Open Access Article
Open Access ArticleApproaching the transit time limit for high-precision spectroscopy on metastable CO around 6 μm
D.
D'Ambrosio
abc,
S.
Borri
 ad,
M.
Verde
a,
A.
Borgognoni
e,
G.
Insero
af,
P.
De Natale
ad,
M.
Verde
a,
A.
Borgognoni
e,
G.
Insero
af,
P.
De Natale
 ad and
G.
Santambrogio
ad and
G.
Santambrogio
 *abd
*abd
aIstituto Nazionale di Ottica, INO-CNR, & European Laboratory for Nonlinear Spectroscopy, LENS, Via Nello Carrara 1, 50019 Sesto Fiorentino, Italy. E-mail: santambrogio@lens.unifi.it
bIstituto Nazionale di Ricerca Metrologica, INRIM, Strada delle Cacce 91, 10135 Torino, Italy
cPolitecnico di Torino, DET-Dipartimento di Elettronica e Telecomunicazioni, Corso Duca degli Abruzzi 24, 10129 Torino, Italy
dIstituto Nazionale di Fisica Nucleare, INFN, Sezione di Firenze, via G. Sansone 1, 50019 Sesto Fiorentino, FI, Italy
eDepartment of Chemistry, University of Florence, Via della Lastruccia 3, 50019 Sesto Fiorentino, Italy
fEuropean Commission, Joint Research Centre (JRC), Karlsruhe, Germany
First published on 29th October 2019
Abstract
As molecular spectroscopy makes its comeback to the limelight of fundamental sciences, scientists need ever better coherent light sources and diagnostic methods. Of particular importance for molecular spectroscopy is the mid infrared spectral region, where strong and narrow ro-vibrational excitations have their fundamental transition frequencies. Unfortunately, much technology in some portions of this spectral region is still rather pioneering. Here we present a high-resolution spectroscopy experiment, based on a molecular beam setup, which pushes the measured linewidth close to the transit time limit, on the order of 100 kHz. Moreover, we discuss the issue of frequency-noise characterization and the linewidth measurement of the ultrastable infrared laser used in the experiment.
I Introduction
Atomic and molecular spectroscopy techniques are gaining a revival of interest due to their application in testing fundamental physics, in subjects such as symmetry violations, variations of fundamental constants, testing of quantum electrodynamics, search for dark energy and dark matter, as well as for a fifth force and so forth.1 This kind of research, traditionally carried out at large particle accelerator facilities, can also be carried out with laboratory-scale experiments by replacing high energies with high precision measurements.2 While it is much easier and efficient to prepare an ultracold atomic sample, molecules offer some advantages, thanks to their richer internal structure.A very convenient spectral window for interrogating molecules is the mid infrared (MIR), because it features intense and very narrow rovibrational molecular transitions. However, laser technology, nonlinear optical elements, electro-optical devices and detectors available for this spectral region are generally much poorer than those for the visible and the near infrared (NIR) region. The situation is somehow less severe for the region below 5 μm wavelength and around 10 μm, which is the operation wavelength of CO2 lasers and beneficial for decades of technological development.
In a recent study, we demonstrated the absolute frequency measurement of a vibrational transition around 5.8 μm on a molecular beam of metastable CO with kHz-level accuracy.3 This measurement was possible thanks to a cw metrological-grade MIR coherent radiation source generated by difference-frequency (DF) mixing in an OP-GaP crystal.4 A fundamental ingredient of the setup was a quantum cascade laser (QCL), emitting at the same wavelength as the DF radiation. The QCL boosted the power by thousand times, from tens of μW of DF radiation to tens of mW, thus enabling spectroscopy on the molecular beam with a better signal-to-noise ratio. In order to maintain the metrological properties of the DF radiation, the QCL was tightly phase-locked to it. The frequency of the transition was accurately measured against the primary frequency standard. The recorded Doppler-broadened absorption profile has a FWHM of ∼1 MHz (ten-minutes scan), whereas 10 hours averaging yielded uncertainty on the line center of 3 kHz. On the basis of noise measurements and considerations on the locking chain, we estimated that the uncertainty on the QCL frequency and its linewidth (expected value ∼few kHz) gave negligible contributions (2 × 10−14 at worst) on the final relative uncertainty (6 × 10−11). However, we were unable to measure the laser line width directly.
In the present work, we reduce the width of the absorption profile, which is mainly due to Doppler broadening, by almost one order of magnitude, approaching the interaction-time limit. This is a qualitative benchmark, because for any further improvement, substantial changes in the experimental approach will be required. To approach natural linewidths, one can either choose a laser-cooled molecular sample or two-photon spectroscopy in a Ramsey interferometer, like in the SF6 experiment around 10 μm by Amy-Klein and co-workers.5 We are not aware of any high resolution spectroscopy in the MIR on laser-cooled molecules, nor of any further application of Ramsey interferometry in the MIR, away from the 10 μm region.
We will discuss the problem of the spectral characterization of narrow-linewidth lasers in the MIR and we will review the recent progress. We argue that high resolution molecular spectroscopy helps in this regard to improve the performance of other standard methods.
II Vibrational transition in a molecular beam
Rovibrational transitions in the MIR have typical linewidths of hundreds Hz. It is thus tempting to exploit such sharp spectral features to characterize a laser source. However, the Doppler broadening of a transition around 50 THz for a molecule with a mass of, say, 50 amu at room temperature is just below 100 MHz. The two most common techniques for sub-Doppler spectroscopy are two-photon spectroscopy and saturation spectroscopy, and they both require overlapped, counter propagating laser beams. We were unable to meet this requirement with our MIR QCL. QCLs are particularly sensitive to back-reflections and optical isolators in the 6 μm region featuring either very poor transmission or very poor isolation.In the first approximation, the Doppler broadening in a crossed-beam configuration is given by Δν·sin(θ), where Δν is the single-photon Doppler broadening and θ is the semi-angle between the laser beams. Therefore, the residual Doppler width, for θ ∼ 1°, is of the order of one MHz.
In a molecular beam, instead, typical translational distributions correspond to temperatures of a few K. This dense phase-space distribution allows for a strong signal even when a subset of molecules with a very narrow velocity distribution is selected. As we show in the following, we achieve a final Doppler width of about 100 kHz.
We used metastable CO, which is rather easy to detect with virtually 100% efficiency. The detailed spectroscopic setup is described in ref. 3. CO has a vibrational transition at 5.83 μm that is within the tuning range of our QCL. Metastable CO in the a3Π1 state has an unpaired electron and is thus rather sensitive to external magnetic fields, with energy shifts of the order of 1 MHz per Gauss. In contrast, the dipole moment of 1.37 Debye makes CO quite insensitive to stray electric fields, which are typically of the order of a few V m−1 (that translates into a broadening contribution <10 kHz).
We produce a supersonic beam of ground-state CO by pulsing a mixture of CO in neon into vacuum with a Jordan valve operating at 10 Hz repetition rate. The source chamber is separated from the main vacuum chamber by a skimmer with an opening diameter of 1 mm. After the skimmer, CO molecules are excited to the a3Π1, v = 0, J = 1 metastable state by about 1 mJ of light at 206 nm, produced by a pulsed OPO (∼10 ns pulses). In the middle of the main vacuum chamber, molecules interact with MIR radiation that transfers the population to the a3Π1, v = 1, J = 1 state. The MIR beam and the molecular beam are overlapped under an angle of 3.1 degrees. This guarantees an interaction time sufficiently long, 20 μs, that limits the transit time broadening to 45 kHz. The relevant velocity component that contributes to Doppler broadening is the one along the molecular beam (plus a ∼5% contribution of the velocity in the plane of the laser and the molecular beam, due to the 3.1 degrees angle). We call z the direction of the molecular beam, x the vertical direction and y is provided by the choice of a right-handed system of coordinates. Finally, we detect the molecules with a second ns-pulsed laser, which ionizes them selectively via the b3Σ+ electronic state in a two-photon process. Ions are generated between two electrodes that accelerate them towards a microchannel plate detector. Both pulsed lasers intersect perpendicularly the molecular beam.
Our measurements and simulations indicate that for small magnetic fields we can control its strength within 50 mG. On the a3Π1 electronic state of CO, we use the vibrational transition from the upper component of the lambda doubling of v = 0, J = 1, positive parity, to the lower component of v = 1, J = 1, negative parity. Transitions with ΔM = 0 are less sensitive to the magnetic field, about 12 kHz G−1, but are close together at low-to-moderate fields, whereas the Zeeman shift of the transitions with ΔM = ±1 is about 500 kHz G−1. Therefore, the contribution of the 50 mG inhomogeneity in the magnetic field is well below the contribution from the Doppler effect for all relevant transitions. We chose to use a ΔM = ±1 transition because at the moderate field strength of 4.5 G it is well separated from all other transitions, whereas the ΔM = 0 transitions are close to each other, making data interpretation more complex. To maximize field homogeneity, the molecular beam is first collimated by the 1 mm skimmer and then by a round opening just before the ionization laser, also 1 mm in diameter (this is the first of the two electrodes mentioned above). Furthermore, we allowed the MIR laser to interact with the molecules only in the central region of our setup, where the magnetic field is the most homogeneous. The interaction time is set at 20 μs, during which molecules at an average speed of 835 m s−1 cover 18.7 mm. We achieve this by two equivalent methods. Either we Stark-shift the transition out of resonance by applying a strong electric field or we rapidly modulate the laser frequency. In both cases, the resonance condition is suppressed before and after the desired interaction time interval. We observe no difference in the measured signal using these two methods.
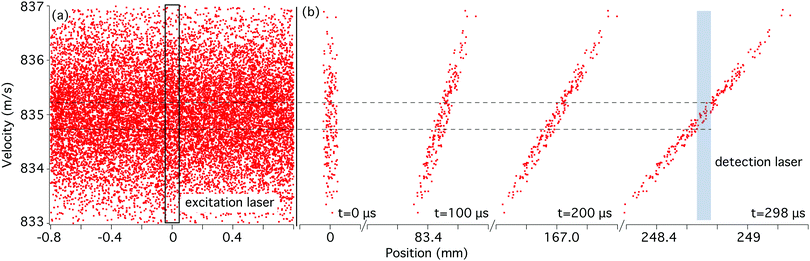
In Fig. 1 and 2 we present the results of some trajectory simulations. Fig. 1(a) shows how the excitation laser selects a subset of molecules in the z–vz phase-space plane among those present in the beam. The molecular cloud propagates toward larger z, with the rotation characteristic of free motion. By the time the molecules reach the ionization laser, their distribution is such that only a very narrow velocity interval is addressed by the laser and thus detected. The vz velocity interval selected by the two lasers depends on the tightness of their beam profiles and on the time delay between them, according to the simple formula
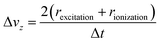 | (1) |
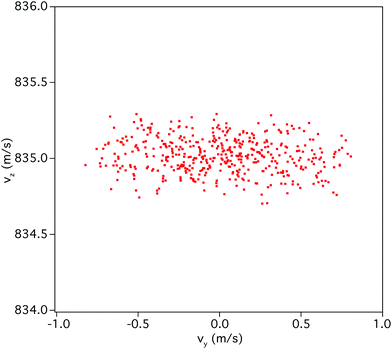 | ||
| Fig. 2 Molecular distribution in the vy–vz plane of the phase space in the experiment. The distribution shows that the vz distribution is much narrower than along vy. | ||
Fig. 2 compares the vy and vz velocity components of the molecules that contribute to the signal under actual experimental conditions. This molecular distribution is due to the apertures that collimate the beam (in the x and y directions) and to the focused pulsed lasers (in the z direction). We see that the vz component is four times narrower than the vy component. This yields a fourfold improvement to the resolution for the quasi-collinear configuration, compared to a configuration where the MIR beam intersects perpendicularly the molecular beam, like in ref. 3.
The precision improvement comes at the cost of a worse accuracy in the determination of the central frequency. Indeed, to compare the central frequency of the laser to the molecular absorption, a good knowledge of the molecular velocity is required. And while we have a very good knowledge of the time delay between the two pulsed lasers, we cannot measure their absolute spatial distance with the same degree of accuracy, at least not in the present setup. More quantitatively, the spatial uncertainty is ±1.5 mm and the time uncertainty is ±5 ns. The former yields a frequency uncertainty of ±400 kHz and the latter ±2 kHz. Reducing the spatial uncertainty to ±0.2 mm is feasible but would require an upgrade of the experimental setup. Correspondingly, the frequency uncertainty would be reduced to ±50 kHz.
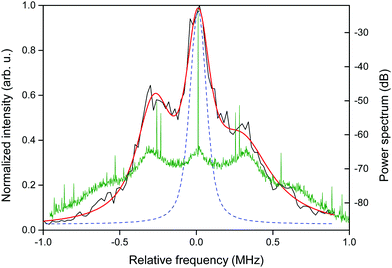
The measured absorption spectrum is shown in Fig. 3. The graph is obtained by scanning the QCL frequency across the molecular rovibrational transition. The vertical axis represents the ion signal obtained by resonant ionization. That is, only when the molecules are transferred to the vibrationally excited state by the QCL, they are efficiently ionized. A triple Voigt function is fitted to the data and the best fit is obtained for a central peak having a width of 180 kHz. The shape of the recorded spectrum can be attributed to the spectral shape of the QCL radiation under locking conditions. As shown by the green trace in Fig. 3, the two side bands in the absorption profile correspond to the bumps in the beat-note spectrum between the locked QCL and the DF radiation.
Apart from the finite laser linewidth, which is discussed in the next paragraph, three effects contribute to the broadening of the measured line. The most important is Doppler broadening. The velocity distribution can be easily extracted from Fig. 2 and yields a linewidth of about 85 kHz. This value can be reduced by slowing down the molecules or by extending the length of the molecular beam. Both approaches are possible but they also reduce the signal-to-noise ratio. Transit time broadening amounts to about 45 kHz. To reduce this broadening contribution, we should increase the size of the experiment in order to achieve a good overlap over a longer distance. Finally, the smallest contribution, 25 kHz, is due to the Zeeman shift of the levels due to the inhomogeneity of the magnetic field. We neglect the spatial intensity distribution of the laser beam. In the Voigt fit of the data shown in Fig. 3, we fixed the Gaussian contribution to 85 kHz, as expected from the residual Doppler broadening. The fit yields a Lorentzian contribution of 138 kHz for the central peak. A Voigt curve with only the calculated Gaussian and Lorentzian contributions is also shown in the figure (dashed line), in order to compare the recorded profile with that expected in the case of negligible laser linewidth.
III Spectral characterization of laser light
In general, the finite laser linewidth affects the spectroscopic measurement by contributing to the spectral broadening of the absorption spectrum. For this reason, the availability of a frequency-stable, narrow-linewidth laser determines the quality of the spectroscopic measurement. The knowledge of the frequency noise characteristics of the laser source is important to appropriately analyze the achieved precision level and to address its limiting factors.The most complete characterization of the spectral purity of a laser is the measurement of its frequency noise power spectral density (FNPSD). On the one hand, one can use it to understand the processes responsible for specific noise functions; on the other hand, it yields a value for the laser linewidth over any accessible timescale.6 For these measurements, the slope of a molecular absorption line or the mode of an optical resonator are used to convert laser frequency fluctuations into more-easily detectable intensity variations. To obtain a precise measurement, the converter lineshape must introduce a negligible noise, while providing a sufficiently high gain factor to bring out the frequency noise to contribution over the laser amplitude noise. In addition, the detector must feature low-noise and high speed, in order to avoid that electronics noise limits the measurement quality.
Between 5.5 μm and 9 μm wavelengths, available opto-electronics perform comparatively poorly. In particular, available detectors have high noise figures, optical resonators have low Q-factors, and optical isolators are inefficient. Indeed, while many papers reported linewidth FNPSDs of lasers at wavelengths below 5 μm,7 only a few studies reported on the noise reduction and frequency noise characterization of laser sources above 5.5 μm. We briefly review here these studies. Fasci et al.8 use a strong N2O absorption line to record the FNPSD of a QCL emitting at 8.6 μm. Although the transition line strength allowed working in the strong absorbance regime, which is good for maximizing the slope of the frequency-to-amplitude converter, the conversion factor was not high enough to allow an appropriate measurement of the laser frequency noise under locking conditions to emerge over the laser intensity noise. The same group reported on a similar noise measurement in a subsequent paper,9 emphasizing the same limitation and giving an estimation of 130 kHz for the laser linewidth under locking conditions. Using the same technique, Mills et al.10 could measure down to 25 kHz over 1 ms (150 kHz over 10 ms) the linewidth of a laser at 9.1 μm, a region where better technology and components have been developed due to the presence of CO2 lasers. It is worth emphasizing that this method requires the availability of a strong molecular absorption within the tuning range of the laser. This can be a serious problem when laser sources with a small tuning range are used, as QCLs. In our case, for example, the QCL operates at room temperature from 1710 and 1716 cm−1, and no strong transitions from simple molecules can be found here to properly implement this method.
An alternative method, although less complete than an FNPSD measurement, is a beat-note measurement of the laser in a heterodyne or homodyne configuration. Here, again, measurement quality depends on the rise-time and sensitivity of the detectors used. However, measuring the radio frequency beat note of two laser beams superimposed onto a fast photo diode is hindered by the relatively large background noise of electro-optical devices in the MIR. Moreover, frequency fluctuations measured from the beat notes are a combination of frequency fluctuations from each contributing laser, and therefore the laser used for the measurement must be at least as stable as the laser under investigation. In the region above 5 μm, this method has been used by the LPL group in Paris,11,12 who used a state-of-the-art secondary frequency standard around 10 μm, a CO2 laser stabilized on an OsO4 saturated absorption line. In principle, one could circumvent the need for a second ultra-stable laser by measuring the beat note of a laser superimposed on itself after a fiber delay loop. But optical fibres in the MIR suffer from low transmittivity, limiting the scope of this method. Some groups implemented up-conversion of the MIR laser under investigation to the NIR and beating it with a narrow-linewidth reference laser. This solution has the advantage to shift the noise analysis in a region where faster and sensitive detectors are available, but to fully exploit this advantage a nonlinear crystal with good conversion efficiency is required. Therefore, it is particularly useful below 5 μm, due to the presence of PPLN crystals. Nonetheless, some groups (including us) use nonlinear conversion for referencing MIR sources above 5 μm to NIR stable references, and some papers10,12–14 report on the use of this technique for linewidth characterization, too.
In cases like ours, the limited tuning range of the laser does not reach any strong and isolated molecular transition that can be used for noise analysis with frequency-to-amplitude conversion. In these cases, when the source is used for high-resolution spectroscopy, the absorption spectra can be used to estimate the laser linewidth. A measurement of the QCL linewidth can be obtained by analysis of the absorption spectrum shown in Fig. 3. By considering the Lorentzian width from the Voigt fit of the central peak and the broadening contributions as calculated in the previous section, an upper limit of 68 kHz can be given for our laser line width. Although it is only an estimation, it compares well with the work reviewed above. As we discuss in the next section, moreover, this estimation is more stringent than a measurement with optical resonators, due to strong limitations of the technology available in certain spectral ranges.
A High-Q whispering-gallery mode resonator
In order to obtain an independent estimation of the laser linewidth, we implemented a standard FNPSD measurement using a crystalline whispering gallery mode resonator (WGMR). This device has the advantage of being made of materials, like fluoride crystals, that are highly transparent over an extremely broad spectral range. CaF2 resonators, for example, are transparent from the UV to the MIR, and Q-factors as high as 1010 in the near infrared (NIR) and 108 in the MIR have been measured.15,16 These devices are already used as a valid alternative to high-finesse Fabry–Perot resonators for MIR laser linewidth narrowing and frequency stabilization,17,18 among other applications.For frequency noise measurements, the transmission mode of a high-Q optical cavity can be used to convert frequency fluctuations into amplitude fluctuations, which can be detected using a photo diode. Of course, the narrower the laser under investigation, the higher must be the Q-factor of the optical cavity. In a classical Fabry–Perot configuration, the Q-factor depends on the reflectivity of the cavity mirrors, which is poorer in the MIR than in the visible-NIR regions. Moreover, a new set of mirrors must be provided for every wavelength that one wants to measure. Whispering-gallery mode resonators do not present these drawbacks. They exploit total reflection inside the material, which makes them independent of optical coatings. To characterize the noise of our MIR source, we used a CaF2 toroidal WGMR (from OEwaves) with a diameter of 3.6 mm. This resonator has a free-spectral range of about 19 GHz at 5.8 μm. The cavity mode can be frequency-tuned by several GHz by changing the resonator temperature. In this way, a cavity mode that suits the frequency of the laser under investigation can be selected. The measured mode width at 5.8 μm is about 20 MHz FWHM, corresponding to a Q-factor of 3 × 106 and a finesse about 1000. These values, although significantly lower than those we recorded at 4.5 μm17 due to the higher absorption of the material, are still very good for the operation wavelength.
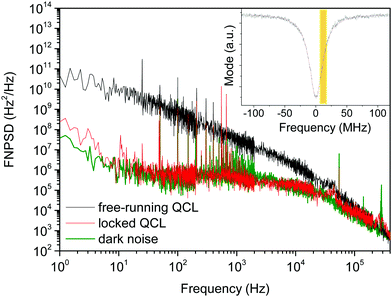
Fig. 4 shows the FNPSD of the QCL both free running and phase-locked to the DF radiation, as measured by using a WGMR as a frequency-to-amplitude converter. In the inset, the resonator mode is sketched, with a Lorentzian fit superimposed to the experimental trace, and the yellow area shows the linear part of the mode slope used as a frequency-to-amplitude converter.
The black trace in the figure is the FNPSD of the free-running QCL. The trace shows the dominant contribution due to flicker noise, in agreement with previous measurements. A numerical integration following ref. 6 gives a free-running line width of 2.1 MHz FWHM over 1 s timescale. The FNPSD of the locked QCL (red trace) cannot be significantly distinguished from the dark noise (green trace). Under these conditions, thus, our measurement can only set a rough upper limit for the linewidth of the locked QCL, which is about 700 kHz (FWHM) over 1 s timescale. From noise measurements and analysis of the locking chain,3,19 we expect a QCL linewidth about 2 orders of magnitude lower under locking conditions.
At present, the limiting factor for the noise measurements is detector noise. For the measurements shown in Fig. 4 we used a liquid-N2-cooled HgCdTe detector from Kolmar (KV104 series), with a noise equivalent power NEP = 2 × 10−12 W and a bandwidth of about 100 MHz. We also used a Peltier-cooled detector from Vigo (PVI-4TE-6) with 10 MHz bandwidth and a similar NEP, but the noise measurements performed with the two detectors show no noticeable difference.
The measurement could be possibly improved by increasing the power coupled to the micro-resonator, thus moving away from the background noise of the detector. In our present setup, the prisms used for evanescent-wave coupling (and extraction) of the light with the whispering-gallery modes of the resonator are made of sapphire, which has a very low transparency at 5.8 μm. BaF2 prisms could be used instead of the sapphire ones. However, coupling large amounts of optical power into tiny mode volumes leads to large frequency instabilities and drifts of the modes due to thermal effects and nonlinear processes, which must be avoided when a high stability is requested, as in frequency noise measurements. Therefore, we are not confident that significant improvement can be achieved with this method.
VI Conclusion
In this paper we have described a setup to observe transition linewidths close to the transit-time limit, ∼100 kHz, even at wavelengths above 5 μm. With respect to a previous study,3 we have improved the linewidth measurement by one order of magnitude, at the cost of a lower accuracy in the absolute frequency. Regarding the laser source used to drive the transition, our method is very general and yields better optical linewidth measurements than other standard techniques, especially in some MIR windows where technology is the main limitation. This work is a step forward for high-precision molecular spectroscopy in the MIR because it provides an additional tool for the characterization of optical sources in a region where the enabling technologies are not readily available, yet. The next natural step for high-precision molecular spectroscopy will be the application of modern laser cooling techniques to produce ultracold molecular samples.Conflicts of interest
There are no conflicts of interest to declare.References
- M. Safronova, D. Budker, D. DeMille, D. F. J. Kimball, A. Derevianko and C. W. Clark, Rev. Mod. Phys., 2018, 90, 025008 CrossRef CAS
.
- D. DeMille, J. M. Doyle and A. O. Sushkov, Science, 2017, 357, 990 CrossRef CAS PubMed
.
- G. Insero, S. Borri, D. Calonico, P. C. Pastor, C. Clivati, D. D'Ambrosio, P. De Natale, M. Inguscio, F. Levi and G. Santambrogio, Sci. Rep., 2017, 7, 12780 CrossRef CAS PubMed
.
- G. Insero, C. Clivati, D. D'Ambrosio, P. De Natale, G. Santambrogio, P. Schunemann, J.-J. Zondy and S. Borri, Opt. Lett., 2016, 41, 5114 CrossRef CAS PubMed
.
- A. Shelkovnikov, R. J. Butcher, C. Chardonnet and A. Amy-Klein, Phys. Rev. Lett., 2008, 100, 150801 CrossRef CAS PubMed
.
- D. S. Elliott, R. Roy and S. Smith, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 12 CrossRef CAS
.
-
S. Schilt, L. Tombez, G. D. Domenico and D. Hofstetter, The wonders of nanotechnology: Quantum and optoelectronic devices and applications, Frequency Noise and Linewidth of Mid-infrared Continous-wave Quantum CascadeLasers: An Overview, ed. M. Razeghi, L. Esaki and K. von Klizing, SPIE, Bellingham, 2013, ch. 12 Search PubMed
.
- E. Fasci, N. Coluccelli, M. Cassinerio, A. Gambetta, L. Hilico, L. Gianfrani, P. Laporta, A. Castrillo and G. Galzerano, Opt. Lett., 2014, 39, 4946 CrossRef PubMed
.
- A. Gambetta, M. Cassinerio, N. Coluccelli, E. Fasci, A. Castrillo, L. Gianfrani, D. Gatti, M. Marangoni, P. Laporta and G. Galzerano, Opt. Lett., 2015, 40, 304 CrossRef CAS PubMed
.
- A. A. Mills, D. Gatti, J. Jiang, C. Mohr, W. Mefford, L. Gianfrani, M. Fermann, I. Hartl and M. Marangoni, Opt. Lett., 2012, 37, 4083 CrossRef CAS PubMed
.
- P. L. T. Sow, S. Mejri, S. K. Tokunaga, O. Lopez, A. Goncharov, B. Argence, C. Chardonnet, A. Amy-Klein, C. Daussy and B. Darquié, Appl. Phys. Lett., 2014, 104, 264101 CrossRef
.
- B. Argence, B. Chanteau, O. Lopez, D. Nicolodi, M. Abgrall, C. Chardonnet, C. Daussy, B. Darquié, Y. L. Coq and A. Amy-Klein, Nat. Photonics, 2015, 9, 456 CrossRef CAS
.
- M. G. Hansen, I. Ernsting, S. V. Vasilyev, A. Grisard, E. Lallier, B. Gérard and S. Schiller, Opt. Express, 2013, 21, 27043 CrossRef PubMed
.
- M. G. Hansen, E. Magoulakis, Q.-F. Chen, I. Ernsting and S. Schiller, Opt. Lett., 2015, 40, 2289 CrossRef CAS PubMed
.
- A. A. Savchenkov, A. B. Matsko, V. S. Ilchenko and L. Maleki, Opt. Express, 2007, 15, 6768 CrossRef PubMed
.
- C. Lecaplain, C. Javerzac-Galy, M. Gorodetsky and T. Kippenberg, Nat. Commun., 2016, 7, 13383 CrossRef CAS PubMed
.
- M. S. de Cumis, S. Borri, G. Insero, I. Galli, A. Savchenkov, D. Eliyahu, V. Ilchenko, N. Akikusa, A. Matsko, L. Maleki and P. D. Natale, Laser Photonics Rev., 2016, 10, 153 CrossRef
.
- S. Borri, M. S. de Cumis, G. Insero, S. Bartalini, P. C. Pastor, D. Mazzotti, I. Galli, G. Giusfredi, G. Santambrogio, A. Savchenkov, D. Eliyahu, V. Ilchenko, N. Akikusa, A. Matsko, L. Maleki and P. De Natale, Sensors, 2016, 16, 238 CrossRef PubMed
.
- D. D'Ambrosio, S. Borri, D. Calonico, C. Clivati, P. De Natale, M. De Pas, G. Insero, F. Levi, M. Verde and G. Santambrogio, 2019, in preparation.
| This journal is © the Owner Societies 2019 |