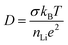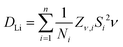Evaluating lithium diffusion mechanisms in the complex spinel Li₂NiGe₃O₈

Abstract

Lithium-ion diffusion mechanisms in the complex spinel Li₂NiGe₃O₈ have been investigated using solid-state NMR, impedance, and muon spectroscopies. Partial occupancy of migratory interstitial 12d sites is shown to occur at lower temperatures than previously reported. Bulk activation energies for Li⁺ ion hopping range from 0.43 ± 0.03 eV for powdered samples to 0.53 ± 0.01 eV for samples sintered at 950 °C for 24 h, due to the loss of Li during sintering at elevated temperatures. A lithium diffusion coefficient of 3.89 × 10⁻¹² cm² s⁻¹ was calculated from muon spectroscopy data for Li₂NiGe₃O₈ at 300 K.

---

1 Introduction

Since Sony's successful commercialisation of lithium-ion batteries (LIBs) in 1990, their numerous desirable properties have been widely reported.^1–3 However, despite becoming ubiquitous in modern society, several safety concerns still remain, predominantly related to the use of flammable and corrosive organic liquid electrolytes in close proximity to highly energetic electrode materials.^4–6 Whilst accidents are relatively rare, these liquid electrolytes can pose significant dangers to consumers and other end-users, as well as reputational damage for device manufacturers.⁷

An all-solid-state battery utilising a solid electrolyte could alleviate many of these concerns, whilst offering improved shock resistance and durability.⁸ To date, research has primarily focused on the development and optimisation of materials with room-temperature Li⁺ ion conductivities (σ_i) of ≥10⁻³ S cm⁻¹, in order to compete with current commercial liquid electrolytes.⁸ Several such materials exist, for instance thio-LISICONs (e.g., Li₁₀GeP₂S₁₂, σ_i = 1.2 × 10⁻² S cm⁻¹) and Li-stuffed garnets (e.g., Li_6.4La₃Zr_1.4Ta_0.6O₁₂, σ_i = 10⁻³ S cm⁻¹).^9–11 Nevertheless, many of these candidate materials suffer a number of drawbacks, which are preventing their commercialisation. For example, thio-LISICONs are unstable in air and decompose at cell voltages >4 V vs. Li/Li⁺.^12,13 Many are also reported to react with lithium metal.¹² Li-stuffed garnets can undergo proton exchange (H⁺/Li⁺), substantially reducing levels of Li⁺ ion conductivity.^14,15 They are also widely reported to exhibit high interfacial resistance with electrode materials (up to ∼2000 Ω cm²).¹⁶ One solution to lowering this interfacial resistance is to use materials with the same crystal structure to enable lattice matching, for example by developing an all-spinel solid-state battery.

The spinel structure, AB₂O₄, has been studied extensively and is known to consist of cubic close packed O²⁻ anions, with A-site cations occupying an eighth of the tetrahedral sites and B-site cations filling half of the available octahedral sites for ‘normal’ spinels.^17,18 Depending on the cations present, the spinel structure may also be inverse ([B]^tet[A,B]^octO₄) or random ([B_0.67A_0.33]^tet[A_0.67B_1.33]^octO₄). Cubic spinels generally crystallise in the Fd3̄m space group. In Li-based spinels, Li⁺ ion conductivity typically follows a two-step conduction mechanism involving Li ions in 8a tetrahedral sites hopping into empty 16c octahedral sites and then onto adjacent 8a sites, forming a three-dimensional 8a-16c-8a pathway for ionic migration¹⁹ that means spinels often exhibit interesting and useful electrical properties. As a result, several manganese-based spinels have been considered as potential high voltage cathode materials (>4.7 V vs. Li⁺/Li), e.g., LiCoMnO₄ and LiNi_0.5Mn_1.5O₄.^20–22 However, these are incompatible with current LIB cell designs due to the breakdown of organic electrolytes above ca. 4.5 V vs. Li⁺/Li. Spinel-based titanates such as Li₄Ti₅O₁₂ are currently of interest as anode materials in LIB applications, as they exhibit excellent dimensional stability during Li (de)intercalation.^23,24 In contrast, spinel-based materials for solid electrolyte applications have received considerably less attention, since they often incorporate redox active transition metals. One potential candidate material is Li₂NiGe₃O₈, previously reported by Kawai et al. to exhibit a modest Li⁺ ion conductivity of ∼10⁻⁷ S cm⁻¹ at 63 °C (comparable to the tetragonal phase of the Li-stuffed garnet Li₇La₃Zr₂O₁₂) and which is electrochemically inactive below 5 V vs. Li⁺/Li.²⁵

Li₂NiGe₃O₈ can be described as an ordered or ‘complex’ spinel in space group P4₃32, with Li⁺ ions occupying tetrahedral 8c sites, and 1 : 3 cation ordering of Ni and Ge on the 4b and 12d octahedral sites, respectively.²⁵ Conduction pathways in complex spinels are less well studied compared to normal spinels, but can involve additional steps depending on the nature of the ordering present. Previous work using variable-temperature time-of-flight neutron powder diffraction (ToF ND) indicated the presence of a second Li 12d octahedral site in Li₂NiGe₃O₈ at high temperatures (∼350–850 °C), leading to the proposition of a three-dimensional 8c-12d-8c conduction pathway.²⁶ Theoretical studies by Nakayama et al. predicted the activation energy for this particular pathway to be 0.47 eV, lower than other previously proposed pathways.¹⁹

An improved understanding of ionic diffusion mechanisms in spinel materials, and Li⁺ ion conductors at large, is crucial if such materials are to be improved and optimised for use as solid electrolytes in all-solid-state LIBs. To this end, we have used a combination of techniques, including impedance, muon and solid-state NMR spectroscopies to enhance our understanding of the crystal structure of the complex spinel Li₂NiGe₃O₈ and the Li⁺ ion diffusion dynamics therein.

2 Experimental methods

2.1 Synthesis and characterisation

Samples of Li₂NiGe₃O₈ were synthesised via traditional solid state methods. Stoichiometric amounts of Li₂CO₃ (Sigma-Aldrich, 99%), NiO (Alfa Aesar, 99%) and GeO₂ (Sigma-Aldrich, 99.999%) were mixed and ground in an agate mortar and pestle, placed into Au boats and fired at 923 K for 5 hours. Prior to heating, the starting reagents were dried at either 453 (for Li₂CO₃) or 773 K (for oxides) for 12 hours. The samples were then calcined at 1173 K for 36 hours, with intermediate regrinding. Identical specimens of Li₂NiGe₃O₈ were used for all XRD, impedance, solid-state NMR and μSR studies.

Samples were characterised by X-ray diffraction (XRD) using a Bruker D2 Phaser diffractometer with Cu Kα (λ = 1.5418 Å) radiation. The ICDD's PDF-4+ database (2019 edition) and SIeve+ software were used for phase analysis. Rietveld refinements were performed using the GSAS-II software.²⁷

2.2 Impedance spectroscopy

Pellets of Li₂NiGe₃O₈ were prepared for impedance spectroscopy measurements by uniaxial pressing. Pellets were placed onto sacrificial powder in an alumina crucible and sintered at 1223 K for 6 or 24 hours, resulting in pellets with 66% and 81% density, respectively. Both pellet faces were polished and gold electrodes applied to each as a paste. Each pellet was then annealed at 1123 K for 2 hours. All heating steps described used heating/cooling rates of 5 °C min⁻¹. Impedance measurements were collected using a Solartron Analytical/Ametek ModuLab XM MTS system from 1 MHz to 30 mHz with a 100 mV applied AC voltage. Measurements were taken during heating from 336 to 541 K.

2.3 Solid-state NMR spectroscopy

Solid-state NMR spectra were acquired using a Bruker 500 Avance III HD spectrometer, equipped with a wide-bore 11.7 T Oxford magnet, using Larmor frequencies of 194.4 MHz for ⁷Li (I = 3/2) and 73.6 MHz for ⁶Li (I = 1). Powdered samples were packed into conventional 4.0 or 1.3 mm ZrO₂ rotors and magic-angle spinning (MAS) rates of 10 and 60 kHz were employed, respectively. Both ⁶Li and ⁷Li chemical shifts were referenced to 1 M LiCl_(aq).

Conventional ⁷Li MAS NMR spectra were obtained using a single-pulse experiment with typical pulse lengths of 3 μs. ⁶Li MAS NMR spectra were acquired using a Hahn echo experiment (90_x–τ–180_y) with a typical π/2 pulse length of 3 μs. Typical radiofrequency field strengths of 84 kHz were employed and an experimentally optimised recycle interval of 0.2 s was used for both ⁷Li and ⁶Li. Standard variable-temperature (VT) ⁶Li MAS NMR experiments were completed between 260 and 412 K using conventional hardware and the parameters stated above. In all cases, temperatures were calibrated using the ¹H signal of MeOH; quoted temperatures thus reflect the true sample temperature during the experiment.

Additional static variable-temperature ⁶Li NMR experiments were completed for Li₂NiGe₃O₈ over the temperature range 204 to 609 K using a Bruker 400 Avance III HD spectrometer, equipped with a wide-bore 9.7 T magnet, using a Larmor frequency of 58.9 MHz for ⁶Li. The sample was packed into a 5.0 mm glass tube and placed into a Bruker 5.0 mm static probe. The static NMR spectra were acquired using a standard solid echo experiment (90_x–τ–90_y), with a typical π/2 pulse length of 5 μs. Here, τ represents an echo delay of 200 μs between 197 and 542 K and 250 μs at 609 K. The interpulse delay was increased in order to acquire the whole echo at higher temperatures. Typical radiofrequency field strengths of 50 kHz were employed and the experimentally optimised recycle interval was 0.05 s. In all cases, true sample temperatures during experiments have been determined using a lead nitrate calibrant.

2.4 Muon spin relaxation (μSR) spectroscopy

All μSR measurements were performed using the EMU instrument at the ISIS pulsed muon facility. Around ∼1 g of sample was packed into a disk of 30 mm diameter and 1.5 mm thickness and sealed in a Ti sample holder with a ∼25 μm thick Ti foil window. The sample was implanted with 3.2 MeV spin-polarised positive muons, and the out-coming positrons detected by 96 scintillator segments arranged in two circular arrays. Data were collected from 39–555 K using a closed cycle refrigerator under three different applied longitudinal magnetic fields (0, 5 and 10 G). Initial symmetry calibrations were conducted using a 20 G transverse magnetic field. Data analysis was conducted using the WiMDA program.²⁸ Collection of data in multiple longitudinal fields enabled (i) the controlled decoupling of interactions between the implanted muons and any local magnetic field distributions, and (ii) additional constraints in and hence more reliable results from the fitting process.

3 Results and discussion

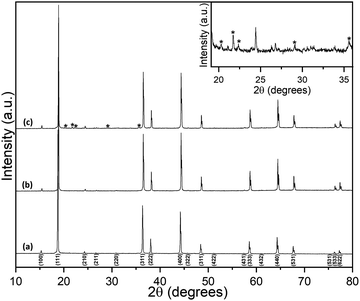
Room-temperature powder XRD data for Li₂NiGe₃O₈ are shown in Fig. 1. Bragg peaks were indexed to the P4₃32 space group, with no additional or missing reflections, giving a refined lattice parameter a = 8.1848(5) Å, in good agreement with previous reports.^25,26 Details of the corresponding Rietveld refinement and a list of refined structural parameters are given in the ESI.† A Li₂NiGe₃O₈ pellet sintered at 1223 K for 24 h showed small additional Bragg peaks which are likely caused by lithium volatilisation, resulting in the onset of thermal decomposition and formation of impurities. Despite a rigorous search of the 2019 edition of the ICDD PDF-4+ database, we were unable to identify the additional phases present. It is noted that these peaks were not observed in data collected for a pellet sintered at the same temperature for 6 h.

Fig. 1 XRD patterns obtained for (a) powdered Li₂NiGe₃O₈ and pellets sintered for (b) 6 h and (c) 24 h. Additional unknown reflections are denoted by *. An expansion of the 2θ range in (c) highlights the additional Bragg peaks present for the 24 h sintered pellet.

3.1 Lithium-ion conductivity analysis by impedance spectroscopy

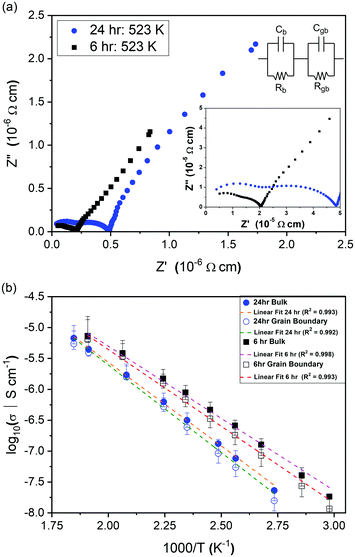
Impedance data were collected for Li₂NiGe₃O₈ pellets sintered for 6 and 24 h. Owing to the lack of mixed valence Ni and Ge species in Li₂NiGe₃O₈, the electrical conductivity is expected to be negligible, as previously reported.^19,25 Hence, the responses observed in impedance data are likely due to Li⁺ ion conduction. The complex impedance spectra obtained in Fig. 2(a) show two partly resolved arcs followed by a low frequency spike.

Fig. 2 (a) Complex impedance spectra collected at ∼523 K for Li₂NiGe₃O₈ pellets prepared using different sintering times: 24 hours (blue circles) and 6 hours (black squares). (b) Arrhenius plots bulk and grain boundary conductivities for Li₂NiGe₃O₈ pellets prepared using different sintering times: 24 hours (circles) and 6 hours (squares). Grain boundary activation energies of 0.56 ± 0.02 eV and 0.49 ± 0.02 eV were calculated for pellets sintered at 24 hours and 6 hours, respectively.

Irrespective of the sintering time, the arc observed at higher frequencies has an associated capacitance of ∼3.1 × 10⁻¹² F, indicative of bulk, intra-granular responses. The second, intermediate frequency arc, with capacitance ∼1 × 10⁻¹¹ F, is attributed to the response from the grain boundary component.²⁹ Under both sintering conditions, a subsequent low-frequency Warburg spike, inclined at ∼50° to the horizontal axis, was observed with associated capacitance of ∼10⁻⁶ F, indicative of complete or partial ion blocking at the electrode, representative of ionic conductivity in Li₂NiGe₃O₈.²⁹

To extract conductivities from the arcs attributed to intra-granular and grain boundary responses in the complex impedance spectra, fitting was performed using Z-View. Bulk conductivities were taken from the intersection of two manually fitted parallel RC semicircles, with errors calculated from the intersection of the semicircles with the Z′ axis. The extracted bulk conductivities, as a function of inverse temperature, are shown in Fig. 2(b). For both samples, the data follows typical Arrhenius-type behaviour, enabling activation energies to be calculated. The pellet sintered for 6 h exhibited an activation energy of 0.46 ± 0.01 eV, whilst the pellet fired for 24 h showed a higher value, 0.53 ± 0.01 eV, closer to that previously reported by Kawai et al. (0.55 eV) for Li₂NiGe₃O₈ sintered for 24 h.²⁵ Assuming all Li in the spinel unit cell contribute to diffusion, an intra-grain diffusion coefficient, D_Li, of 2.26 × 10⁻¹³ cm s⁻¹ can be estimated from impedance data at 336 K using the Nernst–Einstein equation:³⁰

It is evident from Fig. 2(a) and (b) that longer sintering times leads to a concomitant decrease in both bulk and grain boundary conductivities. This difference is attributed to the loss of lithium and subsequent formation of additional phases during sintering at temperatures close to the reported melting point of Li₂NiGe₃O₈ (1243 K).²⁵

3.2 Probing Li diffusion using solid-state NMR

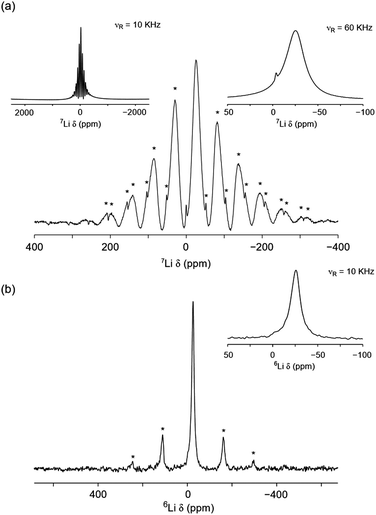
Using solid-state NMR spectroscopy it is possible to probe both local structural changes and ion mobility. Both lithium nuclides (⁶Li and ⁷Li) are suitable for NMR spectroscopy, however, one is often preferred over the other, depending on the specific system under investigation. Typically, ⁷Li is favoured because of its higher natural abundance (92.5%) when compared to ⁶Li (7.5%). However, its large quadrupole moment can give rise to relatively broad lines when Li is in a low symmetry site. In such cases, ⁶Li is often preferred because it can allow close or overlapped resonances to be resolved. Moreover, because of its smaller quadrupolar interaction, the ⁶Li shift may be more closely approximate to the isotropic chemical shift, thereby providing a better measure of the Li bonding environment.³¹ The ⁷Li and ⁶Li MAS NMR spectra obtained for Li₂NiGe₃O₈ are shown in Fig. 3(a) and (b), respectively. The ⁷Li MAS NMR spectrum acquired at 10 kHz exhibits a lineshape characteristic of a paramagnetic-containing species, i.e., a complex manifold of spinning sidebands. The spectrum obtained indicates the presence of two resonances at δ ≈ −25 and 0 ppm, likely corresponding to two distinct Li sites, in good agreement with the reported P4₃32 phase of Li₂NiGe₃O₈.

Fig. 3 (a) ⁷Li and (b) ⁶Li MAS NMR spectra acquired for Li₂NiGe₃O₈. In (a), two different MAS rates were used, 10 and 60 kHz, respectively. In (b), a MAS rate of 10 kHz was used and an expansion of the central transition is also shown as a comparison. All spinning sidebands are denoted by *.

The variation in ^6,7Li chemical shift with coordination number is well reported for a variety of crystalline systems.³² Typically, in diamagnetic systems, LiO₄ environments exhibit chemical shifts between δ_iso = 0–3 ppm, whilst LiO₆ environments are between −1 and 0 ppm.^31,32 In paramagnetic systems, these shifts can be altered substantially by the presence of a paramagnetic species, i.e., the presence of an unpaired electron(s).^33,34

Based on the chemical shifts reported in the literature, coupled with the X-ray diffraction data presented here, and the relative intensities of each resonance, the resonance at δ ≈ −25 ppm is believed to correspond to the tetrahedral 8c site and the resonance at δ ≈ 0.0 ppm corresponds to the octahedral 12d site. Hence, at room temperature, it appears that small amounts of Li occupy the vacant octahedral site, which is in contrast to previous diffraction studies.²⁶ In the spectrum, the tetrahedral site is shifted from its expected position, indicating that it is directly affected by the presence of paramagnetic Ni²⁺, i.e., it is experiencing a Knight shift, although the shift observed here is relatively small when compared to similar reported systems where the resonance can be shifted by several hundreds of ppm.^33,34 A fast spinning (60 kHz) ⁷Li MAS NMR spectrum was also acquired for Li₂NiGe₃O₈ (shown as an inset in Fig. 3(a)), which revealed the presence of two resonances, one broad resonance at δ = −25.3 ppm, belonging to the tetrahedral Li site and a sharper resonance at δ = −3.9 ppm corresponding to the octahedral Li site. It is noted that the extra resolution afforded by faster MAS rates indicates that a Knight shift is also observed for the octahedral site. At slower MAS rates the lineshape is broadened, which hinders the extraction of an accurate shift for this site. Again, the intensities indicate that a small quantity of Li is occupying the octahedral sites. To verify the quantity of Li on each site, the spectrum was fitted to determine the approximate ratio of tetrahedral to octahedral sites. It is noted that this is somewhat challenging based on the broadened nature and overlap of the two sites. Occupancies of 0.024 and 0.976 were obtained for the octahedral and tetrahedral sites, respectively (Fig. S4, ESI†). This is in good agreement with the slow spinning (10 kHz) ⁷Li MAS NMR spectrum.

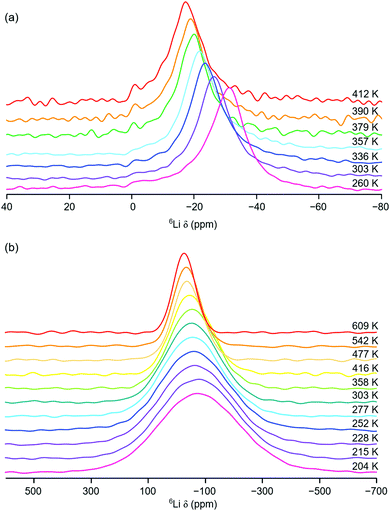
Initial variable-temperature ⁶Li MAS NMR studies of Li₂NiGe₃O₈ were completed over the temperature range 260 to 412 K. The corresponding spectra are shown in Fig. 4(a). Between 260 and 357 K, a single broad resonance is observed. As the temperature is increased to 379 K a second resonance appears at δ = −1.1 ppm, indicating the presence of a second Li site, believed to correspond to the octahedral Li site. The appearance of this site upon heating indicates diffusion of the Li ions from the tetrahedral 8c site onto one of the three neighbouring vacant 12d octahedral sites via a hopping mechanism. The presence of a second site is in good agreement with previous high temperature (∼350–850 °C) ToF ND structural studies of Li₂NiGe₃O₈.²⁶ However, the solid-state NMR data presented indicate that Li diffusion onto the octahedral site(s) occurs at lower temperatures than previously reported.²⁶ In fact, our ⁷Li MAS NMR data (vide supra) suggest that, even at room temperature, some of the vacant octahedral 12d sites are occupied. However, owing to relatively poor signal-to-noise in the VT ⁶Li MAS NMR spectra, it is challenging to accurately determine the precise temperature at which Li ions become mobile and move between the 8c and 12d sites.

Fig. 4 Variable-temperature ⁶Li (a) MAS and (b) static NMR spectra obtained for Li₂NiGe₃O₈. The spectra in (a) were acquired over the temperature range 260 and 412 K and a MAS rate of 10 kHz was used. All of the spectra shown in (b) were acquired under static conditions over the temperature range 204 to 609 K.

As the temperature is increased, there is an obvious, yet gradual, linear change in chemical shift of the resonance corresponding to the tetrahedral site, towards more positive values. For example, the resonance is centred at δ = −31.3 ppm at 260 K and moves to δ = −17.2 ppm at 412 K. This is in contrast to the trend expected with increasing temperature for a paramagnetic system.

Typically, as temperature is increased, Li chemical shift values move to lower (or more negative) values, thereby obeying Curie–Weiss behaviour.³⁵ As stated earlier, a Knight shift is observed for the tetrahedral site in the ⁷Li MAS NMR spectrum obtained at room temperature. This indicates that the tetrahedral Li site is closer in the structure to the paramagnetic Ni²⁺ centre. In contrast, the resonance assigned to the octahedral 12d site exhibits a very small change in chemical shift, moving from δ = −1.1 ppm to δ = −0.9 ppm, with increasing temperature. It is noted that, owing to the relatively low intensity and broad nature of the resonance, it is challenging to accurately determine the precise chemical shift observed. However, the resonance is not shifted to the same extent as that corresponding to the tetrahedral Li site. This suggests that the octahedral 12d site is positioned further away from the Ni²⁺ in the structure and therefore does not experience the same effect of the paramagnetic species, i.e., no significant Knight shift. As temperature is increased and Li ions increasingly migrate from the tetrahedral site onto the octahedral site they move further and further away from the paramagnetic species. As a result, their chemical shift changes (becoming more positive). In Li₂NiGe₃O₈, the octahedral Li site is ∼4 Å from the Ni centre, compared to a separation of ∼3.2 Å between the tetrahedral site to the Ni centre. Similar VT ⁷Li MAS NMR experiments were completed between 260 and 357 K and the same trend in chemical shift was observed, Fig. S5 in the ESI.† Hence, the VT ⁶Li and ⁷Li MAS NMR data are in good agreement.

To further investigate Li⁺ ion mobility in Li₂NiGe₃O₈, additional static variable-temperature ⁶Li NMR experiments were completed over a greater temperature range (204 to 609 K). It is noted that, due to hardware limitations, it is not possible to acquire ⁶Li MAS NMR data over this temperature range. The VT static ⁶Li NMR spectra obtained are shown in Fig. 4(b). Below room temperature, a single broad and relatively featureless lineshape is observed. As the temperature is increased, line narrowing is observed, indicative of Li⁺ ion mobility within Li₂NiGe₃O₈, in good agreement with the VT ⁶Li MAS NMR data.

The variation in ⁶Li chemical shift and full width at half maximum (FWHM) with increasing temperature are shown in Fig. 5, where a linear change in chemical shift is observed and a gradual narrowing of the resonance is also observed, again indicative of Li ion motion. In contrast to the MAS NMR data, it was not possible to resolve distinct Li sites or the individual contributions from the 8c tetrahedral and 12d octahedral Li sites in the observed lineshape. In this instance, the ⁶Li NMR data is only capable of identifying the presence of Li⁺ ion mobility within Li₂NiGe₃O₈ and not the precise contribution of each site. To gain further insight into the ion mobility, ⁶Li T₁ measurements were attempted for Li₂NiGe₃O₈ using a saturation recovery experiment. However, owing to the paramagnetic nature of the sample, the relaxation properties of the system were too fast and could not be accurately measured. Similarly, using the VT NMR data acquired, and analysis of the corresponding FWHM, attempts were made to obtain an activation energy for Li migration. Unfortunately, due to a combination of hardware limitations and the specific characteristics of the system under investigation, we were unable to acquire the full motional narrowing curve for Li₂NiGe₃O₈ (Fig. 5(b)). Hence, we were unable to obtain an activation energy.

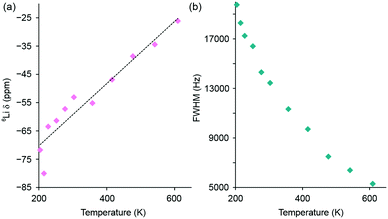Fig. 5 Variation in (a) ⁶Li chemical shift and (b) full width at half maximum (FWHM) with increasing temperature for the ⁶Li static NMR data obtained for Li₂NiGe₃O₈. The corresponding spectra are shown in Fig. 4(b).

3.3 Investigation of intra-grain diffusion by μSR

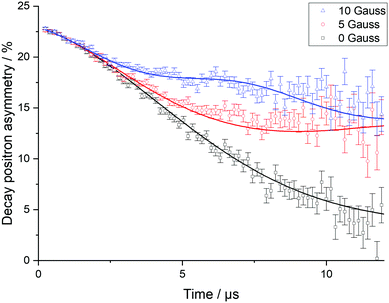
To explore Li⁺ ion diffusion in greater depth, muon spectroscopy, μSR, was used. Positively charged muons, μ⁺, have a lifetime of 2.197 μs and are 100% spin polarised. They can be implanted ∼200 μm into a sample and are expected to reside near oxygen sites.^36–39 The μ⁺ spin can precess depending on the different magnetic fields it experiences, such as external applied fields, fields from nearby nuclei, or those from unpaired electrons in paramagnetic species. The diffusion of Li⁺ ions leads the μ⁺ to undergo a spin flip due to the inherent nuclear magnetic moment of lithium. When the μ⁺ decays, the positron produced is most likely to be emitted in the direction of the μ⁺ spin at decay. By recording the positrons emitted from opposite sides of the sample, the asymmetry of positrons can then be followed as a function of time and the evolution of the muon spin ensemble deduced.

Muon decay asymmetry data collected in longitudinal magnetic fields of 0, 5 and 10 G at various temperatures were fitted using WiMDA. For each temperature point, data from all three fields were fitted to a single model using Keren's analytic generalisation of the Abragam function, multiplied by an exponential relaxation term to account for the presence of paramagnetic Ni.⁴⁰ Example fitted data for Li₂NiGe₃O₈ at room temperature are shown in Fig. 6.

Fig. 6 Raw muon spectroscopy data for Li₂NiGe₃O₈, collected at 300 K in a zero field (squares), and applied longitudinal fields of 5 G (circles) and 10 G (triangles), with fits using the Keren function with a Lorentzian relaxation.

From the different fits, the calculated fluctuation rate, ν, and local magnetic field distribution, Δ, were extracted and their variation with temperature is shown in Fig. 7(a) and (b). The fluctuation rate shows a plateau at lower temperatures, followed by an Arrhenius-like increase due to thermally activated diffusion of lithium ions above ∼300 K. This increase in fluctuation rate continues to 421 K; the subsequent decrease observed at higher temperatures is likely indicative of Li⁺ ions hopping at rates too fast for μSR to capture.^36,37 The values obtained for Δ, Fig. 7(b), support this hypothesis; Δ is constant, within errors, at low temperatures, due to the slow rate of lithium hopping, but then shows a significant decrease from ∼380 K related to the effect of motional narrowing, where Li⁺ ions are moving quickly and their nuclear spins differ from point to point within the sample. Above 442 K, lithium diffusion coefficients become too large for the muons to capture, and Δ values plateau again.

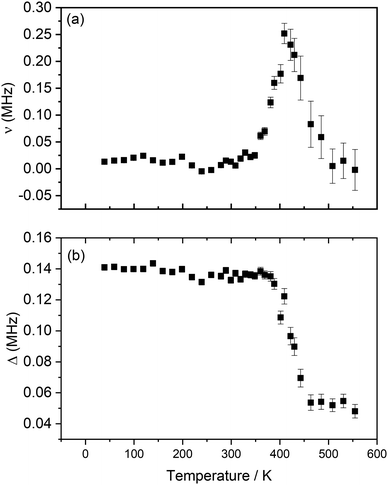Fig. 7 Variation of ν (a) and Δ (b) with temperature obtained from the fitting of raw asymmetry data to the Keren function for Li₂NiG₃O₈, measured from 40 K to 555 K.

3.4 Elucidating diffusion mechanisms

The lithium ion diffusion coefficient for Li₂NiGe₃O₈ can be calculated using the equation:
where N_i is the number of accessible Li sites in the ith path, Z_ν,i is the vacancy fraction of the destination sites in the ith path, S_i is the hopping distance between sites, and ν is the fluctuation rate at 300 K, and assumed to be related to Li⁺ ions hopping between 8c and 12d crystallographic sites, as reported previously.^26,41

Based on the findings obtained using μSR and solid-state NMR spectroscopy, additional analysis was conducted on the crystal structural refinements, using the ToF ND data previously reported by our group.²⁶ Therein, refinements conducted on room temperature data had indicated within standard statistical approaches that the 8c site was fully and solely occupied by Li; occupancy of the 12d migratory interstitial had only been noted where datasets had been collected at temperatures above ambient conditions. This does not preclude the possibility of very low concentrations of lithium hopping between the two sites at, or close to, ambient conditions – such results would merely be statistically indistinguishable from the fully ordered structure reported. This assumption is in good agreement with the ^6,7Li MAS NMR and μSR data presented (Fig. 3 and 7). Therefore, in order to calculate the true diffusion coefficient at 300 K, refined occupancies of both the 8c and 12d sites from 350 ≤ T/°C ≤ 850 were linearly extrapolated (Fig. S6, ESI†) to give proposed fractional occupancies, or Z_ν,i, of 0.97 and 0.03 for the 8c and 12d sites respectively at 300 K (Table S2, ESI†). This is in good agreement with the occupancies obtained from the ⁷Li MAS NMR data (vide supra).

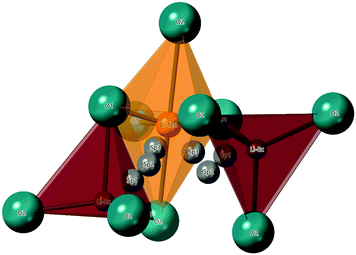
The hopping distance, S_i, in Li₂NiGe₃O₈ can be calculated by considering that an ion hopping between the 8c and 12d sites likely passes through three saddle points (SP) along the way, in the LiO₄ tetrahedral and LiO₆ octahedral faces, and an empty tetrahedral site. Once in the 12d site, Li⁺ ions can hop to one of two neighbouring 8c sites (one of which is the original 8c site). A reasonable hopping distance of 2.95 Å can thus be calculated from the distances between the 8c-SP1-SP2-SP3-12d sites along this proposed conduction pathway (Fig. 8).

Fig. 8 Portion of Li₂NiGe₃O₈ crystal structure showing the proposed 8c-SP1-SP2-SP3-12d conduction pathway. A Li_12d–O₆ octahedron is shown in orange and the two nearest Li_8c–O₄ tetrahedral are shown in red. A hopping distance of 2.95 Å can be calculated from a Li_8c-ion hopping between three possible saddle points (grey) into the neighbouring Li_12d site.

By following these assumptions, the calculated diffusion coefficient, D_Li, for Li₂NiGe₃O₈ at 300 K is found to be 3.89 × 10⁻¹² cm² s⁻¹ (Table S2, ESI†). This is in good agreement with the figure extracted from impedance spectroscopy data, and is similar to values reported for other spinel-type materials, e.g., Li₄Ti₅O₁₂ which has a diffusion coefficient, D_Li of between 3.2 × 10⁻¹¹ to 4.0 × 10⁻¹² cm² s⁻¹, depending on the technique used and precise degree of lithiation.^42,43 By comparison, other solid electrolyte candidate materials based on the Li-stuffed garnet structure, e.g., Li_6.5Al_0.25La_2.92Zr₂O₁₂, with a faster ionic conductivity and shorter hopping distance (1.67 Å), has a Li⁺ ion diffusion coefficient of 4.62 × 10⁻¹¹ cm² s⁻¹.³⁹

An activation energy of 0.43 ± 0.03 eV for lithium hopping in our powdered sample of Li₂NiGe₃O₈ was calculated from an Arrhenius plot of log D_Li over the thermally activated region (Fig. 9), in good agreement with the value obtained from EIS data on a pellet sintered for 6 h (0.46 ± 0.01 eV), but considerably lower than that observed after a 24 h sinter (0.53 ± 0.01 eV). This is further evidence that long dwell times at temperatures close to the melting point result in Li loss through volatilisation. As a result, additional studies aimed at identifying less extreme consolidation methods are currently underway. Length-scale dependent ion dynamics are well known in the literature with LiFePO₄ being a particular prominent example,⁴⁴ where the activation energy changes several-fold and the diffusion constant by several orders-of-magnitude. In Li₂NiGe₃O₈ the change in activation energy is far less pronounced.

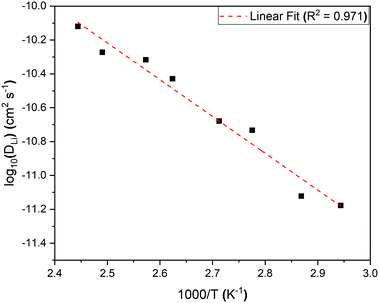Fig. 9 Arrhenius plot of the diffusion coefficient in the temperature range 340 K to 410 K for the complex spinel, Li₂NiGe₃O₈. The calculated activation energy from the slope is 0.43 ± 0.03 eV.

4 Conclusions

Lithium-ion diffusion mechanisms in the complex spinel Li₂NiGe₃O₈ have been investigated using a range of complementary techniques. Building on previous reports of an 8c-12d-8c conduction pathway, using μSR and ^6,7Li solid-state NMR spectroscopy, we have shown that Li⁺ ion hopping becomes thermally activated at ∼300 K, resulting in partial occupancy of the migratory interstitial site at lower temperatures than previously reported. A lithium diffusion coefficient of 3.89 × 10⁻¹² cm² s⁻¹ at 300 K and an activation energy for lithium hopping of 0.43 ± 0.03 eV were determined using μSR on powdered samples. This energy is considerably lower than that observed for sintered pellets (0.46 ± 0.01 and 0.53 ± 0.01 eV, depending on the sintering conditions), suggesting that the investigation of an alternate consolidation route, avoiding Li volatilisation, may be worthwhile. This work also highlights the necessity of using multiple complementary techniques, such as impedance spectroscopy, solid-state NMR and μSR, as local probes in order to gain a more complete understanding of hopping mechanics in important ionic conductors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The PhD work of DZCM under the supervision of NRM and RB was funded by EPSRC through a Doctoral Training Partnership grant awarded to the University of Sheffield. RB acknowledges support by the Lloyd's Register Foundation and Royal Academy of Engineering under the Research Fellowships scheme. The authors extend their gratitude to the ISIS Neutron & Muon Facility for the award of EMU Beamtime. KEJ and ARH would like to thank the EPSRC Doctoral Training Partnership EP/N509462/1 for the award of a studentship to ARH and Dr David Apperley for experimental assistance.

References

1. M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657.
2. J. B. Goodenough and K. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176.
3. N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2015, 18, 252–264.
4. P. G. Balakrishnan, R. Ramesh and T. P. Kumar, J. Phys. Chem. Lett., 2006, 155, 401–414.
5. J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603.
6. Q. Li, J. Chen, L. Fan, X. Kong and Y. Lu, Green Energy Environ., 2016, 1, 18–42.
7. Samsung, 2016, http://www.samsung.com/us/note7recall/.
8. J. C. Bachman, S. Muy, A. Grimaud, H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp and L. Giordano, Chem. Rev., 2016, 116, 140–162.
9. N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama and K. Kawamoto, Nat. Mater., 2011, 10, 682–686.
10. Y. Li, J.-T. Han, C.-A. Wang and J. B. Goodenough, J. Mater. Chem., 2012, 3, 15357–15361.
11. R. Kanno and M. Murayama, J. Electrochem. Soc., 2001, 148, 742–746.
12. A. C. Luntz, J. Voss and K. Reuter, J. Phys. Chem. Lett., 2015, 6, 4599–4604.
13. J. Kasemchainan, P. G. Bruce and J. Matthey, Technol. Rev., 2018, 62, 177–180.
14. V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Rev., 2014, 43, 4714–4727.
15. A. Orera and J. Campo, Inorg. Chem., 2016, 55, 1324–1332.
16. K. Hofstetter, A. J. Samson, S. Narayanan and V. Thangadurai, J. Power Sources, 2018, 390, 297–312.
17. W. H. Bragg, Philos. Mag., 1915, 30, 305–315.
18. S. Nishikawa, Proc. Math. Phys. Soc. Tokyo, 1915, 8, 199–209.
19. M. Nakayama, R. Jalem and T. Kasuga, Solid State Ionics, 2014, 262, 74–76.
20. H. Kawai, M. Nagata, H. Tukamoto and A. R. West, Electrochem. Solid-State Lett., 1998, 1, 212–214.
21. A. Manthiram, K. Chemelewski and E. Lee, Energy Environ. Sci., 2014, 7, 1339–1350.
22. M. M. Thackeray, J. Am. Ceram. Soc., 1999, 54, 3347–3354.
23. B. M. Wagemaker, D. R. Simon, E. M. Kelder, J. Schoonman, C. Ringpfeil, U. Haake, D. Lützenkirchen-hecht, R. Frahm and F. M. Mulder, Adv. Mater., 2006, 18, 3169–3173.
24. T. Ohzuku, A. Ueda and N. Yamamota, J. Electrochem. Soc., 1995, 142, 1431–1435.
25. H. Kawai, M. Tabuchi, M. Nagata, H. Tukamoto and A. R. West, J. Mater. Chem., 1998, 8, 1273–1280.
26. N. Reeves-Mclaren, R. I. Smith and A. R. West, Chem. Mater., 2011, 23, 3556–3563.
27. B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549.
28. F. L. Pratt, Phys. B, 2000, 289–290, 710–714.
29. J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132–138.
30. M. M. Ahmad, RSC Adv., 2015, 25824–25829.
31. K. MacKenzie and S. Mark, Multinuclear Solid-State Nuclear Magnetic Resonance of Inorganic Materials (Pergamon Materials Series), Elsevier Science Ltd, 2002, pp. 629–639.
32. Z. Xu and J. F. Stebbins, Solid State Nucl. Magn. Reson., 1995, 5, 103–112.
33. Y. J. Lee, F. Wang and C. P. Grey, J. Am. Chem. Soc., 1998, 120, 12601–12613.
34. C. P. Grey and Y. J. Lee, Solid State Sci., 2003, 5, 883–894.
35. L. S. Cahill, R. P. Chapman, C. W. Kirby and G. R. Goward, Appl. Magn. Reson., 2007, 32, 565–581.
36. P. J. Baker, I. Franke, F. L. Pratt, T. Lancaster, D. Prabhakaran, W. Hayes and S. J. Blundell, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 1–8.
37. M. Mansson and J. Sugiyama, Phys. Scr., 2013, 88, 1–13.
38. M. J. Ariza, D. J. Jones, J. Roziere, J. S. Lord and D. Ravot, J. Phys. Chem. B, 2003, 107, 6003–6011.
39. M. Amores, T. E. Ashton, P. J. Baker, E. J. Cussen and S. A. Corr, J. Mater. Chem. A, 2016, 4, 1729–1736.
40. A. Keren, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 10039–10042.
41. R. J. Borg and G. J. Dienes, An Introduction to Solid State Diffusion, Academic, San Diego, CA, 1988.
42. J. Sugiyama, H. Nozaki, I. Umegaki, K. Mukai, K. Miwa, S. Shiraki, T. Hitosugi, A. Suter, T. Prokscha, Z. Salman, J. S. Lord and M. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 1–9.
43. W. J. H. Borghols, M. Wagemaker, U. Lafont and E. M. Kelder, J. Phys. Chem. B, 2009, 12, 17786–17792.
44. G. Krishna, P. Dathar, D. Sheppard, K. J. Stevenson and G. Henkelman, Chem. Mater., 2011, 4032–4037.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp02907a

---