Neural network potential energy surface and dynamical isotope effects for the N+(3P) + H2 → NH+ + H reaction
Abstract
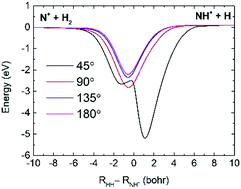
The N+(3P) + H2(X1Σ+g) → NH+(X2Π) + H(2S) reaction is important for initiating the chain reaction of ammonia synthesis in the universe. To study the dynamics of this reaction, a global accurate potential energy surface (PES) of the ground state NH+2 was constructed by combining numerous high-level ab initio energy points with the permutation invariant polynomial neural network method. Utilizing this newly constructed PES, time-dependent wave packet calculations were performed on the state-to-state reactions of N+(3P0) + H2 (v = 0, j = 0) and N+(3P0) + D2 (v = 0, j = 0) in order to study the microscopic reaction mechanisms and dynamical isotope effects. Isotope effects have a significant influence on the rovibrational state distributions and state resolved angle distributions of the product. The total differential cross sections (DCSs) present in the aforementioned reactions are dominated by both forward and backward scattering, as expected from the observable deep well along the reaction path. Meanwhile, the rovibrational state-resolved DCSs show that both reactions are not entirely statistical at the state-to-state level.


 Please wait while we load your content...
Please wait while we load your content...