Unraveling the protonation site of oxazole and solvation with hydrophobic ligands by infrared photodissociation spectroscopy

Abstract

Protonation and solvation of heterocyclic aromatic building blocks control the structure and function of many biological macromolecules. Herein the infrared photodissociation (IRPD) spectra of protonated oxazole (H⁺Ox) microsolvated by nonpolar and quadrupolar ligands, H⁺Ox-L_n with L = Ar (n = 1–2) and L = N₂ (n = 1–4), are analyzed by density functional theory calculations at the dispersion-corrected B3LYP-D3/aug-cc-pVTZ level to determine the preferred protonation and ligand binding sites. Cold H⁺Ox-L_n clusters are generated in an electron impact cluster ion source. Protonation of Ox occurs exclusively at the N atom of the heterocyclic ring, in agreement with the thermochemical predictions. The analysis of the systematic shifts of the NH stretch frequency in the IRPD spectra of H⁺Ox-L_n provides a clear picture of the sequential cluster growth and the type and strength of various competing ligand binding motifs. The most stable structures observed for the H⁺Ox-L dimers (n = 1) exhibit a linear NH⋯L hydrogen bond (H-bond), while π-bonded isomers with L attached to the aromatic ring are local minima on the potential and thus occur at a lower abundance. From the spectra of the H⁺Ox-L(π) isomers, the free NH frequency of bare H⁺Ox is extrapolated as ν_NH = 3444 ± 3 cm⁻¹. The observed H⁺Ox-L₂ clusters with L = N₂ feature both bifurcated NH⋯L₂ (2H isomer) and linear NH⋯L H-bonding motifs (H/π isomer), while for L = Ar only the linear H-bond is observed. No H⁺Ox-L₂(2π) isomers are detected, confirming that H-bonding to the NH group is more stable than π-bonding to the ring. The most stable H⁺Ox-(N₂)_n clusters with n = 3–4 have 2H/(n − 2)π structures, in which the stable 2H core ion is further solvated by (n − 2) π-bonded ligands. Upon N-protonation, the aromatic C–H bonds of the Ox ring get slightly stronger, as revealed by higher CH stretch frequencies and strongly increased IR intensities.

---

1. Introduction

Aromatic molecules play an important role in chemical and biological recognition.^1–4 In particular, heterocyclic azole compounds have attracted the attention of pharmacologists since their first reported antifungal activity.⁵ Good solubility in water and high thermal stability with respect to other heteroaromatic systems make these molecules suitable for the synthesis of therapeutic and natural products.⁶ Among these, the oxazole-containing amino acids are quite ubiquitous in various naturally occurring peptides,^7–12 which possess potential antibiotic and antitumor activity.^13,14 Such compounds have also been used to modify the bioactivity of other macromolecules.^15–17 Additionally, oxazole-bearing drugs exhibit analgesic, antituberculosis, muscle relaxant, antiinflammatory, and HIV-inhibitory properties.^18–27 Protonation of the oxazole (Ox) ring is an important process regarding its bioactivity.^28–30 For example, protonation of the Ox ring in metamifop, the acetyl-coenzyme A carboxylase (ACCase) inhibitor, governs the binding interactions between metamifop and the carboxyltransferase domain.³⁰

The shape and biochemical function of such biological macromolecules are often regulated by their heterocyclic building blocks, such as oxazole (Ox, C₃H₃NO). In the condensed phase, details of their interaction are usually obscured by macroscopic solvent effects, the interaction with other molecules and substrates, and thermal and heterogeneous broadening.^2,3,31 On the other hand, interrogation of the relevant small heterocyclic building blocks in the gas phase, i.e., free from interference with the external bulk environment, provides detailed insight into their physical and chemical properties relevant to the function of the heavier biomolecules. To this end, spectroscopy of cold clusters of heterocyclic molecules in supersonic beams gives direct access to the relevant interaction potentials. Herein, we employ infrared photodissociation (IRPD) spectroscopy in a tandem mass spectrometer to determine fundamental properties of protonated oxazole (H⁺Ox) and its microsolvation interaction with nonpolar (L = Ar) and quadrupolar (L = N₂) ligands with the aid of dispersion-corrected density functional theory (DFT) calculations. In a forthcoming paper, we extend these studies to dipolar ligands (L = H₂O) to characterize the microhydration network. This combined spectroscopic and computational approach has previously been applied in our laboratory to a number of microsolvated solvated aromatic and heterocyclic cations.^32–36

The geometric and spectroscopic properties of the planar Ox molecule have extensively been studied in its neutral S₀ state (¹A′).^37–46 However, no experimental information is available for any neutral Ox-L_n clusters, probably because the broad absorption spectrum prevents the application of convenient size-selective resonant ionization techniques.^47,48 Photoelectron spectra of Ox reveal that ionization into the planar ground electronic state (²A′′) occurs by removal of an electron from a bonding π-orbital localized on the C4–C5 and O1–C2–N3 bonds.^49,50 The high-resolution mass-analyzed threshold ionization spectrum of Ox provides an accurate adiabatic ionization energy, and the analysis of the observed vibrational modes confirms the planarity of the Ox⁺ radical cation and illustrates the changes in geometry upon ionization.⁵⁰ Previous photoelectron imaging of the oxazolide anion indicates selective deprotonation of the Ox ring at the C2 position.⁴² In contrast to neutral and cationic Ox⁽⁺⁾, only very limited information is available for H⁺Ox and its clusters. Previous DFT studies indicate that N-protonation of the heterocyclic ring is strongly preferred over O-protonation,^28,29 and the measured proton affinity is tabulated as 876.4 kJ mol⁻¹.^51,52 Thus far, no spectroscopic data are available for H⁺Ox and its clusters. To this end, our combined IR and DFT studies of H⁺Ox-L_n presented herein provide the first reliable experimental data about the preferred protonation site in H⁺Ox and a first impression of the intermolecular interaction of this prototypical protonated heterocyclic aromatic molecule with hydrophobic aprotic ligands.

2. Experimental and computational methods

IRPD spectra of mass-selected H⁺Ox-L_n clusters are recorded in the CH, NH, and OH stretch range (2650–3600 cm⁻¹) in a tandem quadrupole mass spectrometer coupled to an electron ionization (EI) source and an octupole ion guide.^53,54 Briefly, H⁺Ox-L_n clusters are produced in a pulsed supersonic plasma expansion utilizing electron and chemical ionization close to nozzle orifice. The expanding gas mixture is generated by seeding vapor of Ox (Sigma-Aldrich, 98%) heated to 328 K in Ar (or N₂) and 5% H₂ in He in a 2 : 1 ratio at a backing pressure of 10 bar. Adding H₂ to the expansion gas strongly enhances the yield of H⁺Ox,^55,56 suggesting that H₃⁺ serves as major protonating agent for Ox (although we cannot exclude other ions such as H⁺He, H⁺L, or H₂⁺). The desired H⁺Ox-L_n parent clusters are mass-selected in the first quadrupole and irradiated in the adjacent octupole ion guide with a tunable IR laser pulse (ν_IR, 10 Hz, 2–5 mJ per pulse, bandwidth ∼1 cm⁻¹) emitted from an optical parametric oscillator laser pumped by a Nd:YAG laser. Calibration of ν_IR to better than 1 cm⁻¹ is achieved by a wavemeter. Resonant vibrational excitation leads to the loss of one or more weakly bound ligands. The resulting H⁺Ox-L_m fragment ions (m < n) are mass-selected by the second quadrupole and monitored with a Daly detector as a function of ν_IR to derive the IRPD spectrum of H⁺Ox-L_n. The photofragmentation spectra are linearly normalized for energy fluctuations in the laser pulse. The separation of laser-induced dissociation signal from the signal generated by metastable decay is achieved by triggering the ion source at twice the laser repetition rate and subtracting the signals from alternating triggers. The observed peak widths of the vibrational transitions are mainly due to unresolved rotational structure, sequence hot bands involving low-frequency inter- and intramolecular modes, and possible overlapping contributions from various structural isomers.

Conceivable isomers of H⁺Ox and its H⁺Ox-L_n clusters are calculated at the B3LYP-D3/aug-cc-pVTZ level of DFT theory to assign the measured IRPD spectra and characterize the intermolecular interaction potential.⁵⁷ This dispersion-corrected functional accounts well for the electrostatic, induction, and dispersion forces of the investigated clusters.^56,58–60 Neutral Ox is also computed to establish the influence of protonation on the geometric and vibrational properties. Fully relaxed potential energy surface calculations are performed during the search for stationary points, and their nature as minima or transition states are verified by harmonic frequency analysis. Harmonic intramolecular vibrational frequencies are subjected to a linear scaling factor of 0.9636, derived from a comparison of computed CH and OH stretch frequencies of neutral Ox and water, respectively, to the measured values.^38,61 We consider here also the water modes for optimizing the scaling factor, because we address in a forthcoming paper the vibrational spectroscopy of microhydrated H⁺Ox-(H₂O)_n clusters using the same experimental and computational procedure. Harmonic IR stick spectra are convoluted with a Gaussian line shape (FWHM = 10 cm⁻¹) for convenient comparison to the experimental spectra. All relative energies (E₀) and dissociation energies (D₀) are corrected for harmonic zero-point vibrational energy. Gibbs free energies are evaluated at 298 K (G₀). Previous experience with the chosen computational level illustrates that basis set superposition errors are smaller than 1% and thus not considered here.^58,60 The atomic charge distribution and second-order perturbation energies (E⁽²⁾) of donor–acceptor orbitals involved in the H-bonds are evaluated using the natural bond orbital (NBO) analysis.⁶² Further characterization of the H-bond is obtained from noncovalent interaction (NCI) calculations by evaluating the reduced gradient of the electron density, s(ρ) ∼ |grad(ρ)|/ρ^4/3, as a function of the electron density ρ oriented by the sign of the second eigenvalue λ₂ of the Hessian, ρ* = ρ sign(λ₂).^63,64 The relative strengths of the H-bonding interactions are estimated by comparing the respective ρ* values.

3. Results and discussion

The IRPD spectra of H⁺Ox-L_n recorded between 2950 and 3600 cm⁻¹ are summarized in Fig. 1, and the positions, widths, and vibrational and isomer assignments of the transitions observed (A–D, X) are listed in Table 1, along with the computed frequencies and IR intensities. The considered spectral range covers the OH, NH, and CH stretch fundamentals (ν_OH/NH/CH), which are sensitive to the protonation site and the ligand binding site and bond strength. The positions, band shapes, and relative intensities of bands A–C occurring in the 3300–3450 cm⁻¹ strongly vary with cluster size and type of ligand, suggesting their assignments to free and bound ν_NH modes. In contrast, peaks D1 and D2 observed in the 3150–3220 cm⁻¹ range are relatively insensitive to the ligand type and cluster size and thus can be assigned to aromatic ν_CH modes not involved in ligand bonding. In the following, we discuss the structural, energetic, and vibrational properties of neutral Ox, H⁺Ox, and various H⁺Ox-L_n isomers relevant for the detailed analysis of the experimental spectra. Cartesian coordinates of all relevant optimized structures are provided in the ESI.†

Fig. 1 IRPD spectra of H⁺Ox-L_n with L = Ar (n = 1–2) and N₂ (n = 1–4) recorded in the H⁺Ox-L_m fragment channel (indicated as n–m). The positions, widths, and vibrational and isomer assignments of the transitions observed are listed in Table 1.

Table 1 Positions, widths (FWHM in parentheses), and suggested vibrational and isomer assignments of the transitions observed in the IRPD spectra of H⁺Ox-L_n clusters with L = Ar (n = 1–2) and L = N₂ (n = 1–4) compared to frequencies of the most stable isomers calculated at the B3LYP-D3/aug-cc-pVTZ level. All values are given in cm⁻¹

	Exp.	Calc.^a	Vibration	Isomer
a IR intensities (in km mol^−1) are listed in parentheses. b Ref. 38. c Estimated from the data for H^+Ox-Arn.
Ox	3168^b	3170 (0.4)	ν CH	Ox
	3148^b	3137 (2)	ν CH
		3144 (0.9)	ν CH
H^+Ox	3444 ± 3^c	3446 (202)	ν ^fNH	H^+Ox(N)
	3205 ± 5^c	3181 (27)	ν CH
	3180 ± 10^c	3161 (40)	ν CH
	3170 ± 10^c	3149 (69)	ν CH
H^+Ox-Ar	A 3447	3449 (197)	ν ^fNH	π
	B 3395 (64)	3376 (557)	ν ^bNH	H
	D1 3205 (16)	3182 (28), 3182 (26)	ν CH	H, π
	D2 3174 (32)	3161 (37), 3162 (38)	ν CH	H, π
	D2 3174 (32)	3150 (64), 3151 (67)	ν CH	H, π
H^+Ox-Ar2	B 3401 (25)	3381 (541)	ν ^bNH	H/π
	D1 3204 (11)	3183 (27)	ν CH	H/π
	D2 3175 (18)	3162 (36)	ν CH	H/π
	D2 3175 (18)	3153 (62)	ν CH	H/π
H^+Ox-N2	A 3446	3451 (196)	ν ^fNH	π
	B 3320 (36)	3289 (852)	ν ^bNH	H
	D1 3207 (16)	3182 (32), 3183 (25)	ν CH	H, π
	D2 3172 (24)	3162 (34), 3162 (37)	ν CH	H, π
	D2 3172 (24)	3151 (60), 3153 (65)	ν CH	H, π
H^+Ox-(N2)2	X 3381
	C 3357	3340 (641)	ν ^bNH	2H
	B 3334	3302 (821)	ν ^bNH	H/π
	D1 3208 (11)	3183 (21), 3184 (29)	ν CH	2H, H/π
	D2 3176 (17)	3163 (34), 3163 (32)	ν CH	2H, H/π
	D2 3176 (17)	3166 (65), 3155 (57)	ν CH	2H, H/π
H^+Ox-(N2)3 3-0	C 3368	3352 (616)	ν ^bNH	2H/π
	B 3348	3314 (791)	ν ^bNH	H/2π
	D1 3207 (6)	3185 (18), 3185 (26)	ν CH	2H/π, H/2π
	D2 3179 (30)	3170 (63), 3164 (30)	ν CH	2H/π, H/2π
	D2 3179 (30)	3164 (32), 3159 (54)	ν CH	2H/π, H/2π
H^+Ox-(N2)3 3-1	C 3371 (13)	3352 (616)	ν ^bNH	2H/π
		3185 (18)	ν CH	2H/π
	D2 3168 (25)	3170 (63)	ν CH	2H/π
	D2 3168 (25)	3164 (32)	ν CH	2H/π
H^+Ox-(N2)4 4-1	C 3376 (20)	3363 (591)	ν ^bNH	2H/2π
	B 3358	—	ν ^bNH	H/3π
	D1 3208 (6)	3186 (15), —	ν CH	2H/2π, H/3π
	D2 3168 (14)	3173 (61), —	ν CH	2H/2π, H/3π
	D2 3168 (14)	3165 (30), —		2H/2π, H/3π

---

3.1 Ox and H⁺Ox monomers

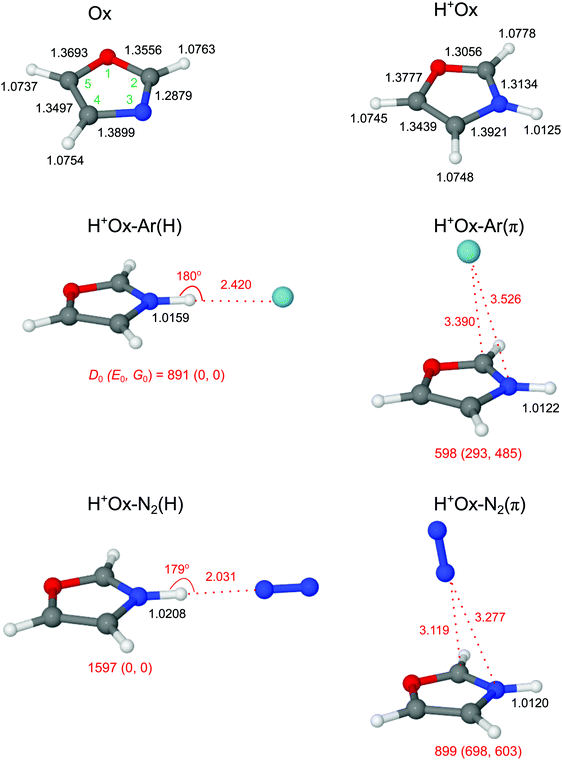
The calculated geometric and vibrational parameters of neutral Ox in its planar ¹A′ ground state (with C_s symmetry) agree satisfactorily with the measurement (Fig. 2 and Table S1 in the ESI†).^38,44 Protonation of Ox may occur at any of the aromatic ring atoms, and their structures are shown in Fig. 3 and Fig. S1 in the ESI.† Apart from the O-protomer, H⁺Ox(O), all protonated structures have C_s symmetry. A detailed potential energy surface, illustrating the relative energies of the various protomers and barriers at the transition states for their interconversion, is shown in Fig. 3. Clearly, H⁺Ox(N) is by far the most stable isomer, and all other protomers are more than ΔE₀ = 120 kJ mol⁻¹ higher in energy. The proton affinity of PA = 876.7 kJ mol⁻¹ predicted for H⁺Ox(N) matches the recommended experimental value of 876.4 kJ mol⁻¹ to better than 1 kJ mol⁻¹,⁵² confirming that the chosen computational level accurately describes the protonation process. Furthermore, the barriers for proton migration between the various protomers are relatively high (>65 kJ mol⁻¹), suggesting that once they are formed in the supersonic expansion, they could kinetically be trapped in deep potential wells.^65–70 All H⁺Ox protomers can readily be distinguished by their predicted IR spectra (Fig. S2 in the ESI†). For example, the C-protomers have characteristic aliphatic CH₂ stretch modes (ν_CH2, calculated below 2950 cm⁻¹), whereas H⁺Ox(O) and H⁺Ox(N) can readily be identified by their unique OH (ν_OH = 3489 cm⁻¹) and NH stretch (ν_NH = 3446 cm⁻¹) oscillators, respectively. The spectral assignment given below demonstrates the exclusive production of H⁺Ox(N), hereafter denoted as H⁺Ox (if not mentioned otherwise), and thus, we mainly focus on the structural details of this protomer.

Fig. 2 Optimized geometries of Ox, H⁺Ox, and H⁺Ox-L isomers with L = Ar and N₂ calculated at the B3LYP-D3/aug-cc-pVTZ level. Binding energies (D₀) and bond lengths are given in cm⁻¹ and Å, respectively. Values in parentheses correspond to relative energies and free energies in cm⁻¹ (E₀, G₀). The atoms are numbered according to IUPAC convention (O1, C2, N3, C4, C5).

Fig. 3 Potential energy surface for proton migration between various protomers of H⁺Ox calculated at the B3LYP-D3/aug-cc-pVTZ level. All energies (E_e in kJ mol⁻¹) are without zero-point energy correction.

Formation of the N–H σ-bond upon protonation at the N atom has a significant influence on the geometry of the aromatic Ox ring skeleton (Fig. 2). For example, the neighboring N–C2 bond elongates by 25.5 mÅ. On the other hand, the effect on the peripheral C–H bonds is comparatively smaller (Δr_CH ≤ 1.5 mÅ). Still, the perturbation is strong enough to increase the average ν_CH frequency with a concomitant enhancement of average IR oscillator strength by Δν_CH = 14 cm⁻¹ and ΔI_CH = 44 km mol⁻¹ (or a factor of 40), respectively (Table 1 and Fig. S2 in the ESI†). The NBO analysis reveals that the additional proton carries almost half of the positive charge (0.465 e), while the rest is delocalized mainly on the peripheral aromatic hydrogens (Fig. S3 in the ESI†).

3.2 H⁺Ox-L dimers

We consider two major binding sites for Ar and N₂ attachment to H⁺Ox, namely H-bonding to the acidic NH proton with high positive partial charge and π-bonding to the aromatic ring. For both ligands, the nearly linear NH⋯L bonded isomers, H⁺Ox-L(H), are the global minima (D₀ = 891/1597 cm⁻¹ for L = Ar/N₂), while the H⁺Ox-L(π) isomers are substantially less stable local minima (D₀ = 598/899 cm⁻¹). The stronger bonds of N₂ arise from its larger parallel polarizability and additional quadrupole moment, leading to stronger electrostatic, inductive and dispersive forces.^71,72 Moreover, the negative sign of the quadrupole moment favors a linear over a T-shaped approach of N₂.^71,72 The difference in the D₀ values between the H-bonded and π-bonded isomers of N₂ is almost 2.5 times larger than for the Ar ligand, owing to the stronger H-bonding affinity of N₂ resulting from its higher proton affinity (PA = 494/369 kJ mol⁻¹ for L = N₂/Ar).⁵² As a consequence of the stronger and shorter NH⋯L H-bond (R = 2.031/2.420 Å), the elongation of the N–H donor bond and corresponding red shift in the H-bonded ν_NH (ν^b_NH) are larger for N₂ (Δr_NH = 8.3/3.4 mÅ, Δν^b_NH = −157/−70 cm⁻¹). The E⁽²⁾ and ρ* values, which both correlate with the strength of the H-bond, are also larger for N₂ (E⁽²⁾ = 42.2/13.7 kJ mol⁻¹, −ρ* = 0.022/0.013, Fig. S4 and S5 in the ESI†). As expected for such weak H-bonds, the charge transfer from H⁺Ox to the H-bonded ligand is small and also scales with the interaction energy (Δq = 0.028/0.017 e). In contrast to H-bonding to the NH group, π-bonding of L to the aromatic ring has a negligible influence on the properties of the N–H bond (Δr_NH ≤ 0.5 mÅ), and thus the free ν^f_NH mode remains nearly unshifted from the monomer (Δν_NH = 3/5 cm⁻¹ for Ar/N₂). For both major binding motifs, the aromatic C–H bonds and ν_CH modes are also essentially unaffected. For completeness, we also consider H⁺Ox-N₂(CH) isomers, in which N₂ forms linear H-bonds to the aromatic CH protons of H⁺Ox. The binding energies obtained for H⁺Ox-N₂(C2H) and H⁺Ox-N₂(C5H) are comparable or weaker than the π-bond (D₀ = 932 and 705 cm⁻¹), and their free ν^f_NH modes are predicted around 3450 cm⁻¹ (Fig. S6 and S7 in the ESI†). Any attempt to optimize H⁺Ox-N₂(C4H) converges to the H⁺Ox-N₂(H) global minimum.

In Fig. 4 the measured IRPD spectra of the H⁺Ox-L dimers are compared to those calculated for the most stable isomers, H⁺Ox-L(H) and H⁺Ox-L(π). The weak transitions A observed at 3447 and 3446 cm⁻¹ for L = Ar and N₂ are attributed to ν^f_NH of the H⁺Ox-L(π) isomers predicted at 3449 and 3451 cm⁻¹, respectively. The more intense bands B at 3395 and 3320 cm⁻¹ can readily be assigned to the ν^b_NH modes of the H⁺Ox-L(H) global minima. The observed red shifts of Δν^b_NH = −52 and −126 cm⁻¹ are somewhat smaller but consistent with the predicted values (−70/−157 cm⁻¹). In addition, the band profile of transition B with a sharp rise on the red side and a long tail on the blue side is characteristic for the excitation of proton-donor stretch modes and thus confirms the given assignments. The large width of such bands arises mainly from sequence hot bands of ν^b_NH with intermolecular modes, which typically occur to higher frequency than the fundamental. The transitions D1/D2 at 3205/3174 and 3207/3172 cm⁻¹ observed for L = Ar and N₂, respectively, are attributed to the three close-lying ν_CH modes of the H⁺Ox-L(π) and H⁺Ox-L(H) isomers, which are predicted in this spectral range with a similar energy spread and intensity ratio. Indeed, as predicted by the calculations, N-protonation increases the ν_CH frequencies. A possible assignment of the bands D1 and D2 to the NH bend overtone, which may gain intensity by anharmonic interaction with the intense ν_NH fundamental,^73,74 can safely be excluded because of the low frequency predicted for the NH bend fundamental (1427 cm⁻¹ for fundamental and 2844 cm⁻¹ for first overtone from anharmonic calculations). For completeness, we also consider an assignment of bands A to combination modes ν^b_NH + ν_s of the H⁺Ox-L(H) isomers involving the intermolecular stretch vibration (ν_s). This scenario would yield ν_s frequencies of 73 and 126 cm⁻¹ for L = Ar and N₂, respectively, which are indeed similar to their harmonic computed values of 70 and 117 cm⁻¹. However, if that assignment were correct, such transitions should also appear in the spectra of the larger H⁺Ox-L_n clusters,^56,75,76 in disagreement with experiment (Fig. 1). Hence, we strongly favor an assignment of bands A to ν^f_NH of the H⁺Ox-L(π) isomers. A definitive isomer assignment, e.g., from hole-burning experiments, is beyond the scope of the present work. In conclusion, all major features of the IRPD spectra of the H⁺Ox-L dimers can readily be reproduced by the spectra predicted for H⁺Ox-L(H) and H⁺Ox-L(π). The analysis of the integrated band intensities of bands A and B, along with the predicted oscillator strengths, results in a rough estimate of the population ratio of H : π ∼ 1.5 and ∼10 for L = Ar and N₂, respectively, consistent with both the absolute and relative binding energies of the two ligand binding motifs.

Fig. 4 Comparison of IRPD spectra of H⁺Ox-L (L = Ar and N₂) to the linear IR absorption spectra of N-protonated H⁺Ox and various H⁺Ox-L isomers obtained at the B3LYP-D3/aug-cc-pVTZ level. The stick spectra are convoluted with Gaussian line profiles with FWHM = 10 cm⁻¹.

In the following, we briefly present arguments for excluding the presence of other protomers and alternative ligand binding sites. In order to test the abundance of H⁺Ox(C) protomers via their characteristic and intense ν_CH2 modes predicted in the 2850–3000 cm⁻¹ range, IRPD spectra of H⁺Ox-L are recorded down to 2650 cm⁻¹ for both Ar and N₂. However, no such transitions are observed in this frequency range, indicating that the concentration of H⁺Ox(C) protomers is below the detection limit (see Fig. S8 in the ESI,† for a comparison with spectra computed for H⁺Ox(C2)-L dimers). We also computed IR spectra of dimers of the H⁺Ox(O) protomer (Fig. S8 in the ESI†). Interestingly, the ν^b_OH mode (3201 cm⁻¹) of H⁺Ox(O)-Ar(H) is predicted with high intensity in the vicinity of band D1. However, the corresponding band of H⁺Ox(O)-N₂(H) predicted at 2887 cm⁻¹ is completely missing in the measured spectrum. As these ν^b_OH bands of H⁺Ox(O)-L(H) have enormous IR oscillator strengths, their absence in the IRPD spectra implies that the H⁺Ox(O) population is negligible (the lack of any ν^f_OH band of this protomer near 3490 cm⁻¹ confirms this view). Thus, in agreement with the thermochemical data in Fig. 3, we detect in the expansion only clusters of the by far most stable H⁺Ox(N) protomer and will not consider other protomers further. Finally, we may also safely exclude CH-bonded isomers of H⁺Ox-N₂. The intense ν^b_CH transition of the most stable of these isomers, H⁺Ox-N₂(C2H), is predicted at 3109 cm⁻¹, and the IRPD spectrum lacks signal in this spectral range (Fig. S8 in ESI†).

3.3 H⁺Ox-L₂ trimers

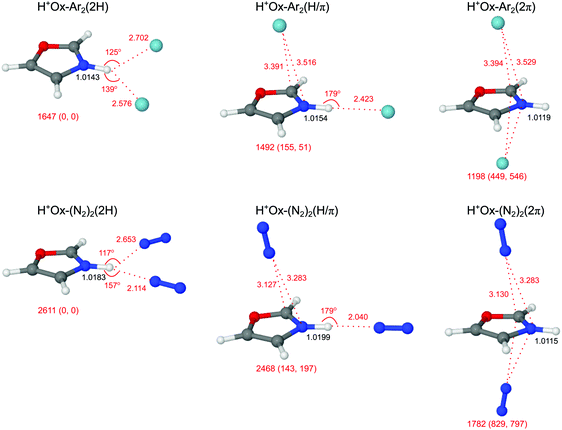
Guided by the analysis of the H⁺Ox-L dimer spectra, addition of the second ligand results in the three different structural isomers of H⁺Ox-L₂ shown in Fig. 5. The planar H⁺Ox-L₂(2H) global minimum features an asymmetric bifurcated NH⋯L₂ H-bond, whereas in H⁺Ox-L₂(H/π) a π-bound ligand is attached to the H⁺Ox-L(H) dimer. These two isomers have comparable stability, with total binding energies of D₀(2H) = 1647/2611 cm⁻¹ and D₀(H/π) = 1492/2468 cm⁻¹ for Ar/N₂. The H⁺Ox-L₂(2π) isomer with two ligands attached to the two opposite sides of the aromatic plane is significantly less stable, D₀(2π) = 1198/1782 cm⁻¹.

Fig. 5 Optimized geometries of various H⁺Ox-L₂ isomers with L = Ar and N₂ calculated at the B3LYP-D3/aug-cc-pVTZ level. Binding energies (D₀) and bond lengths are given in cm⁻¹ and Å, respectively. Values in parentheses correspond to relative energies and free energies in cm⁻¹ (E₀, G₀).

In the 2H isomer with the bifurcated H-bond, the two nonequivalent and strongly nonlinear NH⋯L bonds are substantially weaker than the linear NH⋯L bonds in the dimers. As a result, the N–H bond contracts upon attachment of the second ligand, leading to a significant incremental blue shift in ν_NH (Δr_NH = −1.6/−2.5 mÅ, Δν_NH = 36/51 cm⁻¹ for L = Ar/N₂). The effect is stronger for N₂ due to its higher H-bonding affinity. For the same reason, the asymmetry between the first and second bond is larger for N₂. The E⁽²⁾ energies confirm this view of asymmetric bonding. For example, E⁽²⁾ = 29.8 and 2.7 kJ mol⁻¹ for the two H-bonds in H⁺Ox-(N₂)₂(2H), indicating still a substantial H-bond character to the first ligand, while the strongly nonlinear bond to the second ligand has mostly electrostatic character. In addition, the bent H-bond to the first ligand in the 2H isomer is weaker than in the linearly H-bonded dimer (E⁽²⁾ = 29.8 and 42.2 kJ mol⁻¹). Similar differences between linear and bifurcated H-bonds of acidic proton donors to N₂ ligands have previously been reported for indole⁺–(N₂)₂, pyrrole⁺–(N₂)₂, and tryptamine⁺–(N₂)₂ cluster cations.^59,77,78

In contrast to the 2H isomers, additional π-complexation of the H⁺Ox-L(H) dimer in the H/π isomer induces only a small perturbation on the N–H bond and leads to a minor incremental blue shift of ν^b_NH (Δr_NH = −0.5/−0.9 mÅ, Δν_NH = 5/13 cm⁻¹ for L = Ar/N₂), in line with the slightly smaller E⁽²⁾ energy of the H-bond (41.1 vs. 42.2 kJ mol⁻¹ for L = N₂). Hence, the ν^b_NH mode of the H/π isomer appears red shifted from the 2H isomer (Δν_NH = −31/−38 cm⁻¹) and thus both H-bonded structures can readily be distinguished by their ν^b_NH modes. Finally, the two ligands in the 2π isomer barely influence the NH oscillator, and the associated parameters remain comparable to those of H⁺Ox (Δr_NH = −0.6/−1.0 mÅ, Δν_NH = 6/10 cm⁻¹ for Ar/N₂).

In Fig. 6 the measured IRPD spectra of the H⁺Ox-L₂ trimers are compared to those calculated for the most stable isomers (2H, H/π, 2π). The experimental H⁺Ox-Ar₂ spectrum exhibits three bands at 3401 (B), 3204 (D1) and 3175 (D2) cm⁻¹. Interestingly, band B lies between the predicted ν^b_NH modes of the H/π (3381 cm⁻¹) and 2H (3412 cm⁻¹) isomers split by 31 cm⁻¹, which is somewhat larger than the width of band B (25 cm⁻¹). Because (i) the calculations overestimate the Δν_NH shifts and (ii) the experimental blue shift (Δν_NH = 6 cm⁻¹) with respect to H⁺Ox-Ar(H) agrees well with the one predicted for the statistically favored H/π isomer (Δν_NH = 5 cm⁻¹), we assign band B to the H/π isomer despite its somewhat lower calculated binding energy. The substantially less stable 2π isomer can be excluded because of the absence of any signal near ν^f_NH ∼ 3450 cm⁻¹. Its population is below 5% considering the achieved signal-to-noise ratio and computed oscillator strengths. This result confirms that the H-bond in H⁺Ox-Ar₂ is clearly more stable than the π-bond, as already inferred from the n = 1 spectrum and the calculations. According to this scenario, bands D1 and D2 are assigned to the ν_CH modes of the H/π isomer.

Fig. 6 Comparison of IRPD spectra of H⁺Ox-L₂ (L = Ar and N₂) to the linear IR absorption spectra of various H⁺Ox-L₂ isomers calculated at the B3LYP-D3/aug-cc-pVTZ level. The stick spectra are convoluted with Gaussian line profiles with FWHM = 10 cm⁻¹.

The measured H⁺Ox-(N₂)₂ spectrum displays a triplet structure at 3381 (X), 3357 (C), and 3334 (B) cm⁻¹ in the ν^b_NH range, along with the two ν_CH bands at 3208 (D1) and 3176 (D2) cm⁻¹. Compared to the ν^b_NH band of H⁺Ox-N₂(H) at 3320 cm⁻¹, the relative blue shift for band B is smaller than for band C (Δν_NH = 14 vs. 37 cm⁻¹), and these agree satisfactorily with the computed values of the H/π and 2H isomers (Δν_NH = 13 vs. 51 cm⁻¹), respectively. The ν^b_NH mode of the H/π isomer has a larger IR oscillator strength (821 vs. 641 km mol⁻¹), and this isomer is statistically favored over the 2H isomer (due to the two available π minima). Taking these aspects into account, the higher intensity of band C compared to B may indicate a larger abundance of the 2H isomer, compatible with its higher D₀ value. There is no obvious explanation for the shoulder X, and our currently favored interpretation is a sequence hot band of ν^b_NH of 2H and/or H/π, a conclusion supported by the analysis of the spectra of the colder n = 3 and 4 clusters. Similar to the Ar case, the absence of any weak transition near ν^f_NH ∼ 3450 cm⁻¹ illustrates the lack of the much less stable 2π isomer. The transitions D1 and D2 are then attributed to the ν_CH modes of the two assigned 2H and H/π isomers.

3.4 H⁺Ox-(N₂)_n clusters (n = 3–4)

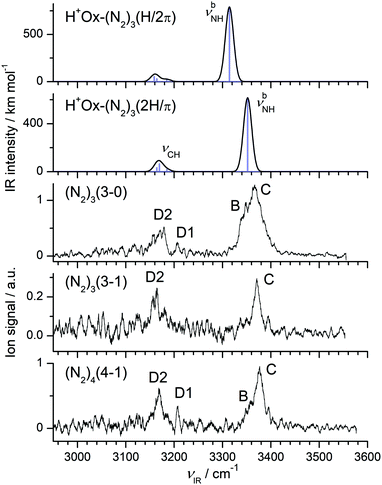
The complex potential energy surface of H⁺Ox-(N₂)₃ is not characterized in detail, and only two relevant structures are optimized (Fig. S9 in the ESI†). Only one calculation is performed for the n = 4 cluster (Fig. S10 in the ESI†). In the most stable 2H/π isomer of H⁺Ox-(N₂)₃ with D₀ = 3482 cm⁻¹, a π-bound N₂ ligand slightly perturbs the bifurcated 2H trimer, whereas the slightly less stable H/2π isomer with D₀ = 3322 cm⁻¹ has a linear H-bonded dimer core solvated by two π-bonded ligands below and above the Ox ring. The structural and vibrational parameters of the N–H bond of 2H/π remain almost the same as in the 2H isomer (Δr_NH = −0.9 mÅ, Δν^b_NH = 12 cm⁻¹). These minor changes result from the small noncooperative effect imposed by the additional π-bound N₂ ligand. The same blue shift of Δν^b_NH = 12 cm⁻¹ is computed for the H/2π structure upon π-complexation of the H/π isomer. For the most stable 2H/2π isomer, we obtain D₀ = 4334 cm⁻¹ and Δν^b_NH = 11 cm⁻¹.

The IRPD spectra of the n = 3 cluster shown in Fig. 7 are obtained in two different fragment ion channels, namely H⁺Ox (denoted 3-0) and H⁺Ox-N₂ (denoted 3-1). The spectrum in the 3-0 channel features a doublet centered at 3368 (C) and 3348 (B) cm⁻¹ in the ν^b_NH range, which is attributed to two different isomers, along with the two weaker ν_CH bands around 3170 (D2) and 3207 (D1) cm⁻¹. We assign transition C to the 2H/π isomer, whose ν^b_NH is blue shifted by 11 cm⁻¹ with respect to the 2H isomer, consistent with its predicted shift of 12 cm⁻¹. Correspondingly, band B at 3348 cm⁻¹ is attributed to the less stable H/2π isomer, whose ν^b_NH blue shift of 14 cm⁻¹ also agrees with the computed value of 12 cm⁻¹.

Fig. 7 Experimental IRPD spectra of H⁺Ox-(N₂)_n with n = 3–4 compared to the linear IR absorption spectra of two isomers of H⁺Ox-(N₂)₃ calculated at the B3LYP-D3/aug-cc-pVTZ level. The stick spectra are convoluted with Gaussian line profiles with FWHM = 10 cm⁻¹.

The spectrum in the 3-1 channel, which is by a factor 5 weaker than the 3-0 channel, contains in the ν^b_NH range only band C at 3371 cm⁻¹ assigned to the 2H/π isomer. Moreover, the width of this transition is smaller than in the 3-0 spectrum. The binding energy of this isomer is calculated as D₀ = 3482 cm⁻¹, i.e. the absorbed photon energy is close to the dissociation energy. Apparently, cold 2H/π clusters can eliminate only two N₂ ligands leading to a narrow ν^b_NH band in the 3-1 channel, while internally warm clusters can eliminate all three N₂ ligands producing the broader ν^b_NH transition in the 3-0 channel. Significantly, the ν^b_NH transition of the H/2π isomer is only detected in the 3-0 channel, because its smaller binding energy calculated as D₀ = 3322 cm⁻¹ allows to fragment all three ligands even for cold clusters. The added intensity of peak C in both fragment spectra is substantially larger than that of peak B. All these experimental results suggest that the 2H/π isomer is indeed more stable than the H/2π isomer, consistent with the calculations. The fact that the branching ratio into the two fragment channels is predicted correctly implies that also the absolute computed binding energies are reliable. The absence of band X in the colder n = 3 and 4 spectra (Fig. 1) is in line with its tentative interpretation as sequence hot band.

The IRPD spectrum of H⁺Ox-(N₂)₄ shown in Fig. 7 is only observed in the H⁺Ox-N₂ fragment channel (4-1), in line with the computed binding energies for π-bonded and H-bonded N₂ ligands (e.g., D₀ = 4334 cm⁻¹ for the most stable 2H/2π isomer). The spectrum in the ν^b_NH range is dominated by band C at 3376 cm⁻¹, which is attributed to the 2H/2π isomer by comparison to the n = 3 spectrum. Similarly, its shoulder B at 3358 cm⁻¹ is the signature of a much less abundant H/3π isomer. Both transitions exhibit small incremental blue shifts of Δν^b_NH ∼ 10 cm⁻¹ typical for π-complexation of H⁺Ox with N₂. The ν_CH bands of the two n = 4 isomers at 3208 (D1) and 3168 (D2) cm⁻¹ are close to the transitions of the n = 1–3 clusters, indicating that all clusters up to n = 4 do not contain any CH-bonded N₂ ligands.

3.5 Cluster growth

The ν_NH frequencies observed for the various H⁺Ox-L_n clusters summarized in Fig. 8 show a clear evolution as a function of the cluster size and the ligand type and binding site, and thus provide a detailed picture of the cluster growth process of the various isomers. The π-bonds are substantially weaker than the H-bonds, and thus H⁺Ox-L_n clusters with only π-bonded ligands (nπ) are merely observed for the cluster size n = 1. At this binding site the perturbation of the NH group is very small, so that we can accurately estimate the ν_NH fundamental of bare N-protonated H⁺Ox as 3444 ± 3 cm⁻¹, in excellent agreement with the predicted value of 3446 cm⁻¹. Clearly, the H-bonded H⁺Ox-L(H) dimers are the global minima on the n = 1 potential, with large incremental red shifts of Δν_NH = −53 and −122 cm⁻¹ for L = Ar and N₂, respectively. Further complexation with π-bonded ligands in the H/(n − 1)π isomers induces small incremental blue shifts of Δν_NH = +6 cm⁻¹ for Ar (n = 2) and +14, +14, and +10 cm⁻¹ for N₂ (n = 2–4). For L = N₂, the most stable binding motif for n ≥ 2 corresponds to the 2H/(n − 2)π isomers with a bifurcated 2H trimer core further solvated by π-bonded ligands. The incremental blue shifts of π-bonding (Δν_NH = +11 and +8 cm⁻¹ for n = 3–4) are slightly smaller than for the H/(n − 1)π series because of the weaker bifurcated H-bonds in the 2H/(n − 2)π isomers.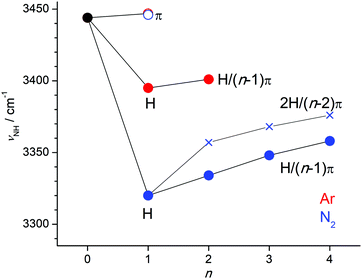

Fig. 8 Plot of experimental ν_NH frequencies obtained from the IRPD spectra of H⁺Ox-L_n with L = Ar (n = 1–2) and L = N₂ (n = 1–4) as a function of cluster size (Table 1). The π and H (and H/(n − 1)π) isomers are indicated by open and filled circles, respectively, while the 2H/(n − 2)π isomers are indicated by crosses. The value for bare H⁺Ox is extrapolated from the H⁺Ox-Ar(π) data point.

4. Concluding remarks

In summary, IRPD spectra of H⁺Ox-L_n with L = Ar (n ≤ 2) and L = N₂ (n ≤ 4) are analyzed in the informative CH, NH, and OH stretch range with dispersion-corrected DFT calculations. Significantly, the IRPD spectra correspond to the first spectroscopic detection of H⁺Ox and its clusters in the gas phase. They provide a reliable determination of the preferred protonation site and a first impression of the interaction of this fundamental protonated heterocyclic molecule with hydrophobic ligands. H⁺Ox ions produced by chemical ionization in a plasma containing H₂ are exclusively protonated at the most basic N position, and protonation at the much less favorable O and C atoms (E₀ > 120 kJ mol⁻¹) is not observed. Size-dependent shifts in the NH stretch frequency of H⁺Ox-L_n provide a clear picture of the ligand binding sites and corresponding bond strengths and the sequential microsolvation process including the formation of solvation subshells. The nonpolar Ar and quadrupolar N₂ ligands prefer H-bonding to the acidic NH proton of H⁺Ox to π-bonding at the aromatic ring. From the spectra of the H⁺Ox-L(π) dimers, the NH stretch frequency of bare H⁺Ox is accurately extracted as 3444 ± 3 cm⁻¹. Similarly, the CH stretching frequencies are extracted as 3205 ± 5, 3180 ± 10, and 3170 ± 10 cm⁻¹, which indicate a strengthening of the C–H bonds upon N-protonation of Ox. The most stable H⁺Ox-L_n clusters with n ≥ 2 have a H⁺Ox-L₂(2H) trimer core with an asymmetric bifurcated NH⋯L₂ H-bond of two nonequivalent ligands to the NH proton. Further solvation in these 2H/(n − 2)π clusters occurs at the π binding sites. A less stable H/(n − 1)π isomer series is also observed for L = Ar and N₂, in which π-bonded ligands are attached to a H⁺Ox-L(H) dimer core with a linear NH⋯L H-bond. The microsolvation of H⁺Ox with hydrophobic ligands reported herein differs substantially from the microsolvation with polar hydrophilic ligands, as inferred from the analysis of IRPD spectra microhydrated H⁺Ox-(H₂O)_n clusters reported in a forthcoming publication.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by Deutsche Forschungsgemeinschaft (DO 729/3-3).

References

1. E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210–1250.
2. M. S. de Vries and P. Hobza, Annu. Rev. Phys. Chem., 2006, 58, 585–612.
3. J.-P. Schermann, Spectroscopy and modelling of biomolecular building blocks, Elsevier, Amsterdam, 2008.
4. L. M. Salonen, M. Ellermann and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 4808–4842.
5. J. A. Maertens, Clin. Microbiol. Infect., 2004, 10, 1–10.
6. P. Ü. Civcir, G. Kurtay and K. Sarıkavak, Struct. Chem., 2017, 28, 773–790.
7. C. Portmann, J. F. Blom, M. Kaiser, R. Brun, F. Jüttner and K. Gademann, J. Nat. Prod., 2008, 71, 1891–1896.
8. E. K. S. Vijaya Kumar, J. Kenia, T. Mukhopadhyay and S. R. Nadkarni, J. Nat. Prod., 1999, 62, 1562–1564.
9. M. L. Chiu, M. Folcher, T. Katoh, A. M. Puglia, J. Vohradsky, B.-S. Yun, H. Seto and C. J. Thompson, J. Biol. Chem., 1999, 274, 20578–20586.
10. R. C. M. Lau and K. L. Rinehart, J. Am. Chem. Soc., 1995, 117, 7606–7610.
11. N. Lindquist, W. Fenical, G. D. Van Duyne and J. Clardy, J. Am. Chem. Soc., 1991, 113, 2303–2304.
12. J. Deeley, A. Bertram and G. Pattenden, Org. Biomol. Chem., 2008, 6, 1994–2010.
13. M. C. Bagley, J. W. Dale, E. A. Merritt and X. Xiong, Chem. Rev., 2005, 105, 685–714.
14. D. Siodłak, M. Staś, M. A. Broda, M. Bujak and T. Lis, J. Phys. Chem. B, 2014, 118, 2340–2350.
15. G. Haberhauer, Á. Pintér, T. Oeser and F. Rominger, Eur. J. Org. Chem., 2007, 1779–1792.
16. S. C. Ceide, L. Trembleau, G. Haberhauer, L. Somogyi, X. Lu, T. Bartfai and J. Rebek, PNAS, 2004, 101, 16727–16732.
17. I. E. Andersson, T. Batsalova, B. Dzhambazov, L. Edvinsson, R. Holmdahl, J. Kihlberg and A. Linusson, Org. Biomol. Chem., 2010, 8, 2931–2940.
18. C. A. Dinarello, Cell, 2010, 140, 935–950.
19. J. Zhang and M. A. Ciufolini, Org. Lett., 2011, 13, 390–393.
20. N. R. Stokes, N. Baker, J. M. Bennett, P. K. Chauhan, I. Collins, D. T. Davies, M. Gavade, D. Kumar, P. Lancett, R. Macdonald, L. Macleod, A. Mahajan, J. P. Mitchell, N. Nayal, Y. N. Nayal, G. R. W. Pitt, M. Singh, A. Yadav, A. Srivastava, L. G. Czaplewski and D. J. Haydon, Bioorg. Med. Chem. Lett., 2014, 24, 353–359.
21. D. J. Kempf, H. L. Sham, K. C. Marsh, C. A. Flentge, D. Betebenner, B. E. Green, E. McDonald, S. Vasavanonda, A. Saldivar, N. E. Wideburg, W. M. Kati, L. Ruiz, C. Zhao, L. Fino, J. Patterson, A. Molla, J. J. Plattner and D. W. Norbeck, J. Med. Chem., 1998, 41, 602–617.
22. Y.-M. Li, J. C. Milne, L. L. Madison, R. Kolter and C. T. Walsh, Science, 1996, 274, 1188–1193.
23. K. Sasahara, Y. Hirao, N. Koyama, K. Kitano, K. Umehara, Y. Shimokawa and M. Shibata, Drug Metab. Dispos., 2015, 43, 1267–1276.
24. G. C. Moraski, M. Chang, A. Villegas-Estrada, S. G. Franzblau, U. Möllmann and M. J. Miller, Eur. J. Med. Chem., 2010, 45, 1703–1716.
25. A. Gürsoy, Ş. Demirayak, G. Çapan, K. Erol and K. Vural, Eur. J. Med. Chem., 2000, 35, 359–364.
26. J. A. Bull, E. P. Balskus, R. A. J. Horan, M. Langner and S. V. Ley, Chem. – Eur. J., 2007, 13, 5515–5538.
27. R. E. Boyd, J. B. Press, C. R. Rasmussen, R. B. Raffa, E. E. Codd, C. D. Connelly, D. J. Bennett, A. L. Kirifides, J. F. Gardocki, B. Reynolds, J. T. Hortenstein and A. B. Reitz, J. Med. Chem., 1999, 42, 5064–5071.
28. B. S. Jursic, J. Chem. Soc., Perkin Trans. 2, 1996, 1021.
29. P. Mátyus, K. Fuji and K. Tanaka, Tetrahedron, 1994, 50, 2405–2414.
30. X. Xia, W. Tang, S. He, J. Kang, H. Ma and J. Li, Sci. Rep., 2016, 6, 34066.
31. G. Haberhauer, E. Drosdow, T. Oeser and F. Rominger, Tetrahedron, 2008, 64, 1853–1859.
32. J. Klyne, M. Schmies, M. Fujii and O. Dopfer, J. Phys. Chem. B, 2015, 119, 1388–1406.
33. K. Chatterjee, Y. Matsumoto and O. Dopfer, Angew. Chem., Int. Ed., 2019, 58, 3351–3355.
34. A. Bouchet, M. Schütz, B. Chiavarino, M. E. Crestoni, S. Fornarini and O. Dopfer, Phys. Chem. Chem. Phys., 2015, 17, 25742–25754.
35. J. Klyne, M. Schmies and O. Dopfer, J. Phys. Chem. B, 2014, 118, 3005–3017.
36. J. Klyne and O. Dopfer, Phys. Chem. Chem. Phys., 2019, 21, 2706–2718.
37. M. H. Palmer, J. Mol. Struct., 2007, 834–836, 113–128.
38. G. Sbrana, E. Castellucci and M. Ginanneschi, Spectrochim. Acta, Part A, 1967, 23, 751–758.
39. E. Borello, A. Zecchina and A. Appiano, Spectrochim. Acta, Part A, 1966, 22, 977–983.
40. M. Der Su, J. Phys. Chem. A, 2015, 119, 9666–9669.
41. D. Kaur and S. Khanna, Comput. Theor. Chem., 2011, 963, 71–75.
42. L. M. Culberson, C. C. Blackstone, R. Wysocki and A. Sanov, Phys. Chem. Chem. Phys., 2014, 16, 527–532.
43. L. M. Culberson, A. A. Wallace, C. C. Blackstone, D. Khuseynov and A. Sanov, Phys. Chem. Chem. Phys., 2014, 16, 3964–3972.
44. A. Kumar, J. Sheridan and O. L. Stiefvater, Z. Naturforsch. A, 1978, 33, 145–152.
45. N. El-Bakali Kassimi, R. J. Doerksen and A. J. Thakkar, J. Phys. Chem., 1996, 100, 8752–8757.
46. A. E. Obukhov and L. I. Belen’kii, Chem. Heterocycl. Compd., 1999, 35, 832–854.
47. M. H. Palmer, G. Ganzenmu and I. C. Walker, Chem. Phys., 2007, 334, 154–166.
48. J. Cao, Z.-Z. Xie and X. Yu, Chem. Phys., 2016, 474, 25–35.
49. M. H. Palmer, R. H. Findlay and R. G. Egdell, J. Mol. Struct., 1977, 40, 191–210.
50. S. Han, T. Y. Kang, S. Choi, K.-W. Choi, S. J. Baek, S. Lee and S. K. Kim, Phys. Chem. Chem. Phys., 2008, 10, 3883–3887.
51. M. Meot-Ner, J. F. Liebman and J. E. Del Bene, J. Org. Chem., 1986, 51, 1105–1110.
52. E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656.
53. O. Dopfer, Int. Rev. Phys. Chem., 2003, 22, 437–495.
54. O. Dopfer, Z. Phys. Chem., 2005, 219, 125–168.
55. E. E. Etim, P. Gorai, A. Das and E. Arunan, Adv. Space Res., 2017, 60, 709–721.
56. K. Chatterjee and O. Dopfer, Astrophys. J., 2018, 865, 114.
57. M. J. Frisch et al. , Gaussian09, D.01, Gaussian, Inc., Walingford, CT, 2009.
58. K. Chatterjee and O. Dopfer, Chem. Sci., 2018, 9, 2301–2318.
59. M. Schütz, Y. Matsumoto, A. Bouchet, M. Öztürk and O. Dopfer, Phys. Chem. Chem. Phys., 2017, 19, 3970–3986.
60. J. Klyne, M. Miyazaki, M. Fujii and O. Dopfer, Phys. Chem. Chem. Phys., 2018, 20, 3092–3108.
61. G. Herzberg, Molecular Spectra and Molecular Structure. II. Infrared and Raman Spectra of Polyatomic Molecules, Krieger Publishing Company, Malabar, Florida, 1991.
62. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry, University of Wisconsin, Madison, 2013.
63. E. R. Johnson, S. Keinan, P. Mori Sánchez, J. Contreras García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
64. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
65. M. Katada and A. Fujii, J. Phys. Chem. A, 2018, 122, 5822–5831.
66. N. Solcà and O. Dopfer, J. Chem. Phys., 2004, 120, 10470–10482.
67. N. Solcà and O. Dopfer, J. Am. Chem. Soc., 2004, 126, 1716–1725.
68. N. Solcà and O. Dopfer, Chem. Phys. Lett., 2001, 342, 191–199.
69. N. Solcà and O. Dopfer, J. Chem. Phys., 2004, 121, 769–772.
70. J. Klyne and O. Dopfer, J. Phys. Chem. B, 2018, 122, 10700–10713.
71. D. Roth and O. Dopfer, Phys. Chem. Chem. Phys., 2002, 4, 4855–4865.
72. R. V. Olkhov and O. Dopfer, Chem. Phys. Lett., 1999, 314, 215–222.
73. J. Klyne, M. Schmies, M. Fujii and O. Dopfer, J. Phys. Chem. B, 2015, 119, 1388–1406.
74. J. Klyne, M. Schmies, M. Miyazaki, M. Fujii and O. Dopfer, Phys. Chem. Chem. Phys., 2018, 20, 3148–3164.
75. O. Dopfer, D. Roth and J. P. Maier, J. Phys. Chem. A, 2000, 104, 11702–11713.
76. R. V. Olkhov, S. A. Nizkorodov and O. Dopfer, Chem. Phys., 1998, 239, 393–407.
77. N. Solca and O. Dopfer, Phys. Chem. Chem. Phys., 2004, 6, 2732–2741.
78. K. Sakota, M. Schütz, M. Schmies, R. Moritz, A. Bouchet, T. Ikeda, Y. Kouno, H. Sekiya and O. Dopfer, Phys. Chem. Chem. Phys., 2014, 16, 3798–3806.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp02787d

---