Deconvolution of BIL-SFG and DL-SFG spectroscopic signals reveals order/disorder of water at the elusive aqueous silica interface
Abstract
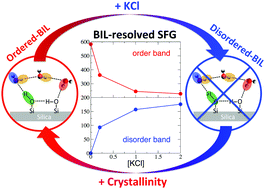
Through the prism of the rather controversial and elusive silica/water interface, ab initio DFT-based molecular dynamics simulations of the structure and non-linear SFG spectroscopy of the interface are analysed. Following our recent work [Phys. Chem. Chem. Phys., 2018, 20, 5190–5199], we show that once the interfacial water is decomposed into BIL (Binding Interfacial Layer) and DL (Diffuse Layer) interfacial regions, the SFG signals can be deconvolved and unambiguously interpreted, and a global microscopic understanding on silica/water interfaces can be obtained. By comparing crystalline quartz/water and amorphous (fused) silica/water interfaces, the dependence of interfacial structural and spectroscopic properties on the degree of surface crystallinity is established, while by adding KCl electrolytes at the quartz/water interface, the chaotropic effect of ions on the interfacial molecular arrangement is unveiled. The evolution of structure and SFG spectra of silica/water interfaces with respect to increasing surface deprotonation, i.e., with respect to pH conditions, is also evaluated. Spectroscopic BIL-SFG markers that experimentally allow one detect the water order/disorder in the BIL as a function of surface hydroxylation and ion concentration are revealed, while the pH-induced modulations in the experimentally recorded SFG spectra are rationalized in terms of changes in both BIL and DL SFG signatures.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...