Dispersion-controlled docking preference: multi-spectroscopic study on complexes of dibenzofuran with alcohols and water

Abstract

The structural preferences within a series of dibenzofuran–solvent complexes have been investigated by electronic, vibrational, and rotational spectroscopic methods probing supersonic jet expansions. The experimental study is accompanied by a detailed theoretical analysis including dispersion-corrected density functional theory, symmetry adapted perturbation theory, as well as coupled cluster approaches. The complementary, multi-spectroscopic results reveal a preferred OH⋯O structure for the smallest complex of dibenzofuran–water, whereas for the methanol complex an OH⋯π isomer is simultaneously observed. For the largest complex, dibenzofuran–tert-butyl alcohol, only a π-bound structure is found. These comprehensive investigations show that a completely inverse trend regarding the docking preference is observed by comparing the present results with the ones for analogous diphenyl ether complexes. This can be rationalized on the basis of the planarity/non-planarity and rigidity/flexibility of the different systems, providing valuable insight into the interplay between different non-covalent interactions. This analysis is a further step towards a quantitative description of very delicate energetic balances with the overall goal of yielding reliable structural predictions for non-covalently bound systems.

---

1 Introduction

Non-covalent attraction plays a key role in molecular recognition and aggregation, which can be fundamental for governing (bio)chemical processes.^1–4 Already small changes within the interplay of intermolecular forces can affect these processes significantly. London dispersion is one of the major attractive contributors, along with ambivalent Keesom and always attractive Debye forces. These forces may compete with or reinforce each other, and most importantly they are balanced by Pauli repulsion at a short distance. London dispersion is particularly able to control the formation of a certain molecular arrangement in anisotropic systems due to its cumulative, non-local nature in contrast to the very local Pauli repulsion.^5,6

The structures of neutral, non-covalently bound molecular complexes involving aromatic moieties and water or alcohol molecules have been extensively studied in the gas phase (see e.g.ref. 7–9 and references therein). Among these studies, several complexes involving heteroaromatic moieties are found including works on indole–water,¹⁰ 7-azaindole–water,¹¹ pyrrole–¹² and carbazole–solvent complexes.^13,14 Moreover, several studies on furan derivatives were carried out, including a comparative FTIR jet and theoretical study on 2,5-dimethylfuran– as well as the 2,3-benzofuran–methanol complexes.¹⁵ The latter have additionally been studied by laser induced fluorescence and IR fluorescence dip spectroscopy, including the respective water complexes.¹⁶ For the 2,5-dimethylfuran–methanol complex, the OH⋯O binding motif was identified as the preferred structure, which exhibits additional CH⋯π stabilization by the interaction of the methyl group with the π-cloud. The OH⋯π-bound isomer was also observed as a slightly less stable structure, although it turned out to cause a stronger OH stretching red-shift than the OH⋯O-bound structure, i.e. the π-cloud causes a stronger distortion of the OH bond than the lone pairs of the ether oxygen. In the case of 2,3-benzofuran–water,¹⁶ a balanced situation was found with the coexisting, nearly isoenergetic OH⋯O and OH⋯π isomers. Within that study, no preferred site could be identified, which agrees with the theoretical predictions of less than 0.5 kJ mol⁻¹ energy difference for the applied methods.¹⁶ However, the methanol complex of 2,3-benzofuran was found to prefer the π-docking site over the oxygen, which was clearly identified by linear FTIR jet spectroscopy.¹⁵ In this case, the π-bound structure exhibits a larger OH stretching red-shift than the OH⋯O structure, whereas theoretical predictions were ambiguous. The competing binding motifs in 2-methylfuran– and furan–methanol complexes are currently being examined in an experimental benchmarking study, with initial FTIR results already published,¹⁷ and a refined analysis with microwave support in preparation.

Several spectroscopic studies on dibenzofuran (DBF) have been performed in the condensed phase^18–23 and in the gas phase,^23–30 including works on the DBF dimer^27,28,31 and mixed dimers of DBF with fluorene and benzofuran.^28,32,33 Auty et al.²⁴ recorded fluorescence excitation spectra of DBF and the DBF–water complex. They assumed that the complex is hydrogen-bonded to the oxygen atom of DBF based on the spectral shift of the fluorescence excitation bands. However, there is a lack of ab initio calculations supporting this assumption as well as further, structurally more sensitive spectroscopic experiments.

In previous studies, we established a multi-spectroscopic approach in order to elucidate the preferred binding sites in different aromatic ether–alcohol and –water complexes.^34–38 Within the series of diphenyl ether (DPE) complexes, we have shown that water and small alcohol molecules prefer the π-docking site, whereas larger alcohols preferably bind to the ether oxygen atom. This observation contradicts the intuitive expectation of a preferred π docking, when the size of the alcohol increases. In that study, the respective contribution of London dispersion to the interaction energy for the different complexes was analyzed in order to explain the observed trend. In addition to that, the distortion of the DPE structure, caused by a twist of the phenyl rings upon aggregation of alcohol or water molecules, was identified as another major aspect influencing the trend.

In order to gain a deeper understanding of the influence of structural deformation upon complex formation, a systematic change in the structure of the ether is valuable. One possible change is the direct connection of the two phenyl rings of DPE, which leads to dibenzofuran (DBF). By doing so, the initial flexibility of DPE is entirely disabled since DBF is planar and rigid. Considering the fact that the π system is delocalized over both phenyl rings via the furan ring, the molecule is expected to remain planar upon solvent aggregation in order to maximize aromaticity. Therefore, there is no deformation of the ether geometry within the solvent complexes that might influence the binding preference, contrary to the case of DPE complexes in which deformation plays a substantial role.³⁷ Moreover, the twisted structure of DPE was shown to enable CH⋯O contacts between ortho CH moieties and the oxygen atom of the alcohol or water molecule. This had a significant influence on the structural preference as well. Since for DBF only in-plane CH groups are available for CH⋯O contacts, structures mainly interacting via the π-cloud should not be affected by CH⋯O contacts. Whatever the relative importance of such qualitative concepts may be, they add up to a computable and experimentally verifiable energy difference between competing solvent docking sites.

Experimental verification of predicted structural preferences of such molecular complexes requires studies on a molecular level, where the isolated molecular aggregates can be investigated without the influence of any environment. These conditions can be fulfilled by molecular beam investigations, allowing the formation of molecular complexes and clusters in a supersonic expansion. A variety of spectroscopic methods can be combined with molecular beam experiments, including FTIR spectroscopy,^15,34,35,38 mass- and isomer-selective IR/UV laser spectroscopy (IR/R2PI^8,39–42) and chirped-pulse Fourier transform microwave (CP-FTMW^43–45) spectroscopy. The combination of these different spectroscopic techniques yields complementary results, providing valuable experimental data ideally suited for benchmarking theoretical approaches.

In the present paper, we investigate a series of DBF complexes with water, methanol and tert-butyl alcohol (ROH with R = H, Me, t-Bu) by a multi-spectroscopic strategy, including FTIR, IR/UV and CP-FTMW spectroscopy. The experimental study is accompanied by a detailed theoretical analysis including dispersion-corrected density functional theory as well as wave function-based methods.

2 Experimental methods

2.1 FTIR spectroscopy

Linear FTIR spectra were recorded using the ‘popcorn’ jet set-up. DBF (alfa aesar, ≥99%) was deposited on molecular sieve and exposed to carrier gas pulses in a heatable sample compartment enclosed by two poppet valves (opening at 70 mbar differential pressure upstream and either 690 or 350 mbar downstream). Helium was used as the carrier gas at 1.5 bar. A gas pulse from a 0.069 m³ reservoir picked up the sample and was supersonically expanded into a 3.6 m³ buffer volume. A sufficiently low background pressure is ensured by a pumping system operating at 500 m³ h⁻¹. Two nozzle variants were applied: a 2 × 10 × 0.5 mm double-slit nozzle and a newly designed 60 × 0.2 mm heatable ‘V-nozzle’, which is angled (162°) to approximately fit the focused IR beam shape. The alcohols (MeOH (Sigma Aldrich, ≥99.8%), MeOD (eurisotop, 99% D), t-BuOH (Roth, ≥99%)) were introduced upstream of the gas reservoir by a coolable saturator or by using premixed gas bottles. Each gas pulse was probed by a single synchronized scan of a Bruker IFS 66v/S FTIR spectrometer. 100–400 scans were averaged to obtain the final spectrum. More details can be found in ref. 34 and 46.

2.2 IR/UV spectroscopy

The experimental set-up for the combined IR/UV experiments is described in detail elsewhere,^42,47 thus only a brief description is given here. The experiments were carried out in a molecular beam apparatus consisting of a differentially pumped linear time-of-flight (TOF) mass spectrometer with a pulsed valve (Series 9 with pulse driver Iota One, General Valve, 500 μm orifice) for skimmed jet expansion. DBF was purchased from Merck (≥97.0%). MeOH (Sigma-Aldrich, ≥99.7%) and t-BuOH (Sigma-Aldrich, ≥99.7%) were each supplied via cooled reservoirs and co-expanded with DBF (held at room temperature) using the carrier gas neon (2.5–3.0 bar).

For the R2PI and IR/R2PI experiments, two tunable nanosecond laser systems were necessary, including one independent UV laser system and one IR laser system. The UV laser radiation is obtained via second harmonic generation in a BBO crystal using the output of a dye laser (Cobra-Stretch, Sirah). The latter is pumped by the second harmonic (532 nm) of a Nd:YAG laser (SpitLight 600, Innolas). The IR laser radiation in the range of 3520–3750 cm⁻¹ is generated by difference frequency mixing (DFM) in a LiNbO₃ crystal using the fundamental (1064 nm) of a Nd:YAG laser (Quanta-Ray Pro-230, Spectra-Physics) and the output of a second dye laser (PrecisionScan, Sirah), which is pumped by the second harmonic (532 nm) of the same Nd:YAG laser. The resulting IR radiation is amplified in an optical parametric amplification (OPA) process in another LiNbO₃ crystal using the output of the DFM process and the fundamental (1064 nm) of the Nd:YAG laser. For the IR/R2PI spectra, the IR laser was irradiated 50 ns prior to the UV laser.

2.3 CP-FTMW spectroscopy

The rotational spectra of the DBF–ROH complexes were recorded with the Hamburg CP-FTMW spectrometer COMPACT, which is operated between 2–8 GHz.^48,49 DBF (stated purity ≥98%) was purchased from Sigma-Aldrich and used without further purification. The molecules were seeded into a supersonic expansion using a modified pulse nozzle (Parker General Valve, Series 9, 1.1 mm orifice diameter) equipped with a heatable reservoir. DBF was placed into the reservoir close to the valve orifice and heated to 100 °C. The solvent (ROH) was placed in an external reservoir upstream of the valve at a second set of tubing to regulate the amount of carrier gas that was flowed over it and thus to regulate the amount of solvent. For all of the experiments, neon (3 bar backing pressure) was used as a carrier gas to form a supersonic expansion into the vacuum chamber. Additional experiments with helium as a carrier gas (3 bar backing pressure) were performed for DBF–MeOH.

For each gas pulse, the ensemble of molecules was polarized with a series of eight microwave chirps with a 4 μs duration and spanning 2–8 GHz, following the fast-frame approach.⁵⁰ The chirps were generated with an arbitrary waveform generator, amplified by a 300 W travelling wave tube amplifier, and transmitted into the vacuum chamber with a horn antenna. Following each excitation chirp, 40 μs of the free induction decay (FID) of the macroscopic ensemble of polarized molecules was recorded, yielding a frequency resolution of 25 kHz. For the experiments, a total of 5 million averages (for DBF–H₂O) and 2 million averages (for DBF–MeOH and DBF–t-BuOH, respectively) were co-added and Fourier transformed with a Kaiser–Bessel window function to give the broadband rotational spectrum in the frequency domain.

All spectra were first fit to an asymmetric rotor Hamiltonian using the JB95 program.⁵¹ The transition frequencies were then refined using the AABS program suite, and the final asymmetric rotor Hamiltonian fits were completed with SPFIT.⁵² Line lists for all three dimers are provided in the ESI.† An analysis of the observed tunneling splitting arising from internal rotation of the methanol methyl group in the dibenzofuran–methanol complex was performed using the XIAM program.⁵³ XIAM is a least squares fitting program specifically designed for analyzing spectra of molecules exhibiting internal rotors by employing the combined axis method of Woods to account for internal rotation through a potential barrier.

3 Computational methods

Input structures were manually constructed with Avogadro⁵⁴ using the MMFF94s force field⁵⁵ for pre-optimization, whereas additional geometries were generated by the simulated annealing conformational search implemented in the GFN-xTB⁵⁶ program (option -siman). Geometry optimizations and harmonic vibrational frequency calculations were performed at the DFT as well as the SCS-CC2⁵⁷ level.

For the DFT calculations, the B3LYP functional^58–60 including the D3 dispersion correction⁶¹ with Becke–Johnson (BJ) damping⁶² was used with the basis sets def2-TZVP,⁶³ def2-QZVP⁶³ and aug-cc-pVTZ⁶⁴ (identical auxiliary basis sets for the RI approximation), while using the Berny optimization algorithm from Gaussian 09⁶⁵ combined with energies and gradients calculated with Turbomole 7.3.^66,67 Similarly, calculations were performed with the M06-2X functional⁶⁸ including the D3 correction and the def2-TZVP basis set.

The SCS-CC2 calculations were carried out with the aug-cc-pVDZ⁶⁴ and def2-TZVP basis sets using Turbomole 7.3, while correspondingly aug-cc-pVDZ-cbas⁶⁹ and def2-TZVP-cbas⁶⁹ were chosen as the auxiliary Coulomb fitting basis sets (cbas) required by the ricc2 module for the RI approximation. Harmonic vibrational frequencies at the SCS-CC2 level were calculated with the NumForce script of Turbomole 7.3.

All geometries were confirmed to be minima with only real harmonic vibrational frequencies. All DFT and SCS-CC2 energies were corrected for the basis set superposition error (BSSE) by applying the counterpoise correction method.⁷⁰

DLPNO-CCSD(T) single-point calculations for the B3LYP-D3(BJ)/aug-cc-pVTZ geometries were carried out with ORCA 4.0.1⁷¹ using the cc-pVTZ and cc-pVQZ basis sets⁶⁴ with corresponding cc-pVTZ/C and cc-pVQZ auxiliary basis sets⁶⁹ for the RI approximation. Additionally, the “TightPNO”⁷² and “TightSCF” options were applied. For comparison of zero-point-vibrational-energy (ZPE)-corrected energies, harmonic ZPE corrections obtained at the B3LYP-D3(BJ)/aug-cc-pVTZ level were added to the DLPNO-CCSD(T)/cc-pVTZ and DLPNO-CCSD(T)/cc-pVQZ energies. Furthermore, a local energy decomposition (LED) scheme^73,74 was applied within the DLPNO-CCSD(T)/cc-pVQZ calculations. This was mainly used for extracting physically meaningful dispersion contributions to the total interaction energies. For comparison, second order SAPT(0) calculations⁷⁵ were carried out with the truncated jun-cc-pVDZ basis set,^64,76,77 using the PSI4 program.⁷⁸

Transition state calculations were performed with the QST3⁷⁹ module of Gaussian 09 (B3LYP-D3(BJ)/def2-TZVP) with initial transition state and barrier guesses from the woelfling⁸⁰ module of Turbomole 7.3 as well as the reaction path finder of the GFN-xTB program (option -path).

4 Results and discussion

4.1 Theoretical results

Fig. 1 shows the optimized minimum structures for DBF complexes with H₂O, MeOH and t-BuOH at the B3LYP-D3(BJ)/def2-TZVP level. The oxygen-bound structure, denoted as OH⋯Op (in the DBF plane), of the DBF–H₂O complex is further stabilized by a CH⋯O interaction, which is reflected in a slight tilt of the water with its oxygen atom towards the C–H group that is in close proximity. Within the structure of the OH⋯π5 isomer, the water molecule is positioned above the furan C–C bond connecting the two phenyl rings, whereas in the OH⋯π6 isomer the water molecule is positioned above the center of one of the six-membered phenyl rings. Upon comparing all three isomers it can be seen that there are two intermolecular contacts within each arrangement: one OH⋯O hydrogen bond along with a CH⋯O contact in OH⋯Op, and two OH⋯π contacts respectively in both OH⋯π isomers. Considering the calculated relative energies obtained at different levels of theory (see Table 1), the OH⋯Op isomer is mostly preferred. This suggests that the OH⋯O hydrogen bond combined with the CH⋯O contact outweighs the sum of two OH⋯π contacts in terms of the strength of the intermolecular interaction.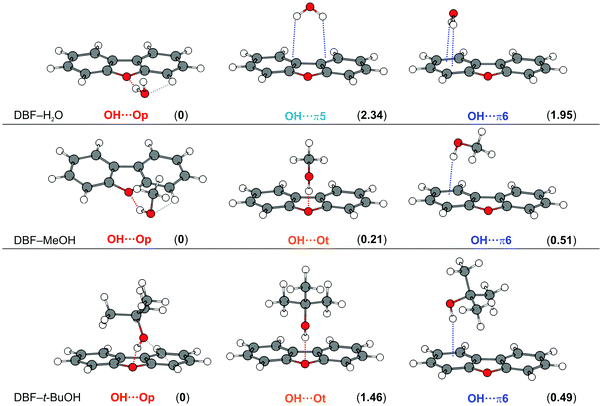

Fig. 1 Optimized minimum structures at the B3LYP-D3(BJ)/def2-TZVP level for DBF–ROH complexes (R = H, Me, t-Bu). Values in parentheses represent relative, ZPE-corrected energies in kJ mol⁻¹ obtained at the DLPNO-CCSD(T)/cc-pVQZ level with ZPE from B3LYP-D3(BJ)/aug-cc-pVTZ calculations (see Table 1). Dashed lines qualitatively indicate different intermolecular contacts.

Table 1 Relative energies for DBF–ROH complexes with (ΔE₀) and without ZPE correction (ΔE) obtained at different levels of theory. All values are given in kJ mol⁻¹ and include BSSE correction

	Isomer	B3LYP-D3(BJ)/def2-TZVP		B3LYP-D3(BJ)/aug-cc-pVTZ		SCS-CC2/def2-TZVP		DLPNO-CCSD(T)/cc-pVQZ^a
		ΔE	ΔE0	ΔE	ΔE0	ΔE	ΔE0	ΔE	ΔE0^b
a Geometries were used from B3LYP-D3(BJ)/aug-cc-pVTZ calculations. b Harmonic ZPE correction obtained from B3LYP-D3(BJ)/aug-cc-pVTZ calculations.
H2O	OH⋯Op	0	0	0	0	0	1.58	0	0
	OH⋯π5	2.42	1.18	2.92	1.88	0.58	0	3.38	2.34
	OH⋯π6	3.79	1.47	3.87	2.02	—	—	3.80	1.95
MeOH	OH⋯Op	0	0.57	0.39	1.06	1.62	3.63	0	0
	OH⋯Ot	1.33	0.96	0	0.05	0.88	1.88	0.85	0.21
	OH⋯π6	1.22	0	0.03	0	0	0	1.21	0.51
t-BuOH	OH⋯Op	1.66	1.57	0	0.21	0.60	1.38	0	0
	OH⋯Ot	0	0	0.16	0.84	0.64	0.85	0.98	1.46
	OH⋯π6	2.35	1.29	0.78	0	0	0	1.48	0.49

---

In order to analyze the respective contributions to the interaction energy of the investigated complexes, SAPT(0)/jun-cc-pVDZ calculations were performed (see Table S1, ESI†) as well as more sophisticated DLPNO-CCSD(T)/cc-pVQZ calculations for which a local energy decomposition (LED) scheme was applied (see Table S2, ESI†). As expected, both approaches yield a larger dispersion contribution in the OH⋯π motifs and significantly more electrostatic contribution for the OH⋯Op structure. This supports the finding that the OH⋯O hydrogen bond, dominated by electrostatics (see Table S1, ESI†), combined with the CH⋯O contact leads to a stronger stabilization than the two OH⋯π contacts within the other isomers.

For the DBF–MeOH complex, the calculated minimum structures at the B3LYP-D3(BJ)/def2-TZVP level are depicted in the second row of Fig. 1. In this case, two oxygen-bound isomers are found: within the C_s-symmetric OH⋯Ot isomer (on top), the methyl group of the methanol molecule is positioned above the furan ring, enabling CH⋯π interactions. The second oxygen-bound structure is denoted as OH⋯Op and exhibits an OH⋯O hydrogen bond in the DBF plane with the methyl group pointing away from the DBF plane. Therefore, the OH⋯Op isomer lacks CH⋯π interactions in contrast to the OH⋯Ot arrangement. However, the in-plane hydrogen bond allows for a stabilizing CH⋯O contact between the MeOH oxygen atom and a CH group of DBF (see Fig. 1), similar to the OH⋯Op isomer of DBF–H₂O. The OH⋯π6 isomer is bound via an OH⋯π contact, and it is stabilized by CH⋯π interactions of the methyl group with the π-cloud. In contrast to the related systems 2,5-dimethylfuran–MeOH and 2,3-benzofuran–MeOH,^15,16 no minimum structure is found with an OH⋯π interaction involving the five-membered furan ring. This might allow for the conclusion that within the extended π system of DBF, the six-membered benzene rings are better hydrogen bond acceptors than the furan moiety. As discussed in previous works on 2-methylfuran, 2,5-dimethylfuran, and 2,3-benzofuran,^15–17 the furan oxygen acceptor site loses attractiveness upon the introduction of methyl groups or one phenyl moiety.

Analyzing the different energy contributions shows that the largest dispersion contribution is in the OH⋯π6 isomer, followed by the symmetric OH⋯Ot structure (see Tables S1 and S2, ESI†). Both arrangements contain CH⋯π stabilization. Accordingly, the dispersion contribution is significantly lower in OH⋯Op, and the structure is clearly dominated by the electrostatic contribution. The large difference in E_elst between the two OH⋯O structures might be explained by the almost coplanar arrangement of the hydrogen bond and the DBF plane in OH⋯Op in contrast to the clearly bent arrangement in OH⋯Ot.

In the latter case, this arrangement obviously reduces the electrostatic stabilization, while it simultaneously increases dispersion stabilization from CH⋯π interactions. Note that the OH⋯O hydrogen bonding angle itself is nearly identical in both structures (155°, Table S3, ESI†), indicating a clearly weakened hydrogen bond as it largely deviates from an ideal linear hydrogen bond. This significantly affects the OH stretching frequencies, which will be discussed in the Experimental results section.

The optimized minimum structures for the t-BuOH complex are shown in the last row of Fig. 1. Similar to the methanol complex, two OH⋯O structures and one OH⋯π arrangement are found as minimum geometries. The OH⋯Ot isomer is C_s-symmetric, identical to the OH⋯Ot isomer of the corresponding MeOH complex. The t-Bu moiety is positioned on top of the furan ring leading to CH⋯π interactions with the π-cloud. In contrast to the analogous MeOH complex, the hydrogen bond is less bent (177° for t-BuOH vs. 155° for MeOH, B3LYP-D3(BJ)/def2-TZVP level, see Table S3, ESI†).

In the OH⋯Op isomer, the t-BuOH moiety is tilted to one side, which indicates a slight CH⋯O interaction between the alcohol oxygen atom and a neighboring CH group, resembling a somehow distorted version of the OH⋯Op isomer of DBF–MeOH with the alcohol being located rather above the π plane due to stronger CH⋯π interactions. Comparing all non-C_s-symmetric OH⋯Op structures, the solvent molecule increasingly approaches the π-cloud above the DBF plane going from water to t-BuOH. In the respective OH⋯π6-bound isomer, the t-Bu moiety is in closer proximity to the DBF π-cloud, resulting in a larger interaction surface for CH⋯π interactions compared to the OH⋯Op isomer. However, CH⋯π interactions should be of similar magnitude in the OH⋯π and the C_s-symmetric OH⋯Ot isomer. This is in line with dispersion contributions obtained at the SAPT(0)/jun-cc-pVDZ and the DLPNO-CCSD(T)/cc-pVQZ levels, which are similar for the two isomers, but clearly smaller for the OH⋯Op isomer. As a hydrogen bond interaction is indicated by the OH stretching red-shift, calculated OH stretching frequencies can be compared for the competing structures. Calculations at the B3LYP-D3 level suggest a stronger OH⋯O hydrogen bond compared to OH⋯π. However, the contrary is predicted at the M06-2X/def2-TZVP and SCS-CC2 levels, indicating a stronger OH⋯π acceptor compared to OH⋯Ot. This aspect will be discussed later in the Experimental results section.

The calculated relative energies for all DBF–ROH complexes at different levels of theory are found in Table 1. The values for the B3LYP-D3(BJ) and SCS-CC2 levels result from geometry optimizations and harmonic frequency calculations, whereas single point calculations were performed at the DLPNO-CCSD(T)/cc-pVQZ level using the geometries obtained at the B3LYP-D3(BJ)/aug-cc-pVTZ level. No anharmonic treatments of the ZPE were used, as anharmonic corrections are expected to be small (assumed to be on the order of <0.5 kJ mol⁻¹), and they have furthermore proven to perform non-systematically in relative energy predictions for similar systems.¹⁷ As shown in previous studies¹⁵ the structures with a rather localized OH⋯O hydrogen bond contain more ZPE than OH⋯π-bound structures. This is reflected in a consistent OH⋯Op destabilization on the order of 0.7–2.3 kJ mol⁻¹ with respect to OH⋯π isomers when electronic (ΔE) and ZPE-corrected energies (ΔE₀) are compared.

For the water complex, the prediction of the energetic order is almost uniform: the OH⋯Op structure is preferred by 0.6 up to 3.4 kJ mol⁻¹, depending on the theoretical level and basis set. The highest applied level suggests the oxygen site to be preferred by about 2 kJ mol⁻¹, which might raise questions about the population of a π-bound structure in molecular beam experiments unless major isomerization barriers prevent relaxation. The SCS-CC2 and M06-2X/def2-TZVP calculations (see Table S4, ESI†) prefer the OH⋯π5 structure. Regarding the DBF–MeOH complex, a rather undecided situation is found with an oscillation of the energetic order between an OH⋯π6, OH⋯Op and even OH⋯Ot preference. The ZPE destabilization of the oxygen-bound structures compared to the OH⋯π6 structure is even more relevant than in the case of water, since it switches the energetic order from a preferred OH⋯O isomer for pure electronic energies towards OH⋯π6 upon ZPE correction for B3LYP-D3(BJ)/def2-TZVP calculations. The most sophisticated theoretical approach at the DLPNO-CCSD(T)/cc-pVQZ level suggests an advantage for OH⋯Op of about 0.5 kJ mol⁻¹ over OH⋯π6 and 0.2 kJ mol⁻¹ over OH⋯Ot, whereas the B3LYP-D3(BJ)/aug-cc-pVTZ calculations even predict the OH⋯Ot and OH⋯π6 isomer to be isoenergetic (within 0.05 kJ mol⁻¹) upon ZPE correction (see Table 1). Considering the energetic range of 0.5 kJ mol⁻¹ for all three binding motifs obtained at the DLPNO-CCSD(T)/cc-pVQZ level – being certainly within the error bar of the method – would not exclude the presence of more than one isomer in molecular beam experiments. In the case of DBF–t-BuOH, the predicted binding preference is undecided as well among the different applied computational approaches: the symmetric OH⋯Ot isomer is preferred at the B3LYP-D3(BJ)/def2-TZVP level, whereas the larger aug-cc-pVTZ basis leads to an OH⋯π6 preference, together with the SCS-CC2 approach. Finally, the DLPNO-CCSD(T) approach favors the OH⋯Op structure by 0.5 kJ mol⁻¹ over OH⋯π6. Overall, the relative ZPE-corrected energies of all three binding motifs are predicted to be within a range of 1.6 kJ mol⁻¹. Thus, the simultaneous presence of more than one isomer cannot be excluded within supersonic jet experiments.

In order to elucidate the aspect of possibly co-existing isomers, being relevant for all investigated DBF–ROH complexes, the analysis of interconversion barriers can be helpful, aside from considering only the relative energies of the isomers. Therefore, transition state calculations were performed with the QST3 method as well as the woelfling module based on transition state guesses from the GFN-xTB method. The obtained interconversion barriers and transition state structures are shown in Fig. S1 (ESI†). In the case of the water complex, the calculated barrier of less than 1 kJ mol⁻¹ between the two π-bound isomers OH⋯π5 and OH⋯π6 suggests that interconversion occurs under the supersonic expansion conditions. However, barriers of about 5 kJ mol⁻¹ between the π-bound structures and the OH⋯Op isomer might allow a kinetic trapping of oxygen- and π-bound isomers, respectively, in the case where they are both initially populated.

For the MeOH complex, a low barrier of about 1 kJ mol⁻¹ is predicted between the two oxygen-bound isomers OH⋯Ot and OH⋯Op, suggesting that interconversion occurs under the experimental conditions. Similar to the water complex, the isomerization barriers between OH⋯O and OH⋯π binding motifs are larger than the ones between the same binding motifs, yet they are slightly lower than that for DBF–H₂O at about 3 kJ mol⁻¹. Nevertheless, kinetic trapping of the respective lower energy isomer can be expected, in the case where more than one isomer is initially populated. Furthermore, the TS calculations suggest that the interconversion of the OH⋯Op structure into the OH⋯π6 isomer involves the C_s-symmetric OH⋯Ot structure as an intermediate state.

Regarding the tert-butyl alcohol complex, the barrier between the oxygen-bound isomers OH⋯Ot and OH⋯Op is calculated to be <1 kJ mol⁻¹, suggesting interconversion. Similar to the case of DBF–MeOH, the TS calculations suggest that conversion of the OH⋯Op structure into the OH⋯π6 isomer occurs via the intermediate OH⋯Ot arrangement. The predicted isomerization barrier from the OH⋯Ot to the OH⋯π6 isomer is approximately 2 kJ mol⁻¹. Hence, interconversion between the binding motifs should not be excluded as well. A discussion of these aspects with respect to the experimental findings will be continued in the Experimental results section.

For a comparison of theory and experiment, the structurally sensitive OH stretching vibration can serve as a spectroscopic probe to be compared to calculated harmonic OH stretching wavenumbers. In some cases, particularly if two competing structures with the same binding motif are present, the OH stretching vibrations might be indistinguishable. Therefore, the experimental rotational constants obtained from rotational spectroscopy combined with calculated dipole moment components can lead to an unambiguous structural assignment. All calculated values relevant for comparison to the experiments are found in Tables S5, S6 and S9–S11 (ESI†) and are discussed in the Experimental results section. In the end, comparison to the experiments will reveal the individual performance of each theoretical approach.

4.2 Experimental results

4.2.1 DBF–H₂O.
IR/UV results. For all investigated systems, R2PI spectra were recorded, revealing isomer-specific electronic excitation energies of the respective complexes (see Fig. S2, ESI†). Based on these findings, IR/R2PI spectra were measured in the OH-stretching region (3520–3750 cm⁻¹) for different excitation energies of the respective complexes.

The R2PI spectrum of the DBF–H₂O complex reveals a S₁ ← S₀ transition that is blue-shifted by +171 cm⁻¹ compared to the DBF monomer transition (see Fig. S2, ESI†). This is in agreement with the findings of fluorescence excitation spectra.²⁴ No additional, red-shifted transitions with respect to the monomer were detected. The experimentally observed shift of +171 cm⁻¹ is in qualitative agreement with the predicted blue-shift of +174 cm⁻¹ for the OH⋯Op isomer at the SCS-CC2/def2-TZVP level with respect to the DBF monomer transition (see Table S5, ESI†). In contrast, the OH⋯π6 isomer is expected to have a red-shifted S₁ ← S₀ transition compared to the DBF monomer (−138 cm⁻¹; see Table S5, ESI†). Based on these findings, the assumption of an OH⋯O binding motif for the DBF–H₂O complex based on the early non-mass-selective study by Auty et al.²⁴ is confirmed by our mass-selective R2PI experiments combined with predicted S₁ ← S₀ excitation energies at the SCS-CC2/def2-TZVP level. These calculations have proven to yield robust predictions.⁵⁷

In order to obtain additional structural information, the OH stretching vibration is used as a spectroscopic probe for identifying the docking motif of the complex. Therefore, an IR/R2PI spectrum was recorded via the electronic resonance at +171 cm⁻¹, which is shown in Fig. 2 for the mass trace of the DBF–H₂O complex compared to calculated harmonic OH stretching frequencies at the B3LYP-D3(BJ)/def2-TZVP level (additional computational results are found in Table S6, ESI†). The IR/R2PI spectrum obtained for the DBF–H₂O complex (Fig. 2(a)) exhibits two OH stretching vibrations at 3623 and 3734 cm⁻¹ (confirming preliminary observations in ref. 81). Calculations uniformly predict a red-shifted symmetric [small nu, Greek, tilde]_OH of the oxygen-bound structure compared to the π-bound structures. Mainly the symmetric [small nu, Greek, tilde]_OH is sensitive to the docking site, whereas the asymmetric [small nu, Greek, tilde]_OH is less affected. It is noticeable that the relative shifts of the symmetric [small nu, Greek, tilde]_OH between OH⋯O and OH⋯π structures are quite large for the B3LYP-D3(BJ) calculations in contrast to the ones for the M06-2X functional as well as the SCS-CC2 predictions. Upon comparison of symmetric [small nu, Greek, tilde]_OH frequencies to the experiment, the OH⋯O isomer matches better than the OH⋯π isomers for all applied theoretical approaches. In order to find a robust assignment, an additional aspect to be considered is the splitting between symmetric and asymmetric [small nu, Greek, tilde]_OH, which is significantly different for the OH⋯O and OH⋯π motifs (see Table S6, ESI†). The experimental splitting is found to be 111 cm⁻¹, while the calculated splittings range from 105–131 cm⁻¹ for the OH⋯Op isomer and only from 83 to 87 cm⁻¹ for OH⋯π structures. Moreover, the changes of the splitting with respect to the splitting of free water clearly suggest the OH⋯Op isomer to be the observed structure. Note that the splittings obtained from the SCS-CC2 calculations are not considered here, as they are found to be unable to reproduce the frequency splitting of the free water molecule correctly.

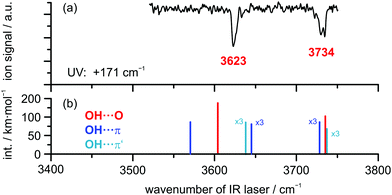Fig. 2 (a) IR/R2PI spectrum of DBF–H₂O obtained via UV excitation at +171 cm⁻¹ compared to calculated OH stretching frequencies (b) at the B3LYP-D3(BJ)/def2-TZVP level; scaling factor: 0.9677.

CP-FTMW results. Rotationally resolved spectroscopy can provide unambiguous proof of the observed clusters (a) via comparison of the experimental rotational constants with the results of quantum chemical calculations and (b) via structure determination using isotopic substitution, either in natural abundance or using enriched samples. The experimental rotational constants for DBF–H₂O obtained from broadband CP-FTMW spectroscopy are summarized in Table 2 together with the results from quantum-chemical calculations. The comparison clearly identifies the observed complex as the OH⋯Op structure, in agreement with the (IR/)R2PI studies, with the rotational constants of the OH⋯π5 isomer being clearly different. Other complexes were not observed under the experimental conditions using neon as a carrier gas. Note that we report an average fit, i.e., fitting the center frequencies of a doublet splitting arising from the internal motion of the water molecule with respect to the DBF moiety. A more detailed analysis of this internal motion is beyond the scope of the present study and will be reported elsewhere. The spectrum is dominated by a- and b-type transitions, while no c-type transitions were observed, which points to averaging due to the internal motion.

Table 2 Molecular rotational parameters of DBF–H₂O: the experimental parameters are based on a fit to an asymmetric rotor Hamiltonian using the JB95 program in comparison to calculated results

Parameters^a	Experiment	B3LYP-D3(BJ)/def2-TZVP	B3LYP-D3(BJ)/def2-TZVP
	OH⋯Op	OH⋯Op	OH⋯π5
a A, B, and C are the experimental rotational constants, ΔJ is the centrifugal distortion constant, and σ is the standard deviation of the fit. b Total number of fitted lines and as distributed over a-, b-, and c-type transitions.
A (MHz)	974.08	973	1339
B (MHz)	575.23	581	479
C (MHz)	362.00	365	447
Δ J (kHz)	0.0334
σ (kHz)	40
N lines (a/b/c)	65(44/21/0)
μ a/μb/μc (D)		1.3/2.2/1.3	1.1/0.2/2.3

---

4.2.2 DBF–MeOH. In contrast to the clear-cut case of DBF–H₂O, where the different experimental and most theoretical methods match nicely in finding a single dominant isomer, a more difficult case is found for DBF–MeOH where the theoretical methods are rather undecided between up to three different structures. Therefore, we include an FTIR study, to provide an overview of the cluster distribution under warmer expansion conditions.
FTIR results. FTIR spectra of the co-expanded DBF–MeOH mixture using the double-slit nozzle are shown in Fig. 3(b). The methanol concentration of 0.15% is chosen such that almost no monomer (3686 cm⁻¹) or homodimer (3575 cm⁻¹) are visible. A distinct band at 3594 cm⁻¹ is observed, but the red-shift upon complexation seems too large to be associated with a heterodimer. Indeed, when comparing to the previously measured spectrum of 2,3-benzofuran–MeOH¹⁵ (Fig. 3(a)) this band lies within the region of larger clusters. Taking the strong cohesion and excess of DBF into account, a trimer including one methanol and two DBF molecules is the most probable assignment. Further discussion on this trimer can be found in the ESI.† Searching for spectral features in proximity to the dimer bands of 2,3-benzofuran–MeOH, two peaks might be located at 3639 and 3646 cm⁻¹, hardly distinguishable from the noise level. In an attempt to alter the expansion conditions to form more mixed dimers, spectrum (c) was recorded. The methanol concentration was increased about two-fold, while the DBF concentration was slightly decreased. However, the major changes were the use of a newly developed V-nozzle, which nominally enhances the absorption path by a factor of about 6, and a simultaneous lowering of the differential opening pressure of the second check valve to 350 mbar. A small and broad spectral feature was observed between 3636 and 3650 cm⁻¹, which supports a dimer origin of the weak bands at 3639 and 3646 cm⁻¹. A further increase of the methanol concentration (spectrum (d) in Fig. 3) did not seem to enhance the dimer abundance any further. Given the weakness and broadness of these bands, only a vague assignment to a specific isomer could be made, but on comparing the dimer band positions of 2,3-benzofuran–MeOH, it is plausible that two dimers are observed due to an OH⋯π isomer further red-shifted than an OH⋯O isomer. The peak intensity of the further red-shifted isomer is at best two-fold higher, but given the lower predicted IR intensity of OH⋯π isomers, the actual excess in abundance may be larger, even in the weakly relaxing helium expansion employed. This tentative assignment called for confirmation by complementary spectroscopic methods.

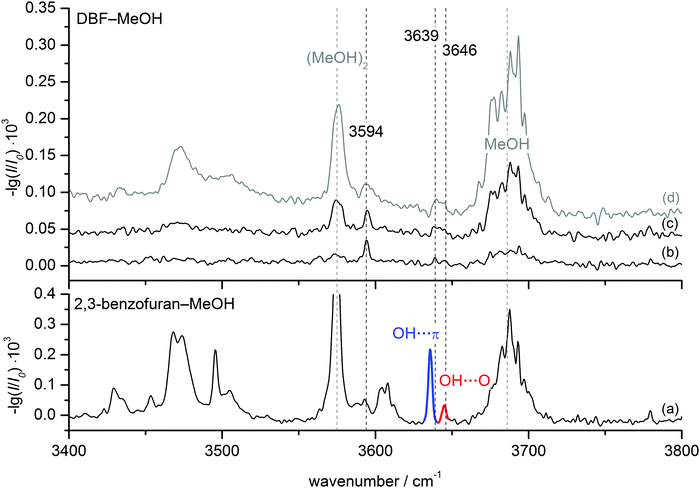Fig. 3 FTIR spectra of DBF–MeOH (b–d) in comparison to 2,3-benzofuran–MeOH (a) taken from ref. 15. Spectrum (b) was measured using the double-slit nozzle (0.15% MeOH, T(DBF) = 120 °C), spectra (c) and (d) using the V-nozzle introducing MeOH via the saturator at temperatures of T(MeOH) = −25 °C (≈0.3%) and T(MeOH) = −10 °C (≈1%), respectively. The DBF concentration is slightly decreased in these spectra (T(DBF) = 110 °C).

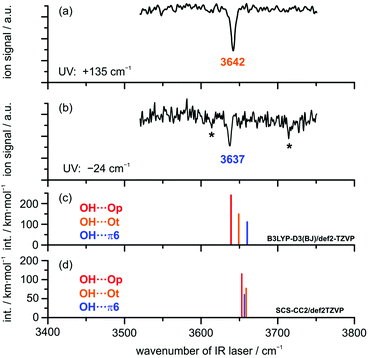
IR/UV results. IR/UV spectroscopy provides additional mass- and isomer-selective insight in addition to the results obtained from the FTIR investigations. The IR/UV experiments on the DBF–MeOH complex revealed the presence of two different isomers with distinct electronic resonances at +135 cm⁻¹ and −24 cm⁻¹ with respect to the DBF monomer transition observed in the R2PI spectrum (see Fig. S2, ESI†; further transitions yield the same IR/R2PI spectra, thus no third isomer is found). The electronic excitation spectrum itself contains valuable information: a comparison to calculated S₁ ← S₀ excitation energies at the SCS-CC2/def2-TZVP level suggests that the blue-shifted transition arises from the OH⋯Ot isomer with a qualitatively matching predicted shift of +126 cm⁻¹. The slightly red-shifted transition observed at −24 cm⁻¹ is in qualitative agreement with the predicted shift for the OH⋯π6 isomer (−245 cm⁻¹). The recorded IR/R2PI spectra via the electronic resonances at +135 cm⁻¹ and −24 cm⁻¹ are depicted in Fig. 4. The spectrum shown in the upper trace (a) exhibits one OH stretching vibration at 3642 cm⁻¹. The spectrum for the second isomer in trace (b) reveals a slightly red-shifted transition at 3637 cm⁻¹.

Fig. 4 IR/R2PI spectra of DBF–MeOH via UV excitations (a) of +135 cm⁻¹ and (b) −24 cm⁻¹ compared to calculated OH stretching frequencies for OH⋯O and OH⋯π isomers (c) at the B3LYP-D3(BJ)/def2-TZVP level and (d) at the SCS-CC2/def2-TZVP level; scaling factors: (c) 0.9674 and (d) 0.9684 derived from reference calculations for MeOH, respectively. Transitions marked with an asterisk result from fragmentation of larger clusters.

The two additional features marked with an asterisk (*) originate from ionization-induced fragmentation of a mixed DBF–MeOH–H₂O cluster (see Fig. S3, ESI†). Given the overlap situation in the FTIR experiment and its relatively high nozzle temperature, as well as the different carrier gas, the wavenumber agreement between the two IR experiments is satisfactory. The observed isomer splitting of 5 cm⁻¹ is probably more reliable than the 7 cm⁻¹ deduced from the FTIR spectrum.

The relative order of calculated OH stretching wavenumbers for the different OH⋯O and OH⋯π structures turns out to be ambiguous: DFT calculations using the B3LYP-D3(BJ) functional predict a red-shifted OH stretch for both OH⋯O-bound structures compared to the OH⋯π6 isomer. Interestingly, calculations at the SCS-CC2 level suggest a switch of the order: the OH⋯π6 structure is predicted to have a lower OH stretching frequency than the OH⋯O equivalent, which suggests the π-cloud to be the stronger acceptor site. The same is observed for calculations with the functional M06-2X (see Table S6, ESI†). Note, however, that these two methods failed in predicting the correct complex with water.

Given the very small OH stretching frequency differences between the observed species, the prediction of the frequency order for a distinct theoretical method is ambiguous. Finally, based on the clear isomer assignment via the electronic resonances, the OH⋯Ot isomer is found to exhibit the less red-shifted OH stretching vibration compared to the OH⋯π6 isomer. This has been observed for similar systems as well (cf. discussion in the ESI† and ref. 15 and 16).

Drawing conclusions on relative populations from the electronic resonances in the R2PI spectrum is difficult in this specific case, as the R2PI spectrum of the DBF–MeOH mass trace is influenced by very strong resonances of the DBF monomer (for further explanation see Fig. S2, ESI†). Additional structural and abundance insight will be gained by rotational spectroscopy.

CP-FTMW results. In the rotational spectrum of the DBF–MeOH mixture, we observed two DBF–MeOH complexes (see Fig. 5). The experimentally obtained rotational parameters are summarized in Table 3. The rotational constants for the two complexes are clearly different, and the spectra also differ in the type of rotational transitions observed (i.e., only a- and b-type transitions but no c-type transitions for one complex and only b- and c-type transitions but no a-type transitions for the other complex). Such observations provide additional input for assigning the structures. Based on a comparison of the rotational constants and the observed type of transition vs. calculated dipole-moment components (see Table 4), the two structures can be unambiguously assigned to the OH⋯π6 and the OH⋯Ot complexes. Thus, the results also allow us to differentiate between the two OH⋯O bound isomers, OH⋯Ot and OH⋯Op.

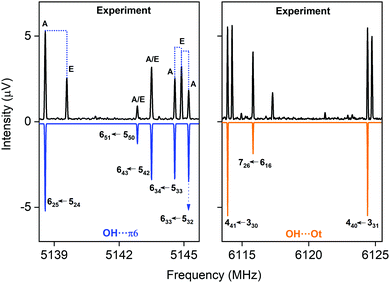Fig. 5 Parts of the CP-FTMW broadband rotational spectrum, indicating the coexistence of the OH⋯π6 and the OH⋯Ot isomer.

Table 3 Molecular parameters of DBF–MeOH: experimental values are based on a fit to an asymmetric rotor Hamiltonian using the AABS software and the XIAM program, respectively. For OH⋯π6, two sets of rotational constants are presented, with and without including the internal rotation of the methyl group (see text)

Parameters^a	OH⋯π6		OH⋯Ot
	Fit 1 A-states	Fit 2 XIAM	Fit 1 A-states
a A, B, and C are the rotational constants, ΔJ, ΔJK, ΔK, δJ and δK are the centrifugal distortion constants, and σ is the standard deviation of the fit. b V 3 is the barrier to internal rotation of the methanol methyl top, F0 is the corresponding rotational constant of the methyl top, and Dpi2J accounts for the internal motion-overall rotation centrifugal distortion, obtained from a global fit of both internal rotational components A and E with the program XIAM. c Total number of fitted lines and as distributed over a-, b-, and c-type transitions.
A (MHz)	987.3953(36)	987.3736(27)	808.91099(33)
B (MHz)	439.33213(28)	439.32995(25)	524.58247(15)
C (MHz)	417.58829(26)	417.58775(21)	375.30332(18)
Δ J (kHz)	0.0529(17)	0.0554(13)	0. 1434(15)
Δ JK (kHz)	0.738(10)	0.7388(82)	1.934(71)
Δ K (kHz)	56.91(80)	56.85(75)	−0. 848(60)
δ J (kHz)	—	—	1.2416(45)
F 0 (cm^−1)	—	159.0	—
V 3 (cm^-1)	—	338.99(89)	—
V 3 (kJ mol^−1)	—	4.055(11)	—
D pi2J (kHz)	—	34.7(2.9)	—
Δ (rad)	—	3.883(13)	—
ε (rad)	—	0.579(23)	—
# A state transitions^c	65 (49/16/0)	65 (49/16/0)	122 (0/94/28)
# E state transitions	—	41 (29/12/0)	—
σ (kHz)	6.9	7.1	7.0

---

Table 4 Theoretical rotational constants for DBF–MeOH obtained at the B3LYP-D3(BJ)/def2-TZVP level of theory

	OH⋯Op	OH⋯Ot	OH⋯π6
A (MHz)	737.4	831.9	1000.3
B (MHz)	515.2	523.1	437.5
C (MHz)	316.9	381.5	418.6
V 3 (kJ mol^−1)	3.8	3.1	5.1
μ a/μb/μc (D)	1.9/1.6/1.3	0.01/3.1/0.5	1.1/1.2/0.2

---

Both complexes show internal rotation splitting due to the internal rotation of the methyl group of the methanol moiety, which results in characteristic doublets for each rotational line. The fact that this internal rotation leads to sizeable splittings and is not locked points to only a loose interaction of the methyl group with DBF. For OH⋯π6, two sets of rotational constants are presented. Fit 1 corresponds to a fit to an asymmetric rotor Hamiltonian including only the A states due to methyl group internal rotation, thus presenting effective rotational constants. Using the program XIAM, these line splittings can be analyzed, resulting in Fit 2. It includes the analysis of the methyl group internal rotation and thus also provides information about the torsional barrier V₃. The V₃ barrier determined from the experimental line splitting into A and E states is V₃(exp) = 4.055(11) kJ mol⁻¹ (Table 3), which is in decent agreement with the calculated barrier of about 5 kJ mol⁻¹ (B3LYP-D3(BJ)/def2-TZVP). For OH⋯Ot, only an A-state fit is presented. An initial global fit including internal rotation via about 20 E-state lines resulted in standard deviations on the order of 100 kHz, potentially pointing to a second internal motion. The obtained rotational parameters of the A-state fit, however, allow a clear identification of the respective isomers.

The wealth of experimental information is thus well suited to identify and further characterize the respective molecules under study and can also be used to benchmark the theoretical models employed. Based on our experimental line intensities, the OH⋯π6 complex is found to be about 10 times stronger than the one for the OH⋯Ot complex. Considering the stronger dipole moment for the OH⋯Ot complex, this points to a clear energetic preference for the OH⋯π6 complex, which is also the global minimum at the B3LYP-D3(BJ)/def2-TZVP, B3LYP-D3(BJ)/aug-cc-pVTZ and the SCS-CC2/def2-TZVP levels. In the case of the B3LYP-D3(BJ)/aug-cc-pVTZ level, OH⋯π6 is nearly isoenergetic with the OH⋯Ot isomer. This finding agrees qualitatively with the FTIR evidence of a higher abundance of the more red-shifted species and the corresponding results for 2,3-benzofuran.¹⁵ It also agrees with the IR/UV experiment, considering the mentioned intensity uncertainty within the R2PI spectra. Interestingly, the third complex, OH⋯Op, was not observed in our microwave study despite intense analysis, even though it is predicted to be the global minimum by the DLPNO-CCSD(T) approach (cf.Table 1). Thus, a low interconversion barrier from the OH⋯Op complex to one or both of the other complexes, OH⋯Ot and OH⋯π6, can be assumed.

4.2.3 DBF–t-BuOH.
FTIR results. The FTIR spectrum of DBF–t-BuOH (see Fig. 6), measured in helium carrier gas with the V-nozzle, shows similar features as DBF–MeOH. The monomer and homodimer bands of tert-butyl alcohol are observed at 3643 cm⁻¹ and 3499 cm⁻¹, respectively. These values are slightly blue-shifted to those reported previously,⁸² which hints at warmer expansion conditions, probably due to the heated nozzle. Fortunately, the proposedly mixed dimer signals are more pronounced than for methanol, revealing one band at 3607 cm⁻¹ with a weak shoulder at 3613 cm⁻¹. Given the similarity of the experimental data, an analogous assignment to the DBF–MeOH clusters is suggestive. Therefore, the band at 3607 cm⁻¹ and the shoulder are tentatively assigned to an OH⋯π and an OH⋯O isomer, respectively. However, without complementary experimental evidence, only a single dominant complex absorbing at 3607 cm⁻¹ can be safely concluded.

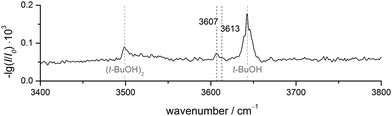Fig. 6 FTIR spectrum of DBF–t-BuOH. The V-nozzle was used and the temperatures set to T(DBF) = 110 °C and T(t-BuOH) = 10 °C.

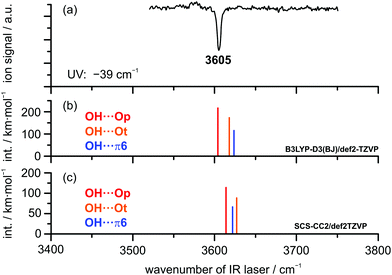
IR/UV results. The IR/UV analysis of the DBF–t-BuOH complex yielded the presence of one single isomer in a conformationally colder neon expansion. Regarding the recorded R2PI spectrum (see Fig. S2, ESI†), containing pronounced vibrational progressions, the observed 0 ← 0 transition for DBF–t-BuOH is red-shifted by −39 cm⁻¹ compared to the DBF monomer. Considering the predicted S₁ ← S₀ transitions, only the OH⋯π6 isomer is found to exhibit a lower S₁ ← S₀ transition than the DBF monomer (−263 cm⁻¹), whereas for the OH⋯O-bound structures blue-shifted excitation energies are predicted (see Table S5, ESI†). Therefore, an assignment of the OH⋯π6 isomer can already be made based on the shift of the electronic origin. Fig. 7 shows the IR/R2PI spectrum obtained via the electronic transition at −39 cm⁻¹ with respect to the DBF monomer transition. It exhibits a single OH stretching vibration at 3605 cm⁻¹. The spectra obtained via all further transitions observed in the R2PI spectrum (see Fig. S2, ESI†) exhibit the same vibrational transition. Therefore, the presence of a second isomer is unlikely (see also the IR_fixed/R2PI spectrum in Fig. S5, ESI†). Based on the aforementioned comparison to calculated electronic excitation energies, the presence of OH⋯O-bound structures would therefore be ruled out. Comparing the recorded IR/R2PI spectrum to the calculated OH stretching frequencies for the different optimized structures does not allow for an unambiguous assignment to one of the isomers. Calculations with the B3LYP-D3(BJ) functional yield a larger OH stretching red-shift for the oxygen-bound structures compared to the OH⋯π isomer (see Fig. 7b and Table S6, ESI†). In contrast, M06-2X/def2-TZVP and SCS-CC2 calculations suggest a stronger red-shift for the OH⋯π6 structure compared to OH⋯Ot and therefore an inverse frequency order compared to B3LYP-D3(BJ) predictions – analogous to the case of DBF–MeOH. According to the B3LYP-D3(BJ) calculations, the OH⋯Op isomer yields the best agreement with the experimentally observed transition. On the other hand, M06-2X/def2-TZVP and SCS-CC2 predictions yield the best match for the OH⋯π6 isomer. Based on the similar findings for DBF–MeOH, an assignment of the OH⋯π6 isomer seems more reasonable, which is however very tentative, since no second isomer is present for comparison of OH stretching vibrations. Additional insight regarding the structural assignment is provided by rotational spectroscopy.

Fig. 7 (a) IR/R2PI spectrum of (a) DBF–t-BuOH via UV excitation at −39 cm⁻¹ compared to calculated OH stretching vibrations (b) at the B3LYP-D3(BJ)/def2-TZVP level (scaling factor 0.9618) and (c) at the SCS-CC2/def2-TZVP level (scaling factor: 0.9686).

As pointed out in the theoretical results section, the isomerization barrier between the OH⋯Op and the OH⋯π structure of the DBF-t-BuOH complex is calculated to be about 2 kJ mol⁻¹, whereas the barrier between OH⋯Ot and OH⋯Op is smaller than 1 kJ mol⁻¹. Since only one isomer is found in the experiment with neon as the carrier gas, it might be concluded that the isomerization barriers are too low for both binding motifs to be stabilized during the supersonic expansion. This would lead to the exclusive population of the global minimum structure in the molecular beam. Comparing the IR/UV and FTIR investigations (see Fig. 6 and 7), the shoulder at 3613 cm⁻¹ exclusively observed in the FTIR spectrum seems to originate either from a less stable DBF–t-BuOH isomer, populated due to different expansion conditions, or from a larger cluster.

CP-FTMW results. The analysis of the broadband rotational spectra for the DBF–t-BuOH mixture also reveals the presence of only one strong spectrum, for which 162 rotational lines, distributed over a-, b-, and c-type transitions, could be identified and fitted to an asymmetric rotor Hamiltonian, with a-type transitions dominating the spectrum (see Fig. 8). The resulting molecular parameters are summarized in Table 5, together with the results from quantum chemical calculations. The widely different rotational constants for the three DBF–t-BuOH complexes allow their identification as the OH⋯π6 isomer, which is stabilized by secondary CH⋯π interactions, in agreement with the IR/UV spectroscopic results. As in the t-BuOH monomer and in other complexes involving t-BuOH, no internal rotation splitting due to internal rotation of the three methyl groups is observed because of the high barrier hindering this motion. The OH⋯π6 structure is predicted to be the global minimum by several quantum chemical methods (including ZPE correction, Table 1). Note the interesting basis set dependence for the dispersion corrected B3LYP-D3(BJ) approach: using the aug-cc-pVTZ basis set, the correct global minimum (after ZPE correction) is predicted, while usage of the def2-TZVP basis set leads to the OH⋯Ot isomer as the energetic minimum structure. The fact that only one species is observed with CP-FTMW and IR/UV spectroscopy employing neon as a carrier gas, while FTIR spectroscopy using helium observes weak evidence for a second isomer gives an indication that the barrier between the OH⋯Ot and OH⋯π6 structures, calculated to be 1.8 kJ mol⁻¹ (Fig. S1, ESI†), is indeed sufficiently low to be overcome in a neon expansion (Fig. 7 and 8).

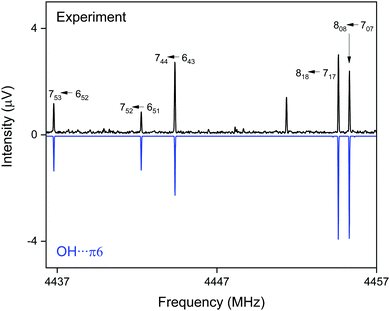Fig. 8 Part of the CP-FTMW broadband rotational spectrum for DBF–t-BuOH, illustrating the presence of the OH⋯π6 isomer.

Table 5 Molecular parameters of DBF–t-BuOH: results of the fit of experimental rotational transitions to an asymmetric rotor Hamiltonian using the AABS software in comparison to the results from density-functional theory calculations (B3LYP-D3(BJ)/def2-TZVP)

Parameters^a	Experiment	B3LYP-D3/def2-TZVP	B3LYP-D3/def2-TZVP	B3LYP-D3/def2-TZVP
	OH⋯π6	OH⋯π6	OH⋯Ot	OH⋯Op
a A, B, and C are the rotational constants, ΔJ, ΔJK, ΔK and δJ are the centrifugal distortion constants, and σ is the standard deviation of the fit. b Total number of fitted lines and as distributed over a-, b-, and c-type transitions.
A (MHz)	513.73023(20)	515	453	473
B (MHz)	351.76117(15)	353	404	376
C (MHz)	269.56523(14)	269	263	246
Δ J (kHz)	0.10324(73)
Δ JK (kHz)	−0.3604(29)
Δ K (kHz)	0.2601(43)
δ J (kHz)	0.03650(54)
σ (kHz)	7.1
N lines (a/b/c)	162 (83/36/43)
μ a/μb/μc (D)		1.3/0.1/0.4	2.2/0/2.0	2.1/0.6/1.7

---

5 Conclusions

A detailed multi-spectroscopic and theoretical analysis on a series of isolated dibenzofuran–alcohol and –water complexes is presented. By combining FTIR, IR/UV and CP-FTMW spectroscopy, the unambiguous assignment of the preferred structures for the respective complexes could be achieved. The most valuable contribution of the FTIR approach, for which DBF complexes are currently at the technological limit, is a survey over the minimum number of relevant complexes under warmer expansion conditions. The IR/UV approach is less limited in molecular size. It provides conformationally resolved IR spectra, and the UV shift from the monomer gives valuable information on the docking position, O vs. π, of the OH group. This is crucial because the spectral shifts between these two docking positions are extremely subtle such that theoretical harmonic predictions remain ambiguous. The CP-FTMW approach provides a firm structural assignment of dominant and also secondary complexes, which goes beyond the O vs. π contact information. It discriminates between O docking geometries, which exploit secondary interactions with either peripheric C–H groups (p) or aromatic π clouds (t) in the planar acceptor molecule. The comparison to theory revealed deficiencies and strengths of different theoretical approaches.

For the DBF–H₂O complex an oxygen bound structure was identified by electronic, vibrational and rotational spectroscopy, building on the early work of Auty et al.²⁴ Despite the prediction of nearly isoenergetic π-bound structures, no second isomer is found. The DLPNO-CCSD(T)/cc-pVQZ method as well as B3LYP-D3(BJ)/aug-cc-pVTZ calculations yield reasonable relative energies that explain the experimental observations. Regarding the methanol complex, two isomers were identified in the molecular beam experiments. The species were identified as the OH⋯π6 isomer and the OH⋯Ot isomer. For the oxygen-bound structure, an interconversion of OH⋯Op to OH⋯Ot is expected due to a low isomerization barrier. Based on the broadband rotational spectroscopic results, the OH⋯π6 isomer is found to be more strongly populated than the OH⋯Ot structure, which is confirmed by the FTIR results and is also reasonable within the uncertainty of the R2PI signal intensities. Nevertheless, within the error of the methods, the predicted relative energies at the DLPNO-CCSD(T)/cc-pVQZ and B3LYP-D3(BJ)/aug-cc-pVTZ level are in agreement with the experimental findings since both theoretical methods indicate two nearly isoenergetic structures. Furthermore, the chosen theoretical approaches largely deviate in predicting OH stretching wavenumbers, which even leads to a switch in the order between the OH stretches of the two docking motifs. This has also been observed for the related 2,5-dimethylfuran–methanol¹⁵ and 2,3-benzofuran–methanol complexes.^15,16 The only approaches that correctly predict a red-shifted OH stretching vibration for the OH⋯π6 isomer compared to OH⋯Ot are the M06-2X functional and calculations at the SCS-CC2 level. This probably indicates a deficiency of the established theoretical approaches including the harmonic approximation, which should be considered in future developments.

The tert-butyl alcohol complex, representing the largest ether–solvent complex in this study, was shown to form only one stable isomer in the molecular beam experiments. Based on a red-shifted S₁ ← S₀ transition, a π-bound structure was identified. Rotational spectroscopy clearly confirmed the observed structure to be the OH⋯π6 isomer.

By comparing all investigated DBF–solvent complexes, we observe a binding preference that switches from oxygen via a balanced situation to the π site when going from small solvent molecules to larger ones (see Fig. 9). This is inverse to the trend that has been observed for the previously studied series of diphenyl ether–solvent complexes. The stabilization due to London dispersion is found to be more pronounced in π-bound structures than in oxygen motifs, indicated by dispersion contributions extracted from both SAPT(0) and DLPNO-CCSD(T) calculations. An exception is found for the t-BuOH complex, where the C_s-symmetric OH⋯Ot and the OH⋯π6 isomers are found to have similar dispersion contributions. We moreover found the influence of CH⋯O contacts on OH⋯Op structures to decrease from the small solvent molecules to the larger ones, while simultaneously enabling stronger CH⋯π interactions in this series. However, their magnitude in the OH⋯O arrangements is always outweighed by the one in the respective OH⋯π structures. Thus, the additional CH⋯O contact leads to preferred oxygen-binding for the smaller solvent molecules, whereas for the larger t-BuOH, London dispersion finally outbalances the CH⋯O-stabilization, leading to preferred π-binding. Regarding relative energies, the overall performance of the B3LYP-D3(BJ)/aug-cc-pVTZ approach is satisfactory and it is, at a first glance surprisingly, even superior to the DLPNO-CCSD(T) approach that seems to slightly underestimate the stability of OH⋯π6 complexes compared to OH⋯Op. Given the fact that the relative energies are mostly below 1 kJ mol⁻¹ and therefore in the order of ZPE corrections, this slight inconsistency might be attributed to the usually less relevant fact that the geometries are not optimized at the DLPNO-CCSD(T) level. Furthermore, neglected anharmonic contributions to the ZPE do not allow for a safe relative ranking of the two electronic structure methods at this subtle level.

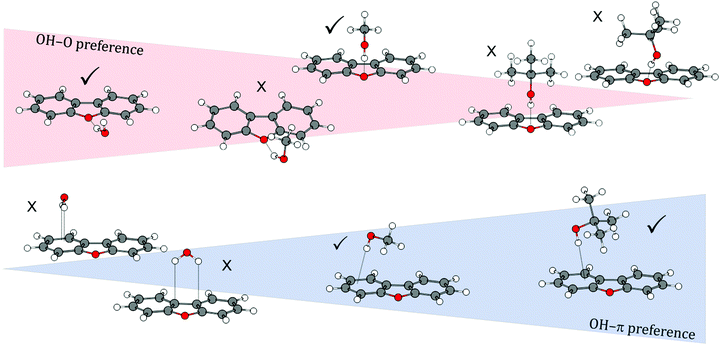Fig. 9 Schematic overview of the transition of binding motif preferences from oxygen-bound to π-bound structures with increasingly larger solvent molecules in DBF–ROH complexes.

Upon comparison to the series of diphenyl ether–solvent complexes³⁷ and also the phenyl vinyl ether–methanol complex,³⁸ the absence of backbone deformation in the DBF complexes proves to be true, as no structures were found involving a non-planar DBF structure, which is not surprising since aromaticity is preserved. The influence of CH⋯O contacts – playing a decisive role in DPE and PVE complexes – partly remains in the DBF–solvent structures as well. However, it is constrained to the oxygen-bound motifs, as the CH moieties of DBF available for CH⋯O contacts are within the DBF plane and therefore not in vicinity to the alcohol oxygen atoms within OH⋯π arrangements. This finally leads to a trend regarding the binding preference that is contrary to the series of DPE–solvent complexes. A further interesting aspect is that the central, five-membered furan moiety in DBF is only a competitive π docking site for the water complex. In the MeOH and t-BuOH complexes, only structures involving the six-membered benzene moieties as π acceptors were observed.

One parameter, namely the rigidity of the aromatic chromophore (DBF vs. DPE), completely changes the preferred binding site within a series of solvent complexes. The big challenge is to quantify the low-temperature abundance by small energy differences between different structures. We succeeded by a comprehensive combination of different experimental and theoretical methods, which finally offers a clear structural assignment. Within the investigated series of DBF–solvent complexes, we found a variable interplay between non-covalent interactions among which London dispersion forces make an important difference in determining the final docking preference.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the Deutsche Forschungsgemeinschaft (DFG, Ge 961/9-2, project number 271505332; Schn 1280/4-2, project number 271359857; Su 121/5-2, project number 271107160) for financial support in the context of the priority program SPP 1807 (Control of London dispersion interactions in molecular chemistry). M. F. acknowledges support from the Hamburg International Max Planck Research School UFAST. This work is part of the PhD theses of D. B., M. F. and A. P.

References

1. J.-M. Lehn, Angew. Chem., Int. Ed. Engl., 1988, 27, 89–112.
2. K. Müller-Dethlefs and P. Hobza, Chem. Rev., 2000, 100, 143–168.
3. E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210–1250.
4. J. Cerný and P. Hobza, Phys. Chem. Chem. Phys., 2007, 9, 5291–5303.
5. S. Rösel, C. Balestrieri and P. R. Schreiner, Chem. Sci., 2017, 8, 405–410.
6. S. Grimme and P. R. Schreiner, Angew. Chem., Int. Ed., 2011, 50, 12639–12642.
7. T. Ebata, A. Fujii and N. Mikami, Int. Rev. Phys. Chem., 1998, 17, 331–361.
8. T. S. Zwier, Annu. Rev. Phys. Chem., 1996, 47, 205–241.
9. B. Brutschy, Chem. Rev., 2000, 100, 3891–3920.
10. J. R. Carney, F. C. Hagemeister and T. S. Zwier, J. Chem. Phys., 1998, 108, 3379–3382.
11. H. Yokoyama, H. Watanabe, T. Omi, S.-I. Ishiuchi and M. Fujii, J. Phys. Chem. A, 2001, 105, 9366–9374.
12. Y. Matsumoto and K. Honma, J. Chem. Phys., 2009, 130, 54311.
13. M. Sakai, K. Daigoku, S.-I. Ishiuchi, M. Saeki, K. Hashimoto and M. Fujii, J. Phys. Chem. A, 2001, 105, 8651–8657.
14. N. A. Borisevich, V. A. Povedailo, E. E. Tselesh and D. L. Yakovlev, J. Appl. Spectrosc., 2007, 74, 838–843.
15. A. Poblotzki, J. Altnöder and M. A. Suhm, Phys. Chem. Chem. Phys., 2016, 18, 27265–27271.
16. H. Sasaki, S. Daicho, Y. Yamada and Y. Nibu, J. Phys. Chem. A, 2013, 117, 3183–3189.
17. H. C. Gottschalk, A. Poblotzki, M. A. Suhm, M. M. Al-Mogren, J. Antony, A. A. Auer, L. Baptista, D. M. Benoit, G. Bistoni, F. Bohle, R. Dahmani, D. Firaha, S. Grimme, A. Hansen, M. E. Harding, M. Hochlaf, C. Holzer, G. Jansen, W. Klopper, W. A. Kopp, L. C. Kröger, K. Leonhard, H. Mouhib, F. Neese, M. N. Pereira, I. S. Ulusoy, A. Wuttke and R. A. Mata, J. Chem. Phys., 2018, 148, 14301.
18. A. Bree, V. V. B. Vilkos and R. Zwarich, J. Mol. Spectrosc., 1973, 48, 124–134.
19. A. Bree, V. V. B. Vilkos and R. Zwarich, J. Mol. Spectrosc., 1973, 48, 135–147.
20. A. Bree, A. R. Lacey, I. G. Ross and R. Zwarich, Chem. Phys. Lett., 1974, 26, 329–333.
21. C. Taliani, A. Bree and R. Zwarich, J. Phys. Chem., 1984, 88, 2357–2360.
22. I. Khasawneh, Talanta, 1988, 35, 267–270.
23. T. D. Klots and W. B. Collier, J. Mol. Spectrosc., 1996, 380, 1–14.
24. A. R. Auty, A. C. Jones and D. Phillips, Chem. Phys. Lett., 1984, 112, 529–533.
25. A. R. Auty, A. C. Jones and D. Phillips, J. Chem. Soc., Faraday Trans. 2, 1986, 82, 1219.
26. C. Weickhardt, R. Zimmermann, U. Boesl and E. W. Schlag, Rapid Commun. Mass Spectrom., 1993, 7, 183–185.
27. T. Chakraborty and E. C. Lim, Chem. Phys. Lett., 1993, 207, 99–104.
28. W. T. Yip and D. H. Levy, J. Phys. Chem., 1996, 100, 11539–11545.
29. M. Baba, K. Mori, M. Yamawaki, K. Akita, M. Ito, S. Kasahara and T. Yamanaka, J. Phys. Chem. A, 2006, 110, 10000–10005.
30. D. Quang Hoa, T. Uchimura, T. Imasaka and N. Dai Hung, Sci. Technol. Adv. Mater., 2016, 7, 714–717.
31. M. Fatima, A. L. Steber, A. Poblotzki, C. Pérez, S. Zinn and M. Schnell, Angew. Chem., 2019, 131, 3140–3145.
32. M. Yamawaki, Y. Tatamitani, A. Doi, S. Kasahara and M. Baba, J. Mol. Spectrosc., 2006, 238, 49–55.
33. J. T. Yi, L. Alvarez-Valtierra and D. W. Pratt, J. Chem. Phys., 2006, 124, 244302.
34. C. Medcraft, S. Zinn, M. Schnell, A. Poblotzki, J. Altnöder, M. Heger, M. A. Suhm, D. Bernhard, A. Stamm, F. Dietrich and M. Gerhards, Phys. Chem. Chem. Phys., 2016, 18, 25975–25983.
35. D. Bernhard, F. Dietrich, M. Fatima, C. Perez, A. Poblotzki, G. Jansen, M. A. Suhm, M. Schnell and M. Gerhards, Phys. Chem. Chem. Phys., 2017, 19, 18076–18088.
36. D. Bernhard, C. Holzer, F. Dietrich, A. Stamm, W. Klopper and M. Gerhards, ChemPhysChem, 2017, 3634–3641.
37. F. Dietrich, D. Bernhard, M. Fatima, C. Pérez, M. Schnell and M. Gerhards, Angew. Chem., Int. Ed., 2018, 57, 9534–9537.
38. D. Bernhard, F. Dietrich, M. Fatima, C. Pérez, H. C. Gottschalk, A. Wuttke, R. A. Mata, M. A. Suhm, M. Schnell and M. Gerhards, Beilstein J. Org. Chem., 2018, 14, 1642–1654.
39. R. H. Page, Y. R. Shen and Y. T. Lee, J. Chem. Phys., 1988, 88, 4621.
40. C. Riehn, C. Lahmann, B. Wassermann and B. Brutschy, Chem. Phys. Lett., 1992, 197, 443–450.
41. M. Mons, E. G. Robertson and J. P. Simons, J. Phys. Chem. A, 2000, 104, 1430–1437.
42. M. Gerhards and C. Unterberg, Phys. Chem. Chem. Phys., 2002, 4, 1760–1765.
43. G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 53103.
44. M. Schnell, Z. Phys. Chem., 2013, 227, 1–22.
45. G. B. Park and R. W. Field, J. Chem. Phys., 2016, 144, 200901.
46. J. Altnöder, S. Oswald and M. A. Suhm, J. Phys. Chem. A, 2014, 118, 3266–3279.
47. C. Unterberg, A. Jansen and M. Gerhards, J. Chem. Phys., 2000, 113, 7945.
48. D. Schmitz, V. Alvin Shubert, T. Betz and M. Schnell, J. Mol. Spectrosc., 2012, 280, 77–84.
49. C. Pérez, A. Krin, A. L. Steber, J. C. López, Z. Kisiel and M. Schnell, J. Phys. Chem. Lett., 2016, 7, 154–160.
50. C. Pérez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Chem. Phys. Lett., 2013, 571, 1–15.
51. D. F. Plusquellic, R. D. Suenram, B. Maté, J. O. Jensen and A. C. Samuels, J. Chem. Phys., 2001, 115, 3057–3067.
52. Z. Kisiel, L. Pszczółkowski, I. R. Medvedev, M. Winnewisser, F. C. de Lucia and E. Herbst, J. Mol. Spectrosc., 2005, 233, 231–243.
53. H. Hartwig and H. Dreizler, Z. Naturforsch., A: Phys. Sci., 1996, 51, 923–932.
54. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
55. T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519.
56. S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009.
57. A. Hellweg, S. A. Grün and C. Hättig, Phys. Chem. Chem. Phys., 2008, 10, 4119–4127.
58. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
59. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
60. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
61. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
62. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
63. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
64. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
65. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc, Wallingford, CT, USA, 2009.
66. TURBOMOLE V7.3 2018, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007. TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
67. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
68. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
69. F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175.
70. S. F. Boys and F. Bernardi, Mol. Phys., 2006, 19, 553–566.
71. F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73–78.
72. D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525–1539.
73. W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2016, 12, 4778–4792.
74. A. Altun, F. Neese and G. Bistoni, Beilstein J. Org. Chem., 2018, 14, 919–929.
75. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930.
76. E. G. Hohenstein, R. M. Parrish, C. D. Sherrill, J. M. Turney and H. F. Schaefer, J. Chem. Phys., 2011, 135, 174107.
77. T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 94106.
78. J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke, M. L. Abrams, N. J. Russ, M. L. Leininger, C. L. Janssen, E. T. Seidl, W. D. Allen, H. F. Schaefer, R. A. King, E. F. Valeev, C. D. Sherrill and T. D. Crawford, WIREs Comput. Mol. Sci., 2012, 2, 556–565.
79. C. Peng and H. Bernhard Schlegel, Isr. J. Chem., 1993, 33, 449–454.
80. P. Plessow, J. Chem. Theory Comput., 2013, 9, 1305–1310.
81. S. Daicho, Y. Yamada and Y. Nibu, in Pacifichem2010, International Chemical Congress of Pacific Basin Societies, Honolulu, HI, United States, December 15–20, 2010 (Conference Abstract).
82. R. Medel, M. Heger and M. A. Suhm, J. Phys. Chem. A, 2015, 119, 1723–1730.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp02635e

---