Quantum chemistry on quantum computers: quantum simulations of the time evolution of wave functions under the S2 operator and determination of the spin quantum number S†
Received
6th May 2019
, Accepted 11th June 2019
First published on 4th July 2019
Abstract
Quantum computers have an enormous impact on quantum chemical calculations. Approaches to calculate the energies of atoms and molecules on quantum computers by utilizing quantum phase estimation (QPE) and the variational quantum eigensolver (VQE) have been well documented, and dozens of methodological improvements to decrease computational costs and to mitigate errors have been reported until recently. However, the possible methodological implementation of observables on quantum computers such as calculating the spin quantum numbers of arbitrary wave functions, which is a crucial issue in quantum chemistry, has been discussed less. Here, we propose a quantum circuit to simulate the time evolution of wave functions under an S2 operator, exp(−iS2t)|Ψ〉, and integrate it into the QPE circuit enabling us to determine the spin quantum number of the arbitrary wave functions. We demonstrate that the spin quantum numbers of up to three spins can be determined by only one qubit measurement in QPE.
1. Introduction
Quantum computing is the focus of current interest in modern society. Although currently available quantum computing devices are noisy and of intermediate scale, quantum computers consisting of more than 100 qubits are expected to appear soon. This reminds us that we are close to “quantum supremacy”,1 in which quantum computing devices solve problems that are practically intractable for classical computers. Among the diverse topics in quantum computing, the electronic structure calculations of atoms and molecules are one of the most studied realms.2–28 Sophisticated quantum chemical calculations on quantum computers can bring a paradigm shift in chemistry and related fields such as nitrogen fixation processes, drug designs, elucidation of catalytic mechanisms of enzymes, and so on.
The ideas to use computers built of quantum mechanical elements to simulate quantum mechanics were proposed by Feynman in the early 1980s.29 An approach to calculate full-CI energy was proposed by Aspuru-Guzik and coworkers in 20052 by using quantum phase estimation (QPE).30 In the QPE-based full-CI calculations, the time evolutions of the wave function |Ψ〉 using a Hamiltonian are simulated and an energy eigenvalue E is extracted as a phase ϕ, as given in eqn (1), using inverse quantum Fourier transformation.31
| | | exp(−iHt)|Ψ〉 = exp(−iEt)|Ψ〉 = exp(−i2πϕ)|Ψ〉 | (1) |
In 2014, a quantum–classical hybrid system known as a variational quantum eigensolver (VQE) was proposed to solve the unitary coupled cluster (UCC) ansatz.19,20 The VQE has attracted attention as the computation model in noisy intermediate-scale quantum (NISQ)32 devices, because coherence times required for the simulations are much lower than the QPE-based approaches.19–26
Despite the rapid progress in the methodologies to calculate molecular energies on quantum computers, approaches to calculate physical quantities other than energies have been less documented. In fact, to our knowledge, there is no theoretical proposal to determine spin quantum numbers of arbitrary wave functions on quantum computers. The determination of spin quantum numbers is an important task, especially for the study of open shell systems. Open shell molecules have many low-lying electronic states with different spin multiplicities and characterization of the spin properties of their electronic ground state is one of the most fundamental issues in quantum chemistry. Molecules and materials having open shell electronic structures play an important role in chemistry and related fields: molecules undergoing covalent bond cleavages, molecular magnets and molecular spin devices, transition metal complexes in active centers of enzymes, etc., and thus the study of open shell electronic structures is crucial in current chemistry and condensed matter physics. The current computational quantum chemistry is based on many approximations and the calculations often fail to predict chemical properties for larger systems. For systems with few electrons/spins, the Lancoz methods or exact diagonalization technique for many body interactions can afford more accurate and reliable energies,33 but the application of such an approach on classical computers is difficult for larger systems due to the exponential scaling of the computational time against the system size. Noticeably, molecular spin quantum technologies and quantum-assisted biomolecular or organic molecular modellings are the topics of ongoing interest in this field. For example, electron spin-mediated nuclear quantum simulations with switchable interaction were studied by using a vanadyl-based two-qubit system,34 adiabatic quantum computations using molecular spins were implemented to execute prime factorization,35 and three-electron spin qubits were exemplified to provide a realistic path forward to solid state quantum information processing.36
Here, we propose a quantum circuit that allows us to efficiently simulate the time evolution of wave functions under the S2 operator to calculate the S2 eigenvalues of arbitrary wave functions by using QPE.
2. Theory
The spin quantum number S of wave functions can be determined using the eigenvalue of the S2 operator as defined in eqn (2)–(4).37| | | S2|Ψ(S)〉 = S(S + 1)|Ψ(S)〉 | (2) |
| | 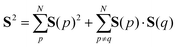 | (3) |
| | 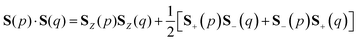 | (4) |
Here, the summation in eqn (3) runs over unpaired electrons. In the quantum chemical calculations on classical computers, equations to calculate the S2 expectation values for spin-unrestricted Hartree–Fock (UHF) and electron correlated wave functions have been reported.38,39 On the other hand, in the quantum chemical calculations on quantum computers, analogous to calculating full-CI energies using QPE, we can readout the S2 eigenvalue as the phase φ by applying QPE if we can simulate the time evolution of wave functions under the S2 operator as given in eqn (5) on quantum computers.| | | exp(−iS2t)|Ψ〉 = exp[−i{S(S + 1)}t]|Ψ〉 = exp(−i2πφ)|Ψ〉 | (5) |
It should be emphasized that the S2 operator can be used not only for the calculation of the spin quantum numbers, but also it is applicable to accelerating quantum simulations and to implementing new algorithms. For example, we can speed up adiabatic state preparations2 of spin-singlet states by using the S2 operator as a penalty function, H(t) = (1 − t)HHF + tHfull-CI + S2 (0 ≤ t ≤ 1). The S2 operator shifts the energy eigenvalue for spin multiplet states depending on the spin quantum number, and therefore the Hamiltonian with the S2 operator has inherently larger energy gaps between singlet and spin-multiplet states. Importantly, the addition of the S2 operator does not change the structure of eigenfunctions because the S2 operator commutes with H. It should be noted that the idea to use the S2 operator as the cost function in the quantum simulations was proposed to avoid kinks in the computations of potential energy surfaces using the VQE.21,22 Spin annihilations based on the Löwdin projection operator40 and adiabatic spin purifications by using a time-dependent Hamiltonian H(t) = H + tS2 are promising applications relevant to the S2 operator.
To simulate the time evolution in eqn (5) on quantum computers, we have to define the S2 operator in the second quantized form and transform it to strings of Pauli operators by using the Jordan–Wigner transformation (JWT) or other wave function mapping techniques.2,41–43 In JWT, each qubit represents the occupation number of a particular spin orbital: |1〉 if the spin orbital is occupied, otherwise |0〉. The first and second terms in eqn (4) can be rewritten as in eqn (6) and (7), respectively, by using creation (a†) and annihilation (a) operators.
| | 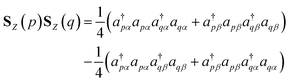 | (6) |
| | 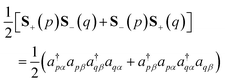 | (7) |
Therefore,
SZ(
p)
SZ(
q) and [
S+(
p)
S−(
q) +
S−(
p)
S+(
q)] terms are expressed as the product of number operators
np (
np =
a†pap) and two-electron excitation operators, respectively, in the second quantized form. By using the JWT and quantum circuit designs proposed by Whitfield and coworkers,
5 the quantum circuits to simulate the time evolution in
eqn (5) can be constructed. For the H
2 molecule with the minimal basis set (two molecular orbitals), the quantum circuit to simulate
eqn (5) can be composed of 76 one-qubit and 54 two-qubit gates in the upper bound (72 one- and 48 two-qubit gates for the [
S+(
p)
S−(
q) +
S−(
p)
S+(
q)] term, 4 one- and 2 two-qubit gates for the
S(
p)
2 term, and 4 two-qubit gates for the
SZ(
p)
SZ(
q) term), without Trotter decompositions. For general molecules, the number of quantum gates scales to
NMO2, where
NMO is the number of molecular orbitals.
The reason why more than 100 quantum gates are required for the quantum simulations of exp(−iS2t)|Ψ〉 in two molecular orbital systems is the fact that the [S+(p)S−(q) + S−(p)S+(q)] term is expressed by two-electron excitation operators in the second quantized form. However, as discussed below, the number of required quantum gates can be drastically reduced by introducing a new wave function mapping method for the spin operators S.
In our previous publications, we introduced a spin coordinate mapping (SCM) to construct spin symmetry-adapted configuration state functions (CSFs) on quantum computers.15,16 In the SCM scheme, the qubit represents the spin degree of freedom of an unpaired electron in the singly occupied molecular orbital (SOMO), namely |0〉 for |α〉 and |1〉 for |β〉. The SCM is convenient for the manipulations of spin degree of freedom, e.g., the [S−(p) + S+(p)] operation becomes a NOT operation, although it corresponds to one-electron excitations in JWT. However, the originally proposed SCM is available only for SOMOs, and here we extend the SCM for general occupations and propose generalized spin coordinate mapping (GSCM).
The correspondence between JWT and GSCM is given in Table 1. As discussed above, in the JWT, qubits store the occupation number of spin orbitals. In Table 1, the first and second qubits correspond to α and β spin orbitals, respectively. In the GSCM, the first qubit specifies whether the molecular orbital is singly occupied or not, and the second qubit represents the occupation number of the β spin orbital. It should be noted that the GSCM has a similarity to the Bravyi–Kitaev transformation (BKT) for wave function mapping in which information on both occupation and parity is stored non-locally.41 Interconversions between JWT and GSCM are achieved by applying controlled-NOT (CNOT) gates; applying a NOT operation to the first qubit if the second qubit is the |1〉 state.
Table 1 Correspondence table of Jordan–Wigner transformation (JWT) and generalized spin coordination mapping (GSCM)
| Electron occupancy of molecular orbitals |
JWT |
GSCM |
| Unoccupied |
|00〉 |
|00〉 |
| Singly occupied by spin-α electrons |
|10〉 |
|10〉 |
| Singly occupied by spin-β electrons |
|01〉 |
|11〉 |
| Doubly occupied |
|11〉 |
|01〉 |
To simulate exp(−iS2t)|Ψ〉 on quantum computers using the GSCM, we rewrite the S2 operator using permutation operators Ppq and number operators of unpaired electrons nspinp = |npα − npβ|, where npα and npβ are number operators acting on the α- and β-spin orbitals, respectively, of the p-th molecular orbital:37
| | 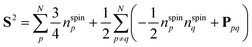 | (8) |
Here,
Ppq interchanges spin coordinates of unpaired electrons in the
p-th and
q-th molecular orbitals, as in
eqn (9).
| | 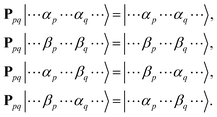 | (9) |
It is clear that
nspinp can be simulated by the one-qubit operation in the GSCM, although it becomes two-qubit operations in the JWT. The time evolution operator arising from
Ppq operators, namely exp(−
iPpqt), seems to be non-trivial at a glance, but it can be expanded as in
eqn (10) by using the relationship (
Ppq)
2 =
1 (identity operator).
| | exp(−iPpqt) = cos(t) − iPpq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(t) sin(t) | (10) |
A quantum circuit for the simulations of
eqn (5) for two molecular orbital systems is illustrated in
Fig. 1. Here, each horizontal line corresponds to the qubit and quantum gates depicted by circles and squares are used from left to right order. Definitions of quantum gates are given in the ESI.
† The quantum circuit consists of five steps: (I) transformation of basis from the JWT to the GSCM, (II) time evolutions by the first term on the right hand side of
eqn (8), (III) time evolutions by the first term in the parenthesis of
eqn (8), (IV) time evolutions by
Ppq terms, and (V) back transformation of the basis from the GSCM to the JWT. Here, we introduced one ancillary qubit to simulate the
Ppq terms. Clearly, the number of quantum gates required for the simulations of exp(−
iS2t)|
Ψ〉 is dramatically reduced by using the GSCM (3, 7, and 3 for one-, two-, and three-qubit operations, respectively). It should also be noted that Trotter decomposition is required only for the
Ppq terms, because [
nspinp,
nspinq] = 0 and [
nspinp,
Ppq] = 0 but [
Ppq,
Pqr] ≠ 0.
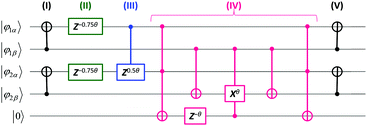 |
| | Fig. 1 A quantum circuit for the simulation of time evolution of the wave function under the S2 operator in two molecular orbital systems like the H2 molecule in the minimal basis, using generalized spin coordinate mapping (GSCM). The circuit consists of five steps: (I) transformation of basis from JWT to GSCM, (II)–(IV) time evolutions caused by the S2 operators (see the text and eqn (8)), and (V) back transformation of the basis from GSCM to JWT. Rotation angle θ = t/π, where t is the time to be evolved. | |
3. Results and discussion
The results of quantum circuit simulations of the time evolution exp(−iS2t)|Ψ〉 for the two- and three-spin systems starting from |Ψ〉 = |αβ〉 and |ααβ〉 are depicted in Fig. 2 and 3, respectively, and several simulations starting from other initial states are given in the ESI.† The simulation programs were developed by using OpenFermion44 and Cirq45 packages. The simulations were carried out with t = 2π and 360 Trotter slices (t = 2π/360 for a single Trotter step) at the first order Trotterizations. The initial wave functions we used (|αβ〉 and |ααβ〉) are not eigenfunctions of the S2 operator but mixtures of two spin eigenfunctions, as given in eqn (11) and (12).| | 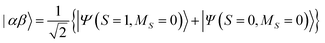 | (11) |
| | 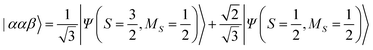 | (12) |
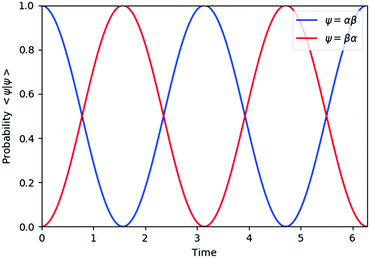 |
| | Fig. 2 Quantum circuit simulation results of the state probability of |αβ〉 and |βα〉 after time evolution exp(−iS2t)|αβ〉. | |
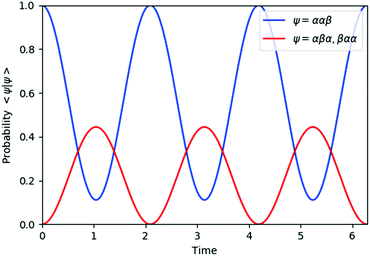 |
| | Fig. 3 Quantum circuit simulation results of the state probability of |ααβ〉, |αβα〉, and |βαα〉 after time evolution exp(−iS2t)|ααβ〉. | |
The spin eigenfunctions with different spin quantum numbers evolve in a different manner, which causes interferences to lead state transformations from |αβ〉 to |βα〉, and |ααβ〉 to |αβα〉 and |βαα〉. The calculated overlaps between the wave functions obtained from the quantum circuit simulations and the wave functions under exact time evolutions are larger than 0.9999996 everywhere.
By integrating the quantum circuit for exp(−iS2t)|Ψ〉 based on the GSCM into the QPE circuit, as illustrated in Fig. 4, we can determine the spin quantum number of the wave function |Ψ〉. For two-spin systems, the spin-triplet wave function evolves as exp(−iS2t)|Ψ〉 = exp(−2it)|Ψ〉 and therefore the measurement of the qubit for QPE always gives |1〉 after time evolution t = π/2, although the spin-singlet wave function does not evolve by S2 operators and the measurement always gives |0〉, because the S2 eigenvalue of spin-singlet states is 0. For three spin systems, the spin states S = 3/2 and S = 1/2 can be discriminated deterministically, by applying time evolution exp(−iS2t)|Ψ〉 with t = π/3 and following phase shift operation Zη with η = π/4 to the qubit to be measured. Detailed discussions are given in the ESI.† For systems of more than three spins, measurements of two or more qubits are required to determine their spin quantum number, but estimations of the number of qubits and optimal time for evolutions are trivial, because the possible spin state is limited by the number of electrons and the eigenvalue of the S2 operator is S(S + 1). The QPE simulation results for two-spin systems are given in Fig. 5. In the QPE simulations in Fig. 5 we gradually changed evolution time t from 0 to π, and plotted the probability to obtain the |1〉 state by using the spin-singlet wave function |Ψ(S = 0)〉 = (|αβ〉 − |βα〉)/√2 and the spin-triplet wave function |Ψ(S = 1)〉 = (|αβ〉 + |βα〉)/√2. The probability was calculated by repetitively performing the QPE quantum circuit simulations 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times for each evolution time and counting how many times the |1〉 state was obtained. In the case of the spin-singlet state, the QPE always returns to the |0〉 state. By contrast, for the spin-triplet state, the probability to measure the |1〉 state depends on the evolution time, and after π/2 of time evolution, the probability becomes maximum as expected. We also performed quantum circuit simulations of QPE using a broken-symmetry wave function |Ψ(BS)〉 = |αβ〉 that corresponds to the 1
000 times for each evolution time and counting how many times the |1〉 state was obtained. In the case of the spin-singlet state, the QPE always returns to the |0〉 state. By contrast, for the spin-triplet state, the probability to measure the |1〉 state depends on the evolution time, and after π/2 of time evolution, the probability becomes maximum as expected. We also performed quantum circuit simulations of QPE using a broken-symmetry wave function |Ψ(BS)〉 = |αβ〉 that corresponds to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of spin singlet and triplet wave functions (see eqn (11)). By running quantum circuit simulations 100
1 mixture of spin singlet and triplet wave functions (see eqn (11)). By running quantum circuit simulations 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times for t = π/2, we obtained the |1〉 state 49
000 times for t = π/2, we obtained the |1〉 state 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 899 times, which is very close to the ideal probability 0.5. Similar results were obtained for the quantum circuit simulations of three-electron systems, as discussed in the ESI.†
899 times, which is very close to the ideal probability 0.5. Similar results were obtained for the quantum circuit simulations of three-electron systems, as discussed in the ESI.†
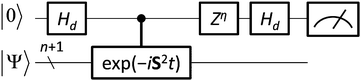 |
| | Fig. 4 A quantum circuit for one-qubit quantum phase estimation. For two- and three-electron systems, spin quantum numbers are calculated in a deterministic manner by setting t = π/2 and η = 0, and t = π/3 and η = π/4, respectively (see text for details). | |
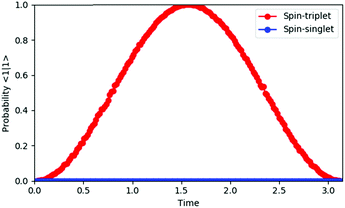 |
| | Fig. 5 Quantum circuit simulation results for the quantum phase estimation of two-electron systems. | |
4. Conclusions
In conclusion, we have developed a quantum circuit for the time evolution of wave functions under the S2 operator, and we use it to determine the spin quantum number of wave functions by means of QPE, illustrating that the quantum circuit approach underlain by quantum algorithms affords extreme efficiency in evaluating observables, which is a seemingly intractable problem. By using the GSCM implemented for the manipulations of wave functions with spin operators, the number of quantum gates required for the simulation is drastically reduced compared with that using the JWT. The spin quantum number of wave functions can be determined from only one qubit readout in QPE for two- and three-spin systems. These results show that rapid computations of the spin quantum numbers S's on quantum computers are possible, by applying the proposed quantum circuits. The approach developed here opens the door toward theoretical characterizations of the spin properties of open shell molecules in their electronic ground state, which is one of the most fundamental issues in open shell chemistry, by using quantum computers. Again, we emphasize that the S2 operator can be used for more than just the calculations of the spin quantum number. Applications of the S2 operator for other quantum chemical problems on quantum computers are underway and will be discussed in a forthcoming paper.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the AOARD Scientific Project on “Molecular Spins for Quantum Technologies” (Grant FA2386-17-1-4040, 4041), USA, and by Grants-in-Aid for Scientific Research B (17H03012), Scientific Research C (18K03465) and C (17K05840) from the MEXT, Japan.
Notes and references
-
J. Preskill, Quantum computing and the entanglement frontier, 2012, arXiv:1203.5813.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Simulated quantum computation of molecular energies, Science, 2005, 309, 1704–1707 CrossRef CAS PubMed.
- B. P. Lanyon, J. D. Whitfield, G. G. Gillett, M. E. Goggin, M. P. Almeida, I. Kassal, J. D. Biamonte, M. Mohseni, B. J. Powell, M. Barbieri, A. Aspuru-Guzik and A. G. White, Towards quantum chemistry on a quantum computer, Nat. Commun., 2010, 2, 106–111 CAS.
- J. Du, N. Xu, X. Peng, P. Wang, S. Wu and D. Lu, NMR implementation of a molecular hydrogen quantum simulation with adiabatic state preparation, Phys. Rev. Lett., 2010, 104, 030502 CrossRef PubMed.
- J. D. Whitfield, J. Biamonte and A. Aspuru-Guzik, Simulation of electronic structure Hamiltonians using quantum computers, Mol. Phys., 2011, 109, 735–750 CrossRef CAS.
- Y. Wang, F. Dolde, J. Biamonte, R. Babbush, V. Bergholm, S. Yang, I. Jakobi, P. Neumann, A. Aspuru-Guzik, J. D. Whitfield and J. Wrachtrup, Quantum simulation of helium hydride cation in a solid-state spin register, ACS Nano, 2015, 9, 7769–7774 CrossRef CAS PubMed.
- P. J. J. O'Malley, R. Babbush, I. D. Kivlichan, J. Romero, J. R. McClean, R. Barends, J. Kelly, P. Roushan, A. Tranter, N. Ding, B. Campbell, Y. Chen, Z. Chen, B. Chiaro, A. Dunsworth, A. G. Fowler, E. Jeffrey, E. Lucero, A. Megrant, J. Y. Mutus, M. Neeley, C. Neill, C. Quintana, D. Sank, A. Vainsencher, J. Wenner, T. C. White, P. V. Coveney, P. J. Love, H. Neven, A. Aspuru-Guzik and J. M. Martinis, Scalable quantum simulation of molecular energies, Phys. Rev. X, 2016, 6, 031007 Search PubMed.
- N. C. Jones, J. D. Whitfield, P. L. McMahon, M.-H. Yung, R. Van Meter, A. Aspuru-Guzik and Y. Yamamoto, Faster quantum chemistry simulation on fault-tolerant quantum computers, New J. Phys., 2012, 14, 115023 CrossRef.
- M. B. Hastings, D. Wecker, B. Bauer and M. Troyer, Improving quantum algorithms for quantum chemistry, Quantum Inf. Comput., 2015, 15, 1–21 CAS.
- N. Mall, A. Fuhrer, P. Staar and I. Tavernelli, Optimizing qubit resources for quantum chemisty simulations in second quantization on a quantum computer, J. Phys. A: Math. Theor., 2016, 49, 295301 CrossRef.
- R. Babbush, D. W. Berry, I. D. Kivlichan, A. Y. Wei, P. J. Love and A. Aspuru-Guzik, Exponentially more precise quantum simulation of fermions in second quantization, New J. Phys., 2016, 18, 033032 CrossRef.
- G. Zhu, Y. Subaşı, J. D. Whitfield and M. Hafezi, Hardware-efficient fermionic simulation with a cavity-QED system, njp Quantum Inf., 2018, 4, 16 CrossRef.
- R. Babbush, N. Wiebe, J. McClean, J. McClain, H. Neven and G. K.-L. Chan, Low-depth quantum simulation of materials, Phys. Rev. X, 2018, 8, 011044 CAS.
- I. D. Kivlichan, J. McClean, N. Wiebe, C. Gidney, A. Aspuru-Guzik, G. K.-L. Chan and R. Babbush, Quantum simulation of electronic structure with linear depth and connectivity, Phys. Rev. Lett., 2018, 120, 110501 CrossRef CAS PubMed.
- K. Sugisaki, S. Yamamoto, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, Quantum chemistry on quantum computers: A polynomial-time quantum algorithm for constructing the wave functions of open-shell molecules, J. Phys. Chem. A, 2016, 120, 6459–6466 CrossRef CAS PubMed.
- K. Sugisaki, S. Yamamoto, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, Open shell electronic state calculations on quantum computers: a quantum circuit for the preparation of configuration state functions based on Serber construction, Chem. Phys. Lett.: X, 2019, 1, 100002 Search PubMed.
- K. Sugisaki, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, Quantum chemistry on quantum computers: a method for preparation of multiconfigurational wave functions on quantum computers without performing post-Hartree–Fock calculations, ACS Cent. Sci., 2019, 5, 167–175 CrossRef CAS PubMed.
-
D. W. Berry, C. Gidney, M. Motta, J. R. McClean and R. Babbush, Qubitization of arbitrary basis quantum chemistry by low rank factorization, 2019, arXiv:1902.02134.
- M.-H. Yung, J. Casanova, A. Mezzacapo, J. McClean, L. Lamata, A. Aspuru-Guzik and E. Solano, From transistor to trapped-ion computers for quantum chemistry, Sci. Rep., 2014, 4, 3589 CrossRef PubMed.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O'Brien, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- J. R. McClean, M. E. Kimchi-Schwartz, J. Carter and W. A. De Jong, Hybrid quantum-classical hierarchy for mitigation of decoherence and determination of excited states, Phys. Rev. A, 2017, 95, 042308 CrossRef.
-
I. G. Ryabinkin, S. N. Genin and A. F. Izmaylov, Constrained variational quantum eigensolver: quantum computer search engine in the Fock space, 2018, arXiv.1806.00461.
- J. I. Colless, V. V. Ramasesh, D. Dahlen, M. S. Blok and M. E. Kimchi-Schwartz, Computation of molecular spectra on a quantum processor with an error-resilient algorithm, Phys. Rev. X, 2018, 8, 011021 CAS.
- J. Romero, R. Babbush, J. R. McClean, C. Hempel, P. Love and A. Aspuru-Guzik, Strategies for quantum computing molecular energies using the unitary coupled cluster ansatz, Quantum Sci. Technol., 2018, 4, 014008 CrossRef.
- Y. Li, J. Hu, X.-M. Zhang, Z. Song and M.-H. Yung, Variational quantum simulation for quantum chemistry, Adv. Theory Simul., 2019, 1800182 CrossRef CAS.
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets, Nature, 2017, 549, 242–246 CrossRef CAS PubMed.
- C. Hempel, C. Maier, J. Romero, J. McClean, T. Monz, H. Shen, P. Jurcevic, B. P. Lanyon, P. Love, R. Babbush, A. Aspuru-Guzik, R. Blatt and C. F. Roos, Quantum chemistry calculations on a trapped-ion quantum simulator, Phys. Rev. X, 2018, 8, 031022 CAS.
-
Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kilvichan, T. Menke, B. Peropadre, N. P. D. Sawaya, S. Sim, L. Veis and A. Aspuru-Guzik, Quantum chemistry in the age of quantum computing, 2018, arXiv:1812.09976.
- R. P. Feynman, Simulating physics with computers, Int. J. Theor. Phys., 1982, 21, 467–488 CrossRef.
- A. Abrams and S. Lloyd, Quantum algorithm providing exponentially speed increase for finding eigenvalues and eigenvectors, Phys. Rev. Lett., 1999, 83, 5162–5165 CrossRef.
-
M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, Cambrigde University Press, Cambridge, 2000 Search PubMed.
- J. Preskill, Quantum computing in the NISQ era and beyond, Quantum, 2018, 2, 79 CrossRef.
- A. N. Kocharian, G. W. Fernando, K. Palandage and J. W. Davenport, Exact study of charge-spin separation, pairing fluctuations, and pseudogaps in four-site Hubbard clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 024511 CrossRef.
- M. Atzori, A. Chiesa, E. Morra, M. Chiesa, L. Sorace, S. Carretta and R. Sessoli, A two-qubit molecular architecture for electron-mediated nuclear quantum simulation, Chem. Sci., 2018, 9, 6183–6192 RSC.
- S. Yamamoto, S. Nakazawa, K. Sugisaki, K. Sato, K. Toyota, D. Shiomi and T. Takui, Adiabatic quantum computing with spin qubits hosted by molecules, Phys. Chem. Chem. Phys., 2015, 17, 2742–2749 RSC.
- M. Russ and G. Burkard, Three-electron spin qubits, J. Phys.: Condens. Matter, 2017, 29, 393001 CrossRef PubMed.
-
R. Pauncz, The Constrution of Spin Eigenfunctions. An Exercise Book, Kluwer Academic/Plenum Publishers, New York, 2000 Search PubMed.
- W. Chen and H. B. Schlegel, Evaluation of S2 for correlated wave functions and spin projection of unrestricted Møller–Plesset perturbation theory, J. Chem. Phys., 1994, 101, 5957–5968 CrossRef CAS.
- J. Wang, A. D. Becke and V. H. Smith, Jr., Evaluation of 〈S2〉 in restricted, unrestricted Hartree–Fock, adn density functional based theories, J. Chem. Phys., 1995, 108, 3477–3480 CrossRef.
- P.-O. Löwdin, Angular momentum wavefunctions constructed by projector operators, Rev. Mod. Phys., 1964, 36, 966–976 CrossRef.
- J. T. Seeley, M. J. Richard and P. J. Love, The Bravyi-Kitaev transformation for quantum computation of electronic structure, J. Chem. Phys., 2012, 137, 224109 CrossRef PubMed.
-
S. Bravyi, J. M. Gambetta, A. Mezzacapo and K. Temme, Tapering off qubits to simulate fermionic Hamiltonians, 2017, arXiv:1701.08213.
- K. Setia and J. D. Whitfield, Bravyi-Kitaev superfast simulation of electronic structure on a quantum computer, J. Chem. Phys., 2018, 148, 164104 CrossRef PubMed.
-
J. R. McClean, K. J. Sung, I. D. Kivlichan, Y. Cao, C. Dai, E. F. Fried, C. Gidney, B. Gimby, P. Gokhale, T. Häner, T. Hardikar, V. Havlíček, O. Higgott, C. Huang, J. Izaac, Z. Jiang, X. Liu, S. McArdle, M. Neeley, T. O'Brien, B. O'Gorman, I. Ozfidan, M. D. Radin, J. Romero, N. Rubin, N. P. D. Sawaya, K. Setia, S. Sim, D. S. Steiger, M. Steudtner, Q. Sun, W. Sun, D. Wang, F. Zhang and R. Babbush, OpenFermion: The electronic structure packeage for quantum computers, 2017, arXiv:1710.07629.
- Cirq. https://github.com/quantumlib/Cirq.
Footnotes |
| † Electronic supplementary information (ESI) available: Definitions of quantum gates, quantum circuit simulations for the time evolution of wave functions under the S2 operator, and quantum circuit simulations for the quantum phase estimation to determine the S2 eigenvalue. See DOI: 10.1039/c9cp02546d |
| ‡ Deceased on March 23, 2019. |
|
| This journal is © the Owner Societies 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Shigeaki
Nakazawa‡
a,
Kazuo
Toyota
a,
Kazunobu
Sato
*a,
Shigeaki
Nakazawa‡
a,
Kazuo
Toyota
a,
Kazunobu
Sato
 *a,
Daisuke
Shiomi
a and
Takeji
Takui
*a,
Daisuke
Shiomi
a and
Takeji
Takui
 *ab
*ab
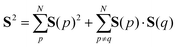
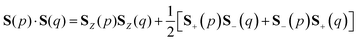
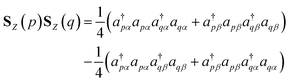
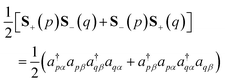
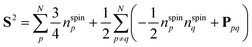
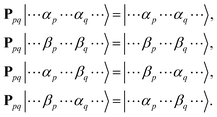
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(t)
sin(t)
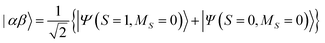
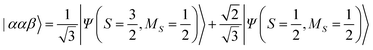


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times for each evolution time and counting how many times the |1〉 state was obtained. In the case of the spin-singlet state, the QPE always returns to the |0〉 state. By contrast, for the spin-triplet state, the probability to measure the |1〉 state depends on the evolution time, and after π/2 of time evolution, the probability becomes maximum as expected. We also performed quantum circuit simulations of QPE using a broken-symmetry wave function |Ψ(BS)〉 = |αβ〉 that corresponds to the 1
000 times for each evolution time and counting how many times the |1〉 state was obtained. In the case of the spin-singlet state, the QPE always returns to the |0〉 state. By contrast, for the spin-triplet state, the probability to measure the |1〉 state depends on the evolution time, and after π/2 of time evolution, the probability becomes maximum as expected. We also performed quantum circuit simulations of QPE using a broken-symmetry wave function |Ψ(BS)〉 = |αβ〉 that corresponds to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of spin singlet and triplet wave functions (see eqn (11)). By running quantum circuit simulations 100
1 mixture of spin singlet and triplet wave functions (see eqn (11)). By running quantum circuit simulations 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times for t = π/2, we obtained the |1〉 state 49
000 times for t = π/2, we obtained the |1〉 state 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 899 times, which is very close to the ideal probability 0.5. Similar results were obtained for the quantum circuit simulations of three-electron systems, as discussed in the ESI.†
899 times, which is very close to the ideal probability 0.5. Similar results were obtained for the quantum circuit simulations of three-electron systems, as discussed in the ESI.†

