Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Are crystallographic B-factors suitable for calculating protein conformational entropy?†
Octav
Caldararu
 a,
Rohit
Kumar
b,
Esko
Oksanen
a,
Rohit
Kumar
b,
Esko
Oksanen
 bc,
Derek T.
Logan
bc,
Derek T.
Logan
 b and
Ulf
Ryde
b and
Ulf
Ryde
 *a
*a
aDepartment of Theoretical Chemistry, Lund University, Chemical Centre, P. O. Box 124, SE-221 00 Lund, Sweden. E-mail: Ulf.Ryde@teokem.lu.se; Fax: +46 46 2228648; Tel: +46 46 2224502
bDepartment of Biophysical Chemistry, Centre for Molecular Protein Science, Lund University, Chemical Centre, P. O. Box 124, SE-221 00 Lund, Sweden
cEuropean Spallation Source Consortium, P. O. Box 176, SE-221 00 Lund, Sweden
First published on 1st August 2019
Abstract
Conformational entropies are of great interest when studying the binding of small ligands to proteins or the interaction of proteins. Unfortunately, there are no experimental methods available to measure conformational entropies of all groups in a protein. Instead, they are normally estimated from molecular dynamics (MD) simulations, although such methods show problems with convergence and correlation of motions, and depend on the accuracy of the underlying potential-energy function. Crystallographic atomic displacement parameters (also known as B-factors) are available in all crystal structures and contain information about the atomic fluctuations, which can be converted to entropies. We have studied whether B-factors can be employed to extract conformational entropies for proteins by comparing such entropies to those measured by NMR relaxation experiments or obtained from MD simulations in solution or in the crystal. Unfortunately, our results show that B-factor entropies are unreliable, because they include the movement and rotation of the entire protein, they exclude correlation of the movements and they include contributions other than the fluctuations, e.g. static disorder, as well as errors in the model and the scattering factors. We have tried to reduce the first problem by employing translation–libration–screw refinement, the second by employing a description of the correlated movement from MD simulations, and the third by studying only the change in entropy when a pair of ligands binds to the same protein, thoroughly re-refining the structures in exactly the same way and using the same set of alternative conformations. However, the experimental B-factors seem to be incompatible with fluctuations from MD simulations and the precision is too poor to give any reliable entropies.
Introduction
All chemical processes are governed by their free energy.1 Gibbs free energy (ΔG) consists of two terms, the enthalpy (ΔH) and the entropy (ΔS), according to ΔG = ΔH − TΔS, where T is the absolute temperature. The enthalpy is often relatively easy to interpret in terms of favourable and unfavourable interactions, e.g. hydrogen bonds, electrostatics, dispersive interactions and steric clashes, which can be directly observed in crystal structures (although it may be hard to determine the relative importance of the various interactions in large systems). However, the entropy is harder to interpret, because it represents the relative probability to obtain a certain state and therefore depends on the dynamic flexibility of the system. Nevertheless, if we want to understand and manipulate biological systems, e.g. in the design of potent medicinal drugs or more efficient enzymes with new reactivity, it is necessary to understand and exploit both enthalpic and entropic effects,2–4 especially as it is normally observed that improvements in enthalpy are counteracted (compensated) by adverse entropy effects, and vice versa.3,5The standard method to measure entropy changes is isothermal titration calorimetry (ITC).6 However, it only estimates the total entropy. It would strongly facilitate understanding if various contributions to the entropy could be measured, e.g. from the solvent, from the translation and rotation of the protein, or from the movement of the various groups in the protein. In particular, the latter term, the conformational entropy, has been shown to play a major role in many biomolecular interactions, in particular in protein–ligand binding, accounting for up to half of the total entropy.7–11 Conformational entropies can be estimated by solution nuclear magnetic resonance (NMR) experiments using order parameters.12–14 Unfortunately, the order parameters are typically measured only for a subset of the protein atoms, e.g. the backbone and some side-chain atoms, so the entropy description from these experiments is incomplete. Moreover, NMR order parameters report only on isolated bond vectors, thus providing no information on correlated motions.15
Therefore, reported conformational entropies have so far relied on computational methods, to fill in the incomplete experimental data.16 Molecular dynamics (MD) simulations are the preferred method of studying protein dynamics computationally and MD-based free energy calculations, for example free energy perturbation, have proved successful in calculating protein–ligand binding free energies.17,18 There are several approaches to estimate conformational entropies from MD simulations, e.g. normal-mode analysis, quasi-harmonic analysis and dihedral histogramming.19–21 However, computational approaches also have significant problems. In particular, protein simulations are based on an empirical molecular mechanics force field, with a limited accuracy. Moreover, it has been shown that the conformational entropy from MD simulations increases logarithmically even after 1 ms of simulation time, making it problematic to extract accurate estimates of the entropy.22
Consequently, there is an urgent need for an experimental method to estimate accurate conformational entropies. A possible source could be protein crystal structures. The crystallographic atomic displacement parameters, more commonly known as B-factors, are reported for all protein X-ray crystal structures and they are directly related to the atomic fluctuations (due to motion or static disorder) in the crystal.23 Polyansky et al. have suggested a method for calculating conformational entropy directly from atomic B-factors, by making use of the standard quasi-harmonic approach.24 This would provide a fast and simple method to obtain conformational entropies, based on readily available experimental data. However, there are multiple issues that arise when dealing with B-factors. First, B-factors do not take into account any correlated motions in the protein, resulting in an overestimate of the absolute conformational entropy. Polyansky et al. accounted for this by using a linear scaling of the entropies without covariance terms, resulting in a corrected entropy that was five times lower than the calculated entropy.24 Another possible way of considering correlation is by using B-factors from a translation–liberation–screw (TLS) model, in which parts of the protein are represented as a rigid body.25,26 Second, data for most protein crystal structures are collected at 100 K. This might lead to an underestimation of conformational entropies, but using room-temperature data may avoid the issue. Third and most importantly, standard B-factors do not always accurately reflect the dynamics in a protein crystal structure.27B-factors also contain a measure of static disorder, arising from differences in equivalent atomic positions in different unit cells within the crystal. In addition, even small errors in the model could significantly change the value of the B-factors.28 A previous study has suggested that X-ray refinement may underestimate B-factors by a factor of up to six.29
In this paper, we study whether crystallographic B-factors can provide accurate conformational entropies compared to those obtained by NMR relaxation experiments or by MD-based methods. To reduce the influence of static disorder and non-fluctuational contributions to the B-factors, we studied only the change in entropy between pairs of structures and re-refined the crystal structures in exactly the same way. Moreover, we employed both cryogenic and room-temperature structures. Finally, we tested using both isotropic and anisotropic B-factors, as well as TLS models and ensemble refinement to obtain entropies. Unfortunately, our results show that crystallographic B-factors are not accurate enough to be used in the calculation of conformational entropy, even after correcting for the missing correlated motions. To understand this failure, we used MD simulations in both solution and in crystals, calculating entropies with four different methods.
Materials and methods
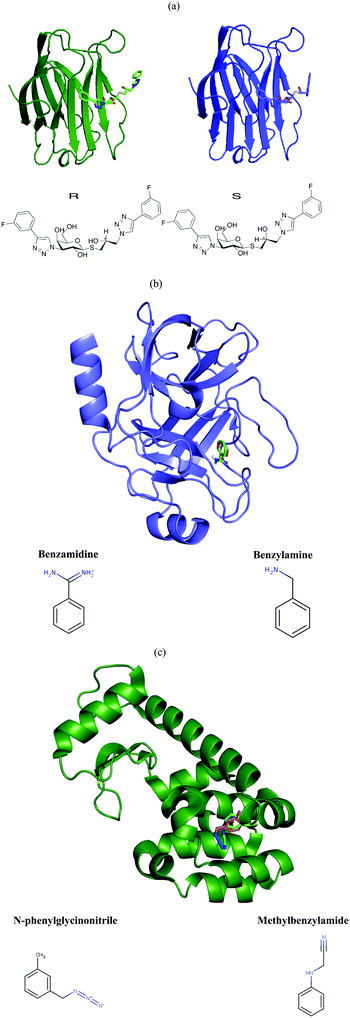
Galectin-3C
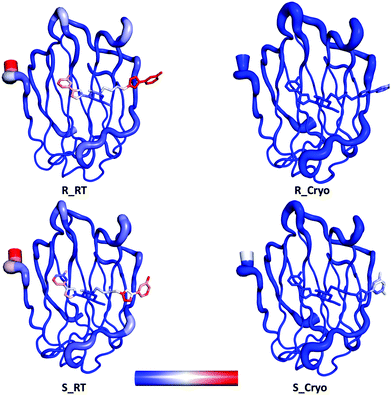
Galectin-3 is a mammalian β-galactoside binding protein involved in glycoprotein trafficking, signalling, cell adhesion, angiogenesis, macrophage activation and apoptosis.30–34 It has been implicated in inflammation, immunity, cancer development and metastasis.35 The C-terminal domain is easily crystallisable with various ligands.36–38 We studied the binding of two diastereomeric ligands, (2R)- and (2S)-2-hydroxy-3-(4-(3-fluorophenyl)-1H-1,2,3-triazol-1-yl)-propyl 2,4,6-tri-O-acetyl-3-deoxy-3-(4-(3-fluorophenyl)-1H-1,2,3-triazol-1-yl)-1-thio-β-D-galactopyranoside, to the C-terminal domain of galectin-3 (galectin-3C). The two ligands, which simply will be denoted R and S in this article, are shown in Fig. 1. Coordinates, B-factors, occupancies and reflection data of the two complexes, collected at 100 K, were obtained from the Protein Data Bank (PDB entries 6QGE and 6QGF).38 The resolutions of these structures were 1.34 Å and 1.19 Å, respectively.The corresponding room temperature data sets were collected with large crystals that were soaked for 15–18 h with the same two ligands. The crystals were then mounted in appropriately-sized loops (0.5 mm) and sealed with a plastic tube using the MicroRT kit from MiTeGen. Data was collected at BioMAX at MAX IV. A defocused beam of size 50 × 50 μm2 was used to avoid radiation damage, but this data turned out to be without ligand for S. On the other hand, positive data were instead collected with a focused beam (20 × 5 μm2). The structure for R then underwent the same refinement procedure as the cryo-temperature structures, described by Verteramo et al.38 The data for S was of a slightly lower resolution, 1.6 Å, so only isotropic B-factor refinement was possible, but all the other parts of the refinement process were similar to that for R. The structures have been deposited in the PDB (IDs 6RHL and 6RHM respectively). Refinement statistics for the final room-temperature structures are given in Table S1 (ESI†). B-Factors for the two sets of structures are compared in Fig. 2.
Next, the two sets of structures were modified, so that both pairs of complexes have alternative conformations for exactly the same residues. This was accomplished by generating extra alternative conformations of sidechains manually in Coot39 after visual inspection. A list of all residues that have alternative conformations is given in Table S2 in the ESI.† These structures were then fully re-refined for seven cycles, refining occupancies for all residues in alternative conformations and anisotropic B-factors for all non-water and non-hydrogen atoms. The B-factors after this refinement were used for entropy calculation. All refinements were done with Phenix v1.11.40 An additional refinement was also run for each protein–ligand complex with TLS parametrization, defining the whole protein and the ligand atoms as one TLS group. Selected refinement statistics for the final structures used for entropy calculation are shown in Table 1.
| R | S | |||||||
|---|---|---|---|---|---|---|---|---|
| Original | Iso | Aniso | TLS | Original | Iso | Aniso | TLS | |
| 100 K | ||||||||
| R | 0.124 | 0.140 | 0.130 | 0.132 | 0.126 | 0.142 | 0.130 | 0.138 |
| R free | 0.158 | 0.176 | 0.163 | 0.166 | 0.156 | 0.177 | 0.162 | 0.171 |
| 〈B〉 | 12.1 | 13.2 | 12.7 | 12.6 (3.5) | 14.8 | 14.7 | 14.0 | 13.9 (3.4) |
| 300 K | ||||||||
| R | 0.137 | 0.160 | 0.139 | 0.153 | 0.179 | 0.171 | 0.171 | |
| R free | 0.165 | 0.185 | 0.169 | 0.173 | 0.190 | 0.190 | 0.191 | |
| 〈B〉 | 26.8 | 27.6 | 28.0 | 29.3 (24.1) | 26.7 | 29.5 | 29.9 (25.2) | |
Ensemble refinement
Ensemble refinement43 of the galectin-3C X-ray diffraction data obtained at both 100 and 300 K was performed using the phenix.ensemble_refinement module in the Phenix software. It was started from the two sets of X-ray crystal structures of the S-galectin-3C and R-galectin-3C complexes, modified as described above. Water molecules observed in the crystal structures were kept and hydrogen atoms and other missing atoms in the crystal structures were added using the leap module from the Amber 1444 software. Ligand restraints and coordinates were the same as those used in the original refinement. The large-scale dynamics of the protein were described using the same TLS model as in the TLS refinement, which included both the protein and the ligand atoms. The fraction of atoms included in the TLS fitting (pTLS) was optimized by testing five different values (0.5, 0.6, 0.7, 0.8 and 0.9) and choosing the one that yielded the lowest Rfree value, which turned out to be pTLS = 0.7 for both protein–ligand complexes at both temperatures. An ensemble of structures was then generated by running MD simulations, in which the model was restrained by a time-averaged X-ray maximum-likelihood target function. The X-ray weight-coupled temperature bath offset was kept at the default value of 5 K. A 1.25 ps relaxation time for the time-averaged restraints was used, resulting in 25 ps long MD simulations, with structures being stored every 0.05 ps. The simulation time-step was 0.5 fs. All structures generated by ensemble refinement were kept, resulting in 500 structures in each ensemble. Atomic fluctuations were calculated using the cpptraj45 module of Amber after removal of the water molecules.Trypsin
Coordinates, B-factors, occupancies and reflection data for two high resolution trypsin complexes, with benzamidine41 (PDB ID 5MNG, 0.86 Å resolution) and with benzylamine41 (PDB ID 5MNK, 0.79 Å resolution) were obtained from the PDB (shown in Fig. 1b). The structures were visually inspected in Coot and it was ensured that they had alternative conformations for the same residues (shown in Table S2, ESI†). Then, the two structures underwent re-refinement analogous to that used for the galectin-3C structures, resulting in three separate sets of B-factors (isotropic, anisotropic and TLS).Lysozyme
Coordinates, B-factors, occupancies and reflection data for two T4 lysozyme L99A complexes, with N-phenylglycinonitrile42 (PDB ID 2RBN, 1.29 Å resolution) and with 3-methylbenzylazide42 (PDB ID 2RB2, 1.46 Å resolution) were obtained from the PDB (shown in Fig. 1c). The structures were visually inspected in Coot and it was ensured that they had alternative conformations for the same residues (shown in Table S2, ESI†). Then, the two structures underwent re-refinement analogous to that used for the two other proteins. As the 3-methylbenzylazide structure has a relatively low resolution, only isotropic and TLS B-factors were obtained for entropy calculation.MD simulations
All MD simulations were run with the Amber 14 software suite.44 Three different types of MD simulation were run: a normal MD simulation in a periodic octahedral water box, a simulation of a single unit cell of the protein crystal and a simulation of two unit cells of the protein crystal. In the latter case, the direction of the adjacent unit cell (i.e. in direction a, b or c) was arbitrarily chosen as a. Crystal simulations were only performed for galectin-3C.All the galectin-3C simulations were started from the X-ray crystal structures of R and S-galectin-3C determined at 100 K. For the normal MD simulations, each galectin-3C complex was solvated in an octahedral box of water molecules extending at least 10 Å from the protein using the tleap module, so that 4965–5593 water molecules were included in the simulations. The simulations were set up in the same way as in our previous studies of galectin-3C.22,37,38,46 All Glu and Asp residues were assumed to be negatively charged and all Lys and Arg residues positively charged, whereas the other residues were assumed to be neutral. The His158 residue was protonated on the ND1 atom, whereas the other three His residues were protonated on the NE2 atom, in accordance with neutron crystal structures, NMR measurements and previous extensive test calculations with MD.47,48 This resulted in a net charge of +4 for the protein. No counter ions were used in the simulations.
The trypsin and lysozyme simulations were started from the crystal structures described above. All the crystal waters were kept and for residues with alternative conformations, the one with the higher occupancy was used (or the first conformation if both had the same occupancy). The proteins were solvated in the same way as for galectin-3C, giving 5580 and 8864 water molecules for trypsin and lysozyme, respectively. All Glu and Asp residues were assumed to be negatively charged and all Lys and Arg residues positively charged. For trypsin, the His residues were protonated as determined in a previous study:47 His40 and His57 were doubly protonated on both the ND1 and NE2 atoms, whereas His91 was protonated only on the NE2 atom. For lysozyme, the protonation of the single His residue was decided by analysing the hydrogen bond network around the residue: His31 was protonated on the ND1 atom.
The proteins were described by the Amber ff14SB force field49 and water molecules with the TIP4P-Ewald model.50 The ligands were treated with the general Amber force field with restrained electrostatic potential charges,51 which have been described before for the galectin-3C ligands,38 whereas those for the trypsin and lysozyme ligands are listed in Table S3 (ESI†). For each complex, the structures were minimised for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, followed by 20 ps constant-volume equilibration and 20 ps constant-pressure equilibration, all performed with heavy non-water atoms restrained towards the starting structure with a force constant of 209 kJ mol−1 Å−2. Finally, the system was equilibrated for 2 ns without any restraints and with constant pressure, followed by 10 ns of production simulation, during which coordinates were saved every 5 or 10 ps. For each protein–ligand complex, 10 independent simulations were run, employing different solvation boxes and starting velocities.52 Consequently, the total simulation time for each complex was 100 ns. Several previous studies have indicated that entropy estimates from MD simulations converge very slowly.53,54 In fact, it has been shown that they change even after 1 ms simulations.22 Therefore, it is unlikely that the results will improve if longer simulations are employed.
000 steps, followed by 20 ps constant-volume equilibration and 20 ps constant-pressure equilibration, all performed with heavy non-water atoms restrained towards the starting structure with a force constant of 209 kJ mol−1 Å−2. Finally, the system was equilibrated for 2 ns without any restraints and with constant pressure, followed by 10 ns of production simulation, during which coordinates were saved every 5 or 10 ps. For each protein–ligand complex, 10 independent simulations were run, employing different solvation boxes and starting velocities.52 Consequently, the total simulation time for each complex was 100 ns. Several previous studies have indicated that entropy estimates from MD simulations converge very slowly.53,54 In fact, it has been shown that they change even after 1 ms simulations.22 Therefore, it is unlikely that the results will improve if longer simulations are employed.
All bonds involving hydrogen atoms were constrained to the equilibrium value using the SHAKE algorithm,55 allowing for a time step of 2 fs. The temperature was kept constant at 300 K using Langevin dynamics,56 with a collision frequency of 2 ps−1. The pressure was kept constant at 1 atm using a weak-coupling isotropic algorithm57 with a relaxation time of 1 ps. Long-range electrostatics were handled by particle-mesh Ewald summation58 with a fourth-order B spline interpolation and a tolerance of 10−5. The cut-off radius for Lennard-Jones interactions between atoms of neighbouring boxes was set to 8 Å.
The two galectin-3C MD simulations in crystal unit cells were set up using the Amber XtalUtilities package, with the unit cell size extracted from the CRYST1 record in the PDB files. One unit cell contained four protein monomers, resulting in four and eight protein monomers simulated for the one and two unit cells simulations, respectively. All crystal water molecules were kept in the simulations. 7Na+ and 11Cl− counter ions were added to match the 0.4 M ionic strength used in the crystallographic experiments. Water molecules were added successively to the existing crystallographic water molecules until all empty space in the unit cell was filled. As this is difficult to evaluate visually, multiple starting structures with 350, 400, 450 and 500 added water molecules per unit cell were tested in the equilibration step. The simulation containing 500 water molecules kept the volume of the system closest to the unit cell volume and was used for the production runs. The same protocol as in the normal MD simulation was used, resulting in 100 ns (10 × 10) of simulation time for each galectin-3C–ligand complex.
Entropy calculations
We employed six different methods to calculate conformational entropies. For all methods, entropies were calculated for the full proteins, including the ligands, without any water molecules. Unless otherwise specified, entropies were calculated separately for each of the 10 individual simulations and the standard error reported over these.In the first approach, the entropies were obtained by dihedral angle histogramming (DH).12,46,59,60 Conformational entropies were calculated from the ensemble of configurations of the protein and ligands by analysing the dihedral-angle fluctuations. Cartesian coordinates were first transformed to internal coordinates. The distribution of the dihedral angles was then approximated by a discrete histogram of 72 bins of 5° each (other number of bins have been tested previously46) and the resulting entropy was calculated from:
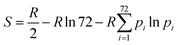 | (1) |
In the second approach, entropies were obtained from quasi-harmonic analysis (QHA) of the covariance matrix.61,62 Thus, the fluctuations were assumed to follow a multivariate Gaussian distribution and quasi-harmonic frequencies were calculated as the eigenvalues of the mass-weighted variance–covariance matrix of the atomic fluctuations determined from an MD simulation. The entropy was then estimated from these frequencies using the harmonic-oscillator approximation:
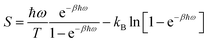 | (2) |
Third, entropies were obtained from B-factors using the method suggested by Polyansky et al.24 The B-factors are directly related to atomic root-mean squared fluctuations (RMSF) according to:
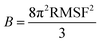 | (3) |
In the case of anisotropic B-factors, RMSFs for each coordinate can be obtained from the diagonal elements of the symmetric displacement tensor, for example:
| U11 = RMSFx | (4) |
To estimate the consistency of our calculations, we also estimated isotropic and anisotropic B-factors from MD simulations using cpptraj and used these to estimate entropies from the MD simulations.
Fourth, entropies were obtained using both B-factors and information from MD simulations, i.e. by combining the QHA and BF methods. The BF approach assumes that all atoms move independently of each other. To try to correct the entropies and take into account some correlated motions, we have calculated quasi-harmonic frequencies from a variance–covariance matrix in which the covariance (off-diagonal) terms were taken from an MD simulation and the variance (diagonal) terms were calculated from crystallographic B-factors as described above (eqn (3) and (4)).
Fifth, alternative conformations also provide a measure of conformational entropy in a crystal structure. Per-residue conformational entropy arising from residues existing in several alternative conformations can be estimated from:
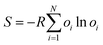 | (5) |
Finally, entropies can also be calculated from a normal-mode analysis (NMA) using an ideal-gas harmonic-oscillator approximation and employing vibrational frequencies calculated at the MM level.63 NMA calculations were performed on the full protein, in vacuum. Before calculating the harmonic frequencies from NMA, the systems were first minimized, also in vacuum, to a gradient of less than 0.001 kcal mol−1 Å−1. The calculations were performed with the nmode module of Amber 14, running in double precision.44
In summary, we used five different methods to obtain the atomic fluctuations:
(1) Traditionally-refined crystal structures with three different types of B-factor refinement: isotropic, anisotropic and TLS refinement.
(2) Crystal structures refined (using the same raw data) with ensemble refinement (which involves dihedral-space MD simulations with time-averaged restraints to the crystallographic data).
(3) A normal MD simulation in water solution, using periodic boundary conditions.
(4) A MD simulation of a single unit cell of the protein (without any crystallographic data, except the size of the unit cell).
(5) A MD simulation of two unit cells of the protein (also without any crystallographic data).
For the first two approaches, we employed two sets of crystal structures, viz. obtained at cryogenic temperature (100 K) or at room temperature (300 K). All crystal structures were first re-refined to ensure that the two structures with different ligands were treated in exactly the same way.
Based on these sets of structures, we have calculated entropies using four different methods:
(A) From the distribution of dihedral angles, using histogramming (DH).
(B) From a quasi-harmonic analysis of the fluctuation covariance matrix (QHA).
(C) From B-factors, using the QHA approach suggested by Polyansky et al.24 (BF).
(D) From a covariance matrix constructed from crystallographic B-factors as the diagonal terms and MD simulation atomic fluctuations for the off-diagonal terms (BF + MD).
The B-factors were obtained either from a refined crystal structure or from the root-mean-squared fluctuations of a MD simulation. Throughout the article, all entropies reported are as TΔS at 300 K, in units of kJ mol−1. Moreover, for the sake of simplicity we will write “entropies”, although we consider only conformational entropies. Uncertainties of entropies calculated from the MD simulations are standard errors over the 10 independent simulations (50 for DH).
Results and discussion
In this paper, we study whether it is possible to obtain reliable entropies from crystallographic B-factors. These are compared to entropies obtained from NMR relaxation experiments and from MD simulations. As discussed in the Methods section, we employed five different methods to obtain the atomic fluctuations and four different methods to calculate entropies. All methods were employed to study the conformational entropy for the binding of two diastereomeric ligands, called R and S (shown in Fig. 1), to the protein galectin-3C. The best methods were also employed on two additional proteins, lysozyme and trypsin. The results of the various methods are presented in separate subsections.Entropy calculations using B-factors for galectin-3C
For the galectin-3C crystal structures, we obtained B-factors in three different ways and then employed the BF method to calculate the corresponding entropies. The isotropic B-factors gave rather consistent results, with large entropies for the individual proteins (∼23 MJ mol−1, shown in Table S4 in the ESI†), and a large and positive difference in entropy between the S and R ligands (ΔSconf = Sconf(S) − Sconf(R) = 469 kJ mol−1; shown in Table 2) for the 100 K structures. If we instead used anisotropic B-factors, the total entropy decreased by 450–471 kJ mol−1 for both ligands, but ΔSconf was reduced by only 20 kJ mol−1. Clearly, these estimates of ΔSconf are too large. Experimentally, the difference in total binding entropy is 3 ± 1 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 and the difference in the conformational entropy of the protein has been estimated by NMR to 16 ± 14 kJ mol−1 (12 ± 8 kJ mol−1 for the backbone and methyl groups actually measured).38 Entropies estimated from MD simulations also give similar results, 10 ± 5 kJ mol−1
38 and the difference in the conformational entropy of the protein has been estimated by NMR to 16 ± 14 kJ mol−1 (12 ± 8 kJ mol−1 for the backbone and methyl groups actually measured).38 Entropies estimated from MD simulations also give similar results, 10 ± 5 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 or 7–12 ± 6 kJ mol−1 in this study, as is discussed below. Moreover, there is no correlation between the per-residue entropy estimated from the B-factors and that obtained from NMR for the backbone N atoms (R = 0.01). One reason for this is that the B-factor of each atom includes the translational and rotational movement of the entire protein.
38 or 7–12 ± 6 kJ mol−1 in this study, as is discussed below. Moreover, there is no correlation between the per-residue entropy estimated from the B-factors and that obtained from NMR for the backbone N atoms (R = 0.01). One reason for this is that the B-factor of each atom includes the translational and rotational movement of the entire protein.
| DH | QHA | BF-iso | BF-aniso | TLS | BF-100 K + MD | BF-300 K + MD | ||
|---|---|---|---|---|---|---|---|---|
| a As S-galectin-3C could not be refined with anisotropic B-factors at room temperature, only the diagonal elements of the MD covariance matrix were replaced in the entropy calculation for S at room temperature. | ||||||||
| Crystallographic refinement | 100 K | 469 | 448 | −29 | ||||
| 300 K | 55 | 67 | ||||||
| Standard MD | 10 ± 5 | −3 ± 26 | 2 ± 227 | 33 ± 87 | 892 ± 156 | −271 ± 56a | ||
| Crystal MD | 1 unit cell | 12 ± 6 | −12 ± 8 | 161 ± 119 | 58 ± 42 | 224 ± 110 | −663 ± 467a | |
| 2 unit cells | 7 ± 5 | 33 ± 6 | 288 ± 122 | 130 ± 42 | 415 ± 134 | −751 ± 358a | ||
| Ensemble refinement | 100 K | −100 ± 11 | 228 ± 4 | 157 ± 560 | −134 ± 280 | 495 ± 379 | ||
| 300 K | 3 ± 19 | −484 ± 3 | 736 ± 817 | 601 ± 621 | 887 ± 602 | |||
An alternative approach to obtain B-factors is to use TLS refinement. By modelling the whole protein as a rigid body (one TLS group), TLS refinement removes the translation and rotation of the entire protein within the crystal lattice. This had a pronounced influence on both the B-factors and the corresponding entropies. For the cryo-structures, the B-factors were reduced, on average, by a factor of about four. Likewise, the entropies were reduced by a factor of ∼6. Consequently, ΔSconf was also reduced, to a more proper order of magnitude, although it is still somewhat too large and it also became negative, ΔSconf = −29 kJ mol−1.
Using B-factors from crystal structures obtained from data collected at room temperature improved the entropy estimates, as these B-factors reflect more accurately the real movements that take place in the protein. The entropy difference was reduced by a factor of 8 for isotropic B-factor refinement, ΔSconf = 55 kJ mol−1. In fact, the entropy difference decreased for 113 of the 138 residues in the protein compared to the cryo structure, showing that this is not a random cancellation effect. However, there is still no correlation between the per-residue entropy estimated from the B-factors and that obtained from NMR for the backbone N atoms (R = 0.06). Moreover, the TLS refinement did not reduce the entropy difference for this data, ΔSconf = 67 kJ mol−1 (Table 2). The B-factors after extracting the TLS components (Table 1) show that rigid body motion is not an important component of the overall motion of the protein at room temperature. Anisotropic B-factor refinement was not possible for the S complex at room temperature so no entropy estimates from anisotropic B-factors are presented.
These results suggest that the room temperature B-factors provide a more realistic picture of movements in the protein, although the entropies are still ∼5 times higher than those estimated by NMR or calculated from the MD simulations. Finally, we note that if we use the original galectin-3C cryo-temperature crystal structures without any re-refinements, we obtain entropy differences, calculated from the anisotropic B-factors (with method BF), that are twice as large as after re-refinement, ΔSconf = 1000 kJ mol−1. This shows that B-factors are very sensitive to what residues are modelled in alternative conformations.
Standard MD simulations
Dihedral histogramming (DH), based on a standard MD simulation of the protein complexes in water solution gave ΔSconf = 10 ± 5 kJ mol−1, as mentioned above. Admittedly, this method focuses at least partly on different types of entropy than the other methods: DH primarily measures major changes in the dihedrals, i.e. different conformations, corresponding to what is treated by alternative conformations in crystal structures. In contrast, the B-factors should primarily reflect local movements (i.e. vibrations) in a single conformation that can be studied by vibrational normal-mode analysis. However, normal-mode analysis of the cryo crystal structure gave a ΔSconf of 47 kJ mol−1, one order of magnitude lower than entropies obtained from the corresponding B-factors. Calculating the entropy that arises only from the alternative conformations in the re-refined crystal structures leads to a ΔSconf of only −2 kJ mol−1. This is to be expected, as the main purpose of re-refinement was to model all differences in dynamics as a difference in B-factors. If we use instead the alternative conformations of the model in the original PDB files (100 K),38 the resulting entropy is −20 kJ mol−1, i.e. a similar magnitude as dihedral histogramming, but with the opposite sign.QHA on the standard MD simulations gave a result of a similar magnitude to dihedral histogramming, albeit with a larger uncertainty, ΔSconf = −3 ± 26 kJ mol−1. Extracting isotropic B-factors from the atomic RMSF in the MD simulation and calculating the entropy with the BF method gives a difference in entropy of 2 ± 227 kJ mol−1, i.e. with an uncertainty that is ∼100 times higher, making the result essentially useless. Extracting anisotropic B-factors instead lowered the uncertainty by a factor of 2, ΔSconf = 33 ± 87 kJ mol−1, but the uncertainty is still clearly too large for the result to be useful.
Crystal MD simulations
To investigate if the differences we observe between standard MD simulations and crystal structures stem from the differences between atomic motions in solution and in the crystal, we performed a MD simulation of galectin-3C in the cryo-temperature crystallographic unit cell (but at 300 K). From such a simulation, we can also calculate both entropies with DH or QHA and B-factors from the atomic fluctuations and then use them to calculate entropies. As can be seen from Table 2, DH gave essentially the same results as the standard MD simulation, ΔSconf = 12 ± 6 kJ mol−1. On the other hand, QHA gave somewhat different entropies, ΔSconf = −12 ± 8 kJ mol−1, a difference from DH that is significant with 97% confidence. This probably reflects that QHA is mainly a harmonic analysis, primarily aimed for molecules in the same conformation; for a dihedral with several minima, it will employ a Gaussian with a single minimum and a wide distribution.On the other hand, entropies obtained from B-factors calculated from the fluctuations during the crystal MD simulation gave ∼5 times larger absolute entropies and a much larger ΔSconf = 161 ± 119 kJ mol−1, with a very large uncertainty, as was also observed for the standard MD simulations. The absolute entropies are of the same magnitude as for the crystal structure, but slightly smaller. Using anisotropic B-factors calculated from the simulation reduced ΔSconf and the uncertainty (58 ± 42 kJ mol−1). It may be argued that the prime problem of the B-factor entropies, calculated in this way, is the poor precision (neither of the two results is significantly different from that of dihedral histogramming). These B-factors do not contain any common translation and rotation of the entire protein, because the structures were overlaid to a common structure before the fluctuations were calculated. However, they also do not contain any information on correlated movements, as no covariance terms are included in the variance–covariance matrix when using isotropic B-factors. A factor of 5, as used in the previous study by Polyansky et al., does not seem enough to correct the entropy differences. In fact, by including only the few off-diagonal terms from the anisotropic displacement tensor, the entropy estimates are drastically improved.
We have also performed calculations based on a MD simulation with two unit cells, in order to check that there are no boundary artefacts when using a single unit cell. The obtained results are comparable to the one-unit-cell simulation: ΔSconf is 7 ± 5 kJ mol−1 for DH, somewhat larger for QHA (33 ± 6 kJ mol−1) and much larger when using calculated B-factors (130 ± 42 kJ mol−1 with anisotropic B-factors). The precision of the latter calculations is still very poor. In fact, the only significant difference in ΔSconf between the two MD simulations is that obtained with QHA.
Ensemble refinement
Next, we employed structures obtained by ensemble refinement.43 These are essentially obtained from MD simulations performed in the crystal structure and restrained to agree with the crystallographic data. They use a TLS model for a large part of the protein (70% in this case), thus eliminating the translation and rotation of the whole protein. Ensemble refinement employs a MD simulation in dihedral space with a simplified energy function (without electrostatics), thus allowing for a much more extensive sampling of phase space than normal MD simulations (although the simulations are much shorter). It gives an ensemble of structures that show a single conformation for crystallographically well-defined groups, but many conformations for parts of the structure that are not well defined by the crystallographic data.38 It gives a different view of the crystal structure, providing very many (in this case ∼500) alternative conformations for less ordered parts of the structure, as an alternative to the B-factors that poorly describe the disorder in such parts of the structure. We then used this ensemble of structures to calculate entropies by DH. This gave almost twice as large absolute entropies as the crystal MD simulations and a much larger ΔSconf with the opposite sign, −100 ± 11 kJ mol−1 for the cryo-temperature structures. The QHA absolute entropies are slightly smaller than for the crystal simulations, but ΔSconf is much larger, 228 ± 4 kJ mol−1. From this ensemble of structures, we can also obtain B-factors, from which entropies can be calculated by the BF method. They gave very large uncertainties, as in the previous simulations, ΔSconf = 157 ± 560 kJ mol−1 with isotropic B-factors and −134 ± 280 with anisotropic B-factors.Ensemble refinement simulations started from the room-temperature structures resulted in slightly better entropy estimates, although still worse than those obtained from MD. The DH entropy was similar to that from MD, but with lower precision, ΔSconf = 3 ± 19 kJ mol−1. On the other hand, the QHA entropies were much larger and ΔSconf was negative, −484 ± 3 kJ mol−1. BF entropies were still too large and had a poor precision, ΔSconf = 736 ± 817 kJ mol−1 with isotropic B-factors and 601 ± 621 with anisotropic B-factors.
Combining experimental B-factors with MD simulations
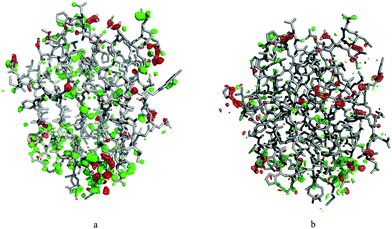
As entropies calculated from B-factors were always too large and imprecise independent on the method used to obtain atomic fluctuations, one can suspect that the prime problem is the lack of correlated movements included in the calculation. Consequently, we attempted to include covariance terms from the MD simulations in the variance–covariance matrix constructed from crystallographic B-factors (BF + MD). This would result in a matrix analogous to the one used in standard QHA. Unfortunately, this method gave the highest ΔSconf in this study, with uncertainties similar to those calculated directly from B-factors. ΔSconf for this method based on B-factors from the cryo-temperature crystal structures ranged from 224 ± 110 kJ mol−1 for covariances obtained from MD simulations in one crystal unit cell to 892 ± 156 kJ mol−1 for covariances obtained from standard MD simulations. Using the B-factors from room-temperature crystallographic data instead, which should be more compatible with MD simulations at 300 K, did not improve the entropy estimates. On the contrary, using room-temperature B-factors and off-diagonal terms from MD simulations in the QHA gave negative ΔSconf ranging from −271 ± 56 kJ mol−1 for solution MD simulations to −751 ± 358 kJ mol−1 for crystal MD simulations (note that this may be partly caused by the fact that we could only use isotropic B-factors for the S complex at room temperature, owing to the lower resolution of the crystal structure). These results suggest that B-factors from crystallographic refinement are not compatible with B-factors obtained from simulations, probably because they contain more information than just the atomic fluctuations, such as random noise or errors in the model.In order to check this hypothesis, we selected a random snapshot from the crystal MD simulation in one unit cell and ran two crystallographic refinements, one against the cryo-temperature data and one against the room-temperature data, keeping the B-factors fixed to those calculated from that simulation. The resulting electron density maps show an abundance of positive difference density peaks for both structures (Fig. 3), suggesting that the structures from MD simulations cannot reproduce the experimental electron density. As the coordinates were minimised in the crystallographic refinement, we can assume that the difference density peaks reflect mostly the incompatibility of the calculated B-factors. This is consistent with the findings of Kuzmanic et al.29 However, correlation of the data is also a significant problem: transferring the (tri-)diagonal elements from the QHA covariance matrix from one simulation to another also significantly deteriorated the calculated entropies.
Entropy calculations on trypsin and lysozyme complexes
In order to verify that the discrepancies between B-factor entropies and entropies calculated from MD simulations are not system specific, we performed a similar investigation on two other sets of protein–ligand systems. To reduce the data obtained, we compare entropies calculated with the BF method only with the most stable method found in the galectin-3C study, DH. Results for the two proteins are presented in Table 3.| Trypsin | Lysozyme | |
|---|---|---|
| BF-isotropic | 1287 | 685 |
| BF-anisotropic | 1385 | |
| BF-TLS | 883 | 565 |
| DH | 19 ± 12 | 21 ± 9 |
First, we studied trypsin in complex with benzamidine and benzylamine, which we will refer to by their PDB IDs, 5MNG and 5MNK. The entropy ΔSconf is always reported as ΔSconf = Sconf(5MNG) − Sconf(5MNK). Calculating the entropy from MD fluctuations gave a rather small entropy difference, 18 ± 12 kJ mol−1. This is expected, as the two complexes differ in only one amino group in the ligand (cf.Fig. 1b). In contrast, entropies calculated from the re-refined B-factors were two orders of magnitude higher, 1286 kJ mol−1 when using isotropic B-factors and 883 kJ mol−1 when using TLS refinement. These results are clearly useless and even worse than in the case of galectin-3C.
We also applied the BF method to two T4 lysozyme complexes, with N-phenylglycinonitrile and 3-methylbenzylazide, which will be referred to by their PDB IDs, 2RB2 and 2RBN. The estimated relative entropy is calculated as the difference ΔSconf = Sconf(2RBN) − Sconf(2RB2). Applying DH to the MD simulations gave an entropy difference of 21 ± 9 kJ mol−1, even though the structural differences between the ligands are larger than for the trypsin or galectin-3C complexes. Calculating the relative entropy using the BF method failed also in this case: the results show an almost 30 times higher relative entropy, 685 kJ mol−1 when using isotropic B-factors and 565 kJ mol−1 when using a TLS refinement. These results clearly show that the incompatibility between entropies obtained from crystallographic B-factors or MD simulations is not a problem specific only to galectin-3C.
Conclusions
We have studied whether reliable estimates of conformational entropies can be obtained from crystallographic B-factors. Such an approach would make conformational entropies directly available for all proteins with known crystal structures and provide a great wealth of thermodynamic information for many processes of great biophysical interest, e.g. ligand binding and protein–protein interactions. Unfortunately, initial estimates of entropies from B-factors (using the approach developed by Polyansky et al.24), gave poor entropies, compared to those obtained by NMR relaxation experiments or extracted from MD simulations. Therefore, we have here investigated whether it is possible to obtain useful entropies for crystallographic B-factors using carefully designed crystal structures and also tried to understand the problem with the B-factor entropies by comparing with entropies obtained from MD simulations, both in solution and in crystals, and employing several different methods to obtain the entropies. We have also tried to combine the data obtained from both B-factors and MD simulations.First, we decided not to study absolute entropies, but rather to restrict the study to the relative conformational entropy of two systems as similar as possible, viz. the same protein bound to two similar ligands. Second, we performed a re-refinement of the original crystal structures, to ensure that they were treated in exactly the same way and that alternative conformations were the same in both structures. Thereby, we minimise differences in contributions to the B-factors that do not come from atomic fluctuations. Third, we have removed contributions from the translation and rotations of the entire protein by using TLS refinement. Fourth, we have solved new crystal structures for galectin-3C at room temperature, because NMR experiments and MD simulations were performed at this temperature. However, conformational entropy estimates from B-factors were still an order of magnitude larger than entropies obtained from NMR experiments or from MD simulations. Moreover, the results may vary by more than 100% when the refinement strategy is changed.
To further understand the failure of the B-factor entropies, we have performed a number of MD simulations under different conditions: in water solution (similar to NMR experiments), in one or two crystal unit cells or using the crystallographic raw data (ensemble refinement). Then, we used a number of different methods to calculate entropies from these MD ensembles: DH, QHA, NMA and by calculating B-factors from the atomic fluctuations and then extract entropies from these B-factors. We showed that simulations in the crystal unit cell gave results similar to those obtained from MD simulations in solution. On the other hand, results obtained from ensemble refinement seemed too unreliable. Most importantly, attempts to calculate entropies from B-factors obtained from the MD simulations were unsuccessful. Including all elements of the anisotropic displacement tensor gave better entropy estimates, but the results were still four times larger than those obtained by QHA or DH. Furthermore, the precision of these calculations was too poor for any quantitative assessment.
It seems that an important reason for the failure of the B-factor entropies is that they lack information about the correlation of the movements. Therefore, we tried to include proper correlation through the off-diagonal terms of the variance–covariance matrix from an MD simulation. Unfortunately, B-factors obtained from crystallographic refinement seem to be incompatible with atomic fluctuations from MD simulations. This was also confirmed for the MD simulations (i.e. that diagonal elements from one simulation cannot be combined with off-diagonal elements from another simulation).
This study also gives some information about the reliability of the various methods to estimate entropies from MD simulations: it seems that DH is the most stable method. It gives the same results 7–12 kJ mol−1 and precision 5–6 kJ mol−1 for all three MD simulations of the two galectin-3 complexes (in solution or in the crystal, using one or two unit cells). QHA gives an appreciably larger variation −12 to 33 kJ mol−1 and also a larger uncertainty, 6–26 kJ mol−1. As discussed above, the two methods measure partly different contributions to the entropy (DH excludes bond and angle vibrations, as well as correlation, whereas QHA treats large variations in dihedrals inappropriately). This difference is strongly enhanced when using ensemble refinement (which samples only dihedral dynamics).
Finally, we show that the discrepancy between entropies calculated via B-factors or via MD simulations is not system-specific. Comparing the entropy estimates from crystallographic B-factors and dihedral histogramming for two other pairs of protein–ligand complexes gave also poor results, with B-factor entropies being one or two orders of magnitude higher than those obtained from MD simulations. Consequently, we have to conclude that it currently is not possible to extract useful entropies from crystallographic B-factors, even if the crystal structures are re-refined or if room-temperature data is employed. Therefore, currently it is only possible to obtain total entropies from isothermal titration calorimetry or contributions from selected groups from NMR experiments, whereas a detailed atomistic interpretation of the entropies can only be gained from molecular simulations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This investigation has been supported by grants from the Swedish Research Council (projects 2014-5540, 2015-05284 and 2018-05003), from the Knut and Alice Wallenberg Foundation (KAW 2013.0022), from eSSENCE: the e-Science Collaboration and from the Royal Physiographic Society in Lund. The computations were performed on computer resources provided by the Swedish National Infrastructure for Computing (SNIC) at Lunarc at Lund University and HPC2N at Umeå University. We thank staff at the BioMAX beamline of MAX IV for assistance with data collection.References
- H.-X. Zhou and M. K. Gilson, Theory of Free Energy and Entropy in Noncovalent Binding, Chem. Rev., 2009, 109, 4092–4107 CrossRef CAS PubMed.
- A. Velazquez-Campoy, I. Luque and E. Freire, The application of thermodynamic methods in drug design, Thermochim. Acta, 2001, 380, 217–227 CrossRef CAS.
- J. D. Chodera and D. L. Mobley, Entropy-Enthalpy Compensation: Role and Ramifications in Biomolecular Ligand Recognition and Design, Annu. Rev. Biophys., 2013, 42, 121–142 CrossRef CAS PubMed.
- Á. Tarcsay and G. M. Keserű, Is there a link between selectivity and binding thermodynamics profiles?, Drug Discovery Today, 2015, 20, 86–94 CrossRef PubMed.
- L. Liu and Q.-X. Guo, Isokinetic Relationship, Isoequilibrium Relationship, and Enthalpy−Entropy Compensation, Chem. Rev., 2001, 101, 673–696 CrossRef CAS PubMed.
- R. J. Falconer, A. Penkova, I. Jelesarov and B. M. Collins, Survey of the year 2008: applications of isothermal titration calorimetry, J. Mol. Recognit., 2010, 23, 395–413 CrossRef CAS PubMed.
- K. K. Frederick, M. S. Marlow, K. G. Valentine and A. J. Wand, Conformational entropy in molecular recognition by proteins, Nature, 2007, 448, 325–329 CrossRef CAS PubMed.
- C. Diehl, O. Engström, T. Delaine, M. Håkansson, S. Genheden, K. Modig, H. Leffler, U. Ryde, U. J. Nilsson and M. Akke, Protein flexibility and conformational entropy in ligand design targeting the carbohydrate recognition domain of galectin-3, J. Am. Chem. Soc., 2010, 132, 14577–14589 CrossRef CAS PubMed.
- S.-R. Tzeng and C. G. Kalodimos, Protein activity regulation by conformational entropy, Nature, 2012, 488, 236–240 CrossRef CAS PubMed.
- M. V. Novotny, M. J. Stone and L. Zídek, Increased protein backbone conformational entropy upon hydrophobic ligand binding, Nat. Struct. Biol., 1999, 6, 1118–1121 CrossRef PubMed.
- M. J. Stone, NMR Relaxation Studies of the Role of Conformational Entropy in Protein Stability and Ligand Binding, Acc. Chem. Res., 2001, 34, 379–388 CrossRef CAS PubMed.
- S. Genheden, M. Akke and U. Ryde, Conformational entropies and order parameters: convergence, reproducibility, and transferability, J. Chem. Theory Comput., 2014, 10, 432–438 CrossRef CAS PubMed.
- M. Akke, R. Brüschweiler and A. G. Palmer, NMR order parameters and free energy: an analytical approach and its application to cooperative calcium(2+) binding by calbindin D9k, J. Am. Chem. Soc., 1993, 115, 9832–9833 CrossRef CAS.
- T. I. Igumenova, K. K. Frederick and A. J. Wand, Characterization of the Fast Dynamics of Protein Amino Acid Side Chains Using NMR Relaxation in Solution, Chem. Rev., 2006, 1672–1699 CrossRef CAS PubMed.
- P. J. Sapienza and A. L. Lee, Using NMR to study fast dynamics in proteins: methods and applications, Curr. Opin. Pharmacol., 2010, 10, 723–730 CrossRef CAS PubMed.
- A. A. Polyansky, R. Zubac and B. Zagrovic, Methods in molecular biology, 2012, vol. 819, pp. 327–353 Search PubMed.
- J. Wereszczynski and J. A. McCammon, Statistical mechanics and molecular dynamics in evaluating thermodynamic properties of biomolecular recognition, Q. Rev. Biophys., 2012, 45, 1–25 CrossRef CAS PubMed.
- N. Hansen and W. F. Van Gunsteren, Practical aspects of free-energy calculations: a review, J. Chem. Theory Comput., 2014, 10, 2632–2647 CrossRef CAS PubMed.
- I. Andricioaei and M. Karplus, On the calculation of entropy from covariance matrices of the atomic fluctuations, J. Chem. Phys., 2001, 115, 6289–6292 CrossRef CAS.
- C.-E. Chang, W. Chen and M. K. Gilson, Ligand configurational entropy and protein binding, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 1534–1539 CrossRef CAS PubMed.
- S. Genheden, O. Kuhn, P. Mikulskis, D. Hoffmann and U. Ryde, The normal-mode entropy in the MM/GBSA method: effect of system truncation, buffer region, and dielectric constant, J. Chem. Inf. Model., 2012, 52, 2079–2088 CrossRef CAS PubMed.
- S. Genheden and U. Ryde, Will molecular dynamics simulations of proteins ever reach equilibrium?, Phys. Chem. Chem. Phys., 2012, 14, 8662–8677 RSC.
- K. N. Trueblood, H. B. Bürgi, H. Burzlaff, J. D. Dunitz, C. M. Gramaccioli, H. H. Schulz, U. Shmueli, S. C. Abrahams and IUCr, Atomic Displacement Parameter Nomenclature. Report of a Subcommittee on Atomic Displacement Parameter Nomenclature, Acta Crystallogr., Sect. A: Found. Crystallogr., 1996, 52, 770–781 CrossRef.
- A. A. Polyansky, A. Kuzmanic, M. Hlevnjak and B. Zagrovic, On the contribution of linear correlations to quasi-harmonic conformational entropy in proteins, J. Chem. Theory Comput., 2012, 8, 3820–3829 CrossRef CAS PubMed.
- V. Schomaker and K. N. Trueblood, On the rigid-body motion of molecules in crystals, Acta Crystallogr., Sect. A: Found. Crystallogr., 1968, 24, 63–76 CrossRef CAS.
- M. D. Winn, G. N. Murshudov and M. Z. Papiz, Macromolecular TLS Refinement in REFMAC at Moderate Resolutions, Methods Enzymol., 2003, 374, 300–321 CAS.
- J. Kuriyan and W. I. Weis, Rigid protein motion as a model for crystallographic temperature factors, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 2773–2777 CrossRef CAS PubMed.
- B. Schneider, J.-C. Gelly, A. G. de Brevern and J. Černý, Local dynamics of proteins and DNA evaluated from crystallographic B factors, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2014, 70, 2413–2419 CrossRef CAS PubMed.
- A. Kuzmanic, N. S. Pannu and B. Zagrovic, X-ray refinement significantly underestimates the level of microscopic heterogeneity in biomolecular crystals, Nat. Commun., 2014, 5, 3220 CrossRef PubMed.
- H. Leffler, S. Carlsson, M. Hedlund, Y. Qian and F. Poirier, Introduction to galectins, Glycoconjugate J., 2002, 19, 433–440 CrossRef CAS PubMed.
- A. C. MacKinnon, S. L. Farnworth, P. S. Hodkinson, N. C. Henderson, K. M. Atkinson, H. Leffler, U. J. Nilsson, C. Haslett, S. J. Forbes and T. Sethi, Regulation of Alternative Macrophage Activation by Galectin-3, J. Immunol., 2008, 180, 2650–2658 CrossRef CAS PubMed.
- D. Delacour, A. Koch and R. Jacob, The Role of Galectins in Protein Trafficking, Traffic, 2009, 10, 1405–1413 CrossRef CAS PubMed.
- F. T. Liu and G. A. Rabinovich, Galectins: regulators of acute and chronic inflammation, Ann. N. Y. Acad. Sci., 2010, 1183, 158–182 CrossRef CAS PubMed.
- A. Grigorian and M. Demetriou, in Glycobiology, ed. M. Fukuda, Academic Press, 2010, vol. 480, pp. 245–266 Search PubMed.
- G. A. Rabinovich, F.-T. Liu, M. Hirashima and A. Anderson, An Emerging Role for Galectins in Tuning the Immune Response: Lessons from Experimental Models of Inflammatory Disease, Autoimmunity and Cancer, Scand. J. Immunol., 2007, 66, 143–158 CrossRef CAS PubMed.
- P. Sörme, P. Arnoux, B. Kahl-Knutsson, H. Leffler, J. M. Rini and U. J. Nilsson, Structural and thermodynamic studies on cation-π interactions in lectin-ligand complexes: high-affinity galectin-3 inhibitors through fine-tuning of an arginine-arene interaction, J. Am. Chem. Soc., 2005, 127, 1737–1743 CrossRef PubMed.
- K. Saraboji, M. Håkansson, S. Genheden, C. Diehl, J. Qvist, U. Weininger, U. J. Nilsson, H. Leffler, U. Ryde, M. Akke and D. T. Logan, The carbohydrate-binding site in galectin-3 is preorganized to recognize a sugarlike framework of oxygens: ultra-high-resolution structures and water dynamics, Biochemistry, 2012, 51, 296–306 CrossRef CAS PubMed.
- M. L. Verteramo, O. Stenström, M. M. Ignjatović, O. Caldararu, M. A. Olsson, F. Manzoni, H. Leffler, E. Oksanen, D. T. Logan, U. J. Nilsson, U. Ryde and M. Akke, Interplay between Conformational Entropy and Solvation Entropy in Protein-Ligand Binding, J. Am. Chem. Soc., 2019, 141, 2012–2026 CrossRef CAS PubMed.
- P. Emsley, B. Lohkamp, W. G. Scott and K. Cowtan, Features and development of Coot, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 486–501 CrossRef CAS PubMed.
- P. D. Adams, P. V. Afonine, G. Bunkóczi, V. B. Chen, I. W. Davis, N. Echols, J. J. Headd, L.-W. Hung, G. J. Kapral, R. W. Grosse-Kunstleve, A. J. McCoy, N. W. Moriarty, R. Oeffner, R. J. Read, D. C. Richardson, J. S. Richardson, T. C. Terwilliger, P. H. Zwart and IUCr, PHENIX: a comprehensive Python-based system for macromolecular structure solution, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 213–221 CrossRef CAS PubMed.
- J. Schiebel, R. Gaspari, T. Wulsdorf, K. Ngo, C. Sohn, T. E. Schrader, A. Cavalli, A. Ostermann, A. Heine and G. Klebe, Intriguing role of water in protein-ligand binding studied by neutron crystallography on trypsin complexes, Nat. Commun., 2018, 9, 3559 CrossRef PubMed.
- A. P. Graves, D. M. Shivakumar, S. E. Boyce, M. P. Jacobson, D. A. Case and B. K. Shoichet, Rescoring Docking Hit Lists for Model Cavity Sites: Predictions and Experimental Testing, J. Mol. Biol., 2008, 377, 914–934 CrossRef CAS PubMed.
- B. T. Burnley, P. V. Afonine, P. D. Adams and P. Gros, Modelling dynamics in protein crystal structures by ensemble refinement, eLife, 2012, 1, e00311 CrossRef PubMed.
- D. A. Case, J. T. Berryman, R. M. Betz, D. S. Cerutti, T. E. Cheatham, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, T. Luchko, R. Luo, B. Madej, K. M. Merz, G. Monard, P. Needham, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. E. Roitberg, R. Salomon-Ferrer, C. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, D. M. York and P. A. Kollman, AMBER 14, University of California, San Francisco, 2014 Search PubMed.
- D. R. Roe and T. E. Cheatham, PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- C. Diehl, S. Genheden, K. Modig, U. Ryde and M. Akke, Conformational entropy changes upon lactose binding to the carbohydrate recognition domain of galectin-3, J. Biomol. NMR, 2009, 45, 157–169 CrossRef CAS PubMed.
- J. Uranga, P. Mikulskis, S. Genheden and U. Ryde, Can the protonation state of histidine residues be determined from molecular dynamics simulations?, Comput. Theor. Chem., 2012, 1000, 75–84 CrossRef CAS.
- F. Manzoni, J. Wallerstein, T. E. Schrader, A. Ostermann, L. Coates, M. Akke, M. P. Blakeley, E. Oksanen and D. T. Logan, Elucidation of Hydrogen Bonding Patterns in Ligand-Free, Lactose- and Glycerol-Bound Galectin-3C by Neutron Crystallography to Guide Drug Design, J. Med. Chem., 2018, 61, 4412–4420 CrossRef CAS PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew, J. Chem. Phys., 2004, 120, 9665–9678 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- S. Genheden and U. Ryde, A comparison of different initialization protocols to obtain statistically independent molecular dynamics simulations, J. Comput. Chem., 2011, 32, 187–195 CrossRef CAS PubMed.
- H. Gohlke and D. A. Case, Converging free energy estimates: MM-PB(GB)SA studies on the protein–protein complex Ras–Raf, J. Comput. Chem., 2004, 25, 238–250 CrossRef CAS PubMed.
- A. Weis, K. Katebzadeh, P. Söderhjelm, I. Nilsson and U. Ryde, Ligand Affinities Predicted with the MM/PBSA Method: Dependence on the Simulation Method and the Force Field, J. Med. Chem., 2006, 49, 6596–6606 CrossRef CAS PubMed.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- X. Wu and B. R. Brooks, Self-guided Langevin dynamics simulation method, Chem. Phys. Lett., 2003, 381, 512–518 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS.
- O. Edholm and H. J. C. Berendsen, Entropy estimation from simulations of non-diffusive systems, Mol. Phys., 1984, 51, 1011–1028 CrossRef CAS.
- N. Trbovic, J. H. Cho, R. Abel, R. A. Friesner, M. Rance and A. G. Palmer, Protein side-chain dynamics and residual conformational entropy, J. Am. Chem. Soc., 2009, 131, 615–622 CrossRef CAS PubMed.
- M. Karplus and J. N. Kushick, Method for estimating the configurational entropy of macromolecules, Macromolecules, 1981, 14, 325–332 CrossRef CAS.
- R. M. Levy, M. Karplus, J. Kushick and D. Perahia, Evaluation of the Configurational entropy for Proteins: Application to Molecular Dynamics Simulations of an alpha-Helix, Macromolecules, 1984, 17, 1370–1374 CrossRef CAS.
- D. A. Case, Normal mode analysis of protein dynamics, Curr. Opin. Struct. Biol., 1994, 4, 285–290 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp02504a |
| This journal is © the Owner Societies 2019 |