Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Error-consistent segmented contracted all-electron relativistic basis sets of double- and triple-zeta quality for NMR shielding constants†
Yannick J.
Franzke
 *a,
Robert
Tre߇
a,
Tobias M.
Pazdera
a and
Florian
Weigend
*a,
Robert
Tre߇
a,
Tobias M.
Pazdera
a and
Florian
Weigend
 *b
*b
aKarlsruhe Institute of Technology (KIT), Institute of Physical Chemistry, Kaiserstraße 12, 76131 Karlsruhe, Germany. E-mail: yannick.franzke@partner.kit.edu
bKarlsruhe Institute of Technology (KIT), Institute of Nanotechnology, Hermann-von-Helmholtz-Platz 1, 76344 Karlsruhe, Germany. E-mail: florian.weigend@kit.edu
First published on 4th July 2019
Abstract
We present property-tailored all-electron relativistic Karlsruhe basis sets for the elements hydrogen to radon. The modifications described herein use at most four additional primitive basis functions and re-optimized contraction coefficients of the inner-most segment. Thus, the shielding constants are improved while maintaining the compactness of the basis set. A large set of 255 closed-shell molecules was used to assess the quality of the developed bases throughout the periodic table of elements.
1 Introduction
All-electron relativistic quantum chemistry has witnessed tremendous progress in the last decade.1–6 Especially the development of the (one-electron) exact two-component theory (X2C)7–14 made all-electron relativistic calculations widely applicable. Here, the basis set expansion in one-particle wave functions is carried out and exploited right from the beginning. The electronic and positronic states are decoupled by block diagonalization of the four-component Dirac matrix leading to an electrons-only two-component Hamiltonian. Thus, the X2C Hamiltonian is only available in matrix form and not within an operator formalism like e.g. in Douglas–Kroll–Hess (DKH)15–17 theory. In quantum chemistry, Gaussian-type orbitals (GTOs) are “usually” chosen for the basis expansion. In this way, the tasks are reduced to the integral evaluation and algebraic operations, which are efficiently carried out on contempory computer architectures. The employed basis sets are characterized by the fixed exponents of the Gaussian functions. For economic reasons, a number of so-called primitive Gaussian-type orbitals (pGTOs) are combined to form a contracted Gaussian-type orbital (cGTO). The conceptionally easiest way is to use the same set of pGTOs to construct every cGTO. Well-known examples of this general contraction scheme for relativistic theories are the atomic natural orbitals basis set, ANO-RCC,18–21 and the bases of Dyall,22–29 which are also employed in “fully” relativistic four-component calculations. On the contrary, atomic shells can also be described by segments. Here, the first cGTO describes the 1s shell and the inner part of the 2s shell. The part of the 2s shell beyond the first radial node is then fitted by the second cGTO and so on. This segmented scheme is exploited in the Karlsruhe X2C30 and Sapporo bases.31–33 In X2C and familiar theories such as the normalized elimination of the small component (NESC),34,35 the Hamiltonian is evaluated in the primitive basis space since the contraction coefficients of the electronic and the positronic states differ significantly. The Hamiltonian is contracted after the relativistic decoupling to be used in the self-consistent field (SCF) procedure. Thus, the contraction coefficients have to be determined for this approach. For the Karlsruhe X2C bases, exponents and contraction coefficients are optimized simultaneously within the one-component X2C approach employing the finite-nucleus model. Basis sets are usually developed by minimizing the total energy with respect to the exponents and the contraction coefficients.30,36–43 In relativistic quantum chemistry, the finite nucleus model based on a Gaussian charge distribution44 is chosen instead of the point charge model to remove the singularity at the nucleus. For basis set optimizations, the finite nucleus approach is mandatory; otherwise the exponents become extremely large, but just model the non-physical singularity of the point-charge approach.Bases developed in this way can be safely used for energy-related properties such as bond energies, geometries and harmonic frequencies.41 The chemically most important region of the atoms are the valence shells. Consequently, so called valence basis sets use a smaller number of basis functions in the core region and thus reduce the computational effort. Typically one cGTO is used for each inner shell (or segment) and X cGTOs are used for the valence shells. Further, sets of higher angular quantum number are needed to describe polarization and – in case of post-Hartree–Fock methods – correlation effects. Often their type and number is chosen according to a strict correlation consistent scheme.45,46 The Karlsruhe basis sets30,41–43 follow these prescriptions concerning contraction and polarization schemes less strictly. They rather focus on consistent errors in structure parameters, bond energies and selected properties in molecular calculations for the entire periodic table.
Electric properties like higher-order multipole moments, polarizabilities and hyperpolarizabilities require additional diffuse functions.47 These basis extensions can still be determined variationally, for instance, by maximizing atomic Hartee–Fock polarizabilities in analytical derivative theory. In contrast, magnetic properties such as nuclear magnetic resonance (NMR) shielding and spin–spin coupling constants depend on the density in the vicinity of the nuclei. Thus, additional steep basis functions may be needed,48,49 in particular for relativistic calculations, where the density is subject to spatial contraction. In this work, we examine the present shortcomings of the Karlsruhe x2c-XVPall (X = S, TZ)30 bases for the calculation of NMR shielding constants and present modifications to overcome these.
2 Design and optimization of the basis set extensions
Bases optimized for NMR shifts cannot be obtained based on the variational principle and the Newton–Raphson algorithm only. Instead a large even-tempered (ET) basis set30 with a factor of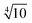 between its exponents up to tight functions was chosen as a reference herein. The property-tailored basis sets, x2c-SVPall-s and x2c-TZVPall-s, were constructed in several steps focusing on the valence and the core region.
between its exponents up to tight functions was chosen as a reference herein. The property-tailored basis sets, x2c-SVPall-s and x2c-TZVPall-s, were constructed in several steps focusing on the valence and the core region.
At first, errors in the valence region of the existing all-electron relativistic Karlsruhe basis sets with respect to the ET bases were determined for a large set50 of more than 250 molecules. This set is based on a previous test set, which was prepared earlier41,51 and contains nearly every element in its common oxidation state. The corresponding structures were optimized at the BP86/def-SV(P)36,38 level using ECPs for the heavy elements. Herein, we only study closed-shell compounds. The Cartesian coordinates of the corresponding molecules are given in the ESI.† All calculations were performed with our recent implementation to calculate NMR shielding tensors52,53 in TURBOMOLE54–56 employing the finite nucleus model for both the scalar potential and the vector potential. PBE functional57 was selected. Symmetry was not exploited to check for basis set deficits being reflected by slightly different results for symmetry equivalent nuclei. The SCF convergence thresholds in all calculations were 10−8Eh. All DFT calculations use grid 4a for the exchange–correlation potential, which was developed in the course of this work. It has been noted previously58 that all-electron relativistic DFT calculations may require extended grids for numerical integration. So, grids optimized in non-relativistic or effective core potential (ECP) calculations may not be sufficient. We have investigated the impact of the number of radial points in X2C-DFT calculations of atoms and molecules (details are given in the ESI†) and found that extended grids (indicated by the appendix “a”) can be obtained by determining the number of radial grid points, r, for an atom based on the atom number, Z, according to
| r = 20 + 5·(n − 1) + Z, | (1) |
The results for the x2c-TZVPall basis sets, the higher polarized variant, x2c-TZVPPall, and the variant for two-component calculations, x2c-TZVPall-2c, that accounts for spatial splitting of inner shells into subshells l ± s (induced by spin–orbit coupling) by additional GTOs, are shown in Fig. 1. It comes as no surprise that the error increases from light to heavy elements and so does the standard deviation. Additional polarizing functions lead to only minor improvements, while the spin–orbit extensions result in a significantly better agreement with the results obtained with the ET bases. However, the standard deviation for the 6p group is still rather large. The x2c-TZVPall-2c basis set employs roughly 30% more functions to describe the spin–orbit splitting. Most of these functions are of p and d type. While the extensions clearly improve the results, the increased size is somewhat disadvantageous. Nevertheless, the spin–orbit extensions of the x2c-TZVPall-2c bases provide a reasonable starting point for the choice of more economic extensions. The additional functions are employed as primitives to ensure a higher flexibility. For the heavy elements, functions with a larger exponent (280 < ζ < 330 for the 6p group) are added to flexibilize the description of the density in the outer-core region. The exponents were optimized with the test set above in several cycles reducing the mean absolute error in the NMR shieldings and form the x2c-TZVPall-s basis set. Exponents for cerium to ytterbium were obtained by systematically increasing that of lanthanum and for luthenium by decreasing the exponents of hafnium.
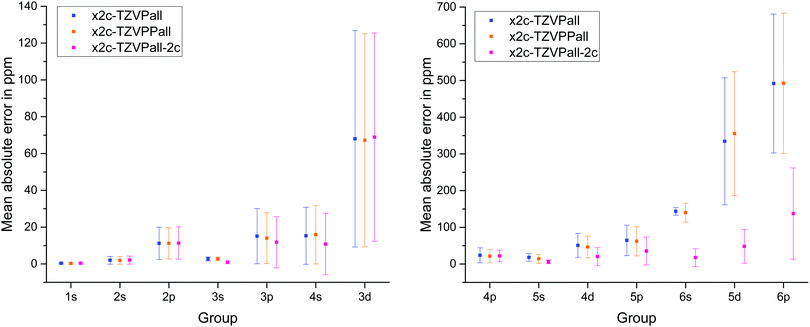 | ||
| Fig. 1 Mean absolute error in the shielding constants and standard deviation of various Karlsruhe triple-ζ bases with respect to an even-tempered basis set. | ||
These extensions mainly correct the outer-core and the valence region. To improve the description of the inner-most shells tight p functions were introduced. In line with ref. 49, a single additional p function was added for each element. Therefore, the exponent of the inner-most primitive function of the parent x2c-SVPall or x2c-TZVPall set was scaled with a factor of 6.5 (test calculations have shown that a factor between 5 and 8 is well suited). Moreover, the outer-most primitive was excluded from the segment and utilized as augmenting function to increase the flexibility. Thus, the contraction coefficients of the new segment need to be re-optimized at the X2C level of theory. The X2C Hamiltonian, hX2C, is evaluated in the primitive space and contracted after the relativistic decoupling. Hence, the relativistic one-electron Hamiltonian, h, reads
| h = C†hX2CC, | (2) |
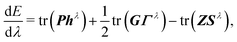 | (3) |
| hλ = C†,λhX2CC + C†hX2CCλ. | (4) |
The contraction coefficients are optimized in atomic calculations utilizing a quasi-Newton algorithm based on the variational principle. The electronic state of the atoms30 was prepared by exploiting symmetry constraints in a restricted open-shell Hartree–Fock (ROHF)61 calculation with SCF and density thresholds of 10−10Eh and 10−10, respectively. The unrestricted Hartree–Fock (UHF) method was used for the lanthanides. The molecular orbital coefficients of the decontracted p shell formed the starting point for the optimization. Table 1 shows the resulting basis set pattern. All exponents of the x2c-TZVPall-s basis set differ at least by a factor of 1.5 to ensure a solid SCF convergence behavior. Furthermore, the x2c-TZVPPall-s is constructed by augmenting the x2c-TZVPall-s basis with the usual polarization functions.41
| Elements | x2c-SVPall-s | x2c-TZVPall-s | ||
|---|---|---|---|---|
| Primitive space | Contracted space | Primitive space | Contracted space | |
| H, He | (4s2p) | [2s2p] | (5p2p) | [3s2p] |
| Li | (7s4p) | [3s3p] | (11s4p) | [5s4p] |
| Be | (7s5p) | [3s3p] | (11s5p1d) | [5s4p1d] |
| B–O, Ne | (7s5p1d) | [3s3p1d] | (11s7p2d1f) | [5s4p2d1f] |
| F | (8s5p1d) | [4s3p1d] | (12s7p2d1f) | [6s4p2d1f] |
| Na | (10s7p1d) | [4s3p1d] | (14s9p3d) | [5s5p3d] |
| Mg | (10s8p1d) | [4s4p1d] | (14s9p3d) | [5s5p3d] |
| Al–Ar | (10s8p1d) | [4s4p1d] | (14s10p3d1f) | [5s6p2d1f] |
| K | (14s10p2d) | [5s4p2d] | (17s12p3d) | [6s5p3d] |
| Ca | (14s10p4d) | [5s4p2d] | (17s13p4d) | [6s6p3d] |
| Sc–Zn | (14s10p7d1f) | [5s4p4d1f] | (17s13p8d1f) | [6s6p5d1f] |
| Ga, Ge | (14s12p6d) | [5s6p3d] | (17s14p8d1f) | [6s7p4d1f] |
| As–Kr | (14s12p6d) | [5s6p3d] | (17s15p8d1f) | [6s7p4d1f] |
| Rb, Sr | (18s15p10d1f) | [6s6p5d1f] | (20s22p11d1f) | [8s8p6d1f] |
| Y–Ag | (18s16p10d1f) | [6s7p5d1f] | (20s22p12d1f) | [8s8p6d1f] |
| Cd | (18s17p10d1f) | [6s8p5d1f] | (20s22p12d1f) | [8s8p6d1f] |
| In–Xe | (18s16p10d) | [6s7p4d] | (20s22p12d2f) | [8s8p5d2f] |
| Cs, Ba | (23s20p11d4f) | [7s7p6d1f] | (24s25p14d4f) | [11s9p7d1f] |
| La | (23s20p14d5f) | [7s7p7d2f] | (24s25p15d5f) | [11s9p8d2f] |
| Ce–Yb | (23s19p14d7f1g) | [7s7p7d3f1g] | (24s24p15d8f1g) | [11s8p8d4f1g] |
| Lu | (23s20p14d6f1g) | [7s8p7d2f1g] | (24s25p15d7f1g) | [11s9p8d2f1g] |
| Hf–Au | (23s20p14d6f) | [7s7p7d2f] | (24s25p15d7f) | [11s9p8d2f] |
| Hg | (23s21p14d6f) | [7s8p7d2f] | (24s25p15d7f) | [11s9p8d2f] |
| Tl–Rn | (23s22p13d6f) | [7s10p5d2f] | (24s26p15d8f) | [11s10p7d3f] |
Test calculations have shown that the contraction pattern of the p functions of the x2c-TZVPall-s set of sulfur and chlorine (421111) needs to be modified compared with aluminum, silicon and phosphorus (511111) in order to significantly improve the shielding constants. This also holds for the x2c-SVPall-s bases where the pattern is changed from (5111) to (4211).
The existing auxiliary bases30 for the resolution of the identity fitting approximation for the Coulomb term (RI-J)38,62–65 can be used. Here, only the total density needs to be fitted. This does not hold for the RI approximation to the exchange integrals66,67 (RI-K) or the application of the RI method to post-Hartee–Fock or post-Kohn–Sham theory,51,68 where the products of the basis functions have to be approximated.
3 Documentation of accuracy and comparison to other relativistic basis sets
For the evaluation of the accuracy, the same test set as above is used. Further, the developed basis sets are compared to the contracted Sapporo triple-ζ31,33 (Sapporo-TZP-2012 and Sappro-DKH3-TZP-2012, here abbreviated as Sapporo-TZP) and Dyall's uncontracted triple-ζ valence22–27,29 (Dyall-VTZ) set. Decontraction was done as suggested by Dyall to decrease linear dependency, e.g. for La the second d function from the SCF set was omitted, and Dunning's uncontracted cc-pVTZ bases46 were used for the lighter elements (1s to 3p, and 3d). All calculations were performed as specified in Section 2 and statistically evaluated. The individual shielding constants are given in the ESI.† There, the shielding constants and the corresponding deviations with different bases are further compared to the range of the experimental NMR shifts and the corresponding double-ζ basis sets are discussed. Equivalent shielding constants were counted only once. We calculated the mean absolute error (MAE) and the standard deviation of the difference of NMR shielding constants, Δσ, for each group instead of a percent-wise error, |Δσ/σET|, as done in ref. 49, since the denominator is very large for heavy elements. The results are listed in Table 2.| Group | n g | ANO-RCC-unc | Dyall-VTZ | Sapporo-TZP | TZVPall | TZVPPall | TZVPall-2c | TZVPall-s |
|---|---|---|---|---|---|---|---|---|
| 1s | 93 | 0.1 ± 0.3 | 0.2 ± 0.3 | 0.2 ± 0.4 | 0.4 ± 0.4 | 0.3 ± 0.4 | 0.4 ± 0.4 | 0.3 ± 1.1 |
| 2s | 19 | 0.9 ± 0.5 | 0.2 ± 0.2 | 5 ± 4 | 2 ± 2 | 2 ± 2 | 2 ± 2 | 1.1 ± 0.9 |
| 2p | 194 | 2 ± 6 | 11 ± 9 | 12 ± 14 | 11 ± 9 | 11 ± 9 | 11 ± 9 | 5 ± 6 |
| 3s | 14 | 0.2 ± 0.1 | 1.1 ± 0.6 | 2 ± 4 | 2.7 ± 1.1 | 2.7 ± 0.9 | 0.8 ± 0.7 | 0.8 ± 0.7 |
| 3p | 76 | 4 ± 11 | 14 ± 19 | 13 ± 19 | 15 ± 15 | 14 ± 14 | 12 ± 14 | 11 ± 13 |
| 4s | 12 | 29 ± 33 | 31 ± 44 | 26 ± 34 | 15 ± 15 | 16 ± 16 | 11 ± 17 | 11 ± 16 |
| 3d | 27 | 3 ± 4 | 22 ± 32 | 72 ± 76 | 68 ± 59 | 67 ± 58 | 69 ± 57 | 30 ± 26 |
| 4p | 24 | 2 ± 5 | 8 ± 12 | 12 ± 8 | 24 ± 20 | 21 ± 18 | 22 ± 16 | 19 ± 17 |
| 5s | 8 | 0.7 ± 0.7 | 10 ± 13 | 54 ± 38 | 18 ± 10 | 14 ± 12 | 6 ± 5 | 13 ± 12 |
| 4d | 21 | 2 ± 3 | 11 ± 11 | 141 ± 113 | 51 ± 33 | 47 ± 30 | 20 ± 25 | 47 ± 45 |
| 5p | 18 | 13 ± 12 | 45 ± 73 | 66 ± 28 | 65 ± 42 | 62 ± 40 | 35 ± 38 | 36 ± 28 |
| 6s | 8 | 16 ± 28 | 10 ± 12 | 78 ± 54 | 144 ± 11 | 140 ± 26 | 18 ± 24 | 28 ± 19 |
| 5d | 21 | 5 ± 6 | 25 ± 37 | 378 ± 259 | 335 ± 173 | 355 ± 169 | 48 ± 46 | 63 ± 52 |
| 6p | 19 | 18 ± 13 | 111 ± 184 | 657 ± 159 | 492 ± 189 | 492 ± 191 | 138 ± 124 | 84 ± 103 |
Even for the light elements (1s to 2p) the standard deviation and the mean absolute error are significantly reduced. Here, the additional tight p function and the re-optimized contraction are the main improvement. The Dyall-VTZ and the Sapporo-TZP basis sets do not feature such tight p functions and show somewhat larger errors. The ANO-RCC-unc bases perform well except for the 4s group, where a large error due to calcium occurs. The ANO-RCC-unc basis set does not employ very tight p functions. Here, the high flexibility allows for an accurate description of the density in the core and the valence region.
For the heavier elements, the x2c-TZVPall-s set shows a rather small standard deviation and is thus error balanced. The main improvement here is achieved by the higher flexibility. In contrast, the Sapporo bases show again larger errors and deviations for the d elements as well as for the 6p group. There the error amounts to 657 ppm while the other sets show errors of 189 ppm (ANO-RCC-unc), 84 ppm (x2c-TZVPall-s) and 111 ppm (Dyall-VTZ). The errors of the latter are smaller than the impact of different functional classes (PBE vs. PBE0). The large error of the Sapporo-TZP set cannot be addressed to a single molecule as all except for RnF2 show errors larger than 500 ppm. For the 3d and 4d elements the error mainly stems from Cu, Mo, Tc and Ru compounds.
In general, the Dyall-VTZ and our tailored basis sets are in rather good agreement. It should be noted that the Sapporo and Dyall's basis sets feature considerably more functions. In total, the Sapporo basis set employs more than 9000 functions for the elements up to Rn whereas x2c-TZVPall and the x2c-TZVPall-s use roughly 6000. For Rn, the x2c-TZVPall-s set uses (24s26p15d8f) functions which are contracted to [11s10p7d3f], that is less than for the x2c-TZVPall-2c set, (24s35p17d8f) contracted to [11s11p9d3f]. The Sapporo-TZP and the uncontracted Dyall-VTZ set consist of (27s21p15d12f2g) functions contracted to [10s9p7d4f1g] and (30s26p17d11f), respectively. To compare with, the ANO-RCC-unc and the even-tempered set employ (25s22p16d12f4g) and (47s35p25d18f8g) functions. Computation times with the different bases are given for W(CO)6 in Table 3, which is one of the largest molecules of the test set. Note that the x2c-TZVPall and the x2c-TZVPall-2c set is identical for light elements such as carbon and oxygen. Therefore, the employment of the x2c-TZVPall-s results in higher computational demands for W(CO)6 but also yielding more accurate results. The CPU times of the Karlsruhe basis sets are similar and differ by only one minute. The use of the Sapporo bases results in an increase of the computation time by a factor of 1.7 whereas the Dyall basis only leads to an increase by a factor of 1.2. This is due to the X2C response (ca. 70% of the total time) in the primitive space. Upon application of the diagonal local approximation to the unitary decoupling,52,69,70 the two-electron integrals are the most demanding part of the NMR shielding calculation and contracted basis sets will become more advantageous. Then, calculations employing the Sapporo and the Dyall basis set take a factor of 1.6 longer compared to the x2c-TZVPall-s bases.
| NBF | SCF | X2C-NMR | DLU-NMR | |
|---|---|---|---|---|
| ANO-RCC-unc | 1497 | 65.8 | 383.8 | 320.6 |
| Dyall-VTZ | 760 | 1.6 | 17.1 | 9.7 |
| Sapporo-TZP | 514 | 2.0 | 23.1 | 9.0 |
| x2c-TZVPall | 453 | 0.9 | 12.9 | 5.0 |
| x2c-TZVPall-2c | 480 | 1.1 | 14.9 | 5.9 |
| x2c-TZVPall-s | 500 | 1.2 | 15.8 | 6.0 |
To allow for a simple comparison of the accuracy and the size of the basis set throughout the periodic table of elements, we propose a weighted overall error, η, which considers the range of the shieldings, wg, and the number of symmetry non-equivalent nuclei, ng, of each group, g. The following nuclei are chosen for the determination of wg: H (1s), Be (2s), O (2p), Mg (3s), S (3p), Ca (4s), Cr (3d), Se (4p), Sr (5s), Mo (4d), Sn (5p), Ba (6s), W (5d), Pb (6p). The weighted overall error then follows as
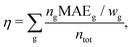 | (5) |
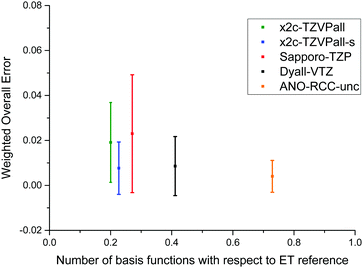 | ||
| Fig. 2 Comparison of various triple-ζ and the ANO-RCC-unc basis sets. The weighted overall error (see eqn (5)) is compared to the total number of contracted basis functions in the spherical atomic orbital (AO) basis. | ||
4 Comparison to other NMR-tailored bases
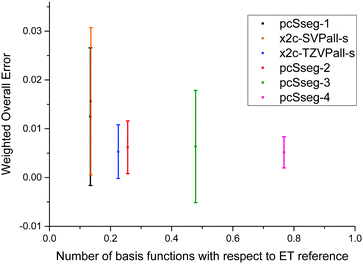
We further compare our tailored basis sets to the pcSseg bases48,49 of Jensen, which are available only for elements up to krypton. Thus, only the corresponding subset of molecules are considered. Computational methods are the same as above, however, a percent-wise error as proposed in ref. 49 serves as the decisive quantity here. The errors are still measured with respect to the ET bases. Concerning the size, the x2c-TZVPall-s lies in between pcSseg-1 and pcSseg-2, and x2c-SVPall-s set is of nearly the same size as pcSseg-1. Moreover, the pcSseg-3 and pcSseg-4 bases employ functions with a higher angular momentum such as g and h functions. The percent-wise error of each group is listed in Table 4 while the individual shielding constants are given in the ESI,† and the weighted overall errors are displayed in Fig. 3. The weighted overall errors were computed as described in the last section. The pcSseg bases do not systematically approach the ET limit with increasing size for all groups due to the pcSseg-3 set. The pcSseg-0 bases lead to large errors for the 2p and the 3d group. There, compounds of copper and fluorine are not well described. Moreover, the x2c-SVPall-s, the pcSseg-1 and the pcSeg-2 basis set show considerably large errors for copper. For the light elements (1s to 3p), the errors of our tailored triple-ζ bases mainly lie in between pcSseg-1 and pcSseg-2, as expected by its construction and size. For the heavier elements, errors of x2c-TZVPall-s clearly drop below pcSseg-2 and even below pcSseg-4 for the 4s and 4p group despite the missing g and h functions. Here, the additional primitive p of the 4p group or d function of the 3d group results in a significant improvement due to the additional flexibility. The x2c-SVPall-s basis set lies in between the pcSseg-0 and pcSseg-1 ones considering performance for the 1s up to the 3s group. However, the error of the 3d group is halved compared to the pcSseg-1 set. For the 4p group, it is the same as obtained with the pcSseg-2 bases. Overall, the x2c-TZVPall-s bases perform significantly better than the pcSseg-3 basis set but use less than half of the functions for the test set. The x2c-SVPall-s bases show a similar accuracy as the pcSeg-1 basis set and are of very similar size (total of 12292 functions vs. 12187).| Group | n g | pcSseg-0 | pcSseg-1 | pcSseg-2 | pcSseg-3 | pcSseg-4 | x2c-SVPall-s | x2c-TZVPall-s |
|---|---|---|---|---|---|---|---|---|
| 1s | 76 | 5.3 | 1.0 | 0.4 | 0.3 | 0.4 | 1.3 | 0.7 |
| 2s | 19 | 1.4 | 0.8 | 0.6 | 1.0 | 1.1 | 1.7 | 1.2 |
| 2p | 127 | 27.6 | 10.3 | 2.0 | 4.7 | 0.4 | 12.0 | 5.0 |
| 3s | 14 | 1.3 | 0.7 | 0.3 | 0.5 | 0.4 | 0.6 | 0.1 |
| 3p | 61 | 9.2 | 1.7 | 1.3 | 1.7 | 1.2 | 8.5 | 2.1 |
| 4s | 11 | 3.1 | 1.5 | 1.5 | 1.5 | 1.5 | 2.2 | 1.1 |
| 3d | 27 | 1049 | 116 | 29.2 | 7.3 | 2.5 | 53.8 | 10.6 |
| 4p | 22 | 9.0 | 5.0 | 3.6 | 3.3 | 2.8 | 3.6 | 1.3 |
5 Conclusions
We presented segmented contracted all-electron relativistic Karlsruhe basis sets for NMR shielding calculations optimized at the scalar X2C level employing the finite nucleus model for the scalar and the vector potential. The basis sets employ at most four additional functions and thus do not significantly enlarge the parent basis. The quality was assessed with a large set of 255 molecules.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Y. J. F. thanks Fonds der Chemischen Industrie for funding via a Kekulé scholarship. The basis sets are available in the ESI and further with TURBOMOLE V7.4 (2019).Notes and references
- T. Saue, ChemPhysChem, 2011, 12, 3077–3094 CrossRef CAS.
- D. Peng and M. Reiher, Theor. Chem. Acc., 2012, 131, 1081 Search PubMed.
- P. Pyykkö, Chem. Rev., 2012, 112, 371–384 CrossRef.
- W. Liu, Mol. Phys., 2010, 108, 1679–1706 CrossRef CAS.
- W. Liu, Phys. Rep., 2014, 537, 59–89 CrossRef.
- W. Liu, Natl. Sci. Rev., 2016, 3, 204–221 CrossRef.
- W. Kutzelnigg and W. Liu, J. Chem. Phys., 2005, 123, 241102 CrossRef PubMed.
- W. Kutzelnigg and W. Liu, Mol. Phys., 2006, 104, 2225–2240 CrossRef CAS.
- W. Liu and D. Peng, J. Chem. Phys., 2006, 125, 044102 CrossRef.
- W. Liu and D. Peng, J. Chem. Phys., 2006, 125, 149901 CrossRef.
- M. Iliaš and T. Saue, J. Chem. Phys., 2007, 126, 064102 CrossRef.
- W. Liu and W. Kutzelnigg, J. Chem. Phys., 2007, 126, 114107 CrossRef.
- D. Peng, W. Liu, Y. Xiao and L. Cheng, J. Chem. Phys., 2007, 127, 104106 CrossRef.
- W. Liu and D. Peng, J. Chem. Phys., 2009, 131, 031104 CrossRef.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 CAS.
- B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748 CrossRef CAS.
- G. Jansen and B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 6016–6017 CrossRef.
- B. O. Roos, V. Veryazov and P.-O. Widmark, Theor. Chem. Acc., 2004, 111, 345–351 Search PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2005, 109, 6575–6579 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov, P.-O. Widmark and A. C. Borin, J. Phys. Chem. A, 2008, 112, 11431–11435 CrossRef CAS.
- K. G. Dyall, Theor. Chem. Acc., 2002, 108, 335–340 Search PubMed.
- K. G. Dyall, Theor. Chem. Acc., 2003, 109, 284 Search PubMed.
- K. G. Dyall, Theor. Chem. Acc., 2006, 115, 441–447 Search PubMed.
- K. G. Dyall, Theor. Chem. Acc., 2004, 112, 403–409 Search PubMed.
- K. G. Dyall and A. S. P. Gomes, Theor. Chem. Acc., 2009, 125, 97 Search PubMed.
- A. S. P. Gomes, K. G. Dyall and L. Visscher, Theor. Chem. Acc., 2010, 127, 369–381 Search PubMed.
- K. G. Dyall, Theor. Chem. Acc., 2012, 131, 1217 Search PubMed.
- Basis sets available from the Dirac web site, http://dirac.chem.sdu.dk.
- P. Pollak and F. Weigend, J. Chem. Theory Comput., 2017, 13, 3696–3705 CrossRef CAS.
- T. Noro, M. Sekiya and T. Koga, Theor. Chem. Acc., 2012, 131, 1124 Search PubMed.
- M. Sekiya, T. Noro, T. Koga and T. Shimazaki, Theor. Chem. Acc., 2012, 131, 1247 Search PubMed.
- T. Noro, M. Sekiya and T. Koga, Theor. Chem. Acc., 2013, 132, 1363 Search PubMed.
- K. G. Dyall, J. Chem. Phys., 1997, 106, 9618–9626 CrossRef CAS.
- D. Cremer, W. Zou and M. Filatov, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 436–467 CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed.
- R. Ahlrichs and K. May, Phys. Chem. Chem. Phys., 2000, 2, 943–945 RSC.
- F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend and A. Baldes, J. Chem. Phys., 2010, 133, 174102 CrossRef.
- R. Gulde, P. Pollak and F. Weigend, J. Chem. Theory Comput., 2012, 8, 4062–4068 CrossRef CAS.
- L. Visscher and K. Dyall, At. Data Nucl. Data Tables, 1997, 67, 207–224 CrossRef CAS.
- K. Jankowski, R. Becherer, P. Scharf, H. Schiffer and R. Ahlrichs, J. Chem. Phys., 1985, 82, 1413–1419 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- F. Jensen, J. Chem. Theory Comput., 2008, 4, 719–727 CrossRef CAS.
- F. Jensen, J. Chem. Theory Comput., 2015, 11, 132–138 CrossRef CAS.
- The molecular test set contains the following 255 compounds: Ag2, AgCl, Al2O3, Al2S3, AlCl3, AlF3, AlH3, Ar2, As4, As4S4, AsCl3, AsH3, At2, AtCl, AtF3, Au2, AuCl, B2H6, B3N3H6, B4H4, Ba4, BaF2, BaH2, BaO, BaS, Be2F4, Be2H4, Be4, BeC2H6, BeF2O2H4, BeH2, BeS, BF3, BH3, BH3CO, BH3NH3, BiF3, BiH3, Br2, BrCl, C2H2, C2H3N, C2H4, C2H6, C4H4, C6H6, CF4, CH2O, CH2O2, CH3N, CH4, CO, CO2, Ca4, CaCl2, CaF2, CaH2, Cd2, Cd2Cl2, CdMe2 (Me denotes CH3), Cl2, ClF, ClF3, Cr(CO)6, CrO3, Cs2, CsF, CsH, Cu2, Cu2O, Cu2S, CuCl, CuCN, CuF, CuH, F2, Fe(CO)5, ferrocene, GaCl, GaCl3, GaF, GaH3, GeCl4, GeF4, GeH4, GeO, GeO2, H2, H2CO3, H2O, H2O2, H2SO4, H3PO4, HBr, HCBr3, HCl, HCN, HCP, He2, HF, HFO, HFO2, Hg2, Hg2Cl2, HgF2, HgMe2, HI, HCN, HNO2, HNO3, H2S, H2S2, I2, ICl, InCl, InCl3, InH, InH3, K2, K2S, K3P, KBr, KCl, KF, KH, KI, Kr2, LaCl3, LaF3, LaH3, Li2, Li2O, Li4C4H12, Li4Cl4, Li4H4, Li8, LiBH4, LiCl, LiF, LiH, Li2S, Mg4, MgCl2, MgF2, MgH2, Mo2, Mo(CO)6, MoO3, N2, N2H2, N2H4, N4, Na2, NF3, NH3, NH4F, Na2O, Na2S, Na3N, Na3P, NaCl, NaF, NaH, NbO2F, Ne2, Ni(CO)4, OF2, Os(CO)5, OsO3, OsO4, P2, PF3, PF5, PH3, PLi3, PbH4, PbO, PbO2, PdBr2, Pd(CO)4, PoBr2, PoCl4, PoF2, PoF6, PoO2, Pt(CO)4, PtO2, Rb2, RbF, RbH, Re2O7, Rn2, RnF2, Ru(CO)5, RuO2, RuO4, S5, SF2, SF4, SF6, SbF3, SbH3, ScCl3, ScF3, ScH3, Se8, SeH2, SeO2, SiCl4, SiF4, SiH4, SiO2, SiS2, SnH4, SnO, SnO2, Sr4, SrF2, SrH2, SrO, SrS, TaF3, TaO2F, Tc2O7, TcO3F, TeH2, TeO2, TiCl4, Ti(CO)4, TiF4, TiH4, TiO2, TiS2, TlCl, TlCl3, TlH, TlH3, VH5, W(CO)6, WO3, XeF2, XeF4, XeOF4, YF, YF3, Zn2, ZnCl2, ZnF2, ZnH2, ZnMe2, ZrO, ZrO2.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- Y. J. Franzke and F. Weigend, J. Chem. Theory Comput., 2019, 15, 1028–1043 CrossRef.
- K. Reiter, F. Mack and F. Weigend, J. Chem. Theory Comput., 2018, 14, 191–197 CrossRef CAS.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 CAS.
- Developer's version of TURBOMOLE V7.4 2019, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- D. A. Pantazis and F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 363–374 CAS.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354 CrossRef CAS.
- P. Pulay, Mol. Phys., 1969, 17, 197–204 CrossRef CAS.
- C. C. J. Roothaan, Rev. Mod. Phys., 1960, 32, 179–185 CrossRef.
- O. Vahtras, J. Almlöf and M. W. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 283–290 CrossRef.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Weigend, M. Kattannek and R. Ahlrichs, J. Chem. Phys., 2009, 130, 164106 CrossRef.
- F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291 RSC.
- F. Weigend, J. Comput. Chem., 2008, 29, 167–175 CrossRef CAS.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- D. Peng and M. Reiher, J. Chem. Phys., 2012, 136, 244108 CrossRef.
- D. Peng, N. Middendorf, F. Weigend and M. Reiher, J. Chem. Phys., 2013, 138, 184105 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Grids for all-electron relativistic DFT, exponents and contractions coefficients of the x2c-SV(P)all-s, x2c-SVPall-s, x2c-TZVPall-s and x2c-TZVPPall-s basis set, Cartesian coordinates and NMR shielding constants of the studied molecules. See DOI: 10.1039/c9cp02382h |
| ‡ Present address: Ruhr-Universität Bochum, Quantum Chemistry Group, Universitätsstraße 150, 44780 Bochum, Germany. |
| This journal is © the Owner Societies 2019 |