View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a Creative Commons Attribution-Non Commercial 3.0 Unported Licence
DOI: 10.1039/C9CP02331C (Paper) Phys. Chem. Chem. Phys., 2019, 21, 24300-24307

Ligand stabilization of manganocene dianions – in defiance of the 18-electron rule†

Monalisa Yadav a, Hong Fang b, Santanab Giri c and Puru Jena *b
aIISER Kolkata, Haringhata Farm, Nadia, West Bengal – 741252, India
bPhysics Department, Virginia Commonwealth University, Richmond, VA 23238, USA. E-mail: pjena@vcu.edu
cSchool of Applied Sciences and Humanities, Haldia institute of Technology, Haldia, 721657, India

Received 24th April 2019 , Accepted 3rd September 2019

First published on 9th September 2019

Abstract

Manganocene [Mn(C5H5)2], a 17-electron system, is expected to have a high electron affinity, as addition of an extra electron would make it a closed-shell 18-electron system. Surprisingly, it has a very low electron affinity of only 0.28 eV. Combined with its high ionization potential of around 7.0 eV, manganocene, therefore, should not be eager to either donate or accept an electron. We show that this property can be fundamentally altered with the proper choice of ligands, even though the total electron count remains the same. For example, the electron affinities of manganocene-derivatives Mn[C5(CN)5]2 and Mn[C5(BO)5]2, created by replacing H with CN or BO, are found to be 4.78 eV and 4.85 eV, respectively, making these species superhalogens. The power of the ligands is further demonstrated by studying the stability of their di-anions. Note that [Mn(C5X5)2]2− (X = H, CN, BO) di-anions, with 19-electrons, have one electron more than necessary to satisfy the 18-electron rule for stability. This factor, combined with the unavoidable repulsion between the two extra electrons, should destabilize [Mn(C5X5)2]2−. While that is the case for [Mn(C5H5)2]2−, we show that both Mn[C5(CN)5]22− and Mn[C5(BO)5]22− are stable against auto-detachment of the second electron by 0.7 eV and 0.38 eV, respectively. These results, based on first-principles calculations, demonstrate that ligand-manipulation can be used as an effective strategy to design and synthesize new materials with novel and tailored properties.

Introduction

Understanding the stability of atoms, molecules, clusters, and solids forms the cornerstone of science. While detailed first-principles calculations of the electronic structure can elucidate the origin of this stability, simple electron counting rules, developed over a century, can help us understand it qualitatively in terms of the electronic shell closure. For example, the octet rule, brought into focus by Lewis in 1916[thin space (1/6-em)]1 and later refined by Langmuir,2 accounts for the observation that main group elements tend to combine in such a way that each atom has eight electrons (s2p6) in their valence shell. Compounds containing transition metal atoms, however, obey a different rule – the 18-electron rule3 where s, p, and d orbitals are full (s2p6d10). Similarly, the stability of benzene (C6H6), closo-borane (B12H122−) and Na clusters containing 2, 8, 20, 40, etc. atoms have been explained by the Huckel's rule,4 Wade–Mingos rule,5 and the jellium rule,6 respectively.

In this paper, we focus on the 18-electron rule. Although, there have been cases where the validity of the 18-electron rule has been questioned,7,8 it generally accounts for the stability of many organo-metallic complexes containing transition metals. In this regard, the discovery of ferrocene, Fe(C5H5)2, a simple compound with two cyclopentadienyl, Cp(C5H5), rings bound to an iron atom (Fe), was a breakthrough in organometallic chemistry. From the fuel to the pharmaceutical industry, ferrocene and its derivatives have resulted in numerous applications, such as antiknock agents in fuels for petrol engines,9 antimalarial drug,10 molecular sensor,11 electrochemical agents,12 liquid crystals,13 non-linear optical films and sensors,14 catalysts,15etc. The stability of ferrocene is due to the 18-electron rule, where the central Fe atom with 3d64s2 orbital configuration contributes eight electrons and the two cyclopentadienyl, Cp rings contribute five electrons each, making a total of 18 electrons. Because of this 18-electron rule, one would expect that manganocene, Mn(C5H5)2 with its 17-valence electrons, will have a large electron affinity and will be reactive. Using first-principles method, based on density functional theory, we found that manganocene defies this rule. For example, the electron affinity of Mn(C5H5)2 is very small, namely, 0.28 eV. However, this can be changed by replacing H ligands with CN or BO groups. The electron affinities of the resulting Mn[C5(CN)5]2 and Mn[C5(BO)5]2 compounds are 4.78 eV and 4.85 eV, respectively. Similarly, Mn[C5X5]22− dianions (X = H, CN, BO), which possess 19-electrons, should not be stable and should auto-eject the second electron because of electron–electron repulsion. While that is the case for Mn(C5H5)22−, Mn[C5(CN)5]22− and Mn[C5(BO)5]22− are stable against auto-detachment of the second electron by 0.7 eV and 0.38 eV, respectively. In this paper, we have analysed these results and illustrate the role the ligands play in ushering unusual chemistry. Our work demonstrates that ligand substitution can be an effective tool for the design and synthesis of compounds with unusual properties.

Computational method

All calculations are based on density functional theory and performed using Gaussian 1616 packages. The geometries of neutral and negatively charged manganocene and its derivatives are optimized using the GDIIS algorithm.17–19 The exchange–correlation potential was incorporated using the B3LYP20,21 functional, which is effective for studying organic molecules and organo-metallic complexes. The 6-31+G(d,p) basis sets are used in our calculations. The stability of these complexes is confirmed by calculating the vibrational frequencies and making sure that they are not imaginary. Since Mn is a transition metal atom and carries a magnetic moment of 5 μB due to its 3d54s2 configuration, we have performed spin-polarized calculations by optimizing the structures of neutral and negative ion species for all possible spin configurations. The optimized geometry and bond lengths for the lowest energy structure have been obtained using the Gauss View 5.0.9 software.22 Nucleus Independent Chemical Shift (NICS)23 calculations have been performed to study and analyse the aromatic behaviour of the organometallic complexes and the effect of ligands on aromaticity. We have computed the NMR properties using the default gauge induced atomic orbital (GIAO) method24–26 in Gaussian. In addition, we have also used Natural Bond Orbital (NBO)27,28 analysis for the charge states of atoms.27,28 To get a better understanding of the electronic structure and charge distribution, we also calculated the energy gaps between the Highest Occupied Molecular Orbital (HOMO)–Lowest Unoccupied Molecular Orbital (LUMO) and the Molecular Orbitals (MO). For these calculations, we have used Gauss View (NBO) and chemissian software.29

Results and discussions

To validate our computational methods and to highlight the role of ligands, we present in Fig. 1 the neutral and anion geometries of C5X5, (X = H, CN, and BO) and compare these with previous calculations and experiments. Note that all the geometries are planar and the C atom of CN and B atom of BO bind to the C atoms of the Cp ring. The electron affinities of these molecules are calculated by taking the energy difference between neutral and their negative ion, each in their lowest energy configuration. The results are given in Table 1 and compared with available experimental and prior theoretical results. We note that these results agree within 0.2 eV with previous results. This is consistent with the accuracy of theoretical results based on density functional theory as the energy depends upon the choice of exchange–correlation functional as well as the basis sets. The electron affinity of CN, namely 4.03 eV, is significantly larger than that of Cl (3.6 eV), which makes it a superhalogen. On the other hand, the electron affinity of BO is only 2.59 eV, which is best described as a pseudo-halogen. Because these electron affinities are much larger than that of H (0.75 eV), the electron affinities C5X5, X = CN, BO are also much larger than that of C5H5. It is also interesting to note that the electron affinity of C5(BO)5 is larger than that of C5(CN)5, even though the electron affinity of BO is significantly smaller than that of CN. The large electron affinities of C5X5, X = H, CN, BO, compared to the negative electron affinity of C6H6, is a consequence of the aromatic rule. Note that C6H6, with its 6π electrons, obeys the Huckel's rule of aromaticity while C5X5 species lack one electron to be aromatic; hence their electron affinities are large. We found that C5X52−, X = CN, BO di-anions are unstable against auto-detachment of the second electron.
image file: c9cp02331c-f1.tif
Fig. 1 Equilibrium geometries of neutral and mono-anionic C5X5, X = CN, BO. (a) C5(CN)5 neutral, (b) C5(CN)5 anion, (c) C5(BO)5 neutral, and (d) C5(BO)5 anion. All bond lengths are given in Angstroms.
Table 1 Comparison of electron affinities (EA in eV) of C5X5, X = H, CN, BO with previous calculations and available experiments. Note, calculated electron affinities of H, CN, and BO are, 0.75 eV, 4.03 eV, and 2.59 eV, respectively
Molecule EA Previous theory32 Experiment33
C5H5 1.73 1.72 1.786 ± 0.020
C5(CN)5 5.55
C5(BO)5 5.72

In order to study the effect of ligands on metallo-organic complexes, we focused on manganocene, Mn(C5H5)2 and its derivatives, Mn(C5X5)2, X = CN, BO. C5(CN)5 anion was first synthesized as early as 1966.30 Later on, its related complex monomeric structures, such as {C5(CN)5}2Co·(H2O)2(THF)2, were also synthesized.31 We note here that Mn(C5X5)2 complexes possess 17 valence electrons and adding one more will satisfy the 18-electron rule. Thus, we expected that electron affinities of Mn(C5X5)2, X = CN, BO will be larger than those of C5X5, X = CN, BO. However, it was not clear to us whether Mn(C5X5)22−, X = CN, BO complexes would be stable. While electron–electron repulsion between excess electrons can be reduced by distributing them on a larger complex, Mn(C5X5)22− complexes possess 19 electrons, which is one more than needed by the 18-electron rule. Our initial thinking was that these di-anions will be unstable. Our calculations proved it to be otherwise.

In Fig. 2 we present the ground state geometries of neutral and mono-anionic Mn(C5X5)2 (X = H, CN, BO) clusters. Note that the Mn atom has five unpaired 3d-electrons and hence Mn(C5X5)2 complexes could carry a net spin magnetic moment. In Fig. 2 we plot only those geometries that correspond to the preferred spin multiplicity. In the ESI,† we provide the total energies of clusters with other spin configurations. The neutral Mn(C5X5)2 (X = H, CN, BO) complexes have high spins (sextets). The mono-anions Mn(C5X5)2− (X = CN, BO), as expected, have quintet spin states. Although the preferred spin state of Mn(C5H5)2− is a singlet, its quintet state is only 0.08 eV higher in energy than the singlet state. Thus, within the accuracy of the DFT results, we conclude that both singlet and quintet states of Mn(C5H5)2− are energetically degenerate. The optimized ground state energy along with the stable spin state for all clusters are given in the ESI.†


image file: c9cp02331c-f2.tif
Fig. 2 Equilibrium geometries of neutral and mono-anionic Mn(C5X5)2 (X = H, CN, BO). The preferred spin multiplicity, 2S + 1, of each cluster is listed in Table 2. The distances between the Mn atom and the centre of the ring are shown in the figure in Angstrom. (a) Mn(C5H5)2 neutral, (b) Mn(C5H5)2 anion, (c) Mn(C5(CN)5)2 neutral, (d) Mn(C5(CN)5)2 anion (e) Mn(C5(BO)5)2 neutral, (f) Mn(C5(BO)5)2 anion.

In Table 2, we present the preferred spin multiplicities and electron affinities (EA) of Mn(C5X5)2 (X = H, CN, BO) complexes, which are calculated using the following equation,

EA = E[Mn(C5X5)2] − E[Mn(C5X5)2−].
E is the total energy of a cluster in its ground state configuration and preferred spin. Note that the electron affinity of manganocene, Mn(C5H5)2 is substantially reduced from that of C5H5. This was unexpected as Mn(C5H5)2 is a 17-electron system and adding an electron would satisfy the 18-electron rule. Hence, the electron affinity of Mn(C5H5)2 was expected to be quite large, possibly making it to a superhalogen. Mn(C5X5)2 (X = CN, BO), on the other hand, are found to be superhalogens, with electron affinities of 4.78 eV and 4.85 eV, respectively. It is interesting to note that the electron affinity of M[C5(BO)5]2 is larger than that of M[C5(CN)5]2, even though the electron affinity of BO is significantly smaller than that of CN.

Table 2 Electron Affinity (EA in eV), and the binding energy (ΔE2) of the subsequent electron added to the mono-anion
Molecule Spin multiplicity (2S + 1) EA (eV) ΔE2 (eV)
Neutral Anion
Mn(C5H5)2 6 1 0.28 −2.70
Mn(C5(CN)5)2 6 5 4.78 0.70
Mn(C5(BO)5)2 6 5 4.85 0.38

We next study the geometry and stability of Mn(C5X5)22− (X = H, CN, BO) dianions. Because these systems contain 19 electrons, we expected these to be unstable for two reasons. First, the two added electrons will repel and second, the cluster contains one more electron than necessary to satisfy the 18-electron shell closure rule. In Fig. 3 we present the optimized geometries of Mn(C5X5)22− (X = H, CN, BO) dianions. The stability of the dianions against electron detachment is calculated by using the following equation,

ΔE2 = E[Mn(C5X5)2−] − E[Mn(C5X5)22−].


image file: c9cp02331c-f3.tif
Fig. 3 Optimized geometries of Mn(C5X5)22− (X = H, CN, BO) dianions. The preferred spin multiplicity, M = 2S + 1, of each cluster is listed in the following. The distance between the centre of the rings and the Mn atom in Angstrom is shown in the figure. (a) Mn(C5H5)22−; M = 6, (b) Mn(C5(CN)5)22−; M = 4, (c) Mn(C5(BO)5)22−M = 4.

The results of ΔE2 are given in Table 2. Mn(C5H5)22− is unstable as expected and the dianion is less stable than the mono-anion by 2.7 eV. However, Mn(C5(CN)5)22− and Mn(C5(BO)5)22− are more stable than their respective mono-anions by 0.70 and 0.38 eV, respectively.

The stability of Mn(C5X5)22− (X = CN, BO) dianions originate from their geometries; the Mn atom is found to be off-centre, in contrast to the case with the mono-anions (Fig. 4). To confirm that the distortion in structure is the cause behind the stability, we calculated the vertical detachment energy (VDE) by taking the energy difference between the ground state geometry of the anion and that of its dianion at the geometry of the anion. Mn(C5(BO)5)22− and Mn(C5(CN)5)22−, thus created, are unstable against auto-detachment of the second electron by 0.60 eV and 0.74 eV, respectively. In addition, the enhanced stability of negatively charged Mn(C5(BO)5)2 and Mn(C5(CN)5)2 over that of Mn(C5H5)2 is due to the fact that the electron affinities of CN and BO are larger than that of H.


image file: c9cp02331c-f4.tif
Fig. 4 Top views showing the displacement of the Mn atom from the centre the ring when the clusters are doubly negatively charged. (a) Mn(C5(CN)5)2 anion; (b) Mn(C5(CN)5)2 dianion; (c) Mn(C5(CN)5)2 anion; (d) Mn(C5(CN)5)2 dianion.

To further examine the role of different ligands in accommodating electrons, we carried out the Natural Bond Orbital Analysis (NBO) for the studied anions. It turns out that the ligands are indeed critical in the stabilization of the charged organometallic compounds. In any charged state, where we have CN and BO, a major part of the added negative charge goes to these ligands in the cluster rather than to the rings or the metal atom. Among these, CN acts as a better ligand than H and BO in terms of its ability to accommodate more charges. This is consistent with the fact that CN has a larger electron affinity than that of BO and H.

The details of the NBO results are given in the ESI.† In the case of H as the ligand, the added electron goes to the d orbital of the metal atom in the neutral Mn(C5H5)2. When the second electron is added to this mono-anion, 78% of the charge goes to the C atoms of (C5H5)2 rings and 22% goes to the Mn atom. In contrast, the added electrons in Mn(C5(BO)5)2 and Mn(C5(CN)5)2 mainly go to the ligands BO and CN, respectively. In the case of Mn(C5(BO)5)2, when the first electron is added, 37% of the charge goes to the Mn atom, while 49% goes to the BO ligands. On adding the second electron, only 8% of the charge goes to the metal atom Mn, while 59% goes to the BO ligands. The trend of adding electrons accommodated by the ligands becomes even more prominent in the case of Mn(C5(CN)5)2. When the first electron is added, 32% of the charge goes to the metal while 65% of the charge goes to the CN ligands. When the second electron is added little charge goes to the metal atom while 66% of the charge goes to the CN ligands.

As mentioned in the Introduction, ferrocene, Fe(C5H5)2, is stable due to the 18-electron rule, where the central Fe atom with 3d64s2 orbital configuration contributes eight electrons and the two cyclopentadienyl, Cp, rings contribute five electrons each, making a total of 18 electrons. Compared to the case of ferrocene, the anionic state of either Mn(C5(CN)5)2 or Mn(C5(BO)5)2 should be stabilized according to the 18-electron rule, given that, compared to the 3d64s2 configuration of Fe, the electron configuration of Mn is 3d54s2 which is one electron less. However, as described in the paper, the di-anions, Mn(C5(CN)5)22− and Mn(C5(BO)5)22−, are more stable than their mono-anion counterparts. We note that it is the total number of electrons involved in the stabilization of the complex as a whole that matters, no matter where the extra electrons go – either to the metal core or to the ligands on the Cp rings. According to the NBO analysis given above, when the first and second electrons are added to the Mn(C5(CN)5)2 and Mn(C5(BO)5)2 to eventually form the di-anions, the electrons are shared by both the ligands of the Cp rings and the metal core, with the former twice as many as the latter. This suggests that all the added electrons participate in stabilizing the complex as a whole and, therefore, the total number of electrons involved in bonding for the di-anions is considered as 19.

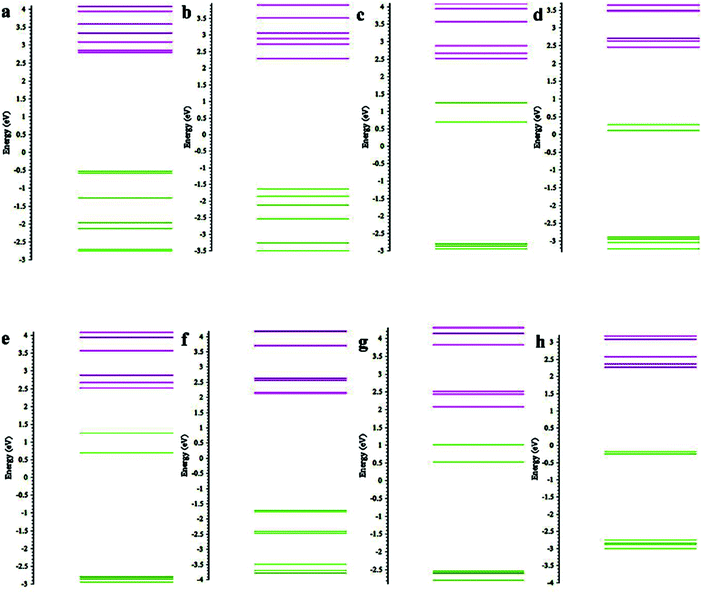
To gain further insight into the stability and electronic structure of the organometallic compounds, we also analysed the energy gap between the Highest Occupied Molecular Orbital (HOMO)–Lowest Unoccupied Molecular Orbital (LUMO). Since all the clusters have an open shell electronic configuration, we analysed HOMO–LUMO and Molecular Orbitals (MO) for both spin-up and spin-down electrons. The results are listed in Table 3. In the case of BO and CN as ligands, the HOMO–LUMO gap decreases as the charge on the cluster increases, undermining the corresponding stability. We can consider the HOMO–LUMO gap as an indicator of chemical stability and chemical reactivity. If the gap is large, it would be unfavourable to donate electron from a low lying HOMO or to accept electron into a high lying LUMO.34,35

Table 3 HOMO–LUMO Gap for spin-up and spin-down electrons for all the organometallic clusters studied
Molecule Spin-up (eV) Spin-down (eV)
Mn(C5H5)2 4.48 4.88
Mn(C5H5)2− 1.83 —
Mn(C5H5)22− 1.98 1.13
Mn(C5(CN)5)2 4.48 3.75
Mn(C5(CN)5)2− 3.84 2.48
Mn(C5(CN)5)22− 3.84 2.46
Mn(C5(BO)5)2 4.82 4.23
Mn(C5(BO)5)2− 4.10 2.68
Mn(C5(BO)5)22− 3.93 2.18

We also analysed the MO to understand the effect of ligands on the energy levels of the clusters. We find that for both spin up and spin down states, the HOMO energy level of the dianions decreases in the order of Mn(C5(H)5)2 > Mn(C5(BO)5)2 > Mn(C5(CN)5)2. (e.g. the HOMO level in the case of spin up are 3.23 eV, −1.64 eV, −1.71 eV, while for spin down they are 2.78 eV, 0.28 eV, −0.19, respectively). This suggests that the CN ligand provides greater stability to the molecules as compared to BO and H (see the ESI†). We further compared the energy levels of Mn(C5(CN)5)2 and Mn(C5(BO)5)2 dianions, both for the ground-state geometries of the dianion and the mono-anion. The spin up HOMO energies of Mn(C5(CN)5)2 and Mn(C5(BO)5)2 dianions at the geometry of the mono-anions are −0.85 eV and −0.51 eV, respectively, which are more than the HOMO energies of the dianions at the ground state geometry. Similarly, HOMO energies of spin down orbitals of Mn(C5(CN)5)2 and Mn(C5(BO)5)2 dianions at the geometry of the mono-anions are −0.52 eV and 1.24 eV, respectively. These levels are higher than the spin down HOMO energy of the ground state of the dianions. Indeed, the HOMO energy is lower for those with distorted structures (see Fig. 5). This suggests that the stability of the molecule increases due to the breaking of the symmetry of the structure caused by the ligands, which in turn lowers the energy of the system, in keeping with the Jahn–Teller-like effect.


image file: c9cp02331c-f5.tif
Fig. 5 Comparison of energy levels between the ground state geometry and at the geometry of the anion. (a), (c), (e), and (g) show the energy levels of Mn(C5(CN)5)2 and Mn(C5(BO)5)2 dianions at the geometry of anions with both up and down spin. (b), (d), (f), and (h) shows the energy levels of the dianions at the ground state geometry, respectively. (a) Mn(C5(BO)5)2 dianion (anion) spin up; (b) Mn(C5(BO)5)2 dianion spin down; (c) Mn(C5(BO)5)2 dianion spin down; (d) Mn(C5(BO)5)2 dianion spin down; (e) Mn(C5(CN)5)2 dianion spin up; (f) Mn(C5(CN)5)2 dianion spin up; (g) Mn(C5(CN)5)2 dianion (anion) spin down; (h) Mn(C5(CN)5)2 dianion spin down.

We also studied the fragment contribution to the various energy levels using the Chemissian software. In the case of neutral and anionic Mn(C5(H)5)2, spin-up LUMO has the highest contribution coming from Mn orbitals. In Mn(C5(H)5)22− dianion, spin-up and spin-down HOMO and LUMO are contributed by s orbital of Mn. The spin-up HOMO of Mn(C5(BO)5)2 is composed of Mn orbitals. In rest of the molecules with BO and H as ligands, the orbitals of the C atoms of the rings contribute to LUMO and HOMO and the nearby energy levels. Similar analysis of the clusters with CN as ligands shows that the orbitals of C atoms of the rings contribute to the energy levels, but we also found some exceptions in neutral and dianionic Mn(C5(CN)5)2, where spin-down orbitals of the CN ligand has the greatest contribution to HOMO–LUMO. We also compared the fragment contributions of clusters with different ligands, but in the same charged state and found that the orbitals of the CN ligand contribute maximum while orbitals of H ligand contribute minimum to the energy levels. The MO energy levels and fragment contribution to various levels are given in the ESI.† As an example, we have shown the HOMOs for spin-up and spin-down electrons of Mn(C5(BO)5)22− in the ESI.† It shows that the main contribution to the HOMO is from the inner skeleton as well as the metal atom.

Finally, Nucleus Independent Chemical Shift (NICS) calculations have been carried out to study the effect of ligands on the aromatic character and hence stability of the C5X5− (X= H, CN, BO) rings. Aromatic compounds are conjugated cyclic π electron systems that are highly stable due to charge delocalisation. Aromaticity cannot be directly measured from experiments36 but there are various descriptors that account for the aromatic behaviour based on energetic, geometric and magnetic criteria.37 Among them, NICS (magnetic criterion) is the most widely used and accepted method for measuring aromaticity.

According to conventions, NICS is taken to be the negative of the magnetic shielding value. In the literature, NICS(0) (calculated at the ring centre) or NICS(1) (calculated at a distance of 1 Å from the plane of the ring to better reflect the π electron effects) are generally reported. In some cases, they have resulted in providing wrong results.23 A better approach for determining NICS based aromaticity has been introduced recently.23 In this method, instead of calculating the NICS value just at a single point, they are calculated perpendicular to the planar ring at small intervals beginning from the centre up to a certain distance from the ring. The results obtained through this approach have proved to be more consistent with the experimental data. In this report, we have adopted the latter technique and have validated this method by using benzene as a benchmark. All calculations have been done using Gaussian 16 package. The NICS values have been calculated using the default gauge induced atomic orbital (GIAO) method for the optimized structures at the same level of theory. We have calculated the NICS values by placing the ghost atoms (Bq) at points ranging from the ring centre to a distance of 4.9 Å at intervals of 0.1 Å. NICS values for the C5X5− (X = H, CN, BO) rings along with that of benzene are given in Fig. 6.


image file: c9cp02331c-f6.tif
Fig. 6 NICS values versus distance from the centre (Å) for benzene, C5H5−, C5(BO)5− and C5(CN)5−.

We, see that NICS values are negative for these complexes, signifying their aromatic character. Benzene has a minimum around 1 Å (−10.5804 ppm at 0.8 Å) which is consistent with the value in the literature. C5(BO)5− has a minimum at 0.4 Å (−13.315 ppm) while C5(CN)5− and C5H5− have the minima at the ring centre (−8.0379 ppm and −15.7059 ppm respectively). Molecules where the σ aromaticity dominates over the π aromaticity have their minima at the ring centre whereas in molecules like C6H6 the π electron delocalisation dominates at certain distances from the ring.38 Presence of the minima in the curves arises due to the out of plane σ contribution, which decays rapidly with distance. The σ contribution is found through a method due to Stanger,39 and is then subtracted from the total to get the π aromaticity. Fig. 6 shows that C5(BO)5− and C5(CN)5− rings, which are closer to benzene, have higher π aromaticity than C5H5− ring and hence provide greater stability to the neutral and charged Mn(C5X5)2 (X = H, BO, CN). This result is consistent with our hypothesis that ligand plays an important role in determining the stability of the organometallic compounds. We can see that C5(CN)5− has a slightly greater aromaticity than C5(BO)5−, which is expected since electron affinity of CN is larger than that of BO. In addition, during the NBO analysis we saw that CN has a greater tendency to add electrons as compared to BO and H and in MO analysis, we found that CN ligand makes maximum contribution to HOMO–LUMO as compared to other ligands.

Conclusion

In summary, we have studied the structure and stability of an organo-metallic complex, manganocene and its derivatives (M(C5X5)2, X = H, CN, BO) using density functional theory. We show that the ligands can have strong influence on their properties and can over-power the effect of the electron counting rule. For example, M(C5X5)2 complexes should have large electron affinity and their dianions should not be stable. This is because these complexes have 17-electrons and adding an electron should make them very stable, according to the 18-electron rule. Thus, their electron affinities should be larger than those of halogens, making them super-halogens. Similarly, their dianions should not be stable not only because of the extra electron–electron repulsion, but also because they will have one-electron more than needed for the 18-electron shell closure. We find this not to be always true. The electron affinity of manganocene, M(C5H5)2 is very small, namely, 0.28 eV. However, in keeping with the expectation from the 18-electron rule, its dianion, Mn(C5H5)22− is unstable against spontaneous emission of the second electron. Things change when H is replaced by more electronegative ligands such as CN and BO. While, as expected, the electron affinities of M(C5X5)2 (X = CN, BO) are much larger than those of the halogens and hence these moieties are superhalogens, Mn(C5X5)22− (X = CN, BO) dianions are stable, in defiance of the 18-electrton rule. This is attributed to the Jahn–Teller-like effect where energy is gained by structural distortion as the Mn atom in Mn(C5X5)22− (X = CN, BO) moves away from the centre of the complex. We also studied Mn(C5X5)23− (X = H, CN, BO) tri-anions and found all of them to be unstable against auto-detachment of the third electron by 4.55 eV, 2.91 eV, and 3.28 eV, respectively. This study demonstrates the power of the ligands in determining the stability of a complex and the role they play in the rational design of multiply charged species.40,41

Conflicts of interest

There are no conflicts to declare.

References

  1. G. N. Lewis, The Atom and the Molecule, J. Am. Chem. Soc., 1916, 38, 762–785 CrossRef CAS.
  2. I. Langmuir, The Arrangement of Electrons in Atoms and Molecules, J. Am. Chem. Soc., 1919, 41, 868–934 CrossRef CAS.
  3. I. Langmuir, Types of Valence, Science, 1921, 54, 59 CrossRef CAS PubMed.
  4. E. Hückel, Quanstentheoretische Beiträge Zum Benzolproblem, Z. Phys., 1931, 72, 310–337 CrossRef; E. Hückel, Zur Quantentheorie Der Doppelbindung, Z. Phys., 1930, 60, 423–456 CrossRef.
  5. K. Wade, The Structural Significance of the Number of Skeletal Bonding Electron-Pairs in Carboranes, the Higher Boranes and Borane Anions, and Various Transition-Metal Carbonyl Cluster Compounds, J. Chem. Soc. D, 1971, 792–793 RSC; K. Wade, Structural and Bonding Patterns in Cluster Chemistry. In Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeléus and A. G. Sharpe, Academic Press, 1976, vol. 18, pp. 1–66 CrossRef CAS; D. M. P. Mingos, Polyhedral Skeletal Electron Pair Approach, Acc. Chem. Res., 1984, 17, 311–319 CrossRef CAS; D. Michael; P. Mingos and R. L. Johnston, Theoretical Models of Cluster Bonding, in Theoretical Approaches, Structure and Bonding, Springer Berlin Heidelberg, Berlin, 1987, vol. 68, pp. 29–87 Search PubMed.
  6. W. D. Knight, K. Clemenger, W. A. de Heer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Electronic Shell Structure and Abundances of Sodium Clusters, Phys. Rev. Lett., 1984, 52, 2141–2143 CrossRef CAS.
  7. M. Gupta, D. J. Singh and R. Gupta, Origin of the 20-Electron Structure of Mg3MnH7: Density Functional Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 092107 CrossRef.
  8. J. J. Concepcion, D. K. Zhong, D. J. Szalda, J. T. Muckerman and E. Fujita, Mechanism of water oxidation by [Ru(bda)(L)2]: the return of the “blue dimer”, Chem. Commun., 2015, 51, 4105–4108 RSC.
  9. V. E. Emel’yanov, L. S. Simonenko and V. N. Skvortsov, Ferrocene – a nontoxic antiknock agent for automotive gasolines, Chem. Technol. Fuels Oils, 2001, 37, 224–228 CrossRef.
  10. C. Roux and C. Biot, Ferrocene-based antimalarials, Future Med. Chem., 2012, 4, 783–797 CrossRef CAS PubMed.
  11. R. Sun, L. Wang, H. Yu, Z. ul-Abdin, Y. Chen, J. Huang and R. Tong, Molecular Recognition and Sensing Based on Ferrocene Derivatives and Ferrocene-Based Polymers, Organometallics, 2014, 33, 4560–4573 CrossRef CAS.
  12. R. R. Gagne, C. A. Koval and G. C. Lisensky, Ferrocene as an internal standard for electrochemical measurements, Inorg. Chem., 1980, 19, 2854–2855 CrossRef CAS.
  13. O. N. Kadkin and Y. G. Galyametdinov, Review on ferrocene-containing liquid crystals, Russ. Chem. Rev., 2012, 81, 675–699 CrossRef CAS.
  14. M. Shadaram, L. Espada, J. Martinez and F. Garcia, Modeling and performance evaluation of ferrocene-based polymer clad tapered optical fiber gas sensors, Opt. Eng., 1998, 37, 1124–1129 CrossRef CAS.
  15. A. Shafir and J. Arnold, Ferrocene-Based Olefin Polymerization Catalysts:[thin space (1/6-em)] Activation, Structure and Intermediates, Organometallics, 2003, 22, 567–575 CrossRef CAS.
  16. M. J. Frisch; G. W. Trucks; H. B. Schlegel; G. E. Scuseria; M. A. Robb; J. R. Cheeseman; G. Scalmani; V. Barone; G. A. Petersson; H. Nakatsuji; X. Li; M. Caricato; A. V. Marenich; J. Bloino; B. G. Janesko; R. Gomperts; B. Mennucci; H. P. Hratchian; J. V. Ortiz; A. F. Izmaylov; J. L. Sonnenberg; D. Williams-Young; F. Ding; F. Lipparini; F. Egidi; J. Goings; B. Peng; A. Petrone; T. Henderson; D. Ranasinghe; V. G. Zakrzewski; J. Gao; N. Rega; G. Zheng; W. Liang; M. Hada; M. Ehara; K. Toyota; R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; T. Vreven; K. Throssell; J. A. Montgomery, Jr.; J. E. Peralta; F. Ogliaro; M. J. Bearpark; J. J. Heyd; E. N. Brothers; K. N. Kudin; V. N. Staroverov; T. A. Keith; R. Kobayashi; J. Normand; K. Raghavachari; A. P. Rendell; J. C. Burant; S. S. Iyengar; J. Tomasi; M. Cossi; J. M. Millam; M. Klene; C. Adamo; R. Cammi; J. W. Ochterski; R. L. Martin; K. Morokuma; O. Farkas; J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
  17. P. Csaszar and P. Pulay, Geometry optimization by direct inversion in the iterative subspace., J. Mol. Struct. THEOCHEM, 1984, 114, 31 CrossRef CAS.
  18. O. Farkas, PhD (CsC) thesis, Eotvos University of Budapest (Budapest, Hungary), Hungarian, 1995.
  19. Ö. Farkas and H. B. Schlegel, Methods for geometry optimization of large molecules, J. Chem. Phys., 1998, 109, 7100 CrossRef.
  20. A. D. Becke, Density-functional Thermochemistry III. The role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
  21. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
  22. R. Dennington; T. Keith and J. Millam, GaussView, Version 5, Semichem Inc., Shawnee Mission, KS, 2009 Search PubMed.
  23. A. Stanger, Nucleus-Independent Chemical Shifts (NICS): Distance Dependence and Revised Criteria for Aromaticity and Antiaromaticity, J. Org. Chem., 2006, 71, 883–893 CrossRef CAS PubMed.
  24. R. Ditchfield, Self-consistent perturbation theory of diamagnetism: I. A gauge-invariant LCAO method for N.M.R chemical shifts, Mol. Phys., 1974, 27, 789 CrossRef CAS.
  25. F. Ribas Prado, C. Giessner-Prettre, J.-P. Daudey, A. Pullman, J. F. Hinton, F. Young and D. Harpool, Nuclear magnetic resonance spectroscopy applied to Li+ complexation by small ligands: An ab initio and experimental study of 7Li chemical shifts, J. Magn. Reson., 1980, 37, 431 Search PubMed.
  26. H. Fukui, K. Miura, H. Yamazaki and T. Nosaka, Calculation of NMR chemical shifts. V. The gauge invariant coupled Hartree–Fock calculation for H2O, H3O+ and OH−, J. Chem. Phys., 1985, 82, 1410 CrossRef CAS.
  27. A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899 CrossRef CAS.
  28. F. Weinhold, Natural bond orbital analysis: a critical overview of relationships to alternative bonding perspectives, J. Comput. Chem., 2012, 33, 2363–2379 CrossRef CAS PubMed.
  29. L. Skripnikov, Chemissian, a computer program to analyze and visualize quantum-chemical calculations; For the current version, see http://www.chemissian.com.
  30. W. Diazotetracyanocyclopentadiene. Webster, J. Am. Chem. Soc., 1966, 88, 3046–3050 CrossRef.
  31. R. J. Less, T. C. Wilson, M. McPartlin, P. T. Wood and D. S. Wright, Transition Metal Complexes of the Pentacyanocyclopentadienide Anion, Chem. Commun., 2011, 47, 10007–10009 RSC.
  32. B. Child, Aromaticity Rules in the development of negative ions, Virginia Commonwealth University, 2014 Search PubMed.
  33. P. C. Engelking and W. C. Lineberger, Laser photoelectron spectrometry of C5H5−: A determination of the electron affinity and Jahn–Teller coupling in cyclopentadienyl, J. Chem. Phys., 1977, 67, 1412 CrossRef CAS.
  34. B. L. Chen, W. G. Sun, X. Y. Kuang, C. Lu, X. X. Xia, H. X. Shi and G. Maroulis, Structural Stability and Evolution of Medium-Sized Tantalum-Doped Boron Clusters: A Half-Sandwich-Structured TaB12− Cluster, Inorg. Chem., 2018, 57, 343–350 CrossRef PubMed.
  35. W. Sun, X. X. Xia, C. Lu, X. Y. Kuang and A. Hermann, Probing the Structural and Electronic Properties of Zirconium Doped Boron Clusters: Zr Distorted B12 Ligand Framework, Phys. Chem. Chem. Phys., 2018, 20, 23740–23746 RSC.
  36. F. Feixas, E. Matito, J. Poater and M. Sola, Quantifying aromaticity with electron delocalisation measures, Chem. Soc. Rev., 2015, 44, 6434–6451 RSC.
  37. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion, Chem. Rev., 2005, 105, 3842 CrossRef CAS PubMed.
  38. J. O. C. Jiménez-Halla, E. Matito, J. Robles and M. Sola, Nucleus independent chemical shift (NICS) profiles in a series of monocyclic planar inorganic Compounds, J. Organomet. Chem., 2006, 691, 4359 CrossRef.
  39. A. Stanger, Obtaining Relative Induced Ring Currents Quantitatively from NICS, J. Org. Chem., 2010, 75, 2281–2288 CrossRef CAS PubMed.
  40. A. Dreuw and L. S. Cederbaum, Multiply charged anions in the gas phase, Chem. Rev., 2002, 102, 181 CrossRef CAS PubMed.
  41. H. Fang and P. Jena, Stable Tetra- and Penta-Anions in the Gas Phase, Angew. Chem., Int. Ed., 2019, 58, 11248–11252 CrossRef CAS PubMed.

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp02331c
This journal is © the Owner Societies 2019
Click here to see how this site uses Cookies. View our privacy policy here.