View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a
Creative Commons Attribution 3.0 Unported Licence
DOI: 10.1039/C9CP02330E (Paper) Phys. Chem. Chem. Phys., 2019, 21, 17142-17151

Elucidation of temperature-programmed desorption of high-coverage hydrogen on Pt(211), Pt(221), Pt(533) and Pt(553) based on density functional theory calculations†

Manuel J. Kolb‡§ a, Anna L. Garden bc, Cansin Badan a, José A. Garrido Torres de, Egill Skúlason b, Ludo B. F. Juurlink a, Hannes Jónsson b and Marc T. M. Koper *a
aLeiden Institute of Chemistry, Leiden University, P.O. Box 9502, 2300 RA Leiden, The Netherlands. E-mail: m.koper@lic.leidenuniv.nl
bFaculty of Industrial Engineering, Mechanical Engineering and Computer Science, University of Iceland, VR-III, 107 Reykjavík, Iceland
cUniversity of Otago, P.O. Box 56, Dunedin 9054, New Zealand
dStanford University, Department of Chemical Engineering, Stanford, California 94305, USA
eSUNCAT Center for Interface Science and Catalysis, Stanford Linear Accelerator Center, Menlo Park, California 94025, USA

Received 24th April 2019 , Accepted 15th July 2019

First published on 16th July 2019

Abstract

In this work we compute high-coverage hydrogen adsorption energies and geometries on the stepped platinum surfaces Pt(211) and Pt(533) which contain a (100)-step type and the Pt(221) and Pt(553) surface with a (111) step edge. We discuss these results in relation to ultra-high-vacuum temperature programmed desorption (TPD) data to elucidate the origin of the desorption features. Our results indicated that on surfaces with a (100)-step type, two distinct ranges of adsorption energy for the step and terrace are observed, which mirrors the TPD spectra for which we find a clear separation of the desorption peaks. For the (111) step type, the TPD spectra show much less separation of the step and terrace features, which we assign to the low individual adsorption energies for H atoms on this step edge. From our results we obtain a much clearer understanding of the surface–hydrogen bonding at high coverages and the origin of the different TPD features present for the two step types studied.

1 Introduction

Platinum surfaces are an important catalyst for hydrogenation reactions in heterogeneous catalysis.1 In these reactions, the interaction between the catalyst and the adsorbed, dissociated hydrogen plays a key role in the catalytic activity. The adsorption of hydrogen also plays an important role in electrocatalysis,2 where it is linked to the hydrogen evolution reaction. Ultra-high-vacuum (UHV) techniques can help in gaining insight into the adsorption properties of hydrogen and the influence of defect sites for both these fields. Accordingly, multiple experimental studies have focused on the interaction of platinum and hydrogen.3–9 These studies investigated not only the Pt(111) facet, but also regularly stepped surfaces such as Pt(211), Pt(533) and Pt(553) and the influence of step edges on the adsorption properties of hydrogen. A study of H2 dissociation dynamics using a curved Pt single crystal recently resolved that dissociation occurs predominantly in parallel at steps and terraces via direct mechanisms.10 From a theoretical standpoint several studies have dealt with hydrogen adsorption on the Pt(111) surface, and its interaction with co-adsorbates.11–13 Due to the larger complexity and higher computational cost, until recently only limited computational work was done on surfaces containing defects.14–16 As yet none of these studies drew a detailed link between the temperature programmed desorption experiments and the theoretical predictions.

A suitable experimental technique to obtain information about interaction and adsorption energies is temperature programmed desorption (TPD). However, in this approach there is not always a clear link between the desorption peak and the microscopic process from which it stems. Density functional theory (DFT) calculations can help provide this link and can therefore give a better view of the desorption pathways involved. One successful example of using theoretical calculations to elucidate TPD spectra is hydrogen desorption from the Pt(110)-(2 × 1)-reconstructed surface.17,18 In these systems, it was found that varying desorption barriers for different coverages can play a large role in determining the desorption pathways. However, to date no systematic study comparing different terrace lengths and step types has been performed.

Previous work in our group discussed the TPD spectra of deuterium desorbing from the Pt(211), Pt(533) and Pt(553) surfaces.6,7 We observed that for deuterium desorption, the surfaces with the (100) step type, namely the Pt(211) and Pt(533) surfaces, exhibit a two peak spectrum. The higher temperature peak was assigned to the desorption stemming from the step edge, while the lower temperature peak was assumed to originate from the (111) terrace, in accordance with the original assignment by Lu and Rye.3 In contrast, the Pt(553) surface, which has a (111)-type step edge, shows a significantly more complex spectrum, with up to four peaks assigned in the evaluation process.

In order to better understand these results, here we present DFT calculations on high-coverage hydrogen adsorption on the Pt(211), Pt(221), Pt(533) and Pt(553) model surfaces and compare these results with the TPD traces obtained in experiment. Furthermore, we present new experimental results on the Pt(221) surface, which completes our dataset for comparison to the other, previously reported, stepped surfaces. We find generally good correlation between the adsorption energies and the peak assignments from TPD elucidation, and are also able to finally assign the origin of the peaks on the surfaces with the (111) step type.

2 Computational methods

The ab initio density functional code VASP19–22 and the PBE functional23 with PAW projectors24,25 were used for all calculations. The step unit cell was replicated two times along the step edge to form a 1 × 2 super cell containing 1 step edge. The Pt(211) surface unit cell consists of a (100) step edge and 3 atom rows in the terrace (see Fig. 1a), while the Pt(533) surface contains the same step edge type, but is 4 atom rows wide, as can be seen in Fig. 1c. In contrast, the Pt(221) surface, shown in Fig. 1b, exhibits a (111) step edge and a 4 atom-row wide terrace and the Pt(553) surface (Fig. 1d) has the same step type, however a 5 atom-row wide terrace. The Brillouin zone was sampled using a 4 × 4 × 1 sampling for the Pt(211) and Pt(221) surface, while the Pt(533) and Pt(553) surfaces used a 3 × 9 × 1 sampling. A plane-wave basis set with a cutoff energy of 550 eV was selected. First-order Methfessel–Paxton smearing26 with a smearing width of 0.2 eV was used and all energies were extrapolated to 0 K. Additional information, including convergence data, about the model surfaces, which consist of 2 bottom layers that are fixed and three layers that are allowed to relax freely, can be found in ref. 27. Structures were relaxed until the remaining forces were below 0.04 eV Å−1.
image file: c9cp02330e-f1.tif
Fig. 1 Adsorption sites on (a) Pt(211), (b) Pt(221), (c) Pt(533) and (d) Pt(553) surfaces. Surface platinum atoms are marked in silver, first sub-surface layer platinum atoms are represented in blue, while the atoms in the second subsurface layer are shown in red. Golden lines indicate the Pt–Pt connectors in the surface plane, while the purple lines indicate the Pt–Pt connectors in the step plane. Subfigures (c) and (d) are taken from ref. 27. Space-filling versions of the images can be found in the ESI.†

The differential adsorption energies Gdiff,n·Hads are calculated as Gibbs free energies and are corrected for zero-point energy (ZPE) and vibrational entropy at 100 K, following the methods described by Loffreda28via the following procedure: the total Gibbs free energy for each adsorption structure was calculated as

 
Gtot,n·Hads = EDFT,n·H + ZPEn·H −T·Sn·H,tot,(1)
while the gas-phase references were calculated as
 
image file: c9cp02330e-t1.tif(2)
The values for SH2,tot are taken from tables for gas-phase species in ref. 29. In order to study the actual energy differences that occur when increasing the coverage, we use the so-called differential adsorption Gibbs free energies, mirroring previous work on this topic.17,18 These are calculated by referencing each energy to the structure with the most favorable energy of all structures with one less hydrogen atom per super cell:
 
Gdiff,n·Hads = Gtot,n·Hads − Gtot,min,(n−1)·Hads.(3)

In order to study the influence of barriers on the desorption characteristics of hydrogen from stepped Pt, we performed nudged-elastic-band (NEB) calculations.30 The barrier calculations were also performed with a cutoff energy of 550 eV, and were relaxed until the remaining forces orthogonal to the reaction coordinate were below 0.04 eV Å−1. The simulations used 7 images along the reaction coordinate. Climbing image NEB calculations31 for the converged pathways were attempted, but had notable convergence problems even after more than 250 structure optimization steps. The few calculations that did converge showed no noticeable change in the barrier height compared to the standard NEB calculations.

We note that in the following the term “coverage” is meant to signify the ratio H[thin space (1/6-em)]:[thin space (1/6-em)]Pt between the number of adsorbed hydrogen atoms per unit cell and the number of surface platinum atoms in the unit cell. For this count, we consider every atom with an on-top site marked in Fig. 1. Experimentally, a full mono-layer is usually defined as the maximum coverage that can be obtained under UHV conditions; however this reference can depend on the exposed facet and also experimental limitations. We choose the ratio between surface platinum atoms and adsorbate atoms to avoid this ambiguity.

In Fig. 1 the naming scheme for the adsorption sites is detailed. We also show space-filling versions of the images in the ESI.† In the following, we will discuss the adsorption structures suggested by our calculations for each surface facet at gradually increasing coverage. Each of the structures shown is the most favorable configuration for each individual coverage, since we expect that high diffusion rates14 allow the hydrogen atoms to move to their most favorable positions before the surface reaches the desorption temperature of hydrogen. For all discussed surfaces we study coverages of up to a maximum of 1[thin space (1/6-em)]:[thin space (1/6-em)]1 H[thin space (1/6-em)]:[thin space (1/6-em)]Pt ratio. From our results we conclude that this coverage in the DFT simulations is adequate to describe the TPD results for the following reasons: firstly, we find that increasing the coverage beyond this point leads to very unfavorable adsorption conditions in all studied cases. Furthermore, due to the already-present high coverage, the adsorption process would also experience a very high barrier, further reducing the probability of these structures being realized. Lastly, we find that the integrals obtained from the experimental TPD spectrum correspond favorably with the ones predicted by the DFT model with this maximum coverage, which implies that no coverages beyond the ratio of 1 hydrogen atom to 1 surface Pt atom are present in the experiment.

3 Experimental procedures

Our equipment and procedures have been discussed previously.32 Summarizing the most important aspects, our home-built (UHV) system has a base pressure of 5 × 10−11 mbar. It contains, among others, LEED optics (VG RVL 900) and a differentially pumped quadrupole mass spectrometer (QMS, Baltzers QMA 400). The samples are 10 mm diameter disc-shaped Pt single crystals of 5 N purity or better. Sample thickness varies between 1 and 2 mm. They are cut and polished with an alignment to expose the indicated stepped surface, i.e. (211), (221), (533), and (553), with a precision better than 0.1° (Surface Preparation Laboratory, Zaandam, The Netherlands). The polished side of the samples is cleaned under UHV conditions by repetitive cycles of Ar-ion sputtering at 1 kV and annealing at 1200 K. Low energy electron diffraction (LEED) confirms long-range order for all samples as shown before for Pt(211) and Pt(533).33 We verify that the expected average terrace width and step direction are maintained across the entire polished surface. Cleaned surfaces are exposed to molecular H2 or D2 by background dosing with the surface temperature generally maintained below 100 K until saturation is reached. The saturation coverage is determined by increasing exposure.33 We observe no isotope dependence for any of the surfaces in desorption experiments. Here, we report only hydrogen desorption having used D2. To minimize contamination by H atoms from residual H2 dissociation we start our dose of D2 already at 700 K while the crystal cools to 100 K. The results were verified for consistency by comparison to previously gathered data from earlier studies in our group, e.g. for Pt(533)34 and Pt(553).35 The heating rate in our TPD experiments is approximately 1.0 K s−1 for all samples.

4 Results and discussion

4.1 High-coverage hydrogen adsorption on Pt(211) and desorption characteristics

The first surface we discuss is Pt(211) which consists of a 3 atom wide (111) terrace and a (100) step edge. We find that the first site to be occupied is the B1 site at the step edge with a Gibbs free energy of adsorption of −0.44 eV (see Fig. 2a). Next, the second B1 site in the studied super cell is filled, with an adsorption energy of −0.51 eV, which is shown in Fig. 2b, indicating a small attractive interaction of ca. 0.03 eV per H between the two step-edge-bound atoms.
image file: c9cp02330e-f2.tif
Fig. 2 Adsorption structures, the coverage, the newly occupied adsorption site, as per Fig. 1a, and their respective differential adsorption Gibbs free energies for increasing coverages from (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, (f) 6 and (g) 7 hydrogen atoms per super cell on Pt(211). The atom with the lowest differential adsorption Gibbs free energy, which is added to increase the coverage, is marked in red. Gold connectors mark the upper step edge.

With all the B1 sites filled, the next most favorable adsorption sites are the on-top sites above the platinum atoms that form the lower step edge (shown in Fig. 2c and d) with adsorption energies of −0.29 and −0.31 eV respectively. Increasing the coverage further, we find the site with the next most favorable adsorption energy to be the two FCC sites next to the step edge with adsorption energies of −0.29 eV and −0.29 eV, which are shown in Fig. 2e and f. It should be noted that for the two OT3 and two FCC sites the differential adsorption energies are very similar, so there is no clear preference for either one. In order to test our initial assumption that coverages beyond the 1[thin space (1/6-em)]:[thin space (1/6-em)]1 Pt[thin space (1/6-em)]:[thin space (1/6-em)]H ratio were not realistic, we simulated a coverage of 7[thin space (1/6-em)]:[thin space (1/6-em)]6 H[thin space (1/6-em)]:[thin space (1/6-em)]Pt for the Pt(211) surface. We find the next most favorable site at a coverage of 7 H-atoms to 6 Pt atoms to be the OT2 site in the middle of the terrace. We find that this adsorption site has a comparatively unfavorable adsorption energy of only +0.04 eV. This is a drastic shift towards a less favorable adsorption energy and indicates that this site will likely not be occupied under UHV conditions.

4.2 Barriers on the Pt(211) surface

Based on the adsorption configurations discussed above, we also calculate NEB desorption pathways from selected structures to calculate any additional barriers present, the results of which are shown in Table 1. We chose structures with an even number of hydrogen atoms to study the desorption from equal sites, since we know that the flat (111) terrace part of the surface generally has low barriers for diffusion and desorption.14 Furthermore, the combination of two non-equal sites will always have a higher barrier for desorption than the combination of two less strongly bound sites. Note that “additional barrier” in this case refers to any energy barrier on top of the desorption energy (adsorption energy) for the two desorbing hydrogen atoms. We observe that the B1–B1 desorption process at the step edge exhibits no additional barrier for any of the studied coverages. The other pathways, namely the OT3–OT3 pathway for a 66% coverage and the FCC1–FCC1 pathway for the 100% coverage case, both show low additional barrier energies of 0.07 eV and 0.10 eV respectively. We note that the OT3–OT3 pathway has quite a high native barrier, so that the NEB calculation shifts the pathway to a diffusion + desorption step that first moves the hydrogen atoms to the HCP2 sites from which they then desorb with the low barrier shown here.
Table 1 Additional reaction barriers for the B1–B1 as well as the lowest energy desorption pathways for increasing coverages on Pt(211). The corresponding NEB profiles are shown in the respective figures in the ESI
H[thin space (1/6-em)]:[thin space (1/6-em)]Pt Pathway 1 E barr [eV] Pathway 2 E barr [eV]
2[thin space (1/6-em)]:[thin space (1/6-em)]6 B1–B1 0.00 — —
4[thin space (1/6-em)]:[thin space (1/6-em)]6 B1–B1 0.00 OT3–OT3 0.07
6[thin space (1/6-em)]:[thin space (1/6-em)]6 B1–B1 0.00 FCC1–FCC1 0.10

4.3 Elucidation of TPD spectra on the Pt(211) surface

Experimentally, the TPD spectrum of the Pt(211) surface under UHV conditions shows two peaks, one low-temperature peak at 277 K and one high-temperature peak at ca. 374 K7 (see Fig. 3b). The two peaks exhibit an area ratio of about 30[thin space (1/6-em)]:[thin space (1/6-em)]70 between the low and the high temperature peak. We find that the DFT-computed differential Gibbs free energies of adsorption show three distinct ranges, which are shown in Fig. 3a and represented by color codes: the first two sites at low coverage are found to be at −0.44 eV and −0.51 eV (located in the area marked green in Fig. 3a), which we propose to be linked to the high temperature peak, also marked green in Fig. 3b. At higher coverages we relate the medium adsorption energy range (located in the area marked blue in Fig. 3a) with the 4 sites on the terrace (OT3 and FCC1) to the low temperature peak at 260 K (colored blue in Fig. 3b). The adsorption energies at coverages above 6H:6Pt are at very low differential binding energies, implying that they are unoccupied. Comparing the ratios from the DFT-calculated sites of 1[thin space (1/6-em)]:[thin space (1/6-em)]2 or 33%[thin space (1/6-em)]:[thin space (1/6-em)]66% to the experimentally obtained peak integral ratio of 30%[thin space (1/6-em)]:[thin space (1/6-em)]70% shows a good correlation between the results and reinforces our assumption that the 1Pt[thin space (1/6-em)]:[thin space (1/6-em)]1H ratio is the maximum realized on this surface.
image file: c9cp02330e-f3.tif
Fig. 3 (a) Differential adsorption Gibbs free energies for Pt(211). The two ranges of adsorption energies discussed below are marked in green (step adsorption) and blue (terrace adsorption), (b) TPD spectrum with the colored areas indicating the origin of the peaks in subfigure (a). The inset in (b) shows the integrals of the deconvolution fits (blue and green) as percentages of the total deconvolution integral (black).

4.4 High-coverage hydrogen adsorption on Pt(221) and desorption characteristics

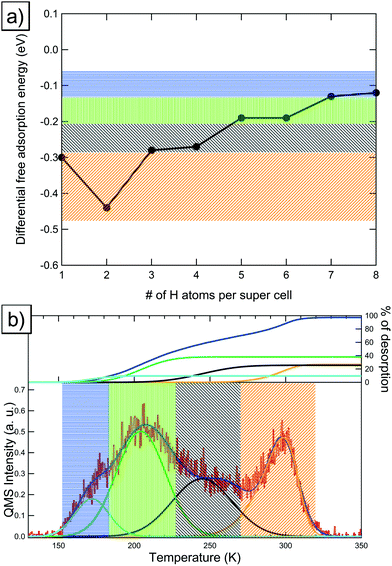
In this section we will discuss our findings for the case of high-coverage adsorption on the Pt(221) surface, which consists of a 4-atom-wide (111) terrace and a (111)-type step edge. At the coverage of 1 H per 8 Pt we observe a preference for the FCC1 site with a differential Gibbs free energy of adsorption of −0.30 eV (shown in Fig. 4a). It should be noted that the FCC1 site is only about 0.01 eV more stable than its neighboring B1 site for a single adsorbed hydrogen atom. Filling the step edge, we observe a noticeable attractive interaction of ca. 0.07 eV per H, leading to a differential adsorption Gibbs free energy of −0.44 eV for the second adsorbed hydrogen atom. Also we observe that the preferred site for the adsorption of the second hydrogen atom shifts away from the FCC1 site and to a B1–B1 structure, as shown in Fig. 4b.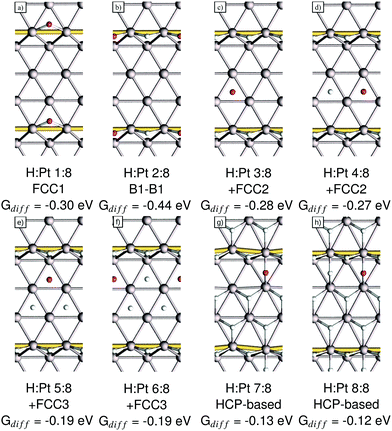
image file: c9cp02330e-f4.tif
Fig. 4 Adsorption structures, the coverage, the newly occupied adsorption site, as per Fig. 1b, and their respective differential adsorption Gibbs free energies for increasing coverages from (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, (f) 6, (g) 7 and (h) 8 hydrogen atoms per super cell on Pt(221). The atom with the lowest differential Gibbs adsorption energy, which is added to increase the coverage, is marked in red. Gold connectors mark the upper step edge.

Additional hydrogen then prefers to sit in the two FCC2 sites in the middle of the terrace with Gibbs free energies of adsorption of −0.28 eV and −0.27 eV, respectively, which are shown in Fig. 4c and d. Increasing the coverage above the 4H:8Pt point, we calculate that the FCC3 sites (shown in Fig. 4e and f) on the terrace closer to the lower step edge are exhibiting the next-best Gibbs free energy of adsorption of −0.19 eV each. Increasing the coverage, again, above 6H:8Pt, we find that the FCC-based structures that we saw up to this point are no longer the most favorable adsorption geometries. We find instead that a surface with all terrace-bound hydrogen atoms shifted to the HCP sites is more stable (Fig. 4g). This change is caused by the initially already small adsorption energy difference between HCP and FCC sites, combined with the repulsion from the upper step edge hydrogen atoms and the reduced adsorption energy of the lower step edge region.

4.5 Barriers on the Pt(221) surface

In order to gauge the influence of additional barriers on the desorption, we calculated minimum energy pathways of desorption for four different coverages. Similar to the Pt(211) surface, we only consider coverages with an even number of hydrogen atoms present on the surface. Our results are tabulated in Table 2. We find that the B1–B1 desorption pathway has no additional barrier at any of the studied coverages, similar to the Pt(211) surface. At medium coverages, the FCC2–FCC2 and FCC3–FCC3 pathways exhibit low additional barrier energies of 0.08 and 0.15 eV respectively. For the very high coverage case of 8H:8Pt, we find that the HCP2–HCP2 pathway has the lowest overall activation energy due to the weak binding of the two HCP2-bound hydrogen atoms; however it exhibits an additional barrier of 0.25 eV due to the unfavorable repulsive interaction with the neighboring adsorbates that is hindering the desorption pathway.
Table 2 Additional reaction barriers for the B1–B1 as well as the lowest energy desorption pathways for increasing coverages on Pt(221). The corresponding NEB profiles are shown in the respective figures in the ESI
H[thin space (1/6-em)]:[thin space (1/6-em)]Pt Pathway 1 E barr [eV] Pathway 2 E barr [eV]
2[thin space (1/6-em)]:[thin space (1/6-em)]8 B1–B1 0.00 — —
4[thin space (1/6-em)]:[thin space (1/6-em)]8 B1–B1 0.00 FCC2–FCC2 0.08
6[thin space (1/6-em)]:[thin space (1/6-em)]8 B1–B1 0.00 FCC3–FCC3 0.15
8[thin space (1/6-em)]:[thin space (1/6-em)]8 B1–B1 0.00 HCP2–HCP2 0.25

4.6 Elucidation of TPD spectra on the Pt(221) surface

Comparing our results to the experimental TPD data shown in Fig. 5b, we find that the deconvolution of the spectrum predicts 4 main peaks: the first peak (marked orange in Fig. 5b) relates to the step-edge adsorption (marked orange in Fig. 5a) while the three low-temperature peaks correspond to the terrace-based sites, which are represented by the black, green and blue areas in Fig. 5a and b. The integrals of the deconvoluted peaks are roughly equal (within the experimental accuracy) for the two high-temperature peaks and the step edge peak, while the low-temperature peaks show a lower combined integral.
image file: c9cp02330e-f5.tif
Fig. 5 (a) Differential adsorption Gibbs free energies for Pt(221) with the step adsorption regime marked in orange and the terrace adsorption regimes marked in green, black and light blue respectively. (b) TPD spectrum with the colored areas indicating the origin of the peaks in (a). The inset in (b) shows the integrals of the deconvolution fits (orange, green, black and light blue) as percentages of the total deconvolution integral (dark blue).

From this result and our calculations, we conclude that the individual deconvoluted peaks correspond reasonably well to the individual sites observed in our calculations. However, for this surface we find that the lower-energy sites are not fully occupied, which we base on the reduced integral for the low-temperature peak obtained from the deconvolution. This is probably due to low adsorption energy of these sites, combined with the prohibitively high barriers associated with a complete shift of the adsorption structure to an HCP-based structure. This implies that the experimentally occupied sites will have an even lower adsorption energy than the HCP-based sites we show here. Furthermore, the increased barriers for HCP-based desorption also imply an increased barrier for adsorption into these sites, which further reduces the coverage under experimental conditions.

4.7 High-coverage hydrogen adsorption on Pt(533) and desorption characteristics

In this section we will discuss adsorption structures for increasing coverages of hydrogen on Pt(533), which consists of a 4-atom-wide (111) terrace and a (100) step edge.

The most favorable adsorption site on the Pt(533) surface for a single isolated hydrogen atom is the B1 site at the step edge, as shown in Fig. 6a, with a differential adsorption energy of −0.55 eV. We find that the site favored for the adsorption of the second hydrogen atom in the super cell is the other B1 site at the step edge. The differential adsorption Gibbs free energy for this site is −0.58 eV and the resulting adsorption geometry can be seen in Fig. 6b. The increase in differential adsorption Gibbs free energy indicates that there is a slight attractive interaction of 0.015 eV per atom between hydrogen atoms absorbed at the step edge of Pt(533). This attractive interaction mirrors the one found on the Pt(211) surface (however the absolute value per atom is smaller by about 0.015 eV per H, which we assume to be within the error of DFT). Further increasing the coverage to include 3 hydrogen atoms per super cell, we find the most favorable site to be the OT4 site with a differential absorption Gibbs free energy of −0.36 eV (see Fig. 6c). It should be noted that, as can be seen in the figure, the OT4 site is located atop the lower step-edge Pt atom and can also be viewed as a bridge site between the upper and lower step-edge platinum atoms. For 4 hydrogen atoms per unit cell we find a preference to occupy the second OT4 site (the resulting adsorption geometry can be found in Fig. 6d). A differential adsorption Gibbs free energy of −0.35 eV was found for this structure. At this point the step edge is completely covered and no further step-related adsorption sites can be occupied without causing strong, unfavorable interactions.


image file: c9cp02330e-f6.tif
Fig. 6 Adsorption structures, the coverage, the newly occupied adsorption site, as per Fig. 1c, and their respective differential adsorption Gibbs free energies for increasing coverages from (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, (f) 6, (g) 7 and (h) 8 hydrogen atoms per super cell on Pt(533). The atom with the lowest differential adsorption Gibbs free energy, which is added to increase the coverage, is marked in red. Gold connectors mark the upper and lower step edge.

Increasing the coverage beyond 4 hydrogen atoms per super cell leads to the occupation of terrace sites. We find that for 5 hydrogen atoms per super cell, the FCC1 site adjacent to the upper step edge is preferred with a differential Gibbs free energy of adsorption of −0.31 eV. The corresponding adsorption geometry can be seen in Fig. 6e. The second terrace-bound atom is found to bind preferentially to the second FCC1 site on the terrace with a differential adsorption Gibbs free energy of −0.31 eV (see Fig. 6f). Increasing the occupation of the super cell further, the two FCC2 sites will be filled next. They exhibit differential adsorption Gibbs free energies of −0.31 eV for the first adsorbate and an identical −0.30 eV for the second adsorbate. The resulting adsorption geometries can be seen in Fig. 6g and h. Note that the differential adsorption Gibbs free energy differences between these 4 sites are very small, independent of the exact order of filling. This observation, combined with the low diffusion barriers for hydrogen on the (111) terrace,14 leads us to conclude that there is no fixed order for filling of, or desorbing from, the terrace.

4.8 Barriers on the Pt(533) surface

In order to estimate the influence of possible desorption barriers, NEB calculations were performed for the B1–B1 and lowest-energy desorption pathway at each ratio of H[thin space (1/6-em)]:[thin space (1/6-em)]Pt: 2[thin space (1/6-em)]:[thin space (1/6-em)]8, 4[thin space (1/6-em)]:[thin space (1/6-em)]8, 6[thin space (1/6-em)]:[thin space (1/6-em)]8 and 8[thin space (1/6-em)]:[thin space (1/6-em)]8. The results are shown in Table 3. We considered the B1–B1 pathway for each coverage and we find that the additional barriers are consistently below 0.05 eV, with no observable barrier at the higher coverages. At a coverage of 4[thin space (1/6-em)]:[thin space (1/6-em)]8 we considered the OT4–OT4 desorption pathway, for which we were unable to achieve a converged minimum energy pathway; however all attempts indicated high remaining additional barriers due to an unfavorable desorption geometry. We expect that the most favorable pathway for desorption from this geometry follows a similar trajectory as for the Pt(211) surfaces, where we observed diffusion to the neighboring HCP site, followed by desorption from these HCP sites. At a coverage of 6[thin space (1/6-em)]:[thin space (1/6-em)]8 we considered the FCC1–FCC1 pathway, for which we observed a small additional barrier of 0.07 eV. However, it should be noted that these calculations did not converge to the force threshold set for the rest of the NEB calculations. At the coverage of 8[thin space (1/6-em)]:[thin space (1/6-em)]8 we calculated the FCC2–FCC2 pathway, for which we obtained an additional barrier of 0.08 eV.
Table 3 Additional reaction barriers for the B1–B1 as well as the lowest energy desorption pathways for increasing coverages on Pt(533). The corresponding NEB profiles are shown in the respective figures in the ESI
H[thin space (1/6-em)]:[thin space (1/6-em)]Pt Pathway 1 E barr [eV] Pathway 2 E barr [eV] ESI
a NEB did not converge with the conventional NEB setup. Calculation details are discussed in the ESI. b Calculation did not converge past 0.1 eV Å−1 remaining forces.
2[thin space (1/6-em)]:[thin space (1/6-em)]8 B1–B1a 0.05 — — Fig. S1
4[thin space (1/6-em)]:[thin space (1/6-em)]8 B1–B1 0.00 OT4–OT4 >0.4a Fig. S2–S5
6[thin space (1/6-em)]:[thin space (1/6-em)]8 B1–B1 0.00 FCC1–FCC1 0.07b Fig. S6 and S7
8[thin space (1/6-em)]:[thin space (1/6-em)]8 B1–B1 0.00 FCC2–FCC2 0.08 Fig. S8 and S9

4.9 Elucidation of TPD spectra on the Pt(533) surface

Experimental TPD spectra show that on Pt(533) there are two main desorption peaks, one at 260 K and another, high-temperature peak at 370 K. The low-temperature peak is generally assigned to the flat Pt(111) terrace.6Fig. 7a plots the DFT-computed differential adsorption Gibbs free energies as a function of the coverage. We observe two general regimes of adsorption energies, namely one regime for the highly favorable B1-bound hydrogen (green area in Fig. 7) and one regime for the rest of the adsorption sites, which have less favorable adsorption energy (blue area in Fig. 7). The step edge related OT4 sites also fall into the latter regime, leading to a 1[thin space (1/6-em)]:[thin space (1/6-em)]3 ratio between the green and the blue areas, which mirrors the experimentally observed ratio of 23[thin space (1/6-em)]:[thin space (1/6-em)]77 or ca. 1[thin space (1/6-em)]:[thin space (1/6-em)]3.6 This implies that hydrogen on Pt(533) reaches the ratio of 1H[thin space (1/6-em)]:[thin space (1/6-em)]1Pt and therefore a true 100% coverage, mirroring the findings on Pt(211). Fig. 7b shows the corresponding temperature regions in the experimental TPD spectrum.
image file: c9cp02330e-f7.tif
Fig. 7 (a) Differential adsorption Gibbs free energies for Pt(533), the two general ranges of adsorption energies discussed below are marked in green (step adsorption) and blue (terrace adsorption), (b) TPD spectrum with the colored areas indicating the origin of the peaks in (a). The inset in (b) shows the integrals of the deconvolution fits (light blue and green) as percentages of the total deconvolution integral (dark blue).

4.10 High-coverage hydrogen adsorption on Pt(553) and desorption characteristics

Lastly, we will describe our findings for the Pt(553) surface. In our earlier publication,27 we identified the FCC1 site (see Fig. 8a) at the upper step edge with a differential adsorption Gibbs free energy of −0.38 eV as the most favorable adsorption site for a single hydrogen atom on Pt(553). However, when increasing the occupation to 2 H per super cell, we find that a combination of two B1 sites (see Fig. 8b), the same as on the Pt(211), Pt(221) and Pt(533) surface, is the most favorable adsorption geometry. A differential adsorption Gibbs free energy of −0.50 eV is observed. Note that this indicates a strong attractive interaction of ∼0.06 eV per H. This behavior mirrors the case on Pt(221) where we also observed a strong attractive interaction combined with a shift in the preferred adsorption site, suggesting that this is a general feature of the interaction of the (111) step edge and hydrogen.
image file: c9cp02330e-f8.tif
Fig. 8 Adsorption structures, the coverage, the newly occupied adsorption site, as per Fig. 1d, and their respective differential adsorption Gibbs free energies for increasing occupations from (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, (f) 6, (g) 7, (h) 8, (i) 9 and (j) 10 hydrogen atoms per super cell on Pt(553). The atom with the lowest differential adsorption Gibbs free energy, which is added to increase the occupation, is marked in red. Gold connectors mark the upper and lower step edge.

Increasing the occupation beyond 2 hydrogen atoms per super cell, we find that now the FCC3 site (see Fig. 8c) in the middle of the terrace is the most favorable site with a differential adsorption Gibbs free energy of −0.35 eV. This preference for the sites in the middle of the terrace was also visible for the single-adsorbate picture.27 Increasing the occupation to 4 hydrogen atoms per super cell, the second FCC3 site (see Fig. 8d) is occupied. A differential Gibbs free energy of adsorption of −0.33 eV is calculated for this site. Further increasing the occupation to 5 and 6 hydrogen atoms per super cell leads to the filling of the two FCC2 sites on the terrace. The respective differential Gibbs energies of adsorption are −0.29 eV in both cases. The adsorption geometries can be seen in Fig. 8e and f. Note that the step-edge adjacent FCC1 sites are not occupied due to the repulsive interaction with the filled B1 sites. Further increasing the occupation beyond 6 H per cell we observe a drastic decrease in differential adsorption Gibbs free energies, to the point that there is little to no energy gain for additional adsorbed H atoms. We will discuss these sites here to arrive at the same 1H[thin space (1/6-em)]:[thin space (1/6-em)]1Pt ratio as for Pt(533); however, we want to point out that it is highly unlikely that these occupations can be reached in the real physical system. For this, we have two main reasons: firstly, for any occupation above 7 atoms per unit cell, we see a distinct shift towards less favorable adsorption energies, which should be reflected in a clearly distinguishable new peak appearing below ca. 180 K, similar to the one seen on Pt(221); however no such peak is observed. Secondly, for the higher occupations of 9 and 10 hydrogen atoms there are no areas in the unit cell that allow for easy dissociative adsorption of the hydrogen molecule (requiring 2 neighboring, empty FCC or HCP sites), leading us to believe that these coverages are seemingly not reached under UHV conditions using molecular hydrogen.

However, for the sake of completeness, we will discuss the adsorption geometries beyond the point which we expect to be reached in experiment. We find that the first adsorption sites to be filled in this regime are the two weak-binding FCC4 sites at the lower step edge both with adsorption energies of −0.19 eV. Their respective adsorption geometries can be seen in Fig. 8g and h. Increasing the occupation further forces the hydrogen to occupy the OT1 site at the step edge (see Fig. 8i), which interacts strongly with the other step-bound hydrogen atoms, especially the B1 site reducing the differential adsorption Gibbs free energy to −0.14 eV. Increasing the occupation to 10 H per super cell, we find that shifting the complete adsorption structure to occupy HCP sites instead of FCC sites leads to a small increase in total adsorption energy compared to the FCC-based 10 H structures. Applying the differential adsorption Gibbs free energy methodology, which is somewhat ill-defined in this case, we arrive at a value of −0.17 eV for this adsorption geometry. Note that the HCP-based geometry for 9 hydrogen atoms per super cell is less favorable than the one containing the OT1-adsorbed hydrogen atom.

4.11 Barriers on the Pt(553) surface

Also for the Pt(553) surface, NEB calculations were performed, the results of which can be found in Table 4. As described earlier, “barrier” denotes any additional barrier that needs to be overcome beyond the desorption energy. We find that without exception all barriers are below 0.1 eV for all adsorption geometries. The B1–B1 pathway generally shows no additional barrier, while the FCC–FCC desorption pathway usually shows very low barriers ranging from 0.03 eV to 0.08 eV. From this we conclude that on the Pt(553) surface additional desorption barriers play no crucial role during the desorption process.
Table 4 Additional reaction barriers for the B1–B1 as well as the lowest energy desorption pathways for increasing coverages on Pt(553). The corresponding NEB profiles are shown in the respective figures in the ESI
H[thin space (1/6-em)]:[thin space (1/6-em)]Pt Pathway 1 E barr [eV] Pathway 2 E barr [eV] ESI
a Occupations beyond the ratio of 8[thin space (1/6-em)]:[thin space (1/6-em)]10 were not investigated with NEB calculations. The reasons for this are discussed in the section of the text dealing with these occupations.
2[thin space (1/6-em)]:[thin space (1/6-em)]10 B1–B1 0.00 — — Fig. S10
4[thin space (1/6-em)]:[thin space (1/6-em)]10 B1–B1 0.00 FCC3–FCC3 0.03 Fig. S11 and S12
6[thin space (1/6-em)]:[thin space (1/6-em)]10 B1–B1 0.03 FCC2–FCC2 0.05 Fig. S13 and S14
8[thin space (1/6-em)]:[thin space (1/6-em)]10a B1–B1 0.00 FCC4–FCC4 0.08 Fig. S15 and S16

4.12 Elucidation of TPD spectra on the Pt(553) surface

For the Pt(553) surface the experimentally obtained TPD spectrum (see Fig. 9b) is quite complex, consisting of a sharp feature at ca. 300 K, followed by a broad peak in the region of 250 K and ending in a broad peak at ca. 210 K. However, a clear indication as to which peak stems from which region of the surface has been elusive. In the following we will try to combine our knowledge from TPD and DFT to arrive at an assignment for the origin of the peaks.
image file: c9cp02330e-f9.tif
Fig. 9 (a) Differential adsorption Gibbs free energies for Pt(553), the four general ranges of adsorption energies discussed in the text are marked in black (step adsorption), light blue and orange (terrace adsorption) and green (low adsorption energy regime), (b) TPD spectrum with the colored areas indicating the origin of the peaks in (a). The inset in (b) shows the integrals of the deconvolution fits (black, light blue, orange and green) as percentages of the total integral (dark blue). (c) Deconvolution of the Pt(553) spectrum done via differential fitting, reproduced from ref. 6.

With the results of the DFT calculations (see Fig. 9a) we find that the most favorable adsorption sites (two B1 sites, located in the orange-marked area) must be linked to the highest-temperature desorption feature, marked orange in Fig. 9b. Also, the sharpness of this peak, suggesting strong attractive interactions, supports this conclusion. Therefore, we associate the high-temperature peak with the step edge sites and from this obtain an estimate for the full occupation by comparing the site-count from DFT to the total integral obtained from the experiment.

Following the same fitting procedures as for the previously discussed surfaces, we observe a significantly changed elucidation of the spectrum compared to the closely related Pt(221) surface. This is probably due to the fact that the Pt(553) spectrum has few obvious maxima in the region from 200 K to 275 K to which Gaussian peaks can be fitted. Furthermore, the low temperature tail below 200 K does not exhibit a clear peak, making a clear peak temperature assignment even harder. Due to this, we also reproduce the initial deconvolution by van der Niet et al.6 in order to allow for a more clear picture.

We find a ratio of 1[thin space (1/6-em)]:[thin space (1/6-em)]4.85 for the integrals of the high-temperature peak and the sum of the integrals of the two low-temperature peaks, suggesting a maximum occupation of ca. 9–10 hydrogen atoms per super cell, which contains 10 surface Pt atoms, in our calculations. As we established for the other surfaces, an occupation beyond 1Pt:1H leads to very unfavorable adsorption energies, leading us to conclude that the surface, at most, reaches a coverage of 1Pt:1H on the Pt(553) surface. The features at temperatures below 300 K (marked in black, green and blue respectively in Fig. 9a and b) are then found to be originating from the terrace sites, with the low-temperature tail caused by the sites located at the lower step edge.

5 Conclusions

From the results described above we conclude that for facets containing a (100) step edge, namely the Pt(211) and Pt(533) surfaces, the TPD analysis is relatively straightforward: the high-temperature feature is associated with the step-edge desorption due to its more favorable binding energy. The low-temperature feature in both cases corresponds to the desorption from the terrace sites. Comparing the predicted adsorption site count of 2[thin space (1/6-em)]:[thin space (1/6-em)]4 for Pt(211) and 2[thin space (1/6-em)]:[thin space (1/6-em)]6 for Pt(533) corresponds very favorably to the observed peak integrals for the low-temperature peaks of 33[thin space (1/6-em)]:[thin space (1/6-em)]66 for Pt(211) and 23[thin space (1/6-em)]:[thin space (1/6-em)]77 for Pt(533) and also suggest that on the surfaces with (100)-step type a full ML of H coverage is reached.

Our calculations for Pt(221) predict a total of four adsorption sites per single surface unit cell combined with a strong attractive interaction at the step edge. The elucidation of the TPD spectrum uses a total of four peaks, where the lowest-temperature peak has a noticeably reduced total integral compared to the other 3, for which the integrals are comparable. From this we conclude that each of the deconvoluted peaks corresponds to one of the desorption peaks, with the last site not being fully occupied, resulting in a total coverage of between 6H:8Pt and 7H:8Pt.

The TPD spectrum for the Pt(553) surface is modeled using similar features as the one on the Pt(221) surface, with a sharp high-temperature feature, a drawn-out medium-temperature feature and a broad low-temperature peak. We combine this knowledge with our calculations, in which we find a strong attractive interaction at the step edge, mirroring the Pt(221) result and assign the high temperature peak to the step-edge-bound hydrogen atoms. Using the peak integral ratios between the high- and the low-temperature features from the TPD measurements, we conclude that we only reach a total coverage of ca. 100%, corresponding to a ratio of 9–10H[thin space (1/6-em)]:[thin space (1/6-em)]10Pt in our super cell.

More generally, we observe that for both surfaces with the (111) step-type the elucidation of the spectra was significantly more complex than for the (100) step-type. From the results presented here, we conclude this to be for two reasons: firstly, the adsorption energy for the step-edge binding site is reduced for the case of Pt(221) and Pt(553). This means that the step-related peaks are also located inside the general temperature range of the peak observed in the Pt(111) TPD experiments, which makes a clear assignment from purely experimental results more challenging. Secondly, the adsorption energy for the binding sites at the lower step edge is qualitatively different for the two step edge types: the (100) step edge has a strongly binding lower step edge, which is the second most favorable site on the surface, while the (111)-type has a weak-binding lower step edge, which is the least-strongly binding site on the surface. This means that under UHV conditions the (100) step-type will have 2 hydrogen atoms sitting at the step edge, while the (111)-type has only one.

Furthermore, as previously observed,33 we find that while step adsorption is relatively invariant to the length of the terrace, adsorption on the terrace itself is affected by the presence of the edge for the Pt(211) and Pt(221) surfaces. Thus, Pt(211) and Pt(221) surfaces are not ideal prototype surfaces for studying high-coverage adsorption in reference to large terrace sizes/isolated steps.

This difference in the effective occupation of hydrogen in the step-edge region will then influence other adsorbates the surface comes into contact with, allowing for a rationalization of the different co-adsorption behavior for the two step-types.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge financial support from the Netherlands Organization for Scientific Research (NWO) as a TOP grant awarded to LBFJ and MTMK. This work was sponsored also by the NWO Exacte Wetenschappen, EW (NWO Physical Sciences Division) for the use of supercomputer facilities, with financial support from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (Netherlands Organisation for Scientific Research, NWO). Furthermore, we would like to thank the Nordic High Performance Computing Center (NHPC) and the New Zealand eScience Infrastructure (NeSi), funded jointly by NeSI's collaborator institutions and through the Ministry of Business, Innovation and Employment's research infrastructure programme. JAGT acknowledges the support of the U.S. Department of Energy, Chemical Sciences, Geosciences, and Biosciences (CSGB) Division of the Office of Basic Energy Sciences, via Grant DE-AC02-76SF00515 to the SUNCAT Center for Interface Science and Catalysis.

References

  1. P. S. Cremer, X. Su, Y. R. Shen and G. A. Somorjai, J. Am. Chem. Soc., 1996, 118, 2942–2949 CrossRef CAS .
  2. B. Conway and B. Tilak, Electrochim. Acta, 2002, 47, 3571–3594 CrossRef CAS .
  3. K. Lu and R. Rye, Surf. Sci., 1974, 45, 677–695 CrossRef CAS .
  4. K. Christmann, G. Ertl and T. Pignet, Surf. Sci., 1976, 54, 365–392 CrossRef CAS .
  5. K. Christmann and G. Ertl, Surf. Sci., 1976, 60, 365–384 CrossRef CAS .
  6. M. J. T. C. van der Niet, A. den Dunnen, L. B. F. Juurlink and M. T. M. Koper, J. Chem. Phys., 2010, 132, 174705 CrossRef PubMed .
  7. C. Badan, M. T. M. Koper and L. B. F. Juurlink, J. Phys. Chem. C, 2015, 119, 13551–13560 CrossRef CAS .
  8. A. T. Gee, B. E. Hayden, C. Mormiche and T. S. Nunney, J. Chem. Phys., 2000, 112, 7660–7668 CrossRef CAS .
  9. B. Poelsema, K. Lenz and G. Comsa, J. Chem. Phys., 2011, 134, 074703 CrossRef PubMed .
  10. R. van Lent, S. V. Auras, K. Cao, A. J. Walsh, M. A. Gleeson and L. B. F. Juurlink, Science, 2019, 363, 155–157 CrossRef CAS PubMed .
  11. J. K. Norskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef CAS .
  12. J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Norskov, Nat. Mater., 2006, 5, 909–913 CrossRef CAS PubMed .
  13. T. Roman and A. Groß, Catal. Today, 2013, 202, 183–190 CrossRef CAS .
  14. R. Olsen, S. Badescu, S. Ying and E. Baerends, J. Chem. Phys., 2004, 120, 11852–11863 CrossRef CAS PubMed .
  15. T. Vehviläinen, P. Salo, T. Ala-Nissila and S. C. Ying, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 035403 CrossRef .
  16. I. T. McCrum and M. J. Janik, ChemElectroChem, 2016, 3, 1609–1617 CrossRef CAS .
  17. S. Gudmundsdóttir, E. Skúlason and H. Jónsson, Phys. Rev. Lett., 2012, 108, 156101 CrossRef PubMed .
  18. S. Gudmundsdottir, E. Skulason, K.-J. Weststrate, L. Juurlink and H. Jonsson, Phys. Chem. Chem. Phys., 2013, 15, 6323–6332 RSC .
  19. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed .
  20. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed .
  21. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS .
  22. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed .
  23. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed .
  24. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed .
  25. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS .
  26. M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed .
  27. M. J. Kolb, F. Calle-Vallejo, L. B. F. Juurlink and M. T. M. Koper, J. Chem. Phys., 2014, 140, 134708 CrossRef .
  28. D. Loffreda, Surf. Sci., 2006, 600, 2103–2112 CrossRef CAS .
  29. M. Chase, C. Davies, J. Downey, D. Frurip, R. MacDonald and A. Syverud, NIST-JANAF Thermodynamical Tables, 1985, vol. 14 Search PubMed .
  30. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS .
  31. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS .
  32. C. Badan, R. G. Farber, Y. Heyrich, M. T. Koper, D. R. Killelea and L. B. Juurlink, J. Phys. Chem. C, 2016, 120, 22927–22935 CrossRef CAS .
  33. C. Badan, M. T. M. Koper and L. Juurlink, J. Phys. Chem. C, 2015, 119, 13551–13560 CrossRef CAS .
  34. M. J. T. C. van der Niet, A. den Dunnen, M. T. M. Koper and L. B. F. Juurlink, Phys. Rev. Lett., 2011, 107, 146103 CrossRef PubMed .
  35. M. J. T. C. van der Niet, A. den Dunnen, L. B. F. Juurlink and M. T. M. Koper, J. Chem. Phys., 2010, 132, 174705 CrossRef PubMed .

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp02330e
‡ Current address: SLAC National Accelerator Laboratory, 2575 Sand Hill Rd, Menlo Park, CA 94025, USA.
§ Current address: University Stockholm, Alba Nova, Roslagstullsbacken 21, 114 21 Stockholm, Sweden.
This journal is © the Owner Societies 2019
Click here to see how this site uses Cookies. View our privacy policy here.