Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chemically-resolved determination of hydrogenated graphene–substrate interaction†
Anders L.
Jørgensen‡
a,
David A.
Duncan
 b,
Claus F. P.
Kastorp
b,
Claus F. P.
Kastorp
 a,
Line
Kyhl
a,
Zeyuan
Tang
a,
Albert
Bruix
a,
Line
Kyhl
a,
Zeyuan
Tang
a,
Albert
Bruix
 c,
Mie
Andersen
c,
Bjørk
Hammer
c,
Mie
Andersen
c,
Bjørk
Hammer
 a,
Tien-Lin
Lee
b,
Liv
Hornekær
a,
Tien-Lin
Lee
b,
Liv
Hornekær
 a and
Richard
Balog
a and
Richard
Balog
 *a
*a
aDepartment of Physics and Astronomy and Interdisciplinary Nanoscience Center (iNANO), Aarhus University, 8000 Aarhus C, Denmark. E-mail: balog@phys.au.dk
bDiamond Light Source Ltd, Harwell Science and Innovation Campus, Didcot, OX11 0DE, UK
cChair for Theoretical Chemistry and Catalysis Research Center, Technische Universität München, Lichtenbergstr. 4, D-85747 Garching, Germany
First published on 4th June 2019
Abstract
Functionalization of graphene on Ir(111) is a promising route to modify graphene by chemical means in a controlled fashion at the nanoscale. Yet, the nature of such functionalized sp3 nanodots remains unknown. Density functional theory (DFT) calculations alone cannot differentiate between two plausible structures, namely true graphane and substrate stabilized graphane-like nanodots. These two structures, however, interact dramatically differently with the underlying substrate. Discriminating which type of nanodots forms on the surface is thus of paramount importance for the applications of such prepared nanostructures. By comparing X-ray standing wave measurements against theoretical model structures obtained by DFT calculations we are able to exclude the formation of true graphane nanodots and clearly show the formation graphane-like nanodots.
Introduction
Chemical functionalization of graphene by hydrogen has been shown to induce novel properties in graphene sheets. For randomly chemisorbed hydrogen, effects such as increased spin–orbit coupling1 and ferromagnetism2,3 have been observed. A nanometer scale periodic functionalization on the other hand has been shown to open a bandgap in graphene where the size of the gap can be controlled by the periodicity of the hydrogen pattern.4 A periodic hydrogen pattern can be prepared in graphene on Ir(111) due to a site selective reactivity driven by the moiré superstructure. Two regions of the moiré unit cell, namely the FCC and the HCP regions, are efficiently hydrogenated.5,6 However, at high temperature (≈600 K) only the HCP regions are populated forming a triangular periodic pattern of H-clusters on macroscopically large areas.7 Here, using the X-ray standing wave (XSW) technique we aim to reveal the geometrical structure of graphene hydrogenated at the HCP regions within the moiré. The primary question, to be addressed by these measurements, is whether the hydrogenation of the graphene in these locations results in a true graphane nanodot configuration, where every C atoms is bound to one hydrogen atom attached alternately from above and below,8 or whether the carbon atoms form a graphane-like configuration with alternating carbon atoms forming a bond with a hydrogen atom and a surface Ir atom.4 This difference between the two structures has important implications. While the graphane-like cluster interacts strongly with the substrate due to C–Ir bond formation, the graphane cluster weakens the interaction owing to the presence of C–H bonds in the gap between graphene and Ir.Previous STM measurements4 demonstrated lateral ordering of H-nanodots and a preference for formation in the HCP regions. However, the significant alteration to the electronic structure of hydrogenated graphene precludes drawing any certain conclusion about the vertical geometric structure of the hydrogenated regions and especially what is occurring below them. DFT calculations predict that both structures are stable with very similar formation energies9 and thus cannot differentiate between them. Hence a spectroscopic probe of the structure is required.
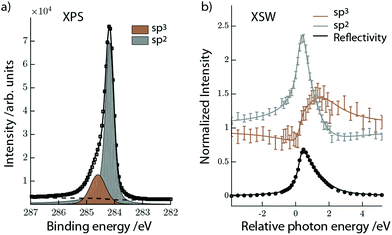
XSW is a highly sensitive method capable of measuring adsorbate-substrate distances with sub-ångstrom resolution.6,10 An XSW field is created by interference between the incoming and the bulk diffracted X-ray waves under Bragg diffraction condition. The standing wave field extending above the surface exhibits the periodicity of the Bragg plane spacing, d. To generate XSW with the (111) reflection of iridium (d = 2.2164 Å), the photon energy is tuned to around 2797 eV. An adsorbate experiencing the XSW field emits electrons with a yield proportional to the standing wave intensity at its position. By measuring the variation of the photoelectron intensity during a photon energy scan around the Bragg energy, which accordingly shifts the phase of the standing wave, we obtain a position specific yield profile for the adsorbate. Utilizing dynamical diffraction theory,10,11 the intensity profile is fitted with two structural parameters referred to as the coherent position PH and the coherent fraction FH. These are related to the relative mean height of the adsorbate and a spread in height around the mean value, respectively.12
Results and discussion
Graphene on Ir(111) was synthesized by combined temperature programmed desorption (TPD) and chemical vapor deposition (CVD)13 (see methods for details). At first, the quality of the graphene layer was inspected. Using X-ray photoelectron spectroscopy (XPS) measurements at photon energy of 435 eV, we obtain a single sp2 component in the C1s spectrum as expected. XSW measurements on the clean graphene (not shown) yield structural parameters P111 = 0.54 ± 0.01 and F111 = 0.74 ± 0.01 that are in line with the earlier results obtained by Busse et al.6 As the coherent positions are given as relative heights modulo and normalized to d111 = 2.2164 Å, the corresponding mean height is![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) = (n + P111) × d111, where n is an integer. Here only n = 1 yields a reasonable height, which is
= (n + P111) × d111, where n is an integer. Here only n = 1 yields a reasonable height, which is ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) = 3.41 ± 0.04 Å. This value is in good agreement with the vdW-corrected density functional theory (DFT) calculations,
= 3.41 ± 0.04 Å. This value is in good agreement with the vdW-corrected density functional theory (DFT) calculations, ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) = 3.54 Å, when referenced against a projected bulk-like truncation (see ESI† for explanation). Additionally the dependence of coherent fraction and the coherent position on the graphene coverage has been studied previously.14 These studies revealed that the coherent position of sp2 carbon remains unaltered with increasing coverage, but the coherent fraction decreases due to an increasing stress in large graphene areas. When using these results, the F111 value in our study gives coverage of about 0.63 ML, which is lower than the expected 1 ML. The lower coverage estimated from the coherent fraction value may, however, be due to the different growth procedures used in the two studies that consequently lead to different extent of stress in graphene sheet (see methods for graphene growth). We note, however, that for sufficiently large graphene islands the coverage plays negligible role for the hydrogenation studies discussed in the article.
= 3.54 Å, when referenced against a projected bulk-like truncation (see ESI† for explanation). Additionally the dependence of coherent fraction and the coherent position on the graphene coverage has been studied previously.14 These studies revealed that the coherent position of sp2 carbon remains unaltered with increasing coverage, but the coherent fraction decreases due to an increasing stress in large graphene areas. When using these results, the F111 value in our study gives coverage of about 0.63 ML, which is lower than the expected 1 ML. The lower coverage estimated from the coherent fraction value may, however, be due to the different growth procedures used in the two studies that consequently lead to different extent of stress in graphene sheet (see methods for graphene growth). We note, however, that for sufficiently large graphene islands the coverage plays negligible role for the hydrogenation studies discussed in the article.
A periodic hydrogen pattern was prepared by exposing the graphene covered Ir(111) to hot H atoms at a sample temperature of 600 K. Fig. 1a shows the corresponding C1s spectrum fitted with two components using a Doniach Sunjic function and a Shirley type background. The two distinguishable components are assigned to sp2 (grey) and sp3 (brown) carbon, representing clean and hydrogenated graphene regions, respectively.15 After the initial XPS measurements we excited the Ir(111) Bragg reflection to measure the XSW-modulated intensity profiles of the individual C1s components. Fig. 1b shows the XSW-modulated C1s intensities of the sp2 and sp3 components in graphene functionalized at high temperature together with their best fits. The coherent position obtained for the sp2 C is P111 = 0.56 ± 0.01, which is clearly very similar to the value found for bare graphene. The adsorption height is then ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) = 3.46 ± 0.02 Å, corresponding to n = 1. For the sp3 component we measure coherent position P111 = 0.02 ± 0.03, which corresponds to two feasible adsorption heights,
= 3.46 ± 0.02 Å, corresponding to n = 1. For the sp3 component we measure coherent position P111 = 0.02 ± 0.03, which corresponds to two feasible adsorption heights, ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) = 2.26 ± 0.07 Å and
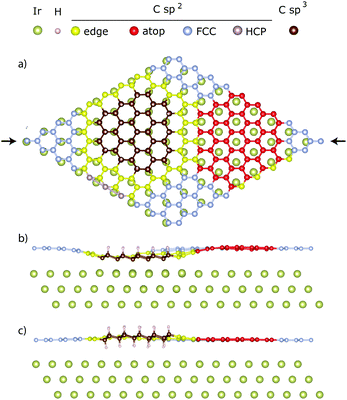
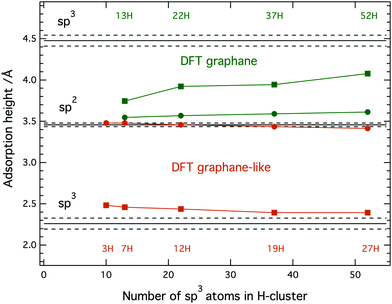
= 2.26 ± 0.07 Å and ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) = 4.48 ± 0.07 Å, with n = 1 and 2, respectively. Neither of these two heights can be immediately ruled out because two types of H-clusters are being considered here, as depicted in Fig. 2. The graphene-like structure where approximately half of the sp3 C atoms within the cluster interact strongly with the underlying Ir, and are thus positioned closer to the substrate than the clean graphane parts (Fig. 2b) and the real graphane cluster where all of the sp3 C atoms are covalently bound to H atoms, and are thus pushed further away from the substrate than the clean graphene parts (Fig. 2c). To determine which cluster is present on the surface, DFT calculations using optimized moiré supercells and vdW-corrected density functionals were employed. The calculated model structures consist of a 10 × 10 supercell of graphene on a 9 × 9 supercell of iridium with a hydrogen cluster positioned on the HCP region of the graphene/Ir(111) moiré. A wide range of H-clusters were explored, specifically, 13–52H atoms for the graphane cluster and 3–27H atoms for the graphane-like cluster. The theoretical coherent positions and fractions (see ESI,† for more details) and adsorption heights of sp2 and sp3 carbon atoms for all model structures, compared against the experimental values, are summarised in Table 1 and shown in Fig. 3. Comparing the calculated values for the graphane structure model (Fig. 3, green symbols) with the experimentally determined heights (black line) show no agreement at any H-cluster size allowing us to exclude the formation of graphane clusters in this system. The graphane-like structure model (Fig. 3, red symbols), however, agrees remarkably well with the experimental values with specifically strong agreement for the 19H cluster. The corresponding structure of the 19H cluster is depicted in Fig. 2a and b.
= 4.48 ± 0.07 Å, with n = 1 and 2, respectively. Neither of these two heights can be immediately ruled out because two types of H-clusters are being considered here, as depicted in Fig. 2. The graphene-like structure where approximately half of the sp3 C atoms within the cluster interact strongly with the underlying Ir, and are thus positioned closer to the substrate than the clean graphane parts (Fig. 2b) and the real graphane cluster where all of the sp3 C atoms are covalently bound to H atoms, and are thus pushed further away from the substrate than the clean graphene parts (Fig. 2c). To determine which cluster is present on the surface, DFT calculations using optimized moiré supercells and vdW-corrected density functionals were employed. The calculated model structures consist of a 10 × 10 supercell of graphene on a 9 × 9 supercell of iridium with a hydrogen cluster positioned on the HCP region of the graphene/Ir(111) moiré. A wide range of H-clusters were explored, specifically, 13–52H atoms for the graphane cluster and 3–27H atoms for the graphane-like cluster. The theoretical coherent positions and fractions (see ESI,† for more details) and adsorption heights of sp2 and sp3 carbon atoms for all model structures, compared against the experimental values, are summarised in Table 1 and shown in Fig. 3. Comparing the calculated values for the graphane structure model (Fig. 3, green symbols) with the experimentally determined heights (black line) show no agreement at any H-cluster size allowing us to exclude the formation of graphane clusters in this system. The graphane-like structure model (Fig. 3, red symbols), however, agrees remarkably well with the experimental values with specifically strong agreement for the 19H cluster. The corresponding structure of the 19H cluster is depicted in Fig. 2a and b.
![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) ) and coherent fraction (F111) derived from the XSW measurements and from the DFT optimized graphane-like and graphane clusters of various sizes
) and coherent fraction (F111) derived from the XSW measurements and from the DFT optimized graphane-like and graphane clusters of various sizes
| #H | P 111 |
![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) /Å /Å |
F 111 | |||
|---|---|---|---|---|---|---|
| sp2 | sp3 | sp2 | sp3 | sp2 | sp3 | |
| DFT-graphane | ||||||
| 13H | 0.60 | 0.69 | 3.54 | 3.75 | 0.97 | 0.75 |
| 22H | 0.61 | 0.77 | 3.57 | 3.92 | 0.97 | 0.75 |
| 37H | 0.62 | 0.78 | 3.59 | 3.95 | 0.96 | 0.72 |
| 52H | 0.63 | 0.84 | 3.61 | 4.07 | 0.93 | 0.72 |
| XSW | ||||||
| 0.56(1) | 0.02(3) | 3.46(2) | 4.47(7) or 2.26(7) | 0.41(2) | 0.43(5) | |
| DFT-graphane-like | ||||||
| 3H | 0.57 | 0.12 | 3.48 | 2.48 | 0.77 | 0.87 |
| 7H | 0.57 | 0.11 | 3.48 | 2.46 | 0.66 | 0.78 |
| 12H | 0.56 | 0.1 | 3.46 | 2.44 | 0.59 | 0.77 |
| 19H | 0.55 | 0.08 | 3.44 | 2.39 | 0.55 | 0.77 |
| 27H | 0.54 | 0.08 | 3.41 | 2.39 | 0.50 | 0.76 |
Our recent work suggests that 5–10% H-coverage per moiré results in the most stable graphane-like structures.7 This coverage corresponds to 10–20H graphane-like clusters in the present study. The 19H cluster found here is thus in excellent agreement with the earlier estimation of the most stable cluster size. All sp2 carbon atoms in Fig. 2 are further divided into four sub-categories depending on the position within the moiré they occupy. Detailed analysis of these sub-groups in the graphane-like model structure (see Table S1 in ESI†) then reveals that the adsorption height of the FCC region, marked silver in Fig. 2, is higher than the same region in bare graphene on iridium, gradually shifting from 3.52 Å to 3.59 Å with increasing cluster size. At the same time the adsorption height of sp2 atoms in the atop region (marked red) decreases from 3.68 Å to 3.61 Å. Thus the heights of the FCC and atop regions have approached each other and on average they have remained at the same mean height as in bare graphene on iridium (≈3.59 Å). Despite this flattening of the FCC and atop region a decrease in the total coherent position of the sp2 atoms, as the H-cluster size increases, is predicted by the DFT calculations, as seen in Fig. 3. This is caused by sp2 atoms at the edge of graphane-like cluster (marked yellow in Fig. 2), which are dragged closer to the substrate due to pinning effect. For the 27H model edge atoms comprise ∼1/3rd of the residual sp2 atoms within the moiré. In fact, due to the adjustment of carbon atom heights in the FCC and ATOP regions in the presence of the graphane-like clusters the shape of hydrogenated graphene approaches the egg box model16 also found for graphene pinned by a periodic array of platinum clusters.17
Though the graphane-like model structure agrees much better with the experiment, we have yet to address the persistent higher position of sp3 atoms appearing in the calculations even for large H-clusters (Table 1 and Fig. 3). We attribute this apparent discrepancy to the fact that in modelled graphane-like cluster structures (12H and 19H), the number of sp3 carbon atoms bonded to hydrogen is slightly higher than those bonded to iridium. Noting, that the selective adsorption height of sp3 carbon atoms involved in C–H bonds and in C–Ir bonds is 2.62 Å and 2.15 Å and thus above and below the experimental value, respectively. In the experiment the ratio between carbon atoms involved in C–H and C–Ir bonds will be lowered due to the variety of clusters structures formed4 but also due to the presence of H-vacancies in the clusters. These vacancies are generally introduced via Eley–Rideal hydrogen abstraction reaction that competes with hydrogen addition reaction during the hydrogenation experiments.18 These effects are clearly not captured in structural parameters obtain from the theoretical model structures were for given value only a single type of H-cluster is considered. Nevertheless, the above-mentioned effects have a tendency to lower the total adsorption height of sp3 atoms. Finally we also comment on the experimental coherent fractions that always appear lower in value than the theoretical ones (see Table 1 for comparison). In general a lower coherent fraction in experiment, compared to DFT, is to be expected due to the latter being estimated for a system at 0 K. The DFT value therefore does not adopt distortions induced by thermal vibrations. Also, a natural variation in the size of the clusters as mentioned above will further decrease the experimental coherent fraction.
Conclusions
In conclusion, we have determined the structure and interaction of graphene on Ir(111) upon patterned hydrogenation at high temperature using the XSW technique and DFT. The hydrogenated graphene regions comprise nanoclusters in the HCP region of graphene/Ir moiré that are found at a mean height of 2.26 ± 0.07 Å. The mean height of sp2 carbon atoms remains broadly unaffected at 3.46 ± 0.02 Å, though theoretical calculations indicate a reduced corrugation between atop and FCC areas. Additionally, the size of H-clusters, estimated from the corrugation of graphene in the present study, agrees remarkably well with the size of most stable graphane-like clusters as found by DFT calculations. We thus decisively conclude that the H-clusters induce strong coupling of graphene to the underlying substrate and thus determine the reaction pathway that has to be considered when altering the properties of graphene sheets on metal substrates by chemical functionalization.Experimental
Materials and methods
The atomic hydrogen beam was formed by passing molecular hydrogen through a hot (2000 K) tungsten capillary. Exposure to atomic hydrogen was conducted at a hydrogen background pressure of pbcg = 4 × 10−7 mbar while keeping the sample at 600 K in front of the beam for about 2 × 20 min. This results in a saturated hydrogen coverage for the given deposition condition. After the hydrogenation process the sample is cooled down to RT.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from VILLUM FONDEN (research grant no. 17547 and 16562 and grant no. 11744 – Villum Centre of Excellence for Dirac. Materials), the Danish Council for Independent Research (grant no. 5137-00049B), Innovation Fund Denmark (NIAGRA) (grant no. 5184-00018B), the European Research Council (CoG GRANN, grant no. 648551), the European Union (EU) and Horizon 2020 funding award under the Marie Skłodowska-Curie action to the EUROPAH consortium, grant number 722346. Affiliation with the Center for Integrated Materials Research (iMAT) at Aarhus University is gratefully acknowledged. We also acknowledge Diamond Light Source for time on beamline I09 under proposal SI16243-1 and thank the I09 technical staff for assistance and support during the measurements.Notes and references
- A. Avsar, J. H. Lee, G. K. W. Koon and B. Özyilmaz, 2D Mater., 2015, 2, 044009 CrossRef.
- W. K. Lee, K. E. Whitener, J. T. Robinson and P. E. Sheehan, Adv. Mater., 2015, 27(10), 1774–1778 CrossRef CAS PubMed.
- M. V. Ulybyshev and M. I. Katsnelson, Phys. Rev. Lett., 2015, 114, 1–5 CrossRef PubMed.
- R. Balog, B. Jørgensen, L. Nilsson, M. Andersen, E. Rienks, M. Bianchi, M. Fanetti, E. Lægsgaard, A. Baraldi and S. Lizzit, et al. , Nat. Mater., 2010, 9, 315–319 CrossRef CAS PubMed.
- A. T. N’Diaye, J. Coraux, T. N. Plasa, C. Busse and T. Michely, New J. Phys., 2008, 10, 043033 CrossRef.
- C. Busse, P. Lazic, R. Djemour, J. Coraux, T. Gerber, N. Atodiresei, V. Caciuc, R. Brako, A. T. N’Diaye and S. Blügel, et al. , Phys. Rev. Lett., 2011, 107, 1–4 CrossRef PubMed.
- J. H. Jørgensen, A. G. Čabo, R. Balog, L. Kyhl, M. N. Groves, A. M. Cassidy, A. Bruix, M. Bianchi, M. Dendzik and M. A. Arman, et al. , ACS Nano, 2016, 10, 10798–10807 CrossRef.
- T. Balgar, H. Kim and E. Hasselbrink, J. Phys. Chem. Lett., 2013, 4, 2094–2098 CrossRef CAS.
- Based on our DFT optimised structures we obtain formation energies that vary depending on the cluster size. The values are, however, similar for both types of clusters of the same size (see ESI,† Fig. S3). For the most stable clusters the formation energy is approx. 2.4–2.5 eV per H. What type of H-cluster dominates on the surface is thus most likely dictated by kinetic barriers for adsorption/desorption and intercalation/deintercalation of hydrogen.
- D. P. Woodruff, Rep. Prog. Phys., 2005, 68, 743 CrossRef CAS.
- B. W. Batterman and H. Cole, Rev. Mod. Phys., 1964, 36, 681–717 CrossRef CAS.
- J. Zegenhagen, Phys. Scr., 1991, T39, 328–332 CrossRef CAS.
- J. Coraux, A. T. N’Diaye, M. Engler, C. Busse, D. Wall, N. Buckanie, F. J. M. Z. Heringdorf, R. V. Gastel, B. Poelsema and T. Michely, New J. Phys., 2009, 11, 023006 CrossRef.
- S. Runte, P. Lazić, C. Vo-Van, J. Coraux, J. Zegenhagen and C. Busse, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(15), 155427 CrossRef.
- R. Balog, M. Andersen, B. Jørgensen, Z. Sljivancanin, B. Hammer, A. Baraldi, R. Larciprete, P. Hofmann, L. Hornekær and S. Lizzit, ACS Nano, 2013, 7, 3823–3832 CrossRef CAS PubMed.
- D. Franz, S. Runte, C. Busse, S. Schumacher, T. Gerber, T. Michely, M. Mantilla, V. Kilic, J. Zegenhagen and A. Stierle, Phys. Rev. Lett., 2013, 110, 1–5 CrossRef PubMed.
- J. Knudsen, P. J. Feibelman, T. Gerber, E. Grånäs, K. Schulte, P. Stratmann, J. N. Andersen and T. Michely, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 1–6 CrossRef.
- T. Zecho, A. Güttler, X. Sha, D. Lemoine, B. Jackson and J. Küppers, Chem. Phys. Lett., 2002, 366, 188–195 CrossRef CAS.
- C. J. Fisher, R. Ithin, R. G. Jones, G. J. Jackson, D. P. Woodruff and B. C. C. Cowie, J. Phys.: Condens. Matter, 1998, 10, L623 CrossRef CAS.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola and H. A. Hansen, et al. , J. Phys.: Condens. Matter, 2010, 22, 253202 CrossRef CAS.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al. , J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed.
- M. Andersen, L. Hornekær and B. Hammer, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 1–9 Search PubMed.
- F. Mittendorfer, A. Garhofer, J. Redinger, J. Klimeš, J. Harl and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 2–5 CrossRef.
- J. Coraux, A. T. N’Diaye, C. Busse and T. Michely, Nano Lett., 2008, 8, 565–570 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Includes complete analysis of adsorption heights for all DFT calculated model structures. See DOI: 10.1039/c9cp02059d |
| ‡ Present address: Newtec Engineering A/S – Stærmosegårdsvej 18, 5000 Odense M, Denmark and University of Southern Denmark, MCI – Alsion 2, 6400 Sønderborg, Denmark. |
| This journal is © the Owner Societies 2019 |