Demonstration of Baird's rule complementarity in the singlet state with implications for excited-state intramolecular proton transfer

Abstract

The aromatic character of an arene is proposed to switch from aromatic in the ground state (S₀) to antiaromatic in the S₁ and T₁ excited states. This behavior is known as Baird's rule and has been invoked to explain excited-state properties, primarily in the triplet state, whereas rationalization of antiaromaticity in the singlet state is less developed. This work demonstrates the first application of Baird's rule to rationalize previously unexplained experimental behavior of the singlet state process known as excited-state intramolecular proton transfer (ESIPT). Further, by analyzing the variations in isotropic magnetic shielding around the base arenes (benzene and naphthalene) of ESIPT fluorophores in the S₀ and S₁ electronic states, different shielding distributions indicate a complementarity to Baird's rule: greater aromaticity in S₀ leads to greater antiaromaticity in S₁ and vice versa. These findings have immediate application in the design of functional ESIPT fluorophores and, more generally, for photochemical reactions that are driven by the relief of antiaromaticity in the excited state. Notably, a tenet of traditional chromophore design states that expansion of conjugation generally leads to a red-shift in absorbance and emission wavelengths. The results of this study show that ESIPT fluorophores run contrary to those conventional design principles and this behavior can only be rationalized by considering Baird's rule.

---

Introduction

Aromaticity plays a major role in the chemical and electronic properties of molecules in the ground state following Hückel's rules.^1–3 Alternatively, the concepts of aromaticity and antiaromaticity have also been shown to influence the properties of singlet and triplet excited states. In general, an annulene with [4n + 2] π-electrons in its aromatic ground state (S₀) can be regarded as antiaromatic in its S₁ and T₁ excited states. The converse is similarly true for annulenes with a 4n π-electron antiaromatic ground states possessing aromatic character in the excited state.^4–9 This inversion of aromaticity between the ground and excited states has colloquially come to be known as Baird's rule.^10,11 Baird originally proposed the inversion of Hückel's rules between S₀ and T₁,⁴ but subsequent theoretical work suggested Baird's rule to be applicable to S₁ states as well.^12–15 While numerous studies¹⁰ have been conducted to investigate the excited-state aromaticity of various annulenes—establishing Baird's rule as a useful convention for understanding electronic states—the application of excited-state aromaticity to rationalize and design photochemical properties is less developed and predominantly focused on triplet aromaticity.^16–19

The goal of this work was to apply Baird's rules to interpret the unconventional behavior of benzoxazole fluorophores that undergo excited-state intramolecular proton transfer (ESIPT), where traditional strategies to red-shift the fluorescent wavelength instead lead to blue-shifted emission.^20,21 In doing so, we demonstrate the complementarity of Baird's rule, where lower aromaticity in S₀ leads to lower antiaromaticity in S₁. These results provide a deeper understanding of excited-state potential energy surfaces for applications in the design of functional chromophores and photochemical pathways.

Excited-state intramolecular proton transfer (ESIPT) is a photochemical process that leads to a dramatically large Stokes shift of the wavelength of fluorescence.²⁰ Briefly, the 2-(2′-hydroxyphenyl)benzoxazole derivative (Fig. 1) exists in its phenolic enol form E in the ground state. After excitation of E, direct fluorescence from E* can produce an emitted photon with a relatively small Stokes shift. Alternatively, the structure of E* is such that an excited-state tautomerization can occur to produce the keto form K* (Fig. 1, ESIPT step). The isomerization from E* to K* is fast (∼ps) and highly favorable. Emission then takes place from K* to the ground-state keto form K—where the quinoidal character of K places it higher in energy in the ground state than E (an example of Hückel [4n + 2] aromatic stability). The net result is that a stabilized K* and destabilized K closes the energy gap (S₁′ → S₀′) such that fluorescence from K* can be >150 nm red-shifted relative to fluorescence from E* (S₁ → S₀).

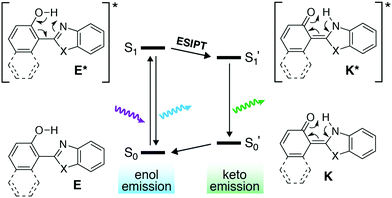Fig. 1 Excited-state intramolecular proton transfer (ESIPT). Isomerization to the keto form closes the energy gap, red-shifts emission and create a large Stokes shift.

The ESIPT process has been applied to the design of new functional molecules for biosensing and imaging.^20,21 Thus, insights into the factors that govern the isomerization and wavelength of emission are immensely valuable to the design and optimization of novel chemical tools based on ESIPT. While the excited-state behavior of derivatives based on E has been extensively studied, one aspect of their emissive behavior has eluded explanation.^22–24

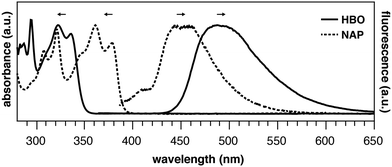
Consider the behavior of two benzoxazole derivatives HBO and NAP (Fig. 2 and Table 1). In general, expansion of conjugation leads to a red-shift in the absorption and emission of a chromophore. Accordingly, the absorbance maximum of NAP is ∼40 nm longer than HBO. In contrast, however, the emission wavelength of NAP is not similarly red-shifted and the Stokes shift is far smaller than for HBO. The origins of this odd behavior have not been adequately explained.^22–24 Additionally, for NAP, two emissive bands are observed. The predominant band is ascribed to emission from NAP-K* (460 nm) with a weaker, poorly defined band from NAP-E* (400 nm).²²

Fig. 2 Absorbance and emission traces of HBO (solid) and NAP (dashed) in toluene.

Table 1 Spectral data of ESIPT fluorophores in toluene

	Abs λmax (nm)	Em λmax (nm)	Stokes shift (nm)
	335	508	173
	378	400, 460	22, 82

---

From the spectral data of HBO and NAP in Table 1, we can develop the potential energy diagrams in Fig. 3.²³ Based on the higher energy of emission from NAP-K* (460 nm) versusHBO-K* (508 nm), HBO-K* is more stabilized relative to HBO-E* than for NAP-K* relative to NAP-E* (e_HBO > e_NAP). Similarly, the smaller energy difference between NAP-E* and NAP-K* (e_NAP) means that a detectable amount of NAP-E* exists and a minor band for enol emission is observed.²⁵ Overall, these results are congruent with the notion that tautomerization of NAP-E* to NAP-K* is not as energetically stabilizing as tautomerization of HBO-E* to HBO-K* despite the larger conjugated system in NAP. Given the utility of ESIPT probes for a variety of sensing and imaging applications,^20,21 it is essential to understand the factors that contribute to the photochemical mechanism to establish reliable design criteria.

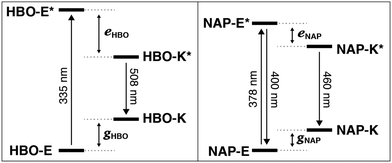Fig. 3 Excited-state intramolecular proton transfer (ESIPT). Isomerization to the keto form closes the energy gap, red-shifts emission and create a large Stokes shift.

It has been proposed theoretically that aromaticity may play a role in the tautomeric proton transfer of phenolic derivatives in the excited state.^26,27 Similarly, according to Baird's rule, the aromatic phenol (E) is antiaromatic in the excited state, and isomerization to the quinoidal keto form (K) can be conceptually understood to relieve the destabilizing effects of antiaromaticity.

Naphthalene is generally understood to be less aromatic than benzene in the ground state.^28–31 We therefore propose that naphthalene is less antiaromatic than benzene in the excited state. This complementarity of greater aromaticity in the ground state leading to greater antiaromaticity in the excited state (and vice versa) is an aspect of Baird's rule that has not been experimentally demonstrated.

Thus, NAP-E* is less antiaromatic relative to HBO-E*, which creates a lower driving force to form NAP-K*. Consequently, NAP-K* is less stabilized in the excited state and a larger energy gap must exist between NAP-K* and NAP-K relative to the energy gap between HBO-K* and HBO-K. As an aside, the reduced Stokes shift of NAP likely also derives from the lower energetic bias between the enol and keto tautomers in the ground state (g_HBO and g_NAP, Fig. 3). The lower ground-state aromaticity of naphthalene versus benzene means that g_HBO > g_NAP. Thus, because NAP-K is not as destabilized relative to NAP-E due to this reduced aromaticity, the energy gap between NAP-K and NAP-K* is necessarily larger than for HBO.

Results and discussion

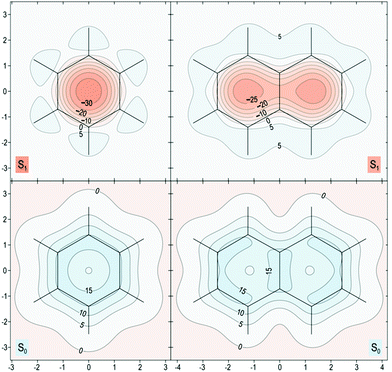
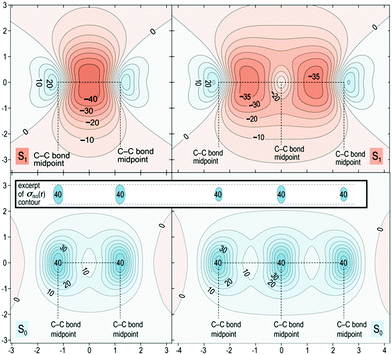
The proposed role that the reduced excited-state antiaromaticity of naphthalene plays in the photophysics of NAP is supported by calculations off-nucleus isotropic magnetic shielding isosurfaces of benzene and naphthalene in the ground and excited state (Fig. 4–6). The comparison of ground and excited-state aromaticity is well-served by this computational approach¹⁵ because the off-nucleus magnetic isotropic shielding, displayed as a function of position in the contour plots of Fig. 4–6, addresses important drawbacks associated with single-point nucleus-independent chemical shift (NICS) values.³² Mainly, the arbitrary position at which a single-point NICS value is calculated may not possess sufficient information to fully characterize the aromaticity of a π-system.^33,34 Additionally, geometric indices of aromaticity are often not applicable for excited-state aromaticity. For example, bond-length alternation is often invoked as an indication of reduced aromaticity in the ground state,³⁵ but benzene maintains the same D_6h symmetry across S₀ and S₁.^36–38 Thus, off-nucleus isotropic magnetic shielding isosurfaces provide one of the most insightful and succinct means of comparing aromaticity between molecules.

Fig. 4 Isotropic shielding contour plots 1 Å above the molecular (horizontal) plane for the S₀ and S₁ states of benzene (left) and naphthalene (right). σ_iso(r) values were obtained using state-optimized π-space CASSCF(6,6)-GIAO/6-311+G* and CASSCF(10,10)-GAIO/6-311+G* wavefunctions for benzene and naphthalene respectively, σ_iso(r) in ppm, axes in Å.

The contour plots in Fig. 4–6 display the spatial variation in the values of the off-nucleus isotropic magnetic shielding, σ_iso(r). The shape of the isotropic shielding surfaces and contour plots in Fig. 4–6 show profoundly different isotropic shielding distributions between the S₀ and S₁ of both benzene and naphthalene, where positive σ_iso(r) values indicate more shielded regions that can be associated with stronger bonding (aromatic) and negative σ_iso(r) values indicate more deshielded regions corresponding to weaker bonding (antiaromatic). Such contour plots have been referred to as “fingerprints” of aromaticity that allow for unambiguous classification of the degree of aromaticity and antiaromaticity in the electronic states of benzene and naphthalene.¹⁵

The isotropic shielding is represented by three plotting plane orientations (Scheme 1) to provide a more comprehensive picture of the spatial variation of σ_iso(r).

Scheme 1 Planes of contour plots in Fig. 4–7.

In general, the contour plots in Fig. 4–6 reveal that benzene is more aromatic relative to naphthalene in the ground state and, conversely, benzene is more antiaromatic relative to naphthalene in the excited state.

The S₀ of benzene in Fig. 4 displays a shielded ring inside of which the isotropic shielding, σ_iso(r), is above 15 ppm. In contrast, the regions where σ_iso(r) exceeds 15 ppm in each of the six-membered rings in S₀ of naphthalene are smaller and discontinuous, indicating a lower aromaticity compared with S₀ of benzene. The S₁ contour plots reveal a complimentary relationship to the aromaticity in S₀. The S₁ of benzene shows σ_iso(r) going down to under −30 ppm in a sizeable central circular region, which indicates that it is more antiaromatic than S₁ of naphthalene where the contour line surrounding the corresponding deshielded regions has σ_iso(r) of −25 ppm.

The spatial variation of σ_iso(r) represented in Fig. 5 reinforces the conclusions from Fig. 4. The areas of strong bonding exhibiting σ_iso(r) over 40 ppm, are larger in the S₀ of benzene than for naphthalene (see inset). Here we have another confirmation that the greater aromaticity of benzene in S₀ leads to greater antiaromaticity in S₁ compared with naphthalene: the most deshielded region extending above and below the central parts of the benzene ring features σ_iso(r) below −40 ppm whereas the corresponding regions in naphthalene are less deshielded by about 5 ppm.

Fig. 5 Isotropic shielding contour plots in the vertical plane slicing through the C–C bonds for the S₀ and S₁ states of benzene (left) and naphthalene (right). Same wavefunctions as for Fig. 4, σ_iso(r) in ppm, axes in Å.

The in-plane variation in σ_iso(r) represented in Fig. 6 is less indicative of differences in aromaticity in S₀. We do note, however, that the area where σ_iso(r) falls to under 10 ppm at the center of each ring is smaller for benzene than for naphthalene, which shows that benzene possesses higher values of σ_iso(r) overall compared with naphthalene. The S₁ contour plots reinforce the observations made in relation to Fig. 5: the central region of the benzene ring features more extensive deshielding that the central regions of the six-membered rings in naphthalene, which is an indication of greater antiaromaticity.

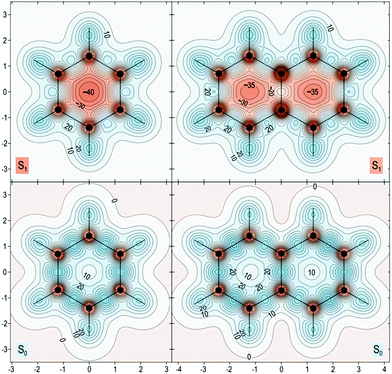Fig. 6 Isotropic shielding contour plots in the molecular (horizontal) plane for the S₀ and S₁ states of benzene (left) and naphthalene (right). Same wavefunctions as for Fig. 4, σ_iso(r) in ppm, axes in Å.

Finally, we introduce a new “fingerprint” of aromaticity switching in Fig. 7, which displays the difference contour plots that result from subtracting σ_iso(r) for S₀ from σ_iso(r) for S₁. Fig. 7 confirms that the overall change in aromatic character from ground to excited state is greater for benzene than for naphthalene by 4–7 ppm.

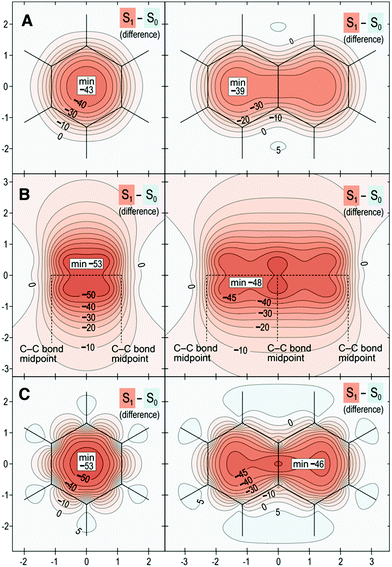Fig. 7 Isotropic shielding difference plots between S₁–S₀ for benzene (left) and naphthalene (right) in three orientations described by Scheme 1: (A) same as for Fig. 4; (B) same as for Fig. 5; (C) same as for Fig. 6. Same wavefunctions as for Fig. 4, σ_iso(r) differences in ppm, axes in Å.

The overall conclusion from all of the contour plots is that differences in aromaticity and bonding between benzene and naphthalene are smaller in S₀ relative to S₁. Indeed, differences in ground-state aromaticity are small (these are more obvious in the S₀ shielding plots 1 Å above the molecular plane, see Fig. 4, whereas the S₀ shielding plots in Fig. 5 and 6 display very similar bonding patterns). This finding, albeit based on a single comparative example, may imply that small differences in ground state aromaticity can lead to much larger differences in antiaromaticity in the excited state.

Collectively, these results affirm the greater aromaticity of benzene compared with naphthalene in S₀.^28–31 Conversely, benzene is more antiaromatic in S₁ than naphthalene. Therefore, the greater aromaticity of benzene in S₀ similarly leads to greater antiaromaticity in S₁ relative to naphthalene (Δσ_iso(r) of about −5 ppm). These results demonstrate that, when applied to singlet states, Baird's rule is complimentary between S₀ and S₁, where greater aromaticity in S₀ leads to greater antiaromaticity in S₁. The implications of this observation build a compelling case for the role that aromaticity effects play in the ESIPT process of HBO and NAP.

The greater antiaromaticity in the phenol of HBO-E* creates a larger energetic difference between HBO-E* and the quinoidal HBO-K* (which could be considered nominally nonaromatic by Hückel's rules). In contrast, the reduced antiaromaticity of NAP-E* relative to HBO-E* creates a smaller energetic driving force to form NAP-K*. We therefore propose that these aromaticity effects are responsible for the reduced Stoke's shift for NAP. Similarly, the smaller energetic bias between NAP-E* and NAP-K* means that enol emission from NAP-E* can be detected relative to keto emission.

Finally, we note that Baird's rules of excited-state aromaticity have primarily been validated in arenes with (π,π*) excited states.¹⁰ The ESIPT process similarly occurs in the (π,π*) excited state,²⁴ which justifies our application of Baird's rule to explain the behavior of NAP.

The potential energy diagrams in Fig. 3 were constructed based on the observable spectral properties of HBO and NAP. To gain further insight into the ESIPT process, we calculated the energetic parameters defined in Fig. 8.

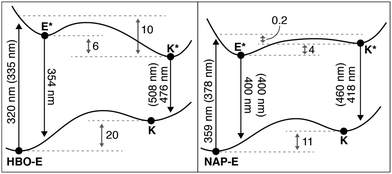Fig. 8 Computed TD-DFT potential energy diagram for HBO and NAP (at the TD-DFT B3LYP 6-311+G(d,p) level). All vertical transitions are reported in nm with experimentally determined values from Table 1 provided in brackets. Adiabatic energy differences reported in kcal mol⁻¹.

The computed wavelengths of absorption and emission correspond to the Frank–Condon vertical transitions from the ground state and the optimized excited state geometry for both HBO and NAP. All electronic energies were normalized to the ground state energy of the enol form (E) for both HBO and NAP. As anticipated, based on the lower aromaticity of naphthalene versus benzene discussed above, there is a smaller energy difference between the E and K species of NAP relative to HBO.

Alternatively, in the excited state, the analysis in Fig. 4–7 predict a greater stabilization of HBO-K* compared with HBO-E*, in accord with Baird's rule. Indeed, we compute a favorable stabilization (6 kcal mol⁻¹) of HBO-K* following ESIPT, whereas the energetic stabilization of NAP-K* was computed to be energetically uphill (4 kcal mol⁻¹) relative to NAP-E*. The spontaneous formation of NAP-K* has been spectroscopically confirmed,²² implying an exothermic ESIPT process to form NAP-K*. We therefore conclude that our computed endothermic process likely arises from error associated with excited-state geometry optimization of K*. TD-DFT geometry optimizations have been characterized to significantly underestimate CO bond lengths and as a result, will give inaccurate emission energies.^39,40 Nevertheless, the reported gas phase transition energies (in nm) match experimental observables within documented TD-DFT errors (0.2–0.3 eV),⁴¹ where emission from NAP-K* shows the most inaccurate computed value (418 nm) relative to experiment (460 nm). This inaccuracy further suggests that an error in the computed geometry is responsible for the discrepancy in energy between theory and experiment of NAP-E* and NAP-K*.

Conclusion

We present compelling evidence that aromaticity plays a key role in determining the energetic difference between tautomeric species in the excited state. This result has immediate implications for the design of ESIPT chromophores based on HBO. The ESIPT process has been applied to the development of new functional molecules and sensors.^20,21,42 Thus, an understanding of how structure relates to spectral features is critical to the design of novel ESIPT materials. This work reveals that expansion of conjugation is not a viable strategy to red-shift the emissive properties of ESIPT fluorophores unless expansion of the π-system leads to a more aromatic phenolic partner than the base phenol in HBO. Notably, this result runs contrary to traditional chromophore design principles in which expansion of conjugation generally leads to a red-shift in absorbance and emissive properties. These results can only be rationalized by considering Baird's rule (see below).

We propose that the aromaticity of the phenolic ring should be given strong consideration during the design of novel ESIPT chromophores as it can dramatically impact the Stokes shift of keto emission. Further, we predict that strategies centered around using electron-donating and electron-withdraw substitution (so called “push–pull” chromophores) may provide more fruitful avenues to increase the Stokes shift of keto emission, as has been demonstrated.⁴³ To date, however, a systematic investigation of the role that substitution of the HBO core can play in tuning the absorbance and enol vs. keto emission features of HBO has not been experimentally demonstrated.²⁵

More generally, this work corroborates the tenets of Baird's rule that [4n + 2] Hückel aromatic character in the ground state flips to antiaromatic character in the excited state.¹⁰ Furthermore, experimental evidence for Baird's rule operating in the singlet excited state is lacking.^12–15 This report provides experimental demonstration of Baird's rule in the singlet state, where the excited-state isomerization observed in HBO can be rationalized to be a process by which excited-state antiaromaticity is alleviated via intramolecular proton transfer to a quinoidal isomer.

Finally, this work proposes and demonstrates a largely intuitive concept within Baird's rule that greater aromaticity in S₀ leads to greater antiaromaticity in S₁, and presumably vice versa in terms of antiaromaticity in S₀.

Computational details

All complete-active-space self-consistent field calculations with gauge-including atomic orbitals (CASSCF-GIAO) on benzene and naphthalene reported in this paper were carried out using the MCSCF-GIAO (multiconfigurational SCF with GIAOs) methodology^44,45 and implemented in the Dalton 2016.2 program package,⁴⁶ within the 6-311+G* basis set.

The S₀ (1 ¹A_1g) and S₁ (1 ¹B_2u) electronic states of benzene were described using state-optimized π-space CASSCF(6,6) wavefunctions (with ‘6 electrons in 6 orbitals’), at the experimental D_6h gas-phase ground-state geometry established through analysis of the ν₄ vibration–rotation bands of C₆H₆ and C₆D₆.⁴⁷ The geometry of benzene chosen for the current calculations is identical to that used in previous shielding studies.^12,15,48

In the calculations on the S₀ (1 ¹A_g) and S₁ (1 ¹B_3u) electronic states of naphthalene we employed state-optimized π-space CASSCF(10,10) wavefunctions (with ‘10 electrons in 10 orbitals’), at the D_2h gas-phase ground-state geometry determined through a combination of ultrahigh-resolution laser spectroscopy and ab initio calculations.⁴⁹

As ground-state geometries were used in excited state calculations, the comparisons between the properties of the S₀ and S₁ electronic states of benzene and naphthalene are in the context of vertical excitations.

σ _iso(r) contour plots for the S₀ and S₁ electronic states of benzene and naphthalene were constructed using regular grids of points with a spacing of 0.05 Å. To reduce computational effort, for each grid σ_iso(r) values were calculated within one quadrant of the respective grid only and replicated by symmetry.

The CASSCF(6,6)/6-311+G* and CASSCF(10,10)/6-311+G* S₁ ← S₀ vertical excitation energies of 4.98 eV and 4.22 eV that we obtained for benzene and naphthalene, respectively, agree well with experimental data and other theoretical results.^12,50

Additional data on NICS and magnetic susceptibilities for the S₀ and S₁ electronic states of benzene and naphthalene, calculated at the CASSCF(6,6)-GIAO/6-311+G* and CASSCF(10,10)-GIAO/6-311+G* levels of theory, respectively, are reported in Table 2. The selection of NICS indices includes the original NICS index, NICS(0),⁵¹ defined as −σ_iso (at ring center), NICS(1) = −σ_iso (at 1 Å above ring center),^52,53 NICS(0)_zz = −σ_zz (at ring center)^54,55 and NICS(1)_zz = −σ_zz (at 1 Å above ring center).⁵⁶ The magnetic susceptibility data is comprised of the isotropic magnetic susceptibilities, χ_iso, and the out-of-plane components of the magnetic susceptibility tensor, χ_zz.

Table 2 NICS values (ppm) and magnetic susceptibilities (ppm cm³ mol⁻¹) for the S₀ and S₁ states of benzene and naphthalene

		NICS(0)	NICS(1)	NICS(0)zz	NICS(1)zz	χ iso	χ zz
C6H6	S0	−8.3	−9.9	−11.3	−27.2	−59.7	−99.8
	S1	44.4	33.3	143.1	100.1	1.3	76.6
C10H8	S0	−8.1	−9.8	−8.2	−25.4	−99.3	−176.2
	S1	37.7	28.3	127.8	87.9	9.9	147.2

---

The comparison between the CASSCF-GIAO NICS values for the S₀ and S₁ electronic states of benzene and naphthalene shows clearly that whereas, in the electronic ground states, the six-membered ring in benzene is more aromatic than a six-membered ring in naphthalene, in the first singlet excited states a six-membered ring in naphthalene is less antiaromatic (or, more aromatic) than the six-membered ring in benzene. The NICS(0)_zz and NICS(1)_zz indices suggest more pronounced differences between the aromaticities of the six-membered rings in the two molecules in each electronic state than do NICS(0) and NICS(1). The CASSCF(6,6)-GIAO/6-311+G* NICS values for the S₀ and S₁ electronic states of benzene are in good agreement with the corresponding CASSCF(6,6)-GIAO/6-311++G(2d,2p) NICS data from literature,¹² which is an indication that the accuracy afforded by the 6-311+G* basis is sufficient for the purposes of the current investigation. As expected, the NICS data in Table 2 fully supports the conclusions following from the analyses of Fig. 4–7.

When comparing the isotropic magnetic susceptibilities and the out-of-plane components of the magnetic susceptibility tensor for the two molecules, it is important to remember that these are ‘entire molecule’ and not ‘per ring’ values, so each of χ_iso and χ_zz for naphthalene needs to be divided by 2 before juxtaposing it with the correspond value for benzene. A comparison of this type leads to conclusions analogous to those derived from the NICS values, with one exception: due to the larger differences between the diagonal components of the S₁ magnetic susceptibility tensor for naphthalene, the corresponding χ_iso value turns out to be higher than the corresponding value for benzene.

Finally, we note that HBO and NAP possess large π-systems making calculation of the full π-space by CASSCF impractical. For this reason, we chose TD-DFT to analyze these molecules in Fig. 8 (see ESI† for details). TD-DFT allowed for computation of these systems in a straightforward manner, introducing correlation effects for both core and valence electrons. However, TD-DFT cannot be used to describe singlet excited state (anti)aromaticity as the required methodology has not been developed and implemented in code.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful for support of this work by Iowa State University of Science and Technology and a Pfizer Global ASPIRE Award (WI241789).

Notes and references

1. R. Gleiter and G. Haberhauer, Aromaticity and Other Conjugation Effects, Wiley-VCH, Weinheim, Germany, 2012.
2. N. Martin, M. M. Haley and R. Tykwinski, Aromaticity: A Web Themed Issue, Chem. Commun., 2012, 48, 10471.
3. P. v. R. Schleyer, Chem. Rev., 2005, 105(10), 3433–3435.
4. N. C. Baird, J. Am. Chem. Soc., 1972, 94, 4941–4948.
5. J. Aihara, Bull. Chem. Soc. Jpn., 1978, 51, 1788–1792.
6. F. Fratev, V. Monev and R. Janoschek, Tetrahedron, 1982, 38, 2929–2932.
7. B. Wrackmeyer, H. J. Schanz, M. Hofmann and P. V. R. Schleyer, Angew. Chem., Int. Ed., 1998, 37, 1245–1247.
8. M. Kataoka, J. Chem. Res., 2004, 573–574.
9. A. Soncini and P. W. Fowler, Chem. Phys. Lett., 2008, 450, 431–436.
10. M. Rosenberg, C. Dahlstrand, K. Kilsa and H. Ottosson, Chem. Rev., 2014, 114, 5379–5425.
11. H. Ottosson, Nat. Chem., 2012, 4, 969–971.
12. P. B. Karadakov, J. Phys. Chem. A, 2008, 112, 7303–7309.
13. P. B. Karadakov, J. Phys. Chem. A, 2008, 112, 12707–12713.
14. F. Feixas, J. Vandenbussche, P. Bultinck, E. Matito and M. Sola, Phys. Chem. Chem. Phys., 2011, 13, 20690–20703.
15. P. B. Karadakov, P. Hearnshaw and K. E. Horner, J. Org. Chem., 2016, 81, 11346–11352.
16. M. Ueda, K. Jorner, Y. M. Sung, T. Mori, Q. Xiao, D. Kim, H. Ottosson, T. Aida and Y. Itoh, Nat. Commun., 2017, 8, 346.
17. L. J. Fischer, A. S. Dutton and A. H. Winter, Chem. Sci., 2017, 8, 4231–4241.
18. R. Ayub, R. Papadakis, K. Jorner, B. Zietz and H. Ottosson, Chem. – Eur. J., 2017, 23, 13684–13695.
19. J. Oh, Y. M. Sung, H. Mori, S. Park, K. Jorner, H. Ottosson, M. Lim, A. Osuka and D. Kim, Chem, 2017, 3, 870–880.
20. J. Zhao, S. Ji, Y. Chen, H. Guo and P. Yang, Phys. Chem. Chem. Phys., 2012, 14, 8803–8817.
21. A. C. Sedgwick, L. Wu, H. H. Han, S. D. Bull, X. P. He, T. D. James, J. L. Sessler, B. Z. Tang, H. Tian and J. Yoon, Chem. Soc. Rev., 2018, 47, 8842–8880.
22. T. Iijima, A. Momotake, Y. Shinohara, T. Sato, Y. Nishimura and T. Arai, J. Phys. Chem. A, 2010, 114, 1603–1609.
23. T. Kanda, A. Momotake, Y. Shinohara, T. Sato, Y. Nishimura and T. Arai, Bull. Chem. Soc. Jpn., 2009, 82, 118–120.
24. H. Roohi, F. Hejazi, N. Mohtamedifar and M. Jahantab, Spectrochim. Acta, Part A, 2014, 118, 228–238.
25. C. Azarias, S. Budzak, A. D. Laurent, G. Ulrich and D. Jacquemin, Chem. Sci., 2016, 7, 3763–3774.
26. L. Gutierrez-Arzaluz, F. Cortes-Guzman, T. Rocha-Rinza and J. Peon, Phys. Chem. Chem. Phys., 2015, 17, 31608–31612.
27. N. Nishina, T. Mutai and J. I. Aihara, J. Phys. Chem. A, 2017, 121, 151–161.
28. D. Setiawan, E. Kraka and D. Cremer, J. Org. Chem., 2016, 81, 9669–9686.
29. M. Giambiagi, M. S. de Giambiagi, C. D. D. Silva and A. P. de Figueiredo, Phys. Chem. Chem. Phys., 2000, 2, 3381–3392.
30. E. Clar, The Aromatic Sextet, Wiley, London, NY, 1972.
31. T. M. Krygowski and M. K. Cyranski, Chem. Rev., 2001, 101, 1385–1419.
32. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. Schleyer, Chem. Rev., 2005, 105, 3842–3888.
33. S. Fias, P. W. Fowler, J. L. Delgado, U. Hahn and P. Bultinck, Chem. – Eur. J., 2008, 14, 3093–3099.
34. S. Van Damme, G. Acke, R. W. A. Havenith and P. Bultinck, Phys. Chem. Chem. Phys., 2016, 18, 11746–11755.
35. T. M. Krygowski, H. Szatylowicz, O. A. Stasyuk, J. Dominikowska and M. Palusiak, Chem. Rev., 2014, 114, 6383–6422.
36. I. J. Palmer, I. N. Ragazos, F. Bernardi, M. Olivucci and M. A. Robb, J. Am. Chem. Soc., 1993, 115, 673–682.
37. J. Dreyer and M. Klessinger, Chem. – Eur. J., 1996, 2, 335–341.
38. E. J. P. Malar and K. Jug, J. Phys. Chem., 1984, 88, 3508–3516.
39. E. Brémond, M. Savarese, C. Adamo and D. Jacquemin, J. Chem. Theory Comput., 2018, 14, 3715–3727.
40. D. Jacquemin, J. Chem. Theory Comput., 2018, 14, 1534–1543.
41. A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039.
42. B. J. Lampkin, C. Monteiro, E. T. Powers, P. M. Bouc, J. W. Kelly and B. VanVeller, Org. Biomol. Chem., 2019, 17, 1076–1080.
43. J. Seo, S. Kim and S. Y. Park, J. Am. Chem. Soc., 2004, 126, 11154–11155.
44. K. Ruud, T. Helgaker, R. Kobayashi, P. Jørgensen, K. L. Bak and H. J. r. A. Jensen, J. Chem. Phys., 1994, 100, 8178–8185.
45. K. Ruud, T. Helgaker, K. L. Bak, P. Jørgensen and J. Olsen, Chem. Phys., 1995, 195, 157–169.
46. K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, R. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. Sánchez de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, The Dalton Quantum Chemistry Program System, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 , Dalton, a Molecular Electronic Structure Program, Release Dalton 2016.2, 2016.
47. A. Cabana, J. Bachand and J. Giguère, Can. J. Phys., 1974, 52, 1949–1955.
48. P. B. Karadakov and K. E. Horner, J. Phys. Chem. A, 2013, 117, 518–523.
49. M. Baba, Y. Kowaka, U. Nagashima, T. Ishimoto, H. Goto and N. Nakayama, J. Chem. Phys., 2011, 135, 054305.
50. T. Hashimoto, H. Nakano and K. Hirao, J. Chem. Phys., 1996, 104, 6244–6258.
51. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
52. P. v. R. Schleyer, H. Jiao, N. J. R. v. E. Hommes, V. G. Malkin and O. L. Malkina, J. Am. Chem. Soc., 1997, 119, 12669–12670.
53. P. v. R. Schleyer, M. Manoharan, Z.-X. Wang, B. Kiran, H. Jiao, R. Puchta and N. J. R. van Eikema Hommes, Org. Lett., 2001, 3, 2465–2468.
54. I. Cernusak, P. W. Fowler and E. Steiner, Mol. Phys., 2000, 98, 945–953.
55. E. Steiner, P. W. Fowler and L. W. Jenneskens, Angew. Chem., Int. Ed., 2001, 40, 362–366.
56. H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Org. Lett., 2006, 8, 863–866.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp02050k

‡ These authors contributed equally to this manuscript.

---