Open Access Article
Open Access ArticleVibrational spectroscopy of the hexahydrated sulfate dianion revisited: role of isomers and anharmonicities†
Harald
Knorke
a,
Huiyan
Li
bc,
Zhi-Feng
Liu
*bc and
Knut R.
Asmis
 *a
*a
aWilhelm-Ostwald-Institut für Physikalische und Theoretische Chemie, Universität Leipzig, Linnéstr. 2, 04103 Leipzig, Germany. E-mail: knut.asmis@uni-leipzig.de
bDepartment of Chemistry and Centre for Scientific Modelling and Computation, Chinese University of Hong Kong, Hong Kong, China. E-mail: zfliu@cuhk.edu.hk
cShenzhen Research Institute, Chinese University of Hong Kong, No. 10, 2nd Yuexing Road, Shenzhen, China
First published on 13th May 2019
Abstract
We report on the gas phase vibrational spectroscopy of the hexahydrated sulfate dianion, SO42−(H2O)6, and its fully deuterated isotopologue, SO42−(D2O)6, using infrared photodissociation (IRPD) spectroscopy of the D2-tagged dianions in combination with density-functional-theory calculations on minimum-energy structures as well as finite temperature ab initio molecular dynamics (AIMD) simulations. The IRPD spectra were recorded at an ion trap temperature of 12 K and in the spectral range from 650 to 3800 cm−1, covering the intramolecular modes of the solvent (OH/OD stretches and H2O/D2O bends) at higher energies, those of the solute (sulfate stretches) at intermediate energies and the intermolecular solute librational modes at the lowest energies. Isomer-specific double resonance in combination with messenger-tag dependent IRPD spectra show that only a single isomer is contributing significantly and that this isomer is not the highly symmetric Td but rather the lower symmetry C3 isomer. Temperature-dependent IR multiple photon dissociation spectra of bare SO42−(H2O)6 suggest that the C3 isomer remains the most stable one up to 200 K. The AIMD simulations reveal that the IRPD spectra can only be fully understood when anharmonic effects as well as entropy-driven hydrogen bond network fluctuations are considered.
Introduction
Hydrated sulfate dianions, SO42−, play a key role in the homogeneous nucleation of ice particles by sulfate aerosols in the upper troposphere1 and in the regulation of many metabolic and cellular processes.2 The presence of water on the Martian surface has been inferred from sulfate geochemistry.3 Due to its compact and doubly charged nature, the interaction of sulfate with water is strong and sulfate adopts a distinct position in the famous Hofmeister series as one of the most kosmotropic anions.4 Microhydrated sulfate dianions in the gas phase serve as prototypical model systems for understanding anion solvation, in general, and that of multiply-charged anions, in particular.5,6 The structure of the hexahydrated sulfate dianion has been the subject of ongoing discussions over the last two decades.7–15 Two low-energy structures exist (see Fig. 1), which differ in the way the six water molecules function as hydrogen-bond acceptors (A) and donors (D). The C3 isomer contains two types of water molecules, three DD and three ADD ones, and is referred to as the 6.9.3 isomer, since it contains six water molecules that form nine anion-water and three water–water hydrogen bonds.13 In contrast, the six DD water molecules in the Td isomer 6.12.0 are symmetry equivalent, forming twelve anion–water and no water–water hydrogen bonds. Here, we study the vibrational spectroscopy of the hexahydrated sulfate dianions, SO42−(H2O)6, and its fully deuterated isotopologue, SO42−(D2O)6, in order to unambiguously resolve, which isomers contribute to its gas phase IR spectrum at cryogenic temperatures and above. | ||
| Fig. 1 B3LYP-D3/aug-cc-pVTZ minimum-energy structures, including label (see text and ref. 7 for details) and symmetry, of the two lowest energy structures of SO42−(H2O)6. Bond lengths are reported in pm. Water molecules are classified according to their function as hydrogen bond acceptor (A) or donor (D). | ||
Blades and Kebarle5 were the first to detect SO42−(H2O)n dianions with n ≥ 3 in the gas phase and subsequently determined some of their hydration energies.16 Wang and co-workers performed the first spectroscopic investigations using anion photoelectron (APE) spectroscopy and suggested that the signal carrier is the C3 isomer 6.9.3 (see Fig. 1), based on density functional theory (DFT) calculations.7 Subsequently, second-order Møller–Plesset (MP2) calculations by Pye and Rudolph identified the Td isomer 6.12.0 (see Fig. 1) as the global minimum.8 Computational studies that directly followed provided evidence for several energetically low-lying isomers and could not convincingly resolve this issue.9 The first gas phase vibrational spectra, in the form of infrared multiple photon photodissociation (IRMPD) spectra of cryogenically-cooled ions at ∼20 K in the mid-IR range (550 to 1800 cm−1) using the widely-tunable IR radiation from a free electron laser were published in 2006.10 Comparison to simulated harmonic IR spectra from MP2 calculations yielded slightly better agreement with the Td isomer 6.12.0 in this spectral range. Shortly thereafter, Williams and co-workers measured an IRMPD spectrum of slightly hotter anions (130 K), but now in the O–H stretching region, and came to the conclusion that multiple isomers, in particular the C3 and Td isomers, are present and contribute to the IRMPD spectra.11 APE experiments on cryogenically cooled dianions at 12 K, which allow for a more accurate determination of the vertical detachment energy, combined with higher level calculations, on the other hand, confirmed the initial assignment by Wang et al. to the C3 isomer.12 The authors also noted that at room temperature multiple isomers should be populated. Head-Gordon, Xantheas and co-workers performed the first coupled cluster calculations, also in combination with anharmonic vibrational corrections and estimates of the basis set effects up to the complete basis set limit using MP2, on this system.13,14 Interestingly, these calculations predict yet another structure, a 6.6.6 structure containing two three-membered water rings, to be the global minimum, but after zero-point energy corrections are taken into account the C3 isomer (6.9.3) is predicted to be the most stable one at 0 K for both isotopologues. However, the authors also note that “the errors in the different theoretical treatments might still be too large to make a clear distinction between very closely spaced isomers possible”.14 Since anharmonic as well as entropic effects are important for a reliable description of such systems a molecular dynamics description of this system may prove more appropriate.13,17
In this publication we consider many of the previously made suggestions and report messenger-tagged spectra of cold, hexahydrated sulfate dianions. We explicitly explore anharmonic effects by studying the effect of (i) isotope-substitution, (ii) the number of messenger tags and (iii) temperature on the vibrational spectra. Furthermore, we apply an established IR double-resonance detection scheme18 to identify the contributions to the vibrational spectra isomer-specifically. The interpretation of the experimental data is aided by the results from harmonic and anharmonic vibrational frequency calculations as well as ab initio molecular dynamics (AIMD) simulations using DFT.
Methods
Experimental methods
IRPD experiments were performed using the 6 K ion trap triple mass spectrometer described previously.19 In brief, microhydrated sulfate dianions are produced in a nanospray ion source from a 20 mM solution of sulfuric acid in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 water/methanol mixture. A typical mass spectrum of this solution is shown in Fig. S1 of the ESI.† The beam of anions is skimmed, collimated in a gas-filled radio frequency (RF) ion guide, mass-selected using a quadrupole mass-filter and focused in a RF ring-electrode ion trap, held at a temperature in-between 6 and 300 K using a closed-cycle helium cryostat. To allow for continuous ion loading and ion thermalization, the trap is continuously filled with buffer gas, either He (for bare ions) or D2 (for messenger-tagged ions). Many collisions of the trapped ions with the buffer gas provide gentle cooling of the internal degrees of freedom close to the ambient temperature. At sufficiently low ion-trap temperatures, ion–messenger complexes are formed via three-body collisions.20 Every 100 ms, all ions are extracted from the ion trap and focused both temporally and spatially into the center of the extraction region of an orthogonally-mounted double-focussing reflectron time-of-flight (TOF) tandem photofragmentation mass spectrometer. The ion packet is accelerated into the reflectron stage, ions spread out in space according to their mass-to-charge ratio (m/z) and are refocused at the initial extraction region. Prior to reacceleration towards the MCP detector, ions with a particular m/z value are irradiated by a properly timed, widely wavelength tunable IR laser pulse (bandwidth: 2.5 cm−1), supplied by an optical parametric oscillator/amplifier (LaserVision: OPO/OPA/AgGaSe2) laser system.21 An IRPD spectrum is measured by continuously scanning the laser wavelength, which is monitored online using a HighFinesse WS6-600 wavelength meter, with a scan speed such that an averaged TOF mass spectrum (over 150 laser shots) is obtained every 2 cm−1. Typically, at least three scans are measured and averaged and the photodissociation cross section σIRPD is determined as described previously.19
2 water/methanol mixture. A typical mass spectrum of this solution is shown in Fig. S1 of the ESI.† The beam of anions is skimmed, collimated in a gas-filled radio frequency (RF) ion guide, mass-selected using a quadrupole mass-filter and focused in a RF ring-electrode ion trap, held at a temperature in-between 6 and 300 K using a closed-cycle helium cryostat. To allow for continuous ion loading and ion thermalization, the trap is continuously filled with buffer gas, either He (for bare ions) or D2 (for messenger-tagged ions). Many collisions of the trapped ions with the buffer gas provide gentle cooling of the internal degrees of freedom close to the ambient temperature. At sufficiently low ion-trap temperatures, ion–messenger complexes are formed via three-body collisions.20 Every 100 ms, all ions are extracted from the ion trap and focused both temporally and spatially into the center of the extraction region of an orthogonally-mounted double-focussing reflectron time-of-flight (TOF) tandem photofragmentation mass spectrometer. The ion packet is accelerated into the reflectron stage, ions spread out in space according to their mass-to-charge ratio (m/z) and are refocused at the initial extraction region. Prior to reacceleration towards the MCP detector, ions with a particular m/z value are irradiated by a properly timed, widely wavelength tunable IR laser pulse (bandwidth: 2.5 cm−1), supplied by an optical parametric oscillator/amplifier (LaserVision: OPO/OPA/AgGaSe2) laser system.21 An IRPD spectrum is measured by continuously scanning the laser wavelength, which is monitored online using a HighFinesse WS6-600 wavelength meter, with a scan speed such that an averaged TOF mass spectrum (over 150 laser shots) is obtained every 2 cm−1. Typically, at least three scans are measured and averaged and the photodissociation cross section σIRPD is determined as described previously.19
Computational methods
Electronic structure calculations were performed using the Gaussian 16 rev. A.03 program.22 Previously reported geometries10,13 were used as initial guesses for geometry optimizations followed by vibrational frequency calculations using the B3LYP functional23 in combination with the aug-cc-pVTZ24 basis set. The influence of dispersion interactions was considered by using the D3 version of Grimme's dispersion correction with Becke–Johnson damping.25 To account for anharmonic effects as well as systematic errors on the harmonic force constants, we determined scaling factors on the basis of a comparison of the IRPD spectra to harmonic spectra of both isotopologues (all-H and all-D). To assess these effects more carefully, we performed anharmonic frequency calculations using the second-order vibrational perturbation theory (VPT2) method as implemented by Bloino and Barone.26 Relevant optimized geometries, minimum energies and harmonic and anharmonic vibrational spectra are reported in the ESI.†To uniquely identify the numerous isomers, we adopt the labelling proposed by Lambrecht et al.13,14 The label of each individual SO42−(H2O)n structure is given in the n.s.w-l notation, where n, s and w refer to the number of water molecules, of sulfate–water hydrogen bonds and of water–water hydrogen bonds, respectively. Within each n.s.w category the structures are sorted according to increasing electronic energy determined by Lambrecht et al.14 and indicated with number l (l = 1, 2,…). Note, when l is omitted l = 1 is implied.
In AIMD simulations, the electronic energy and atomic forces are obtained within the framework of DFT, while the atomic motion is treated within Newtonian mechanics, as implemented in the CP2K package.27 The wave functions are expanded in a double zeta Gaussian basis set, while the electron density is expanded in Gaussians and auxiliary plane waves (GPW)28 with an energy cut-off at 350 Rydberg for the electron density. The atomic cores are modelled by the Goedecker–Teter–Hutter (GTH) type pseudopotentials.29 The exchange and correlation energy is calculated using the BLYP functional30 in combination with Grimme's D3 dispersion correction.25 A cluster ion is put at the center of a periodic cubic box, and the effects of the periodic charge density images are corrected by the decoupling technique developed by Martyna and Tuckerman.31 The box length is 16 to 20 Å depending on the cluster size. The convergence criterion for the SCF electronic procedure is set to be 10−7 a.u. at each time step. For molecular dynamics, the temperature is controlled by a Nose–Hoover thermostat,32 with a time step of 0.5 fs. An equilibration period of up to 15 ps is performed first, while a production run for data collection at 100 K lasts more than 100 ps.
A vibrational spectrum can be directly simulated by the Fourier transform of the dipole time-correlation function (DTCF),33
![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) is the total dipole moment of the system, calculated by the polarization including both ionic and electronic contributions at each time step. The temperature and dynamic effects produced by the fluctuations of HBs on the vibrations are automatically captured by AIMD simulations and contained in such a DTCF spectrum.
is the total dipole moment of the system, calculated by the polarization including both ionic and electronic contributions at each time step. The temperature and dynamic effects produced by the fluctuations of HBs on the vibrations are automatically captured by AIMD simulations and contained in such a DTCF spectrum.
Results and discussion
IRPD spectra of the all-H and all-D isotopologues
IRPD spectra of D2-tagged SO42−(H2O)6 and SO42−(D2O)6 in the O–H(D) stretching and the mid-IR spectral regions are shown in Fig. 2. Band positions and assignments are summarized in Table 1. The IRPD bands are labelled according to their assignment, i.e., either as hydrogen-bonded water stretching (a), D2 stretching (b), water bending (c), antisymmetric sulfate stretching (d) and water wagging (e) modes, numbered from highest to lowest energy. An apostrophe indicates the bands of the deuterated complex. For better comparability of the bands assigned to water modes, a scaling factor of 1.361 is used to align the O–H/O–D stretching and H2O/D2O bending regions. The scaling factor is close to the value expected for isolated O–H vs. O–D oscillators (1/1.374). Note, non-water modes, like SO42− and D2 stretches (indicated by the broken lines in Fig. 2), which are centred at similar wavenumbers in the spectra of the two isotopologues, are not aligned in this representation. | ||
| Fig. 2 IRPD spectra of the D2-tagged all-H and all-D isotopologues of the hexahydrated sulfate dianion: SO42−(H2O)6·D2 (top) and SO42−(D2O)6·D2 (bottom). Note, for better comparability the spectra are plotted against opposing vertical axes and the horizontal axis of the lower spectrum was scaled 1/1.361, such that the bands corresponding water modes, i.e. bands a/a′ and c/c′ appear at similar horizontal positions (see text). See Table 1 for band labels, positions and assignments. | ||
| Labelb | IRMPD | IRPD | B3LYP-D3 | Assignmentc | ||||
|---|---|---|---|---|---|---|---|---|
| All-H | All-D | Ratio | All-H | All-D | Ratio | |||
| a Ref. 14. b IRPD bands associated with the all-D isotopomer are labelled with an apostrophe in Fig. 2. c Abbreviations: hydrogen-bonded (HBed), donor–donor (DD), acceptor–donor–donor (ADD, see text). | ||||||||
| a1/a1′ | 3560 | 3559 | 2625 | 1.36 | 3658 | 2662 | 1.37 | HBed O–H/O–D stretch (ADD water–ADD water) |
| a2/a2′ | 3528 | 3528 | 2606 | 1.35 | 3614 | 2638 | 1.37 | HBed O–H/O–D stretch (ADD water–ADD water) |
| a3/a3′ | 3459 | 3457 | 2546 | 1.36 | 3626, 3616 | 2628, 2623 | 1.38, 1.38 | HBed O–H/O–D stretch (DD water–sulfate) |
| a4/a4′ | 3416 | 3416 | 2488 | Overtone/combination band | ||||
| a5/a5′ | 3385 | 3383 | 2445 | Overtone/combination band | ||||
| a6 | 3272 | 3278 | Overtone/combination band | |||||
| a7 | 3237 | 3246 | Overtone/combination band | |||||
| a8/a8′ | 3167 | 3172 | 2371 | 1.34 | 3390, 3342 | 2459, 2432 | 1.38, 1.37 | HBed O–H/O–D stretch (ADD water–sulfate) |
| b1/b1′ | 2944 | 2944 | 1.00 | 3019 | 3019 | 1.00 | D2 stretch (bound to SO42−) | |
| b2/b2′ | 2929 | 2929 | 1.00 | 3001, 2997 | 3001, 2997 | 1.00, 1.00 | D2 stretch (bound to water) | |
| c1/c1′ | 1710 | 1256 | 1.36 | 1719 | 1260 | 1.36 | Water bend | |
| c2/c2′ | 1690a | 1694 | 1245 | 1.36 | 1709, 1698 | 1249, 1243 | 1.37, 1.37 | Water bend |
| d1/d1′ | 1088a | 1088 | 1087 | 1.00 | 1057, 1055 | 1054, 1051 | 1.00, 1.00 | Antisymmetric SO42− stretch |
| e1 | 771a | 772 | 856, 748 | 621, 539 | 1.38, 1.39 | Water wag | ||
| 621a | 640, 593 | 614, 590 | 1.04, 1.01 | SO42− bend | ||||
Taking into account the expected isotopic shifts, the IRPD spectra of the two isotopologues shown in Fig. 2 look very similar, indicating that the same isomer (or isomers) is (are) probed in both cases. The spectra show no sign of free O–H (>3650 cm−1) or O–D (>2700 cm−1) stretching modes, but a rather complicated pattern of at least eight (five) bands in the hydrogen-bonded O–H(D) stretching region extending from 3600 to 3100 cm−1 (2650 to 2300 cm−1). This characteristic IR signature in the hydrogen-bonded O–H(D) stretching region is similarly broad to that observed previously by Bush et al. in their IRMPD study.11 This supports their previous assignment to a lower-symmetry isomer containing hydrogen-bonded O–H(D) oscillators in various environments, i.e. exhibiting a broader distribution of red-shifted O–H stretching transitions, like the 6.9.3 isomer, which contains weak (water–water), intermediate (DD water–sulfate) and stronger (ADD water–sulfate) hydrogen bonds. The highly symmetric Td isomer 6.12.0, on the other hand, exhibits only a single type of hydrogen bonded O–H(D) oscillator (DD water–sulfate) and consequently should yield a less red-shifted and much narrower absorption profile.
In more detail, both spectra contain three intense bands at 3559/2625 cm−1 (a1/a1′), 3457/2546 cm−1 (a3/a3′) and 3172/2371 cm−1 (a8/a8′), which we assign, in agreement with previous calculations,10–14 to the stretching modes involving the predominantly decoupled O–H/(D) oscillators of the ADD waters hydrogen-bonded to either the adjacent ADD water molecules (a1/a1′) or to the sulfate core (a8/a8′) and the symmetric combination of coupled O–H(D) oscillators of the DD waters (a3/a3′). Note, while the band position ratios a1/a1′ (1.356) and a3/a3′ (1.358) are nearly identical, the ratio a8/a8′ (1.338) is smaller, indicating a larger anharmonicity in the all-H isotopologue of the latter mode and hence a less pronounced red-shift of a8′ (compared to a1′ and a3′, see Fig. 2) as a result of the lower zero-point energy (ZPE) in the all-D isotopologue. The weaker features a4–7 are attributed to combination and overtone excitations. The band position ratio a2/a2′ (1.354) is similar to that of a1/a1′, while features a4–7 seem to exhibit a similar behaviour to a8, suggesting that this mode (a8) contributes to some of these combination bands. In addition, the intensities of non-fundamental transition are markedly suppressed in the all-D spectrum, in agreement with smaller anharmonicities and hence less strong couplings with low-energy modes in the all-D isotopologue.
The nominally IR-forbidden D–D stretching mode of the messenger tag, which gains IR-activity upon polarization, is observed red-shifted (50–65 cm−1) from its value in free D2 (2994 cm−1).34 Interestingly, this region exhibits more than one peak, an intense one at 2944 cm−1 (b1, b1′) and a roughly seven (four) times weaker one at 2929 cm−1 (b2, b2′), suggesting more than one D2 binding site. Note, three type of D2 binding sites (see below) are present in the 6.9.3 isomer, while the 6.12.0 isomer exhibits only a single type.
A pair of peaks, at 1710 cm−1 (c1) and 1694 cm−1 (c2) in the all-H and at 1256 cm−1 (c1′) and 1245 cm−1 (c2′) in the all-D spectrum, are observed in the water bending region. These bands exhibit the same band position ratios (c1/c1′: 1.361, c2/c2′: 1.361) as well as similar band intensity ratios (c1/c2: 59%, c1′/c2′: 71%). This suggests a similar number of water molecules in two type of binding environments, again favouring an assignment to the 6.9.3 isomer, which contains three DD and three ADD waters, rather than to the 6.12.0 isomer with its six symmetry-equivalent DD waters.
A single peak d1 (d1′) with a width of 23 cm−1 (17 cm−1) is observed at 1088 cm−1 (1087 cm−1) in the sulfate stretching region of the IRPD spectra of the all-H (all-D) isotopologue. The absence of any significant splitting (considering the experimental resolution of a few cm−1) of the antisymmetric sulfate stretching mode suggest that the microhydration environment does not significantly perturb the triply degenerate transition, in agreement with the predictions for both isomers.12 However, bands d1 and d1′ do have slightly different band shapes: band d1 is more symmetrically broadened at its base, while d1′ is narrower, presumably due to the smaller rotational constants of the all-D isotopologue, and asymmetric.
Isomer-specific IR2MS2 spectra
In order to determine how many different isomers contribute to the IRPD spectrum of SO42−(H2O)6·D2 we performed isomer-selective IR2MS2 measurements.28,29 More precisely, the method is sensitive to laser-induced population changes that are maintained longer than the delay between the two IR laser pulses (∼10−5 s). The IR spectra of more quickly interconverting isomers cannot be isolated using this technique. IR2MS2 spectra probed in O–H oscillator region (3800–2900 cm−1) at 3559 cm−1 (a1), 3457 cm−1 (a3) and 3172 cm−1 (a8) are shown in Fig. 3 along with the (single-resonance) IRPD spectrum from Fig. 2. The three IR2MS2 spectra look very similar and thus provide strong evidence for the predominant presence of only a single isomer under these experimental conditions. | ||
| Fig. 3 Comparison of the (single resonance) IRPD spectrum of SO42−(H2O)6·D2 (a) from Fig. 2 to isomer-specific double-resonance IR2MS2 spectra probed at 3172 cm−1 (b), 3457 cm−1 (c) and 3559 cm−1 (d), corresponding to bands a8, a3 and a1, respectively, each marked by an arrow. | ||
Influence of the messenger tag
Additional information regarding the identity of the isomer can be obtained by comparing the IRPD spectra of complexes containing a different number of D2 tags n (see Fig. 4). The spectra were measured in the O–H stretching region and at an ion trap temperature of 12 K. While the overall appearance of the spectra is similar, two apparent messenger-tag dependent effects are observed. First, the lower energy bands shift to higher energies as n increases. This effect is most pronounced for band a8 and amounts to ∼6 cm−1 per D2 molecule. Secondly, the relative intensities of the two D2 stretches (b1, b2) increase and change their ratio from roughly 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 6
1 to 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 with increasing n (see Fig. S6 and Table S2, ESI†). In more detail, D2 binding to the site corresponding to b1 is initially favoured, but saturation leads to binding of additional messenger tags to the other binding site (b2). Both these observations support an assignment to a lower symmetry isomer. Isomer 6.9.3, indeed, has three types of D2 binding sites, the O-atoms of the three DD waters and the three ADD waters as well as three undercoordinated O-atoms of SO42−. Our DFT calculations suggest that adsorption at the DD–H2O and SO42− sites is slightly favoured energetically and results in the blue shift of band a8 that is apparent in Fig. 4.
5 with increasing n (see Fig. S6 and Table S2, ESI†). In more detail, D2 binding to the site corresponding to b1 is initially favoured, but saturation leads to binding of additional messenger tags to the other binding site (b2). Both these observations support an assignment to a lower symmetry isomer. Isomer 6.9.3, indeed, has three types of D2 binding sites, the O-atoms of the three DD waters and the three ADD waters as well as three undercoordinated O-atoms of SO42−. Our DFT calculations suggest that adsorption at the DD–H2O and SO42− sites is slightly favoured energetically and results in the blue shift of band a8 that is apparent in Fig. 4.
 | ||
| Fig. 4 Comparison of the IRMPD spectrum of SO42−(H2O)6 (top trace) to IRPD spectra of the D2-tagged clusters SO42−(H2O)6·(D2)n with n = 1–4 measured at an ion trap temperature of 12 K. | ||
Temperature-dependent IRMPD spectra
Fig. 5 shows the comparison of the IRPD spectrum of D2-tagged SO42−(H2O)6 measured at an ion trap temperature of 12 K, with IRMPD spectra of bare SO42−(H2O)6 for temperatures between 6 and 200 K in the O–H stretching region. The IRMPD spectrum at 6 K shows the same number peaks as the IRPD spectrum of the D2-tagged species, indicating that the same isomer is probed. However, the relative intensities of some of the peaks are different, in particular, those at higher energies, like those of a1 are smaller and those of the bands at lower energies, like a6 and a7, are larger in the IRMPD spectrum of untagged SO42−(H2O)6. Note, photodissociation of bare SO42−(H2O)6 (at 0 K) requires at least two IR photons in this spectral region in order to overcome the predicted dissociation limit of ∼70 kJ mol−1.14 We attribute the low intensity of a1 to less efficient IRMPD compared to the more anharmonic O–H oscillators further to the red. Practically, the situation is more complex and mode-dependent details need to be considered. With increasing temperature the spectral features widen and merge into a single broad, asymmetric absorption band with a maximum around 3150 cm−1 at approximately 100 K. Note, at higher energies the form of this absorption feature remains the same, providing no evidence for the population of additional isomers. This is significant, since the IRMPD spectrum reported by Williams and co-workers,11 obtained at 130 K and under different experimental conditions, lies in the same spectral region, but is more structured, with a strong absorption band at 3550 cm−1, which was attributed to the 6.12.0 isomer. We observe no such feature up to 200 K, suggesting that this isomer is not populated thermally in our experiment. Hence, the different time scales in the two experiments lead to different isomer populations. In the present experiment the ions are irradiated by a single IR laser pulse (12 mJ) of ∼5 ns duration and this leads to the detection of only a single isomer (6.9.3), suggesting that isomerization is inefficient on this time scale. In the previous experiment the ions are irradiated by 70 to 1200 IR laser pulses (10 Hz, 8–21 mJ), which gives them up to 120 s to isomerize (and/or radiatively decay) after the first photon is absorbed. In this way, the 6.12.0 isomer as well as others could be efficiently populated. Gibbs free energy calculations (see Table 2) show that the all-H (all-D) isotopologue of the 6.9.3 isomer is favoured by 6 kJ mol−1 (8 kJ mol−1) over the 6.12.0 isomer at 0 K. However, the higher symmetric (!) 6.12.0 isomer is entropically favoured at higher temperatures and its population is predicted to become relevant near room temperature. | ||
| Fig. 5 IRMPD spectra of SO42−(H2O)6 for ion trap temperatures from 6 to 200 K. The D2-tagged IRPD spectrum measured at 12 K, as well as, the spectrum measured by Williams and coworkers13 is also shown at the top. | ||
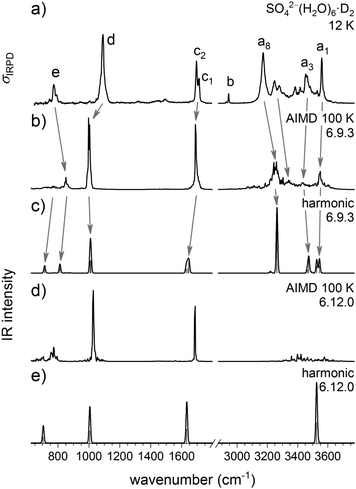
Harmonic and DTCF spectra
Fig. 6 shows the comparison of the experimental D2-tagged IRPD spectrum of SO42−(H2O)6 with simulated harmonic as well as 100 K DTCF spectra of the two isomers 6.9.3 and 6.12.0. Calculated IR spectra of other isomers are shown in the Fig. S2 of the ESI.† The scaled harmonic IR spectra for the two isomers (panels c and e in Fig. 6) are rather similar over the complete spectral range and both show similarities with the experimental spectrum. However, there are two differences, which favor an assignment to isomer 6.9.3. The most obvious is the prediction of five O–H stretching bands in the range from 3200–3600 cm−1, in particular the intense band at 3263 cm−1, assigned to the hydrogen bonded (ADD–H2O/sulfate) O–H stretching modes, in contrast to the single O–H stretching band at 3525 in the harmonic spectrum of isomer 6.12.0. Note, the B3LYP-D3 calculations slightly underestimate the strength of the ADD–H2O/sulfate hydrogen bonds. The broader water bending band in the 6.9.3 spectrum also agrees better with the experimental spectrum. On the other hand, the harmonic spectrum of 6.9.3 predicts two water wagging modes of comparable IR intensity, of which only one is observed in the IRPD spectrum. This was one of arguments in favor of an assignment to isomer 6.12.0 in the original IRMPD study, which was based on measurements exclusively in the mid-IR spectral range (540–1850 cm−1).10Additional insights can be gained from the results of the AIMD simulations (panels b and d of Fig. 6). Compared to the harmonic IR spectrum the DTCF spectrum of the 6.9.3 isomer qualitatively improves the agreement with the experimental one, in particular because the AIMD simulation also accounts for temperature as well as dynamic aspects.17 The predicted absorption profile over the complete spectral range, but especially in the O–H stretching region, captures the widths and relative intensities rather well, without the need for convolution as for the harmonic spectra. Moreover, the AIMD simulations predict only a single prominent band in the water wag region below 900 cm−1, in better agreement with experiment. Unexpectedly, the results of the AIMD simulations for 6.12.0 also reveal an improved agreement compared to the harmonic IR spectrum. Instead of a single O–H stretching peak, a 400 cm−1 broad, low intensity feature is predicted, suggesting that it may be difficult to rule out the presence of the 6.12.0 isomer, since its characteristic absorptions overlap with those of the 6.9.3 isomer. Moreover, these calculations suggest that the highest energy experimental band a1, previously assumed to contain significant contributions from isomer 6.12.0 based on the harmonic spectra,11 predominantly contains contributions from 6.9.3 (even if 6.12.0 were present). Summarizing, the current experimental IR(M)PD spectra are best rationalized by assuming the predominant presence of isomer 6.9.3, possibly with minor contributions from 6.12.0.
More detailed, atom-dependent information on the dynamic effects of the solvent molecules can be gained from the vibrational density of states (DOS) obtained by the Fourier transform of the velocity autocorrelation function for a particular atom, shown in Fig. 7. This shows that the OH–stretch vibration of the DD–H2O covers a range of 300 cm−1. As demonstrated in a previous study on HCO3−(H2O),35 the DD–H2O is in an indifferent equilibrium since it's impossible to achieve a co-linear O–H⋯O alignment for both hydrogen bonds, similar to the situation in NO3−(H2O).36 The DD–H2O can easily rock to one side, making one hydrogen bond shorter and better aligned, while sacrificing the other hydrogen bond. This motion leads to a broadening of the OH stretching and water wagging modes of the DD–H2O's, which are particularly sensitive to the length of the hydrogen bond. In addition, the harmonic calculations confirm that the vibrations associated with this rocking motion are predicted at 72 and 107 cm−1, which coincides with the observed difference of 76 cm−1 (a7–a8) and 105 cm−1 (a6–a8). As a result, the IR intensity of the DD–H2O wagging vibrations is smeared out over a broader spectral range (∼150 cm−1) due to the dynamic effects and therefore less apparent in the IRPD spectrum. In contrast, the rocking motion of the three ADD–H2O's has a much smaller amplitude as a result of the additional fixation by the third hydrogen bond. The DOS plots in Fig. 7 also support the assignment of bands a1 and a8 to O–H stretches of the ADD–H2O's hydrogen-bonded to a water molecule or the sulfate core, respectively. Finally, our calculations confirm that the three-membered water ring in 6.9.3 is stable over the whole simulation time, even when the simulation temperature is raised to 200 K.
 | ||
| Fig. 7 Vibrational density of states plots for the O- and H-atoms of the DD-H2O (a) and ADD-H2O (b) hydrogen bonded water molecules based on the AIMD simulation of 6.9.3 at 100 K (c). | ||
Summary and conclusions
The present study shows that predominantly a single spectroscopic species, namely the 6.9.3 and not the 6.12.0 isomer, is probed in IRPD experiments on SO42−(H2O)6 as well as its fully deuterated isotopologue at temperatures up to 200 K. While the vibrational signature of these two isomers is quite similar in the mid-IR region, in particular, when dynamic effects are considered, measurements in the O–H(D) region prove to be more diagnostic, in this particular case, as was suggested previously.11,12 However, also in this spectral region the assignment is not as straight-forward as one would expect based on the harmonic simulations of the IR spectra, but anharmonic, temperature and tagging effects need to be considered as well and only the one- and two-color IRPD spectra obtained at cryogenic temperatures in combination with AIMD simulations allow for an unambiguous structural assignment.The anharmonic spectra obtained from the AIMD simulations on SO42−(H2O)6 accurately account for the most of the features across the IRPD spectrum. The simulations confirm the stability of the 6.9.3 isomer also at elevated temperatures (∼200 K) and show that the two types of water molecules (ADD vs. DD) behave quite differently. The position of the ADD waters are fixed by the ring, the DD waters (of both isomers) perform larger amplitude motion, leading to the broadening of the corresponding O–H stretch and H2O wagging vibrations. Population of the 6.12.0 isomer is predicted to become favorable near room temperature and above. However, its spectral identification will be challenging, since it contains only DD water molecules, which are prone to large amplitude motion and hence lead to particularly broad features in the vibrational spectrum, especially at 300 K. Nonetheless, the insights obtained in the present study should prove helpful to reliably assign structures of sulfate–water clusters of different size.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the German Research Foundation (DFG) as part of the individual research Grant No. AS133/3-1 “Spectroscopic Characterization of Salt Dissolution in Microhydrated Cluster Ions and at the Water/Vapor Interface.” ZFL thanks the support from the National Natural Science Foundation of China (Grant No. 21473151) and from CUHK through a Direct Grant (3132676). The authors are grateful to Alexandra Giermann (Universität Leipzig) for her assistance in preparing and handling sulfuric acid solutions. K. R. A. acknowledges instrumental support from the Fritz-Haber-Institute of the Max-Planck Society.References
- V. Ramanathan, P. J. Crutzen, J. T. Kiehl and D. Rosenfeld, Science, 2001, 294, 2119–2124 CrossRef CAS PubMed.
- A. Lee, P. A. Dawson and D. Markovich, Int. J. Biochem. Cell Biol., 2005, 37, 1350–1356 CrossRef CAS PubMed.
- S. W. Squyres, J. P. Grotzinger, R. E. Arvidson, J. F. Bell, W. Calvin, P. R. Christensen, B. C. Clark, J. A. Crisp, W. H. Farrand, K. E. Herkenhoff, J. R. Johnson, G. Klingelhofer, A. H. Knoll, S. M. McLennan, H. Y. McSween, R. V. Morris, J. W. Rice, R. Rieder and L. A. Soderblom, Science, 2004, 306, 1709–1714 CrossRef CAS PubMed.
- Y. J. Zhang and P. S. Cremer, Curr. Opin. Chem. Biol., 2006, 10, 658–663 CrossRef CAS PubMed.
- A. T. Blades and P. Kebarle, J. Am. Chem. Soc., 1994, 116, 10761–10766 CrossRef CAS.
- W. R. Cannon, B. M. Pettitt and J. A. McCammon, J. Phys. Chem., 1994, 98, 6225–6230 CrossRef CAS; X. B. Wang, X. Yang and L. S. Wang, Int. Rev. Phys. Chem., 2002, 21, 473–498 Search PubMed.
- X. B. Wang, J. B. Nicholas and L. S. Wang, J. Chem. Phys., 2000, 113, 10837–10840 CrossRef CAS.
- C. C. Pye and W. W. Rudolph, J. Phys. Chem. A, 2001, 105, 905–912 CrossRef CAS.
- R. L. Wong and E. R. Williams, J. Phys. Chem. A, 2003, 107, 10976–10983 CrossRef CAS; C. G. Zhan, F. Zheng and D. A. Dixon, J. Chem. Phys., 2003, 119, 781–793 CrossRef; B. Gao and Z. F. Liu, J. Chem. Phys., 2004, 121, 8299–8306 CrossRef PubMed; B. Gao and Z. F. Liu, J. Chem. Phys., 2005, 123, 224302 CrossRef PubMed.
- J. Zhou, G. Santambrogio, M. Brümmer, D. T. Moore, G. Meijer, D. M. Neumark and K. R. Asmis, J. Chem. Phys., 2006, 125, 111102 CrossRef PubMed.
- M. F. Bush, J. T. O'Brien, J. S. Prell, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2007, 129, 1612–1622 CrossRef CAS PubMed.
- X. B. Wang, A. P. Sergeeva, J. Yang, X. P. Xing, A. I. Boldyrev and L. S. Wang, J. Phys. Chem. A, 2009, 113, 5567–5576 CrossRef CAS PubMed.
- D. S. Lambrecht, G. N. Clark, T. Head-Gordon and M. Head-Gordon, J. Phys. Chem. A, 2011, 115, 5928–5935 CrossRef CAS PubMed.
- D. S. Lambrecht, L. McCaslin, S. S. Xantheas, E. Epifanovsky and M. Head-Gordon, Mol. Phys., 2012, 110, 2513–2521 CrossRef CAS.
- N. Mardirossian, D. S. Lambrecht, L. McCaslin, S. S. Xantheas and M. Head-Gordon, J. Chem. Theory Comput., 2013, 9, 1368–1380 CrossRef CAS PubMed.
- A. T. Blades, J. S. Klassen and P. Kebarle, J. Am. Chem. Soc., 1995, 117, 10563–10571 CrossRef CAS; A. T. Blades and P. Kebarle, J. Phys. Chem. A, 2005, 109, 8293–8298 CrossRef PubMed.
- L. Jiang, S.-T. Sun, N. Heine, J.-W. Liu, T. I. Yacovitch, T. Wende, Z.-F. Liu, D. M. Neumark and K. R. Asmis, Phys. Chem. Chem. Phys., 2014, 16, 1314–1318 RSC.
- R. A. Relph, B. M. Elliott, G. H. Weddle, M. A. Johnson, J. Ding and K. A. Jordan, J. Phys. Chem. A, 2009, 113, 975–981 CrossRef CAS PubMed; N. Heine, M. R. Fagiani, M. Rossi, T. Wende, G. Berden, V. Blum and K. R. Asmis, J. Am. Chem. Soc., 2013, 135, 8266–8273 CrossRef PubMed.
- N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2014, 34, 1–34 Search PubMed; N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2016, 35, 507 Search PubMed.
- M. Brümmer, C. Kaposta, G. Santambrogio and K. R. Asmis, J. Chem. Phys., 2003, 119, 12700–12703 CrossRef CAS; D. J. Goebbert, T. Wende, R. Bergmann, G. Meijer and K. R. Asmis, J. Phys. Chem. A, 2009, 113, 5874–5880 CrossRef PubMed.
- W. R. Bosenberg and D. R. Guyer, J. Opt. Soc. Am. Soc. B, 1993, 10, 1716–1722 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS; D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. Bloino and V. Barone, J. Chem. Phys., 2012, 136, 124108 CrossRef PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- G. Lippert, J. r. Hutter and M. Parrinello, Theor. Chem. Acc., 1999, 103, 124–140 Search PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS; C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef; M. Krack, Theor. Chem. Acc., 2005, 114, 145–152 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS; C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef.
- G. J. Martyna and M. E. Tuckerman, J. Chem. Phys., 1999, 110, 2810–2821 CrossRef CAS.
- S. Nose, J. Chem. Phys., 1984, 81, 511–519 CrossRef CAS.
- D. A. McQuarrie, Statistic Mechanics, Harper-Collins Publishers, New York, 1976 Search PubMed.
- P. J. Brannon, C. H. Church and C. W. Peters, J. Mol. Spectrosc., 1968, 27, 44–54 CrossRef CAS.
- X. Kong, S.-T. Sun, L. Jiang and Z.-F. Liu, Phys. Chem. Chem. Phys., 2018, 20, 4571–4578 RSC.
- X. B. Wang, X. Yang, L. S. Wang and J. B. Nicholas, J. Chem. Phys., 2002, 116, 561–570 CrossRef CAS; D. J. Goebbert, E. Garand, T. Wende, R. Bergmann, G. Meijer, K. R. Asmis and D. M. Neumark, J. Phys. Chem. A, 2009, 113, 7584–7592 CrossRef PubMed; N. Heine, E. G. Kratz, R. Bergmann, D. P. Schofield, K. P. Asmis, K. D. Jordan and A. B. McCoy, J. Phys. Chem. A, 2014, 118, 8188–8197 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Mass spectrum, relative electronic energies and Gibbs free energies, simulated harmonic and anharmonic IR spectra, fit parameters. See DOI: 10.1039/c9cp01802f |
| This journal is © the Owner Societies 2019 |