Biological relevance of charge transfer branching pathways in photolyases

Abstract

The repair of sun-induced DNA lesions by photolyases is driven by a photoinduced electron transfer from a fully reduced FAD to the damaged DNA. A chain of several aromatic residues connecting FAD to solvent ensures the prior photoreduction of the FAD cofactor. In PhrA, a class III CPD photolyase, two branching tryptophan charge transfer pathways have been characterized. According to previous experiments, both pathways play a role in the FAD photoreduction. To provide a molecular insight to the charge transfer abilities of both pathways, we perform multiscales simulations where the protein motion and the positive charge are simultaneously propagated. Our computational approach reveals that one pathway drives a very fast charge transfer whereas the other pathway provides a very good thermodynamic stabilization of the positive charge. During the simulations, the positive charge firstly moves on the fast triad, while a reorganization of the close FAD˙⁻ environment occurs. Then, backward transfers can lead to the propagation of the positive charge on the second pathway. After one nanosecond, we observe a nearly equal probability to find the charge at ending tryptophan of either pathway; eventually the charge distribution will likely evolve towards a charge stabilization on the last tryptophan of the slowest pathway. Our results highlight the role the protein environment, which manages the association of a kinetic and a thermodynamic pathways to trigger a fast and efficient FAD photoreduction.

---

1 Introduction

Photolyases and cryptochromes belong to a family of light sensitive flavoproteins involved in the repair of DNA UV-induced lesions or in cellular signaling. Their function arises from the photo-activation of a non covalently bound FAD cofactor: a photoinduced electron transfer from reduced FAD to the damaged DNA initiates the catalytic cycle in photolyases, while the signaling function of cryptochromes is based on the formation of a radical pair state in the protein after FAD photoreduction.^1–4

A tryptophan triad, first identified in the Escherichia coli photolyase structure,⁵ conducts charge transfers (CT) from the photoactivated oxidized FAD to the protein surface. Many recent experimental and computational studies addressed this photoreduction mechanism in several cryptochromes and photolyases.^6–18 They describe an efficient subnanosecond process, essential to recover the active form of the protein in vitro. Since the first description of the common tryptophan triad, different CT pathways have been reported: a fourth Trp,^7,12 tyrosines or alternative pathways^6,18,19 can participate in the photoreduction mechanism. These different features of the CT cascade help to understand the evolution within the cryptochrome–photolyase family.

PhrA is a class III cyclobutane pyrimidine (CPD) photolyase from Agrobacterium tumefaciens.²⁰ Plant cryptochromes probably arose from class III CPD photolyases, both appear as sister groups in phylogenetic studies. At least two possible CT pathways have been characterized in this protein (see Fig. 1) and participate in the FAD photoreduction. The first one corresponds to the classical tryptophan triad previously described in Escherichia coli photolyase and contains Trp384, Trp361 and Trp308 (respectively A, B1 and C1 in Fig. 1). The alternative triad includes Trp384, Trp318 and Trp367 (A, B2 and C2 in Fig. 1). Though close to Trp367, a fourth tryptophan, Trp336 (D2 in Fig. 1), was not considered in the previous experiments. We expect that this tryptophan can participate in the alternative pathway. Moreover, this residue forms a π-stack complex with the other chromophore of PhrA, a methenyltetrahydrofolate (MTHF) antenna which harvests light energy to transfer it to FAD. The mutant of this tryptophan loses this chromophore,²⁰ so it becomes harder to experimentally characterize its impact on the photoreduction. Indeed, site-directed mutagenesis experiments are often used to assess the charge transfer ability of a pathway by replacing a hypothetical electron transmitter by a redox-inactive amino acid such as phenylalanine. Most of the time, such photolyase and cryptochrome mutants show a blocked or a reduced FAD photoreduction. The presence of an alternative pathway can be demonstrated by the persistence of the CT process when the classical triad is interrupted.⁶ However, the PhrA mutants contrast with the previously described behaviour: while the absorption spectra indicate a classical monoexponential decay of oxidized FAD in wild-type (WT) PhrA, it shows a transition between a slow initial decay and a very fast decay when a tryptophan from either pathway is mutated to phenylalanine or alanine.²⁰ These two components reduction patterns imply a slower secondary mechanism such as a conformational rearrangement.²⁰ The monoexponential photoreduction observed in WT PhrA seems to require the full “classical” and “alternative” ET pathways.

Fig. 1 PhrA structure (PDB: 4U63)²⁰ and the charge migration within the two CT pathways: the classical path with Trp384 (A, black), Trp361 (B1, red) and Trp308 (C1, green); the alternative path with Trp384 (A), Trp318 (B2, blue), Trp367 (C2, orange), Trp336 (D2, purple). FAD is colored in cyan. Arrows represent the hole transfers from excited FAD to A (cyan), along the classical triad (pink) or along the alternative tetrad (yellow). Hydrogen atoms are omitted for clarity. Picture made with VMD.²¹

In this work, we focus on the comparison and the interplay between the two tryptophan pathways. We consider Trp336 in the so-called alternative pathway, which is thus a tryptophan tetrad. We use an unbiased quantum mechanics/molecular mechanics (QM/MM) scheme which was successfully applied to characterize CT in DNA,^22–25 in photolyases, cryptochromes^16–18 and also in organic materials.^26–28 We found a good agreement between the experimental values and our computational results for the classical tryptophan triad in the Escherichia coli CPD photolyase¹⁶ or in the Arabidopsis thaliana plant cryptochrome:¹⁷ we obtained rate constants differing by one order of magnitude or less from experimental data for forward charge transfer. Our QM/MM scheme allows the direct simulation of the charge motion along the different redox cofactors without any bias, which unravels the relative stability of the different redox states and the possible backward CT mechanisms (albeit the calculated backward rate constants are often overestimated). In our previous studies, the electrostatic environment provided by the protein structure and the solvent accessibility generates a downhill picture for the CT along the triad where the positive charge is stabilized on the last tryptophan, far from FAD.^17,18 Such a stabilization is required in the signaling function of cryptochrome or to allow the protonation of FAD which occurs at larger timescales (see for example ref. 29). Some alternative pathways, which are activated in Xenopus laevis cryptochrome DASH mutants, have also been tested using the same approach and computational results reproduced the experimental data.^6,30 Our main goal here is to establish, at a molecular level, the pertinence of the branching pathways in the FAD photoreduction in terms of CT rate. We firstly consider each pathway separately to analyze their own characteristics and interactions with the protein environment. We then include the two branching CT pathways in the simulation protocol in order to define the interplay of different CT mechanisms in PhrA.

2 Computational details

2.1 Classical MD-simulation

We started our simulations with the crystal structure of PhrA (PDB-ID: 4U63).²⁰ The construction of the simulation box and all the classical simulations were performed using the GROMACS 5.0.4 package^31,32 and the AMBER-SB99-ILDN force field.^33–35 The force field parameters for the different FAD redox states were previously described.^16,17 The atomic charges of the MTHF antenna chromophore were generated from restrained fitting on the electrostatic potential (RESP)^36,37 calculated at HF/6-31G*^38,39 using Gaussian09 software.⁴⁰ Other nonstandard force field parameters were derived from the general AMBER force field (GAFF).^41,42 The pK_a of titratable residues has been determined using PROPKA 3.0 program.^43,44 The protein was solvated in a 118 × 118 × 118 Å TIP3P water⁴⁵ cubic box. Three chloride anions were added to neutralize the system.

The equilibration of the solvated protein PhrA starts with a minimization step, followed by 100 ps MD in the canonical ensemble and 100 ps in the isothermal–isobaric ensemble (300 K, 1 atm) using Nosé–Hoover thermostat⁴⁶ and Parrinello–Rahman barostat.⁴⁷ 150 ns of production of MD simulations in the isothermal–isobaric ensemble (300 K, 1 atm) were performed afterwards with a time step of 2 fs and covalent hydrogen bonds were fixed on a constant length by the use of the LINCS algorithm.⁴⁸

2.2 QM/MM

We extracted 29 geometries from our 150 ns classical MD trajectory. The structures were separated by one nanosecond in 6 intervals: 25–29 ns, 35–39 ns, 71–74 ns, 96–100 ns, 121–125 ns and 146–150 ns. For our QM/MM simulations, we follow the same procedure as in our previous studies.^16–18 Only the first photoreduction is considered, namely the reduction of oxidized FAD to semi-quinone FAD˙⁻. We exclude the subpicosecond CT between the photoexcited FAD and the closest site A from our simulations. The flavin is described using classical force field on its negatively charge FAD˙⁻ state. The QM part contains the side chain of the tryptophans from the considered pathway(s). QM/MM boundaries, defined on the C_α–C_β bond, are treated using hydrogen link atoms.

Three QM/MM partitions are used, depending on the considered CT cascade. The first possible QM part concerns the classical triad and the QM part contains only the side chains of A, B1 and C1. The second QM partition corresponds to the alternative tetrad A, B2, C2 and D2. The last partition includes both pathways, namely sites A, B1, C1, B2, C2 and D2. All QM/MM simulations last 1 ns. We performed 25 or 29 QM/MM charge propagation simulations along the individual pathways or the branching pathways respectively.

We use a in-house GROMACS 4.6 version which allows site energies and electronic coupling calculations at Fragment Orbital Tight Binding Density Functional Theory (FO-DFTB) level. DFTB⁴⁹ is a semi-empirical approach, based on GGA-DFT methods, but two to three orders of magnitude faster than standard DFT calculations. To reduce the computational cost of the charge propagation, we split the quantum region into several fragments, corresponding to the individual tryptophan side chains. For each fragment, only the HOMO, for a hole transfer, or the LUMO, for an electron transfer, is considered in the Hamiltonian of the whole system. Further calculation details are described elsewhere.^16,25,50 Practically, our approach is based on a quantum description of the charge propagation included in a classical MD protocol (see Fig. 2) of the system and is propagated over the system solving the time-dependent Schrödinger equation. Before each atomic forces calculation following the Newton's laws, the charges are updated according to the electronic wave function.

Fig. 2 Scheme of our direct fast charge transfer simulation protocol using classical force field for atomic motions and a fragment orbital (FO)-DFTB/MM scheme for charge propagation.

The different steps of the calculation can be described as below:

• The whole system, i.e. the fragments involved in charge transfer as well as the environment, i.e., the protein and water solvent are treated using a classical force field. Forces are computed and used to compute MD-trajectories.

• In every time-step of this classical MD, the IP (or site energies) and charge transfer couplings are computed from the FO-DFTB/MM method. DFTB has been benchmarked before for this purpose and it has been shown, that IP's and couplings can be computed with very high accuracy.^22,51–53 The couplings are computed from the orbitals of the fragments ‘i’ and ‘j’ as:

T_ij = 〈Φ_i|Ĥ|Φ_j〉;. (1)

• The site energy ε_i and the couplings are fused to a fragment-orbital Hamiltonian, which describes the electronic structure of the quantum subsystem. The charge is treated as a second order perturbation of the neutral Hamiltonian:

Solving the time-dependent Schrödinger-equation for this reduced system, leads to a time-dependence of the coefficients a_i of Ψ,This equation, therefore, describes the dynamics of the hole-charge wavefunction.

• At this stage, the dynamics of the atoms is governed purely by the classical force-field (FF). This force field has fixed atomic charges, therefore, is in principle not able to describe charge transfer. However, after propagation of the wavefunction one step with the time-dependent Schrödinger-equation, we project the wave-function onto atomic charges, and update the charges in the force-field according to the electronic wave-function. Therefore, we perform a ‘on-the-fly’ reparametrisation of the force-field depending on the electronic structure of the quantum sub-system. Atomic forces for the whole system are computed with these new charges. Such scheme allows the dynamic relaxation of the environment around the moving charges which is the microscopic cause of the phenomenological Marcus reorganization parameters, when the equilibrium is reached. I.e., without the projection of the charges, one would neglect reorganization energy, which is often the most important factor for the dynamics.

The charge occupation of each fragment, which changes between 0 (neutral residue) and 1 (positively charged residue) is collected along the different trajectories and then averaged. The obtained time dependent averaged occupations can be fitted using a kinetic model¹⁷ to compute theoretical rate constants characterizing forward and backward CT.

Additionally, we performed FO-DFTB/MM simulations in which the positive charge stays on A, B1, C1, B2, C2 or D2 during 1 ns while the FAD cofactor is negatively charged. The difference between the site energy for each positively charged tryptophan and their neutral state corresponds to the stabilization of the positive charge by the surrounding environment. We split this energy gap into two components: one corresponds to the contribution from FAD and the 6 tryptophan residues (called CT-pathway), and the other one to the interaction with the environment, namely the solvent and the protein excluding the tryptophan residues from the CT-pathway. The first contribution was obtained by calculating the site energy of the charged tryptophan along the previously obtained 1 ns simulation with all the atomic charges equal to zero except ones of the FAD cofactor and the tryptophan side chains. The difference between the total energy (including all interactions) and the CT-pathway contribution provides the environment contribution.

3 Results and discussion

3.1 Charge transfer along the independent pathways

A first tryptophan (A in Fig. 1) is in a suitable position to give an electron to the photoexcited FAD. Afterwards, two branching pathways can be considered: the classical one, a triad of the three tryptophans A, B1 and C1, or the alternative one, a tryptophan tetrad which includes A, B2, C2 and D2 (see Fig. 1). We firstly sampled the conformational space around the different tryptophans along a 150 ns classical MD (the electronic couplings calculated during this simulation are reported in Table S1, ESI†). Thereafter, we performed unbiased QM/MM MD simulations of the CT propagation along the classical triad or the alternative tetrad. In a first set of simulations, we considered the two pathways individually in order to compute the CT rates for the respective pathways.

Starting from 25 different structures which were randomly extracted from the long classical MD simulation, we performed 25 direct CT simulations over the classical triad. Only A, B1 and C1 compose the QM part in these first simulations, therefore, no transfer to the alternative pathway or to FAD can be described. Exactly the same procedure is applied to the alternative tetrad, considering A, B2, C2 and D2 in the QM part. The occupation of each tryptophan, which directly relates to its charge (0 means neutral site and 1 fully oxidized site), is evaluated as a function of time during the 1 ns QM/MM simulations. Afterwards, this occupation was averaged on the 25 simulations to draw kinetic profiles (see Fig. 3). Rate constants (see Table 1) are determined from the time dependence of the averaged occupations following a numerical fitting procedure described elsewhere.¹⁷

Fig. 3 Time dependent evolution of the averaged charge occupation along the classical triad (a) or the alternative one (b) in PhrA. Black line: A; red line: B1; green line: C1; blue line: B2; orange line: C2; purple line: D2. A time-scale change is represented by the grey dashed line: on the left hand, the first decades of picoseconds are zoomed to provide a picture of the first fast CT events; then the scale is modified to account for the fluctuation of the charge localisation at hundreds of picoseconds time-scale: error bars denote the standard deviation of the occupations each 0.1 ns. The charge is on A at the starting point of the simulation. The fitting curves from our kinetic model are also shown using the same relative colors.

Table 1 Rate constants in ns⁻¹ for the different CT transfers between tryptophan in PhrA. The first subscripted letter indicates the positive charge donor and the second the acceptor. Each line corresponds to a different QM part: only A, B1 and C1 for the “classical triad”; A, B2, C2 and D2 for the “alternative tetrad” and finally all tryptophans for “both” pathways

	k A–B1	k B1–A	k B1–C1	k C1–B1	k A–B2	k B2–A	k B2–C2	k C2–B2	k C2–D2	k D2–C2
Classical triad	1010.3	778.3	219.6	20.0	—	—	—	—	—	—
Alternative tetrad	—	—	—	—	48.6	56.6	1195.5	318.0	176.7	25.4
Both	738.6	601.6	435.1	71.4	26.9	46.0	398.4	196.5	61.1	7.7

---

The kinetic profile for the classical triad A–B1–C1 (Fig. 3a) describes a very fast CT cascade: B1 is transiently occupied and the charge is stabilized on the well-solvated last site C1 after 20 ps of simulation. We observe a remarkably high rate constant of 1010.3 ns⁻¹ for the forward CT from A to B1 (1), which is about 5 times the B1 to C1 CT rate constant and about 10 times the corresponding rate constant in cryptochrome.¹⁷ The slowest backward transfer from C1 to B1 reflects the stabilization of the charge on the last tryptophan C1 (1).

The same procedure was applied on the alternative tetrad A–B2–C2–D2. The corresponding kinetic profile presents a charge stabilization on D2 after 60 ps (Fig. 3b). The occupation increases on site D2 and decreases on site A in a symmetrical way, whereas the occupation on site B2 and C2 stays very low. The C2 occupation slightly grows in the first 20 ps to get an averaged occupation of 10% which remains stable during at least 1 ns. The large standard deviation values in Fig. 3b of the occupation of C2 and D2 denotes different final distribution of the charge along this tetrad. Actually, in most of the QM/MM simulations but two, the positive charge is stabilized on D2, supporting the hypothesis of a participation of this tryptophan to the alternative pathway. In the two remaining simulations, the positive charge is stabilized on C2. We observe a conformational change in these two simulations: the distance between the centres of mass of C2 and D2 increases from 7.6 to 10.0 Å. As a result, the electronic coupling is diminished by two orders of magnitude, thereby blocking the transfer to site D2. The CT between C2 and D2 is thus coupled to conformational changes. Similar observation has been already mentioned for the transfer between B1 and C1 homologous tryptophans in Arabidopsis thaliana cryptochrome.¹⁷

The rate constant of the first transfer between A and B2 is around 50 ns⁻¹, so 20 fold slower than between A and B1 (see Table 1). Besides, the corresponding backward transfer from B2 to A occurs on the same time-scale. On the contrary, the second CT between B2 and C2 happens on a similar time-scale as the A–B1 (thousand ns⁻¹). This combination of a slow oxidation of B2 and a fast oxidation of C2 leads to an unoccupied B2 site. The CT from C2 to D2 is slower, with a rate around two hundreds of ns⁻¹, but still one order of magnitude higher than the corresponding backward transfer. This difference between k_C2–D2 and k_D2–C2 attests to the stability of the charge on the last tryptophan D2. In this alternative tetrad, the first CT constitutes the kinetic limiting step while the charge is then quickly transferred to D2, in agreement with the symmetric time-dependent profiles of A and D2 occupations (Fig. 3b).

The individual analysis of the QM/MM simulations provides further details about the relative stability of the charge on the last residue of each pathways. We determined the frequency of the backward transfers from the last residue C1 or D2 to A. On average, 8 backward transfers occur during the classical triad trajectories and are randomly distributed in the 1 ns simulation time. On the contrary; in the alternative tetrad, the number of backward transfers is 2.4 on average, and they happen only at the beginning of the simulations: no backward transfer is observed after 250 ps. Most of the simulation time, the positive charge stays localized on D2 or C2, which decreases the probability of a charge recombination on FAD. This observation suggests that the conformation of the close environment rapidly adjusts to stabilize the positive charge on D2.

Though isoenergetic in gas phase, the different tryptophans in PhrA have different ionization potentials (IP) due to the heterogeneous environment of the solvated protein (see Fig. 4). The energy of neutral and oxidized tryptophans are averaged over 1 ns. The large fluctuations are due not only to the thermal fluctuation but also to the modification of the electrostatic field around each tryptophan. The energy of B2 is slightly higher than A, therefore, the observation of the slow rate constant of A–B2 transfer is consistent with the energetics. Conversely, the large energy differences between A and B1 (about 0.6 eV) or B2 and C2 (about 1 eV) correlates with the very fast forward CT between these tryptophans (note that these differences correspond to maxima after the relaxation of the environment around each radical state, which is not reach during the charge propagation simulations). Even tough in Marcus theory the existence of the invert region supposes that a larger driving force does not necessarily lead to a higher rate constant, the energy of the radical states in photolyases relaxes on timescales overlapping that of CT. Indeed, in a previous study,¹⁵ we found that Marcus theory fails to described the fast CT occuring in E. coli photolyase. We observe for both pathways a downhill energy profile which was previously highlighted in cryptochromes and photolyases.^16–18 We decompose the energy difference between the neutral and the oxidized states into two contributions (Fig. 4 bottom): (i) the interaction with the CT-pathway, containing the tryptophan side chains and charged FAD˙⁻, and (ii) the interaction with the protein and the solvent molecules. A localized positive charge on A is stabilized by the interaction with the negatively charged FAD˙⁻. As expected, the contribution associated with this interaction decreases when the FAD-tryptophan distance increases. The stabilization of the oxidized state of B1, C1 and D2 is mainly due to interactions with the protein and the solvent molecules. On the contrary, the contribution from the CT-pathway constitutes the major part of the stabilization of B2 and the stabilization of C2 results also mainly from the CT-pathway contribution (ca. frac23).

Fig. 4 Site energies of the different Trp (A, black; B1, red; C1, green; B2, blue; C2, orange; D2, purple) at a neutral state (top graph, highest values) and oxidized state (top graph, lowest values). Energy values are averaged along one nanosecond QM/MM MD trajectory. The error bars denote the standard deviation of the site energies. The energy gap between the two states (bottom graph) is divided into two contributions for each tryptophan: the contribution from the CT-pathway (tryptophans and FAD˙⁻) (bar filled with diagonal lines) and the interaction with PhrA and solvent (solid bar).

The radial distribution function of water molecules around the positively charged sites is given in Fig. 5. The classical triad presents an increasing solvation from A to C1, comparable to the water molecules distribution around the tryptophan triad in the plant cryptochrome.¹⁷ Much less water molecules interact with B2 than with B1. A look at the structure reveals that B2 is actually located in a hydrophobic pocket, which can explain its relatively high site energy. C1 and C2 have a similar solvation, and D2 has the highest degree of solvation because it is in direct contact with the bulk.

Fig. 5 Radial distribution function of water molecules around the center of mass of the different tryptophans in the branching pathway: black line: A; red line: B1; green line: C1; blue line: B2; orange line: C2; purple line: D2.

As we demonstrated for other photolyases and cryptochromes, the typical downhill profile for the CT results from better solvation of the residues, the closer they are to the bulk solvent.^16–18 The radical is stabilized by the deprotonation of the last tryptophan of a pathway, leading to the neutral radical indol ring. The deprotonation of the homologs of C1 occurs in 350 ps in a class II CPD photolyase,⁵⁴ 200 ns in plant cryptochrome,⁵⁵ 300 ns in Escherichia coli photolyase⁵⁶ and 2.5 μs in Xenopus laevis photolyase.⁷ The subnanosecond deprotonation in the class II CPD photolyase is explained by the presence of an acidic wire, which consists of a water cluster, an aspartate and a histidine in the tryptophan neighbourhood. In PhrA, several water molecules can also constitute a hydrogen bond wire around C1, however, no acidic residue is available to support the deprotonation of the positively charged C1. The C1 pocket is relatively similar to the Trp324 pocket in plant cryptochrome, except for the presence of a salt bridge close to C1 in PhrA. Considering these structural comparisons, we can expect that the deprotonation of C1 is faster than in plant cryptochrome, but not as fast as in the class II photolyase. In absence of any experimental value, the competition between the transfer to the alternative tetrad and the deprotonation of C1 remains conceivable, but we do not consider it in our simulations. In most of our simulations, the nitrogen atom of D2 is in hydrogen bond interaction with the backbone of Thr319. However, some D2 side chain rotations are observed leading to the complete solvation of the indol group. In such position, the tryptophan deprotonation can happen very fast.

In summary, our results on the independent CT pathways confirm the relative importance of the different tryptophans from both pathways. Once A is oxidized, the charge moves faster on the classical triad than on the alternative tetrad. The positive charge is stabilized on C1 following a downhill mechanism. A similar profile is observed for the alternative tetrad but the A–B2 transfer is two orders of magnitude slower than the A–B1 CT. However, the stabilization of the charge is stronger on the last tryptophan D2 of the alternative tetrad than on the site C1 of the classical triad. The good solvation of C2 also allows a significant stabilization of the charge on the alternative pathway. Moreover, the backward transfer is energetically impeded by the high cost of a reoxidation of B2. Consequently, our simulations draw a distinction between a kinetic triad A–B1–C1 and a thermodynamic tetrad A–B2–C2–D2, with their own advantages and drawbacks.

3.2 Charge transfer along the branching pathways

Site-directed mutagenesis of tryptophans from both pathways leads to a complex photoreduction process which contrasts with the monoexponential decay observed after excitation of oxidized FAD in the WT and suggests an important role of the combination of two CT pathways.²⁰ The simulations reported above neglect the interplay between these pathways. We thus simulated unbiased CT describing A, B1, C1, B2, C2, D2 at a QM level at the same time. We started 29 individual 1 ns QM/MM MD from different structures including an oxidized site A and a classical FAD˙⁻. As we did in the previous part, we averaged the occupations of each tryptophan over the different simulations to draw the kinetic profile presented in Fig. 6.

Fig. 6 Time dependent evolution of the averaged charge occupation along both pathways in PhrA. Black line: A; red line: B1; green line: C1; blue line: B2; orange line: C2; purple line: D2. The charge is on A at the starting point of the simulation. The fitting curves from our kinetic model are also shown using the same relative colors.

During the first 10 ps, the charge promptly goes from A to C1, so, maximum of C1 occupation (about 70%) is observed after 20 ps. Subsequently, the C1 occupation slowly decreases whereas the D2 occupation conversely increases. After 1 ns, the final occupation of C1 and D2 is between 40% and 50%. Because of the larger stabilization of the charge on the alternative tetrad, one can expect a complete transfer of the charge on D2 after several nanoseconds. The occupations of the intermediate tryptophans B1, B2 and C2 remain very low as well as the A occupation. Actually, in 27 of the 29 simulations, the charge moves to B1 first. In the two remaining trajectories, the charge is directly propagated along the alternative tetrad. Transfers causing crossings between pathways occur at low frequency (at maximum 3 crossings per simulation) but they lead to a 40–60% distribution of the charge on the two pathways: after 1 ns, 12 trajectories present an oxidized C1 and 17 an oxidized D2.

The rate constants (Table 1) are influenced by the extension of the QM zone to the six tryptophans. As expected, we observe a decrease of the rate constants involving site A as the Y-shaped pathway induces a competition between A–B1 and A–B2 transfer. Obviously, the classical triad has the better kinetic parameters and enables a fast transfer of the positive charge. However, the rate constant of the second CT, from B1 to C1, is lower than the backward CT rate from B1 to A. The charge thus fluctuates along the classical triad (see also the movie and the graphs in ESI†). On the contrary, if the first transfer from A to B2 is slow, the second transfer from B2 to C2 is ten fold faster than the backward transfer from B2 to A. The barrier for backward CT in the alternative tetrad is higher than in the classical triad so the charge is more stabilized on C2 or D2 than on C1 (see also Fig. 4).

We also performed QM/MM simulations where the positive charge is constrained on one site and the FAD is negatively charged. The starting structure is taken from the 150 ns classical MD simulation where the FAD is fully oxidized and the tryptophan are neutral. We can thus observe the conformational changes around each redox partner induced by the charge separation and the positive charge propagation. After almost 100 ps, we observe that the FAD˙⁻ IP increases by 0.2–0.4 eV, making the FAD oxidation harder (see Fig. 7), i.e., the energy of the hole on FAD is increased by environment reorganization. An example for reorganization is represented by the snapshot in Fig. 7: the rotation of Asn380, the rotation of the guanidinium group of Arg346 from π-stacked conformation to π–cation interaction with FAD, the formation of a hydrogen bond between Asp376 backbone and FAD. Thermodynamically, this will not have a big impact on the driving force of the charge recombination, but the reorganization, in a Marcus picture, would change the curvature of the diabatic states and may thereby introduce a small kinetic barrier. However, the electronic coupling between A and FAD does not change, so it is not affected by these structural reorientations. Overall, a recombination due to backward transfer along the classical triad seems likely. Then, a competition between the charge recombination on FAD and the transfer to alternative pathway arises. Once the charge is on C2 or D2, however, backward transfer is strongly inhibited by the large energy gap in the C2–B2 transfer. Despite the use of numerous and various simulations, no specific conformational change has been detected with regards to the control of the charge transfer across the branches. We expect an ensemble of small contributions allowing the site energies fluctuations and triggering the charge transfer from to B1 or B2.

Fig. 7 Fluctuation of the ionization potential of FAD˙⁻ when the charge is fixed on C1. The starting and the last conformations (upper pictures) of the FAD pocket illustrate different modifications of the environment occurring after the FAD photoreduction. Orange dashed lines indicate the hydrogen bond and purple dashed line the π–cation interaction. Hydrogen atoms of FAD have been deleted for clarity.

The mechanism observed in our simulation can be described by three steps also resumed in Fig. 8: (1) the charge is rapidly transferred to C1 through B1; (2) the environment stabilizes the negative charge on the isoalloxazine ring of the FAD, and the charge is transferred back to A; (3) the charge is stabilized on D2. The fast transfer to C1 avoids the immediate charge recombination between A and FAD. However, backward CT along the triad are frequent so the risk of FAD reoxidation may grow when A is again transiently positively charged. Two mechanisms can counteract the charge recombination: (i) the deprotonation of positively charged C1 (likely several nanoseconds) or (ii) the transfer of the positive charge to D2 (about several hundreds of ps). A reorganization of the environment around the FAD chromophore seems to follow the redox state modification of the isoalloxazine ring. On the contrary, the hydrophobic pocket of B2 appears mostly insensitive to the redox state of B2 (Fig. 4), so the charge can be transferred from A to C2 through B2 without a big outer sphere reorganization. The final stabilization of the positive charge on C2 or D2 prevents any charge recombination.

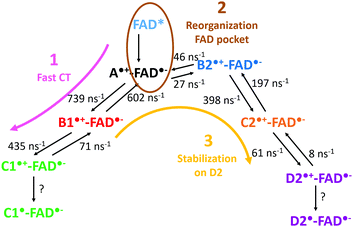Fig. 8 Scheme summarizing a possible mechanism involving both kinetic and thermodynamic pathways in the CT transfer in PhrA.

4 Conclusion

Photolyases and cryptochromes are able to efficiently photoreduce FAD. Several pathways of aromatic residues participate in the charge transfer from the flavin cofactor to the solvent. PhrA possesses two related CT pathways, starting from the same tryptophan, A. One of these pathways is called the classical triad with reference to the homologous pathway which was firstly described in Escherichia coli photolyase. The second one represents an alternative pathway which was also previously described in other proteins.^6,57,58 Such a pathway contributes to the photoreduction of FAD if the charge transfer along the classical triad is hindered. Unexpectedly, in PhrA, in vitro FAD photoreduction is altered by mutations on both pathways.²⁰

Our computational study provides a new insight on the respective role of these two pathways. First of all, we demonstrate the importance of a fourth tryptophan in the alternative pathway. Its IP is the most convenient one for a good stabilization of the positive charge. However, the classical pathway presents the highest rate constant for the first CT from the first tryptophan A to the second tryptophan of the CT cascade. The comparison between the rate constants of the different CT and the IP of the different tryptophan leads us to describe the classical triad as the “kinetic” one and the alternative one as the “thermodynamic” CT. Our unbiased CT simulations reflect these different behaviors. In most of our 1 ns trajectories, the charge goes to the classical triad in few ps. In about 100 ps, a reorganization of the FAD pocket leads to a small stabilization of FAD˙⁻. From time to time, a transfer to the alternative tetrad occurs and then the charge is stabilized on the last tryptophan D2. After 1 ns, we obtain a similar probability to have the charge on C1 or D2, but the kinetic profiles and the energetic values suggest a final stabilization of the charge on D2 after several ns. We also found that thermal motions that result in changed tryptophans distances can have a major impact on charge transfer. Conformational changes during photoreduction could also lead to the biexponential photoreduction curves that were observed during the measurements on tryptophans mutants.

The ubiquity of an efficient charge transfer pathway in all members of the photolyase–cryptochrome family underlines the importance of the photoreduction process leading to a stable radical state. Several strategies have been followed during the evolution to maintain the positive charge from the FAD: the fast charge transfers to the first and the second tryptophans which avoid the fast charge separation-recombination mechanism which occurs in a solvated U-shape FAD;^59,60 the common downhill process due to the environment which creates a stable charge separation state;^17,18 the fast deprotonation of the last tryptophan which stabilizes its oxidation;⁵⁴ or in the case of PhrA, the presence of alternative pathways. We prove that the combination of both CT pathways in PhrA ensures a fast and stable FAD photoreduction. This strategy can be followed by many cryptochromes and photolyases containing homologs of the branching pathway of PhrA.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thanks the state of Baden-Württemberg for providing computational resources through bwHPC. We also acknowledge Eike Hollesen for his help in the PhrA simulations. Natacha Gillet thanks the Alexander von Humboldt Foundation for a postdoctoral funding.

Notes and references

1. A. Sancar, Chem. Rev., 2003, 103, 2203–2238.
2. M. Müller and T. Carell, Curr. Opin. Struct. Biol., 2009, 19, 277–285.
3. I. Chaves, R. Pokorny, M. Byrdin, N. Hoang, T. Ritz, K. Brettel, L.-O. Essen, G. T. J. van der Horst, A. Batschauer and M. Ahmad, Annu. Rev. Plant Biol., 2011, 62, 335–364.
4. M. Zhang, L. Wang and D. Zhong, Photochem. Photobiol., 2017, 93, 78–92.
5. H. W. Park, S. T. Kim, A. Sancar and J. Deisenhofer, Science, 1995, 268, 1866–1872.
6. T. Biskup, B. Paulus, A. Okafuji, K. Hitomi, E. D. Getzoff, S. Weber and E. Schleicher, J. Biol. Chem., 2013, 288, 9249–9260.
7. P. Müller, J. Yamamoto, R. Martin, S. Iwai and K. Brettel, Chem. Commun., 2015, 51, 15502–15505.
8. J. Yamamoto, K. Shimizu, T. Kanda, Y. Hosokawa, S. Iwai, P. Plaza and P. Müller, Biochemistry, 2017, 56, 5356–5364.
9. I. A. Solov’yov, T. Domratcheva, A. R. Moughal Shahi and K. Schulten, J. Am. Chem. Soc., 2012, 134, 18046–18052.
10. I. A. Solov'yov, T. Domratcheva and K. Schulten, Sci. Rep., 2014, 4, 3845.
11. F. Cailliez, P. Müller, M. Gallois and A. de la Lande, J. Am. Chem. Soc., 2014, 136, 12974–12986.
12. F. Cailliez, P. Müller, T. Firmino, P. Pernot and A. de la Lande, J. Am. Chem. Soc., 2016, 138, 1904.
13. T. Firmino, E. Mangaud, F. Cailliez, A. Devolder, D. Mendive-Tapia, F. Gatti, C. Meier, M. Desouter-Lecomte and A. de la Lande, Phys. Chem. Chem. Phys., 2016, 18, 21442–21457.
14. R. Martin, F. Lacombat, A. Espagne, N. Dozova, P. Plaza, J. Yamamoto, P. Muller, K. Brettel and A. de la Lande, Phys. Chem. Chem. Phys., 2017, 19, 24493–24504.
15. P. B. Woiczikowski, T. Steinbrecher, T. Kubař and M. Elstner, J. Phys. Chem. B, 2011, 115, 9846–9863.
16. G. Lüdemann, P. B. Woiczikowski, T. Kubař, M. Elstner and T. B. Steinbrecher, J. Phys. Chem. B, 2013, 117, 10769–10778.
17. G. Lüdemann, I. A. Solov’yov, T. Kubař and M. Elstner, J. Am. Chem. Soc., 2015, 137, 1147–1156.
18. D. Holub, H. Ma, N. Krauß, T. Lamparter, M. Elstner and N. Gillet, Chem. Sci., 2018, 9, 1259–1272.
19. C. Aubert, P. Mathis, A. P. M. Eker and K. Brettel, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 5423–5427.
20. P. Scheerer, F. Zhang, J. Kalms, D. v. Stetten, N. Krauß, I. Oberpichler and T. Lamparter, J. Biol. Chem., 2015, 290, 11504–11514.
21. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
22. T. Kubař, P. B. Woiczikowski, G. Cuniberti and M. Elstner, J. Phys. Chem. B, 2008, 112, 7937–7947.
23. T. Kubař and M. Elstner, J. Phys. Chem. B, 2010, 114, 11221–11240.
24. T. Kubař and M. Elstner, J. Phys. Chem. B, 2008, 112, 8788–8798.
25. T. Kubar and M. Elstner, J. R. Soc., Interface, 2013, 10, 20130415.
26. A. Bashir, A. Heck, A. Narita, X. Feng, A. Nefedov, M. Rohwerder, K. Mullen, M. Elstner and C. Woll, Phys. Chem. Chem. Phys., 2015, 17, 21988–21996.
27. A. Heck, J. J. Kranz, T. Kubař and M. Elstner, J. Chem. Theory Comput., 2015, 11, 5068–5082.
28. A. Heck, J. J. Kranz and M. Elstner, J. Chem. Theory Comput., 2016, 12, 3087–3096.
29. P. Müller, K. Brettel, L. Grama, M. Nyitrai and A. Lukacs, ChemPhysChem, 2016, 17, 1329–1340.
30. E. Sjulstok, G. Lüdemann, T. Kubař, M. Elstner and I. A. Solov’yov, Biophys. J., 2018, 114, 2563–2572.
31. H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56.
32. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
33. J. Wang, P. Cieplak and P. A. Kollman, J. Comput. Chem., 2000, 21, 1049–1074.
34. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725.
35. D. E. Shaw, P. Maragakis, K. Lindorff-Larsen, S. Piana, R. O. Dror, M. P. Eastwood, J. A. Bank, J. M. Jumper, J. K. Salmon, Y. Shan and W. Wriggers, Science, 2010, 330, 341–346.
36. U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145.
37. B. H. Besler, K. M. Merz and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439.
38. G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218.
39. G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009.
41. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
42. J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260.
43. C. R. Søndergaard, M. H. M. Olsson, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 2284–2295.
44. M. H. M. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537.
45. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
46. D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069.
47. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
48. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
49. M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260.
50. T. Kubař and M. Elstner, Phys. Chem. Chem. Phys., 2013, 15, 5794–5813.
51. A. Kubas, F. Hoffmann, A. Heck, H. Oberhofer, M. Elstner and J. Blumberger, J. Chem. Phys., 2014, 140, 104105.
52. A. Kubas, F. Gajdos, A. Heck, H. Oberhofer, M. Elstner and J. Blumberger, Phys. Chem. Chem. Phys., 2015, 17, 14342–14354.
53. N. Gillet, L. Berstis, X. Wu, F. Gajdos, A. Heck, A. de la Lande, J. Blumberger and M. Elstner, J. Chem. Theory Comput., 2016, 12, 4793–4805.
54. P. Müller, E. Ignatz, S. Kiontke, K. Brettel and L.-O. Essen, Chem. Sci., 2018, 9, 1200–1212.
55. P. Müller, J.-P. Bouly, K. Hitomi, V. Balland, E. D. Getzoff, T. Ritz and K. Brettel, Sci. Rep., 2014, 4, 5175.
56. C. Aubert, M. H. Vos, P. Mathis, A. Eker and K. Brettel, Nature, 2000, 405, 586–590.
57. Y. F. Li, P. F. Heelis and A. Sancar, Biochemistry, 1991, 30, 6322–6329.
58. Z. Liu, C. Tan, X. Guo, J. Li, L. Wang, A. Sancar and D. Zhong, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12966–12971.
59. J. Brazard, A. Usman, F. Lacombat, C. Ley, M. M. Martin and P. Plaza, J. Phys. Chem. A, 2011, 115, 3251–3262.
60. Z. Liu, C. Tan, X. Guo, J. Li, L. Wang, A. Sancar and D. Zhong, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12966–12971.

---

Footnotes

† Electronic supplementary information (ESI) available: A movie of one unbiased simulation of the charge transfer including all the sites from both pathways. Tryptophans from left to right in the movie: C1, B1, A, B2, C2 and D2. The color scale varies from red (occupation equal to 0) to blue (occupation equal to 1) through green (occupation equal to 0.5). Details about the occupation of each tryptophan along the simulations corresponding to the movie are also given. See DOI: 10.1039/c9cp01609k

‡ Present address: Department of Integrative Structural Biology, Institut de Génétique et de Biologie Moléculaire et Cellulaire (IGBMC), Centre National de Recherche Scientifique (CNRS) UMR 7104, Institut National de Santé et de Recherche Médicale (INSERM) U964, Université de Strasbourg, 67404 Illkirch, France.

---