A comparative test of different density functionals for calculations of NH₃-SCR over Cu-Chabazite

Abstract

A general challenge in density functional theory calculations is to simultaneously account for different types of bonds. One such example is reactions in zeolites where both van der Waals and chemical bonds should be described accurately. Here, we use different exchange–correlation functionals to explore O₂ dissociation over pairs of Cu(NH₃)₂⁺ complexes in Cu-Chabazite. This is an important part of selective catalytic reduction of NO_x using NH₃ as a reducing agent. The investigated functionals are PBE, PBE+U, PBE+D, PBE+U+D, PBE-cx, BEEF and HSE06+D. We find that the potential energy landscape for O₂ activation and dissociation depends critically on the choice of functional. However, the van der Waals contributions are similarly described by the functionals accounting for this interaction. The discrepancies in the potential energy surface are instead related to different descriptions of the Cu–O chemical bond. By investigating the electronic, structural and energetic properties of reference systems including bulk copper oxides and (Cu₂O₂)²⁺ enzymatic crystals, we find that the PBE+U approach together with van der Waals corrections provides a reasonable simultaneous accuracy of the different bonds in the systems.

---

1 Introduction

Selective catalytic reduction of NO_x by NH₃ (NH₃-SCR) over ion-exchanged zeolites is the basis of the current technology for emission control of diesel engines.¹ The understanding of relevant reaction mechanisms and atomic structures for the reaction over Cu-Chabazite (Cu-CHA) has advanced significantly during recent years.^2–5 The development is thanks to a range of spectroscopic techniques in combination with density functional theory (DFT) calculations. The NH₃-SCR reaction over Cu-CHA proceeds by adsorption of different (N,O) and (N,H) ligands on the active Cu ions. The adsorbates react with N₂ and H₂O during the catalytic cycle while the Cu ions change the oxidation states between Cu(I) and Cu(II). The NH₃-SCR reaction over Cu-CHA is challenging for electronic structure calculations as different types of bonds should be described simultaneously with appropriate accuracy. In addition to the Cu–N and Cu–O bonds with different oxidation states of the metal ion, the applied methodology should account for the weak van der Waals (vdW) interactions with the zeolite framework.

The inclusion of vdW interactions in DFT calculations has been a long-standing issue.⁶ It is generally difficult to describe chemical bonding and vdW-interactions simultaneously. The common local, semi-local and hybrid functionals are designed to describe local chemical bonding rather than the long-range electron correlation giving rise to dispersion interactions.^7,8 One strategy has been to add vdW-interactions in a semi-empirical manner as suggested by Grimme and co-workers⁹ whereas another approach has been to develop density functionals including dispersion.^8,10,11 The performance of the different approaches for reactions in zeolites is generally difficult to assess due to the lack of clear comparisons between calculated and experimental data.

The dissociation of oxygen is a key step in the NH₃-SCR reaction over Cu zeolites.² It is known that the adsorption and dissociation of O₂ on Cu-CHA requires the presence of Cu(I).^2,5,12,13 Under typical reaction conditions and at temperatures below ∼523 K, the Cu(I)-ion is solvated by NH₃ ligands forming a Cu(NH₃)₂⁺ complex.^5,12,14–16 Recent publications^3–5,17 have addressed O₂ dissociation over Cu(NH₃)₂⁺ complexes with DFT calculations using different exchange–correlation functionals. The reported potential energy surfaces appear to depend strongly on the functional. One of the potential reasons for the discrepancies between the reports^3,12,17 could be the well-known difficulty of describing the oxygen bonding to binuclear Cu-amine complexes by first principles calculations,^18–20 as the system is highly correlated.^21–23

To understand the origin of functional-differences and simultaneously establish a preferred methodology for DFT calculations of Cu-CHA systems, we explore eight functionals with three common approaches to account for van der Waals interactions, namely (i) DFT with D2 and D3 corrections,^9,24–26 (ii) BEEF-vdW²⁷ and (iii) the vdW-density functional PBE+cx.²⁸ To describe the highly localized 3d-electrons in oxidized Cu, we also investigate the DFT+U methodology. By investigating the electronic, structural and energetic properties of bulk copper oxides and (Cu₂O₂)²⁺ enzymatic crystals as reference systems, we find that the DFT+U approach together with vdW-corrections provides a reasonable description of the different bonds in the systems.

2 Computational methods

Spin-polarised density functional theory (DFT) calculations are performed with the Vienna Ab Initio Simulation Package (VASP).^29–33 The Kohn–Sham orbitals are expanded with plane waves using an energy cut-off of 480 eV and the interaction between the valence electrons and the cores is described with the plane augmented wave (PAW) method.^34,35 The number of valence electrons used in the calculations is 11(Cu), 4(Si), 3(Al), 6(O), 5(N) and 1(H).

Structures are optimized with the conjugate gradient method and geometries are considered to be converged when the electronic energy difference between subsequent steps is smaller than 1 × 10⁻⁵ eV and the largest force is smaller than 3 × 10⁻² eV Å⁻¹. Reaction barriers are calculated by the use of the climbing image Nudged Elastic Band (NEB)^36,37 technique as implemented in the transition state tools of VASP. Five images are generated between the initial and final states and the spring constant between the images is set to 5 eV Å⁻². Harmonic vibrational frequencies are computed using the finite-difference approach. The identified transition states are confirmed by the vibrational analysis with one imaginary frequency towards the product coordinate. The k-point sampling is restricted to the Γ-point.³⁸

The potential energy surface of species not directly bonded to the zeolite framework is highly complex with many local minima. Here, Born–Oppenheimer ab initio molecular dynamics (AIMD) simulations in the NVT ensemble are performed to explore the low-energy configurations of the Cu species in CHA. The temperature in the simulation is controlled to be 300 K using a Nosé–Hoover thermostat.^39,40 The mass of hydrogen is replaced by the mass of tritium to facilitate the integration of the equations of motion which is done using a time step of 1 fs. The simulations are performed for 6 ps and low-energy configurations are relaxed from this trajectory.

The chabazite structure is modeled using a rhombohedral unit cell which includes 12 Si atoms in tetrahedral (T) positions. The optimized cell parameters are a = 9.42 Å. The lattice parameters are kept fixed during the geometry relaxations and molecular dynamics. We also performed some tests where the lattice parameters were relaxed. This was found to change the adsorption energies by less than 0.05 eV. The Si/Al ratio is 11 when the sequential adsorption energy of NH₃ bonded with the Cu(NH₃)₂⁺ complex is investigated, whereas the ratio is 5 when the direct O₂ dissociation on the Cu(NH₃)₂⁺-pairs is calculated. Both ratios are within the common experimental range with Si/Al ratios between 5 and 20.^12,41–43

The calculations are performed with different functionals. The generalized gradient approximation according to Perdew–Burke–Ernzerhof (PBE)⁴⁴ is used to describe local and semi-local exchange–correlation effects. To account for the highly localized 3d-electrons of oxidized copper, PBE is also used together with a Hubbard term (PBE+U). The U-parameter for Cu 3d is set to 6 eV as proposed by Isseroff et al.⁴⁵ The U-value in ref. 45 was determined from comparisons with the experimental lattice constant for Cu₂O and showed good results for the dielectric constant. We also investigate the effect of including non-local exchange by using the hybrid functional HSE06.⁴⁶

A common approach to account for vdW-interactions is to include a semi-empirical correction as proposed by Grimme and co-workers.^9,24–26 The D2 approach²⁴ uses dispersion coefficients fitted to experimental values, whereas the dispersion coefficients D3 are computed from first-principles.^25,26 Here, the D2 and D3 corrections are used together with either PBE, PBE+U or HSE06. Another approach to incorporate vdW-interactions is to use a nonlocal correlation term in the exchange–correlation functional (vdW-DF).^6,8,28,47,48 In this work, we use the consistent-exchange (cx) functional²⁸ together with PBE. The third approach we explore for taking vdW-interactions into account is the Bayesian error estimation functional (BEEF).²⁷ BEEF is a semi-empirical density functional developed by fitting experimental data for molecules, surfaces and bulk materials.¹⁰

3 Results

An important reaction step during low-temperature NH₃-SCR in Cu-CHA is the activation and dissociation of O₂ over copper species.^4,14,49 This has recently been investigated by several groups^4,5,17,49 and it has been established that the reaction is facile over pairs of Cu(NH₃)₂⁺ complexes. Although these studies agree that direct dissociation preferably takes place over Cu-pairs, the reported energy landscapes differ significantly. This can, in part, be due to different choices of functionals.^3–5,17 In ref. 4 and 49, PBE was used in combination with D2 and D3 whereas the BEEF functional was applied in ref. 5 and 17. Here, we systematically investigate these reactions with different functionals and the different implementations of the vdW interactions.

3.1 Direct dissociation of O₂ on the Cu(NH₃)₂⁺-pair

The potential energy landscape for direct O₂ dissociation on a Cu(NH₃)₂⁺-pair in CHA with different functionals is shown in Fig. 1. Because the potential energy surface is shallow⁵ with several local minima, AIMD is employed to facilitate the sampling of low-energy configurations. The AIMD simulations are performed using the BEEF functional.

Fig. 1 The potential energy landscape of direct O₂ dissociation on Cu(NH₃)₂⁺-pairs in CHA by different functionals. The structure for each step is shown on top. The triplet to singlet transition for O₂ occurs between steps C2 and C3. TS stands for the transition state from C2 to C3 and the barriers are listed below the curves with the corresponding colors. The stars in the potential energy landscape stand for the singlet state of O₂ adsorbed on the pair. All energies are zero-point energy corrected. Atom color codes: copper (pink), aluminum (purple), nitrogen (blue), silicon (yellow), oxygen (red) and hydrogen (white).

The oxygen dissociation path is divided into steps with five structures denoted C1 to C5. It is clear that calculations with the different functionals result in different reaction paths and also reaction products. In general, all functionals indicate that Cu-pairs are favorable for oxygen adsorption. However, whereas some of the PBE-based functionals predict the dissociated molecule (C5) to be the stable configuration, BEEF, PBE+U, PBE+U+D3 and HSE06+D3 favor activated O₂ (C4).

Following the path for O₂ activation and dissociation in detail, the initial configuration (C1) consists of O₂ in the gas-phase and two Cu(NH₃)₂⁺ complexes in one CHA unit cell. For adsorption of O₂ (C1 to C2), the eight functionals predict the O₂ adsorption energy to be in the range from 0.12 eV (HSE06+D3) to −0.46 eV (PBE+cx). PBE, PBE+U+D3 and BEEF yield similar values (about −0.24 eV). Addition of vdW-corrections to PBE stabilizes the adsorption by 0.1 eV (D2) and 0.2 eV (D3). The increased adsorption energy of O₂ is related to the vdW interaction with the framework as the interaction energy of O₂ to the bare CHA is calculated to be −0.01 (PBE), −0.07 (PBE+D2), −0.09 (PBE+D3) and −0.15 eV (PBE+cx).

Our result with PBE+D3 agrees with the report of Gao et al.³ when subtracting the O₂ gas-phase entropy from the value in ref. 3. Using PBE+D2, we get a weaker adsorption energy (−0.33 eV) than that reported in ref. 4 (−0.61 eV) despite the use of the same DFT implementation and Al-distribution. We find that this apparent disagreement is due to different reference energies of the bare Cu-pair structures. The reference structure used in ref. 4 is 0.21 eV less stable than the reference used for Fig. 1.⁵⁰ The O₂ adsorption step is endothermic using the HSE06+D3 functional, which disagrees with the experimental observation of O₂ adsorption.^4,49

The barrier from C2 to C3 includes the spin-transition from triplet to singlet¹⁷ and is calculated using the Minimum Energy Crossing Point (MECP) approach for the two potential energy curves.⁵¹ We note that the coupling between the two states is needed to estimate the rate for the reaction.⁵² The point of transition is marked with a star in the energy diagram. The triplet–singlet excitation energy is functional dependent. We have calculated the triplet–singlet excitation energy for gas phase O₂ (see the ESI†) and found that the gas phase excitation energy has a functional dependence following the trend in Fig. 1. The excitation is the dominant part of the C2 to C3 barrier for PBE+D3 and PBE+cx, whereas the excitation occurs before the transition state for the other functionals.

The O₂ activation is completed by changing the orientation of the molecule from C3 to a symmetric configuration (C4) where both Cu-ions are bonded to two oxygen atoms (μ-η²:η² peroxo). Here, this structure will be referred to as “side-on”. This step is exothermic in all functionals, although the energy difference for BEEF is small. O₂ dissociation is completed in the step from C4 to C5. The structure of dissociated O₂ is bis(μ-oxo) which we will denote “bis”. The energetics of the dissociated molecule (C5) is found to be strongly functional dependent. The process is predicted to be endothermic by HSE06+D3 (0.31 eV), PBE+U (0.19 eV), BEEF (0.08 eV) and PBE+U+D3 (0.07 eV), whereas it is exothermic in PBE (−0.43 eV), PBE+D2 (−0.51 eV), PBE+D3 (−0.52 eV) and PBE+cx (−0.85 eV).

The activation and dissociation of O₂ over the pairs of complexes are accompanied by changes of the oxidation state of the Cu-ions. Based on the calculated magnetic moment of the Cu ions, we find that the oxidation state of Cu is Cu(I) in C1 and C2. The magnetic moment of the ions is calculated to be close to zero and the Bader charge^53,54 is +0.5 e. The asymmetric configuration in C3 has different charge states and magnetic moments on the copper ions. The oxidation state of the Cu-ions which are linearly coordinated to NH₃ is 1+, whereas it is 2+ for the other ions. The oxidation state of Cu in C4 is formally 2+ which is signalled by Bader charges of +0.94 e and the magnetic moments. The system is singlet with two antiferromagnetically coupled magnetic moments (∼0.6 μ_B). The spin-density is predominantly located on the two copper ions. The Bader charges on the copper ions for the configuration with dissociated O₂ (C5) are about +1.03 e. The system is singlet and the magnetic moments are zero, implying a formal oxidation state of 3+. Even though this is an unusual oxidation state of Cu, it has been identified earlier for similar Cu₂O₂ motifs in enzymatic catalysts.^23,55,56

To investigate the effect of the incorporation of vdW interaction, the oxidation of Cu with oxygen in the gas phase is investigated using the BEEF and PBE-cx functionals. The spatial confinement in the zeolite cages is expected to give substantial vdW interactions with the Cu-complexes. We find that the vdW interactions for both functionals result in a stabilization of 0.5 ± 0.1 eV for C2, C4 and C5 (see the ESI†). This shows that the vdW contributions to the adsorption energy are similar for the two functionals and it can be concluded that the differences in the potential energy landscape are due to different descriptions of the Cu–N or Cu–O bonds.

3.2 Sequential adsorption of Cu⁺(NH₃)_x (x = 1–4)

To investigate how the different functionals perform for the Cu–N bond, we calculated the sequential binding energies of Cu⁺(NH₃)_x (x = 1–4) in the gas phase and compared with experimental results. Walter and Armentrout⁵⁷ have experimentally studied the sequential bond dissociation of Cu⁺(NH₃)_x (x = 1–4) in the gas phase. The bond dissociation energies were determined by analysis of the kinetic energy dependence of the collision-induced dissociation reactions of the Cu⁺(NH₃)_x (x = 1–4) complexes with xenon in a guided ion beam mass spectrometer.

The sequential binding energies of Cu⁺(NH₃)_x (x = 1–4) in the gas phase were calculated and the results are shown in Fig. 2(a). The experimental data show that the second NH₃ binds slightly stronger to the Cu⁺ ion than the first NH₃. This is a consequence of the Cu 4s–3d σ hybridization, which is an effective way to reduce the metal–ligand repulsion for doubly ligated systems.⁵⁷ Our calculations verify this phenomenon showing that the second NH₃ ligand binds stronger with the Cu⁺ ion than the first NH₃ ligand in all functionals except HSE06+D3 which have similar stability for the adsorption of the first and second ammonia. Except PBE+U and BEEF, the different functionals predict the binding energies of the first and second NH₃ ligand within 0.1 eV of the experimental value. PBE+U and BEEF underestimate the binding energies by ∼0.3 eV.

Fig. 2 (a) Calculated sequential binding energies of Cu⁺(NH₃)_x (x = 1–4) in the gas phase using different functionals compared with experimental values (dashed lines). The experimental sequential adsorption energies are 2.49, 2.60, 0.52 and 0.42 eV, respectively. (b) Calculated sequential adsorption energies of Cu⁺(NH₃)_x (x = 1–4) in 12T-site Cu-CHA using different functionals. The binding energies are calculated with respect to gas phase NH₃. All calculated energies include zero point energy corrections. Atom color codes: copper (pink), aluminum (purple), nitrogen (blue), silicon (yellow), oxygen (red) and hydrogen (white).

There is a large decrease in binding energies for the third and fourth NH₃ molecule, as compared to the first two molecules. This is a result of the increased ligand–ligand repulsion and the loss of the Cu 4s–3d σ hybridization because the 4s–3d σ hybrids are effective for only two ligands coordinated linearly to the metal site.⁵⁸ Also for these systems, BEEF underestimates the binding energies whereas the other functionals predicted the stability within ∼0.1 eV with respect to the experimental value. Even if the difference is small, PBE+cx and PBE+D3 give the overall best performance among the investigated functionals for the sequential binding energies of Cu⁺(NH₃)_x (x = 1–4) in the gas phase.

As a next step, we investigated the sequential binding energies of Cu⁺(NH₃)_x (x = 1–4) in CHA, Fig. 2(b). The sequential binding energies from the PBE functional are lower than the results from the other functionals including vdW-corrections, which all are within 0.1 eV. Compared with the 1st NH₃ binding energy in the gas phase, the binding energy in CHA is much lower as the bare Cu⁺ ion is stabilized by the CHA framework. This is also the reason why the second NH₃ binding energy in Cu-CHA is lower than the gas phase value. It should be noted that the second NH₃ ligand binds weaker to the Cu species in CHA than the first NH₃ ligand. The reason for this is that the adsorption of the second ligand involves the penalty of breaking the bond between Cu⁺ and an oxygen atom in the CHA framework to form the linear Cu⁺(NH₃)₂ complex. The sequential adsorption of the 3rd and 4th NH₃ ligand is much weaker than the 1st and 2nd molecule, similarly to the gas-phase values.

We do not have any direct experimental comparison in the case of sequential NH₃ adsorption in CHA. However, our results indicate that vdW-interactions have an effect as the adsorption energies for PBE are consistently lower by 0.1–0.2 eV. The differences between the functionals including vdW-effects are, however, small. Given the good agreement between the calculated and experimental NH₃ adsorption energies, we conclude that all investigated functionals describe the Cu–N bond with reasonable accuracy.

3.3 Electronic structures of bulk Cu_xO (x = 1,2)

To elucidate the differences in the description of the Cu–O bond with the functionals, we have analyzed the electronic density of states. To have experimental references, we consider bulk oxides (Cu₂O and CuO) in addition to the side-on (C4) and bis (C5) complexes in Fig. 1. These calculations are done with PBE, PBE+cx, BEEF and PBE+U. The projected density of states (PDOS) of Cu 3d and O 2p for Cu₂O and CuO are shown in Fig. 3a and b together with experimental XPS and UPS spectra.⁵⁹ As noted in ref. 59, XPS primarily probes the Cu-3d states while the UPS spectra are more sensitive to O-2p.

Fig. 3 Projected density of states (PDOS) of Cu 3d (in blue) and O 2p (in red) by different functionals for (a) bulk Cu₂O, (b) bulk CuO, (c) side-on Cu₂O₂ in CHA (C4 configuration in Fig. 1), and (d) bis Cu₂O₂ in CHA (C5 in Fig. 1). The PBE+U results are obtained with U = 6 eV. The UPS and XPS spectra of bulk Cu₂O and bulk CuO are taken from ref. 59.

The oxidation states of Cu₂O and CuO are +1 and +2, respectively. This is corroborated by a Bader charge analysis, which reveals that the copper ions have a charge of +0.53 e in Cu₂O and of +0.93 in CuO. CuO has an antiferromagnetic ordering^59,60 and the magnetic moment is calculated to be ±0.6 μ_B. The center of the d-band is for Cu₂O within the PBE, PBE+cx and BEEF functionals situated at about −2.1 eV below the Fermi energy. For PBE+U (with U = 6 eV), the d-band is shifted to lower energies by about 1 eV, which places the center close to the experimental XPS-value. The O 2p states are mainly situated in the energy range from −8 eV to −4 eV. The differences between the functionals are in this case small and the position with respect to the Fermi energy is similar to the UPS spectrum. Similar trends apply for CuO; PBE, PBE+cx and BEEF place the d-band center at higher energies as compared to PBE+U and the experiments. This comparison is in agreement with previous reports⁵⁹ and indicates that a Hubbard-U term is needed to describe the electronic structure and bonding in copper oxides.^45,61,62

The conclusions regarding the effect of including a Hubbard-U term for oxidization are similar for the side-on (C4) and bis (C5) configurations, see Fig. 3c and d. The d-state for PBE+U is for the side-on structure shifted to lower binding energies by about 1 eV with respect to the other functionals. This is similar to the value for bulk CuO. The stabilization of the d-state influences the degree of delocalization and hybridization to the oxygen states and, consequently, the bonding. It is known that the magnetic coupling constant (J) between the metal sites in di-nuclear copper complexes is sensitive to the degree of d-electron localization.^63,64 Using the broken symmetry approach⁶⁵ for C4, we calculate J to be −230 and −70 meV within PBE+D3 and PBE+U+D3, respectively. This trend is similar to the results obtained for other copper complexes⁶⁴ and demonstrates the d-electron localization when a Hubbard-U term is applied.

3.4 Energetics of crystals with Cu₂O₂ motifs

It is known that Cu–O bonds are difficult to describe accurately with DFT-calculations.^{18–20,45,59} The main reason is strong correlation effects in systems with oxidized copper having highly localized 3d-states. Moreover, it has also been difficult to obtain accurate energies with ab initio wave-function based methods^18–20 to benchmark DFT-results. To assess the performance of the functionals with respect to the Cu–O bond, we have chosen to compare with experimentally determined crystals with Cu₂O₂ motifs, which exist in enzymatic systems. A range of such crystals have been synthesized and structurally characterized by single crystal diffraction,^23,66,67 thus providing accurate experimental data for the structure on the relevant Cu₂O₂ complexes. As the structure of the Cu–O complexes in the crystals is known, the performance of the functionals can be assessed by computationally considering both the side-on and bis motifs. We consider the full crystals as the relative stability of the side-on and bis-configurations depends on ligand-interaction and counter-ions. By explicit calculations, we have found that smaller gas-phase models cannot capture the experimental structure.

Crystal structures have been reported for both side-on and bis-motifs with different N-donor ligands.^68–71 Here we investigate the energetics of one bis-crystal⁶⁸ and two side-on crystals.^69,70 The Cu atoms are for the bis-crystal coordinated with two N-ligands constrained by the molecular structure to favor a four-fold coordination around the ion and therefore the bis-configuration.^23,66 The side-on crystals have three N-ligands which have some structural flexibility. We do these calculations for PBE+U, PBE+U+D3, PBE+cx and BEEF. The experimentally reported crystal structures were completely relaxed with the Cu₂O₂ motif in the side-on and the bis-structures. The energetics and relevant bond lengths are reported in Table 1 whereas the crystal structures are reported in the ESI.†

Table 1 The relative energy (in eV) between the side-on and bis-configurations. The energy of the preferred structure is taken as reference (0). Selected bond lengths are reported for the experimentally stable structure. Atom color codes: copper (pink), nitrogen (blue), oxygen (red), carbon (grey) and hydrogen (white)

Exp. crystal	Cu2O2^2+ fragment structure	Functional & Exp.	Bond length (Å)			Relative energy (eV)
			Cu–Cu	Cu–O	O–O	Side-on	Bis
Bis		PBE+cx	2.72	1.81	2.38	—	0
		BEEF	2.77	1.83	2.39	1.98	0
		PBE+U	2.73	1.80	2.35	1.57	0
		PBE+U+D3	2.70	1.80	2.37	1.93	0
		Exp.^68	2.75	1.81	2.34	—	0
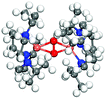
Side-on		PBE+cx	3.55	1.93	1.49	0.36	0
		BEEF	3.61	1.96	1.49	0.16	0
		PBE+U	3.58	1.94	1.46	0	0.21
		PBE+U+D3	3.57	1.93	1.46	0	0.31
		Exp.^69	3.52	1.89	1.37	0	—
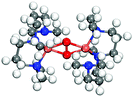
Side-on		PBE+cx	3.63	1.96	1.47	0.37	0
		BEEF	3.67	1.98	1.47	+0.00	0
		PBE+U	3.65	1.96	1.45	0	0.28
		PBE+U+D3	3.62	1.95	1.45	0	0.13
		Exp.^70	3.53	1.93	1.54	0	—

---

All functionals predict the correct energetic ordering for the experimental bis-crystal. The side-on structure is clearly unfavored and for PBE+cx, we do not find this structure as a minimum on the potential energy surface. As to the two experimental side-on crystals,^69,70 PBE+cx and BEEF functionals fail to predict the correct structural ground state. The correct experimental structure is instead given by the PBE+U and PBE+U+D3 functionals. The geometrical differences between the functionals and the experimental structures are in all cases within 0.1 Å.

The results show that PBE+U(+D) successfully predicts the correct structure for the known enzymatic systems with side-on and bis-configurations, where BEEF and PBE+cx fail. The PBE+cx preference for bis-configurations is consistent with the potential energy diagram in Fig. 1 where the C5 structure is clearly favored.

4 Conclusions

We have investigated O₂ dissociation over pairs of Cu⁺(NH₃)₂ complexes in CHA. This is, from a computational point of view, a challenging system as strong chemical bonds should be described simultaneously with weak van der Waals interactions. Additionally, the Cu–O bonds can be expected to be affected by strong correlation effects. We have explored different functionals which use different strategies to account for exchange–correlation effects including van der Waals interactions.

The potential energy diagram for O₂ dissociation is found to depend critically on the choice of functional. Some functionals predict dissociation of O₂ to be preferred (PBE, PBE+D, and PBE+cx), whereas others do not (HSE06+D, BEEF, PBE+U, and PBE+U+D3). By comparing the calculations with respect to experimental results for the binding of NH₃ to copper ions, the stability of Cu₂O₂ crystals and XPS/UPS spectra of copper oxides, we can assess the performance of the functionals. For the zeolite reactions, van der Waals interactions are found to be important and should be accounted for in some way; either by semi-empirical corrections or by vdW exchange–correlation functionals. The Cu–NH₃ bond strength is found to be reasonably described by all functionals. The main challenge for different functionals was instead the Cu–O bond. We found that only the functional with a Hubbard-U term could correctly describe the experimental preference for both bis- and side-on Cu₂O₂ crystals.

A fundamental challenge for structural characterization of NH₃-SCR over Cu-CHA is that the active site (Cu(NH₃)₂⁺) only exists during reaction conditions. Because of this, we have here assessed the performance of different density functionals by comparison to reference systems. Our work highlights the need for experimental benchmarks with atomistic information in zeolite reactions and we hope that our work could stimulate such studies.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Hanne Falsig and Mohamed Ali Al-Badri for stimulating discussions. The Competence Centre for Catalysis is hosted by Chalmers University of Technology and financially supported by the Swedish Energy Agency and the member companies AB Volvo, ECAPS AB, Johnson Matthey AB, Preem AB, Scania CV AB, Umicore AG & Co. KG and Volvo Car Corporation AB. Additional financial support from the Swedish Research Council (2016-05234) and the Chalmers Area of Advance Transport is acknowledged. The calculations have been performed at C3SE (Göteborg) and PDC (Stockholm) through a SNIC grant.

Notes and references

1. A. M. Beale, F. Gao, I. Lezcano-Gonzalez, C. H. Peden and J. Szanyi, Chem. Soc. Rev., 2015, 44, 7371–7405.
2. T. Janssens, H. Falsig, L. Lundegaard, P. Vennestrøm, S. Rasmussen, P. Moses, F. Giordanino, E. Borfecchia, K. Lomachenko, C. Lamberti and S. Bordiga, ACS Catal., 2015, 5, 2832–2845.
3. F. Gao, D. Mei, Y. Wang, J. Szanyi and C. Peden, J. Am. Chem. Soc., 2017, 139, 4935–4942.
4. C. Paolucci, I. Khurana, A. Parekh, S. Li, A. Shih, H. Li, J. Di Iorio, J. Albarracin-Caballero, A. Yezerets, J. Miller and W. Delgass, Science, 2017, 357, 898–903.
5. L. Chen, H. Falsig, T. Janssens and H. Grönbeck, J. Catal., 2018, 358, 179–186.
6. H. Rydberg, B. Lundqvist, D. Langreth and M. Dion, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 6997–7006.
7. D. Langreth and S. Vosko, Adv. Quantum Chem., 1990, 175, 175–199.
8. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
9. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
10. J. J. Mortensen, K. Kaasbjerg, S. L. Frederiksen, J. K. Nørskov, J. P. Sethna and K. W. Jacobsen, Phys. Rev. Lett., 2005, 95, 216401.
11. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
12. C. Paolucci, A. Parekh, I. Khurana, J. Di Iorio, H. Li, J. Albarracin Caballero, A. Shih, T. Anggara, W. Delgass, J. Miller and F. Ribeiro, J. Am. Chem. Soc., 2016, 138, 6028–6048.
13. H. Falsig, P. Vennestrøm, P. Moses and T. Janssens, Catal. Today, 2016, 59, 861–865.
14. A. Marberger, A. Petrov, P. Steiger, M. Elsener, O. Kröcher, M. Nachtegaal and D. Ferri, Nat. Catal., 2018, 1, 221–227.
15. F. Giordanino, E. Borfecchia, K. Lomachenko, A. Lazzarini, G. Agostini, E. Gallo, A. Soldatov, P. Beato, S. Bordiga and C. Lamberti, J. Phys. Chem. Lett., 2014, 5, 1552–1559.
16. L. Chen, T. Janssens, M. Skoglundh and H. Grönbeck, Top. Catal., 2019, 62, 93–99.
17. L. Chen, H. Falsig, J. Jansson, T. Janssens, M. Skoglundh and H. Grönbeck, Catal. Sci. Technol., 2018, 8, 2131–2136.
18. C. Cramer, M. Włoch, P. Piecuch, C. Puzzarini and L. Gagliardi, J. Phys. Chem. A, 2006, 110, 1991–2004.
19. C. Cramer, A. Kinal, M. Włoch, P. Piecuch and L. Gagliardi, J. Phys. Chem. A, 2006, 110, 11557–11568.
20. C. Cramer, B. Smith and W. Tolman, J. Am. Chem. Soc., 1996, 118, 11283–11287.
21. Y. He, J. Gräfenstein, E. Kraka and D. Cremer, Mol. Phys., 2000, 98, 1639–1658.
22. J. Gräfenstein and D. Cremer, Mol. Phys., 2005, 103, 279–308.
23. E. Solomon, D. Heppner, E. Johnston, J. Ginsbach, J. Cirera, M. Qayyum, M. Kieber-Emmons, C. Kjaergaard, R. Hadt and L. Tian, Chem. Rev., 2014, 114, 3659–3853.
24. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
25. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2010, 132, 154104.
26. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
27. J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149.
28. K. Berland and P. Hyldgaard, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035412.
29. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118.
30. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
31. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 64, 11169–11186.
32. G. Kresse and J. Furthmüller, J. Comput. Mater. Sci., 1996, 6, 15–50.
33. We used VASP version 5.4.1.
34. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
35. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
36. G. Mills, H. Jónsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337.
37. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
38. We performed tests with denser k-point samplings (2 × 2 × 2 and 3 × 3 × 3) and the adsorption energy differencies are within 0.02 eV of the calculations with only the gamma point.
39. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
40. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695.
41. A. K. S. Clemens, A. Shishkin, P.-A. Carlsson, M. Skoglundh, Z. M. F. J. Martínez-Casado, O. Balmes and H. Härelind, ACS Catal., 2015, 5, 6209–6218.
42. A. Shishkin, H. Kannisto, P. A. Carlsson, H. Härelind and M. Skoglundh, Catal. Sci. Technol., 2014, 4, 3917–3926.
43. E. A. Eilertsen, M. H. Nilsen, R. Wendelbo, U. Olsbye and K. P. Lillerud, Stud. Surf. Sci. Catal., 2008, 174, 265–268.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. L. Isseroff and E. Carter, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235142.
46. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906.
47. H. Rydberg, M. Dion, N. Jacobson, E. Schröder, P. Hyldgaard, S. I. Simak, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2003, 91, 126402.
48. T. Thonhauser, V. Cooper, S. Li, A. Puzder, P. Hyldgaard and D. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125112.
49. F. Gao, E. D. Walter, E. M. Karp, J. Luo, R. G. Tonkyn, J. H. Kwak, J. Szanyi and C. H. Peden, J. Catal., 2013, 300, 20–29.
50. The low stability of the reference configuration has consequencies for the analysis of the potential energy surface in ref. 4. In particular, the O₂ adsorption energy does not balance energy cost for pair formation.
51. J. N. Harvey, Phys. Chem. Chem. Phys., 2007, 9, 331–343.
52. D. Schröder, S. Shaik and H. Schwarz, Acc. Chem. Res., 2000, 33, 139–145.
53. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, London, 1994.
54. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
55. I. Garcia-Bosch, R. Cowley, D. Díaz, R. Peterson, E. Solomon and K. Karlin, J. Am. Chem. Soc., 2017, 139, 3186–3195.
56. C. Elwell, N. Gagnon, B. Neisen, D. Dhar, A. Spaeth, G. Yee and W. Tolman, Chem. Rev., 2017, 117, 2059–2107.
57. D. Walter and P. B. Armentrout, J. Am. Chem. Soc., 1998, 120, 3176–3187.
58. C. W. Bauschlicher, S. R. Langhoff and H. Partridge, J. Chem. Phys., 1991, 94, 2068–2072.
59. Y. Wang, S. Lany, J. Ghanbaja, Y. Fagot-Revurat, Y. Chen, F. Soldera, D. Horwat, F. Mücklich and J. Pierson, Phys. Rev. B, 2016, 94, 245418.
60. M. Heinemann, B. Eifert and C. Heiliger, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 115111.
61. L. Y. Isseroff and E. A. Carter, Chem. Mater., 2013, 25, 253–265.
62. K. Bhola, J. Varghese, L. Dapeng, Y. Liu and S. Mushrif, J. Phys. Chem. C, 2017, 121, 21343–21353.
63. R. Valero, R. Costa, I. D. P. R. Moreira, D. G. Truhlar and F. Illas, J. Chem. Phys., 2008, 128, 114103.
64. P. Rivero, C. Loschen, I. D. P. R. Moreira and F. Illas, J. Comput. Chem., 2009, 30, 2316–2326.
65. L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743.
66. L. Mirica, X. Ottenwaelder and T. Stack, Chem. Rev., 2004, 104, 1013–1046.
67. M. Metz and E. Solomon, J. Am. Chem. Soc., 2001, 123, 4938–4950.
68. V. Mahadevan, Z. Hou, A. Cole, D. Root, T. Lal, E. Solomon and T. Stack, J. Am. Chem. Soc., 1997, 119, 11996–11997.
69. B. Lam, J. Halfen, V. Young, J. Hagadorn, P. Holland, A. Lledós, L. Cucurull-Sánchez, J. Novoa, S. Alvarez and W. Tolman, Inorg. Chem., 2000, 39, 4059–4072.
70. G. Park, M. Qayyum, J. Woertink, K. Hodgson, B. Hedman, A. Narducci Sarjeant, E. Solomon and K. Karlin, J. Am. Chem. Soc., 2012, 134, 8513–8524.
71. A. Cole, V. Mahadevan, L. Mirica, X. Ottenwaelder and T. Stack, Inorg. Chem., 2005, 44, 7345–7364.

---

Footnote

† Electronic supplementary information (ESI) available: Triplet–singlet excitation energies for O₂, structures, vibrational analysis, O₂ adsorption over gas-phase complexes and crystal structures. See DOI: 10.1039/c9cp01576k

---