Spectroscopic and theoretical investigation of the [Fe₂(bdt)(CO)₆] hydrogenase mimic and some catalyst intermediates

Abstract

In [Fe–Fe] hydrogenase mimic systems the ene-1,2-dithiolene ligands play an important role in the stabilisation of the redox-active metal center. This is demonstrated by the benzenedithiolene (bdt) analogue, featuring six terminal carbonyl ligands connected to a di-iron metal center, i.e. [Fe₂(bdt)(CO)₆]. Here we present a combined experimental and theoretical study that elucidates key intermediates [Fe₂(bdt)(CO)₆]¹⁻ and [Fe₂(bdt)(μ-CO)(CO)₅]²⁻ in the electrocatalytic production of dihydrogen. A DFT study shows that [Fe₂(bdt)(CO)₆]¹⁻ is the kinetic product after the first one electron reduction, while the previously proposed bridging intermediate species [Fe₂(bdt)(μ-CO)(CO)₅]¹⁻ is kinetically inaccessible. The doubly reduced species [Fe₂(bdt)(μ-CO)(CO)₅]²⁻ was for the first time structurally characterized using EXAFS. XANES analysis confirms the existence of reduced iron zero species and confirms the distorted geometry that was suggested by the DFT calculations. Combining IR, UV-vis and XAS spectroscopic results with TD-DFT and FEFF calculations enabled us to assign the key-intermediate [Fe₂(bdt)(CO)₆]²⁻. This study emphasizes the strengths of combining computational chemistry with advanced spectroscopy techniques.

---

1 Introduction

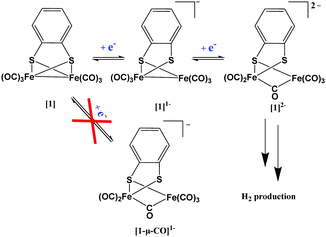
The ever-increasing demand to replace our current fossil fuel-driven economy by sustainable alternatives has intensified the research field on alternative energy sources. A good candidate as clean fuel could be molecular hydrogen, but only when generated in a sustainable manner. Water splitting using green energy would be sustainable, but for proton reduction catalysis the best catalysts are still based on non-abundant metals like platinum.¹ In order to make the switch to a sustainable economy, we should strive to develop cheap, robust and reliable catalysts. In nature, dihydrogen is efficiently produced by hydrogenase enzymes and research into hydrogenase mimics is an active field. Many simple bio-mimetic analogues have been synthesised^2,3 and characterised⁴ over the past decades. To characterize these systems, many techniques like, cyclic voltammetry (CV),⁵ electron paramagnetic resonance spectroscopy (EPR),⁶ infrared spectroscopy (IR)^7,8 and X-ray absorption spectroscopy (XAS)⁹ have been used. In order to design more productive hydrogen evolution catalysts, detailed understanding on their performance, including their reaction mechanism is required. For example, accurate information on the charge transfer (resulting in changes in oxidation state) within these systems is essential to understand the electronic properties and reactivity. Felton et al.¹⁰ reviewed the electrochemical performance of over 240 complexes containing the Fe₂S₂ core-motif and showed that only [Fe₂(bdt)(CO)₆] ([1]) is capable of high catalytic efficiency with three different acids. Together with a relatively mild over-potential (∼500 mV), a reversible and stable reduction process makes [1] an interesting hydrogenase mimic system.^11,12 This complex is well established in the field of bio-inorganic chemistry^13,14 and modifications have also been performed by the group of Rauchfuss¹⁵ and Kaur.¹⁶

The proton reduction process utilizing [Fe₂(bdt)(CO)₆] has previously been theoretically modelled and monitored by spectro-electrochemical methods and from these results a variety of (catalytic) mechanisms have been proposed.^17,18 Felton et al.¹⁰ and Capon et al.¹⁹ for example postulated, based on electrochemical and computational methods, that the first one-electron reduction step would lead to a structural rearrangement in which one CO bridges between both iron atoms and one Fe–S bond cleaves ([1-μ-CO]¹⁻). Note that none of these studies provide experimental structural characterisation of any of the intermediates. Femtosecond transient IR spectroscopy, however, suggested a terminal binding mode of all the CO fragments in the mono-reduced state ([1]¹⁻) which was further supported by DFT calculations.^20,21 Wright et al.¹¹ demonstrated that by using an excess of sodium, {[Na₂(THF)(OEt₂)][Fe₂(bdt)(CO)₆]²⁻}₂ could be isolated, which was characterised by X-ray crystallography. In solution, however, multiple bridging CO signals were observed by IR spectroscopy hinting at the presence of multiple species.¹¹

A proposed mechanism for the formation of the singly and doubly reduced Fe species (before formation of H₂) is shown in Scheme 1. Despite the fact that there is experimental evidence of solely terminal CO species after the first reduction, theory often also suggests the formation of [1-μ-CO]¹⁻, as both structures are close in energy.^10,19 In order to clarify why only [1]¹⁻ is experimentally observed, we have conducted a DFT study focussing on the possible formation and interconversion between the two structures. Although the overall mechanism is dependent on the acid strength, the singly reduced catalyst [1]¹⁻ was shown to be a key intermediate in the photocatalytic H₂ formation, whereas in electrochemical reduction the di-anion [Fe₂(bdt)(μ-CO)(CO)₅]²⁻ ([1]²⁻) is inevitably formed. Thus far, this key doubly reduced [1]²⁻ intermediate has not been structurally characterized in solution, and could help in further understanding and development of proton reduction catalysts.

Scheme 1 Proposed electrochemical reduction mechanism of [1] prior to the formation of H₂.

To structurally characterize this reduced complex in solution, X-ray absorption spectroscopy (XAS) has been combined with a computational study. XAS combines electronic and structural characterisation, in solid state and solution, and is therefore a powerful method for the identification of intermediates in mechanistic studies.^22,23 Herein we report the characterisation of reduced intermediates present in an active hydrogenase mimic system [Fe₂(bdt)(CO)₆] [1]. Unfortunately, the singly-reduced [1]¹⁻ or [1-μ-CO]¹⁻ could not be isolated for structural analysis and the first electron reduction was thus solely investigated computationally. The overall two-electron reduced species was spectroscopically characterised using Fe K-edge XAS and spectro-electrochemistry (UV-vis and IR). Additional TD-DFT and FEFF9 calculations have provided detailed insights in the structural and electronic properties of the reduced intermediate [Fe₂(bdt)(CO)₆]²⁻ [2]²⁻.

2 Experimental

2.1 General experimental details

Starting materials were obtained commercially or prepared and purified according to the references given below. All solvents were dried by using standard procedures.²⁴ All air-sensitive materials were manipulated using standard Schlenk techniques or by the use of a glovebox. ¹H and ¹³C NMR spectra were recorded on a Bruker AVANCE 300 MHz spectrometer. IR spectra were recorded on a Nicolet Nexus FT-IR spectrometer. Elemental analyses were performed by Mikroanalytischen Laboratorium Kolbe in Germany.

2.2 Sample preparation

[Fe₂(bdt)(CO)₆] ([1]). A modified literature procedure²⁵ was used. 4.3 g (8.5 mmol) Fe₃(CO)₁₂ was treated with 1.20 g (8.5 mmol) benzene-1,2-dithiol in THF and refluxed for exactly two hours. The resulting red solution was directly filtered over cotton. Unreacted Fe(CO)₅ was evaporated by rotary evaporation as a yellow solution. Silica column chromatography was conducted using petroleum ether/pentane (40/60) as eluent. Only the red band was collected and further dried in vacuo, resulting in red crystalline powder in a 76% yield. ¹H NMR (300 MHz, CDCl₃) δ 7.16 (dd, J = 5.5, 3.2 Hz, 2H), 6.66 (dd, J = 5.5, 3.2 Hz, 2H). ¹³C{¹H} NMR (300 MHz, CDCl₃): δ = 207.48 (s, CO), 147.45 (s, SC̲), 127.96 (s, SCC̲H), 126.80 (s, SCCHC̲H) IR (CO) (MeCN) (cm⁻¹): 2078 (m), 2043 (s), 2002 (s). Elemental analysis: calculated (expected): C, 34.35 (34.32); H, 0.93 (0.96); Fe, 26.42 (26.59); S, 15.02 (15.27).

[Fe₂(bdt)(CO)₆]¹⁻ ([1]¹⁻). [Fe₂(bdt)(CO)₆] ([1]) + 1.05 eq. of CoCp₂* (5 mM), added to Fe₂(bdt)(CO)₆ (5.0 mM) in acetonitrile under nitrogen or argon atmosphere. IR (CO) (MeCN) (cm⁻¹): 2078 (m), 2043 (s), 2002 (s), 1963 (s), 1914 (s), 1881 (w), 1863 (m), 1842 (w), 1688 (b).

[Fe₂(bdt)(μ-CO)(CO)₅]²⁻ ([1]²⁻). 2.1 eq. of CoCp₂* (5 mM) was added to Fe₂(bdt)(CO)₆ (5.0 mM) in acetonitrile under nitrogen or argon atmosphere. IR (CO) (MeCN) (cm⁻¹): 1963 (s), 1914 (s), 1881 (w), 1863 (m), 1842 (w), 1688 (b).

2.3 X-ray absorption spectroscopy

Fe K-edge (7112 eV) X-ray absorption measurements were performed at beamline B18 of the Diamond Light source (Didcot, UK) using a Si (111) crystal monochromator. Solutions were measured in fluorescence mode, using a Germanium 9 element detector, or in transmission using ionisation chambers. The measurements were performed on 5.0 mM complexes in acetonitrile. Samples were prepared in Kapton tubes and subsequently frozen in liquid nitrogen under argon atmosphere (to prevent further reaction as well as beam damage). During the measurements the samples were kept frozen using a cryojet (100 K) setup. Data processing analysis was conducted with Athena and Artemis (Demeter software package).²⁶

2.4 UV-vis and IR spectro-electrochemistry

Electrochemical experiments were performed in an optically transparent thin-layer (200 μm) electrochemical (OTTLE)²⁷ cell equipped with CaF₂ optical windows and a platinum minigrid working electrode. The difference absorbance IR spectra were recorded on a Nicolet Nexus FT-IR spectrometer and the UV-vis spectra were recorded on a Shimadzu UV-2700 spectrophotometer. The cyclic voltammetry scanning process (ν = 0.5 mV s⁻¹) was controlled by a PGSTAT (Eco-Chemie) potentiostat. The measurements were performed on 5.0 mM complexes in acetonitrile containing 0.1 M nBu₄NPF₆ as a supporting electrolyte.

2.5 Computational details

All geometry optimisations and IR simulations were conducted using ADF^28,29 with the TZ2P basis set and BP86³⁰ or OPBE³¹ functional. COSMO solvent models were carried out employing acetonitrile.³² Transition states were located using a linear transit method,³³ and were validated by a single imaginary frequency. TD-DFT XANES calculations were performed with a 50 Davidson excitation restriction window where only singlet quadrupole- and dipole-allowed transitions are selected from the Fe 1s orbitals.^34,35 In all TD-DFT calculations, the B3LYP – d3 functional and a QZ4P Slater-type basis set was applied.³⁶ The intensities include second-order contributions due to the magnetic-dipole and electric-quadrupole transition moments.³⁷ The spectra were shifted by 151.0 eV for comparison to experiment. These shifts are chosen such that the energy of the first peak in the calculated spectrum agrees with the first peak in the experimental spectrum. While these shifts are rather large, they do not affect the relative position of the peaks.³⁸

Redox potentials were determined using the Born–Haber cycle approach³⁹ (see Scheme S1, ESI†). By applying formula (1), the change in free energy of the redox process in solution can be obtained.⁴⁰ Now by the use of formula (2), the standard absolute redox potential (E⁰) can be calculated, where F is the Faraday constant (23.061 kcal per volt gram equivalent) and Z equals 1.0 (one-electron redox processes).⁴⁰

−ΔG⁰(soln, redox) = ΔG⁰(gas, redox) + ΔG⁰(solv, [Fe₂(bdt)(CO)₆]⁻¹) − ΔG⁰(solv, [Fe₂(bdt)(CO)₆]) (2)

Fe K-edge XANES spectra were simulated with FEFF9.^41,42 These XANES calculations were carried out using both the crystallographic data as well as DFT geometry optimised coordinates. In all cases a Hedin–Lundqvist potential was utilized.⁴³ The many-body reduction factor (S₀²) was kept at 1.0. A default core-hole broadening (1/3 of the energy step) was applied for spectral plots, with no additional experimental broadening.

3 Results and discussion

3.1 Fe K-edge XANES

Fig. 1 displays the experimental and DFT calculated Fe K-edge XANES spectra of [1]. At lower energies (7113 eV), multiple pre-edge absorption signals arise that are mainly attributed to electric dipole-forbidden transitions of the 1s core electrons into valence metal 3d orbitals.⁴⁴ The relatively high pre-edge intensities in the spectra are typical for five-coordinated iron species, compared to octahedral complexes.⁴⁵ The pre-edge features at 7120 eV mainly arise due to quadrupole allowed 3d–4p_z hybridized orbital final states, as shown by the calculated DFT contributions (see ESI,† Section 5). Utilizing the calculated TD-DFT excitations, we can determine whether a transition from the iron 1s to the unoccupied molecular orbitals will have dipolar and/or quadrupole contributions, which is further illustrated in ESI,† Section 5. The reduced complex [1]²⁻ also plotted in Fig. 1, displays a significant edge shift of −1.5 eV, corresponding to a reduction of Fe¹–Fe¹ to Fe⁰–Fe⁰.⁴⁶ The pre-edge features again hint at a 5-coordinated geometry, with similar transitions as observed in [1]. The singly-reduced [1]¹⁻ or [1-μ-CO]¹⁻ system was attempted to be prepared and measured. Unfortunately, the data point to a combination of starting compound [1] (60%) and doubly-reduced [1]²⁻ (40%) species (see Fig. S1 of the ESI† for linear combination fit of the singly-reduced XANES data), rather than a unique singly-reduced structure. This confirms that the singly-reduced species is very short-lived, explaining the results in literature as discussed above,^{10,11,13,15,16} and confirmed by our computational study (vide infra). The white line possesses no distinct pre-edge features at higher energies. This is also reflected in the calculated XANES spectrum of [1]²⁻ where the transitions are mainly from iron 1s to the lowest lying unoccupied orbitals now more localized on the Fe–Fe core (see ESI,† Section 5). These electric-dipole-allowed transitions are in line with the selection rules. At higher energies (7140 eV) multiple scattering and charge transfer effects play a dominant factor,⁴⁷ which is not accounted for in our DFT calculations. In order to simulate the full XANES (including edge), FEFF9 was used. The pre-edge features both resemble their experimental value in terms of energy position and shape. The main edge position is shifted to lower energies, reproducing the reduction of the two central iron atoms. The drop in intensity after the edge at 7140 eV is well-reproduced by the FEFF calculation and is due to the reduced multiple scattering features of the neighbouring carbonyl groups and overall changes in (less constraint) geometry.

Fig. 1 Experimental (solid) and computational (dashed) Fe K-edge XANES spectrum of [1] (red) and reduced [1]²⁻ (blue) using TD-DFT (top) and FEFF9 (bottom).

3.2 Fe K-edge EXAFS

Structural information of [1] and [1]²⁻ was obtained from a frozen acetonitrile solution in a Kapton tube. The k²-weighted Fe K-edge EXAFS spectra are shown in Fig. 2 [top]. Iron K-edge EXAFS analysis of the non-reduced species show three main contributions: Fe–C (A), Fe–S (B) and the multiple scattering Fe–CO (C) interactions. The carbonyl multiple scattering is highly contributing due to the linearity of the Fe–CO bond in these Fe₂S₂ butterfly structures.⁴⁸ The coordination numbers (N) and inter-atomic distances (R) in the fitting model, closely resembles its single crystal structure as shown in Table 1. The main features of EXAFS are reproduced with good accuracy, as observed in both EXAFS and Fourier Transforms. EXAFS analysis of [1]²⁻ also shows three main contributions: Fe–C (D), Fe–S (E) and the less pronounced multiple scattering Fe–CO (F), depicted in Fig. 3 [bottom]. The overall reduction in amplitude resembles a loss of symmetry, earlier observed in the XANES region. The Fe–S contribution is fitted with a bond distance of 2.32(2) Å with a coordination number of 1.5. This supports the cleavage of the Fe₂S₂ butterfly structure and the loss of symmetry, resulting in two inequivalent iron atoms. A further Fe–S scattering path with a distance of 3.76(4) Å can be added, but with a low reliability of the fit, as this distance exceeds the limit of the data. The Fe–C shell is split in to a coordination number of one carbon at a distance of 2.03(3) Å and 2.5 carbons at 1.78(1) Å. Further analysis shows a decreasing CO contribution which can be explained by the bridging mode observed by earlier IR and DFT results. The use of this model where CO is bridging and bond breakage between Fe–S had to be included in order to obtain a good and reliable fit. The reduction of both iron atoms logically causes an elongation of the bond, as was proven by our DFT calculations. Hence, the calculated bond distance of 2.58 Å in [1]²⁻ compared to the 2.48 Å bond distance in [1] was applied in the EXAFS fitting model (2.55(2) Å), resulting in an overall better fit, while further elongation of the bond (e.g. >2.61 Å) gave a worse fit. The results confirm the structure of the hydrogenase mimic [1] and the formation of its reduced equivalent [1]²⁻ as proposed in Scheme 2.

Fig. 2 (Top) k²-Weighted Fe K-edge EXAFS data of [1] (left) and [1]²⁻ (right). (Bottom) k²-weighted Fourier Transforms of the EXAFS data for 2 < k < 10.5 Å of [1] (left) and [1]²⁻ (right). In all plots the data are represented by the solid lines (red), whereas the corresponding fits are the dotted lines (blue).

Table 1 Fe K-edge EXAFS fitting parameters for [Fe₂(bdt)(CO)₆] (crystal structure) and [Fe₂(bdt)(CO)₆]²⁻ (DFT geometry optimized), where N = coordination number, σ² = Debye Waller factor [Å⁻²], R = fitted bond length [Å]

Sample	Shell	N	σ ^2	R XRD/DFT (Å)	R fit (Å)
a k-range = 2–12.8 Å, R-range = 1–3.2 Å; k-weighted fit = 1, 2, 3 E0 = −0.8(8) eV, S0^2 = 0.90, R-factor fit: 0.0174. b k range = 2–12.8 Å, R range = 1–3.2 Å; k-weighted fit = 1, 2, 3 E0 = −0.12 eV, S0^2 = 0.90, R-factor fit: 0.0069.
[Fe2(bdt)(CO)6]^a	Fe–C	3.0	0.004(1)	1.79	1.80(1)
	Fe–S	2.0	0.006(3)	2.27	2.29(1)
	Fe–Fe	1.0	0.006(3)	2.48	2.48(2)
	Fe–O	3.0	0.0002(2)	2.92	2.97(1)
	Fe–CO	6.0	0.002(2)	2.92	2.97(1)
	Fe–COC	3.0	0.004(2)	2.92	2.97(1)
[Fe2(bdt)(CO)6]^2−^b	Fe–C	2.5	0.0051(9)	1.76	1.776(6)
	Fe–C	1.0	0.006(4)	1.98	2.00(2)
	Fe–S	1.5	0.0046(9)	2.33	2.310(6)
	Fe–Fe	1.0	0.009(2)	2.58	2.57(1)
	Fe–O	3.0	0.0002(8)	2.93	2.970(2)
	Fe–CO	5.0	0.0026(9)	2.93	2.972(5)
	Fe–COC	2.5	0.0052(9)	2.93	2.974(5)

---

Fig. 3 (top) Normalized experimental (solid lines) and theoretical (dashed lines) infrared spectrum of [1] (red) and [1]²⁻ (blue). (bottom) Spectro-electrochemistry of [Fe₂(bdt)(CO)₆] in the infrared region.

Scheme 2 Proposed reduction mechanism of [1].

The EXAFS analysis of [1] with one equivalent of CoCp₂* again indicates, like in the XANES, that a combination of [1] and [1]²⁻ is obtained (see Fig. S2 and Table S1 of ESI† for EXAFS fit results).

3.3 The reduction mechanism of [Fe₂(bdt)(CO)₆]

Computational study. In order to reliably assign possible intermediate structures and obtain more insights in the singly-reduced species, additional calculations were performed. In the current study calculations have been performed with the often applied BP86 functional (in combination with scaling factors)⁴³ and these have been compared to the results obtained with the OPBE functional, which is often applied for the accurate description of open-shell inorganic systems.³¹ Although the structure with the lowest energy is often depicted as the most relevant structure, it is also important to evaluate if the structure is kinetically accessible by conducting a transition state analysis of the possible pathways. Additionally, comparison of the calculated infrared spectra and redox potentials to the experimental data should support the theory (see Tables S2 and S3, ESI†).

Complex [1] possesses a clear fingerprint of mainly four CO vibrational modes in the IR region, resulting in two sharp signals at 2078 cm⁻¹ and 2044 cm⁻¹, and two unresolved signals around 2001 cm⁻¹ (see Fig. 3). Comparing the different functionals and models, it is evident that the neutral molecule is best described by the use of the OPBE functional in combination with a solvent model (based on the comparison of calculated and experimental IR signals). The calculated redox potential show only minor variations between the functionals, with OPBE giving a value of −1.41 V, which is quite close to the literature value of −1.33 V.¹⁰ Upon the first reduction, all calculated structures show Fe–S (∼1.2 Å) and Fe–Fe (∼0.1 Å) bond elongation compared to the neutral state. The CO ligands can either all stay in a terminal binding mode or one can move to a bridging mode. The energy difference between bridged [1-μ-CO]¹⁻ and terminally bonded CO [1]¹⁻ is relatively low (0.65 kcal mol⁻¹), in favour of the non-bridging structure. The addition of one electron was found to be energetically downhill, therefore proceeding barrierless. Due to the fact that the two structures are so close in total bonding energy, carbonyl displacement forming [1-μ-CO]¹⁻ could be feasible. The energy barrier from [1]¹⁻ towards [1-μCO]¹⁻ is calculated to be +11.9 kcal mol⁻¹ (see Scheme 3). This corresponds to an approximate half time (τ_1/2) in the millisecond regime calculated via the Eyring equation at ambient conditions.⁴⁶ The second electron transfer takes place on a much faster timescale,²⁰ explaining why the formation of [1-μCO]¹⁻ is not experimentally observed.

Scheme 3 Energy diagram of [1] towards [1]¹⁻, followed by the corresponding transition state towards [1-μCO]¹⁻ and finally [1]²⁻. All the relative energies are in kcal mol⁻¹.

The Gibbs free energy of the calculated reduction potential of [1]¹⁻ at −1.13 V (−89 kcal mol⁻¹) compared to [1] at −1.41 eV (−84 kcal mol⁻¹) nicely models a potential inversion and also underpins an expected fast second electron transfer as ΔG₀ increases by a very small amount.⁴⁷ The calculated infrared spectrum of [1]¹⁻, indeed only shows terminal CO fragments best described by again an OPBE functional. This analysis is in line with our spectro-electrochemical UV-vis data showing an isobestic points at 330 and 350 nm indicating the transformation of [1] to [1]²⁻ without the observation of an intermediate state (Fig. 4). The calculated reduction potential of [1-μ-CO]¹⁻ (−1.13 V OPBE and −0.97 V BP86) and [1]¹⁻ (−1.13 V OPBE and −1.07 V BP86) are all in the same range, slightly underestimating the earlier simulated second reduction potential. This implies that Fe–S bond breakage only is sufficient to lower the overall basicity of the complex. Regardless of the functional employed, the second reduction step always converges to a CO bridged incorporated structure [1]²⁻. This results in an IR spectral profile where all three carbonyl vibrations undergo a blue shift towards lower wavenumbers (Fig. 3). This can be explained by stronger π back donation into the carbonyl anti-bonding orbital from the electron enriched iron centres, thereby weakening the carbonyl bond.⁴⁹ This reduction was performed experimentally by the addition of 2.05 eq. CoCp₂* to 5.0 mM of [1] in acetonitrile. Due to the presence of the cationic [CoCp₂*]⁺, ion paired species are likely to be present, assigning minor signals around 1750 cm⁻¹ (see Fig. 1). Note, a bridging CO moiety between two iron atoms will give a signal at even lower wavenumbers, (1687 cm⁻¹), an assignment that is supported by our spectro-electrochemistry data (see Fig. 3). Looking at the calculated data, the OPBE functional resulted in an infrared spectrum matching the different experimental CO vibrational modes. The bridging CO signal at 1682 cm⁻¹, often calculated at much higher wavenumbers is herein conclusive. Moreover, in order to match our infrared spectra with experimental data, no additional shift or scaling factor was applied, contrary to earlier literature research.⁵⁰ Although the calculated reduction potentials show some variation, in all cases they are able to replicate the experimental potential inversion.

Fig. 4 Spectro-electrochemistry of [Fe₂(bdt)(CO)₆] in the UV-vis region.

Based on all experimental and theoretical results, we have proposed the following reduction mechanism, where the mono-reduced species indeed have all CO's in terminal position and only move to a bridging position upon the second electron reduction (see Scheme 2). The Fe–S bond will elongate upon the first reduction and slightly reorganize after the second reduction.

4 Conclusions

We have investigated the reduction of hydrogenase mimic [Fe₂(bdt)(CO)₆] with a combined XAS-DFT study, revealing the structural rearrangement of the catalyst after the second electron reduction. DFT predicts that upon the first reduction only Fe–S and Fe–Fe bond elongation is likely to take place, supporting the latest findings. The conversion of the reduced [1]¹⁻ to [1-μ-CO]¹⁻, the isomeric structure with a bridging carbonyl, is associated with an energy barrier of +12 kcal mol⁻¹, which is considered (kinetically) prohibitive. Consecutive reduction of [1]¹⁻, leads to a structure that has a bridging iron carbonyl moiety (Fe–μ-CO–Fe), as supported by both DFT calculations and infrared spectroscopy. The suggested open dianionic structure [Fe₂(bdt)(μ-CO)(CO)₅]²⁻ was for the first time structurally characterized by the use of XAS. In here, the XANES region clearly shows the reduction by a significant edge shift of −1.5 eV. TD-DFT calculations are sufficiently accurate to allow a qualitative assignment and analysis of the pre-edge region in the experimental XAS spectra. The reduced multiple scattering effects above the edge support the structural reorganization, which was further characterized in great detail by EXAFS analysis. This shows that the coordination number of Fe–S drops from 2 to 1.5. Both the observed increase in the Fe–Fe bond length from 2.48 Å to 2.55(2) Å as the fitted bridging carbonyl ligand are in good agreement with theory. Overall, our DFT calculations are in excellent agreement with the experimentally derived structural parameters and provide complementary insights into the electronic structures of the species presented. To the best of our knowledge, direct evidence of Fe–S bond breakage has not been experimentally observed before an as this is a key intermediate in the reaction mechanism it facilitates in understanding the operational mode of hydrogenase mimics. The presented methodology should be directly applicable to other postulated intermediates in the mechanistic characterization of alternative catalyst systems. Future work to focus on the elucidation of other intermediates postulated in the reaction mechanism, e.g. the subsequent protonation of the mono or double reduced intermediate.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the Netherlands Organisation for Scientific Research (NWO) for funding (VIDI grant 723.014.010 to MT (MT, JPHO, DJM and BV), VENI grant 722.016.012 to TJK (TJK)). The authors thank the staff of the beamline B18, Diamond Light Source (proposal number SP13069) in Didcot for support and access to their facilities. The authors thank Michelle Hammerton and Lukas Wolzak for support during synchrotron measurements. The authors thank Dr Andreas Ehlers for support with the performed DFT calculations.

Notes and references

1. N. Armaroli and V. Balzani, ChemSusChem, 2011, 4, 21–36.
2. C. Tard and C. J. Pickett, Chem. Rev., 2009, 109, 2245–2274.
3. I. K. Pandey, M. Natarajan and S. Kaur-Ghumaan, J. Inorg. Biochem., 2015, 143, 88–110.
4. T. R. Simmons, G. Berggren, M. Bacchi, M. Fontecave and V. Arteroa, Coord. Chem. Rev., 2014, 270–271, 127–150.
5. F. Gloaguen, Inorg. Chem., 2016, 55, 390–398.
6. P. S. Singh, H. C. Rudbeck, P. Huang, S. Ezzaher, L. Eriksson, M. Stein, S. Ott and R. Lomoth, Inorg. Chem., 2009, 48, 10883–10885.
7. O. F. Erdem, L. Schwartz, M. Stein, A. Silakov, S. Kaur-Ghumaan, P. Huang, S. Ott, E. J. Reijerse and W. Lubitz, Angew. Chem., Int. Ed., 2011, 50, 1439–1443.
8. S. Tschierlei, S. Ott and R. Lomoth, Energy Environ. Sci., 2011, 4, 2340–2352.
9. D. E. Schwab, C. Tard, E. Brecht, J. W. Peters, C. J. Pickett and R. K. Szilagyi, Chem. Commun., 2006, 3696–3698.
10. G. A. N. Felton, A. K. Vannucci, J. Chen, L. T. Lockett, N. Okumura, B. J. Petro, U. I. Zakai, D. H. Evans, R. S. Glass and D. L. Lichtenberger, J. Am. Chem. Soc., 2007, 129, 12521–12530.
11. R. J. Wright, W. Zhang, X. Yang, M. Fasulo and T. D. Tilley, Dalton Trans., 2012, 41, 73–82.
12. J. Zhao, Z. Wei, X. Zeng and X. Liu, Dalton Trans., 2012, 41, 11125–11133.
13. L. Schwartz, P. S. Pradyumna, S. Singh, L. Eriksson, R. Lomoth and S. Ott, C. R. Chim., 2008, 11, 875–889.
14. Y. C. Liu, T. H. Yen, K. T. Chu and M. H. Chiang, Comments Inorg. Chem., 2016, 36, 141–181.
15. I. K. Pandey, S. M. Mobin, N. Deibel, B. Sarkar and S. Kaur-Ghumaan, Eur. J. Inorg. Chem., 2015, 2875–2882.
16. F. Gloaguen, J. D. Lawrence, M. Schmidt, S. R. Wilson and T. B. Rauchfuss, J. Am. Chem. Soc., 2001, 123, 12518–12527.
17. J. Chen, A. K. Vannucci, C. A. Mebi, N. Okumura, S. C. Borowski, M. Swenson, L. T. Lockett, D. H. Evans, R. S. Glass and D. L. Lichtenberger, Organometallics, 2010, 29, 5530–5540.
18. Y. C. Liu, K. T. Chu, Y. L. Huang, C. H. Hsu, G. H. Lee, M. C. Tseng and M. H. Chiang, ACS Catal., 2016, 6, 2559–2576.
19. J. F. Capon, F. Gloaguen, F. Y. Pétillon, P. Schollhammer and J. Talarmin, C. R. Chim., 2008, 11, 842–851.
20. M. Mirmohades, S. Pullen, M. Stein, S. Maji, S. Ott, L. Hammarström and R. Lomoth, J. Am. Chem. Soc., 2014, 136, 17366–17369.
21. S. Wang, A. Aster, M. Mirmohades, R. Lomoth and L. Hammarström, Inorg. Chem., 2018, 57, 768–776.
22. M. Tromp, G. P. F. Strijdonck, S. S. Berkel, A. van den Hoogenband, M. C. Feiters, B. de Bruin, S. G. Fiddy, A. M. J. van der Eerden, J. A. van Bokhoven, P. W. N. M. van Leeuwen and D. C. Koningsberger, Organometallics, 2010, 29, 3085–3097.
23. S. A. Bartlett, P. P. Wells, M. Nachtegaal, A. J. Dent, G. Cibin, G. Reid, J. Evans and M. Tromp, J. Catal., 2011, 284, 247–258.
24. W. L. F. Armarego and C. Chai, Purification of Laboratory Chemicals, Elsevier, 6th edn, 2009.
25. J. A. Cabeza, M. A. Martınez-Garcıa and V. Riera, Organometallics, 1998, 17, 1471–1477.
26. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
27. (a) M. Krejčik, M. Daněk and F. Hartl, J. Electroanal. Chem., 1991, 317, 179–187; (b) M. Swart, A. W. Ehlers and K. Lammertsma, Mol. Phys., 2004, 102, 2467–2474.
28. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, J. A. Gisbergen, G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
29. C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 101, 391–403.
30. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
31. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
32. C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396–408.
33. L. Fan and T. Ziegler, J. Am. Chem. Soc., 1992, 114, 10890–10897.
34. A. J. Atkins, M. Bauer and C. R. Jacob, Phys. Chem. Chem. Phys., 2015, 17, 13937–13948.
35. M. Stener, G. Fronzoni and M. de Simone, Chem. Phys. Lett., 2003, 373, 115–123.
36. E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
37. S. Bernadotte and A. J. Atkins, J. Chem. Phys., 2012, 137, 204106.
38. S. DeBeer George, T. Petrenko and F. Neese, J. Phys. Chem. A, 2008, 12, 12936–12943.
39. J. Li, C. L. Fisher, J. L. Chen, D. Bashford and L. Noodleman, Inorg. Chem., 1996, 35, 4694–4702.
40. L. E. Roy, E. Jakubikova, M. G. Guthrie and E. R. Batista, J. Phys. Chem. A, 2009, 113, 6745–6750.
41. J. J. Rehr, J. J. Kas, F. D. Vila, M. P. Prange and K. Jorissen, Phys. Chem. Chem. Phys., 2010, 12, 5503–5513.
42. J. J. Rehr, J. J. Kas, M. P. Prange, A. P. Sorini, Y. Takimoto and F. Vila, C. R. Phys., 2009, 10, 548–559.
43. L. Hedin and S. Lundqvist, J. Phys. C: Solid State Phys., 1971, 4, 2064–2083.
44. T. E. Westre, P. Kennepohl, J. G. Witt, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1997, 119, 6297–6314.
45. A. L. Ankudinov, B. Ravel, J. J. Rehr and S. D. Conradson, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7565–7576.
46. H. Eyring, J. Chem. Phys., 1935, 3, 107–115.
47. L. Schwartz, P. S. Singh, L. Eriksson, R. Lomoth and S. Ott, C. R. Chim., 2008, 11, 875–889.
48. S. Löscher, L. Schwartz, M. Stein, S. Ott and M. Haumann, Inorg. Chem., 2007, 46, 11094–11105.
49. R. H. Crabtree, The organometallic chemistry of the transition metals, John Wiley and Son, Inc., New Jersey, 6th edn, 2014.
50. L. Yu, C. Greco, M. Bruschi, U. Ryde, L. Gioia and M. Reiher, Inorg. Chem., 2011, 50, 3888–3900.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp01393h

‡ Current address: University of Groningen, Zernike Institute for Advanced Materials, Materials Chemistry, Nijenborgh 4, 9747 AG Groningen, The Netherlands. E-maii: Moniek.Tromp@rug.nl

---