Halogen bonding in differently charged complexes: basic profile, essential interaction terms and intrinsic σ-hole

Abstract

Studies on halogen bonds (XB) between organohalogens and their acceptors in crystal structures revealed that the XB donor and acceptor could be differently charged, making it difficult to understand the nature of the interaction, especially the negatively charged donor's electrophilicity and positively charged acceptor's nucleophilicity. In this paper, 9 XB systems mimicking all possibly charged halogen bonding interactions were designed and explored computationally. The results revealed that all XBs could be stable, with binding energies after removing background interaction as strong as −1.2, −3.4, and −8.3 kcal mol⁻¹ for Cl, Br, and I involved XBs respectively. Orbital and dispersion interactions are found to be always attractive while unidirectional intermolecular electron transfer from a XB acceptor to a XB donor occurs in all XB complexes. These observations could be attributed to the intrinsic σ-hole of the XB donor and the intrinsic electronic properties of the XB acceptor regardless of their charge states. Intramolecular charge redistribution inside both the donor and the acceptor is found to be system-dependent but always leads to a more stable XB. Accordingly, this study demonstrates that the orbital-based origin of halogen bonds could successfully interpret the complicated behaviour of differently charged XB complexes, while electrostatic interaction may dramatically change the overall bonding strength. The results should further promote the application of halogens in all related areas.

---

1. Introduction

Precursory research on halogen bonding can probably be traced back to 1814, conducted by Colin, revealing that dry iodine forms a metallic-colored liquid with dry gaseous ammonia.¹ Subsequently, various unconventional iodinated complexes were reported throughout the whole 19th century,² and extended to other halogens,³ indicating the potential ability of halogen atoms to interact with Lewis bases. In the middle of the 20th century, reports on the X-ray structure of the Br₂:dioxane adduct⁴ revealed a substantially shorter distance of Br⋯O than the sum of their van der Waals radii, which also demonstrated the inconsistent role of halogens that are traditionally accepted as nucleophiles.

Following these early studies, intermolecular charge transfer was indicated by Mulliken to rationalize the structure of halogen–aromatic–molecule complexes,⁵ while the structure of the Br₂:dioxane adduct was described as electron-pair donors bridged by halogen molecules according to Bent.⁶ These findings partially demonstrated an orbital-based origin of the interaction between halogenated molecules and Lewis bases, which was also discussed in various pioneering research studies.⁷ With the development of modern quantum mechanics, it was eventually revealed that a covalently bonded halogen atom, owing to the anisotropy of its electron density distribution,⁸ could generate a locally electron-depleted region, namely the σ-hole,⁹ upon elongation of the covalent bond, which is able to form attractive interactions with Lewis bases possibly through an electrostatic way.¹⁰ To precisely define the interaction, IUPAC launched a project¹¹ which concluded that “A halogen bond occurs when there is evidence of a net attractive interaction between an electrophilic region associated with a halogen atom in a molecular entity and a nucleophilic region in another, or the same, molecular entity”.¹² In general, the electrophilic halogenated molecule is referred to as the halogen bond (XB) donor, and the nucleophile as the XB acceptor.¹³ While the definition of a halogen bond as a net attractive interaction between electrophilic and nucleophilic regions offers a wonderful answer to the question of the role halogens could play in their complexes, the origin of this interaction is still in lively discussion as either electrostatic or electronic or both in nature.^10a,14

Promoted by both theoretical and experimental studies, halogen bonding is accepted nowadays as an important intermolecular interaction and applied in many research fields including materials science and medicinal chemistry.¹⁵ Numerous reports are available, which tremendously enriched our knowledge of halogen bonds and demonstrated their complexity. For example, based on UV-Vis and X-ray results and M06-2X/6-311+G(d,p) density functional theory (DFT) computations, Rosokha et al.¹⁶ found that electrophilic bromocarbons could form XBs with pseudohalide anions with considerable binding strengths up to about −20 kcal mol⁻¹ in the gas phase. The XB binding strength could be even stronger between a cationic XB donor and an anionic XB acceptor, as reported by Riley et al.¹⁷ using DFT (ωB97X-D/def2-TZVP) and the symmetry-adapted perturbation theory (SAPT) method, revealing extreme negative values up to about −80 kcal mol⁻¹ in a vacuum. However, the strong ion-pair XB may weaken considerably in solvents,¹⁸ which should thus be taken into account to evaluate the binding strength more realistically. The solvent effects on the XB estimated using ¹⁹F NMR titrations by Sarwar et al. revealed that the purely electrostatic description of the XB may have limitations,¹⁹ which was suggested by Huber et al. as well.¹⁴ In recent years, Cotrina et al. reported that a XB formed between anionic diflunisal derivatives and the neutral residue of the TTR Y78F variant could lead to an increase in ligand bioactivity up to 4 fold moving from H to F, Cl, Br and I.²⁰ Wang et al.²¹ showed that anion–anion halogen bonding is also stable in polar environments, with bonding strength possibly being stronger than classic neutral–neutral interactions while the calculations revealed that the anionic XB donor has no positively charged σ-hole region and thus should not be a conventional electrophile. Another investigation by Quiñonero et al.²² revealed the existence of halogen bonding interactions in cation–cation complexes, albeit that the cationic XB acceptor is traditionally not considered as a nucleophile. Meanwhile, Mo et al.²³ demonstrated that XBs between ions of like charges are anti-electrostatic in nature using the block-localized wave function (BLW) method and associated energy decomposition analysis. All these explorations might bring enlightenment for designs in molecular recognition, crystal engineering and catalyzing chemical reactions.²⁴

The database survey of the Protein Data Bank (PDB)²⁵ revealed the complexity of interactions between organohalogens and proteins as well.²⁶ While the interaction between the halogen atom of the organohalogen and the heavy atom of the residues in the binding pocket is revealed by the short intermolecular distance compared to the sum of their van der Waals radii, both the organohalogen and the residue could be neutral or positively or negatively charged, leading to 9 different types of XB-like interactions (Fig. S1, ESI†). As the anionic organohalogen and cationic residues have no classic electrophilic and nucleophilic regions, the survey raises again the concern whether there is really a net attractive interaction, especially between the like-charge pairing organohalogens and the protein residues, or if the short distance is just a geometrical constraint in the protein binding pocket but without attraction. If there are XBs in the charged systems, what are the essential attractive terms shared in all 9 types of XB interactions; what makes the like-charge repulsion under vacuum change to attraction in the ligand binding pocket of the protein; what is the basic profile of a XB; how strong is the interaction between the halogen atom and the XB acceptor in the charged complexes if the background electrostatic interaction is removed; whether the less negatively charged “σ-hole” region in anionic XB donors²¹ has intrinsic similarities with the conventional positively charged region; how to understand “electrophilic” and “nucleophilic” in the XB definition; is the IUPAC recommended definition still suitable in the charged systems? However, the reported investigations were mostly performed by different groups with different methods on different XB systems for different purposes, which make it difficult to compare the results for systematically answering the above raised questions.

Hence, we designed 9 highly comparable halogen bonding systems in this study to explore the multiple effects of the molecular charge state, environmental dielectric constant and halogen with the density functional theory (DFT) method. Systematic analysis of the complexity of halogen bonding was then conducted based on the optimized geometries and predicted binding energies followed by wave function analyses at the identical calculation level. The results showed that the existence of a XB depends on a combined effect of electrostatic and electronic interactions that may act either in balance or synergy with each other, as well as environmental polarity, featuring electron transfer always from the XB acceptor to donor no matter what kind of charge is present on the XB donor and acceptor in all 9 halogen bonding systems, allowing the IUPAC definition to be still applicable in all differently charged XB systems. Therefore, the study could help us to precisely understand the basic profile and essential attractive terms of XB and accurately interpret the electrophilicity and nucleophilicity of the XB donor and acceptor, and thus, the IUPAC recommended definition of XB.

2. Model systems and theoretical methods

2.1. Model systems

Considering that both the donor and the acceptor could be neutral or positively or negatively charged (Fig. S1, ESI†), 3-amino-5-halobenzoic acid and glycine were considered as the XB donor and acceptor (Fig. 1a) respectively. The charge state of the designed complex could be adjusted simply by protonation of amino groups and deprotonation of carboxyl groups to mimic all the 9 possible differently charged halogen bonding interactions discovered between organohalogens and proteins in PDB (Fig. 1b). As expected, the molecular surface electrostatic potential alters from totally positive to totally negative (Fig. 1c and d) if the protonated states of the substituent groups are changed.

Fig. 1 (a) Designed models of the selected halogen bond (XB) donor and acceptor (X = Cl, Br, and I). The molecular charges are modified by the protonation or deprotonation of the substituent amino (blue) or carboxyl (red) groups. (b) Schematic models of 9 possible differently charged XB complexes and geometric parameters. d represents the interaction distance while θ the interaction angle. (c) Electrostatic potentials (ESPs) mapped on the 0.001 electrons/Bohr³ isosurface of electronic density for cationic (left), neutral (middle), and anionic (right) XB donors. (d) ESPs for cationic (left), neutral (middle), anionic (right) XB acceptors.

2.2. Geometry optimization

The geometries of the designed XB complexes were optimized with the Gaussian 09 program suite²⁷ using the M06-2X²⁸ functional, owing to its satisfactory performance in describing weak interactions such as halogen bonds.²⁹ Calculations were conducted either in a vacuum or with implicit solvents, including chloroform (trichloromethane, TCM, ε = 4.71), dichloroethane (DCE, ε = 10.13), acetone (ε = 20.49), DMSO (ε = 46.83) and water (ε = 78.36), to determine the effect of the dielectric environments of protein binding pockets.²⁶ The triple-ζ basis set 6-311++G(d,p) was employed for all atoms except iodine, for which the Stuttgart/Dresden effective core pseudopotentials (SDD) and its associated basis set were adopted. Frequency analysis was performed for all optimized geometries to confirm them as the local energy minima.

2.3. Binding energy calculation

The binding energy based on the optimized geometry is determined by eqn (1).

E_bind = E_complex − E_donor − E_acceptor + BSSE (1)

where E_bind represents the binding energy between the XB donor and acceptor; E_complex is the electronic energy of the complex; E_donor and E_acceptor are the electronic energies of the donor and the acceptor extracted from their complex geometry, respectively; BSSE stands for the basis set superposition error estimated by counterpoise corrections³⁰ performed in a vacuum.²⁶

2.4. Energy decomposition analysis

Energy decomposition analysis was performed using the ETS-NOCV (Extended Transition State coupled with Natural Orbitals for Chemical Valence) method and the Amsterdam Density Functional (ADF)³¹ program package with the optimized geometries. The exchange–correlation functional Perdew–Burke–Ernzerhof (PBE)³² combined with dispersion correction³³ improved by a moderate BJ damping function³⁴ was applied to take dispersion terms into consideration. The double-ζ STO basis set DZP was used for the hydrogen atom while the triple-ζ STO basis set TZP was used for other atoms except bromine and iodine, for which relativistic effects were considered with zero-order regular approximation (ZORA) and the triple-ζ STO basis set TZ2P was adopted. The scaling-factor corrected³⁵ COSMO solvent model³⁶ was employed to assess the solvation energy.²⁶

2.5. Other analyses

Wave function analyses including quantum theory of atoms in molecules (QTAIM),³⁷ the non-covalent interaction (NCI) index,³⁸ Hirshfeld population analysis (HPA),³⁹ the electron density difference (EDD) and surface electrostatic potential (ESP) were carried out using the Multiwfn (version 3.4) program⁴⁰ with wave functions obtained from Gaussian 09 results. The natural bond orbital (NBO) analysis⁴¹ was conducted with the NBO program implemented in Gaussian 09 at the same calculation level as geometry optimizations. The outer-sphere electron transfer activation barriers by the Marcus theory⁴² were calculated with Gaussian 09 following the scheme to include the carbon–halogen bond dissociation energy into the total reorganization energy⁴³ (refer to the ESI,† for technical details).

3. Results and discussion

3.1. Attractive binding energy (E_bind) between the XB donor and acceptor in 9 types of XB complexes

The binding energies are summarized in Table 1, which were calculated using eqn (1) based on the optimized complex structures without imaginary frequency unless otherwise stated.²⁶ The results revealed that all the XB interactions in the 9 model systems are attractive in polar environments except that between the 3-amino-5-chlorobenzoic anion and the glycine anion, indicating that both neutral and like-charge pairing XBs could be stable. The formation of intermolecular XBs is further confirmed by both QTAIM⁴⁴ (Fig. S2 and Tables S2–S4, ESI†) and NCI^31d,38,45 (Fig. S3–S5, ESI†) analyses besides the fulfilment of the geometric criteria (Table 2 and Table S1, ESI†). As expected,²¹ the local electrostatic potential maxima (V_S,max) maintain on halogen atoms of all differently charged XB donors in all studied solvents (Fig. S6 and Table S5, ESI†), although the overall molecular surface of the anionic XB donors is negatively charged (Fig. 1c). These results suggested that a favorable XB could even form between the ligand and the residue of the like charges in the protein binding pocket that may enhance the bioactivity of the organohalogen, especially considering that charged residues (e.g., Lys, Arg, Glu and Asp) are usually in agreement with high local dielectric constant values.⁴⁶

Table 1 Calculated binding energies for halogen-bonded complexes between differently charged 3-amino-5-halobenzoic acid and glycine^a

Environment	Cation–anion			Cation–neutral			Cation–cation
	Cl	Br	I	Cl	Br	I	Cl	Br	I
a All values are in kcal mol^−1. b Results of constrained optimization.^26 c Results of single-point energy calculations using the TCM-optimized geometries.
Vacuum	−60.21^b	−65.28^b	−76.52	−6.72	−7.99	−10.23	28.38^c	27.89^c	27.09^c
TCM	−10.38^b	−12.51	−17.03	−1.80	−2.72	−4.25	4.49	3.86	2.84
DCE	−4.78	−6.52	−10.19	−1.14	−2.00	−3.37	1.66	1.02	0.12
Acetone	−2.65	−4.21	−7.40	−0.88	−1.69	−2.99	0.49	−0.11	−1.10
DMSO	−1.55	−3.01	−5.93	−0.74	−1.52	−2.79	−0.13	−0.73	−1.70
Water	−1.21	−2.62	−5.48	−0.70	−1.48	−2.72	−0.32	−0.92	−1.88

---

Environment	Neutral–anion			Neutral–neutral			Neutral–cation
	Cl	Br	I	Cl	Br	I	Cl	Br	I
Vacuum	−4.59^b	−8.15	−15.39	−0.45^b	−1.24^b	−2.69	−2.46^c	−2.78^c	−2.90^c
TCM	0.25	−1.48	−4.85	−0.28	−0.91	−2.13	−0.85	−1.33	−2.01
DCE	0.20	−1.16	−3.83	−0.33	−0.93	−2.02	−0.64	−1.07	−1.83
Acetone	0.02	−1.19	−3.54	−0.37	−0.95	−1.99	−0.56	−1.00	−1.74
DMSO	−0.12	−1.24	−3.43	−0.40	−0.99	−1.99	−0.51	−0.94	−1.69
Water	−0.18	−1.26	−3.39	−0.41	−1.00	−1.98	−0.50	−0.92	−1.67

---

Environment	Anion–anion			Anion–neutral			Anion–cation
	Cl	Br	I	Cl	Br	I	Cl	Br	I
Vacuum	37.69^c	36.36^c	31.07	3.94^c	3.16^c	1.63^b	−32.11^c	−32.23^c	−31.78^c
TCM	8.00	6.92	4.23	0.90^b	0.29^b	−0.77	−5.96^b	−6.32	−6.72
DCE	3.97	2.85	0.65	0.33	−0.24^b	−1.11	−2.86	−3.23	−3.77
Acetone	1.97	0.97	−1.00	0.02	−0.51	−1.37	−1.56	−1.93	−2.54
DMSO	0.82	−0.07	−1.91	−0.17	−0.67	−1.51	−0.89	−1.28	−1.87
Water	0.48	−0.40	−2.19	−0.24	−0.72	−1.54	−0.68	−1.07	−1.67

---

Table 2 Optimized halogen bonding distances in complexes between differently charged 3-amino-5-halobenzoic acid and glycine^a

Environment	Cation–anion			Cation–neutral			Cation–cation
	Cl	Br	I	Cl	Br	I	Cl	Br	I
a All values are in angstrom. b The complex geometry is obtained by constrained optimization.^26 c The complex geometry is the optimized structure in TCM.
Vacuum	2.53^b	2.43^b	2.40	2.81	2.83	2.86	3.09^c	3.03^c	3.04^c
TCM	2.78^b	2.75	2.65	2.90	2.92	2.94	3.09	3.03	3.04
DCE	2.85	2.79	2.71	2.94	2.94	2.96	3.04	3.00	3.03
Acetone	2.88	2.83	2.76	2.96	2.95	2.96	3.04	3.01	3.02
DMSO	2.89	2.85	2.77	2.98	2.99	2.97	3.04	3.01	3.01
Water	2.90	2.86	2.78	2.98	2.99	2.97	3.04	3.01	3.01

---

Environment	Neutral–anion			Neutral–neutral			Neutral–cation
	Cl	Br	I	Cl	Br	I	Cl	Br	I
Vacuum	2.75^b	2.70	2.63	3.05^b	3.02^b	3.05	3.15^c	3.12^c	3.12^c
TCM	2.98	2.85	2.79	3.07	3.04	3.03	3.15	3.12	3.12
DCE	3.02	2.89	2.85	3.08	3.05	3.05	3.15	3.12	3.10
Acetone	3.06	2.92	2.87	3.09	3.07	3.04	3.14	3.10	3.08
DMSO	3.05	2.95	2.87	3.09	3.09	3.04	3.14	3.09	3.08
Water	3.09	2.93	2.89	3.10	3.09	3.05	3.14	3.09	3.08

---

Environment	Anion–anion			Anion–neutral			Anion–cation
	Cl	Br	I	Cl	Br	I	Cl	Br	I
Vacuum	3.16^c	2.98^c	2.97	3.25^c	3.20^c	3.34^b	3.10^c	3.15^c	3.18^c
TCM	3.16	2.98	2.93	3.25^b	3.20^b	3.15	3.10^b	3.15	3.18
DCE	3.08	3.10	2.94	3.23	3.18^b	3.12	3.12	3.15	3.16
Acetone	3.10	3.05	2.94	3.21	3.16	3.10	3.13	3.15	3.15
DMSO	3.19	3.04	2.94	3.19	3.16	3.09	3.18	3.17	3.15
Water	3.16	3.04	2.94	3.16	3.16	3.11	3.18	3.19	3.14

---

Taking organobromine complexes as examples, the binding in a vacuum between the cationic donor and the anionic acceptor (hereinafter referred to as cation–anion and so forth for others) presents the strongest attraction (−65.28 kcal mol⁻¹), which is almost two times that for the anion–cation complex (−32.23 kcal mol⁻¹). The significantly weaker binding in the anion–cation complex than that in the cation–anion complex indicated that the cationic donor's σ-hole and anionic acceptor's Lewis basicity should play important roles in the halogen bonding interaction.⁴⁷ As expected,^21,48 complexes formed by ions of like charges are unstable and repulsive in a vacuum.

Different from the results in a vacuum, almost all the repulsive interactions eventually become attractive as the environment becomes more and more polar. If the intermolecular interaction is just a simple electrostatic repulsion, the corresponding binding energies in different solvents should be in line with the environmental dielectric constants. Therefore, the observed change from repulsion to attraction demonstrates that there should be non-electrostatic profiles in these like-charge pairing XBs. The assumption is obviously tenable as well for other neutral or charged complexes (Table 1). For instance, the ratio of binding energy in TCM and water is approximately 5 : 1 or 6 : 1 for cation–anion or anion–cation organobromine complexes, respectively, while that of the dielectric constants is approximately 17 : 1 (78.36 : 4.71), demonstrating again the existence of additional intermolecular interactions besides the Coulombic terms.

Notably, the cation–cation organobromine complex tends to have less repulsive or more attractive binding energies than the anion–anion complex in different environments. The binding energy of the anion–anion organobromine complex is 36.36 kcal mol⁻¹ in a vacuum, approximately 8.5 kcal mol⁻¹ larger than that for the cation–cation complex (27.89 kcal mol⁻¹). This might indicate that the donor's electrophilicity (σ-hole) possibly plays a more important role than the acceptor's nucleophilicity in forming such XBs even taking into consideration the different distances between charge centers in the two complexes, which may result in an energy difference of only about 2.9 kcal mol⁻¹ in a vacuum.⁴⁹ This indication might also be suggested by the more favorable binding energy for the cation–neutral organobromine complex (e.g., −1.48 kcal mol⁻¹ in water) than that for the neutral–anion complex (e.g., −1.26 kcal mol⁻¹ in water), as well as the similar binding strength for the neutral–cation (e.g., −1.00 to −0.92 kcal mol⁻¹) and the classic neutral–neutral complex (e.g., −0.95 to −1.00 kcal mol⁻¹) in highly polar environments.

The geometry parameters for all optimized structures are listed in Table 2 and Table S1 (ESI†). In general, the halogen bonding angle tends to be linear and varies from 173.3° to 179.1° in all differently charged complexes (Table S1, ESI†). All interaction distances are shorter than the sum of the typical van der Waals radii of the corresponding atoms, while the anion–cation complexes have the longest halogen bonding length (larger than 3.10 Å) in polar solvents, and the cation–anion the shortest (smaller than 2.90 Å). It was found that the optimized interaction distances (Table 2) are in general always longer in polar environments for complexes except those with the anionic donor or the cationic acceptor, which probably results from the combined effect of the dielectric environment and polarization of the halogen atom.⁵⁰ The interaction distances in the anion–cation organochlorine and organobromine cases also become longer in polar environments, in which background electrostatic attractions are formed which may dominate the changes in the interaction distance besides the halogen's σ-hole character. Notably, a significant portion of organoiodine complexes exhibit shorter interaction distances than that of organochlorine complexes while the atomic radius of iodine is much larger than that of chlorine, reflecting the flatter shape (Fig. S7 and Tables S6–S8, ESI†) and the larger σ-hole region of heavier halogens which may result in less Pauli repulsion and more favorable binding energy (the so-called polar flattening).⁵¹

In general, the dielectric environment influences both the binding strength and geometry parameters of XB by weakening electrostatic interactions, making it possible to form attractive interaction even for the like-charge pairing XBs in polar environments. This result further enriches our knowledge in applying XBs to different systems especially those formed by the negatively charged donors and the positively charged acceptors, which are traditionally regarded as nucleophiles and electrophiles respectively.

3.2. Net binding energy (E_{bind_X}) between a halogen atom and a XB acceptor after removing background electrostatic interaction

Although overall binding energy (E_bind) has long been a classic parameter when discussing the strength of XBs, intermolecular Coulombic interaction has significant contributions to total binding strength,^18,21,22,52 especially in charged complexes (Table 1). A strategy of applying the classic point-to-point Coulombic formula via fixing the charges at specific points was considered to remove the background Coulombic interaction, and has been successfully utilized on charged XB systems to obtain net halogen bonding energy between the charged donor and acceptor.^22,48a Considering the possible charge delocalization in the whole complex and the possible electrostatic interaction even in neutral XB systems,²⁶ we proposed a “free radical” approach to estimate the net binding energy between the halogen atom and the XB acceptor (E_{bind_X}) by subtracting the background Coulombic interaction (E_bg, calculated with eqn (2)) from the total binding energy (E_bind) (eqn (3)).

E_bg = E_{bind_FR} − E_{orb_SCF} (2)

E_{bind_X} = E_bind − E_bg (3)

where E_{bind_FR} represents the binding energy between the XB donor radical, obtained by removing the halogen atom from the donor, and the acceptor (Fig. S8, ESI†). E_{orb_SCF} stands for the contribution of the potential orbital interactions between the radical and the acceptor, which may be induced especially by strong intermolecular Coulombic attraction and is evaluated by comparing the corresponding electronic energy of wave functions acquired after and before the self-consistent field iteration (SCF) process,²⁶ as defined in Multiwfn.⁴⁰

Comparing scanning curves of E_bind (Fig. S9–S11, ESI†) and E_{bind_X} (Fig. 2 and Fig. S12, S13, ESI†) against the interaction distance, it is found that E_{bind_X} tends to zero at distances longer than approximately 6 Å, suggesting that the background electrostatic term has been successfully removed and thus demonstrating the rationality of the “free radical” approach.^22,48a The E_{bind_X} values at the optimized distance are found to almost always have negative values in all types of halogen bonding systems except some of the anion–anion organochlorine complexes (Table 3 and Tables S9, S10, ESI†). As expected, attractive E_{bind_X} still follows the trend of I > Br > Cl, with values ranging from −1.33 to −5.44, −0.72 to −2.22 and 0.04 to −0.62 kcal mol⁻¹ respectively in highly dielectric environments.

Fig. 2 Net binding energy (E_{bind_X}) between the Br atom and the acceptor versus the intermolecular Br⋯O distance of the complexes between differently charged 3-amino-5-bromobenzoic acid and glycine in different environments including vacuum (black, those based on optimized structures in TCM are shown in dashed line), TCM (red), DCE (blue), acetone (magenta), DMSO (green), and water (midnight blue).

Table 3 Net binding energies (E_{bind_X}) between the halogen atom and acceptor for complexes between differently charged 3-amino-5-bromobenzoic acid and glycine at the optimized distance^a

Complex	Environment
	Vacuum	TCM	DCE	Acetone	DMSO	Water
a All values are in kcal mol^−1. b The complex geometry is obtained by constrained optimization.^26 c The complex geometry is the optimized structure in TCM.
Br cation–anion	−16.98^b	−3.36	−2.51	−2.22	−2.10	−2.05
Br neutral–anion	−8.38	−2.12	−1.50	−1.34	−1.26	−1.24
Br anion–anion	−2.60^c	−1.19	−0.94	−0.87	−0.83	−0.82
Br cation–neutral	−3.82	−1.69	−1.48	−1.41	−1.37	−1.36
Br neutral–neutral	−1.47^b	−1.09	−1.01	−0.97	−0.96	−0.96
Br anion–neutral	−0.44^c	−0.81^b	−0.79^b	−0.77	−0.75	−0.74
Br cation–cation	−1.35^c	−1.36	−1.27	−1.21	−1.18	−1.17
Br neutral−cation	−1.89^c	−1.06	−0.94	−0.90	−0.87	−0.86
Br anion–cation	−2.78^c	−0.89	−0.79	−0.73	−0.72	−0.72

---

Notably, even if the contribution of background interactions has been excluded, differently charged substituent groups still influence E_{bind_X}. Taking the organobromine complexes as examples (Table 3), the E_{bind_X} at the optimized interaction distance varies from −0.72 to −3.36 kcal mol⁻¹ in different solvents. The cation–anion complex has the strongest E_{bind_X} strength while the anion–cation complex is the weakest, which is precisely in line with the corresponding interaction distances, as shown in Table 2. In general, the E_{bind_X} follows the trend of cationic > neutral > anionic donors for the same acceptor especially in solvents, which could be attributed to the electron density redistribution and σ-hole reshaping (Table S6, ESI†) of the halogen atom induced by the cationic or anionic substituent groups.⁵³ Similarly, the charge state of the acceptor also affects E_{bind_X} owing to the influence of the acceptor's nucleophilicity. E_{bind_X} for the cation–cation organobromine complex is still more negative than that for the anion–anion complex in general, indicating again the possibly more important role of the XB donor's electrophilicity.

Additionally, with the increase of environmental polarity, E_{bind_X} weakens steadily and eventually tends to be a constant in different solvents. Unlike the overall binding energy (E_bind), E_{bind_X} always weakens as the environment becomes more polar (Table 3). While there is a big difference in E_{bind_X} between the vacuum and solvent cases, E_{bind_X} changes little in different solvents and tends to be convergent to a constant in highly polar environments with variation of <20% from TCM onward for complexes with neutral XB acceptors and <10% from acetone onward for all studied complexes. Considering that the average dielectric value inside the protein is about 6–7 (ε_TCM = 4.71) while that around charged residues are probably larger than 20 (ε_acetone = 20.49),⁴⁶ this finding provides us with a new insight into describing halogen bonding interactions, which may pave a new way in developing new halogen bonding scoring functions or force fields. However, we are still not clear about the common energy terms composing the net attractive interactions between the halogen atom and the XB acceptor.

3.3. Essential attraction terms in all types of XB

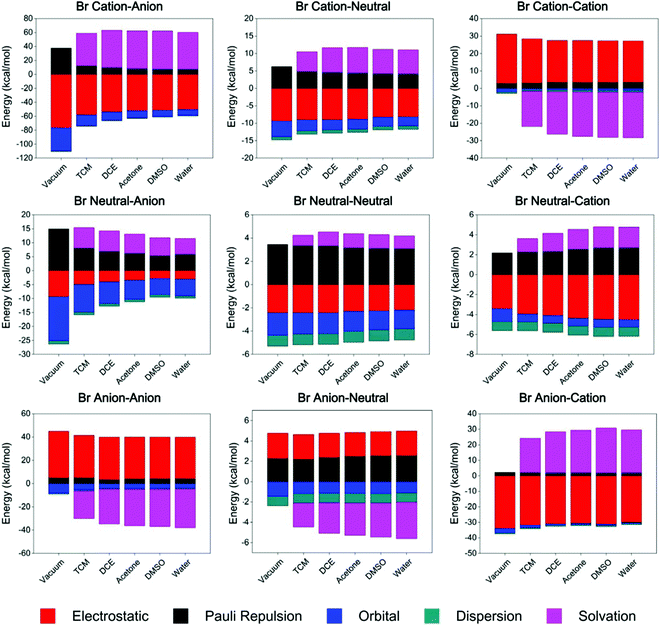
In order to identify the common interaction terms existing in all types of XB with different charge states, we performed energy decomposition analysis using the ETS-NOCV scheme based on the ADF program package to decompose the total binding energy (E_bind) into electrostatic (E_elest), Pauli repulsion (E_Pauli), orbital (E_orb) and dispersion (E_disp) terms. The solvation energy (E_solv) is included, for solvent cases (eqn (4)).

E_bind = E_elest + E_Pauli + E_orb + E_disp + E_solv (4)

The ETS-NOCV results (Tables S11–S13, ESI†) revealed that orbital interaction and dispersion terms always have negative values and contribute to the stability of complexes with all types of charge states. This observation indicates that, the orbital and dispersion terms may play essential roles in the formation of a XB, and show non-negligible contributions to the total binding energy.

Taking organobromine complexes as examples (Fig. 3 and Table S12, ESI†), regardless of the solvation energy, the orbital interaction plays the most or second most important role in the overall binding energy. Notably, the orbital interaction decreases significantly as the donor's charge state changes from cationic to anionic and the acceptor's from anionic to cationic (Fig. 4), revealing the stronger ability of the cationic donor to obtain electrons and that of the anionic acceptor to provide electrons in the formation of a XB. Hence, as expected,^18,52b remarkable electron transfer interaction takes place in the cation–anion complex, which is also indicated by the QTAIM analysis results (Tables S2–S4, ESI†), such that the corresponding net halogen bonding strength is the strongest while that of the anion–cation complex is the weakest in polar solvents (Table 3). Although the orbital interaction decreases for most systems in polar environments, it increases in the cation–cation complex, partially as a result of intramolecular charge redistribution (part 3.5). The dispersion energy was found to be insensitive to the charge state and environmental polarity, ranging approximately from −0.9 to −1.2 kcal mol⁻¹ in different complexes (Fig. 4). Although the dispersion term is in general relatively weak in strength, it still contributes a considerable percentage⁵⁴ to the total binding energy, especially for weak attractive halogen-bonded complexes, for instance the neutral–neutral cases.

Fig. 3 ETS-NOCV based energy decomposition for all complexes between differently charged 3-amino-5-bromobenzoic acid and glycine. The binding energy (E_bind) is decomposed into electrostatic (E_elest, red), Pauli repulsion (E_Pauli, black), orbital (E_orb, blue) and dispersion (E_disp, dark cyan) terms. The solvation energy (E_solv, magenta) is included for solvent cases.

Fig. 4 Changes in orbital interaction (blue) and dispersion term (dark cyan) in systems represented by that between differently charged 3-amino-5-bromobenzoic acid and glycine in TCM and water.

The overall electrostatic interaction is not always attractive in differently charged complexes (Tables S11–S13, ESI†). For instance, the electrostatic repulsion of around 1.2 and 4.3 kcal mol⁻¹ was found in neutral–anion and anion–neutral organochlorine complexes in polar environments, respectively. Complexes with heavier halogens tend to exhibit stronger electrostatic attraction or weaker electrostatic repulsion,⁵⁵ indicating the two sources for electrostatic contribution, namely, the background Coulombic term and that involving the σ-hole region.

Similar to literature reports,^17,18,48b,56 the solvation energy has comparable strength to the electrostatic term in all types of differently charged complexes, but in general always with opposite symbols in numerical value. Especially in complexes composed of both charged subunits, the solvation energy term even presents a larger absolute value than the electrostatic term. These observations actually originate from the dielectric properties of solvents, which by definition stands for the ability in weakening the Coulombic interaction strength and electric field intensity by generating inductive charges and may be able to change both size and magnitude⁵⁷ of the σ-hole (Fig. S14–S15 and Table S5, ESI†). Therefore, for the like-charge pairing complexes that are unstable in a vacuum, contribution from the highly dielectric solvents shields the donor and the acceptor from repulsive background interactions, allowing these complexes to overcome the energy barrier for Coulombic repulsion and create a halogen bonding potential energy well allowing the formation of stable geometries. Yet for the charge-assisted complexes, especially with oppositely charged subunits, intermolecular electrostatic attraction is greatly weakened by polar environments, thus resulting in weaker XB attraction.

Overall, while electrostatic interaction changes from repulsive to attractive in differently charged complexes, orbital and dispersion terms always have negative values and contribute to the system's stability, and are therefore essential terms for all halogen bonds. Meanwhile, solvation energy also plays a remarkable role in overcoming the intermolecular electrostatic repulsion, especially for the like-charge pairing complexes. Contributed by all these energy terms, favorable binding energies and stable XB geometries are presented in all 9 differently charged complexes in highly dielectric solvents, with binding strength at the same order of magnitude (several kcal mol⁻¹).

3.4. Basic profile of halogen bonding reflected by unidirectional electron transfer

Considering the significant character of orbital interactions, we conducted a study of the electron transfer utilizing the natural bond orbital (NBO) method. The NBO analysis results showed that electrons always transfer from the acceptor's lone pair electron orbital of the oxygen atom (n_O) to the donor's antibonding orbital of the carbon–halogen bond (σ*_C–X) in not only the classic XB system,⁵⁸ but all 9 types of differently charged complexes (Tables S14–S16, ESI†). For a small portion of complexes especially those involving heavy halogens, intermolecular electron transfer with a relatively small second-order perturbation stabilization energy (E(2))^41a between the lone pair electron orbital of the other oxygen atom (n_O′) in the carboxyl group and σ*_C–X is also observed, indicating the existence of multiple halogen bonding interactions^15e in the designed model systems. Contributed by all these inter-orbital electron transfers, the direction of overall intermolecular electron transfer is always from the XB acceptor to the XB donor in solvents (Tables S17–S19, ESI†), at least in the studied cases, even for anion–cation complexes, though much less in amount. Taking the organobromine complexes with both charged subunits as examples (Q_CT in Table 4), the cation–anion complex has the largest amount of electrons transferred from the XB acceptor to donor (0.0351–0.0208 a.u. in solvents) while the anion–cation generally has the least (0.0042–0.0059 a.u. in solvents). Solvents are found to affect the amount of electrons transferred as well,^18,57 and in general lead to less electron transfer in polar environments for charge-assisted XB complexes (e.g., cation–anion, neutral–anion and cation–neutral) and more for the others, which may explain the preference of polar solvents for the classic neutral–neutral halogen-bonded co-crystals.⁵⁹ All these observations from the natural population analysis (NPA) are similarly indicated by the Hirshfeld population analysis (HPA) (Tables S20–S22, ESI†) as well. Stabilization contributions from electron transfer are estimated by the sum of E(2) values for all electron transfer from n_O and n_O′ to σ*_C–X, which in general show a linear relationship with the entire orbital interaction obtained using the ETS-NOCV method (Fig. S16, ESI†), indicating that such electron transfer from the acceptor to the donor probably plays the most important role in the overall orbital interaction, and therefore, should be distinguished as the basic profile of a XB.

Table 4 Calculated atomic charge and electron transfer results from natural population analysis for complexes between both charged 3-amino-5-bromobenzoic acid and glycine^a

Complex	Environment	Q CT	q(X)monomer^c	q(X)complex^d	Δq(X)^e	ΔQCTX^f
a All values are in atomic units. b Amount of electrons transferred from the XB acceptor to donor. c Atomic charge of the halogen atom in the monomer determined by natural population analysis (NPA). d Atomic charge of the halogen atom in the complex determined by NPA. e Difference between d and c. f ΔQCTX = −QCT − Δq(X), negative ΔQCTX value means electron transfer from the halogen atom to the rest of the XB donor molecule and vice versa. g The complex geometry is obtained by constrained optimization.^26 h The complex geometry is the optimized structure in TCM.
Br cation–anion	Vacuum^g	0.1119	0.1775	0.2852	0.1077	−0.2195
	TCM	0.0351	0.1289	0.1859	0.0570	−0.0920
	DCE	0.0282	0.1188	0.1612	0.0423	−0.0705
	Acetone	0.0239	0.1141	0.1486	0.0345	−0.0584
	DMSO	0.0222	0.1113	0.1412	0.0299	−0.0520
	Water	0.0208	0.1105	0.1386	0.0282	−0.0489
Br anion–anion	Vacuum^h	0.0143	−0.0044	0.1066	0.1110	−0.1253
	TCM	0.0139	0.0247	0.0786	0.0539	−0.0679
	DCE	0.0121	0.0308	0.0672	0.0364	−0.0484
	Acetone	0.0130	0.0337	0.0647	0.0310	−0.0440
	DMSO	0.0130	0.0354	0.0626	0.0272	−0.0403
	Water	0.0131	0.0359	0.0620	0.0261	−0.0392
Br cation–cation	Vacuum^h	0.0056	0.1775	0.1483	−0.0292	0.0236
	TCM	0.0073	0.1289	0.1319	0.0030	−0.0103
	DCE	0.0079	0.1188	0.1266	0.0078	−0.0156
	Acetone	0.0081	0.1141	0.1227	0.0087	−0.0167
	DMSO	0.0082	0.1113	0.1208	0.0094	−0.0177
	Water	0.0083	0.1105	0.1202	0.0097	−0.0180
Br anion–cation	Vacuum^h	−0.0011	−0.0044	−0.0200	−0.0156	0.0166
	TCM	0.0042	0.0247	0.0304	0.0057	−0.0099
	DCE	0.0048	0.0308	0.0394	0.0086	−0.0135
	Acetone	0.0052	0.0337	0.0433	0.0096	−0.0149
	DMSO	0.0051	0.0354	0.0432	0.0078	−0.0129
	Water	0.0059	0.0359	0.0446	0.0087	−0.0146

---

The universal orbital interaction and unidirectional electron transfer from the acceptor to the donor may greatly help us to gain further insights into the concept of “electrophilicity” and “nucleophilicity” in the IUPAC recommended XB definition. In other words, for the anionic XB donor, despite the overall negative surface electrostatic potential, the less negatively charged “σ-hole” region on the halogen atom still has the ability to accept electrons from the XB acceptor, and thus should be regarded as the “intrinsic σ-hole” which could still be electrophilic in nature. Similarly, for the cationic acceptor, the intrinsic electronic properties were not fundamentally changed by the charge state. The original lone pair of electrons on the oxygen atom probably still results in a nucleophilic region that is able to transfer electrons to the intrinsic σ-hole region of the XB donor, even though the overall molecular surface is positively charged. This “intrinsic” electronic property is further demonstrated in complexes with the six-membered oxocarbenium, dimethyloxidanium and methylguanidinium cations as the XB acceptors (Fig. S17, ESI†). Calculations showed that all these cationic acceptors have a locally less positively charged region (Fig. S18, ESI†) resulting from a lone pair of electrons or a π system that could form stable XB interactions with organohalogens in the polar environment (Table S23, ESI†). Consequently, all the analyses suggested that an attractive XB exists, especially in polar environments, as long as the donor and the acceptor have the intrinsic σ-hole region and maintain the intrinsic electronic properties respectively, regardless of their charge states and the sign of electrostatic potential on the molecular surface, thus indicating that the IUPAC definition should be applicable in these systems.

3.5. Charge redistribution for either enhancing binding or reducing repulsion

Besides intermolecular electron transfer, intramolecular charge redistribution was found to take place simultaneously in all XB systems according to both NPA and HPA results. As shown in Tables S17–S22 (ESI†), although the direction of intermolecular electron transfer is in general always from the acceptor to the donor, the atomic charge of the donor's halogen has become more positive in most of the complexes. This observation suggests that the halogen atom transfers more electrons to the rest of the XB donor molecule than it obtains from the XB acceptor.²¹ Taking the natural population analysis results of the cation–anion organobromine complex in a vacuum as an example (Table 4), the intermolecular electron transfer of 0.1119 a.u. (Q_CT) takes place from the acceptor to the donor. However, the difference of the halogen's atomic charge (Δq(X)) between its XB complex and free XB donor could be as much as 0.1077 a.u., indicating an intramolecular charge redistribution (ΔQ_CTX) of 0.2195 a.u. from Br to the rest of the donor during the formation of the XB. As a result, the reduced electron density on the Br atom probably enhances the attraction between the σ-hole and the oxygen atom of the anionic acceptor to form a stronger XB. In contrast, for a small amount of complexes represented by the cation–cation organobromine case in a vacuum (Table 4), more negative charge is found on Br than the amount from intermolecular electron transfer (ΔQ_CTX = 0.0236), suggesting the additional electron flow from the rest of the XB donor to Br, which thus leads to the increased electron density on the Br atom that could reduce electrostatic repulsion and enhance the XB strength.

The intramolecular electron flows are further demonstrated using electron density difference (EDD) maps (Fig. 5). Comparing the EDD maps for the cation–anion and cation–cation organobromine complexes that differ only in the acceptor's charge state (Fig. 5a), the electron density increases in a particular region of the donor in the cation–anion system, and it decreases in the corresponding region of the cation–cation one, and vice versa. These observations thus indicate the opposite intramolecular electron transfer direction within the XB donor, which is affected by the acceptor's charge state. It is obvious that a relatively strong intermolecular electrostatic repulsion is presented in the cation–cation complexes. Hence, partial electron transfer from the non-halogen part of the XB donor to the halogen atom should be able to produce a relatively stronger cation–cation XB via reducing the repulsive interaction between the two cations while still maintaining a significant positive σ-hole. Electron transfers in the XB acceptor are similarly affected by the donor's charge state. As shown in Fig. 5b, comparing the EDD maps of the anion–cation and cation–cation cases, the electrons transfer from the carboxyl oxygen atom to the rest of the acceptor molecule in the anion–cation complex, while the electrons transfer in the opposite direction for the repulsive cation–cation complex, such that the overall binding energy is more attractive and less repulsive in general.

Fig. 5 Electron density difference (EDD) maps for complexes of the (a) cationic 3-amino-5-bromobenzoic acid donor, and anionic (left) and cationic (right) glycine acceptors in a vacuum, and complexes of (b) anionic (left) and cationic (right) 3-amino-5-bromobenzoic acid donors, and the cationic glycine acceptor in TCM. Electrons transfer from the electron density decreased regions (red) to increased regions (blue). The corresponding isovalues are listed below the EDD maps.

It is noteworthy that, with the exception of the vacuum case, the direction of intramolecular electron flow in the cation–cation organobromine complex is still from the halogen atom to the rest of the donor (Table 4), which might indicate the possible balance between decreasing positive charges to reduce repulsive electrostatic interaction (electron flow direction from donor to halogen) and maintaining the ability of the σ-hole to extract electrons from other molecular entities (electron flow direction from halogen to the donor). Whenever the repulsive electrostatic interaction is partly shielded by highly dielectric solvents, the balance moves towards maintaining or strengthening the electrophilicity of the σ-hole, allowing more electrons to be able to transfer from the halogen atom to the rest of the XB donor in polar solvents for the cation–cation organobromine complex, and thus the orbital interactions are stronger in water compared to that in TCM, as shown in Fig. 4. However, for complexes represented in the cation–anion cases, electronic effects act synergistically with electrostatic interactions, leading to the strengthening of σ-hole's electrophilicity, and thus the electrostatic attraction.

To validate the bidirectional charge redistribution phenomena, further calculations were conducted to provide more evidence (Fig. S19, S20 and Tables S24, S25, ESI†). The results revealed that, once we switch the acceptor to the cationic methylguanidinium molecule, which has a more positively charged electrostatic potential surface (Fig, S19, ESI†), charge redistribution from the rest of the XB donor to the halogen atom could exist in complexes with all types of solvents, not only in a vacuum, thus demonstrating that the charge state based electron redistribution tendency could exist widely in stable geometries in various environments. These findings might indicate the lowering of activation barriers for intermolecular electron transfer as reported by Rosokha et al.^43c Actually, our calculations of the organobromine complexes showed that the outer-sphere electron transfer activation barriers according to the Marcus theory^26,42 are extremely high for all differently charged XB complexes in various solvents (Table S26, ESI†), which might indicate the existence of an inner-sphere mechanism and redox centers that are strongly coupled upon the formation of halogen bonds.^43c

Therefore, supported by the natural bond orbital and EDD results, it can be concluded that while the electrons always transfer from the acceptor to the donor, the intramolecular charge redistribution in either the donor or the acceptor is bidirectional, which may act in balance or synergy with the background electrostatic interaction and always contributes to more favorable complex stability and binding energy.

4. Conclusions

To explore the basic profile and essential interaction terms of halogen bonding, 9 highly comparable XB complexes with different charge states were designed and optimized by a quantum chemistry method at the M06-2X/6-311++G(d,p) level (M06-2X/SDD for iodine), followed by systematic wave function analyses. Based on theoretical explorations, orbital and dispersion terms turn out to be always attractive in all types of differently charged complexes, and thus are essential terms to all XBs. The electron transfer from the lone pair electron orbital of the heavy atom in the XB acceptor to the antibonding orbital of the carbon–halogen bond in the XB donor is widely presented as the basic profile in all halogen-bonded complexes. This basic profile causes the overall intermolecular electron transfer to be always from the XB acceptor to the XB donor. The result suggests that the intrinsic electronic properties of both anionic XB donors and cationic XB acceptors are not fundamentally changed by the molecular charge state, which should still be electrophilic and nucleophilic in nature. In other words, the locally less negatively charged region (conventional σ-hole area) on the halogen atom of the anionic XB donor is still capable of receiving electrons from the XB acceptor and thus should be regarded as the intrinsic σ-hole, while the locally less positively charged region (e.g., a lone pair of electrons or a π system) on the cationic XB acceptor is able to provide its electrons to the XB donor as well, resulting in effective XB-acceptor-to-XB-donor electron transfer in all differently charged XB complexes. Meanwhile, intramolecular charge redistribution inside both XB donors and acceptors always makes the overall binding strength more attractive or less repulsive, making it possible for the halogen atom to be more or less negatively charged upon the formation of a XB. Benefitting from all these contributions, stable complexes with favorable binding energies are widely formed in highly polar environments. Removal of the “background” electrostatic interactions was conducted by employing a “free radical” strategy to demonstrate that the net binding strength between the halogen atom and the XB acceptor is almost always attractive, regardless of the complex charge state, which weakens steadily to approximately a constant with variation less than 10% in highly dielectric solvents.

All the results discussed above suggest that the orbital-based origin of halogen bonds could be successfully applied to rationalize the complicated behaviors of halogen bonding complexes with different charge states, while the charge state and electrostatic interaction may dramatically change the overall bonding strength. These conclusions should be helpful in identifying the criteria for classifying σ-hole bonding interactions involving Group 14–16 elements in the newly launched IUPAC project⁶⁰ and thus provide new insights into introducing σ-hole interactions in materials science and rational drug design⁶¹ and promote the development of related research areas.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors would like to thank Dr Zhaoning Zhu and Dr Adam Smalley at UCB Biopharma for discussion and proofreading the manuscript. This work was supported by the National Key Research and Development Program (Grant 2016YFA0502301) and the National Natural Science Foundation of China (Grant No. 81573350 and 31870717). The calculations were partially run at TianHe-2 supercomputer in Guangzhou, supported by the Special Program for Applied Research on Super Computation of the NSFC-Guangdong Joint Fund (the second phase) under Grant No. nsfc2015_447.

Notes and references

1. G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601.
2. (a) F. Guthrie, J. Chem. Soc., 1863, 16, 239–244; (b) O. Rhoussopoulos, Ber. Dtsch. Chem. Ges., 1883, 16, 202–203.
3. I. Remsen and J. F. Norris, Am. Chem. J., 1896, 18, 90–95.
4. (a) O. Hassel and J. Hvoslef, Acta Chem. Scand., 1954, 8, 873; (b) O. Hassel, Science, 1970, 170, 497–502.
5. R. S. Mulliken, J. Am. Chem. Soc., 1950, 72, 600–609.
6. H. A. Bent, Chem. Rev., 1968, 68, 587–648.
7. (a) A. E. Reed, F. Weinhold, R. Weiss and J. Macheleid, J. Phys. Chem., 1985, 89, 2688–2694; (b) N. Ramasubbu, R. Parthasarathy and P. Murrayrust, J. Am. Chem. Soc., 1986, 108, 4308–4314; (c) A. C. Legon, Angew. Chem., Int. Ed., 1999, 38, 2687–2714.
8. (a) T. Brinck, J. S. Murray and P. Politzer, Int. J. Quantum Chem., 1992, 44, 57–64; (b) T. Brinck, J. S. Murray and P. Politzer, Int. J. Quantum Chem., 1993, 48, 73–88.
9. T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296.
10. (a) T. Clark and A. Hesselmann, Phys. Chem. Chem. Phys., 2018, 20, 22849–22855; (b) P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189.
11. Project No. 2009-032-1-100, Chem. Int., 2010, 32, 20–21 , http://publications.iupac.org/ci/2010/3202/pp1_2009-032-1-100.html.
12. G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711.
13. To get in line with the IUPAC definition, “electrophile” and “nucleophile” are used in this article instead of “Lewis acid” and “Lewis base” respectively in the thermodynamics contexts.
14. (a) J. Thirman, E. Engelage, S. M. Huber and M. Head-Gordon, Phys. Chem. Chem. Phys., 2018, 20, 905–915; (b) S. M. Huber, E. Jimenez-Izal, J. M. Ugalde and I. Infante, Chem. Commun., 2012, 48, 7708–7710.
15. (a) P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Angew. Chem., Int. Ed., 2008, 47, 6114–6127; (b) G. M. Espallargas, F. Zordan, L. A. Marin, H. Adams, K. Shankland, J. van de Streek and L. Brammer, Chem. – Eur. J., 2009, 15, 7554–7568; (c) Y. Lu, T. Shi, Y. Wang, H. Yang, X. Yan, X. Luo, H. Jiang and W. Zhu, J. Med. Chem., 2009, 52, 2854–2862; (d) A. R. Voth, P. Khuu, K. Oishi and P. S. Ho, Nat. Chem., 2009, 1, 74–79; (e) R. Wilcken, M. O. Zimmermann, A. Lange, A. C. Joerger and F. M. Boeckler, J. Med. Chem., 2013, 56, 1363–1388; (f) A. Priimagi, G. Cavallo, P. Metrangolo and G. Resnati, Acc. Chem. Res., 2013, 46, 2686–2695; (g) A. Mukherjee, S. Tothadi and G. R. Desiraju, Acc. Chem. Res., 2014, 47, 2514–2524; (h) F. Topic and K. Rissanen, J. Am. Chem. Soc., 2016, 138, 6610–6616.
16. S. V. Rosokha, C. L. Stern, A. Swartz and R. Stewart, Phys. Chem. Chem. Phys., 2014, 16, 12968–12979.
17. K. E. Riley and K.-A. Tran, Faraday Discuss., 2017, 203, 47–60.
18. R. Nunes and P. J. Costa, Chem. – Asian J., 2017, 12, 586–594.
19. M. G. Sarwar, B. Dragisic, L. J. Salsberg, C. Gouliaras and M. S. Taylor, J. Am. Chem. Soc., 2010, 132, 1646–1653.
20. E. Y. Cotrina, M. Pinto, L. Bosch, M. Vila, D. Blasi, J. Quintana, N. B. Centeno, G. Arsequell, A. Planas and G. Valencia, J. Med. Chem., 2013, 56, 9110–9121.
21. G. M. Wang, Z. Q. Chen, Z. J. Xu, J. N. Wang, Y. Yang, T. T. Cai, J. Y. Shi and W. L. Zhu, J. Phys. Chem. B, 2016, 120, 610–620.
22. D. Quiñonero, I. Alkorta and J. Elguero, Phys. Chem. Chem. Phys., 2016, 18, 27939–27950.
23. C. W. Wang, Y. Z. Fu, L. N. Zhang, D. Danovich, S. Shaik and Y. R. Mo, J. Comput. Chem., 2018, 39, 481–487.
24. S. H. Jungbauer and S. M. Huber, J. Am. Chem. Soc., 2015, 137, 12110–12120.
25. (a) F. C. Bernstein, T. F. Koetzle, G. J. Williams, E. F. Meyer, Jr., M. D. Brice, J. R. Rodgers, O. Kennard, T. Shimanouchi and M. Tasumi, J. Mol. Biol., 1977, 112, 535–542; (b) H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242.
26. See “1. Computational Details” in supporting information for details.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford, CT, 2009.
28. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
29. (a) M. H. Kolář and P. Hobza, Chem. Rev., 2016, 116, 5155–5187; (b) S. Kozuch and J. M. Martin, J. Chem. Theory Comput., 2013, 9, 1918–1931; (c) A. Forni, S. Pieraccini, S. Rendine and M. Sironi, J. Comput. Chem., 2014, 35, 386–394.
30. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
31. (a) ADF 2013, SCM, Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands, 2013, http://www.scm.com; (b) C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403; (c) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967; (d) B. Pinter, N. Nagels, W. A. Herrebout and F. D. Proft, Chem. – Eur. J., 2013, 19, 518–529; (e) K. Dyduch, M. P. Mitoraj and A. Michalak, J. Mol. Model., 2013, 19, 2747–2758.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
33. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
34. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
35. (a) A. Klamt, C. Moya and J. Palomar, J. Chem. Theory Comput., 2015, 11, 4220–4225; (b) J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
36. A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
37. (a) R. F. W. Bader, Atoms in Molecules – A Quantum Theory, Oxford University, London, 1994; (b) R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323.
38. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
39. F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138.
40. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592.
41. (a) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926; (b) A. Shahi and E. Arunan, Phys. Chem. Chem. Phys., 2014, 16, 22935–22952; (c) M. Jablonski and M. Palusiak, J. Phys. Chem. A, 2012, 116, 2322–2332.
42. (a) R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322; (b) B. S. Brunschwig and N. Sutin, Coord. Chem. Rev., 1999, 187, 233–254.
43. (a) J. M. Saveant, Acc. Chem. Res., 1993, 26, 455–461; (b) A. Cardinale, A. A. Isse, A. Gennaro, M. Robert and J. M. Saveant, J. Am. Chem. Soc., 2002, 124, 13533–13539; (c) S. V. Rosokha and M. K. Vinakos, Phys. Chem. Chem. Phys., 2014, 16, 1809–1813.
44. (a) S. Scheiner and J. Lu, Chem. – Eur. J., 2018, 24, 8167–8177; (b) Y. Segawa, Y. Suzuki, M. Yamashita and K. Nozaki, J. Am. Chem. Soc., 2008, 130, 16069–16079; (c) N. Castillo and R. J. Boyd, J. Chem. Theory Comput., 2006, 2, 271–280.
45. L. Maugeri, J. Asencio-Hernandez, T. Lebl, D. B. Cordes, A. M. Z. Slawin, M. A. Delsuc and D. Philp, Chem. Sci., 2016, 7, 6422–6428.
46. L. Li, C. Li, Z. Zhang and E. Alexov, J. Chem. Theory Comput., 2013, 9, 2126–2136.
47. (a) B. Nepal and S. Scheiner, Chem. – Eur. J., 2015, 21, 13330–13335; (b) A. Brown and P. D. Beer, Chem. Commun., 2016, 52, 8645–8658.
48. (a) I. Alkorta, I. Mata, E. Molins and E. Espinosa, Chem. – Eur. J., 2016, 22, 9226–9234; (b) S. M. Chalanchi, I. Alkorta, J. Elguero and D. Quinonero, ChemPhysChem, 2017, 18, 3462–3468.
49. Calculated using the Coulomb formula with charge-center distance of about 9.16 Å and 9.95 Å for the corresponding anion–anion and cation–cation complexes respectively, the previous reported scheme by Quiñonero et al.²² was applied to take the middle of the C–NH₃⁺ bond as the positive charge center while the middle of the C–CO₂⁻ bond as the negative center.
50. (a) Y. Lu, H. Li, X. Zhu, W. Zhu and H. Liu, J. Phys. Chem. A, 2011, 115, 4467–4475; (b) M. Hennemann, J. S. Murray, P. Politzer, K. E. Riley and T. Clark, J. Mol. Model., 2012, 18, 2461–2469.
51. (a) A. J. Stone, J. Am. Chem. Soc., 2013, 135, 7005–7009; (b) A. El Kerdawy, J. S. Murray, P. Politzer, P. Bleiziffer, A. Heßelmann, A. Görling and T. Clark, J. Chem. Theory Comput., 2013, 9, 2264–2275; (c) R. Sedlak, M. H. Kolar and P. Hobza, J. Chem. Theory Comput., 2015, 11, 4727–4732.
52. (a) S. M. Walter, F. Kniep, L. Rout, F. P. Schmidtchen, E. Herdtweck and S. M. Huber, J. Am. Chem. Soc., 2012, 134, 8507–8512; (b) M. Domagala, A. Lutynska and M. Palusiak, J. Phys. Chem. A, 2018, 122, 5484–5492; (c) O. Donoso-Tauda, P. Jaque, J. Elguero and I. Alkorta, J. Phys. Chem. A, 2014, 118, 9552–9560.
53. (a) K. J. Donald, B. K. Wittmaack and C. Crigger, J. Phys. Chem. A, 2010, 114, 7213–7222; (b) D. J. R. Duarte, G. L. Sosa, N. M. Peruchena and I. Alkorta, Phys. Chem. Chem. Phys., 2016, 18, 7300–7309.
54. K. E. Riley and P. Hobza, Phys. Chem. Chem. Phys., 2013, 15, 17742–17751.
55. (a) K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2008, 4, 232–242; (b) M. Kolar, J. Hostas and P. Hobza, Phys. Chem. Chem. Phys., 2014, 16, 9987–9996.
56. Z. Q. Chen, G. M. Wang, Z. J. Xu, J. A. Wang, Y. Q. Yu, T. T. Cai, Q. Shao, J. Y. Shi and W. L. Zhu, J. Phys. Chem. B, 2016, 120, 8784–8793.
57. D. Shen, P. Su and W. Wu, Phys. Chem. Chem. Phys., 2018, 20, 26126–26139.
58. (a) J.-W. Zou, Y.-J. Jiang, M. Guo, G.-X. Hu, B. Zhang, H.-C. Liu and Q.-S. Yu, Chem. – Eur. J., 2005, 11, 740–751; (b) C. Wang, D. Danovich, Y. Mo and S. Shaik, J. Chem. Theory Comput., 2014, 10, 3726–3737; (c) J. Thirman, E. Engelage, S. M. Huber and M. Head-Gordon, Phys. Chem. Chem. Phys., 2018, 20, 905–915.
59. C. C. Robertson, J. S. Wright, E. J. Carrington, R. N. Perutz, C. A. Hunter and L. Brammer, Chem. Sci., 2017, 8, 5392–5398.
60. Project No. 2016-001-2-300, Chem. Int., 2016, 38, 22–24,  DOI:10.1515/ci-2016-0617.
61. (a) S. Scheiner, Acc. Chem. Res., 2013, 46, 280–288; (b) A. Lange, M. Gunther, F. M. Buttner, M. O. Zimmermann, J. Heidrich, S. Hennig, S. Zahn, C. Schall, A. Sievers-Engler, F. Ansideri, P. Koch, M. Laemmerhofer, T. Stehle, S. A. Laufer and F. M. Boeckler, J. Am. Chem. Soc., 2015, 137, 14640–14652; (c) V. R. Mundlapati, D. K. Sahoo, S. Bhaumik, S. Jena, A. Chandrakar and H. S. Biswal, Angew. Chem., Int. Ed., 2018, 57, 16496–16500.

---

Footnotes

† Electronic supplementary information (ESI) available: Computational details; Fig. S1–S20 and Tables S1–S29 and discussions; Cartesian coordinates of all optimized geometries. See DOI: 10.1039/c9cp01379b

‡ Z. Z. and G. W. contributed equally to this work.

---