Molecular-scale thermally activated fractures in methane hydrates: a molecular dynamics study

Abstract

We perform multiple large molecular dynamics simulations to study the fracture behaviour of monocrystalline methane hydrates under tension. We examine the fracture initiation phase and find that the fracture process can be divided into two phases: slow crack growth and rapid crack propagation. The time of the slow crack growth phase can be predicted by a thermal activation model [L. Vanel et al., J. Phys. D: Appl. Phys., 2009, 42, 214007] where an energy barrier has to be overcome in order for the crack to propagate. Our simulations predict that the slow growth phase vanishes when the stress intensity factor approaches .

---

Introduction

Clathrates are substances consisting of a lattice trapping-enclathrating-molecules. Gas hydrates are realizations of clathrates where the lattice is made up of water molecules and the enclathrated molecules would be gaseous under standard atmospheric conditions. The most common gas hydrate is the methane hydrate. Methane hydrates form out of an aqueous methane solution at moderate pressure and low temperature conditions.¹ They are common in marine sediments on continental margins and in the arctic tundra, where these conditions are prevalent.²

Hydrates make up an important, sometimes essential, part of the mechanical and failure properties of hydrate bearing sediments.³ In particular, hydrates make their surrounding sediments sensitive to pressure and temperature changes that may result either from geological driving forces, such as climate change or resource exploitation. Producing natural gas from methane hydrates is inherently different from producing from a conventional reservoir with a porous matrix, since the process destroys solid material. This destruction of the sediment itself has mechanical consequences, and it is therefore crucial to establish the strength of hydrate-bearing sediments under changing thermodynamic conditions.

Methane is frequently found to seep out of reservoirs below the seafloor.⁴ Under the right thermodynamic circumstances, this leads to hydrate crusted methane bubbles rising in the water column. These bubbles may persist for longer periods of time, even though they are thermodynamically unstable, because the initial creation of a hydrate shell shuts of the methane supply, hindering further growth.⁵ Such bubbles show clearly visible crack-like damage as they move in the water column both in nature⁴ and in controlled experiment.⁶ These cracks have been hypothesized to play an important role in bubble gas exchange. The mechanical response of hydrate crusted bubbles at rest has been studied more in detail experimentally,⁷ but it remains difficult to obtain accurate data, and the detailed mechanisms on the molecular level remain experimentally unavailable.

Beyond Earth, hydrates have been suggested to be of importance to ice shell thickness of Jupiter's moon Europa,⁸ since the lower thermal conductivity of clathrates⁹ would isolate the heat generated by tidal flexing more efficiently than pure water ice. The presence of methane hydrates have been inferred on Europa based on reflectance spectra.¹⁰ Estimates of seismic activity on Europa have been made, based on tidal cracking of the ice shell,¹¹ and these estimates would have to be adjusted if it turns out that Europa's icy shell contains a significant proportion of clathrates.

All of these phenomena rely on the mechanical and failure properties of methane hydrates. Due to the high water content and hydrogen-bonded nature of clathrates, one could expect the mechanical properties to be similar to those of ice. However, experiments have shown that methane hydrates are more than an order of magnitude more creep resistant than ice.¹² Therefore, fundamental micro-mechanical properties of methane hydrates have to be established specifically. Micro-mechanical properties of pure methane hydrates are largely unknown because measuring the failure properties of methane hydrates experimentally is hard.¹³

Molecular dynamics simulations can provide important complementary information to the problem, suggest mechanisms, and shed light on the following rather simple question: What is the behaviour of small cracks in methane hydrates when they are close to mechanical failure conditions?

Previous molecular-scale modeling studies of the mechanical properties of hydrates have explained the strain hardening of polycrystalline systems¹⁴ and the mechanical and tensile failure of perfect monocrystalline crystal lattices.^15–17 However, the failure of monocrystalline hydrates with preexisting flaws have not been studied. This is the fracture mechanics way: using an imperfect sample to account for the way materials actually fail, through the growth of existing impurities. A notch impurity may for instance form at the triple junction between two hydrate monocrystals and a mineral surface.¹⁸

In this paper, we describe the fracture initiation process in crystalline methane hydrates from direct molecular dynamics simulations of samples with a penny-shaped crack. We find that the failure initiation can be divided into two phases: slow crack growth and rapid crack propagation, and that the slow phase can be explained as thermally activated brittle fracture. The waiting time associated with this slow phase follows a simple Arrhenius-based functional relationship¹⁹ incorporating the stress and the temperature of the hydrate. The range of stresses that result in a thermally activated fracture is wide enough for failure to happen at stresses well below the nominal fracture toughness.

Simulations

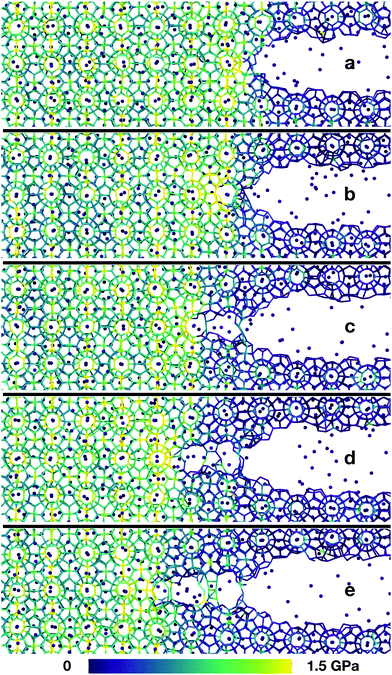
To study the failure of monocrystalline methane hydrates, we performed large-scale molecular dynamics simulations of the fracture initiation in flawed hydrate single crystals. We prepared an unstrained cubic sample with L = 29 nm of structure I methane hydrate at full occupancy and introduced a controlled flaw in the hydrate cube. This flaw was an 8 nm wide oblate ellipsoidal cavity at the centre of the sample. The system was equilibrated at a designated temperature, and then gradually subjected to uniaxial strain normal to the major plane of the ellipsoidal cavity to induce mechanical failure. The simulation setup is shown in Fig. 1.

Fig. 1 Modeled system (a) and close-up of the crack (b). (a) is the system cut in half to show the crack. (c) Tensile stress through time in several simulations at 280 K. The stress decreases after applying strain, and the plot shows that the stress decrease can be divided into a slow phase and a rapid phase. Furthermore, high strains lead to high stresses and a short slow phase, whereas lower strains lead to lower stresses and longer slow phases of the crack development. The light gray markers indicate the point of largest stress, and the dark grey markers indicate the measured corresponding waiting time for fracture. Colors of the curves indicate the strain applied to the system during the loading phase.

When the uniaxial strain reaches a sufficient level, the sample fails by fracturing. Snapshots from a typical crack propagation event are shown in Fig. 2. The crack evolves by opening subsequent hydrate cages, and all material destruction happens in the failure plane, that is with no dislocations away from the crack, thus the hydrate behaves brittle under our simulation conditions.

Fig. 2 Molecular mechanism during fracture along the (001) plane. First, a small cage opens (a), then a large one (b). In (c) we see how the stress concentrates on a half-cage when a large cage is open on one side, but not yet broken on the other side. Panels (d) and (e) show that this process continues, and that the cages open sequentially. There are no dislocations forming far from the crack tip, and there is no reformation of the hydrate after a cage has opened. The colors indicate the virial stress in the direction of the applied tension, averaged over 1 ps. The snapshots are taken from a simulation at 280 K with a maximum strain level of 5.7%. The stress peak moves as the crack propagates.

Quantification–scaling relation

To systematically determine the effect of the temperature and the strain on the fracture initiation, we performed multiple simulations with temperatures ranging from 120 K to 325 K and strains from 4.9% to 7.3%. The choice of the strain level is particular to the geometry of the system; the combination of the system size and crack length were chosen in order to give a stress intensity that allows us to study the fracture initiation phase on the timescales of molecular dynamics simulations. The general trend from this series of simulations is that warm and highly strained samples fail immediately, or even before the strain has reached its final value, and that cold samples subjected to a low strain do not fail at all during the simulation. For samples at an intermediate stress level, however, the crack development can be separated into two distinct phases: slow crack growth and rapid crack propagation. This shows up in the time-evolution of the tensile stress in the system after straining (Fig. 1c). A relatively long phase of slow crack evolution can be seen from the slowly decreasing tensile stress. Then, a relatively short period of fast crack propagation can be seen from a sudden and rapid stress decrease. At some point, the crack spans a whole plane of the simulation box, at which point the sample has been divided into two parts and vibrates such that the measured tensile stress fluctuates around zero. Furthermore, the crack growth during the slow crack evolution looks irreversible in all of our simulations – the crack area is growing monotonously.

To quantify this behaviour, we measure the waiting time, t_w, from the conclusion of the ramp up of strain until a critical crack has developed. Because the slow crack evolution phase is the relatively longer period, we define t_w as the time it takes for the tensile stress along the axis of applied strain to be reduced from its maximum level (typically when straining stops) to half of that maximum value. Whether we choose half of the maximum stress level or a different fraction is unimportant, since the fast stress drop associated with rapid fracture is much more abrupt than the slow stress drop associated with slow cracks. The measured waiting times as a function of the applied stress for different temperatures are shown in Fig. 3a. It shows that the waiting time decreases with maximum stress for a given temperature. Also, the waiting time decreases with increasing temperature for a given stress. Interestingly, we see that over the relatively short range of waiting times that are accessible when doing many large-scale simulations, the maximum stresses vary by almost a factor of two.

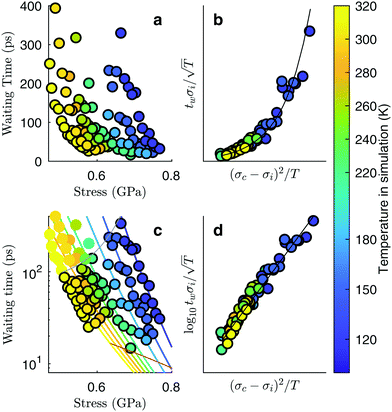Fig. 3 Slow cracks follow the equation of thermally activated brittle fracture. Simulations at different temperatures according to the colour bar. (a) Waiting time from maximum stress to the stress has fallen to half of that maximum value, as measured in Fig. 1c, but with more data points. (b) Data collapses onto a common scaling function. (c) Data points plotted together with the fitted functional relationship. The validity range of the local elastic barrier model is the region between the gray lines, and points within this range are drawn with a black border. The region below the lower line is the region where the energy requirement does not hold, and the region above the upper line is the region where the initial crack length requirement does not hold. Only points within the validity range are included in the subsequent fitting of the data to the model. (d) A linear data collapse on a logarithmic y-axis shows that the scaling function is an exponential function.

To obtain the functional relationship between the waiting time, the maximum stress level and the temperature, we try to explain our data by a thermal activation model. This means we expect a process supporting crack growth to operate at a rate given by Arrhenius' equation: k ∝ e^ΔU/k_BT, with ΔU an energy barrier, T the system temperature and k_B the Boltzmann constant. For crack propagation, the relevant energy barrier is the energy difference between the system at its actual stress level and the system at its nominal critical stress level. A detailed calculation of such a waiting time, assuming irreversible fracture propagation that has to overcome a local elastic barrier leads to the following model:¹⁹

where l_i is the initial crack length, σ_i the initial stress near the crack tip, σ_c the critical (failure) stress level near the crack tip, v₀ a characteristic propagation velocity, Y the Young's modulus, T the system temperature, k_B the Boltzmann constant and V an activation volume. This equation is valid when the energy barrier is sufficiently big compared to the temperature, (σ_c − σ_i)²V ≫ 2Yk_BT and when the initial crack length is close to the crack length at which the system would fail immediately, that is the critical crack length, l(σ_c) ∼ l(σ_i). We indicate in Fig. 3c what points fulfill these conditions with and . The stresses σ_c and σ_i are stresses over the activation volume.

The values of the parameters of eqn (2) translated to the present study are as follows: the initial crack length is a the width of the initial flaw we introduce, l_i = 8 nm. Youngs modulus for the force field we use has been reported to vary between 9.71 GPa at 283.15 K to 7.68 GPa at 200 K.¹⁴ For simplicity in the scaling analysis, we choose to regard the Young's modulus as constant, Y = 9 GPa, since the temperature variation is a second order effect. V and v₀ are model parameters that will be determined by the subsequent scaling analysis.

The activation energy, ΔU, can also be written in terms of the stress intensity factor, and therefore in terms of the faraway stress (in our case the stress over the simulation cell) and the crack length:

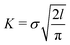where λ is the cut-off length of stress divergence due to the discrete nature of matter on atomic scales. The rightmost expression above assumes the stress intensity factor of the penny-shaped crack under tension on an infinite domain, (see e.g. Anderson²⁰). This form of the activation energy resolves an apparent unphysical property of eqn (2), namely that the waiting time seems to be proportional to the initial crack length. Using the latter form of the activation energy, we see that an increase in the initial crack length results in a smaller energy barrier.

We choose λ = 3 Å because this is approximately the distance between water molecules in hydrates and thus the cut-off distance of the hydrogen-bonding. We then insert in the scaling analysis, and try to choose an appropriate value for our only fitting parameter, , in order to make the data collapse onto a common scaling function. If such a common scaling function is consistent with eqn (2), we may calculate the characteristic propagation velocity v₀ and the activation volume V from the parameters obtained when fitting the data to eqn (2).

We find that the data collapse onto a common scaling function for σ_c = 4.7 GPa on the axes shown in Fig. 3b. Note that this value is much larger than the stresses measured over the simulation box (Fig. 3a and c). This is due to stress concentration. The simulation cell stress corresponding to this number is σ = 1.15 GPa, giving an estimate of which stress level would make the waiting time vanish in the local elastic barrier model for a methane hydrate with an 8 nm penny-shaped crack. We may also express this in terms of the stress intensity factor, which gives us an upper limit of the fracture toughness: 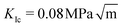for this molecular hydrate model. This value is close to the experimentally reported fracture toughness of water ice, which typically comes out around 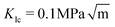.^21,22 The data collapse indicates that we have chosen the right governing parameters, and the linearity of the collapsed data on logarithmic axes (Fig. 3d) shows that the data is consistent with an exponential functional form.

Even though the functional form of the waiting time is an exponential function, the variance of the data compared to the fit line is lower that one would expect from an exponential distribution. This indicates that the failure of the system is the result of several successive bond opening events, rather than a single activation event. This is in line with the assumptions of the local elastic barrier model: The crack is assumed to maintain a slow propagation velocity v for some time. Our simulations therefore provide an estimate for the relation between stress, σ_i, temperature, T, and the time until failure, t_w:

with and .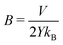

The data collapse allows us to extract parameters to be used to compare the effect of thermally activated cracks to other mechanisms of failure and deformation. By fitting the collapsed data to eqn (4) we find and 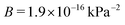. Since the model formula includes both the length of the initial cavity and the critical stress level, these parameters should hold when changing the system size, allowing for the prediction of thermal activation times of larger hydrate systems. We can also estimate the values of v₀ and V. By rearranging the expressions for A and B, we find that V^1/3 = 3.6 Å, which is consistent with the thermal activation process happening on the scale of hydrate cages and hydrogen bonds. We also find the characteristic propagation velocity v₀ = 6.3 km s⁻¹. Since this value is on the same order of magnitude as the sound velocity in the material, it suggests an attempt rate on the order of the natural oscillation frequency of the crystal lattice.

Simulation details

We performed a series of simulation using the mW water potential combined with a united atom methane model.²³ All simulations were performed using LAMMPS.²⁴ The equations of motion were integrated using the Velocity Verlet scheme with a timestep of 10 fs. We performed simulations using the following procedure: a methane hydrate in the sI structure at full occupancy was initialized. Atoms were then deleted in the cavity region, which was an oblate ellipsoid with a major plane of diameter 8 nm parallel to the (001) crystal plane, and a height of 1.2 nm. Mathematically, this cavity can be represented as with a = 4 nm, c = 0.6 nm and (x₀, y₀, z₀) being the geometrical center of the simulated system. Particle velocities were set to the Boltzmann distribution at 1.8T with T the wanted system temperature, since approximately half of the kinetic energy will move to the potential degrees of freedom during equilibration. The system was then allowed to equilibrate during 20 ps subjected to a Nosé–Hoover thermo-barostat (NPT) at P = 10 MPa with time constants of 2 ps. This equilibration was performed to allow the hydrate to assume its preferred shape at the temperature of that simulation. After equilibration, the barostat was turned off, while the thermo-couple was kept on, but with the simulation box expanding in the z direction to induce a prescribed strain level on the hydrate sample during 100 ps. Expansion was turned off upon arrival at the prescribed strain level, and the simulation was then continued at constant volume with the thermo-couple still on. To reach strains of 4.9–7.3% in 100 ps, we applied a strain rate of 4.9–7.3 × 10⁸ s⁻¹. We chose to use a high strain rate to get the system quickly to a strained state without allowing the crack to start propagating before the prescribed strain level was reached. At the same time, the strain rate was chosen sufficiently low to prevent oscillations of the whole system. The stress–strain curves of Fig. 1c show that there are no significant stress oscillations in the bulk, and the upward slope of the stress–strain curve is much steeper just before expansion is turned off than just after, showing that the loading phase and the waiting phase do not interfere significantly. For further details, see LAMMPS input scripts and thermodynamic output data from the simulations.†

Discussion

We have shown simulations indicating that the mechanical failure of a methane hydrate crystal can happen at loads well below the nominal fracture toughness of the hydrate, and thermally activated fracture leads to catastrophic failure of a sample under high stress. Furthermore, the duration of the slow thermal initiation phase before rapid fracture obeys consistently and accurately a simple functional relationship. From visual inspection of the simulations, we could have anticipated this because we see that the structure decomposes cage by cage in an irreversible manner as seen in Fig. 2.

Due to the limited spatial range of molecular dynamics simulations, sizes are small, timescales short and the stresses high in this study. This does not mean that the stresses must be this high to observe the effects of thermal activation in a laboratory setting, where the stresses are on the order of MPa or tens of MPa.²⁵ The relevant parameter for observing this effect is stress intensity, i.e. the stress near the crack tip. Stress intensity goes like 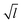, where l is the size of flaws in the material subjected to stress. Extrapolating with this formula yields that materials with flaws of for instance 1 μm will reach the same stress intensity as our simulations at a stress of around 20 MPa, which is a relevant stress in a natural hydrate setting. For instance, the dissociation of hydrates itself can increase the pore pressure by tens of megapascals in tight sediments.²⁶ Increasing the flaw size and reducing the stress level within the validity range of the local elastic barrier model should lead to longer waiting times, and in the above-mentioned extrapolation scenario, the waiting time would translate to around 0.1 μs. When the timescale increases, the effect of dissociation may become important, so one should for instance consider whether dissociation of the hydrate could interfere with the crack propagation, either by promoting crack growth or by blunting the crack.

Further progress in understanding hydrates in nature from a microscopical scale depends on also studying shear properties of hydrates, both in monocrystalline, bi-crystalline and polycrystalline systems. Shear is fundamentally different from tension, since it allows for inducing mechanical failure without changing the confining pressure, and thus failure of the hydrate can be studied without worrying about going outside the stability thermodynamic conditions of the hydrate. Shear also allows for a thorough study of grain boundary sliding properties of hydrate interfaces. That could be pure hydrate–hydrate interfaces with some crystal mismatch to create a grain boundary, or interfaces that combine hydrates with other substances such as minerals, water and water ice, which are coexisting with hydrates in natural reservoirs.³

Finally, we want to stress the fracture mechanics approach. Stresses concentrate around preexisting weaknesses, leading to materials becoming much weaker than one would expect from the strength of atomic bonds. Therefore, when possible, strengths should be reported in fracture toughness rather than fracture stress. This is of course not always viable, for instance when the size of preexisting cracks is unknown. But from a fracture mechanics point of view, it is unsurprising that the strength of hydrates is reported to be relatively weak in experiments,²⁵ stronger in molecular dynamics simulations,¹⁴ and even stronger in DFT simulations.²⁷

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Research Council of Norway, FRINATEK, grant number 231621. Some of the simulations were performed using computer resources provided by Notur, project number NN9272K.

References

1. E. D. Sloan, Nature, 2003, 426, 353–363.
2. C. D. Ruppel and J. D. Kessler, Rev. Geophys., 2017, 55, 126–168.
3. W. F. Waite, J. C. Santamarina, D. D. Cortes, B. Dugan, D. N. Espinoza, J. Germaine, J. Jang, J. W. Jung, T. J. Kneafsey, H. Shin, K. Soga, W. J. Winters and T.-S. Yun, Rev. Geophys., 2009, 47, RG4003.
4. B. Wang, S. A. Socolofsky, J. A. Breier and J. S. Seewald, J. Geophys. Res.: Oceans, 2016, 2203–2230.
5. X. Fu, L. Cueto-Felgueroso and R. Juanes, Phys. Rev. Lett., 2018, 120, 144501.
6. R. P. Warzinski, R. Lynn, I. Haljasmaa, I. Leifer, F. Shaffer, B. J. Anderson and J. S. Levine, Geophys. Res. Lett., 2014, 41, 6841–6847.
7. S. L. Li, C. Y. Sun, G. J. Chen, Z. Y. Li, Q. L. Ma, L. Y. Yang and A. K. Sum, Chem. Eng. Sci., 2014, 116, 109–117.
8. K. P. Hand, C. F. Chyba, R. W. Carlson and J. F. Cooper, Astrobiology, 2006, 6, 463–482.
9. E. D. Sloan and C. A. Koh, Clathrate hydrates of natural gases, CRC Press, 2007.
10. V. V. Busarev, A. M. Tatarnikov and M. A. Burlak, Sol. Syst. Res., 2018, 52, 301–311.
11. M. P. Panning, S. C. Stähler, H. H. Huang, S. D. Vance, S. Kedar, V. C. Tsai, W. T. Pike and R. D. Lorenz, J. Geophys. Res.: Planets, 2018, 123, 163–179.
12. W. B. Durham, S. H. Kirby, L. A. Stern and W. Zhang, J. Geophys. Res.: Solid Earth, 2003, 108, 2182.
13. F. Ning, Y. Yu, S. Kjelstrup, T. J. H. Vlugt and K. Glavatskiy, Energy Environ. Sci., 2012, 5, 6779.
14. J. Wu, F. Ning, T. T. Trinh, S. Kjelstrup, T. J. H. Vlugt, J. He, B. H. Skallerud and Z. Zhang, Nat. Commun., 2015, 6, 8743.
15. P. Cao, J. Wu, Z. Zhang, B. Fang and F. Ning, J. Phys. Chem. C, 2018, 122, 29081–29093.
16. J. Jia, Y. Liang, T. Tsuji, S. Murata and T. Matsuoka, Sci. Rep., 2017, 7, 1–11.
17. J. Jia, Y. Liang, T. Tsuji, S. Murata and T. Matsuoka, Sci. Rep., 2016, 6, 23548.
18. M. Chaouachi, A. Falenty, K. Sell, F. Enzmann, M. Kersten, D. Haberthür and W. F. Kuhs, Geochem., Geophys., Geosyst., 2015, 16, 1711–1722.
19. L. Vanel, S. Ciliberto, P.-P. Cortet and S. Santucci, J. Phys. D: Appl. Phys., 2009, 42, 214007.
20. T. L. Anderson, Fracture Mechanics: Fundamentals and Applications, 3rd edn, 2005, p. 640.
21. H. W. Liu and K. J. Miller, J. Glaciol., 1979, 22, 135–143.
22. P. P. Benham, R. J. Crawford and C. G. Armstrong, Mechanics of engineering materials, Longman, Harlow, 1996.
23. L. C. Jacobson and V. Molinero, J. Phys. Chem. B, 2010, 114, 7302–7311.
24. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
25. J. W. Jung and J. C. Santamarina, Geochem., Geophys., Geosyst., 2011, 12, Q08003.
26. W. Xu and L. N. Germanovich, J. Geophys. Res., 2006, 111, B01104.
27. T. M. Vlasic, P. Servio and A. D. Rey, AIP Adv., 2016, 6, 085317.

---

Footnote

† Data set available from Zenodo, http://doi.org/10.5281/zenodo.3229900

---