London dispersion effects in the coordination and activation of alkanes in σ-complexes: a local energy decomposition study

Abstract

Local energy decomposition (LED) analysis decomposes the interaction energy between two fragments calculated at the domain-based local pair natural orbital CCSD(T) (DLPNO-CCSD(T)) level of theory into a number of chemically meaningful contributions. Herein, this scheme is applied to the interaction between the transition metal (TM) and the alkane in σ-complexes. It is demonstrated that the often-neglected London dispersion (LD) energy is a fundamental component of the TM–alkane interaction for a wide range of experimentally characterized σ-complexes. LD effects determine the structure and the thermodynamic stability of σ-complexes and influence the selectivity of CH activation reactions. The magnitude of the LD energy can be modulated by increasing the size of the alkane and of the ancillary ligands on the TM. These results provide further evidence on the fundamental role that London dispersion plays in organometallic chemistry.

---

1 Introduction

The London dispersion (LD) energy constitutes the attractive part of the van der Waals potential and it is omnipresent in chemistry. In the Symmetry Adapted Perturbation Theory (SAPT) framework,² the leading dipole–dipole term of the LD energy grows with the polarizabilities of the interacting fragments and decays asymptotically as R⁻⁶, with R being the interfragment distance.³ Hence, as the molecular system size increases, the magnitude of the LD energy increases, often making it stronger than covalent or electrostatic interactions.⁴ Due to its size dependence, LD is responsible for the stability of seemingly too crowded molecules, such as diamantyl,⁵ all-meta ^tBu-triphenylmethane,⁶ and all-meta ^tBu-hexaphenylethane dimers.⁷ Moreover, its importance has been widely recognized in biochemistry,⁸ material science,⁹ and organic chemistry.¹⁰

On the other hand, LD is typically considered weaker than covalent or other non-covalent interactions, especially for small systems.¹¹ In particular, although recent studies have underlined its importance in organometallic chemistry,^4,10,12–22 its contribution to coordinate covalent bonds is still often ignored or assumed to be negligible. In fact, the interaction between a transition metal (TM) and a ligand (L) is still often described as a simple donor–acceptor interaction and the structure, the catalytic behaviour and the spectroscopic properties of TM complexes are in most cases discussed using orbital models such as the popular Dewar–Chatt–Duncanson (DCD) bonding model.^23,24

Despite the success of these simple interpretative frameworks, a unified understanding of intermolecular interactions in the various fields of chemical research would require models that explicitly include LD as one of the components of the chemical bond, irrespective of the intermolecular distance or of the interaction strength. Unfortunately, rigorous perturbative approaches like SAPT are not applicable to strong TM–L interactions.

More in general, the LD energy, as well as all the other physical components of the interaction typically discussed in chemical models, is not a quantum mechanical observable. Hence, its theoretical definition is ambiguous, especially when the interacting fragments are close to each other and their electron density significantly overlap.³

Another major problem is that the computational modeling of organometallic complexes requires the accurate inclusion of electron correlation for systems with many electrons and complicated electronic structures. The most commonly used computational methodology to practically address this problem is Density Functional Theory (DFT). Although it is well-known that DFT does not properly describe LD forces,²⁵ several strategies have been suggested to deal with this shortcoming,^26,27 thus allowing the calculation of accurate structures and energies for organometallic complexes. In particular, a force-field like correction term (the -D correction) is typically added to the DFT energy to account for long-range LD effects, which are not or poorly described by the exchange–correlation functional. Hence, the magnitude of the -D correction can be used as a qualitative estimate for the LD energy, albeit with caution in those cases when short- to mid-range LD effects are important.¹³

Recently,^28–30 we proposed a new strategy called Local Energy Decomposition (LED) analysis, which provides a decomposition of interaction energies computed at the domain-based local pair natural orbital coupled cluster DLPNO-CCSD(T)^31–33 level into various terms representing the most important chemical components of the interaction. This scheme allows for a simple definition of the LD energy at the DLPNO-CCSD(T) level^29,34,35 and has been already applied in a wide range of different chemical situations.³⁶ Importantly, the LED analysis can be applied for obtaining a consistent quantification of the LD energy for virtually any system within the range of applicability of DLPNO-CCSD(T) scheme, going from weak noncovalent interactions²⁹ to strong ionic and covalent bonds.^13,34,37

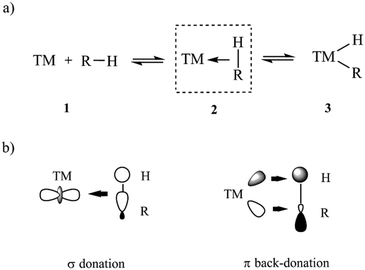
Herein, the DLPNO-CCSD(T)/LED approach is used to quantify the LD component of TM–L bonds of various strength and to elucidate the factors that contribute to its magnitude in organometallic complexes. As a case study, we consider the bond between the TM and the CH bond of an alkane in σ-complexes. These complexes have been suggested as crucial intermediates for alkane C–H activation reactions,^38–44 which are of paramount importance in various chemical industries. In particular, the development of chemical processes for the conversion of alkanes from fossil sources to more-valuable compounds has attracted great attention over past decades.^44–48 In the simplest mechanistic scenario, the CH bond initially coordinates to the TM to form a σ-complex (intermediate 2 in Scheme 1a), eventually leading to the cleavage of the CH bond through oxidative addition to the TM.

Scheme 1 (a) Oxidative addition of an alkane to a TM. R denotes an alkyl group. (b) Simple orbital representation describing the donor acceptor interaction between the R–H bond and the TM in alkane σ-complexes.

The chemical bond between the TM and the CH bond in σ-complexes is typically described as a donor–acceptor in the framework of the DCD model (Scheme 1b). In this model, the C–H group formally donates electrons from its filled σ orbital to the metal center (TM ← HC σ-donation) while at the same time the TM back-donates d electrons into the empty C–H σ* orbital in the alkane (TM → HC π-backdonation).^49–51 This model can be considered as an extension of the three-center two-electron (3c-2e) model initially adopted by Brookhart⁵² and later corroborated by energy decomposition schemes at the density functional theory (DFT) level of theory.^42,53 Both σ-donation and π-backdonation are expected to decrease the CH bond order, thus favoring the oxidative addition to the TM.⁵⁴

Although alkane σ-complexes have been proposed for decades, their direct experimental characterization has constituted one of the major challenges for organometallic chemists.^54,55 The few experimental characterized σ-complexes can be grouped into three families, differing for the complex structure and their synthetic route. Herein, we base our analysis on a series of σ-complexes that includes representative systems of each class.

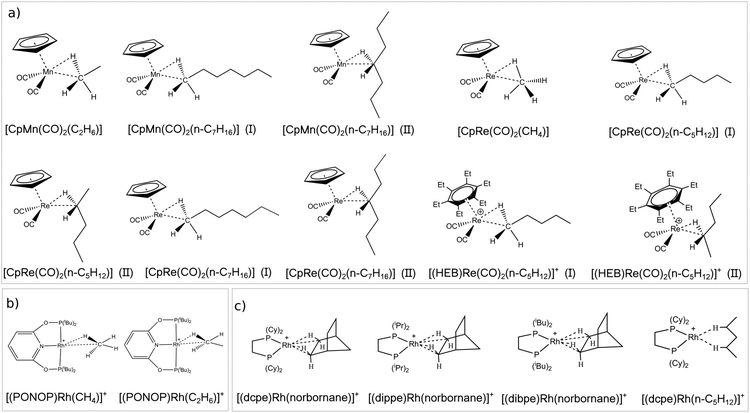
The first class of σ-complexes investigated herein is a series of group VII TM complexes that were previously characterized mainly by means of IR spectroscopy. Their structure is shown in Scheme 2a. The series includes neutral complexes differing for the size of the alkane such as [CpMn(CO)₂(alkane)] (alkane = C₂H₆, n-C₇H₁₆)^56–59 and [CpRe(CO)₂(alkane)] (alkane = CH₄, n-C₅H₁₂, n-C₇H₁₆)^56,57,60 as well as the positively charged [(HEB)Re(CO)₂(n-C₅H₁₂)]⁺ (HEB = hexaethylbenzene).⁶¹ Note that for the longer alkanes many conformers are possible, depending on their relative orientation with the TM. As case studies, two conformers are investigated for each complex, in which the TM interacts with a CH bond located on either the methyl or the methylene carbon. Conformers of the first type are denoted hereafter as “head-on” structures, whilst the latter are denoted as “side-on” structures.

Scheme 2 TM–alkane complexes investigated and nomenclature used in this work.

The second family of σ-complexes investigated herein is shown in Scheme 2b and includes two Rh complexes bearing the same tridentate ligand (PONOP = 2,6-(^tBu₂PO)₂C₅H₃N) but different alkanes [(PONOP)Rh(alkane)]⁺ (alkane = CH₄, C₂H₆). These complexes were characterized by means of NMR spectroscopy.^62,63

Finally, the last class includes Rh complexes of norbornane bearing different diphosphine ligands [(L)Rh(norbornane)]⁺ (L = dpce, dippe, dibpe) as well as the [(dcpe)Rh(n-C₅H₁₂)]⁺ complex. All these complexes were fully characterized by X-ray crystallography and solid state NMR.^49,64–66 Their structures are shown in Scheme 2c.

For all these complexes, the main factors contributing to their formation, the coordination preference of the alkane and the activation of the CH bond are discussed in the framework of the LED analysis and the role played by LD in all these situations is elucidated. Moreover, the factors that contribute to the magnitude of the LD energy are identified and designing principles for σ-complexes with tailored bonding features are given.

2 Method

Geometry optimizations were carried out using the TPSS functional⁶⁷ and including the -D3 dispersion correction term⁶⁸ with Becke–Johnson damping parameters.⁶⁹ The def2-TZVP basis set⁷⁰ was used. The def2-ECP effective core potential was used for Re and Rh atoms. Frequencies were calculated at the same level of theory to verify the nature of minima and transition states and to compute free energies. The optimized geometries and vibrational frequencies obtained with these computational settings were found to be in good agreement with available X-ray structures and IR data, as shown in Table S1 in the ESI.† Moreover, these settings were shown to provide geometries and IR frequencies in good agreement with experimental data for the closely related agostic complexes.¹²

Single point energies at the DLPNO-CCSD(T) level were computed using TightPNO settings.^31–33 The def2-TZVPP basis set was used in conjunction with the def2-TZVPP/C auxiliary basis set. Table S2 (ESI†) shows that the DLPNO-CCSD(T) results are at convergence with respect to the basis set size. The RIJCOSX approximation⁷¹ was used for the calculation of Coulomb and exchange integrals in the HF reference. The def2/J auxiliary basis set was used. The COSX grid was set to GridX5.

Binding energies (ΔE) at the DLPNO-CCSD(T) level were calculated as the electronic energy difference between the σ-complex and its constituting fragments (the alkane and the remaining metallic moiety) at their equilibrium TPSS-D3 geometry. The binding energies were decomposed into dispersive (E_disp) and non-dispersive (ΔE_no-disp) contributions by means of the LED technique.²⁸

The dominant term in E_disp is the DLPNO-CCSD contribution E^C-CCSD_disp, which was calculated by summing up all the instantaneous dipole–dipole excitations between the two fragments. It includes contributions from both strong and weak pairs, as detailed in ref. 29. For the sake of simplicity, an effective triples correction contribution to the LD energy was also included. It was estimated by multiplying the intermolecular component of the perturbative triples correction, i.e., the contribution coming from triples of occupied orbitals located on different fragments E^(X,Y)_C-(T),²⁸ by a correction factor γ. The γ correction was defined as the ratio between the dispersion contribution from the strong pairs and the total intermolecular strong pair contribution. Hence, the total LD energy reads:

E_disp = E^C-CCSD_disp + γE^(X,Y)_C-(T) (1)

For the systems studied in this work E^C-CCSD_disp amounts to about 90% of the overall E_disp contribution, as shown in Table S3 (ESI†).

The remaining part of the correlation contribution to the binding energy is denoted as ΔE^C-CCSD(T)_no-disp. The sum of this term with the overall HF contribution to the binding energy ΔE^HF gives the overall non-dispersive contribution to the binding energy, i.e., ΔE_no-disp.

In order to provide an in-depth analysis of the factors contributing to the LD energy, the Dispersion Interaction Density (DID) plot^29,72 were employed. They provide a useful spatial analysis of the LD energy and were calculated as detailed in ref. 29.

Finally, the orbital relaxation contribution to the binding energy was calculated as detailed in ref. 29. It provides a useful estimate for the charge transfer and polarization energy at the reference level of theory, consistent with that provided by standard energy decomposition schemes.⁷³

3 Results and discussion

3.1. The London dispersion component of the TM–CH₄ bond in [CpRe(CO)₂(CH₄)]

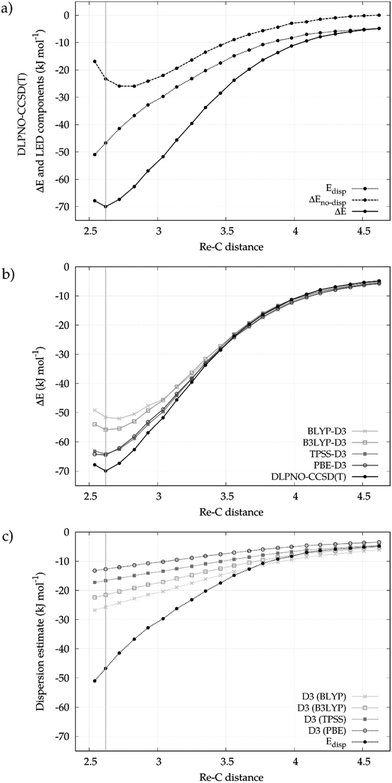
We first describe here a detailed investigation of the Re⋯CH bond in the [CpRe(CO)₂(CH₄)] complex. The analysis will be then extended to the whole series of σ-complexes shown in Scheme 2 in the next section.

The Re⋯CH₄ binding energy profile as a function of the Re⋯C distance calculated at the DLPNO-CCSD(T) level of theory is shown in the upper panel of Fig. 1. In the same panel, the decay of the LD energy (E_disp) and of the non-dispersive component of the binding energy (ΔE_no-disp) is also reported. As expected, the binding energy is dominated by LD forces in the long range where no significant charge transfer occurs between the fragments. As the fragments approach each other, the relative contribution of E_disp to the binding energy slightly decreases. At the equilibrium geometry, E_disp amounts to −46.7 kJ mol⁻¹, which is about the 67% of the overall binding energy (−69.8 kJ mol⁻¹). The remaining 33% comes from ΔE_no-disp. It describes the balance between the orbital relaxation energy at the HF level (−135.2 kJ mol⁻¹) and the other components of the interaction (+112.1 kJ mol⁻¹), such as permanent electrostatics, electronic preparation and the correlation correction for these terms ΔE^C-CCSD(T)_no-disp.²⁹ For the sake of simplicity, only E_disp and ΔE_no-disp will be discussed in the following. Additional information on the various terms of the decomposition can be found in the ESI.†

Fig. 1 (a) DLPNO-CCSD(T) binding energy decay with the Re⋯CH₄ distance in [CpRe(CO)₂(CH₄)]. Its decomposition into dispersive (E_disp) and non-dispersive (ΔE_no-disp) contributions is also shown. (b) Binding energy profiles with different computational methods. (c) Comparison of LED (E_disp) and -D3 estimate for the London dispersion. The vertical line marks the equilibrium geometry.

Although Re⋯CH₄ is a relatively weak coordination bond, the fact that the E_disp amounts to the 67% of the overall binding energy is surprising. These results are consistent with the ones recently¹² found in the context of agostic interactions, i.e. the intramolecular interaction between a C–H bond and a coordinatively unsaturated TM. It was found that short-range LD forces between the agostic C–H bond and the metal center are largely responsible for the stability of a wide range of agostic complexes, consistent with a large number of experimental findings, including the fact that many agostic complexes do not show evidence of significant C–H bond activation.⁷⁴

In order to compare different computational methodologies, the binding energy profile obtained with different functionals is compared with the DLPNO-CCSD(T) one in the central panel of Fig. 1. In the bottom panel of the same figure the decay of the -D3 correction for different functionals is compared with the E_disp values extracted from the LED scheme.

In the long range, all methods provide similar Re⋯CH₄ binding energies. At the equilibrium geometry, the difference between the various functionals increases, with binding energies being −51.6, −55.8, −64.2 and −64.5 kJ mol⁻¹ for BLYP-D3, B3LYP-D3, TPSS-D3 and PBE-D3, respectively. The corresponding -D3 correction follows the opposite trend, being −25.7, −21.6, −16.6 and −12.7 kJ mol⁻¹. The differences between the -D3 estimates are mostly due to the effect of the damping functions, as also recently discussed by Grimme et al.¹³ By comparing these figures with the E_disp value (−46.7 kJ mol⁻¹), one finds that the functionals that better reproduce the DLPNO-CCSD(T) binding energy (e.g. PBE) are those for which the -D3 correction is smaller and far from the accurate LED values. Hence, in the following only DLPNO-CCSD(T)/LED results will be discussed.

In summary our results clearly show that LD is fundamental for both the formation and the thermodynamic stability of [CpRe(CO)₂(CH₄)]. In fact, it dominates the TM–alkane interaction in the long range and significantly contributes to the magnitude of the binding energy at the equilibrium geometry.

3.2. London dispersion in σ-complexes

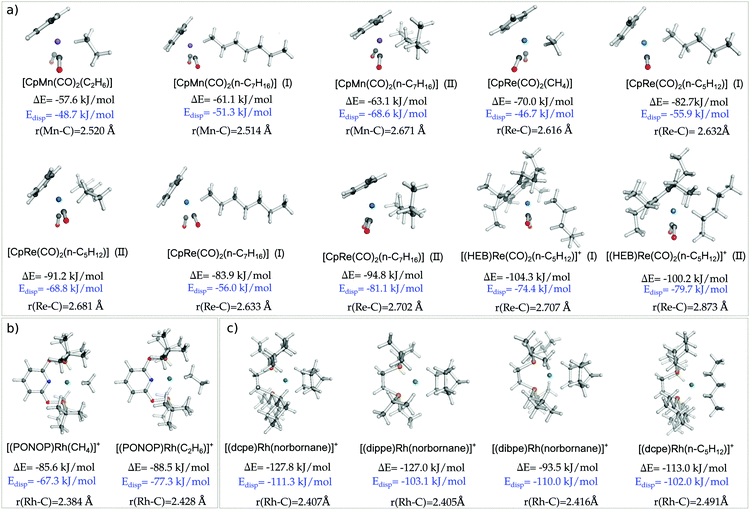
In order to test the generality of our findings for the Re⋯CH₄ interaction in [CpRe(CO)₂(CH₄)], geometries, binding energies and the corresponding LD contributions were calculated for the whole series of σ-complexes investigated in this work. The results obtained are summarized in Fig. 2. Note that, for the sake of simplicity, only electronic energies are discussed in this section, while the free energies at experimental conditions are reported in Table S4 (ESI†).

Fig. 2 Comparison of TM⋯alkane binding energies (ΔE) and the associated LD contribution (E_disp) for the systems investigated in this work. The distance between the TM and the closest carbon atom on the alkane r_(TM–C) is also reported.

Binding energies span a broad range of values, going from −57.6 to −127.8 kJ mol⁻¹ for [CpMn(CO)₂(C₂H₆)] and [(dcpe)Rh(norbornane)]⁺, respectively. Similarly, the LD energy ranges from −46.7 to −111.3 kJ mol⁻¹ for [CpRe(CO)₂(CH₄)] and [(dcpe)Rh(norbornane)]⁺, respectively.

Remarkably enough, E_disp amounts to at least the 67% of the binding energy for all complexes. For [CpMn(CO)₂(C₇H₆)] (II) and [(dibpe)Rh(norbornane)]⁺, its magnitude exceeds the binding energy. Hence, without this important component of the interaction, these experimentally characterized complexes would not be stable. These results are consistent with our previous findings on the agostic EtTiCl₃(dmpe) complex.¹²

Having established the fundamental importance of LD for the thermodynamic stability of σ-complexes, we aim at identifying the most important factors contributing to its magnitude in a view of aiding to the development of designing principle for stable TM–alkane adducts.

As mentioned in the introduction, LD increases with the polarizability of the interacting fragments and decreases with the intermolecular distance. Hence, the size of the ancillary ligands and of the alkane, the nature and the oxidation state of the TM, and the coordination mode of the alkane (i.e. whether it forms head-on or side-on structures) are all expected to contribute to its magnitude.

A revealing insight into this aspect comes from the analysis of the DID plots (Fig. 3), which provide a simple mean of visualizing the most important contacts contributing to the magnitude of the LD energy of the TM⋯alkane interaction.⁷²

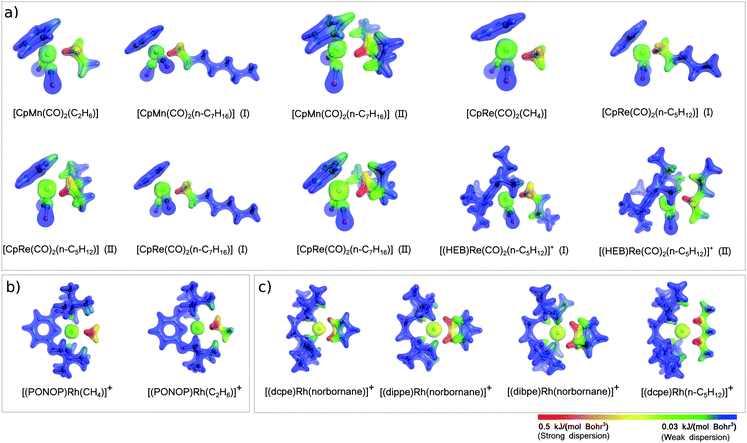Fig. 3 Dispersion interaction density (DID) plots for selected TM–alkane σ-complexes experimentally characterized (see Scheme 2). The density isosurfaces were generated for a contour value of 0.1 e Bohr⁻³. The DID color scheme ranges from highest value (red) to zero dispersion energy (blue).

The first eye-catching feature of these plots is that the most significant contribution to the LD energy originates from short TM⋯H–C contacts, as evidenced by the red color of the density isosurfaces around the C–H groups in close proximity of the TM. In Mn and Re complexes, only one C–H group strongly interacts with the TM, whilst all Rh complexes (Fig. 2b and c) are stabilized by two short TM⋯H–C contacts. For this reason, the LD energy in Rh complexes is typically larger than in the other σ-complexes investigated in this work.

The size of the alkane also plays an important role in affecting the magnitude of the LD contribution. By comparing [CpRe(CO)₂(CH₄)], [CpRe(CO)₂(n-C₅H₁₂)] (I), and [CpRe(CO)₂(n-C₇H₁₆)] (I), in which alkanes of different size interact through their methyl carbon with the same TM fragment, it can be found that the LD increases with the size of the alkane, in line with the above considerations. However, [CpRe(CO)₂(n-C₅H₁₂)] (I) and [CpRe(CO)₂(n-C₇H₁₆)] (I) have essentially the same amount of LD energy. This occurs because the tail of the heptane chain in [CpRe(CO)₂(n-C₇H₁₆)] is too far away from the Re atom to affect the LD energy, as shown by the blue color that the DID plot assumes in this region. The same trend can also be observed for other pair of complexes, i.e., [CpMn(CO)₂(C₂H₆)] vs. [CpMn(CO)₂(n-C₇H₁₆)] (I) and [(PONOP)Rh(CH₄)]⁺vs. [(PONOP)Rh(C₂H₆)]⁺. As these variations in the LD energy correlate well with the corresponding variations in the binding energies, it can be concluded that the size of the alkane does not significantly affect the other components of the interaction.

Similarly, the use of bulky ligands on the TM also increases the LD contribution to the binding energy. In fact, going from [(dippe)Rh(norbornane)]⁺ to [(dbpe)Rh(norbornane)]⁺, E_disp increases from 103 to 110 kJ mol⁻¹ as a consequence of the substitution on the four ⁱPr groups on the diphosphine ligand with the more polarizable ^tBu groups. However, these figures do not correlate with the corresponding variations in the binding energy. This is probably due to steric effects associated with the inclusion of bulkier ^tBu groups, as shown by the fact that r_(TM–C) distance slightly increases going from [(dippe)Rh(norbornane)]⁺ (2.40 Å) to [(dbpe)Rh(norbornane)]⁺ (2.42 Å).

As mentioned above, different coordination modes (e.g. side-on vs. head-on) are possible for the longer alkanes. To investigate the effect of LD on the coordination preference of the alkane, it is useful to compare binding and LD energies for the pairs [CpMn(CO)₂(n-C₇H₁₆)] (I/II), [CpRe(CO)₂(n-C₅H₁₂)] (I/II), [CpRe(CO)₂(n-C₇H₁₆)] (I/II) and [(HEB)Re(CO)₂(n-C₅H₁₂)]⁺.

In all cases, LD is larger for side-on than for head-on structures. In fact, the former are more compact and feature many TM⋯HC contacts. Consistent with this observation, the TM–alkane binding energy is always slightly larger for side-on structures, with the only exception being the positively charged [(HEB)Re(CO)₂(n-C₅H₁₂)]⁺. In this case, the positive charge on the metal probably increases the relative importance of the non-dispersive interaction components, such as polarization and TM ← CH σ-donation. Indeed, by subtracting the LD energy from the binding energy, one finds that the non-dispersive contributions favour head-on structures over side-on structures in all cases. In fact, due to the less congested environment around the TM center, the head-on structures feature slightly smaller r_(TM–C) values (Fig. 2), and charge transfer and polarization effects decay quickly with the intermolecular distance.^29,73 This aspect will be further discussed in Section 3.3 while investigating the physical components affecting the selectivity of CH activation reactions.

These results demonstrate that two opposing effects, i.e., dispersive and non-dispersive energy contributions, determine the coordination preference of σ-complexes. Although LD typically dominates in σ-complexes, the non-dispersive contributions are also important and particularly significant in charged species. These results are consistent with previous experimental NMR studies showing that [CpRe(CO)₂(n-C₅H₁₂)] has a slight preference to form side-on structures,^1,75 whilst [(HEB)Re(CO)₂(n-C₅H₁₂)]⁺ favors head-on structures.⁷⁶

In summary, LD is fundamental for the thermodynamic stability of σ-complexes. It favors the formation of σ-complexes of long alkanes, influences the alkane coordination preference and favors the formation of compact structure with many TM⋯CH contacts.

3.3. Activation of alkanes in σ-complexes

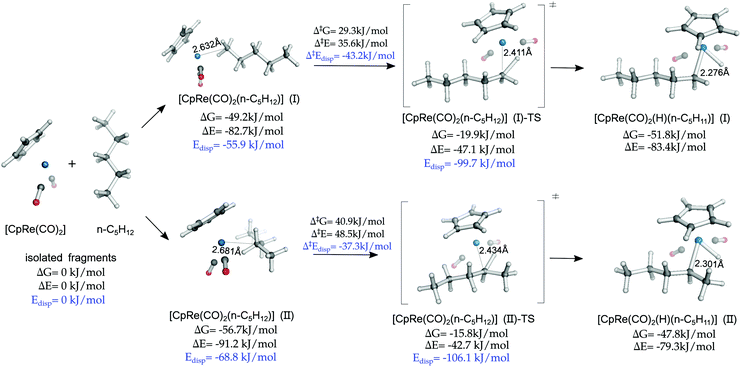
The finding that LD forces determine to a large extent the coordination preference of the alkane, favoring the formation of compact side-on structures, is in apparent contrast with the fact that the majority of alkane CH activation reactions take place at the methyl carbon, which is usually qualitatively explained in terms of steric effects.^77,78

To provide an insight into this aspect, we investigated a model oxidative addition step in which n-pentane interacts with CpRe(CO)₂ to form the oxidative addition product via the formation of the σ-complex intermediate [CpRe(CO)₂(n-C₅H₁₂)] (Scheme 2a). This reaction has been recently studied by means of DFT calculations, but the role played by the LD energy in this context was not discussed.⁵³ The computed mechanism at the DLPNO-CCSD(T) level of theory is shown in Fig. 4.

Fig. 4 Oxidative addition of pentane to the CpRe(CO)₂ fragment. Electronic energies (ΔE) and free energies (ΔG) at 190 K are reported relative to the isolated fragments. The distance between the TM and the closest carbon atom on the alkane r_(TM–C) is also reported.

As [CpRe(CO)₂(n-C₅H₁₂)] (II) is the absolute minimum in the section of the potential energy surface investigated, the oxidative addition is thermodynamically disfavored. This is consistent with the fact that the [CpRe(CO)₂(n-C₅H₁₂)] intermediate can be characterized by NMR spectroscopy.¹

Although the side-on [CpRe(CO)₂(n-C₅H₁₂)] (II) is thermodynamically more stable than the head-on [CpRe(CO)₂(n-C₅H₁₂)] (I) conformer, consistent with the above mentioned experimental observation, the cleavage of the coordinated CH bond in the former requires a larger free energy barrier (ΔG^‡ = 40.9 kJ mol⁻¹) than in the latter (ΔG^‡ = 29.3 kJ mol⁻¹). These results are consistent with previous experimental findings on closely related systems.⁷⁹

These results can be explained by considering that the CH bond has to be in close proximity to the TM in order to be activated towards the oxidative addition. However, the equilibrium TM⋯C distance in [CpRe(CO)₂(n-C₅H₁₂)] (II) is significantly longer than that of [CpRe(CO)₂(n-C₅H₁₂)] (I) (2.68 vs. 2.63 Å) and this difference is partially retained also in the corresponding transition states (2.43 vs. 2.41 Å) and products (2.30 vs. 2.28 Å). This effect probably originates from significant steric effects in the side-on conformation, due to the congested environment around the TM center.

Consistent with these observations, the non-dispersive contribution to the binding energy amounts to −22.4 and −26.8 kJ mol⁻¹ for [CpRe(CO)₂(n-C₅H₁₂)] (II) and [CpRe(CO)₂(n-C₅H₁₂)] (I), respectively, and to +63.4 and +52.6 kJ mol⁻¹ for the corresponding transition states. Hence, polarization and charge transfer effects seem to favor the activation of the CH bond at the methyl carbon.

In summary, even though LD determines to a large extent the thermodynamic stability of σ-complexes, the activation barrier associated with the oxidative addition step is determined by an interplay of LD, steric and charge transfer effects.

4 Conclusions

The recently introduced DLPNO-CCSD(T)/LED scheme was used to compute TM⋯alkane binding energies for a broad range of experimentally characterized σ-complexes and to provide an accurate quantification of the London dispersion component of the coordination bond.

It was found that London dispersion significantly contributes to the TM⋯alkane interaction and is largely responsible for the thermodynamic stability of σ-complexes. Its magnitude can be modulated by modifying the size of the substituents on the TM fragment or by increasing the number of carbons in the alkane.

Moreover, LD influences the coordination preference of the alkane to the TM. As LD increases with the number of TM⋯CH contacts, side-on structures are generally favored over head-on structures, consistent with previous experimental findings. On the other hand, due to the steric effects, head-on structures feature a shorter distance between the TM and the coordinated carbon, leading to larger polarization and charge transfer interactions.

As charge transfer effects weaken the CH bond, activating it towards the cleavage, the oxidative addition of methyl CH bonds to the TM is expected to be kinetically preferred, as shown in a prototype oxidative addition reaction and consistent with previous experimental findings.

As LD is ubiquitous in nature, it is expected that our findings concerning its importance in organometallic chemistry can be applied to other TM–L interactions, such as the wide range of σ-complexes that serve as intermediates in CH activation reactions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the Priority Program “Control of Dispersion Interactions in Molecular Chemistry” (SPP 1807) of the Deutsche Forschungsgemeinschaft for financial support. Open Access funding provided by the Max Planck Society.

References

1. G. E. Ball, C. M. Brookes, A. J. Cowan, T. A. Darwish, M. W. George, H. K. Kawanami, P. Portius and J. P. Rourke, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6927.
2. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887.
3. A. Stone, The theory of intermolecular forces, OUP Oxford, 2013.
4. J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274.
5. A. A. Fokin, T. S. Zhuk, S. Blomeyer, C. Perez, L. V. Chernish, A. E. Pashenko, J. Antony, Y. V. Vishnevskiy, R. J. F. Berger, S. Grimme, C. Logemann, M. Schnell, N. W. Mitzel and P. R. Schreiner, J. Am. Chem. Soc., 2017, 139, 16696.
6. S. Rosel, H. Quanz, C. Logemann, J. Becker, E. Mossou, L. Canadillas-Delgado, E. Caldeweyher, S. Grimme and P. R. Schreiner, J. Am. Chem. Soc., 2017, 139, 7428.
7. S. Grimme and P. R. Schreiner, Angew. Chem., Int. Ed., 2011, 50, 12639.
8. C. N. Pace, J. M. Scholtz and G. R. Grimsley, FEBS Lett., 2014, 588, 2177.
9. S. Parveen, S. Rana and R. Fangueiro, J. Nanomater., 2013, 19.
10. D. J. Liptrot and P. P. Power, Nat. Rev. Chem., 2017, 1, 0004.
11. M. Strauss and H. A. Wegner, Eur. J. Org. Chem., 2019, 295.
12. Q. Lu, F. Neese and G. Bistoni, Angew. Chem., Int. Ed., 2018, 57, 4760.
13. M. Bursch, E. Caldeweyher, A. Hansen, H. Neugebauer, S. Ehlert and S. Grimme, Acc. Chem. Res., 2019, 52, 258.
14. P. Sliwa and J. Handzlik, Chem. Phys. Lett., 2010, 493, 273.
15. M. S. G. Ahlquist and P. O. Norrby, Angew. Chem., Int. Ed., 2011, 50, 11794.
16. Y. Minenkov, G. Occhipinti, W. Heyndrickx and V. R. Jensen, Eur. J. Inorg. Chem., 2012, 1507,  DOI:10.1002/ejic.201100932,.
17. A. Hansen, C. Bannwarth, S. Grimme, P. Petrovic, C. Werle and J. P. Djukic, ChemistryOpen, 2014, 3, 177.
18. L. P. Wolters, R. Koekkoek and F. M. Bickelhaupt, ACS Catal., 2015, 5, 5766.
19. G. Lu, R. Y. Liu, Y. Yang, C. Fang, D. S. Lambrecht, S. L. Buchwald and P. Liu, J. Am. Chem. Soc., 2017, 139, 16548.
20. T. R. Cundari, B. P. Jacobs, S. N. MacMillan and P. T. Wolczanski, Dalton Trans., 2018, 47, 6025.
21. E. Detmar, V. Muller, D. Zell, L. Ackermann and M. Breugst, Beilstein J. Org. Chem., 2018, 14, 1537.
22. A. A. Thomas, K. Speck, I. Kevlishvili, Z. H. Lu, P. Liu and S. L. Buchwald, J. Am. Chem. Soc., 2018, 140, 13976.
23. J. Dewar, Bull. Soc. Chim. Fr., 1951, 18, C71.
24. J. Chatt and L. Duncanson, J. Chem. Soc., 1953, 2939.
25. S. Kristyán and P. Pulay, Chem. Phys. Lett., 1994, 229, 175.
26. S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105.
27. R. Peverati and D. G. Truhlar, Philos. Trans. R. Soc., A, 2014, 372, 20120476.
28. W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2016, 12, 4778.
29. A. Altun, F. Neese and G. Bistoni, J. Chem. Theory Comput., 2019, 15, 215.
30. A. Altun, M. Saitow, F. Neese and G. Bistoni, J. Chem. Theory Comput., 2019, 15, 1616–1632.
31. C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106.
32. C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134103.
33. C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109.
34. G. Bistoni, A. A. Auer and F. Neese, Chem. – Eur. J., 2017, 23, 865.
35. A. Altun, F. Neese and G. Bistoni, Beilstein J. Org. Chem., 2018, 14, 919.
36. F. Neese, M. Atanasov, G. Bistoni, D. Maganas and S. Ye, J. Am. Chem. Soc., 2019, 141, 2814–2824.
37. V. M. Schmiedel, Y. J. Hong, D. Lentz, D. J. Tantillo and M. Christmann, Angew. Chem., Int. Ed., 2018, 57, 2419.
38. C. L. Gross and G. S. Girolami, J. Am. Chem. Soc., 1998, 120, 6605.
39. D. D. Wick, K. A. Reynolds and W. D. Jones, J. Am. Chem. Soc., 1999, 121, 3974.
40. W. H. Bernskoetter, S. K. Hanson, S. K. Buzak, Z. Davis, P. S. White, R. Swartz, K. I. Goldberg and M. Brookhart, J. Am. Chem. Soc., 2009, 131, 8603.
41. T. A. Mobley, C. Schade and R. G. Bergman, J. Am. Chem. Soc., 1995, 117, 7822.
42. E. A. Cobar, R. Z. Khaliullin, R. G. Bergman and M. Head-Gordon, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6963.
43. S. E. Bromberg, H. Yang, M. C. Asplund, T. Lian, B. K. McNamara, K. T. Kotz, J. S. Yeston, M. Wilkens, H. Frei, R. G. Bergman and C. B. Harris, Science, 1997, 278, 260.
44. M. Lersch and M. Tilset, Chem. Rev., 2005, 105, 2471.
45. B. G. Hashiguchi, S. M. Bischof, M. M. Konnick and R. A. Periana, Acc. Chem. Res., 2012, 45, 885.
46. W. D. Jones, Inorg. Chem., 2005, 44, 4475.
47. Y. Qin, L. H. Zhu and S. Z. Luo, Chem. Rev., 2017, 117, 9433.
48. T. Brent Gunnoe, in Alkane C-H Activation by Single-Site Metal Catalysis, ed. P. Pedro, Springer, Dordrecht, Heidelberg, New York, London, 2012, pp. 1–15.
49. F. M. Chadwick, T. Kramer, T. Gutmann, N. H. Rees, A. L. Thompson, A. J. Edwards, G. Buntkowsky, S. A. Macgregor and A. S. Weller, J. Am. Chem. Soc., 2016, 138, 13369.
50. M. L. H. Green and G. Parkin, Struct. Bonding, 2017, 171, 79.
51. J. M. Buchanan, J. M. Stryker and R. G. Bergman, J. Am. Chem. Soc., 1986, 108, 1537.
52. W. Lamanna and M. Brookhart, J. Am. Chem. Soc., 1981, 103, 989.
53. M. Thenraj and A. G. Samuelson, J. Comput. Chem., 2015, 36, 1818.
54. D. Balcells, E. Clot and O. Eisenstein, Chem. Rev., 2010, 110, 749.
55. C. Hall and R. N. Perutz, Chem. Rev., 1996, 96, 3125.
56. A. J. Cowan, P. Portius, H. K. Kawanami, O. S. Jina, D. C. Grills, X. Z. Sun, J. McMaster and M. W. George, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6933.
57. G. I. Childs, C. S. Colley, J. Dyer, D. C. Grills, X. Z. Sun, J. X. Yang and M. W. George, J. Chem. Soc., Dalton Trans., 2000, 1901–1906,  10.1039/b001987i.
58. O. Torres, J. A. Calladine, S. B. Duckett, M. W. George and R. N. Perutz, Chem. Sci., 2015, 6, 418.
59. F. P. A. Johnson, M. W. George, V. N. Bagratashvili, L. N. Vereshchagina and M. H. Palmer, Mendeleev Commun., 1991, 1, 26.
60. X. Z. Sun, D. C. Grills, S. M. Nikiforov, M. Poliakoff and M. W. George, J. Am. Chem. Soc., 1997, 119, 7521.
61. H. M. Yau, A. I. McKay, H. Hesse, R. Xu, M. He, C. E. Holt and G. E. Ball, J. Am. Chem. Soc., 2016, 138, 281.
62. W. H. Bernskoetter, C. K. Schauer, K. I. Goldberg and M. Brookhart, Science, 2009, 326, 553.
63. M. D. Walter, P. S. White, C. K. Schauer and M. Brookhart, J. Am. Chem. Soc., 2013, 135, 15933.
64. S. D. Pike, A. L. Thompson, A. G. Algarra, D. C. Apperley, S. A. Macgregor and A. S. Weller, Science, 2012, 337, 1648.
65. F. M. Chadwick, N. H. Rees, A. S. Weller, T. Kramer, M. Iannuzzi and S. A. Macgregor, Angew. Chem., Int. Ed., 2016, 55, 3677.
66. S. D. Pike, F. M. Chadwick, N. H. Rees, M. P. Scott, A. S. Weller, T. Kramer and S. A. Macgregor, J. Am. Chem. Soc., 2015, 137, 820.
67. J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
68. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
69. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101.
70. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
71. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98.
72. A. Wuttke and R. A. Mata, J. Comput. Chem., 2017, 38, 15.
73. M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962.
74. W. Scherer and G. S. McGrady, Angew. Chem., Int. Ed., 2004, 43, 1782.
75. D. J. Lawes, S. Geftakis and G. E. Ball, J. Am. Chem. Soc., 2005, 127, 4134.
76. R. D. Young, D. J. Lawes, A. F. Hill and G. E. Ball, J. Am. Chem. Soc., 2012, 134, 8294.
77. A. Sivaramakrishna, P. Suman, E. V. Goud, S. Janardan, C. Sravani, T. Sandeep, K. Vijayakrishna and H. S. Clayton, J. Coord. Chem., 2013, 66, 2091.
78. J. A. Labinger and J. E. Bercaw, Nature, 2002, 417, 507.
79. M. C. Asplund, P. T. Snee, J. S. Yeston, M. J. Wilkens, C. K. Payne, H. Yang, K. T. Kotz, H. Frei, R. G. Bergman and C. B. Harris, J. Am. Chem. Soc., 2002, 124, 10605.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp01309a

---