Open Access Article
Open Access ArticleNeutron reflectometry to measure in situ the rate determining step of lithium ion transport through thin silicon layers and interfaces†
Erwin
Hüger
 *a,
Jochen
Stahn
b,
Paul
Heitjans
*a,
Jochen
Stahn
b,
Paul
Heitjans
 c and
Harald
Schmidt
c and
Harald
Schmidt
 ad
ad
aAG Mikrokinetik, Institut für Metallurgie, TU Clausthal, D-38678 Clausthal-Zellerfeld, Germany. E-mail: erwin.hueger@tu-clausthal.de
bLaboratory for Neutron Scattering and Imaging, Paul Scherrer Institut, CH-5232 Villigen, Switzerland
cInstitut für Physikalische Chemie und Elektrochemie, and ZFM – Zentrum für Festkörperchemie und Neue Materialien, Leibniz Universität Hannover, D-30167 Hannover, Germany
dClausthaler Zentrum für Materialtechnik, Technische Universität Clausthal, D-38678 Clausthal-Zellerfeld, Germany
First published on 16th May 2019
Abstract
Li ion transport through thin (14–22 nm) amorphous silicon layers adjacent to lithium metal oxide layers (lithium niobate) was studied by in situ neutron reflectometry experiments and the control mechanism was determined. It was found that the interface between amorphous silicon and the oxide material does not hinder Li transport. It is restricted by Li diffusion in the silicon material. This finding based on in situ experiments confirms results obtained ex situ and destructively by secondary ion mass spectrometry (SIMS) depth profiling investigations. The Li permeabilities obtained from the present experiments are in agreement with those obtained from ex situ SIMS measurements showing similar activation enthalpies.
1. Introduction
The design and tailoring of advanced materials that will support emergent energy technologies (photovoltaics, hydrogen storage, lithium based energy storage) is a challenge for the future. In appropriate devices different types of materials are often combined which are separated by interfaces, e.g. electrolyte and electrodes in batteries. A central aspect regarding the functionality of such devices is the transport of ions or atoms through different classes of materials like the transport of Li ions between electrodes in Li storage technology. Interfaces between different materials may represent obstacles for ion migration counteracting the requirement for a smooth material flow in energy storage and energy conversion device operation. For example, interface limited Li transport was suggested to be present in solid-state Li ion batteries (LIB) possessing silicon as active material.1 A reduction of the transport distances by downsizing the active material to, e.g., nanoparticles, is thought to be indispensable for improved energy storage devices.2 In that case, Li migration has to surpass a large number of interfaces in nanosized materials. Consequently, the time needed to cross materials interfaces can be similar to the total migration time. In that case, Li transport over interfaces may dominate the overall material transport, a phenomenon thought to happen in all-solid-state LIBs.1–9A promising negative electrode active material for electrochemical energy storage in LIBs is silicon.10–13 Silicon is earth-abundant, light-weight, low-cost and can store a high amount of lithium, i.e., up to 4 Li ions per one Si atom. On the positive electrode side, thin LiNbO3 layers inserted between the electrolyte and the positive electrode were found to be beneficial for LIB operation.14–23 The interface between these two materials is also of interest because LiNbO3 adjacent to silicon thin layers might be important for the fabrication of self-charging LIBs that hybridize mechanical energy harvesting and ion storage processes into one process.24,25
In general, the reduction of the interface impedance is a challenge for proper all-solid state LIB operation.1–9 Criteria for a rational electrode design are based on Li transport parameters.2 For example, the knowledge of the Li transport parameters is of importance for the understanding of the lithiation process (ref. 26), maximum storage capacity, charging/discharging times and for the mechanical stress built up during LIB operation.27 Not at least, Li transport parameters are of importance for the design, the dimensioning, and the use of barrier layers.
In that context, a well-suited transport parameter is the permeability (P) defined as
| P = S·D | (1) |
Unfortunately, there are not many analytical techniques suitable for transport measurements which are specific and sensitive to light elements such as hydrogen and lithium. Neutron reflectometry (NR) is such a technique. Hydrogen and lithium possess negative neutron scattering lengths in contrast to the other elements which have almost all positive values. This fact enables appropriate hydrogen and lithium detection by neutron-based techniques. Due to their predominant scatter at atomic nuclei, neutrons can discern between isotopes of Li and H. Furthermore, neutrons have high penetration and escape lengths in and from almost all materials. NR permits the detection of buried interfaces deep within complex sample environments in a non-destructive manner and allows the study of in-operando processes in LIBs during device operation.30–38
This work describes the use of neutron reflectometry to measure the transport of Li across Si layers in a multilayer. It is the latest in a series of related articles26,29,35,39–41 of increasing sophistication and quality of information. More information on this issue is given in the first section of the ESI† accompanying this work. Briefly, the methodology to measure Li permeation in silicon thin layers was established in ref. 26, 29, 35 and 39–41. It is based on multilayers (MLs) as that sketched in Fig. S1 of the ESI† accompanying this work. The MLs were produced by ion-beam sputter deposition.42 There,26,29,35,39–41 a sequence of [6LiNbO3/Si/7LiNbO3/Si] structural units were used for the experiments. The 6LiNbO3 and 7LiNbO3 layers are enriched with 6Li and 7Li isotopes, respectively. Each of these two isotope enriched Li reservoir layers are adjacent to a Si layer. Amorphous LiNbO3 was used as a Li reservoir due to its high Li diffusivity, stability against air corrosion and heating procedures.26,29,40,41,43 The high diffusivity of Li in amorphous LiNbO3 as compared to crystalline and even nanocrystalline LiNbO3 had earlier been shown.44–47 Similar results were found for other Li metal oxides like LiTaO3, LiAlO2 or LiGaO2 studied partly also by NR, secondary ion mass spectrometry (SIMS), nuclear magnetic resonance spectroscopy or impedance spectroscopy (see ref. 48 for a review). A mutual exchange of Li isotopes through the Si layer and adjacent interfaces appears by thermally activated Li permeation during annealing. The mutual isotope exchange is modifying and balancing the Li isotope fraction in each of the two Li reservoir layers. In first approximation, the chemical composition of the Li reservoir is unchanged because the solubility of Li in silicon is very low.26 The Li permeability is obtained by measuring the relative fraction of 6Li and 7Li isotopes in the Li reservoirs as a function of Li permeation time as described in ref. 26 and 29. Up to now, with the exception presented below, only ex situ investigations for the determination of Li permeabilities in Si layers are published which were done by NR or SIMS (see the ESI† accompanying this work).26,29,39–41Ex situ means that the isothermal annealing procedure necessary to initiate the Li permeation process was interrupted and the sample was cooled to room temperature before analysis is carried out. Ref. 35 demonstrates exemplarily that in situ measurements of Li permeabilities are feasible with NR, were neutron experiments are done directly during annealing. This work presents NR experiments that allow the in situ determination of permeabilities in thin films and of the rate controlling step of Li transport through thin Si layers and their interfaces to an oxide material.
2. Materials and methods
The MLs were investigated by X-ray reflectometry (XRR), grazing incidence X-ray diffraction (GI-XRD), SIMS and NR. Details on XRR, GI-XRD, SIMS and sample preparation are given in the ESI† accompanying this work. Investigations with XRD revealed an amorphous structure of the whole multilayer. The results obtained from XRR, SIMS and NR investigations are given and discussed in detail in the ESI accompanying this work. In situ NR was carried out using the reflectometer AMOR located at SINQ (Paul Scherer Institut, Villigen, Switzerland). During NR experiments, a neutron beam strikes the sample surface under a small angle (θ), is reflected at each isotope or composition interface and is afterwards detected. Due to the interference of the individual partial beams a characteristic interference pattern36 is formed (e.g., a Bragg reflection or Bragg peak, Fig. 1). The intensity of the reflected beam is measured as a function of the scattering vector normal to the surface Qz = 4π(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/λ, with λ the neutron wavelength. In situ NR measurements were done with the Selene focussing optics35,49 recently implemented at AMOR. This experimental arrangement improves the intensity at the sample significantly so that the reflected intensity can be measured continuously and pinned down to 1 min time resolution for in situ studies. For the experiments a specially designed rapid thermal annealing setup (AO 500, MBE-Komponenten GmbH, Germany) was employed being optimized for use in the neutron beam. Here, extremely fast heating rates are possible which allow one to reach temperatures up to 500 °C in less than 30 s in argon gas. For the NR experiments, the samples were positioned on an alumina heating stage inside the rapid thermal annealing device.
θ)/λ, with λ the neutron wavelength. In situ NR measurements were done with the Selene focussing optics35,49 recently implemented at AMOR. This experimental arrangement improves the intensity at the sample significantly so that the reflected intensity can be measured continuously and pinned down to 1 min time resolution for in situ studies. For the experiments a specially designed rapid thermal annealing setup (AO 500, MBE-Komponenten GmbH, Germany) was employed being optimized for use in the neutron beam. Here, extremely fast heating rates are possible which allow one to reach temperatures up to 500 °C in less than 30 s in argon gas. For the NR experiments, the samples were positioned on an alumina heating stage inside the rapid thermal annealing device.
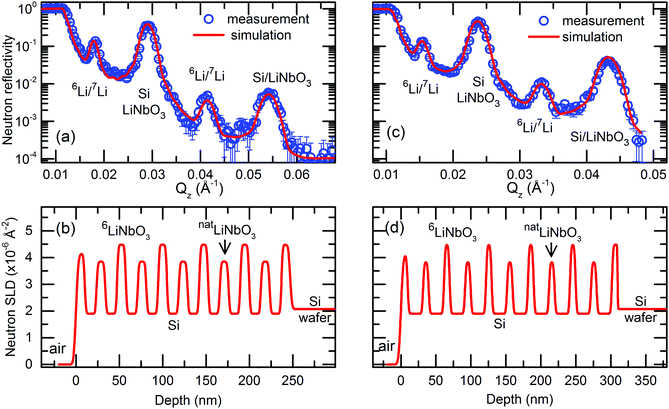 | ||
| Fig. 1 (a and c) Measured NR patterns (open symbols) and corresponding Parratt32 simulations (red lines) for MLs with (a) 14 nm and (c) 22 nm Si layers in the as-deposited state. (b and d) Neutron scattering length density (SLD) obtained from the simulations given in panel (a and c). Parameters used for NR simulations are given in Table S1 of the ESI† accompanying this work. | ||
3. Results and discussions
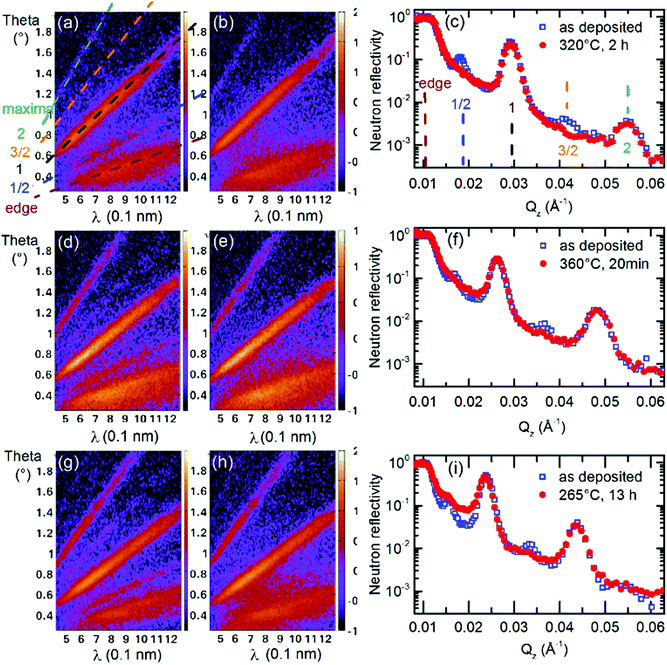
Fig. 1 presents NR patterns recorded for MLs containing 14 and 22 nm thin Si layers, respectively. For data analysis the program Parratt32 is used. The neutron scattering length density (SLD) obtained by comparing the NR simulation (lines in Fig. 1a and c) to the measured data (open symbols in Fig. 1a and c) is given in Fig. 1b and d. This gives also the individual layer thicknesses which are listed in Tables S1, S3 and S4 of the ESI† accompanying this work.Strong Bragg reflections located at scattering vectors of ∼0.029 and ∼0.054 Å−1 in Fig. 1a and of ∼0.023 and ∼0.043 Å−1 in Fig. 1c, originate from the double layer Si/LiNbO3 periodicity of the ML with 14 nm and 22 nm thin Si layers, respectively. They correspond to the Bragg reflections of first and second order. The four-layer periodicity introduced by the different Li isotopes fractions of consecutive LiNbO3 layers, i.e., the four-layer unit Si/6LiNbO3/Si/7LiNbO3, give rise to the half order Bragg reflections (1/2 and 3/2). They are located at the scattering wave vectors of ∼0.018 and ∼0.041 Å−1 in Fig. 1a and of ∼0.016 and ∼0.033 Å−1 in Fig. 1c, respectively. Fig. S2 of the ESI† shows by NR simulations that the halve order Bragg reflections are resulting from the Li isotope contrast difference of the LiNbO3 layers.
Fig. 2 presents typical NR patterns recorded at room temperature from the as-deposited ML in comparison to that recorded at elevated temperatures. The NR intensity maps are recorded with the help of the Selene focusing device.35,49 The intensity up to the edge of the total reflection and the intensity at the Bragg reflections positions produces intensity bands in the intensity maps. They are marked in Fig. 2a with dashed lines. Neutron reflectivity curves are obtained by a projection of the intensity map onto a scattering wave vector Qz grid.49 The intensity bands (Fig. 2a) produce intensity maxima in the NR curves as marked in Fig. 2c with dashed lines in accordance with Fig. 2a.
The Li isotope and chemical contrast does not change for years of sample storage at room temperature in air. Consequently, the Li permeation at room temperature has to be extremely low. If the ML arrangement is annealed, e.g., at 320 °C, Li diffusion through the interfaces and silicon layer from one to the next Li isotope reservoir is induced. This reduces the Bragg reflections of half orders but not that of integral order. The lack of considerable change of the total reflection edge and of integral order Bragg reflections indicates that during annealing there is no layer intermixing between the layers of the MLs (see Fig. S16 in the ESI† of ref. 40). The decrease of solely the half order Bragg reflection is an indicator for the 6Li and 7Li isotope exchange through the Si layer without chemical phase formation.
The Li isotope contrast that can be determined from the measurements is defined as given in ref. 26
 | (2) |
Fig. 3 presents the modification in Li isotope contrast in dependence on annealing time as determined from the in situ NR measurements (see the ESI†) reflecting the progression of the Li permeation. The Li contrast decreases as a function of annealing time for all temperatures investigated.
 | ||
| Fig. 3 Annealing time behaviour of the 6Li contrast in the 6Li reservoir layers obtained from in situ NR measurements (open symbols) during Li permeation through thin Si layers at different temperatures. Further details on error limit calculations and layer thicknesses are given in Sections S4 and S6 of the ESI.† The fit of eqn (2) is shown by solid lines. | ||
The time constant characterizing the decay rate of the Li isotope contrast is presented in Fig. 4a for each investigated Si layer thickness and temperature. The thicknesses of the Si and LiNbO3 layers were determined from the reflectivity measurements as presented in the ESI.† The time constant of Li isotope intermixing by Li permeation through the Si layers and interfaces should obviously be also dependent on how much Li is present in the Li reservoirs. Thinner LiNbO3 layers possess a lower amount of Li available for the Li permeation process and in that way the Li isotope fraction should diminish faster for thinner than for thicker Li reservoir layers. Fig. 4b addresses this issue by dividing the time constant by the thickness of the LiNbO3 layers. However, no significant differences to Fig. 4a are found.
Except for 265 °C (MLs with 14 and 17 nm thin Si layers), the time constant increases with larger Si layer thickness. This happens at all temperatures. The thinner the Si layer, the faster is the Li isotope exchange through the Si layer and the lower the necessary time constant. This means that Li transport through the LiNbO3/Si interface is much faster than through the Si layers. Otherwise, the time constants would be expected to be independent of Si layer thickness. The in situ NR experiments confirm the results obtained by ex situ SIMS experiments41 that Li transport through thin Si layers is strongly dependent on the Si layer thickness and is consequently controlled by the Li permeation/diffusion process in the Si layers and not by the transport of Li through the LiNbO3/Si interface. This shows that the LiNbO3/Si interface is not an obstacle for the Li transport process. Further elaboration presented in Section S7 of the ESI† confirms this finding. However, the contact of pure Si material to a solid-state Li reservoir (such as a solid-state Li electrolyte) is in a real LIB present only at the very first operation sequence, i.e., at the start of the first Si electrode lithiation cycle. For most of the LIB operation time, the solid-state Li electrolyte is in contact rather to a LixSi alloy than to pure Si material. In that case, the rate determining step of Li transport may change to interface control. This may happen if Li permeation through the LixSi layer becomes very fast. According to eqn (1), Li permeation is enhanced by a higher Li content (Li solubility) in the intermediary layer. This is the case for LixSi. Moreover, the higher Li content in LixSi enhances Li diffusivity.50 SIMS50 and NR51 experiments were performed in our laboratory to determine Li diffusivity and Li permeability in amorphous LixSi layers. It was found that Li permeability in LixSi layers with a low amount of x is close to that of pure amorphous silicon.51 Further, systematic diffusion studies in LixSi revealed that Li diffusivities are significantly enhanced with increasing Li content.50 Consequently, as a perspective, the application of the NR methodology to determine in situ the rate determining step of Li permeation through LixSi alloys and their interfaces to, e.g., different oxide based solid electrolyte materials is desirable in the context of battery applications.
The Li permeability (eqn (1)) is calculated using the molar masses (MSi, MLiNbO3), mass densities (ρLiNbO3, ρSi), layer thicknesses (dLiNbO3, dSi) and time constants (eqn (2)) by (see the ESI† of ref. 26)
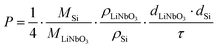 | (3) |
The obtained Li permeabilities are presented in Fig. 5 by full symbols. The open symbols in Fig. 5 represent Li permeabilities obtained ex situ by the means of SIMS depth profiling for Si layer thicknesses of 12, 17 and 25 nm.41 The results of the different methods are in acceptable agreement. The temperature dependence of Li permeabilities follows the Arrhenius law with an enthalpy of Li permeation of about 1 eV (see Table S5 of the ESI†) which is also in good agreement to the values obtained ex situ from SIMS investigations.41 The ex situ SIMS experiments revealed a Si layer dependence of the Li permeability between 10 and 100 nm thickness.41 Thinner Si layers show a higher Li permeability.41 This result is also reflected in the present in situ data. The Li permeability increase for thinner Si layers was attributed in ref. 41 to a change of the Li diffusion mechanism from trap-limited Li diffusion in thick Si layers to trap-free Li diffusion in thinner Si layers. A higher Li solubility in thinner Si layers could also contribute to this effect.41
 | ||
| Fig. 5 Li permeabilities in thin amorphous Si layers (different thicknesses) as function of reciprocal temperature determined by in situ NR measurements (full symbols) in comparison that obtained by ex situ SIMS measurements41 (open symbols). | ||
Before concluding, let us mention that, as described already in the Introduction section, the knowledge of permeability is sometimes of higher interest than solely diffusion. It takes also into account the amount of Li which is transported during diffusion. Other groups measured solely the Li diffusivity in amorphous silicon.52–56 In Fig. 10 of ref. 26 the Li diffusion coefficients obtained from the study of Li permeation to that obtained by other groups by classical diffusion experiments are compared.
4. Conclusions
A methodology based on NR is used to determine in situ the rate determining step of the Li permeation process through thin silicon layers and their interfaces in contact to amorphous LiNbO3 material. Li diffusion inside the Si material is controlling the Li transport. The LiNbO3/Si interface is no significant obstacle for the Li permeation process. This result obtained from the present in situ experiments confirms the results obtained from ex situ experiments performed destructively by SIMS. Also the absolute size and activation enthalpy of Li permeabilities derived by both methods are identical within error limits.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Deutsche Forschungsgemeinschaft (DFG) under the contract HU 2170/2-1 is gratefully acknowledged. This research project has been supported by the European Commission under the 7th Framework Program through the ‘Research Infrastructures’ action of the ‘Capacities’ Program, NMI3-II grant number 283883. This work is based on experiments performed at the Swiss spallation neutron source (SINQ), at the instruments AMOR and Morpheus, PSI Villigen, Switzerland. Thanks are due to E. Witt (U Hannover) for preparing the LiNbO3 sputter targets in the frame of DFG FOR 1277. P. H. is grateful to Niedersächsisches Ministerium für Wissenschaft und Kultur (MWK) for support within a Niedersachsen Professorship (VWZN3095).Notes and references
- D. Santhanagopalan, D. Qian, Th. McGilvray, Z. Wang, F. Wang, F. Camino, J. Graetz, N. Dudney and Y. S. Meng, J. Phys. Chem. Lett., 2014, 5, 298 CrossRef CAS PubMed.
- C. Zhu, R. E. Usiskin, Y. Yu and J. Maier, Science, 2017, 358, 1400 CrossRef CAS PubMed.
- K. Takada, T. Ohno, N. Ohta, T. Ohnishi and Y. Tanaka, ACS Energy Lett., 2018, 3, 98 CrossRef CAS.
- F. S. Gittleson and F. El Gabaly, Nano Lett., 2017, 17, 6974 CrossRef CAS PubMed.
- W. Zhang, D. A. Weber, H. Weigand, T. Arlt, I. Manke, D. Schröder, R. Koerver, T. Leichtweiss, P. Hartmann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2017, 9, 17835 CrossRef CAS PubMed.
- R. Koerver, I. Aygün, T. Leichtweiß, C. Dietrich, W. Zhang, J. O. Binder, P. Hartmann, W. G. Zeier and J. Janek, Chem. Mater., 2017, 29, 5574 CrossRef CAS.
- R. Koerver, F. Walther, I. Aygün, J. Sann, C. Dietrich, W. G. Zeier and J. Janek, J. Mater. Chem. A, 2017, 5, 22750 RSC.
- L. Sang, R. Haasch, A. A. Gewirth and R. G. Nuzzo, Chem. Mater., 2017, 29, 3029 CrossRef CAS.
- B. Wu, S. Wang, W. G. Evans IV, D. Z. Deng, J. Yang and J. Xiao, J. Mater. Chem. A, 2016, 4, 15266 RSC.
- M. T. McDowell, S. W. Lee, W. D. Nix and Y. Cui, Adv. Mater., 2013, 25, 4966 CrossRef CAS PubMed.
- E. Hüger, B. Jerliu, L. Dörrer, M. Bruns, G. Borchardt and H. Schmidt, Z. Phys. Chem., 2015, 229, 1375 Search PubMed.
- M. T. McDowell, S. W. Lee, C. Th. Harris, B. A. Korgel, C. Wang, W. D. Nix and Y. Cui, Nano Lett., 2013, 13, 758 CrossRef CAS PubMed.
- J. W. Wang, Y. He, F. Fan, X. H. Liu, S. Xia, Y. Liu, C. Th. Harris, H. Li, J. Y. Huang, S. X. Mao and T. Zhu, Nano Lett., 2013, 13, 709 CrossRef CAS PubMed.
- J. F. M. Oudenhoven, L. Baggetto and P. Notten, Adv. Energy Mater., 2011, 1, 10 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682 CrossRef CAS PubMed.
- M. Ogawa, R. Kanda, K. Yoshida, T. Uemura and K. Harada, J. Power Sources, 2012, 205, 487 CrossRef CAS.
- N. Ohta, K. Takada, I. Sakaguchi, L. Zhang, R. Ma, K. Fukuda, M. Osada and T. Sasaki, Electrochem. Commun., 2007, 9, 1486 CrossRef CAS.
- M. Kato, H. Hayashi, G. Hasegawa, X. Lu, T. Miyazaki, Y. Matsuda, N. Kuwata, K. Kurihara and T. Kawamura, Solid State Ionics, 2017, 308, 54 CrossRef CAS.
- J. Haruyama, K. Sodeyama, L. Han, K. Takada and Y. Tateyama, Chem. Mater., 2014, 26, 4248 CrossRef CAS.
- T. Teranishi, M. Inohara, J. Kano, H. Hayashi, A. Kishimoto, K. Yoda, H. Motobayashi and Y. Tasaki, Solid State Ionics, 2018, 314, 57 CrossRef CAS.
- S. Xin, Y. You, S. Wang, H. Gao, Y.-G. Yin and Y.-G. Guo, ACS Energy Lett., 2017, 2, 1385 CrossRef CAS.
- Z. Gao, H. Sun, L. Fu, F. Ye, Y. Zhang, W. Luo and Y. Huang, Adv. Mater., 2018, 30, 1705702 CrossRef PubMed.
- H. Kim, D. Byun, W. Chang, H.-G. Jung and W. Choi, J. Mater. Chem. A, 2017, 5, 25077 RSC.
- Z. Wang, Z. Li and Y. Q. Fu, ChemElectroChem, 2017, 4, 1523 CrossRef CAS.
- Z. Wang, ACS Appl. Mater. Interfaces, 2017, 9, 15893 CrossRef CAS PubMed.
- E. Hüger, L. Dörrer and H. Schmidt, Chem. Mater., 2018, 30, 3254 CrossRef.
- D. Wang, Y. Wang, Y. Zou, C. Lu and Z. Ma, Acta Mech., 2018, 229, 3293 CrossRef.
- R. Kirchheim, Defect Diffus. Forum, 1997, 143-147, 911 CAS.
- E. Hüger, L. Dörrer, J. Rahn, T. Panzner, J. Stahn, G. Lilienkamp and H. Schmidt, Nano Lett., 2013, 13, 1237 CrossRef PubMed.
- B. Jerliu, L. Dörrer, E. Hüger, G. Borchardt, R. Steitz, U. Geckle, V. Oberst, M. Bruns, O. Schneider and H. Schmidt, Phys. Chem. Chem. Phys., 2013, 15, 7777 RSC.
- B. Jerliu, L. Dörrer, E. Hüger, B.-K. Seidlhofer, R. Steitz, U. Geckle, V. Oberst, M. Bruns and H. Schmidt, J. Phys. Chem. C, 2014, 118, 9395 CrossRef CAS.
- B.-K. Seidlhofer, B. Jerliu, M. Trapp, E. Hüger, S. Risse, R. Cubitt, H. Schmidt, R. Steitz and M. Ballauff, ACS Nano, 2016, 10, 7458 CrossRef CAS PubMed.
- B. Jerliu, E. Hüger, M. Horisberger, J. Stahn and H. Schmidt, J. Power Sources, 2017, 359, 415 CrossRef CAS.
- E. Hüger, F. Strauß, J. Stahn, J. Deubener, M. Bruns and H. Schmidt, Sci. Rep., 2018, 8, 17607 CrossRef PubMed.
- E. Hüger, J. Stahn and H. Schmidt, J. Electrochem. Soc., 2015, 162, A7104 CrossRef.
- J. A. Dura, E. D. Rus, P. A. Kienzle and B. B. Maranville, Nanolayer Analysis by Neutron Reflectometry, in Nanolayer research: Methodology and Technology for Green Chemistry, ed. T. Imae, Elsevier, Amsterdam, Oxford, Cambridge, 2017, ch. 5, ISBN: 978-0-444-63739-0 Search PubMed.
- J. Daillant and A. Gibaud, X-ray and neutron reflectivity: principles and applications, Lecture notes in physics, Berlin, Springer, 1999, vol. 58 Search PubMed.
- H. Wang, R. G. Downing, J. A. Dura and D. S. Hussey, In Situ Neutron Techniques for Studying Lithium Ion Batteries, Polymers for Energy Storage and Delivery: Polyelectrolytes for Batteries and Fuel Cells, ACS Symposium Series, 2012, ch. 6, vol. 1096, pp. 91–106, DOI:10.1021/bk-2012-1096.ch006, ISBN13: 9780841226319.
- E. Hüger, L. Dörrer, J. Stahn, T. Geue and H. Schmidt, Defect Diffus. Forum, 2015, 363, 49 Search PubMed.
- E. Hüger, L. Dörrer, R. Yimnirun, J. Jutimoosik, J. Stahn and A. Paul, Phys. Chem. Chem. Phys., 2018, 20, 23233 RSC.
- E. Hüger and H. Schmidt, J. Phys. Chem. C, 2018, 122, 28528 CrossRef.
- F. Strauß, E. Hüger, P. Heitjans, V. Trouillet, M. Bruns and H. Schmidt, RSC Adv., 2015, 5, 7192 RSC.
- J. Rahn, E. Hüger, L. Dörrer, B. Ruprecht, P. Heitjans and H. Schmidt, Z. Phys. Chem., 2012, 226, 439 CrossRef CAS.
- A. M. Glass, K. Nassau and T. J. Negran, J. Appl. Phys., 1980, 51, 3756 CrossRef CAS.
- M. Masoud and P. Heitjans, Defect Diffus. Forum, 2005, 237–240, 1016 CAS.
- D. Bork and P. Heitjans, J. Phys. Chem. B, 1998, 102, 7303 CrossRef CAS.
- P. Heitjans, M. Masoud, A. Feldhoff and M. Wilkening, Faraday Discuss., 2007, 134, 67 RSC.
- J. Uhlendorf, B. Ruprecht, E. Witt, C. V. Chandran, L. Dörrer, E. Hüger, F. Strauß, P. Heitjans and H. Schmidt, Z. Phys. Chem., 2017, 231, 1423 CAS.
- J. Stahn and A. Glavic, Nucl. Instrum. Methods Phys. Res., Sect. A, 2016, 821, 44 CrossRef CAS.
- F. Strauß, L. Dörrer, M. Bruns and H. Schmidt, J. Phys. Chem. C, 2018, 122, 6508 CrossRef.
- F. Strauß, E. Hüger, P. Heitjans, T. Geue, J. Stahn and H. Schmidt, Energy Technol., 2016, 12, 1582 CrossRef.
- U. Zastrow, W. Beyer and J. Herion, Fresenius’ J. Anal. Chem., 1992, 346, 92 CrossRef.
- D. Fink, J. P. Biersack, H. P. Schoelch, M. Weiser, S. Kalbitzer, M. Behar, J. P. De Souza, F. C. Zawislak, A. M. Mazzone and H. Kranz, Radiat. Eff. Defects Solids, 1989, 108, 185 CrossRef CAS.
- D. Fink, K. Tjan, J. P. Biersack and L. Wang, Radiat. Eff. Defects Solids, 1989, 108, 27 CrossRef CAS.
- D. Fink, K. Tjan and L. Wang, Radiat. Eff. Defects Solids, 1990, 114, 21 CrossRef CAS.
- A. Ruzin, A. Abrosimov and P. Litovchenko, Nucl. Instrum. Methods Phys. Res., Sect. A, 2010, 617, 588 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: A literature survey, details on multilayer deposition and measurement techniques, microscopy on multilayers, layer thickness determination by reflectometry, secondary ion mass spectrometry data, additional neutron reflectometry data and error analysis, and additional references. See DOI: 10.1039/c9cp01222b |
| This journal is © the Owner Societies 2019 |