Open Access Article
Open Access ArticleWeak-field coherent control of photodissociation in polyatomic molecules†
A.
Serrano-Jiménez
a,
L.
Bañares
b and
A.
García-Vela
 *a
*a
aInstituto de Física Fundamental, Consejo Superior de Investigaciones Científicas, Serrano 123, 28006 Madrid, Spain. E-mail: garciavela@iff.csic.es
bDepartamento de Química Física, Facultad de Ciencias Químicas (Unidad Asociada I+D+i al CSIC), Universidad Complutense de Madrid, 28040 Madrid, Spain
First published on 18th March 2019
Abstract
A coherent control scheme is suggested to modify the output of photodissociation in a polyatomic system. The performance of the scheme is illustrated by applying it to the ultrafast photodissociation of CH3I in the A-band. The control scheme uses a pump laser weak field that combines two pulses of a few femtoseconds delayed in time. By varying the time delay between the pulses, the shape of the laser field spectral profile is modulated, which causes a change in the initial relative populations excited by the pump laser to the different electronic states involved in the photodissociation. Such a change in the relative populations produces different photodissociation outputs, which is the basis of the control achieved. The degree of control obtained over different photodissociation observables, like the branching ratio between the two dissociation channels of CH3I yielding I(2P3/2) and I*(2P1/2) and the fragment angular distributions associated with each channel, is investigated. These magnitudes are found to oscillate strongly with the time delay, with the branching ratio changing by factors between two and three. Substantial variations of the angular distributions also indicate that the scheme provides a high degree of control. Experimental application of the scheme to general polyatomic photodissociation processes should be straightforward.
1 Introduction
Control of molecular photodissociation and reaction processes has been pursued for a long time.1–28 For this purpose, a variety of control strategies have been designed in order to steer the evolution of the molecular dynamics towards a desired target, using both weak and strong laser fields. While control of molecular processes in the strong-field regime has been very successful,7,12,23,27 in some cases it can lead to undesired multiphoton ionization and fragmentation processes of the system under study. Thus, in several situations it is desirable to work in weak-field, one-photon conditions where the above processes are minimized and the inherent dynamics of the system is not significantly altered by the field applied. Effective weak-field control, however, still poses several challenges.It has been shown experimentally8,29–31 and theoretically32 for atomic and diatomic systems that when a weak electric field combining two pulses delayed in time is applied, by varying the time delay between the pulses it is possible to modify the shape of the spectral profile associated with the field, which implies changing the relative populations of the different states excited within a superposition. The shape of the profile changes as the delay between the pulses is varied due to interference between the pulses. Such a combination of pulses produces a spectral profile with a fixed bandwidth that is independent of the delay between the pulses. Thus, the spectral bandwidth of the laser field applied is not modified when the time delay between the pulses is varied.
Based on the above interference effect, a weak-field coherent control scheme has been recently proposed for the first time to modify the asymptotic photofragment state distribution of a polyatomic system, Ne-Br2(B,ν′), produced upon resonance decay.33,34 The scheme was applied to control the long-time, final vibrational distribution of the Br2(B,νf < ν′) fragment produced upon dissociation from an initial superposition of either intermolecular overlapping or isolated resonances,33 and also from initial single isolated resonances.34 The control scheme applied an electric field consisting of two pulses that overlap spectrally with a time delay between them. When the time delay is varied, the shape of the corresponding fixed bandwidth spectral profile changes, causing modulation of the initial population of the different resonances in the superposition, leading to variation of the asymptotic Br2(B,νf < ν′) fragment vibrational distribution. Thus, control of the final fragment distribution is possible just by varying the time delay between the two pulses.
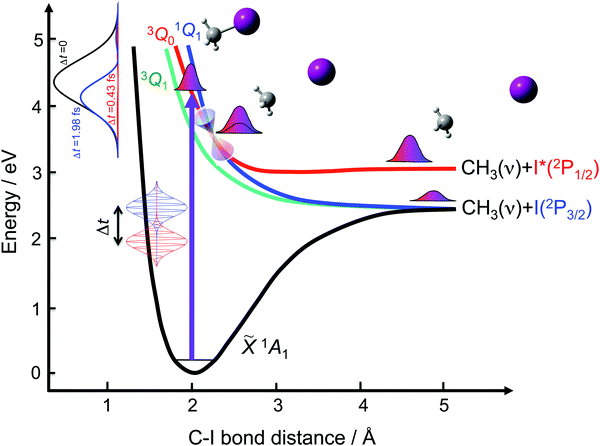
In the previous applications of the control scheme,33,34 the specific interest was to control the fragment state distribution produced in a resonance-mediated photodissociation process on a single excited electronic state. Thus, the spectral bandwidths associated with the laser fields applied were correspondingly narrow, of a few wavenumbers (≤6 cm−1). While it has been shown that for overlapping resonances the fragment state distribution produced upon resonance decay can vary significantly within those narrow energy ranges,35 using a narrow spectral bandwidth limits remarkably the potential performance of the control scheme. It is expected that the scheme will display its largest potential when a broad spectral bandwidth (associated with pulses on the femtosecond or even the attosecond time scale) is used to excite the several electronic states that are usually involved in general polyatomic photodissociation processes. This work pursues investigation of the application of the control scheme under these general conditions of photodissociation. In this sense, the photodissociation process associated with the A-band of the CH3I molecule, which involves excitation to three different electronic states, is an ideal case in order to test the performance of the control scheme.
A great deal of effort has been devoted to investigating the A-band photodissociation of methyl iodide, both experimentally27,36–46 and theoretically.43,44,47–59 In brief, the absorption spectrum associated with this band involves excitation from the ground electronic state ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 to the three excited states 3Q0, 1Q1, and 3Q1 (in Mulliken's notation60). The parallel transition to the 3Q0 state dominates at most of the excitation wavelengths, and particularly at the maximum of the band at 260 nm. Weak perpendicular transitions to 1Q1 and 3Q1 take place at the blue and red edges of the band, respectively. In addition, a conical intersection couples the 3Q0 and 1Q1 states. The 3Q0 state correlates adiabatically with the CH3(
1A1 to the three excited states 3Q0, 1Q1, and 3Q1 (in Mulliken's notation60). The parallel transition to the 3Q0 state dominates at most of the excitation wavelengths, and particularly at the maximum of the band at 260 nm. Weak perpendicular transitions to 1Q1 and 3Q1 take place at the blue and red edges of the band, respectively. In addition, a conical intersection couples the 3Q0 and 1Q1 states. The 3Q0 state correlates adiabatically with the CH3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2′′) + I*(2P1/2) products, while both 1Q1 and 3Q1 correlate with CH3(
2A2′′) + I*(2P1/2) products, while both 1Q1 and 3Q1 correlate with CH3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2′′) + I(2P3/2). Photodissociation through each excited electronic state produces a different output, and thus varying the initial relative population of the three states implies controlling the final global photodissociation yield. As schematically depicted in Fig. 1, the goal of the present work is to investigate to what extent such control can be achieved for different product fragment distributions by applying the above-mentioned control scheme based on two time-delayed excitation pulses.
2A2′′) + I(2P3/2). Photodissociation through each excited electronic state produces a different output, and thus varying the initial relative population of the three states implies controlling the final global photodissociation yield. As schematically depicted in Fig. 1, the goal of the present work is to investigate to what extent such control can be achieved for different product fragment distributions by applying the above-mentioned control scheme based on two time-delayed excitation pulses.
2 Theoretical methodology
The photodissociation of CH3I in the A-band is modeled using a wave packet treatment very similar to that used previously,44 with some modification. The modification has to do with the fact that in the present simulations excitation of the system from the ground electronic state is carried out by means of a laser field with a given time dependence, while in ref. 44 a laser pulse independent of time was used, assuming a Franck–Condon transition of the vibronic ground state to the excited electronic states. The method applied here is briefly described in the following.In order to describe the CH3I system the reduced-dimensionality model of Guo48 has been used. In this model the CH3I molecule is considered as a CXI pseudotriatomic molecule where the pseudoatom X (X = H3) is located at the center-of-mass (CM) of the three H atoms. The model considers three degrees of freedom (DOF) represented by the (R,r,θ) Jacobi coordinates. The dissociation coordinate R is the distance between I and the CH3 (or C–X) CM, r is the C–X distance, which represents the umbrella bend of the C–H3 group (ν2), and θ is the angle between the vectors associated with R and r, and represents the X–C–I bend (ν6). The specific form of the nuclear kinetic energy operator within this model has been given in detail in previous work.43 Since the purpose is to calculate angular distributions of the photofragments, an additional DOF, θR, which is the angle between the laser electric field polarization direction and the CH3–I molecular axis R, is also included.
In the present model four electronic states are considered, namely the ground state ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 and the three excited states 3Q0, 1Q1, and 3Q1. The potential-energy surfaces used to represent these four states, as well as the transition dipole moment functions that couple them, have been described in detail earlier.43,44 Thus, the total wave packet of the system can be expressed as
1A1 and the three excited states 3Q0, 1Q1, and 3Q1. The potential-energy surfaces used to represent these four states, as well as the transition dipole moment functions that couple them, have been described in detail earlier.43,44 Thus, the total wave packet of the system can be expressed as
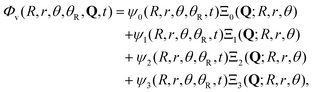 | (1) |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , 3Q0, 1Q1, and 3Q1 states, respectively, and Q denotes the electronic coordinates. The time evolution of the amplitudes ψ0, ψ1, ψ2, and ψ3 is governed by a set of time-dependent coupled equations,
, 3Q0, 1Q1, and 3Q1 states, respectively, and Q denotes the electronic coordinates. The time evolution of the amplitudes ψ0, ψ1, ψ2, and ψ3 is governed by a set of time-dependent coupled equations,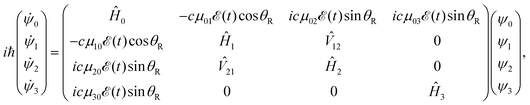 | (2) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) +
+ ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) i (i = 1–3),
i (i = 1–3), ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 12 (
12 (![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 12 =
12 = ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 21) is the nonadiabatic coupling term between the 3Q0 and 1Q1 surfaces, μ0i = μi0 are the transition dipole moments coupling the ground and the excited states,
21) is the nonadiabatic coupling term between the 3Q0 and 1Q1 surfaces, μ0i = μi0 are the transition dipole moments coupling the ground and the excited states, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t) is the pump laser field applied, c = (1/8π2)1/2 is a constant, and the functions c
(t) is the pump laser field applied, c = (1/8π2)1/2 is a constant, and the functions c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR and −ic
θR and −ic![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR determine the parallel and perpendicular character, respectively, of the transitions to 3Q0 on the one hand, and to 1Q1 and 3Q1 on the other hand. The solution of eqn (2) is subject to the initial condition ψ0(R,r,θ,θR,t = 0) = ϕ
θR determine the parallel and perpendicular character, respectively, of the transitions to 3Q0 on the one hand, and to 1Q1 and 3Q1 on the other hand. The solution of eqn (2) is subject to the initial condition ψ0(R,r,θ,θR,t = 0) = ϕ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ν=0(R,r,θ), ψ1(R,r,θ,θR,t = 0) = ψ2(R,r,θ,θR,t = 0) = ψ3(R,r,θ,θR,t = 0) = 0, where ϕ
ν=0(R,r,θ), ψ1(R,r,θ,θR,t = 0) = ψ2(R,r,θ,θR,t = 0) = ψ3(R,r,θ,θR,t = 0) = 0, where ϕ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ν=0(R,r,θ) is the ground vibrational state of CH3I. The total wave packet is propagated until all the amplitude pumped by the laser field to the excited states has reached the asymptotic region. In order to obtain the observable distributions of interest, the wave packet is projected out in the asymptotic region onto the states of the product fragments, namely CH3 + I* and CH3 + I, corresponding to a given total energy of CH3I. In the reduced-dimensionality model applied, the vibrational states of the CH3 fragment correspond to the umbrella and bending modes. The spectral bandwidth of the pump laser applied is taken into account by projecting out the wave packet to calculate the fragment distributions for 9000 total energies of CH3I covering the whole energy range populated by the pump laser, and then averaging over that range to obtain the final product fragment distribution for the observable magnitude of interest.58 Details on the wave packet propagation and projection onto the fragments states have been given elsewhere.43,44,58 As mentioned above, the basis of the control scheme is the pump laser field applied,
ν=0(R,r,θ) is the ground vibrational state of CH3I. The total wave packet is propagated until all the amplitude pumped by the laser field to the excited states has reached the asymptotic region. In order to obtain the observable distributions of interest, the wave packet is projected out in the asymptotic region onto the states of the product fragments, namely CH3 + I* and CH3 + I, corresponding to a given total energy of CH3I. In the reduced-dimensionality model applied, the vibrational states of the CH3 fragment correspond to the umbrella and bending modes. The spectral bandwidth of the pump laser applied is taken into account by projecting out the wave packet to calculate the fragment distributions for 9000 total energies of CH3I covering the whole energy range populated by the pump laser, and then averaging over that range to obtain the final product fragment distribution for the observable magnitude of interest.58 Details on the wave packet propagation and projection onto the fragments states have been given elsewhere.43,44,58 As mentioned above, the basis of the control scheme is the pump laser field applied, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t), which consists of a combination of two Gaussian pulses
(t), which consists of a combination of two Gaussian pulses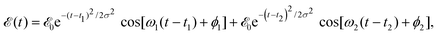 | (3) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 0 = 1.0 × 10−6 a.u., which corresponds to a maximum pulse intensity of about 3.5 × 104 W cm−2, within the weak-field regime. The frequency amplitude profile
0 = 1.0 × 10−6 a.u., which corresponds to a maximum pulse intensity of about 3.5 × 104 W cm−2, within the weak-field regime. The frequency amplitude profile 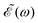 associated with
associated with ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t) is
(t) is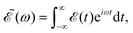 | (4) |
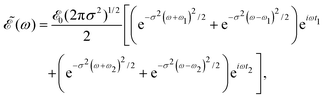 | (5) |
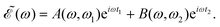 | (6) |
Thus, the spectral profile 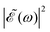 can be expressed as
can be expressed as
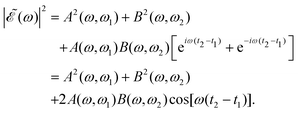 | (7) |
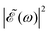 in eqn (7) is a phase dependence term that can be modulated just by varying the time delay Δt = t2 − t1 between the two pulses of
in eqn (7) is a phase dependence term that can be modulated just by varying the time delay Δt = t2 − t1 between the two pulses of ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t). Such a modulation will change the phase of the electric field
(t). Such a modulation will change the phase of the electric field ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t), and correspondingly also the shape of the
(t), and correspondingly also the shape of the 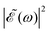 profile, but still keeping the same fixed spectral bandwidth. Actually, varying the time delay between the pulses causes a similar effect as a chirp, because when the time delay between the pulses changes, the different frequencies excited by the two pulses are populated at different times, the same as happens when a chirp is applied. When the
profile, but still keeping the same fixed spectral bandwidth. Actually, varying the time delay between the pulses causes a similar effect as a chirp, because when the time delay between the pulses changes, the different frequencies excited by the two pulses are populated at different times, the same as happens when a chirp is applied. When the 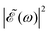 profile prepares a superposition of different quantum states of a system (vibrational and electronic), the change in the shape of
profile prepares a superposition of different quantum states of a system (vibrational and electronic), the change in the shape of 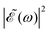 involves a variation of the relative populations initially excited in the superposition, leading to different product fragment distributions. This is the basis of the control scheme.
involves a variation of the relative populations initially excited in the superposition, leading to different product fragment distributions. This is the basis of the control scheme.
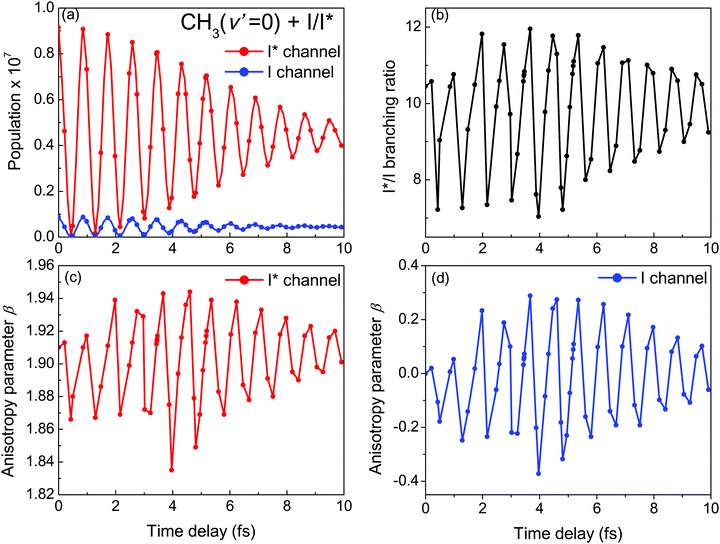
The phase dependence term 2A(ω,ω1)B(ω,ω2)cos(ωΔt) is actually an interference term that arises when 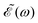 is squared. The requirement for this term to be nonzero is that the product A(ω,ω1)B(ω,ω2) must be nonzero, that is, the bandwidths A(ω,ω1) and B(ω,ω2) of the two pulses of eqn (3) must overlap in a certain range of frequencies ω. When this happens, this term will modulate the spectral profile in that range of frequencies. It is important to notice that the maximum value of cos(ωΔt) = 1 (which occurs at Δt = 0) leads to the maximum intensity of
is squared. The requirement for this term to be nonzero is that the product A(ω,ω1)B(ω,ω2) must be nonzero, that is, the bandwidths A(ω,ω1) and B(ω,ω2) of the two pulses of eqn (3) must overlap in a certain range of frequencies ω. When this happens, this term will modulate the spectral profile in that range of frequencies. It is important to notice that the maximum value of cos(ωΔt) = 1 (which occurs at Δt = 0) leads to the maximum intensity of 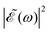 . For all other values cos(ωΔt) < 1, the contribution of the interference term will produce a
. For all other values cos(ωΔt) < 1, the contribution of the interference term will produce a 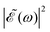 profile with a smaller intensity, reaching a minimum when cos(ωΔt) = −1.
profile with a smaller intensity, reaching a minimum when cos(ωΔt) = −1.
In the present simulations, it is assumed that the two Gaussian pulses of eqn (3) are identical, i.e., ω1 = ω2. In this case A(ω,ω1) = B(ω,ω2), and 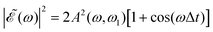 . The implication of this condition is that for those values of Δt leading to cos(ωΔt) = −1, the
. The implication of this condition is that for those values of Δt leading to cos(ωΔt) = −1, the 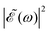 intensity is suppressed. The specific ω1 = ω2 frequencies used correspond to the energy of the maximum of the calculated absorption spectrum of the CH3I A band, namely 38
intensity is suppressed. The specific ω1 = ω2 frequencies used correspond to the energy of the maximum of the calculated absorption spectrum of the CH3I A band, namely 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680 cm−1, associated with the excitation wavelength λ = 258.6 nm from the ground electronic state. The temporal full width at half-maximum (FWHM) of both pulses of eqn (3) is
680 cm−1, associated with the excitation wavelength λ = 258.6 nm from the ground electronic state. The temporal full width at half-maximum (FWHM) of both pulses of eqn (3) is 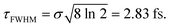
3 Results and discussion
The calculated spectrum associated with the A-band of CH3I is displayed in Fig. 2, along with the sub-bands associated with the adiabatic photodissociation that takes place upon the transitions 3Q0 ←![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1, 1Q1 ←
1A1, 1Q1 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1, and 3Q1 ←
1A1, and 3Q1 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1.44 The sub-band corresponding to 3Q0 is the dominant one, as mentioned above. It is noted that in the calculated spectrum, the intensity of the sub-band associated with the 1Q1 ←
1A1.44 The sub-band corresponding to 3Q0 is the dominant one, as mentioned above. It is noted that in the calculated spectrum, the intensity of the sub-band associated with the 1Q1 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 and 3Q1 ←
1A1 and 3Q1 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 transitions is overestimated with respect to the experimental spectrum.36
1A1 transitions is overestimated with respect to the experimental spectrum.36
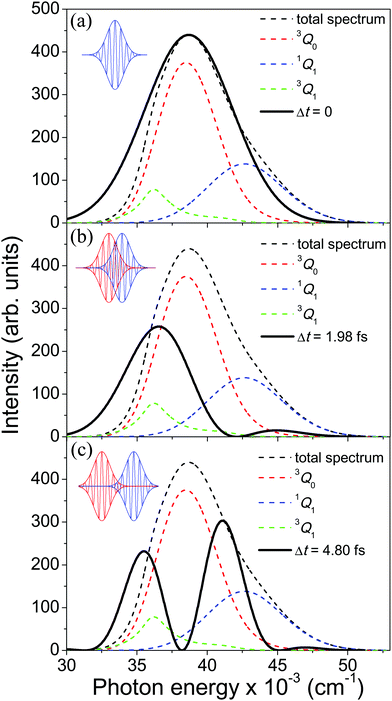 | ||
Fig. 2 Calculated absorption spectrum of the A-band of CH3I, along with the sub-bands associated with the transitions 3Q0 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1, 1Q1 ← 1A1, 1Q1 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1, and 3Q1 ← 1A1, and 3Q1 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1. Also shown are the spectral profiles 1A1. Also shown are the spectral profiles 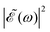 (eqn (7)) of the laser field of eqn (3) applied with three different time delays, (a) Δt = 0, (b) 1.98, and (c) 4.80 fs. (eqn (7)) of the laser field of eqn (3) applied with three different time delays, (a) Δt = 0, (b) 1.98, and (c) 4.80 fs. | ||
As discussed above, the interference term governed by cos(ωΔt) (see eqn (7)) allows one to modify the shape of the laser field spectral profile 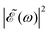 when Δt > 0. By choosing appropriately the delay time between the two pulses of eqn (3),
when Δt > 0. By choosing appropriately the delay time between the two pulses of eqn (3), 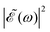 can be shaped so that population of a given region (and therefore of a given sub-band) of the absorption spectrum is favored. This is shown in Fig. 2, where the
can be shaped so that population of a given region (and therefore of a given sub-band) of the absorption spectrum is favored. This is shown in Fig. 2, where the 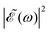 profiles associated with three different time delays, namely Δt = 0, 1.98, and 4.80 fs, are displayed. For Δt = 0 the spectral profile nearly covers all the absorption spectrum, thus populating the three sub-bands associated with 3Q0, 1Q1, and 3Q1. However, for Δt = 1.98 fs the corresponding
profiles associated with three different time delays, namely Δt = 0, 1.98, and 4.80 fs, are displayed. For Δt = 0 the spectral profile nearly covers all the absorption spectrum, thus populating the three sub-bands associated with 3Q0, 1Q1, and 3Q1. However, for Δt = 1.98 fs the corresponding 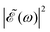 profile populates mainly the 3Q0 and 3Q1 states, minimizing the population of 1Q1, while for Δt = 4.80 fs population of the 1Q1 state is favored. The photodissociation yield in each case is expected to be different.
profile populates mainly the 3Q0 and 3Q1 states, minimizing the population of 1Q1, while for Δt = 4.80 fs population of the 1Q1 state is favored. The photodissociation yield in each case is expected to be different.
A deeper physical insight into how interference between the two pulses operates can be gained by analyzing the behavior of the laser field for different values of Δt. This is done in Fig. 3, where the behavior of both 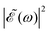 and
and 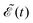 is shown for three time delays which correspond to the situations of maximum (Δt = 0), nearly minimum (Δt = 0.43 fs), and intermediate (Δt = 1.98 fs) intensity of
is shown for three time delays which correspond to the situations of maximum (Δt = 0), nearly minimum (Δt = 0.43 fs), and intermediate (Δt = 1.98 fs) intensity of 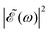 , as displayed in Fig. 3(a). Indeed, for Δt = 0.43 fs we have that cos(ωΔt) ≈ −1, and
, as displayed in Fig. 3(a). Indeed, for Δt = 0.43 fs we have that cos(ωΔt) ≈ −1, and 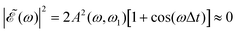 . For simplicity, let us rewrite eqn (3) in a more compact form
. For simplicity, let us rewrite eqn (3) in a more compact form
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t) = (t) = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1(t) + 1(t) + ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 2(t), 2(t), | (8) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) i(t) =
i(t) = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 0e−(t−ti)2/2σ2
0e−(t−ti)2/2σ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos[ωi(t − ti) + ϕi]. The two pulses
cos[ωi(t − ti) + ϕi]. The two pulses ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1(t) and
1(t) and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 2(t), along with the sum of them,
2(t), along with the sum of them, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t), are shown in Fig. 3(b)–(d) for the three Δt values. For Δt = 0,
(t), are shown in Fig. 3(b)–(d) for the three Δt values. For Δt = 0, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1(t) and
1(t) and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 2(t) are identical pulses with the same temporal phase, and the sum of them gives rise to a field
2(t) are identical pulses with the same temporal phase, and the sum of them gives rise to a field ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t) with double the amplitude of each individual pulse. When Δt ≠ 0,
(t) with double the amplitude of each individual pulse. When Δt ≠ 0, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1(t) and
1(t) and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 2(t) become dephased in time, as shown in Fig. 3(c) and (d), which causes destructive interference between them. As a result,
2(t) become dephased in time, as shown in Fig. 3(c) and (d), which causes destructive interference between them. As a result, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t) has a smaller amplitude, even nearly vanishing, for Δt = 0.43 fs, as shown in Fig. 3(c). The decrease of the amplitude of
(t) has a smaller amplitude, even nearly vanishing, for Δt = 0.43 fs, as shown in Fig. 3(c). The decrease of the amplitude of ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t) due to destructive interference is reflected in the decrease of the intensity of the spectral profiles (see Fig. 3(a)). It is interesting to note that interference changes not only the amplitude but also the shape of the temporal profile
(t) due to destructive interference is reflected in the decrease of the intensity of the spectral profiles (see Fig. 3(a)). It is interesting to note that interference changes not only the amplitude but also the shape of the temporal profile ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t) with respect to the Δt = 0 situation. In contrast, if Δt = 1.98 fs, an intermediate situation arises in between maximum (Δt = 0) and minimum (Δt = 0.43 fs)
(t) with respect to the Δt = 0 situation. In contrast, if Δt = 1.98 fs, an intermediate situation arises in between maximum (Δt = 0) and minimum (Δt = 0.43 fs) 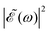 intensity, as depicted in Fig. 3(a).
intensity, as depicted in Fig. 3(a).
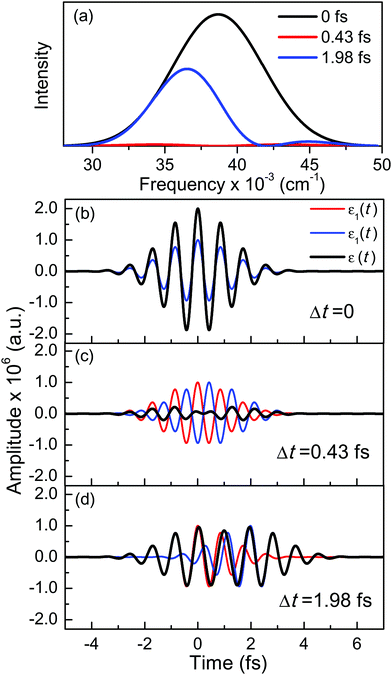 | ||
Fig. 3 (a) Spectral profile 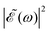 (eqn (7)) of the laser field applied with three different time delays between the two Gaussian pulses, Δt = 0, 0.43, and 1.98 fs, and temporal profiles of the two Gaussian pulses (eqn (7)) of the laser field applied with three different time delays between the two Gaussian pulses, Δt = 0, 0.43, and 1.98 fs, and temporal profiles of the two Gaussian pulses ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1(t) and 1(t) and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 2(t) along with their sum 2(t) along with their sum ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (t) for the time delays (b) Δt = 0, (c) Δt = 0.43 fs, and (d) Δt = 1.98 fs. (t) for the time delays (b) Δt = 0, (c) Δt = 0.43 fs, and (d) Δt = 1.98 fs. | ||
Several quantities have been analyzed in order to assess the degree of control achieved over the output of the CH3I photodissociation process when the time delay Δt between the two excitation pulses is varied. Such quantities include the final populations (when t → ∞) in the CH3(ν′) + I* and CH3(ν′) + I dissociation channels (from now on referred to as the I* and I channels), the branching ratio between these two final populations, and the anisotropy parameter β associated with the angular distributions produced through both channels. The analysis is carried out for the final states ν′ = 0, 1, and 2 of the umbrella mode of the CH3 fragment, and the results are shown in Fig. 4 for ν′ = 0 and in Fig. S1 and S2 (ESI†) for ν′ = 1 and ν′ = 2, respectively (reported as ESI†).
 | ||
| Fig. 4 Behavior of different observables with the time delay Δt between the two excitation pulses of the laser field of eqn (3) for the vibrational state ν′ = 0 of the CH3 fragment. (a) Final populations in the I* and I dissociation channels. (b) Branching ratio I*/I between the final populations in the I* and I dissociation channels. (c) Anisotropy parameter β associated with the angular distribution produced by dissociation through the I* channel. (d) Same as panel (c) for the I channel. | ||
The most interesting result of Fig. 4 and Fig. S1 and S2 (ESI†) is that all quantities investigated display a strongly oscillating behavior with Δt. This behavior is caused by the oscillating nature between 1 and −1 of the cos(ωΔt) term in 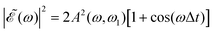 . The oscillations are qualitatively similar for the three vibrational states of the CH3 fragment. The main difference found with the final vibrational quantum number ν′ is the relative population of the I* and I channels (and therefore the branching ratio), determined by the CH3 product vibrational distribution associated with each channel. Around the maximum of the CH3I A-band spectrum, the CH3 vibrational distribution associated with the I* channel is very cold, with most of the population located at ν′ = 0 and little population for ν′ > 0, while the distribution of the I channel is hotter, peaking at ν′ = 1.43
. The oscillations are qualitatively similar for the three vibrational states of the CH3 fragment. The main difference found with the final vibrational quantum number ν′ is the relative population of the I* and I channels (and therefore the branching ratio), determined by the CH3 product vibrational distribution associated with each channel. Around the maximum of the CH3I A-band spectrum, the CH3 vibrational distribution associated with the I* channel is very cold, with most of the population located at ν′ = 0 and little population for ν′ > 0, while the distribution of the I channel is hotter, peaking at ν′ = 1.43
Fig. 4(a) shows the final populations of the CH3(ν′ = 0) fragment produced through the I* and I channels in a range of time delays of nearly 10 fs. As mentioned above, the maximum population occurs in both channels for Δt = 0, which implies that cos(ωΔt) = 1. Then cos(ωΔt) ≈ −1 for Δt = 0.43 fs, and the population of both channels nearly vanishes. A second maximum of the populations occurs at Δt = 0.99 fs, and a second minimum is found at Δt = 1.29 fs. Successive maxima and minima occur in the populations for longer Δt. Since the maxima and minima are determined by cos(ωΔt) = 1 and −1, respectively, the corresponding Δt values can be determined from the conditions
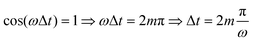 | (9) |
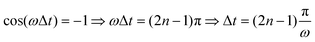 | (10) |
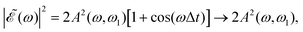 as Δt → ∞, and thus for large Δt the populations converge to an asymptotic value which is half the value found for Δt = 0, as shown by the curves of Fig. 4(a) and Fig. S1(a) and S2(a) (ESI†). In summary, the main finding is that just by varying the time delay Δt, the populations in the two dissociation channels oscillate initially between their maximum values and zero, converging finally to half their maximum value.
as Δt → ∞, and thus for large Δt the populations converge to an asymptotic value which is half the value found for Δt = 0, as shown by the curves of Fig. 4(a) and Fig. S1(a) and S2(a) (ESI†). In summary, the main finding is that just by varying the time delay Δt, the populations in the two dissociation channels oscillate initially between their maximum values and zero, converging finally to half their maximum value.
The variation of the branching ratio between the populations of the two dissociation channels (denoted by I*/I) with Δt is probably even more interesting than that of the populations themselves. The branching ratios corresponding to ν′ = 0, 1, and 2 are shown in Fig. 4(b) and Fig. S1(b) and S2(b) (ESI†), respectively. The three branching ratios display a qualitatively similar structure of pronounced oscillations, related to the oscillations of the populations themselves. The I*/I ratio varies between 7 and 12 for ν′ = 0, between 0.7 and 1.4 for ν′ = 1, and between 0.1 and 0.3 for ν′ = 2. This means a variation of the ratio by about a factor of two for ν′ = 0 and ν′ = 1, and by a factor of three for ν′ = 2 when Δt is changed. In addition, while the maxima and minima of the I* and I populations always coincide, they do not necessarily coincide with the maxima and minima of the corresponding ratios. The interesting implication is that despite the qualitatively similar, in phase oscillations of the I* and I populations with Δt, the quantitative variation of the two populations is significantly different, giving rise to strong variations of the I*/I ratio by factors of two or three that allow for a high degree of control.
Three regions can be distinguished in the behavior of the I*/I ratios of Fig. 4 and Fig. S1 and S2 (ESI†). There is a central region 2–3 fs < Δt < 7 fs where the oscillations of the ratios are more pronounced, while in the side regions Δt < 2–3 fs and Δt > 7 fs the intensity of the oscillations is somewhat weaker. A trivial explanation would be that this effect is due to a lack of resolution in the grid of points of Δt used that would prevent finding the correct position and value of the maxima and minima, which would have a similar value across the whole range of Δt. It is noted, however, that for Δt = 0 (where a possible lack of resolution has no effect) the I* and I populations reach the maximum value possible, but still the value of the corresponding ratio is smaller than the values of the maxima at 2–3 fs < Δt < 7 fs.
While a lack of resolution could contribute to some extent to the effect, an additional explanation is that the variation of the intensity of the oscillations in the ratios as Δt increases is also due to the different behavior of the effect of interference between the two pulses when Δt changes, and how it affects the population of the electronic states correlating with the I* and I channels. For relatively short delays Δt < 2–3 fs the spectral profile 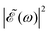 displays few ocillations due to the cos(ωΔt) term. This may favor population of the 1Q1 and 3Q1 states, which lead to the I channel, causing lower maximum and higher minimum values of the I*/I ratio in this region of Δt. In the intermediate region 2–3 fs < Δt < 7 fs the number of oscillations in
displays few ocillations due to the cos(ωΔt) term. This may favor population of the 1Q1 and 3Q1 states, which lead to the I channel, causing lower maximum and higher minimum values of the I*/I ratio in this region of Δt. In the intermediate region 2–3 fs < Δt < 7 fs the number of oscillations in 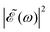 gradually increases, which may alternately favor population of either the 3Q0 or the 1Q1 and 3Q1 states, producing higher differences between the maxima and the minima of the ratio oscillations. Finally, for Δt > 7 fs the effect of the cos(ωΔt) term is vanishing, as shown by the behavior of the individual I* and I populations, and then
gradually increases, which may alternately favor population of either the 3Q0 or the 1Q1 and 3Q1 states, producing higher differences between the maxima and the minima of the ratio oscillations. Finally, for Δt > 7 fs the effect of the cos(ωΔt) term is vanishing, as shown by the behavior of the individual I* and I populations, and then 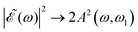 . This spectral profile would populate the whole CH3I absorption spectrum, approaching a situation very similar to that of Δt = 0, which would explain the similar behavior of the ratios for Δt > 7 fs and for Δt = 0. While the present behavior of the I*/I ratios is due to the specific structure of the sub-bands of the CH3I absorption spectrum, the behavior of
. This spectral profile would populate the whole CH3I absorption spectrum, approaching a situation very similar to that of Δt = 0, which would explain the similar behavior of the ratios for Δt > 7 fs and for Δt = 0. While the present behavior of the I*/I ratios is due to the specific structure of the sub-bands of the CH3I absorption spectrum, the behavior of 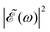 with increasing Δt described above is general for any photodissociation process, and will affect it correspondingly.
with increasing Δt described above is general for any photodissociation process, and will affect it correspondingly.
Angular distributions were calculated for photodissociation into the CH3 + I* and CH3 + I product channels in order to investigate the behavior of these distributions when Δt is varied. In the absence of any conical intersection in between excited states, the only contribution to the I* channel angular distribution would come from the 3Q0 state, while in the case of the I channel the angular distribution would be the sum of the contributions produced upon dissociation through both the 1Q1 and 3Q1 electronic states. The angular distributions obtained for both dissociation channels were fitted to the familiar expression61
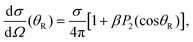 | (11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θR) is the second order Legendre polynomial. From the fits of the angular distributions to eqn (11), the values of β are obtained for the two dissociation channels as the time delay between the two pulses is varied. The 3Q0 ←
θR) is the second order Legendre polynomial. From the fits of the angular distributions to eqn (11), the values of β are obtained for the two dissociation channels as the time delay between the two pulses is varied. The 3Q0 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 transition is a parallel one, while the 1Q1 ←
1A1 transition is a parallel one, while the 1Q1 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 and 3Q1 ←
1A1 and 3Q1 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 transitions have a perpendicular character. This implies that in the absence of a conical intersection, the angular distributions produced through the I* and I channels would have associated parameters β = 2 and β = −1, respectively. However, the existence of a conical intersection that couples 3Q0 and 1Q1 allows transfer of population from one state to the other (in both directions), causing a mix of characters that may produce values of the anisotropy parameter β < 2 and β > −1, for the I* and I channels, respectively. As we shall see below, this transfer of population through the conical intersection is what makes possible the control over the angular distributions by changing the initial population of the three excited electronic states when Δt is varied.
1A1 transitions have a perpendicular character. This implies that in the absence of a conical intersection, the angular distributions produced through the I* and I channels would have associated parameters β = 2 and β = −1, respectively. However, the existence of a conical intersection that couples 3Q0 and 1Q1 allows transfer of population from one state to the other (in both directions), causing a mix of characters that may produce values of the anisotropy parameter β < 2 and β > −1, for the I* and I channels, respectively. As we shall see below, this transfer of population through the conical intersection is what makes possible the control over the angular distributions by changing the initial population of the three excited electronic states when Δt is varied.
The β parameters associated with the angular distributions of the I* and I channels are shown vs. Δt in the (c) and (d) panels of Fig. 4 and Fig. S1, S2 (ESI†) for ν′ = 0–2, respectively. Not surprisingly, the anisotropy parameters for both dissociation channels display a similar structure of oscillations to those found in the upper panels for the populations and the branching ratios. In the case of the I* channel, the oscillating values of β are very close to 2, reflecting the parallel character of the 3Q0 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 transition, and the fact that little population is transferred from the 1Q1 state through the conical intersection across all the range of Δt investigated. Consistently with this small contribution of the 1Q1 population the variation of the I* channel β with Δt is rather small, the largest variations being from 1.84 to 1.94 for ν = 0, from ∼1.965 to ∼1.985 for ν = 1, and from ∼1.865 to ∼1.92 for ν = 2. Such small variations imply very little (or negligible) control of the I* channel angular distribution.
1A1 transition, and the fact that little population is transferred from the 1Q1 state through the conical intersection across all the range of Δt investigated. Consistently with this small contribution of the 1Q1 population the variation of the I* channel β with Δt is rather small, the largest variations being from 1.84 to 1.94 for ν = 0, from ∼1.965 to ∼1.985 for ν = 1, and from ∼1.865 to ∼1.92 for ν = 2. Such small variations imply very little (or negligible) control of the I* channel angular distribution.
The situation, however, is quite different for the I dissociation channel. Indeed the β parameter for this channel shows remarkably larger variations with Δt. The reason is that in the CH3I excitation, the 3Q0 state is the most populated one (as shown by the absorption spectrum of Fig. 2), and thus the fraction of this population that is transferred to the 1Q1 state through the conical intersection is large enough to cause substantial changes in the angular distribution of the I channel. The largest variations found are from −0.4 to 0.3 for ν′ = 0, from ≈−0.4 to ≈0.2 for ν′ = 1, and from ≈−0.4 to ≈0.1 for ν′ = 2. Those variations imply large changes in the exit angle of the photoproducts, and thus a large degree of control of the angular distribution of the I channel.
It is interesting to note that for the three vibrational states of the CH3 fragment, the shape of the β dependence on Δt is very similar for the two dissociation channels, with coinciding positions of the maxima and minima. Moreover, the shape of the two β curves is also very similar to the shape of the corresponding I*/I ratio as a function of Δt, showing three distinct regions, with the most intense oscillations appearing at intermediate Δt values. The coincidence in the shape of the branching ratio and β curves seems to support that their trend is determined by the behavior of the interference cos(ωΔt) term as Δt increases, as discussed above. A close or even exact coincidence (for most of the points) in the position of the maxima and minima of the β curves with those of the branching ratio is found. Such a correlation is not very surprising since when the I*/I ratio reaches a maximum (involving an increase of the I* population), it is expected that the β value of the I* and I channels will also reach a maximum (i.e., becoming closer to 2 and more positive for the I* and I channels, respectively), while when the I*/I ratio reaches a minimum (decreasing the I* population) the expected result is also a minimum of the two β parameters (i.e., becoming farther away from 2 and less positive for the I* and I channels, respectively). The important implication is that by controlling the initial relative population of the different excited electronic states, it is possible to control the photodissociation output of all the observables affected by those states.
For simplicity the present work was restricted to the situation where the two pulses of eqn (3) overlap completely in the frequency domain (ω1 = ω2). It is interesting to comment briefly on what it is expected in the more general scenario of only partial overlap of both pulses (ω1 ≠ ω2). In this case the interference term cos(ωΔt) operates only in the region of frequency overlap (see eqn (3)), and thus control by varying Δt could only be exerted in the region of the absorption spectrum that coincides with that overlapping region. In some cases it may be desirable to restrict the action of control to a limited region of the absorption spectrum, and this can be done by varying the size of the pulse overlap region, changing the carrier frequencies ω1 and ω2 and the spectral width of the two pulses of eqn (3).
4 Conclusions
This work has investigated the performance of a coherent control scheme to modify the output of the ultrafast photodissociation of a polyatomic molecule, with specific application to the photodissociation of CH3I in the A-band. The control scheme applies a pump laser field consisting of two phase-locked few femtosecond pulses of the same frequency delayed in time. By varying the time delay between the pulses, the laser spectral profile is modulated, which changes the initial relative population of the different electronic states involved in the photodissociation process, and produces different photodissociation outputs. Several observable quantities associated with the CH3 + I* and CH3 + I dissociation channels, like the final populations in those channels, the branching ratio between them, and the anisotropy parameters associated with the angular distributions produced through both channels, are investigated to assess the degree of control achieved. It is found that all the quantities studied oscillate strongly across the range of time delays analyzed, giving rise to large variations in general that allow for a high degree of control. In particular, the branching ratio between the two dissociation channels is found to change by factors between two and three. Large variations in the anisotropy parameter of the I channel are also obtained, indicating a remarkable degree of control of the corresponding fragment angular distributions. A conical intersection between two excited states of CH3I is found to play an important role in the control scheme. The present control scheme is envisioned as a powerful tool of straightforward experimental application to control the photodissociation of polyatomic molecules, and experiments are in preparation in our lab.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was funded by the Ministerio de Economía y Competitividad (MINECO, Spain), Grant No. CTQ2015-65033-P, and COST Action program, Grant No. CM1401 and CM1405. A. S.-J. acknowledges a contract from the Programa Operativo de Empleo Juvenil 2014-2020 of Fondo Social Europeo. The Centro de Supercomputación de Galicia (CESGA, Spain) is acknowledged for the use of its resources.References
- D. J. Tannor and S. A. Rice, J. Chem. Phys., 1985, 83, 5013 CrossRef CAS.
- D. J. Tannor and S. A. Rice, J. Chem. Phys., 1986, 85, 5805 CrossRef CAS.
- P. Brumer and M. Shapiro, Chem. Phys. Lett., 1986, 126, 541 CrossRef CAS.
- A. Assion, T. Baumert, M. Bergt, T. Brixner, B. Kiefer, V. Seyfried, M. Strehle and G. Gerber, Science, 1998, 282, 919 CrossRef CAS PubMed.
- P. Anfinrud, R. de Vivie-Riedle and V. Engel, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 8328 CrossRef CAS.
- S. A. Rice and M. Zhao, Optical Control of Molecular Dynamics, Wiley, New York, 2000 Search PubMed.
- R. J. Levis, G. M. Menkir and H. Rabitz, Science, 2001, 292, 709 CrossRef CAS PubMed.
- E. Skovsen, M. Machholm, T. Ejdrup, J. Thøgersen and H. Stapelfeldt, Phys. Rev. Lett., 2002, 89, 133004 CrossRef PubMed.
- C. Daniel, J. Full, L. González, C. Lupulescu, J. Manz, A. Merli, S. Vajda and L. Wöste, Science, 2003, 299, 536 CrossRef CAS PubMed.
- W. Shiu, J. J. Lin and K. Liu, Phys. Rev. Lett., 2004, 92, 103201 CrossRef PubMed.
- M. Wollenhaupt, V. Engel and T. Baumert, Annu. Rev. Phys. Chem., 2005, 56, 25 CrossRef CAS PubMed.
- B. J. Sussman, D. Townsend, M. I. Ivanov and A. Stolow, Science, 2006, 314, 278 CrossRef CAS PubMed.
- H. Katsuki, H. Chiba, B. Girard, C. Meier and K. Ohmori, Science, 2006, 311, 15891592 CrossRef PubMed.
- G. Katz, M. A. Ratner and R. Kosloff, Phys. Rev. Lett., 2007, 98, 203006 CrossRef PubMed.
- M. P. A. Branderhorst, P. Londero, P. Wasylczyk, C. Brif, R. L. Kosut, H. Rabitz and I. A. Walmsley, Science, 2008, 320, 638 CrossRef CAS PubMed.
- O. Atabek, R. Lefebvre, M. Lepers, A. Jaouadi, O. Dulieu and V. Kokoouline, Phys. Rev. Lett., 2011, 106, 173002 CrossRef CAS PubMed.
- M. Shapiro and P. Brumer, Quantum Control of Molecular Processes, Wiley-VCH Verlag GmbH and Co. KGaA, Singapore, 2nd edn, 2012 Search PubMed.
- A. B. Henson, S. Gersten, Y. Shagam, J. Narevicius and E. Narevicius, Science, 2012, 338, 234 CrossRef CAS PubMed.
- A. García-Vela, J. Phys. Chem. Lett., 2012, 3, 1941 CrossRef.
- Z. Hu, S. Singha, Y. Zhao, G. E. Barry, T. Seideman and R. J. Gordon, J. Phys. Chem. Lett., 2012, 3, 2744 CrossRef CAS.
- E. Wells, C. E. Rallis, M. Zohrabi, R. Siemering, B. Jochim, P. R. Andrews, U. Ablikim, B. Gaire, S. De, K. D. Carnes, B. Bergues, R. de Vivie-Riedle, M. F. Kling and I. Ben-Itzhak, Nat. Commun., 2013, 4, 2895 CrossRef CAS PubMed.
- F. Calegari, et al. , Science, 2014, 346, 336 CrossRef CAS PubMed.
- P. Ranitovica, C. W. Hoglea, P. Rivierec, A. Palacios, X.-M. Tongd, N. Toshimad, A. González-Castrillo, L. Martina, F. Martín, M. Murnane and H. Kapteyn, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 912 CrossRef PubMed.
- A. Bergeat, J. Onvlee, C. Naulin, A. van der Avoird and M. Costes, Nat. Chem., 2015, 7, 349 CrossRef CAS PubMed.
- A. García-Vela and N. E. Henriksen, J. Phys. Chem. Lett., 2015, 6, 824 CrossRef PubMed.
- C. Naulin and M. Costes, Chem. Sci., 2016, 7, 2462 RSC.
- M. E. Corrales, J. González-Vázquez, G. Balerdi, I. R. Solá, R. de Nalda and L. Bañares, Nat. Chem., 2014, 6, 785 CrossRef CAS PubMed.
- A. García-Vela, Phys. Rev. Lett., 2018, 121, 153204 CrossRef PubMed.
- M. Wollenhaupt, A. Assion, D. Liese, C. Sarpe-Tudoran, T. Baumert, S. Zamith, M. A. Boucheme, B. Girard, A. Flettner, U. Weichmann and G. Gerber, Phys. Rev. Lett., 2002, 89, 173001 CrossRef CAS PubMed.
- K. Ohmori, Y. Sato, E. E. Nikitin and S. A. Rice, Phys. Rev. Lett., 2003, 91, 243003 CrossRef PubMed.
- C. Petersen, E. Péronne, J. Thϕgersen, H. Stapelfeldt and M. Machholm, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 033404 CrossRef.
- M. Lein, M. Erdmann and V. Engel, J. Chem. Phys., 2000, 113, 3609 CrossRef CAS.
- A. García-Vela, Phys. Chem. Chem. Phys., 2016, 18, 10346 RSC.
- A. García-Vela, J. Chem. Phys., 2016, 144, 141102 CrossRef PubMed.
- A. García-Vela, Chem. Sci., 2017, 8, 4804 RSC.
- A. Gedanken and M. D. Rowe, Chem. Phys. Lett., 1975, 34, 39 CrossRef CAS.
- B. R. Johnson, C. Kittrell, P. B. Kelly and J. L. Kinsey, J. Phys. Chem., 1996, 100, 7743 CrossRef CAS.
- D. W. Chandler and P. L. Houston, J. Chem. Phys., 1987, 87, 1445 CrossRef CAS.
- I. Powis and J. F. Black, J. Phys. Chem., 1989, 93, 2461 CrossRef CAS.
- D. W. Chandler, J. W. Thoman Jr., M. H. M. Janssen and D. H. Parker, Chem. Phys. Lett., 1989, 156, 151 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, J. Chem. Phys., 1998, 109, 4758 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, J. Chem. Phys., 1999, 110, 832 CrossRef CAS.
- R. de Nalda, J. Durá, A. García-Vela, J. G. Izquierdo, J. González-Vázquez and L. Bañares, J. Chem. Phys., 2008, 128, 244309 CrossRef PubMed.
- L. Rubio-Lago, A. García-Vela, A. Arregui, G. A. Amaral and L. Bañares, J. Chem. Phys., 2009, 131, 174309 CrossRef CAS PubMed.
- M. E. Corrales, P. S. Shternin, L. Rubio-Lago, R. de Nalda, O. S. Vasyutinskii and L. Bañares, J. Phys. Chem. Lett., 2016, 7, 4458 CrossRef CAS PubMed.
- M. E. Corrales, R. de Nalda and L. Bañares, Nat. Commun., 2017, 8, 1345 CrossRef PubMed.
- H. Guo and G. C. Schatz, J. Chem. Phys., 1990, 93, 393 CrossRef CAS.
- H. Guo, J. Chem. Phys., 1992, 96, 6629 CrossRef CAS.
- A. D. Hammerich, U. Manthe, R. Kosloff, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1994, 101, 5623 CrossRef.
- Y. Amatatsu, S. Yabushita and K. Morokuma, J. Chem. Phys., 1996, 104, 9783 CrossRef CAS.
- D. Xie, H. Guo, Y. Amatatsu and R. Kosloff, J. Phys. Chem. A, 2000, 104, 1009 CrossRef CAS.
- I. Thanopulos and M. Shapiro, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 031401 CrossRef.
- I. Thanopulos and M. Shapiro, J. Chem. Phys., 2006, 125, 133314 CrossRef PubMed.
- A. B. Alekseyev, H.-P. Liebermann, R. J. Buenker and S. N. Yurchenko, J. Chem. Phys., 2007, 126, 234102 CrossRef PubMed.
- A. B. Alekseyev, H.-P. Liebermann and R. J. Buenker, J. Chem. Phys., 2007, 126, 234103 CrossRef PubMed.
- I. Thanopulos and M. Shapiro, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 074010 CrossRef.
- C. R. Evenhuis and U. Manthe, J. Phys. Chem. A, 2011, 115, 5992 CrossRef CAS PubMed.
- A. García-Vela, R. de Nalda, J. Durá, J. González-Vázquez and L. Bañares, J. Chem. Phys., 2011, 135, 154306 CrossRef PubMed.
- W. Arbelo-González, L. Bonnet and A. García-Vela, Phys. Chem. Chem. Phys., 2013, 15, 9994 RSC.
- R. S. Mulliken, J. Chem. Phys., 1940, 8, 382 CrossRef CAS.
- R. N. Zare, Angular Momentum: Understanding Spatial Aspects in Chemistry and Physiscs, Wiley, New York, 1998 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Trends of different observables with the time delay between two excitation laser pulses for the product vibrational states ν′ = 1 and 2 of the CH3 fragment: final populations in the I* and I dissociation channels, branching ratios between the final populations in the I* and I dissociation channels and anisotropy parameters. See DOI: 10.1039/c9cp01214a |
| This journal is © the Owner Societies 2019 |