 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the preparation and NMR spectroscopic characterization of potassium aluminium tetrahydride KAlH4†
Bodo
Zibrowius
 * and
Michael
Felderhoff
* and
Michael
Felderhoff
 *
*
Max-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany. E-mail: zibrowius@mpi-muelheim.mpg.de; felderhoff@mpi-muelheim.mpg.de
First published on 17th May 2019
Abstract
Potassium aluminium tetrahydride KAlH4 of high phase purity (space group Pnma (62)) was synthesized via a mechanochemical route. The thus obtained material was studied by 27Al and 39K MAS NMR spectroscopy. For both nuclei precise data for the isotropic chemical shift and the quadrupole coupling at T = 295 K were derived (27Al: δiso = (107.6 ± 0.2) ppm, CQ = (1.29 ± 0.02) MHz and η = 0.64 ± 0.02; 39K: δiso = (6.1 ± 0.2) ppm, CQ = (0.562 ± 0.005) MHz and η = 0.74 ± 0.02). The straightforward NMR spectroscopic approach applied here should also work for other complex aluminium hydrides and for many other materials containing half-integer nuclei experiencing small to medium-sized quadrupole couplings.
Introduction
In the quest for materials for reversible hydrogen storage, complex aluminium hydrides have attracted much scientific interest in the last two decades.1–3 Because of its excellent dehydrogenation reversibility under the influence of a catalyst at moderate conditions,4 sodium aluminium tetrahydride NaAlH4 is certainly one of the most studied potential hydrogen storage materials. Besides other methods, X-ray5–8 and neutron diffraction,6–9 Raman scattering10–12 and X-ray absorption13,14 and nuclear magnetic resonance (NMR) spectroscopy5,15–17 have been applied to study NaAlH4 and its decomposition in great detail. Nevertheless, some important questions concerning the mechanism of hydrogen release and uptake remain open.18,19The number of papers devoted to the characterization of the next heavier alkali aluminium hydride KAlH4 is rather limited. Morioka et al.20 have shown that potassium aluminium hydride can reversibly be dehydrogenated and rehydrogenated in the temperature range from 523 to 613 K without any catalysts. The decomposition of KAlH4 into potassium hydride and aluminium metal releases only 4.3 wt% hydrogen compared to 5.6 wt% for the corresponding decomposition of NaAlH4. So, KAlH4 is of course a rather unlikely candidate for a widespread application as hydrogen storage material. Nevertheless, the elucidation of structural details and mechanisms of dehydrogenation and rehydrogenation of KAlH4 and other alkali aluminium hydrides, interesting in its own right, may help to better understand the more promising NaAlH4 hydrogen storage system. Indeed, studies of the decomposition of KAlH4 have revealed the formation of an unknown intermediate either instead of ref. 21 or alongside with ref. 22 the expected formation of the hexahydride K3AlH6. In an in situ powder X-ray diffraction study using synchrotron radiation, three different intermediates with hitherto unknown structures have been found during the decomposition and formation of KAlH4.23 More recently, Ares et al.24 have detected only K3AlH6 as intermediate in both the mechanochemical synthesis and the subsequent decomposition of KAlH4. These at least partially contradictory findings might indicate that the release and uptake reactions in alkali aluminium hydrides are more complex than hitherto thought and might also depend on the experimental conditions used.
There are at least two straightforward preparation methods for KAlH4. The first is a direct synthesis reported by Ashby et al.25 starting from metallic potassium (or potassium hydride) and metallic aluminium under hydrogen pressure at elevated temperatures in diglyme. After precipitation with a nonpolar solvent, filtration and careful drying, a pure KAlH4 material can be obtained. Alternatively, the direct hydrogenation can be performed under mechanochemical conditions.24,26 Another, less demanding preparation method for KAlH4 is the salt metathesis reaction starting from a potassium halide and NaAlH4 or LiAlH4 under mechanochemical conditions.21 To remove the produced alkali halide, a subsequent treatment with diglyme is necessary. The pure KAlH4 can once again be obtained after precipitation, filtration and drying.
To the best of our knowledge, there are only four reports on NMR studies of potassium aluminium tetrahydride. Tarasov et al.27 studied KAlH4 by using 27Al and 39K NMR on stationary (non-spinning) samples. They reported chemical shift and quadrupole coupling data for both nuclei. Surprisingly, the authors found three different aluminium species with distinctly different quadrupole couplings. They interpreted their findings in terms of a static orientational disorder of the [AlH4]− anions. According to the widely accepted structure solutions for KAlH428 and KAlD4,29 all aluminium atoms are equivalent. Later on, Tarasov et al.30 studied the thermal decomposition of KAlH4 by the same methods. They identified the decomposition products potassium hydride KH and aluminium metal and the intermediate hexahydride K3AlH6.
The third, more recently published paper by Sorte et al.31 is mainly devoted to the study of the dynamics of the [AlH4]− anions. To this end, 1H and 27Al NMR measurements on a stationary sample were performed in a wide temperature range. The experimental results with respect to the quadrupole coupling do not really fit those obtained earlier. The 27Al NMR line measured for the stationary sample at room temperature is broad, but the singularities typical of quadrupole coupling are missing. This holds also for the sideband pattern observed in the 27Al MAS NMR spectrum. The authors assume “that the quadrupolar singularities were broadened by some disorder, resulting in a distribution of the parameters” which are describing the quadrupole coupling. For the additionally given 39K NMR spectrum, the disagreement with the earlier work27 is even more evident. Sorte et al.31 finally arrive at the rather unsatisfactory conclusion “that there may be other crystal structures present in our KAlH4 or that used in the previous study.” In the fourth, above already mentioned paper, Ares et al.24 used 27Al and 1H MAS NMR spectroscopy to characterize their KAlH4 samples obtained via direct hydrogenation under ball milling conditions. Although the spectral resolution achieved in the 27Al MAS NMR spectra is way better than in the earlier papers, the authors have to admit that the “lack of sharp feature in the first-order quadrupolar spinning-sideband pattern suggests that structural disorder exists.” Since materials produced by ball milling usually consist of very small particles with a large number of defects this finding is not surprising.
Recent papers5,15,16 on the sodium aluminium hydrides NaAlH4 and Na3AlH6 have shown that the NMR parameters, which mirror the site geometry, can reliably be determined for both the aluminium atom and the alkali cation if well-defined alkali aluminium hydride samples are used. In our very recent study on CsAlH432 we were able to unambiguously distinguish two different polymorphs present in the freshly precipitated hydride on the basis of well resolved 27Al and 133Cs MAS NMR spectra.
The aim of the present paper is to demonstrate that KAlH4 with the previously described structure29 can readily be synthesized following the established metathesis procedure. The thus obtained material exhibits a sufficient crystallinity and phase purity and allows the NMR chemical shift and quadrupole coupling parameters to be determined with high accuracy. The precise determination of these parameters combined with state-of-the-art DFT calculations offers an alternative approach to high-quality structures for polycrystalline materials. This NMR crystallographic approach is particularly helpful when diffraction-based methods are hampered by crystal twinning and stacking faults.33
To ease the understanding of the procedure used for the extraction of the relevant parameters, we give a brief summary of important peculiarities of solid-state NMR spectroscopy of quadrupolar nuclei. The procedure outlined for 27Al can be considered as a blueprint for NMR studies of materials containing half-integer quadrupolar nuclei with small to medium values of the coupling constant.
Experimental
Synthesis of KAlH4
All procedures were performed under argon as protective gas atmosphere and with carefully dried solvents. 3.00 g (40.2 mmol) KCl and 2.15 g (40.2 mmol) of NaAlH4 were mechanochemically treated in a planetary ball mill for 3 h (Pulverisette P7, 500 rpm, hardened steel milling vial 45 ml with 7 balls 13.5 g each, 15 min milling, 10 min break after each milling period, 12 repetitions). The resulting powder was suspended in 25 ml diglyme and stirred for 12 h. After filtration, KAlH4 was precipitated through the addition of toluene and filtered off. The carefully dried KAlH4 contained small amounts of unreacted NaAlH4 observable in the X-ray diffraction pattern. Pure KAlH4 was obtained after treatment with 20 ml tetrahydrofurane for 12 h, filtration and drying in vacuum.X-ray diffraction
The X-ray diffraction (XRD) measurements were carried out in Debye–Scherrer transmission geometry on a STOE STADI P diffractometer using Cu Kα1 (λ = 1.5460 Å) radiation. To avoid any contact with air, sealed 0.5 mm diameter glass capillaries were used. The data were collected with a linear position sensitive detector fabricated by Stoe in the 15–80° 2Θ range.Solid-state NMR spectroscopy
The NMR spectra were recorded on a Bruker Avance III HD 500WB spectrometer using double-bearing MAS probes (DVT BL4) at resonance frequencies of 130.3 MHz and 23.3 MHz for 27Al and 39K, respectively. The magic angle was adjusted by maximizing the rotational echoes of the 23Na resonance of solid NaNO3.For the 27Al MAS NMR spectra, single π/12 pulses (tp = 0.6 μs) were applied at a repetition time of 2 s (2000–16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 scans) and spinning frequencies (νMAS) between 1.4 and 8.0 kHz. High-power proton decoupling (SPINAL-64) was used for all spectra shown in this paper, although its influence on the spectral resolution was hardly noticeable at spinning frequencies above 5 kHz. The 27Al chemical shifts were referenced relative to an external 1.0 M aqueous solution of aluminium nitrate. The same solution was used for determining the flip-angle.
000 scans) and spinning frequencies (νMAS) between 1.4 and 8.0 kHz. High-power proton decoupling (SPINAL-64) was used for all spectra shown in this paper, although its influence on the spectral resolution was hardly noticeable at spinning frequencies above 5 kHz. The 27Al chemical shifts were referenced relative to an external 1.0 M aqueous solution of aluminium nitrate. The same solution was used for determining the flip-angle.
For the 39K MAS NMR spectra, single π/8 pulses (tp = 3.0 μs) were applied at a repetition time of 6 s (4000–24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 scans) and spinning frequencies between 4.0 and 6.0 kHz. The 39K chemical shifts are given with respect to 1.0 M aqueous solution of potassium chloride using solid potassium chloride (νMAS = 6 kHz) with its sharp resonance at δ = 47.8 ppm34 as secondary standard. Solid potassium chloride was also used for determining the flip-angle.
000 scans) and spinning frequencies between 4.0 and 6.0 kHz. The 39K chemical shifts are given with respect to 1.0 M aqueous solution of potassium chloride using solid potassium chloride (νMAS = 6 kHz) with its sharp resonance at δ = 47.8 ppm34 as secondary standard. Solid potassium chloride was also used for determining the flip-angle.
Both the spinning-sideband patterns of the 27Al MAS NMR spectra and the centrebands of the 39K MAS NMR spectra were simulated by using the solids lineshape analysis module implemented in the TopSpin™ 3.2 NMR software package from Bruker BioSpin GmbH. Throughout the paper any effect of chemical shift anisotropy on the 27Al NMR lineshape is neglected.
Results and discussion
Structure
Fig. 1 shows the X-ray powder diffraction pattern measured for our KAlH4 sample in comparison with a calculated diffraction pattern based on the structural data for KAlD4.29 To account for the difference between KAlH4 and KAlD4, the lattice parameters (in Å) were slightly adjusted: a = 8.8475 (8.8514), b = 5.81428 (5.8119) and c = 7.3448 (7.3457). The values in parentheses are those reported by Hauback et al.29 for KAlD4 at T = 295 K. The agreement between the calculated and the observed pattern shows that the material under study is structurally identical to the previously reported orthorhombic potassium aluminium tetrahydride KAlH4.20,28,29,35 No crystalline by-product can be identified in the powder pattern in Fig. 1. According to the structure solutions for KAlH4 in space group Pnma (62)29 or Pbnm (62),28 both the aluminium and the potassium atoms as well as half of the hydrogen atoms are located in Wyckoff position 4c, i.e., they sit on mirror planes.27Al MAS NMR spectroscopy
Different regions of a 27Al MAS NMR spectrum of the above structurally characterized KAlH4 sample are depicted in Fig. 2. The bottom trace shows the centreband region with an almost symmetrical line at 106.9 ppm. This position of the resonance line agrees with those reported in the previous studies of KAlH424,27,31 and fits into the range generally obtained for isolated [AlH4]− units in alkali aluminium hydrides.36 The linewidth of about 190 Hz (full width at half height, FWHH) is comparable with that measured for the isostructural orthorhombic CsAlH4 under the same experimental conditions.32 It should be noted that spinning the sample at about 3 kHz results in the best spectral resolution. A further increase in the spinning speed leads to a significant broadening and a high-field shift of the centreband. This effect can easily be explained by a non-uniform increase in temperature over the length of the sample brought about by frictional heating.37,38 At νMAS = 8 kHz, a centreband with a width of about 230 Hz is observed at 106.8 ppm. Although no indication of crystalline by-products was found in the XRD powder pattern of the sample after the treatment with tetrahydrofurane, a close inspection of the spectrum in Fig. 2 reveals the presence of traces of both NaAlH4 and Na3AlH6 (see ESI,† Fig. S1).Since 27Al is a nucleus with a spin  , the NMR spectrum consists not only of the central transition
, the NMR spectrum consists not only of the central transition 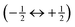 , but comprises also the pair of inner satellite transitions
, but comprises also the pair of inner satellite transitions  and
and 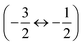 and the pair of outer satellite transitions
and the pair of outer satellite transitions  and
and  .39,40 These pairs of satellite transitions are symmetric, i.e., the lineshape of a satellite transition (−m ↔ −m + 1) is a mirror image of the lineshape of the transition (m − 1 ↔ m). The quadrupole interaction does not only cause several, usually broad, resonance lines per nucleus, but also shifts the positions of the resonance lines with respect to those given by the Larmor equation. This additional shift of the resonance lines occurs with and without sample spinning. Hence, as distinct from the case of nuclei with
.39,40 These pairs of satellite transitions are symmetric, i.e., the lineshape of a satellite transition (−m ↔ −m + 1) is a mirror image of the lineshape of the transition (m − 1 ↔ m). The quadrupole interaction does not only cause several, usually broad, resonance lines per nucleus, but also shifts the positions of the resonance lines with respect to those given by the Larmor equation. This additional shift of the resonance lines occurs with and without sample spinning. Hence, as distinct from the case of nuclei with 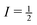 , the position of the centreband is not identical with the isotropic chemical shift δiso. Instead, the position of the centre of gravity of the resonance line δcg of the (m − 1 ↔ m) transition of a quadrupolar nucleus differs from δiso by the so-called quadrupole-induced shift δqis(m):
, the position of the centreband is not identical with the isotropic chemical shift δiso. Instead, the position of the centre of gravity of the resonance line δcg of the (m − 1 ↔ m) transition of a quadrupolar nucleus differs from δiso by the so-called quadrupole-induced shift δqis(m):
| δcg(m) = δiso + δqis(m). | (1) |
 | (2) |
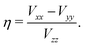 | (3) |
 | (4) |
Although the effects of the quadrupole interaction on shape and position of NMR lines are well known to experts in the field, line positions observed in NMR spectra of quadupolar nuclei are very often erroneously reported as chemical shifts. For the central transition, the quadrupole-induced shift is always negative, i.e., the resonance line is shifted to higher field. By determining δcg(m) for two different values of m, the isotropic chemical shift δiso can be experimentally obtained in a reliable way. In particular, for a nucleus with 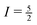 the quadrupole-induced shift of the inner satellite transitions is given by
the quadrupole-induced shift of the inner satellite transitions is given by 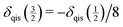 .41 Hence, the isotropic chemical shift can easily be calculated from the following relation:
.41 Hence, the isotropic chemical shift can easily be calculated from the following relation:
 | (5) |
For the sample under study, the centreband and the first spinning sidebands (enlarged in the blue insets above the bottom trace of Fig. 2) obviously contain contributions of both the central transition and the satellite transitions. The top trace of Fig. 2 shows the third to fifth spinning sidebands of the same spectrum. These spinning sidebands contain only the well-resolved contributions of the inner and outer satellite transitions. The width of the symmetric spinning sidebands of the inner satellites is about 115 Hz (FWHH). From the positions of the spinning sidebands +5 to +3 and −3 to −5, we obtain 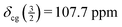 . With
. With 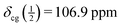 we arrive at δiso = (107.6 ± 0.2) ppm at T = 295 K. The margin of error given is a rather conservative estimate, taking into account possible errors in the calibration with the external standard and the above mentioned effect of a temperature increase by frictional heating under MAS.
we arrive at δiso = (107.6 ± 0.2) ppm at T = 295 K. The margin of error given is a rather conservative estimate, taking into account possible errors in the calibration with the external standard and the above mentioned effect of a temperature increase by frictional heating under MAS.
The well-resolved MAS NMR spectrum in Fig. 2 does not only allow the correct isotropic chemical shift to be determined, but also the strength of the quadrupole coupling to be estimated. The splitting between the maxima of the spinning sidebands of the two pairs of satellite transitions amounts to (2.3 ± 0.1) ppm. Eqn (1) implies that the splitting is caused by the difference in the quadrupole-induced shifts. Eqn (4) shows that for  this difference is given by
this difference is given by
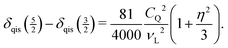 | (6) |
 | (7) |
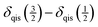 . However, this difference is only one third of that given in eqn (6). Provided that the spinning sidebands of the outer satellite transitions are well resolved, calculations based on eqn (6) are more precise.
. However, this difference is only one third of that given in eqn (6). Provided that the spinning sidebands of the outer satellite transitions are well resolved, calculations based on eqn (6) are more precise.
We can even go one step further. At sufficiently low spinning speeds, the envelope of the spinning sidebands agrees with the lineshape one would obtain for a stationary sample. The total spread of the resonance line caused by a pair of satellite transitions (ΔνTS(m)) depends on the quadrupole coupling constant CQ, but is independent of the asymmetry parameter η.46 Hence, the range over which the spinning sidebands can be observed yields a rather good estimate for CQ. If the range over which sidebands are actually detected is limited by the finite bandwidth of the probe, the excitation or the receiver, spectra with various frequency offsets can be taken to overcome these limitations. For the 27Al nucleus (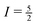 ), the relation between ΔνTS(m) and CQ reads as39,46
), the relation between ΔνTS(m) and CQ reads as39,46
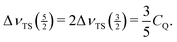 | (8) |
27Al MAS NMR spectra of KAlH4 measured at different spinning frequencies are summarized in Fig. 3. The spectrum in the middle shows the same spectrum as Fig. 2, but now in a wide range of 6700 ppm corresponding to about 0.87 MHz. The two sets of spinning sidebands caused by the inner and outer satellite transitions can easily be discerned. In the spectrum measured at the lowest spinning frequency (top trace in Fig. 3), the sidebands of the inner satellites spread from 1620 ppm to −1410 ppm ( ) and those of the outer satellites from 3130 ppm to −2920 ppm (
) and those of the outer satellites from 3130 ppm to −2920 ppm (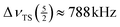 ). Since the range of the spinning sidebands of the outer satellite is about twice as wide as the range of the inner satellite, we can exclude detection problems caused by a limited bandwidth. With the estimate for
). Since the range of the spinning sidebands of the outer satellite is about twice as wide as the range of the inner satellite, we can exclude detection problems caused by a limited bandwidth. With the estimate for  , eqn (8) yields a value for the quadrupole coupling constant of CQ ≈ 1.32 MHz. This result falls into the range derived above from the splitting of the spinning sidebands of the satellite transitions. From this value for CQ and the above determined value for the quadrupolar interaction product P, we obtain a first estimate for the asymmetry parameter: η ≈ 0.6. The non-vanishing asymmetry parameter corresponds to the fact that the aluminium atoms are located in Wyckoff position 4c in Pnma KAlH4. There is no Cn axis with n ≥ 3 going through this position.
, eqn (8) yields a value for the quadrupole coupling constant of CQ ≈ 1.32 MHz. This result falls into the range derived above from the splitting of the spinning sidebands of the satellite transitions. From this value for CQ and the above determined value for the quadrupolar interaction product P, we obtain a first estimate for the asymmetry parameter: η ≈ 0.6. The non-vanishing asymmetry parameter corresponds to the fact that the aluminium atoms are located in Wyckoff position 4c in Pnma KAlH4. There is no Cn axis with n ≥ 3 going through this position.
A more precise estimate of the asymmetry parameter can be obtained when the ratio between the splitting of the maxima of the inner satellite transition ( ) and the total spread of this transition (
) and the total spread of this transition (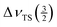 ) is used. From the definition of η (eqn (3)) and the fact that the field gradient tensor is traceless, it follows that for any transition m the asymmetry parameter is related to the characteristic points of the first-order quadrupole lineshape by the following equation:
) is used. From the definition of η (eqn (3)) and the fact that the field gradient tensor is traceless, it follows that for any transition m the asymmetry parameter is related to the characteristic points of the first-order quadrupole lineshape by the following equation:
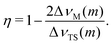 | (9) |
The spectrum measured at νMAS = 1.4 kHz (top trace in Fig. 3) yields  . With the above derived value for
. With the above derived value for 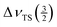 we obtain η ≈ 0.65. This value of the asymmetry parameter and the above derived one for the quadrupole coupling constant have been used to simulate the lineshape of the satellite transitions one would obtain for a non-spinning sample (cf.Fig. 3).
we obtain η ≈ 0.65. This value of the asymmetry parameter and the above derived one for the quadrupole coupling constant have been used to simulate the lineshape of the satellite transitions one would obtain for a non-spinning sample (cf.Fig. 3).
Fig. 3 shows that spinning at 1.4 kHz is still too fast to avoid significant deviations of the envelope of the sideband pattern from the lineshape of the stationary sample. Almost three decades ago, Jakobsen and co-workers have demonstrated that these characteristic intensity modulations of the spinning sidebands of the satellite transitions can be used to determine the values of the parameters CQ and η with high accuracy.44,45 Nowadays, the software to perform this kind of lineshape simulations comes with the spectrometer. Using the above derived values for the parameters δiso, CQ and η as starting values for the fit, only a few iteration cycles are necessary to reach a nice agreement between experiment and simulation, as shown in Fig. 4. The reduced intensities in the outer wings of the experimental sideband pattern are mainly caused by the limited excitation width of the rf pulses used. The quality of the fit can better be judged from the enlarged version of Fig. 4 given as Fig. S2 in the ESI.†
By varying the simulation parameters and carefully comparing the simulated with the experimental spectrum we finally derived the following values for the parameters describing the quadrupole interaction: CQ = (1.29 ± 0.02) MHz and η = 0.64 ± 0.02. A comparison between experiment and simulation for νMAS = 3.0 kHz (Fig. S3) and a complete list of the parameters used for the simulation of the sideband patterns (Table S1) can be found in the ESI.†
From the strength of the quadrupole coupling found for 27Al in KAlH4, it is apparent why the centreband of the central transition in Fig. 2 does not show any indication of second-order quadrupolar broadening. The mathematical expressions for the characteristic features of the lineshape for a quadrupolar nucleus with a half-integer spin I under MAS conditions were derived decades ago. With the expressions given by Freude and Haase42 for the minimum and maximum frequencies, the total width of the MAS centreband of the central transition is obtained as
 | (10) |
 and the above determined values of CQ and η, eqn (10) yields
and the above determined values of CQ and η, eqn (10) yields  . The total broadening caused by second-order quadrupole interaction exceeds the experimental FWHH of the centreband of the central transition by only a few Hertz. Other broadening mechanisms such as the homonuclear dipole–dipole interaction or the line broadening caused by structural defects mask the effect of second-order quadrupole interaction.
. The total broadening caused by second-order quadrupole interaction exceeds the experimental FWHH of the centreband of the central transition by only a few Hertz. Other broadening mechanisms such as the homonuclear dipole–dipole interaction or the line broadening caused by structural defects mask the effect of second-order quadrupole interaction.
The two-dimensional one pulse (TOP) presentation of 1D MAS NMR spectra47 can offer an alternative convenient way to extract the relevant parameters for half-integer quadrupolar nuclei. We have added such a presentation of an experimental spectrum shown in Fig. 3 as Fig. S4 to the ESI.† The line positions of the central transition and the satellite transitions can be read out directly from this plot. The lack of any significant second-order quadrupolar broadening is obvious.
Provided that neither other broadening mechanisms nor the presence of by-products obscure the characteristic features of the quadrupolar lineshape, the parameters describing the quadrupole interaction can alternatively be derived from spectra measured without spinning the sample under the magic angle. Because of the width of these spectra, corresponding to a very fast decay of the NMR signal, the spectra of stationary samples have to be measured with an appropriate echo technique to overcome the inevitable dead time problems after a strong radio pulse. For molecular aluminophosphate compounds containing aluminium nuclei with quadrupole coupling constants slightly larger than the one observed here, the Solomon echo sequence48 has successfully been applied as an alternative approach for the determination of CQ and η.49
The values determined for CQ and η in the present paper do not agree with any of the pairs of quadrupole coupling parameters determined by Tarasov et al.27 for the three different sites they found (CQ in MHz/η: 0.58/0.1, 2.07/0.0, 2.8/0.05). The authors inferred the presence of these different sites with different quadrupole couplings from a pattern of very weak resonance lines on both sides of the strong central line of KAlH4. On the other hand, the authors mention the presence of a by-product giving rise to a broad line in the 27Al NMR spectrum. Unfortunately, no diffraction data are reported. Based on chemical analysis, the authors state a phase purity of no more than 95–97%. Hence, we refrain from speculating about the origin of this obvious disagreement with our data.
Sorte et al.31 reported first-order quadrupole patterns “from both MAS and quadrupole echoes, with no sharp singularities.” The lack of well-defined lineshapes is obviously due to the rather questionable quality of the KAlH4 sample used. It should be noted that the NMR measurements were performed on the unannealed material, i.e., not on the material whose XRD pattern is given in the paper. Apart from the obvious presence of a significant amount of metallic aluminium, the authors mention several reflections in the XRD pattern of the unannealed material that do not correspond to Pnma KAlH4 and assign them to unknown impurities or to other crystal phases of KAlH4.31 With these characteristics of the material it is debatable as to which extent the experimental results obtained mirror intrinsic properties of KAlH4 and not the peculiarities of the sample measured.
Ares et al.24 reported rather well resolved 27Al MAS NMR spectra for KAlH4 samples synthesized via direct hydrogenation under mechanochemical conditions with and without the presence of different metal chlorides. To further compare our material with those used in this recent study, we measured 1H MAS NMR spectra at different spinning frequencies (cf. Fig. S5 in the ESI†). The 1H resonance line of KAlH4 at about 3 ppm (FWHH ≈ 1.3 kHz at νMAS = 8 kHz) is very similar to those reported by Ares et al.,24 except that our spectra do not show any indication of the presence of KH. Their 27Al MAS NMR spectra are also very similar to those we recorded for samples directly after the salt metathesis, i.e., prior to the recrystallisation procedure described above. We believe that the lack of sharp features in the first-order quadrupolar spinning-sideband patterns noticed by the authors24 is typical of materials produced by ball milling since they usually consist of very small particles with a large number of defects. In particular, the presence of strong spinning sidebands of the central transition masks the minimum in the envelope of the spinning sidebands of the inner satellite transition in the centre of the line. This leads to the erroneous assumption of a small or even vanishing asymmetry parameter. Furthermore, we have never achieved a sufficient resolution of the sidebands of the outer and inner satellite transition for samples obtained directly from ball milling. The attempt undertaken by Ares et al.24 to fit the sideband envelope by using the parameters reported by Tarasov et al.27 was bound to fail. Hence, we are left without any 27Al NMR study on KAlH4 we can compare our results with.
For the much better studied NaAlH4, which crystallises in the tetragonal space group I41/a,9 a significantly stronger quadrupole coupling has been found (CQ = 3.15 MHz15). Since the Al atoms in NaAlH4 are located in Wyckoff position 4b, i.e., on a C4 axis, the asymmetry parameter is zero. For the monoclinic LiAlH4 (space group P21/c50) an even stronger quadrupole coupling (CQ = 3.90 MHz51,52) has been reported. The asymmetry parameter for LiAlH4 has been determined as 0.3051 or 0.24.52 For both the orthorhombic and the tetragonal phases of CsAlH4, centrebands of the 27Al central transition have been observed32 that are almost as narrow and without any indication of second-order quadrupole interaction as the centrebands obtained here for KAlH4. Hence, we estimate that the strength of the quadrupole coupling for both modifications of CsAlH4 is similar to that of KAlH4.
39K MAS NMR spectroscopy
Because of the relatively low gyromagnetic ratio of the 39K isotope (natural abundance: 93.3%, ), the intensity of the resonance line is much weaker than in the case of the same number 27Al nuclei at the same field. Furthermore, quadrupole coupling constants of up to 3.2 MHz have been found for the cation in simple potassium salts.53 For
), the intensity of the resonance line is much weaker than in the case of the same number 27Al nuclei at the same field. Furthermore, quadrupole coupling constants of up to 3.2 MHz have been found for the cation in simple potassium salts.53 For  a quadrupole coupling of this strength leads to much wider resonance lines than in the case of
a quadrupole coupling of this strength leads to much wider resonance lines than in the case of  . As can be seen in eqn (10), the total width of the central transition due to second-order quadrupole interaction scales with the factor
. As can be seen in eqn (10), the total width of the central transition due to second-order quadrupole interaction scales with the factor 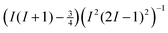 . However, with the sensitivity of modern NMR spectrometers operating at sufficiently high magnetic fields the detection of 39K NMR lines for solids is usually no serious problem, provided that the samples are well defined.
. However, with the sensitivity of modern NMR spectrometers operating at sufficiently high magnetic fields the detection of 39K NMR lines for solids is usually no serious problem, provided that the samples are well defined.
A 39K MAS NMR spectrum of our KAlH4 sample is shown in Fig. 5. The shape of the centreband of the central transition is clearly governed by second-order quadrupole interaction. The spectrum exhibits the discontinuities characteristic of this type of interaction. The overall lineshape indicates a non-vanishing asymmetry parameter.39 Since the potassium cation sits in Wyckoff position 4c in Pnma KAlH4,29 this finding is not surprising. The total spread of the resonance line  is about 920 Hz. Assuming an asymmetry parameter of 0.8, eqn (10) yields an estimate for the quadrupole coupling constant: CQ ≈ 0.5 MHz. These values were used as starting values for an iterative simulation of the lineshape. As Fig. 5 shows, the simulation does not only reproduce the characteristic features of the centreband of the central transition, but identifies the spectral intensity on the low-field side of this line as the much weaker centreband of the satellite transitions
is about 920 Hz. Assuming an asymmetry parameter of 0.8, eqn (10) yields an estimate for the quadrupole coupling constant: CQ ≈ 0.5 MHz. These values were used as starting values for an iterative simulation of the lineshape. As Fig. 5 shows, the simulation does not only reproduce the characteristic features of the centreband of the central transition, but identifies the spectral intensity on the low-field side of this line as the much weaker centreband of the satellite transitions  and
and  . There is no indication of the presence of any potassium-containing by-product. By comparing simulated and experimental spectra measured at different spinning speeds we derived the following parameters: δiso = (6.1 ± 0.2) ppm, CQ = (0.562 ± 0.005) MHz and η = 0.74 ± 0.02.
. There is no indication of the presence of any potassium-containing by-product. By comparing simulated and experimental spectra measured at different spinning speeds we derived the following parameters: δiso = (6.1 ± 0.2) ppm, CQ = (0.562 ± 0.005) MHz and η = 0.74 ± 0.02.
At first glance, there is a large discrepancy between our data and those reported by Tarasov et al.: δiso = (−49 ± 5) ppm, CQ = (1.12 ± 0.07) MHz and η = (0.83 ± 0.05).27 However, this discrepancy can easily be resolved. Tarasov et al.27 used a procedure outlined by Granger54 to extract the parameters of the quadrupole interaction from their spectrum measured for a stationary sample. Unfortunately, they overlooked an obvious typo in the original paper. The correct equation for CQ should read
 | (11) |
 , using a factor (2I + 1) instead of the correct (2I − 1) accounts for a factor of two for the quadrupole coupling constant. Hence, our data for the quadrupole coupling actually agree very nicely with those found by Tarasov et al.27Eqn (11) follows directly from the mathematical expressions found for the minimum and maximum frequencies of the central transition for a half-integer nucleus that is subjected to second-order quadrupole interaction.42 In analogy to eqn (10) for a sample under MAS conditions, the total spread of the resonance line for a stationary sample is given by:
, using a factor (2I + 1) instead of the correct (2I − 1) accounts for a factor of two for the quadrupole coupling constant. Hence, our data for the quadrupole coupling actually agree very nicely with those found by Tarasov et al.27Eqn (11) follows directly from the mathematical expressions found for the minimum and maximum frequencies of the central transition for a half-integer nucleus that is subjected to second-order quadrupole interaction.42 In analogy to eqn (10) for a sample under MAS conditions, the total spread of the resonance line for a stationary sample is given by: | (12) |
 this shift is given by
this shift is given by | (13) |
In the more recent paper by Sorte et al.,31 a 39K NMR line at −10.9 ppm with FWHH = 800 Hz and a total spread of about 3 kHz is reported for a stationary sample. Under the same experimental conditions, Tarasov et al.27 observed a resonance line with a splitting of 614 Hz and a total spread 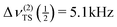 . According to eqn (12), one would expect a total spread of the resonance line of about 4.92 kHz from the above determined parameters. Hence, we have to conclude that the 39K NMR line reported by Sorte et al.31 is not caused by the potassium ions in Pnma KAlH4.
. According to eqn (12), one would expect a total spread of the resonance line of about 4.92 kHz from the above determined parameters. Hence, we have to conclude that the 39K NMR line reported by Sorte et al.31 is not caused by the potassium ions in Pnma KAlH4.
Conclusions
We have shown that potassium aluminium tetrahydride KAlH4 of high phase purity can easily be synthesized via a mechanochemical route. The thus obtained material crystallises in space group Pnma (62). We believe that a sufficient quality of the hydride sample is not only important for obtaining a convincing resolution in the MAS NMR spectra, but will be of paramount importance in future studies of dynamical properties and the decomposition process.Using a well-established procedure and spectral simulation we have derived precise data for the isotropic chemical shift and the quadrupole coupling for both nuclei studied. Apart from the quadrupole coupling data for 27Al, the results agree fairly well with those of an earlier study by Tarasov et al.27
Provided that samples of sufficient crystallinity and phase purity are used, the approach applied in the present paper should also work for other alkali aluminium hydrides and, more generally, for many other materials containing half-integer nuclei experiencing small to medium-sized quadrupole couplings.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are very much indebted to Dr Thomas Bernert for measuring and evaluating the X-ray data. Open Access funding provided by the Max Planck Society.References
- F. Schüth, B. Bogdanović and M. Felderhoff, Chem. Commun., 2004, 2249–2258 RSC.
- S. Orimo, Y. Nakamori, J. R. Eliseo, A. Züttel and C. M. Jensen, Chem. Rev., 2007, 107, 4111–4132 CrossRef CAS PubMed.
- L. Li, C. Xu, C. Chen, Y. Wang, L. Jiao and H. Yuan, Int. J. Hydrogen Energy, 2013, 38, 8798–8812 CrossRef CAS.
- B. Bogdanović and M. Schwickardi, J. Alloys Compd., 1997, 253–254, 1–9 CrossRef.
- B. Bogdanović, M. Felderhoff, M. Germann, M. Härtel, A. Pommerin, F. Schüth, C. Weidenthaler and B. Zibrowius, J. Alloys Compd., 2003, 350, 246–255 CrossRef.
- H. Brinks, C. Jensen, S. Srinivasan, B. Hauback, D. Blanchard and K. Murphy, J. Alloys Compd., 2004, 376, 215–221 CrossRef CAS.
- B. Hauback, Z. Kristallogr., 2008, 223, 636–648 CAS.
- T. D. Humphries, J. W. Makepeace, S. Hino, W. I. F. David and B. C. Hauback, J. Mater. Chem. A, 2014, 2, 16594–16600 RSC.
- B. C. Hauback, H. W. Brinks, C. M. Jensen, K. Murphy and A. J. Maeland, J. Alloys Compd., 2003, 358, 142–145 CrossRef CAS.
- D. J. Ross, M. D. Halls, A. G. Nazri and R. F. Aroca, Chem. Phys. Lett., 2004, 388, 430–435 CrossRef CAS.
- E. H. Majzoub, K. F. McCarty and V. Ozoliņš, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 024118 CrossRef.
- H. Yukawa, N. Morisaku, Y. Li, K. Komiya, R. Rong, Y. Shinzato, R. Sekine and M. Morinaga, J. Alloys Compd., 2007, 446–447, 242–247 CrossRef CAS.
- C. P. Baldé, A. E. Mijovilovich, D. C. Koningsberger, A. M. J. van der Eerden, A. D. Smith, K. P. de Jong and J. H. Bitter, J. Phys. Chem. C, 2007, 111, 11721–11725 CrossRef.
- A. Léon, A. Balerna, G. Cinque, C. Frommen and M. Fichtner, J. Phys. Chem. C, 2007, 111, 3795–3798 CrossRef.
- J. Zhang, M.-A. Pilette, F. Cuevas, T. Charpentier, F. Mauri and M. Latroche, J. Phys. Chem. C, 2009, 113, 21242–21252 CrossRef CAS.
- M. H. W. Verkuijlen, P. J. M. van Bentum, E. R. H. van Eck, W. Lohstroh, M. Fichtnern and A. P. M. Kentgens, J. Phys. Chem. C, 2009, 113, 15467–15472 CrossRef CAS.
- M. H. W. Verkuijlen, P. J. M. van Bentum, O. Zabara, M. Fichtner and A. P. M. Kentgens, J. Phys. Chem. C, 2011, 115, 13100–13106 CrossRef CAS.
- T. J. Frankcombe, Chem. Rev., 2012, 112, 2164–2178 CrossRef CAS PubMed.
- Z. Ö. Kocabas Atakli, E. Callini, S. Kato, P. Mauron, S.-I. Orimo and A. Züttel, Phys. Chem. Chem. Phys., 2015, 17, 20932–20940 RSC.
- H. Morioka, K. Kikizaki, S.-C. Chung and A. Yamada, J. Alloys Compd., 2003, 353, 310–314 CrossRef CAS.
- M. Mamatha, C. Weidenthaler, A. Pommerin, M. Felderhoff and F. Schüth, J. Alloys Compd., 2006, 416, 303–314 CrossRef CAS.
- J. R. Ares, K.-F. Aguey-Zinsou, F. Leardini, I. J. Ferrer, J.-F. Fernandez, Z.-X. Guo and C. Sanchez, J. Phys. Chem. C, 2009, 113, 6845–6851 CrossRef CAS.
- L. M. Arnbjerg and T. R. Jensen, Int. J. Hydrogen Energy, 2012, 37, 345–356 CrossRef CAS.
- J. R. Ares, J. Zhang, T. Charpentier, F. Cuevas and M. Latroche, J. Phys. Chem. C, 2016, 120, 21299–21308 CrossRef CAS.
- E. C. Ashby, G. J. Brendel and H. E. Redman, Inorg. Chem., 1963, 2, 499–504 CrossRef CAS.
- D. Pukazhselvan, D. P. Fagg and O. N. Srivastava, Int. J. Hydrogen Energy, 2015, 40, 4916–4924 CrossRef CAS.
- V. P. Tarasov, S. I. Bakum and A. V. Novikov, Russ. J. Inorg. Chem., 2000, 45, 1890–1896 Search PubMed.
- S.-C. Chung and H. Morioka, J. Alloys Compd., 2004, 372, 92–96 CrossRef CAS.
- B. C. Hauback, H. W. Brinks, R. H. Heyn, R. Blom and H. Fjellvåg, J. Alloys Compd., 2005, 394, 35–38 CrossRef CAS.
- V. P. Tarasov, S. I. Bakum and A. V. Novikov, Russ. J. Inorg. Chem., 2001, 46, 409–414 Search PubMed.
- E. G. Sorte, S. B. Emery, E. H. Majzoub, T. Ellis-Caleo, Z. L. Ma, B. A. Hammann, S. E. Hayes, R. C. Bowman and M. S. Conradi, J. Phys. Chem. C, 2014, 118, 5725–5732 CrossRef CAS.
- D. Krech, B. Zibrowius, C. Weidenthaler and M. Felderhoff, Eur. J. Inorg. Chem., 2014, 5683–5688 CrossRef CAS.
- F. A. Perras and D. L. Bryce, J. Phys. Chem. C, 2012, 116, 19472–19482 CrossRef CAS.
- S. Hayashi and K. Hayamizu, Bull. Chem. Soc. Jpn., 1990, 63, 913–919 CrossRef CAS.
- J.-P. Bastide, P. Claudy, J.-M. Letoffe and J. El Hajri, Rev. Chim. Miner., 1987, 24, 248–263 CAS.
- V. P. Tarasov and G. A. Kirakosyan, Russ. J. Inorg. Chem., 2008, 53, 2048–2081 CrossRef.
- J. Brus, Solid State Nucl. Magn. Reson., 2000, 16, 151–160 CrossRef CAS PubMed.
- S. Antonijevic and G. Bodenhausen, Angew. Chem., Int. Ed., 2005, 44, 2935–2938 CrossRef CAS PubMed.
- D. Freude, in Encyclopedia of Analytical Chemistry, ed. R. A. Meyers, John Wiley & Sons Ltd, Chichester, 2000, ch. Quadrupolar Nuclei in Solid-state Nuclear Magentic Resonance, pp. 12188–12224 Search PubMed.
- P. P. Man, in Encyclopedia of Nuclear Magnetic Resonance, ed. R. K. Harris and R. E. Wasylishen, John Wiley & Sons Ltd, Chichester, 2012, ch. Quadrupolar Interactions, pp. 3689–3698 Search PubMed.
- A. Samoson, Chem. Phys. Lett., 1985, 119, 29–32 CrossRef CAS.
- D. Freude and J. Haase, in NMR Basic Principles and Progress, ed. P. Diehl, E. Fluck, H. Guenther, R. Kosfeld and J. Seelig, Springer Verlag, Berlin, 1993, vol. 29, ch. Quadrupole Effects in Solid-State Nuclear Magnetic Resonance, pp. 1–90 Search PubMed.
- G. Engelhardt, A. P. M. Kentgens, H. Koller and A. Samoson, Solid State Nucl. Magn. Reson., 1999, 15, 171–180 CrossRef CAS PubMed.
- H. J. Jakobsen, J. Skibsted, H. Bildsøe and N. C. Nielsen, J. Magn. Reson., 1989, 85, 173–180 CAS.
- J. Skibsted, N. C. Nielsen, H. Bildsøe and H. J. Jakobsen, J. Magn. Reson., 1991, 95, 88–117 CAS.
- P. C. Taylor, J. F. Baugher and H. M. Kriz, Chem. Rev., 1975, 75, 203–240 CrossRef CAS.
- D. Massiot, J. Hiet, N. Pellerin, F. Fayon, M. Deschamps, S. Steuernagel and P. Grandinetti, J. Magn. Reson., 2006, 181, 310–315 CrossRef CAS PubMed.
- I. Solomon, Phys. Rev., 1958, 110, 61–65 CrossRef CAS.
- T. Azaïs, C. Bonhomme, L. Bonhomme-Coury, J. Vaissermann, Y. Millot, P. P. Man, P. Bertani, J. Hirschinger and J. Livage, J. Chem. Soc., Dalton Trans., 2002, 609–618 RSC.
- B. C. Hauback, H. W. Brinks and F. Fjellvåg, J. Alloys Compd., 2002, 346, 184–189 CrossRef CAS.
- L. Kellberg, H. Bildsøe and H. J. Jakobsen, J. Chem. Soc., Chem. Commun., 1990, 1294–1295 RSC.
- J. Wiench, V. P. Balema, V. K. Pecharsky and M. Pruski, J. Solid State Chem., 2004, 177, 648–653 CrossRef CAS.
- I. L. Moudrakovski and J. A. Ripmeester, J. Phys. Chem. B, 2007, 11, 491–495 CrossRef PubMed.
- P. Granger, Magn. Reson. Chem., 1989, 28, 156–158 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp01059a |
| This journal is © the Owner Societies 2019 |





