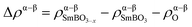Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational study of the mixed B-site perovskite SmBxCo1−xO3−d (B = Mn, Fe, Ni, Cu) for next generation solid oxide fuel cell cathodes†
Emilia
Olsson
 a,
Jonathon
Cottom
a,
Jonathon
Cottom
 b,
Xavier
Aparicio-Anglès
b,
Xavier
Aparicio-Anglès
 a and
Nora H.
de Leeuw
a and
Nora H.
de Leeuw
 *ac
*ac
aDepartment of Chemistry, University College London, WC1H 0AJ, London, UK. E-mail: k.olsson.12@ucl.ac.uk
bDepartment of Physics and Astronomy, University College London, WC1E 6BT, London, UK
cSchool of Chemistry, Cardiff University, Main Building, Park Place, CF10 3AT, Cardiff, UK. E-mail: deleeuwn@cardiff.ac.uk
First published on 18th April 2019
Abstract
SmCoO3 is a promising perovskite material for the next generation of intermediate temperature solid oxide fuel cells (SOFC), but its potential application is directly linked to, and dependent on, the presence of dopant ions. Doping on the Co-site is suggested to improve the catalytic and electronic properties of this cathode material. Fe, Mn, Ni, and Cu have been proposed as possible dopants and experimental studies have investigated and confirmed the potential of these materials. Here we present a systematic DFT+U study focused on the changes in electronic, magnetic, and physical properties with B-site doping of SmCoO3 to allow cathode optimization. It is shown that doping generally leads to distortion in the system, thereby inducing different electron occupations of the Co d-orbitals, altering the electronic and magnetic structure. From these calculations, the 0 K electronic conductivity (σe) was obtained, with SmMnxCo1−xO3 having the highest σe, and SmFexCo1−xO3 the lowest σe, in agreement with experiment. We have also investigated the impact of dopant species and concentration on the oxygen vacancy formation energy (Ef), which is related to the ionic conductivity (σO). We found that the Ef values are lowered only when SmCoO3 is doped with Cu or Ni. Finally, thermal expansion coefficients were calculated, with Mn-doping showing the largest decrease at low x and at x = 0.75. Combining these results, it is clear that Mn-doping in the range x = 0.125–0.25 would imbue SmCoO3 with the most favorable properties for IT-SOFC cathode applications.
1. Introduction
Solid oxide fuel cells (SOFC) are low-emission, high efficiency electrical generators, which show great promise as an emerging energy technology.1–3 However, in order to decrease costs and to prolong cell lifetimes, a concerted research effort is required to lower SOFC operating temperatures into the temperature range 500–800 °C.1–3 Unfortunately, traditional cathode materials such as LaxSr1−xMnO3−d (LSM), which has long been the state-of-the-art SOFC cathode, have been shown to be inefficient under these operating conditions.4,5 It is the main task of the cathode to catalyze the oxygen reduction reaction (ORR) and facilitate oxygen diffusion through the electrolyte towards the anode. To this end, it should have high electronic conductivity (σe), which depends on the electronic structure, and ionic conductivity (σO) which is dependent on the concentration of oxygen vacancies (VO) and therefore on the oxygen vacancy formation energy (Ef).1–3,6 The cathode should further be chemically and physically compatible with the coupled electrolyte. Hence, having thermal expansion coefficients (TEC) close to those of traditional electrolytes (10–13 × 10−6 K−1) is important to minimize strain in the cell to prevent premature failure.7In view of the above, new cathode materials are sought, which has led to interest in cobalt-based cathodes.8 These materials have shown excellent SOFC cathode properties at intermediate temperatures, with high σO and σe.8 A promising material is SmCoO3, which is in itself a semiconductor, but by doping this perovskite on the Co-site with manganese, nickel, iron, or copper, σe can be increased through modification of its electronic structure.9–12 Such doping makes SmCoO3 a p-type semiconductor, and samarium oxide perovskites doped with transition metals on the B sites, show excellent promise as intermediate temperature (IT-SOFC) cathodes.13 Fullarton et al. discovered that partial substitution on Sm- (with Sr and Ca) and/or Co- (with Ni, Cu, and Fe) sites in SmCoO3 greatly improves σO.14 In combination with doping on the Sm site, substitutional Co-site doping of SmCoO3 with other transition metals has the potential to increase σe, by making the materials metallic and magnetic, as well as having an impact on the TEC which decreases.10,15 For example, Mn-doping of SmCoO3-type cathode materials has been shown experimentally to decrease the TEC, alter the catalytic properties, and increase conduction – property changes that have also been shown for La-based systems.11 Fe-, Ni- and Cu-doping have been suggested to greatly modify the oxygen diffusion, oxygen surface-to-bulk incorporation, and the catalytic oxygen reduction activity of SmCoO3.14 Ni-doped SmCoO3 has also been shown experimentally to alter the electronic conduction, and be capable of accommodating oxygen deficiency.15 Furthermore, Ni-, Fe- and Mn-doping have also been shown to readily reduce the TEC of SmCoO3-based cathode materials.13,16
However, the full substitution of Co by dopants leads to completely different types of perovskite materials (SmBO3), which, compared to LaBO3, have been subject to few experimental and only some theoretical studies. Previous computational research has focused on SmFeO317–20 and SmMnO321,22 whereas computational information on SmNiO3 and SmCuO3 is scarce.23–27 However, experimental studies exist, providing the basis for this study,15,28–30 where both Ni and Cu are proposed to readily decrease the TEC in SOFC cathodes, and to be possible dopants in SmCoO3.14,25
Taking into account previous work and the promise of SmCoO3 as an IT-SOFC cathode material, here we present a systematic study on the doping of SmCoO3 with Mn, Fe, Ni, and Cu at different concentrations, as well as the fully substituted SmBO3 pseudo-cubic structures. We pay special attention to the effect of the dopant concentrations on the geometric, electronic and magnetic structures, as well as the electronic and ionic conductivities. In addition, the energetics and electronic implications of the oxygen vacancy formation is also investigated. Each of these data points are combined to allow the optimization of properties for B-site doping of SmCoO3.
2. Computational details
2.1 Density functional theory (DFT) calculations
All calculations except for the thermal expansion, discussed below, in this study employed the Vienna ab initio simulation package (VASP, version 5.3.5).31–34 We have applied the projector-augmented wave method (PAW) to describe the ion–electron interaction,35 and, based on convergence tests, the energy cut-offs for all systems were set to 500 eV. Spin-polarized calculations were executed using the Perdew–Burke–Ernzerhof (PBE)36,37 functional under electronic (convergence criterion of 10−5 eV) and ionic (convergence criterion of 10−3 eV Å−1) self-consistence. The following valence electrons were considered for the atomic species involved: Sm (5s25p66s2), Mn (3p63d64s1), Fe (3p63d64s2), Co (4s23d7), Ni (4s23d8), Cu (4s13d10) and O (2s22p4). Furthermore, the tetrahedron method with Blöchl corrections for smearing38 was applied, together with a 4 × 4 × 4 Γ-centered Monkhorst–Pack grid.39 Bader AIM (Atoms in Molecules) charges40 were calculated using the Henkelman algorithm.41 The supercell used throughout this work is the 2 × 2 × 2 Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m pseudo-cubic cell, as this was found to be large enough to model bulk properties and defect structures within reasonable computational resources.
m pseudo-cubic cell, as this was found to be large enough to model bulk properties and defect structures within reasonable computational resources.
To describe electronic structures, we have used the on-site coulombic interaction (DFT+U) for the B 3d-electrons. Normal exchange correlation functionals (LDA or GGA) cannot correct the electron self-interaction problem, leading to a metallic description of perovskites or at least an underestimation of their band gaps.42–44 In this work, we have employed Dudarev's approach,45 in which an effective Hubbard parameter (Ueff) is applied to the B d-states. The Ueff-parameters for B ions in perovskites have been extensively fitted and tested elsewhere, based on lattice parameters, band gaps and properties such as magnetic structures, enthalpy of formation, and defect formation energies. Based on this prior work, here we have used the following Hubbard parameters: Ueff = 4 eV46 for Mn, Ueff = 4.3 eV47 for Fe, Ueff = 3 eV48 for Co, Ueff = 6.4 eV46 for Ni, and Ueff = 3 eV49 for Cu. The electronic conductivity is calculated for the 0 K optimized electronic structures from the frequency dependent dielectric matrix, where the electronic conductivity can be calculated from the dielectric constant, dielectric loss factor, and the loss tangent, which are then obtained from the dielectric parameters.50–53
2.2 Molecular dynamics (MD) simulations
Thermal expansion coefficients were calculated from molecular dynamics (MD) simulations using the DL_POLY 4 program.54 20 × 20 × 20 supercells based on the DFT+U optimized SmBxCo1−xO3 structures were simulated under NPT conditions (constant number of particles, pressure and temperature), with a Nosé–Hoover thermostat.55 All statistics were collected after a 10 ps system equilibration, with a 100 ps production phase and a time step of 0.1 fs. To account for electrostatic interactions, the Ewald summation was employed, and the Verlet algorithm was employed to evaluate the atomic motions. Short-range atomic interactions were calculated with Buckingham potentials (eqn (1)), which are used extensively within the Born model for ionic solids.56–58Eqn (1) shows the Buckingham potential expression, with r defining the distance between ions i and j, and A, ρ, and C being empirically fitted parameters.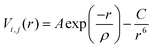 | (1) |
To describe the electronic polarization of the atoms (α), the shell model is included,48,59 where ions are modelled as cores, connected by a harmonic spring (k) to a massless shell with charge Y (eqn (2)).
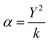 | (2) |
The relevant interatomic potentials are taken from the Cherry et al. library, as these have previously been used to model σO in perovskites,60 and have already been evaluated for SmCoO3.61 The full set of interatomic potentials is presented in Table S1 in the ESI.†
3. Results and discussion
3.1 Dopant configuration
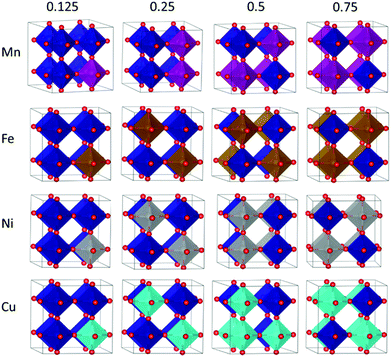
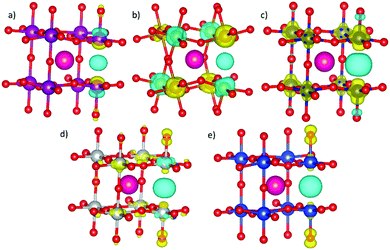
As a first step, the non-equivalent dopant configurations in SmBxCo1−xO3 were evaluated using the Site-Occupancy Disorder Program (SOD).62 The 2 × 2 × 2 supercell includes eight Co lattice positions, thus a substitution of one Co by a dopant ion B represents a dopant concentration of x = 0.125 (for which only one non-equivalent structure can be found), for two Co substitutions x = 0.25, four substitutions x = 0.50, and finally in x = 0.75 we have two Co and six B. Three inequivalent configurations exist for x = 0.25 and 0.75, and six for x = 0.5. The different SmBxCo1−xO3 configurations were optimized with VASP, with their relative energies collected in Table S2 of the ESI,† after which the lowest energy configurations were selected for further study (Fig. 1). In real systems, a degree of disorder between dopant configurations would be expected. However, in order to avoid confusion, and as the smallest energy difference between the different dopant configurations for any particular dopant and dopant level was more than 0.1 eV, only the lowest energy configurations have been considered here. It was found that the lowest energy dopant configurations were dependent on both the dopant type and dopant configuration.In order to further understand the trends in doped SmBxCo1−xO3, we have also studied the SmBO3 perovskites. Cubic SmBO3 perovskites are isostructural, with differences in the B–O bond lengths ranging from 0 to 0.6 Å related to the differences in B ionic radii between the materials (Table S3 in ESI†). As a result, variations in lattice parameter are observed over the periodic series (Table 1), according to the nature of B, in terms of ionic radii and electronegativity, which will influence the chemistry and physical properties of these materials.
| B | x = 0.125 | x = 0.25 | x = 0.5 | x = 0.75 | x = 1.0 | |
|---|---|---|---|---|---|---|
| Mn | a | 3.76 | 3.78 | 3.83 | 3.85 | 3.87 (3.89)22 |
| μ Mn | 3.4 | 3.5 | 3.5 | 3.8 | 3.9 | |
| μ Co | 0.2, 0.06 | 0.2 | 2.4, 0.4 | 0.4 | ||
| FM | FM | FM | FM | FM | ||
| q Mn | 1.74 | 1.74 | 1.70 | 1.68 | 1.71 | |
| q Co | 1.28 | 1.25 | 1.14, 1.35 | 1.13 | ||
| E g | 0.78 (α), 0 (β) | 0 (α), 0.97 (β) | 0 (α), 1.66 (β) | 0 (α), 2.16 (β) | 0.0 (α), 2.90 (β) | |
| Fe | a | 3.78 | 3.78 | 3.81 | 3.85 | 3.89 |
| μ Fe | 4.2 | 4.2 | 4.2 | 4.3 | 4.2 | |
| μ Co | 0.0, 0.2 | 0.2 | 0.3 | 0.4 | ||
| FM | FM | FM | FM | CAFM | ||
| q Fe | 1.70 | 1.73 | 1.71 | 1.68 | 1.61 | |
| q Co | 1.28 | 1.26 | 1.17 | 1.18 | ||
| E g | 0.18 (α), 0.48 (β) | 0.46 (α), 0 (β) | 2.23 (α), 1.67 (β) | 1.04 (α), 1.69 (β) | 2.16 | |
| Ni | a | 3.77 | 3.81 | 3.77 | 3.77 | 3.78 (3.81)23 |
| μ Ni | 1.7 | 1.7 | 1.6 | 1.7, 0.9, 1.6 | 1.3 | |
| μ Co | 0.5, 0.7, 2.9, 3.0 | 0.01, 1.7, 1.8 | 1.5 | 1.3 | ||
| FM | FM | FM | FM | FM | ||
| q Ni | 1.17 | 1.29 | 1.27 | 1.33, 1.12 | 1.21 | |
| q Co | 1.17, 1.55 | 1.21, 1.36 | 1.35 | 1.31 | ||
| E g | 1.49 (α), 0 (β) | 0 (α), 0.40 (β) | 1.12 (α), 0 (β) | 0 (α), 1.22 (β) | 0.0(α), 2.25 (β) | |
| Cu | a | 3.76 | 3.81 | 3.80 | 3.81 | 3.80 |
| μ Cu | 0.8 | 0.7 | 0.6 | 2.6, 0.7 | 0.0 | |
| μ Co | 0.1, 0.0 | 1.1, 0.4, 3.0 | 1.3 | 0.6 | ||
| FM | FM | GAFM | GAFM | NM | ||
| q Cu | 1.32 | 1.28 | 1.25 | 1.18, 1.20 | 1.15 | |
| q Co | 1.30 | 1.19, 1.30, 1.53 | 1.34, 1.24 | 1.40 | ||
| E g | 0.66 (α), 0 (β) | 1.02 (α), 0 (β) | 0 (α), 0.67 (β) | 0.06 (α), 0.21 (β) | 0.0 | |
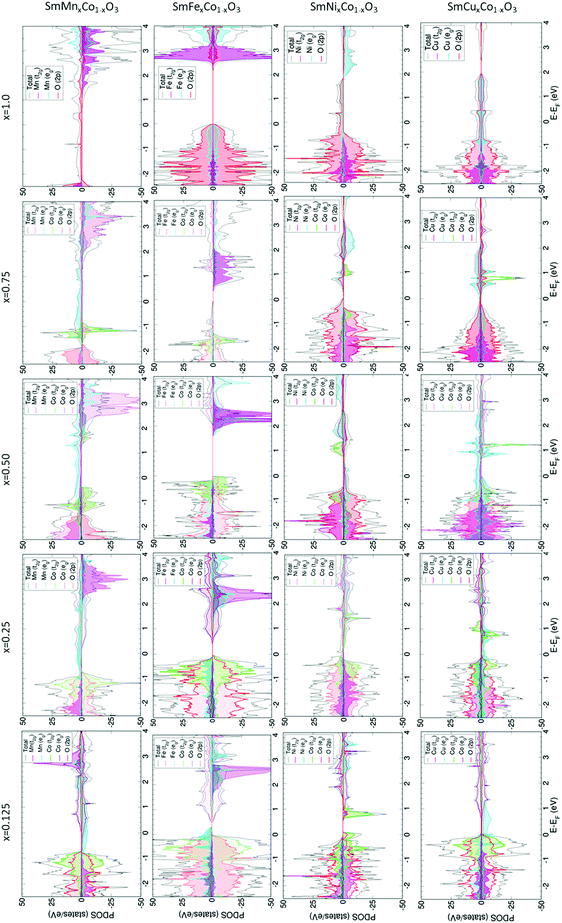
3.2 Electronic and magnetic structures
Co and B can exist in different spin states, depending on the d-orbital occupation. Co3+ (3d6) has a low-spin ground state (LS, t62ge0g), and a negligible magnetic moment (μ) of 0 μB.63 However, upon distortion of the CoO6-octahedra, the d-orbital occupation can be altered, resulting in different spin states, specifically intermediate (IS, t52ge1g) or high (HS, t42ge2g) states, thus modifying the magnetic properties of the system.48,64 In addition, the dopants considered in this work can also present different d-orbital occupations and consequently different spin states.46,65The spin arrangement is important as it determines the magnetic structure of the material. Three general magnetic structures are possible: non-magnetic (NM), antiferromagnetic (AFM), and ferromagnetic (FM). Additionally, AFM can be presented in different configurations: C-type, A-type, and G-type, all schematically represented in Fig. S1 (ESI†). We evaluated all the potential magnetic structures for all dopants and concentrations. Interestingly, almost all SmBxCo1−xO3 compositions were calculated to have a FM structure, whereas we could not obtain either AFM or NM structures. However, there were two exceptions; SmCu0.5Co0.5O3 and SmCu0.75Co0.25O3 converged for the G-AFM structure, indicating a clear preference by this type of system for the ferromagnetic structure (Table 1). We were also able to converge different magnetic structures for pure SmBO3, whose relative energies can be found in Table S5 of the ESI.† SmFeO3 was found to have a C-AFM ground state, with G-AFM being the energetically second-most stable configuration, found to be 0.11 eV per formula unit higher in energy. For SmMnO3 and SmNiO3, FM configurations are more stable than AFM, where in both cases the difference in energy to the second-most stable magnetic structure was more than 0.4 eV per formula unit, in agreement with previous data on cubic phase lanthanide manganate perovskites, and cubic SmNiO3 (which undergoes an insulator-to-metal transition at ∼400 K).15,66 Finally, for SmCuO3, our calculations could only obtain the FM and NM structures, and, according to their relative energies, this material is expected to be non-magnetic, with the FM structure 0.66 eV per formula unit higher in energy.
For SmMnxCo1−xO3, regardless of the dopant concentration, an overlap between the Co and Mn eg-bands (Fig. 2) is always found at the Fermi level, anticipating a high electron conductivity, as high σe has been reported to go through eg-bands.67,68 The contribution of each band depends on the dopant concentration, with larger contributions of the Co eg-bands at lower dopant concentrations, and vice versa when the material is heavily doped. Increasing the dopant concentration does not affect the Co t2g/eg-splitting. We know from previous publications that the change in the spin state, and thus the occupation of the d-orbitals in Co, can be directly related to the distortion of the octahedral environment, i.e. distortions in the Co–O bonds.64 Indeed, for x = 0.125, x = 0.25 and x = 0.75, these bonds are only distorted by ≈0.01 Å with respect to the ideal Co–O bond of 1.88 Å. However, for x = 0.50, the range of Co–O bond lengths is wider (1.88–1.95 Å), thus altering the Co d-orbital crystal field splitting, and consequently, the orbital occupation.
This exception for x = 0.5 can also be observed in the variation of the cobalt magnetic moment. As shown in Table 1, μCo is close to 0 for all concentrations, with the exception of x = 0.50 with a μCo of 2.4 that can be associated to an intermediate spin (IS) state. This behavior is also observed in the PDOS, with the occupation of the Co eg-orbitals on the one hand and β-t2g-orbitals at positive energies on the other. Moving through the PDOS with increasing x, it can be seen that this material becomes gradually more like SmMnO3. The β-band gap increases with increasing x, reaching a maximum in SmMnO3. Also noticeable is the magnetic moment of Mn, which is found to be between 3.76 and 3.85, indicating that Mn is found in its higher spin state, with the highest Mn magnetic moment observed in SmMnO3. Furthermore, μMn decreases with decreasing Mn-content (xMn), a behaviour that has been observed previously in LaMn1−xCoO3.69
The crystal field splitting for cobalt is further observed to remain unchanged with increasing Fe concentration (Fig. 2), which is mainly due to the low degree of distortion suffered by the Co–O bonds upon Fe-doping, as can be seen in Table S3 of the ESI.† At x = 0.125, Fe-doped SmCoO3 is metallic, with an overlap of Fe eg- and Co t2g-bands at the Fermi level, where we thus may expect a relatively large electronic conductivity. However, with increasing dopant concentration, the material becomes increasingly semi-conducting, disqualifying it as a good cathode candidate. As was observed for SmMnxCo1–xO3, SmFexCo1−xO3 gains more SmFeO3 character with increasing x, with the band gap becoming increasingly symmetrical, resulting in pure semi-conductor behaviour at x = 1.0. On the other hand, the iron magnetic moment remains mostly constant over the series at 4.2 μB, whereas the Co magnetic moments are very low for the entire series, oscillating between 0.0 and 0.4 μB. In SmFeO3, all Fe–O bond lengths are equal, which results in a symmetrical electronic structure. It is worth noting that all Fe–O bonds are equal for x = 0.5 as well, but the Co–O bond lengths, whilst all the same, are different to the Fe–O bonds, thus inducing distortions in the oxygen sub-lattice resulting in an asymmetric PDOS.
The electronic structures of SmNixCo1−xO3 and SmCuxCo1−xO3 show different behaviour to the Fe- and Mn-doped systems. In SmNixCo1−xO3, the Co t2g-bands are not fully occupied whereas the eg-bands are partially occupied, which can be related directly to a change in the Co spin moment, and thus to the changes in the Co–O distances (Table S3, ESI†). Interestingly, for x = 0.125 the system is a conductor, but conduction occurs only through the Co t2g-bands and as soon as the dopant concentration increases, the system becomes half-metallic and the conduction occurs through the nickel eg-bands. The half-metallic nature is preserved in SmNiO3, thus inferring that Ni-doping, even at low concentrations, induces more SmNiO3-type behavior than SmCoO3-type. It is worth noting that there is no overlap between the bands of Co and Ni, which is indicative of poor electronic conductivity.
For SmCuxCo1−xO3 (Fig. 2), the Cu eg-bands are partially occupied over the Fermi level for x = 0.125, x = 0.25 and x = 0.5, indicating that electronic conductivity should be possible. For x = 0.75, a change in the electronic structure is seen around the Fermi level, resulting in a small band gap, which would suggest a decrease in σe. For SmCuO3, the electronic structure becomes fully metallic and ferromagnetic. Additionally, for all xCu, the cobalt octahedral environment is distorted, resulting in the Co t2g-levels splitting over the valence and conduction bands, which again can be related directly to a change in the cobalt spin moment, and thus to distortions in the Co–O distances, as listed in Table S3 (ESI†).
Moreover, Bader charges and magnetic moments for cobalt at different concentrations suggest the presence of different mixed valence states, for example when x = 0.125. In this situation, Co charges decrease and increase by ∼0.2 e with respect to the Co charge in SmCoO3. This difference could be seen as a partial change in oxidation state, but neither the magnetic moments nor the electronic structure are clear enough to support this idea. On the other hand, nickel's magnetic moment is around 1.7 for all concentrations, indicating that nickel is found in a mixed spin state.
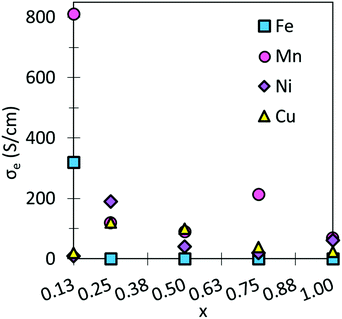
The largest σe are obtained for SmMn0.125Co0.875O3, and SmFe0.125Co0.875O3. These large σe can be attributed to the overlapping between the d-bands of Co and the dopants.74,75 It is further expected that at higher temperatures, these σe could be increased. Moreover, all σe are in line with general IT-SOFC cathode requirements and experimentally obtained data.10,70,71,76
3.3 Hole and oxygen vacancy formation
A critical property for SOFC cathodes is their high combined electronic and ionic conductivity. Mixed ionic and electronic conductors (MIECs) have electronic conductivity (as presented above) reinforced by ionic conductivity. Ionic conductivity in these perovskites proceeds via an oxygen vacancy hopping mechanism, inferring that a high concentration of oxygen vacancies is important. Oxygen vacancies are generally formed as the result charge compensation, but can also be formed as a function of oxygen partial pressure and temperature. Furthermore, it has been demonstrated that hole formation could lead to higher electronic conductivity.72,77 Hence, we below investigate both hole and oxygen vacancy formation in SmBxCo1−xO3.| B | x = 0.125 | x = 0.25 | x = 0.5 | x = 0.75 |
|---|---|---|---|---|
| Mn | −0.13 | −0.23 | −0.47 | −0.15 |
| Fe | −1.28 | −0.27 | −0.40 | −1.39 |
| Ni | −0.66 | −1.03 | −1.27 | −1.07 |
| Cu | −1.12 | −0.79 | −1.02 | −0.13 |
Examining Table 2, we can see that the hole formation energies as a result of Ni- and Cu-doping are quite high, with similar energies seen for Fe-doping at x = 0.125, and 0.75. Hence, the hole polarons formed in these systems represent the deep hole states that would be expected to remain localized at device operating temperatures. Mn-doping on the other hand leads to much smaller hole formation energies, which is in line with previous work on manganese-based perovskites.72 The hole formation in Mn-containing systems has been assigned to the breakdown of the Mn3+ charge state to Mn2+ and Mn4+, which furthermore leads to high electronic conductivity as these states are shallow and hence mobile at elevated temperatures.72
| Ef = EDefective − EBulk + μO | (3) |
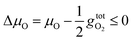 | (4) |
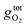 is the free energy of the oxygen molecule (O2(g)).80–85 It is widely accepted that
is the free energy of the oxygen molecule (O2(g)).80–85 It is widely accepted that 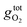 can be approximated by the DFT energy of O2(g) (EO2) when calculations are performed under oxygen-rich conditions, and the material is in thermodynamic equilibrium with the surface, and that the latter is in equilibrium with the gas phase.83 However, it is necessary to determine first whether the material is stable or not for ΔμO = 0, which is evaluated through chemical potential phase diagrams. A more detailed explanation on how to construct these diagrams can be found in the ESI.†
can be approximated by the DFT energy of O2(g) (EO2) when calculations are performed under oxygen-rich conditions, and the material is in thermodynamic equilibrium with the surface, and that the latter is in equilibrium with the gas phase.83 However, it is necessary to determine first whether the material is stable or not for ΔμO = 0, which is evaluated through chemical potential phase diagrams. A more detailed explanation on how to construct these diagrams can be found in the ESI.†
3.3.2.1 Oxygen vacancy formation in SmB1−xCoxO3. For SmCoO3, it was shown in our previous work that the upper limit to ΔμO is −0.5 eV.48 In this work, we thus constructed phase diagrams for SmMnO3 and SmFeO3, from which we found that the upper limits of the oxygen potential (eqn (4)) for SmMnO3 (based on experimental data from Pawlas-Foryst et al.86) is ΔμO ≤ 0 eV, whereas for SmFeO3 (based on experimental data from Parida et al.87) it is ΔμO ≤ −0.7 eV. The lack of experimental data for SmCuO3 and SmNiO3 meant that we could not calculate their respective phase diagrams, although it has been reported that both materials are unstable under high partial oxygen pressures.24,26,27
As such, for ease of comparison ΔμO = −0.5 eV has been used for all materials and concentrations, and we have assumed that the ensuing error for SmFeO3 is negligible for the purpose of this discussion.13,48 However, we have considered ΔμO = 0 for SmMn0.75Co0.25O3−x, since its stoichiometry is closer to SmMnO3 than it is to SmCoO3.
Comparing the oxygen vacancy formation energies with respect to undoped SmCoO3 (2.08 eV), Co-site doping with B does not markedly lower Ef, except when doped with Cu, and at xNi > 0.75. The calculated oxygen vacancy formation energies for Ni- and Cu-doped SmCoO3 (Table 3, and Table S7 in ESI†) indicate – in agreement with experimental studies15,24,26,27 – that only SmNixCo1−xO3−d and SmCuxCo1−xO3−d lead to meaningful reduction in the VO formation energy at higher dopant concentrations. As such, these systems are expected to be oxygen-deficient at IT-SOFC operating temperatures and oxygen partial pressures. However, the effect of Co-site doping on the VO formation energies is limited when compared to Sm-site doping, where spontaneous formation of oxygen vacancies are observed. Sm-site doping reduces the oxygen vacancy formation energy by more than 2.5 eV,61 whereas the maximum reduction in oxygen vacancy formation energy seen here is 1.66 eV. Hence, this doping scheme has a much larger effect on the electrical conductivity than the ionic conductivity. This finding is in accordance with B-site doping having a limited effect on σO, with a much larger impact seen from Sm-site doping.
| B | x = 0.125 | x = 0.25 | x = 0.5 | x = 0.75 | x = 1.0 |
|---|---|---|---|---|---|
| Mn | 1.77 | 1.85 | 2.06 | 2.20 | 2.36 |
| Fe | 1.82 | 2.20 | 3.03 | 1.49 | 5.65 |
| Ni | 1.66 | 1.09 | 2.15 | 0.44 | 0.55 |
| Cu | 1.69 | 0.55 | 0.79 | 0.42 | 0.54 |
3.3.2.2 Oxygen vacancy formation in SmBO3. Comparison of Ef in SmBO3 is presented in Fig. 4. SmBO3 show a non-linear Ef trend (comparable to LaBO3),6,46 with Fe-based lanthanide oxides having the highest Ef. What is notable in comparison with LaBO3,6,46 is that the trend is more extreme, where Ef for SmFeO3 is higher by ∼1 eV, whereas Ef for SmMnO3 and SmCoO3 is lower. Ef in SmNiO3 and SmCuO3 are very low, as was also seen for SmCu/NixCo1−xO3. These low Ef are a consequence of the instability of the Ni and Cu 3+ oxidation state, as was observed previously in LaNiO3 and LaCuO3.88
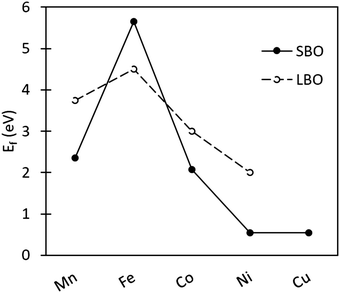 | ||
| Fig. 4 Oxygen vacancy formation energy as a function of transition metal ion in SmBO3 (B = Mn, Fe, Co, Ni, and Cu). Solid line SBO is SmBO3, and dashed line LBO is LaBO3 with the values taken from Lee et al.46 | ||
To investigate the impact of VO formation on the charge distribution in SmBO3, we have plotted the change in spin density (Δρα–β) upon VO formation (Fig. 5) as
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NN
NN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VO = 1.16 and 2.1, which is compatible with iron going from a d5-occupancy (Fe3+) to d4 (Fe2+). This change in iron d-occupancy is unfavorable and has been suggested previously to cause the high Ef in LaFeO3.89 A thorough discussion on VO formation in SmCoO3 has been presented in a previous publication48 and is thus only briefly mentioned here.
VO = 1.16 and 2.1, which is compatible with iron going from a d5-occupancy (Fe3+) to d4 (Fe2+). This change in iron d-occupancy is unfavorable and has been suggested previously to cause the high Ef in LaFeO3.89 A thorough discussion on VO formation in SmCoO3 has been presented in a previous publication48 and is thus only briefly mentioned here.
3.4 Thermal expansion coefficient (TEC)
The TECs of traditional electrolyte materials are in the region of ∼10–13 × 10−6 K−1 and SmCoO3 has a calculated TEC of 17.7 × 10−6 K−1. These high TECs are commonplace for cobalt perovskites, and they are known to increase with Sm-site doping, as this increases oxygen deficiency in the lattice, leading to further lattice volume expansion upon heating. Co-site doping can decrease TEC, as seen in Fig. 6 and Table S8 (ESI†), which would make the materials more practical as SOFC cathodes, making the electrolyte and cathode compatible. Encouragingly, most systems investigated here do show lowered TEC compared to SmCoO3, although none are directly in the range of common SOFC electrolytes. As such, none of the materials are suitable as SOFC cathodes in their current compositions. Mn-doping is seen to decrease TEC the most, but it also varies greatly with x. On the other hand, Fe-doping barely affects the TEC at any x. Doping with copper shows no significant change in TEC at low x, but it increases for x = 0.5. Finally, Ni-doping shows similar behaviour to Mn-doping, but does not reduce TEC as readily. Although these results are generally positive in terms of lowering TEC, they are not sufficient to match an acceptable TEC range.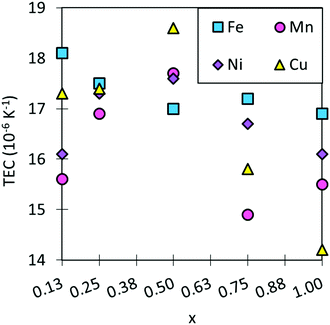 | ||
| Fig. 6 The trend in TEC for SmBxCo1−xO3 calculated over a temperature range of 600–1200 K. TECs for typical SOFC electrolytes are ∼10–13 × 10−6 K−1, which is outside the range of this graph. | ||
4. Conclusion
In this paper we have presented a detailed atomic-level computational study of SmBxCo1−xO3 materials, where B = Fe, Mn, Ni, and Cu, and x = 0.125, 0.25, 0.5, 0.75 and 1.00. After a complete study of the dopant configurations, the most stable dopant distributions and concentrations were determined, from which the electronic and magnetic properties, hole formation, oxygen vacancy formation energies, and thermal expansion coefficients were calculated.Regardless of the dopant, doping on the Co-site induces a distortion of the Co–O bond that forces different Co d-orbital occupations. This effect, in combination with the d-orbital occupation of the dopants, explains why the majority of the systems become ferromagnetic, with the exception of SmCu0.5Co0.5O3 and SmCu0.75Co0.25O3. The overlap between the eg-orbitals of the dopant and cobalt around the Fermi level explains the impressively high electrical conductivity found for SmMn0.125Co0.875O3 compared to SmFe0.125Co0.875O3, where the presence of an electronic band explains the insignificant calculated electronic conductivity. We have also illustrated that doping with Cu and Ni does not significantly improve the electronic conductivity of the perovskite. Hence, only Mn-doping would be beneficial for this material as an SOFC cathode, as electronic conductivity is of vital importance for intermediate temperature SOFC cathodes.
Furthermore, B-site doping was not found to reduce significantly the oxygen vacancy formation energy when B = Mn or Fe, but it does decrease with B = Cu or Ni. In general, the most common VO configuration was found to be Co–VO–Co, with the reduction of cobalt. Finally, TECs were calculated, where Mn-doping showed the largest decrease at low x. Thus, from the results obtained from the combination of our DFT calculations and MD simulations, we conclude that SmMnxCo1−xO3 at x = 0.125 or x = 0.25 would be the most favorable composition to improve SmCoO3 as an IT-SOFC cathode material, but that doping with Fe would be disadvantageous due to the low electronic conductivity. However, to realize the potential of doped SmCoO3 as a SOFC cathode material, studies would need to be conducted combining both the Co-site doping studied here with Sm-doping.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the Engineering and Physical Sciences Research Council (EPSRC) for financial support (Grants references EP/K016288/1 and EP/K001329/1). We also acknowledge the use of the UCL Legion High Performance Computing Facility (Legion@UCL) and the UCL Grace High Performance Computing Facility (Grace@UCL), and associated support services, in the completion of this work. Finally, via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work made use of the facilities of ARCHER, the UK's national high-performance computing service, which is funded by the Office of Science and Technology through EPSRC's High End Computing Programme. DL_POLY_4 has been obtained from STFC's Daresbury Laboratory via the website http://www.ccp5.ac.uk/DL_POLY. We acknowledge use of STFC Hartree Centre resources in this work. The STFC Hartree Centre is a research collaboratory in association with IBM providing High Performance Computing platforms funded by the UK's investment in e-Infrastructure. E. O. gratefully acknowledges EPSRC funding from the UCL Centre for Doctoral Training in Molecular Modelling and Materials Science (EP/G036675/1).References
- W. C. Chueh and S. M. Haile, Electrochemistry of mixed oxygen ion and electron conducting electrodes in solid electrolyte cells, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 313–341 CrossRef CAS PubMed.
- S. M. Haile, Fuel cell materials and components, Acta Mater., 2003, 51, 5981–6000 CrossRef CAS.
- B. C. Steele and A. Heinzel, Materials for fuel-cell technologies, Nature, 2001, 414, 345–352 CrossRef CAS PubMed.
- R. M. Ormerod, Solid oxide fuel cells, Chem. Soc. Rev., 2003, 32, 17–28 RSC.
- J. Van Herle, A. J. J. McEvoy and K. Ravindranathan Thampi, A study on the La1−xSrxMnO3 oxygen cathode, Electrochim. Acta, 1996, 41, 1447–1454 CrossRef CAS.
- M. Pavone, A. M. Ritzmann and E. A. Carter, Quantum-mechanics-based design principles for solid oxide fuel cell cathode materials, Energy Environ. Sci., 2011, 4, 4933 RSC.
- J. A. Kilner and M. Burriel, Materials for Intermediate-Temperature Solid-Oxide Fuel Cells, Annu. Rev. Mater. Res., 2014, 44, 365–393 CrossRef CAS.
- X. Jiang, Q. Xu, Y. Shi, X. Li, W. Zhou, H. Xu and Q. Zhang, Synthesis and properties of Sm3+-deficient Sm1−xBaCo2O5+δ perovskite oxides as cathode materials, Int. J. Hydrogen Energy, 2014, 39, 10817–10823 CrossRef CAS.
- J. H. Kim, S.-W. Baek, C. Lee, K. Park and J. Bae, Performance analysis of cobalt-based cathode materials for solid oxide fuel cell, Solid State Ionics, 2008, 179, 1490–1496 CrossRef CAS.
- K. H. Jung, S. Choi, H.-H. Park and W.-S. Seo, High temperature thermoelectric properties of Sr and Fe doped SmCoO3 perovskite structure, Curr. Appl. Phys., 2011, 11, S260–S265 CrossRef.
- Y. Wang, X. Zhao, S. Lü, X. Meng, Y. Zhang, B. Yu, X. Li, Y. Sui, J. Yang, C. Fu and Y. Ji, Synthesis and characterization of SmSrCo2−xMnxO5+δ (x = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0) cathode materials for intermediate-temperature solid-oxide fuel cells, Ceram. Int., 2014, 40, 11343–11350 CrossRef CAS.
- M. M. Natile, G. Eger, P. Batocchi, F. Mauvy and A. Glisenti, Strontium and copper doped LaCoO3: new cathode materials for solid oxide fuel cells?, Int. J. Hydrogen Energy, 2017, 42, 1724–1735 CrossRef CAS.
- S. W. Baek, J. H. Kim and J. Bae, Characteristics of ABO3 and A2BO4 (A = Sm, Sr; B = Co, Fe, Ni) samarium oxide system as cathode materials for intermediate temperature-operating solid oxide fuel cell, Solid State Ionics, 2008, 179, 1570–1574 CrossRef CAS.
- I. Fullarton, J. Jacobs and H. Van Benthem, Study of oxygen ion transport in acceptor doped samarium cobalt oxide, Ionics, 1995, 1, 51–58 CrossRef CAS.
- J. Perez-Cacho, J. Blasco, J. Garcia and R. Sanchez, Relationships between Structure and Physical Properties in SmNi1−xCoxO3, J. Solid State Chem., 2000, 150, 145–153 CrossRef CAS.
- H. Ullmann, N. Trofimenko, F. Tietz, D. Stöver and A. Ahmad-Khanlou, Correlation between thermal expansion and oxide ion transport in mixed conducting perovskite-type oxides for SOFC cathodes, Solid State Ionics, 2000, 138, 79–90 CrossRef CAS.
- Y. Sun, W. Ren, S. Cao, H. Zhou, H. J. Zhao and H. Xu, Hydrostatic pressure driven spin, volume and band gap collapses in SmFeO3: a GGA+U study, Philos. Mag., 2016, 96, 1613–1622 CrossRef CAS.
- H. J. Zhao, W. Ren, Y. Yang, X. M. Chen and L. Bellaiche, Effect of chemical and hydrostatic pressures on structural and magnetic properties of rare-earth orthoferrites: a first-principles study, J. Phys.: Condens. Matter, 2013, 25, 466002 CrossRef PubMed.
- S. Sahoo, P. K. Mahapatra and R. N. P. Choudhary, The structural, electrical and magnetoelectric properties of soft-chemically-synthesized SmFeO3 ceramics, J. Phys. D: Appl. Phys., 2016, 49, 035302 CrossRef.
- P. Ciambelli, S. Cimino, S. De Rossi, L. Lisi, G. Minelli, P. Porta and G. Russo, AFeO3 (A = La, Nd, Sm) and LaFe1−xMgxO3 perovskites as methane combustion and CO oxidation catalysts: structural, redox and catalytic properties, Appl. Catal., B, 2001, 29, 239–250 CrossRef CAS.
- R. Choithrani, N. K. Gaur and R. K. Singh, Thermodynamic properties of SmMnO3, Sm0.55Sr0.45MnO3 and Ca0.85Sm0.15MnO3, J. Phys.: Condens. Matter, 2008, 20, 415201 CrossRef.
- W. Lee, J. W. Han, Y. Chen, Z. Cai and B. Yildiz, Cation size mismatch and charge interactions drive dopant segregation at the surfaces of manganite perovskites, J. Am. Chem. Soc., 2013, 135, 7909–7925 CrossRef CAS PubMed.
- N. Shukla, T. Joshi, S. Dasgupta, P. Borisov, D. Lederman and S. Datta, Electrically induced insulator to metal transition in epitaxial SmNiO3 thin films, Appl. Phys. Lett., 2014, 105, 2012–2017 Search PubMed.
- I. V. Nikulin, M. A. Novojilov, A. R. Kaul, S. N. Mudretsova and S. V. Kondrashov, Oxygen nonstoichiometry of NdNiO3−d and SmNiO3−d, Mater. Res. Bull., 2004, 39, 775–791 CrossRef CAS.
- R. Pelosato, G. Cordaro, D. Stucchi, C. Cristiani and G. Dotelli, Cobalt based layered perovskites as cathode material for intermediate temperature solid oxide fuel cells: a brief review, J. Power Sources, 2015, 298, 46–67 CrossRef CAS.
- M. Karppinen, H. Yamauchi, H. Suematsu, K. Isawa, M. Nagano, R. Itti and O. Fukunaga, Control on the Copper Valence and Properties by Oxygen Content Adjustment in the LaCuO3−y System (0 ≤ y ≤ 0.5), J. Solid State Chem., 1997, 130, 213–222 CrossRef CAS.
- M. Karppinen, H. Yamauchi, T. Ito, H. Suematsu and O. Fukunaga, High-pressure synthesis and thermal decomposition of LaCuO3, Mater. Sci. Eng., B, 1996, 41, 59–62 CrossRef.
- J. Perez-Cacho, J. Blasco, J. Garcia, M. Castro, J. Stankiewicz, M. C. Sanchez and R. D. Sanches, Magnetic Properties of SmNiO3, J. Magn. Magn. Mater., 1999, 196–197, 541 CrossRef.
- A. Gupta, B. Mercey, H. Hervieu and B. Raveau, Thin-Film Stabilization of Metastable Phases in the Sm1−xSrxCuOy System, Chem. Mater., 1994, 6, 1011–1016 CrossRef CAS.
- N. J. C. Ingle, R. H. Hammond and M. R. Beasley, Molecular beam epitaxial growth of SrCu2O3: metastable structures and the role of epitaxy, J. Appl. Phys., 2002, 91, 6371 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for Ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. Perdew, K. Burke and M. Ernzerhof, Errata: Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 1396 CrossRef PubMed.
- J. Perdew, K. Burke and M. Ernzerhof, Errata: Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- T. Geng, Z. Han and S. Zhuang, Effective Coulomb interaction in LaMnO3, Phys. B, 2010, 405, 3714–3716 CrossRef CAS.
- P. Ravindran, A. Kjekshus, H. Fjellvåg, A. Delin and O. Eriksson, Ground-state and excited-state properties of LaMnO3 from full-potential calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 064445 CrossRef.
- P. Ravindran, R. Vidya, H. Fjellvåg and A. Kjekshus, Electronic Structure and Excited-state Properties of Perovskite-like Oxides, J. Cryst. Growth, 2004, 268, 554–559 CrossRef CAS.
- S. Dudarev, G. Botton and S. Savrasov, Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- Y.-L. Lee, J. Kleis, J. Rossmeisl and D. Morgan, Ab initio energetics of LaBO3(001) (B = Mn, Fe, Co, and Ni) for solid oxide fuel cell cathodes, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 224101 CrossRef.
- A. M. Ritzmann, J. M. Dieterich and E. A. Carter, DFT+U analysis of the electronic structure and defect chemistry of LSCF, Phys. Chem. Chem. Phys., 2016, 18, 12260–12269 RSC.
- E. Olsson, X. Aparicio-Anglès and N. H. de Leeuw, Ab initio study of vacancy formation in cubic LaMnO3 and SmCoO3 as cathode materials in solid oxide fuel cells, J. Chem. Phys., 2016, 145, 014703 CrossRef PubMed.
- S. Vázquez, L. Suescun and R. Faccio, Effect of Cu doping on Ba0.5Sr0.5Fe1−xCuxO3−δ perovskites for solid oxide fuel cells: a first-principles study, J. Power Sources, 2016, 311, 13–20 CrossRef.
- S. Fares, Frequency dependence of the electrical conductivity and dielectric constants of polycarbonate (Makrofol-E) film under the effects of γ-radiation, Nat. Sci., 2011, 03, 1034–1039 CAS.
- M. Mehedi Hassan, A. S. Ahmed, M. Chaman, W. Khan, A. H. Naqvi and A. Azam, Structural and frequency dependent dielectric properties of Fe3+ doped ZnO nanoparticles, Mater. Res. Bull., 2012, 47, 3952–3958 CrossRef CAS.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Linear optical properties in the projector-augmented wave methodology, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 1–9 CrossRef.
- J. D. Baran, M. Molinari, N. Kulwongwit, F. Azough, R. Freer, D. Kepaptsoglou, Q. M. Ramasse and S. C. Parker, Tuning Thermoelectric Properties of Misfit Layered Cobaltites by Chemically Induced Strain, J. Phys. Chem. C, 2015, 119, 21818–21827 CrossRef CAS.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, DL_POLY, J. Mater. Chem., 2006, 16, 1911–1918 RSC.
- W. G. Hoover, Canonical dynamics: equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- M. Born and J. Mayer, Lattice theory of ionic solids, Phys. B, 1932, 75, 1–18 CAS.
- J. E. Mayer, Dispersion and Polarizability and the van der Waals Potential in the Alkali Halides, J. Chem. Phys., 1933, 1, 270–279 CrossRef CAS.
- M. S. Islam, M. Cherry and C. R. A. Catlow, Oxygen Diffusion in LaMnO3 and LaCoO3 Perovskite-Type Oxides: A Molecular Dynamics Study, J. Solid State Chem., 1996, 124, 230–237 CrossRef CAS.
- M. A. Farhan and M. J. Akhtar, Negative pressure driven phase transformation in Sr doped SmCoO3, J. Phys.: Condens. Matter, 2010, 22, 075402 CrossRef PubMed.
- M. Cherry, M. S. Islam and C. R. A. Catlow, Oxygen ion migration in perovskite-type oxides, J. Solid State Chem., 1995, 118, 125–132 CrossRef CAS.
- E. Olsson, X. Aparicio-Anglès and N. H. de Leeuw, A computational study of the electronic properties, ionic conduction, and thermal expansion of Sm1−xAxCoO3 and Sm1−xAxCoO3−x/2 (A = Ba2+, Ca2+, Sr2+, and x = 0.25, 0.5) as intermediate temperature SOFC cathodes, Phys. Chem. Chem. Phys., 2017, 19, 13960–13969 RSC.
- R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. de Leeuw, Symmetry-adapted configurational modelling of fractional site occupancy in solids, J. Phys.: Condens. Matter, 2007, 19, 256201 CrossRef.
- T. N. Vasil’chikova, T. G. Kuz’mova, A. A. Kamenev, A. R. Kaul’ and A. N. Vasil’ev, Spin states of cobalt and the thermodynamics of Sm1−xCaxCoO3−δ solid solutions, JETP Lett., 2013, 97, 34–37 CrossRef.
- E. Olsson, X. Aparicio-Anglès and N. H. de Leeuw, A DFT+U study of the structural, electronic, magnetic, and mechanical properties of cubic and orthorhombic SmCoO3, J. Chem. Phys., 2016, 145, 224704 CrossRef PubMed.
- T. Arima and Y. Tokura, Optical Study of Electronic Structure in Perovskite-Type RMO3 (R = La, Y; M = Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu), J. Phys. Soc. Jpn., 1995, 64, 2488–2501 CrossRef CAS.
- H. Y. Lee, K. Huang and J. B. Goodenough, Sr- and Ni-Doped LaCoO3 and LaFeO3 Perovskites, J. Electrochem. Soc., 1998, 145, 3220–3227 CrossRef.
- I. Loa, P. Adler, A. Grzechnik, K. Syassen, U. Schwarz, M. Hanfland, G. Rozenberg, P. Gorodetsky and M. P. Pasternak, Pressure-induced quenching of the Jahn-Teller distortion and insulator-to-metal transition in LaMnO3, Phys. Rev. Lett., 2001, 87, 125501 CrossRef CAS PubMed.
- M. Pavone, A. B. Muñoz-Garcia, A. M. Ritzmann and E. A. Carter, First-Principles Study of Lanthanum Strontium Manganite: new Insights into Electronic Structure and Oxygen Vacancy Formation, J. Phys. Chem. C, 2014, 118, 13346–13356 CrossRef CAS.
- J. H. Park, S. Cheong and C. T. Chen, Double-exchange ferromagnetism in La(Mn1−xCoxO)3, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 11072–11075 CrossRef CAS.
- W. Zhou, R. Ran and Z. Shao, Progress in understanding and development of Ba0.5Sr0.5Co0.8Fe0.2O3−δ-based cathodes for intermediate-temperature solid-oxide fuel cells: a review, J. Power Sources, 2009, 192, 231–246 CrossRef CAS.
- L. W. Tai, M. M. Nasrallah, H. U. Anderson, D. M. Sparlin and S. R. Sehlin, Structure and electrical properties of La1−xSrxCo1−yFeyO3. Part 2. The system La1−xSrxCo0.2Fe0.8O3, Solid State Ionics, 1995, 76, 273–283 CrossRef CAS.
- J. Richter, P. Holtappels, T. Graule, T. Nakamura and L. J. Gauckler, Materials design for perovskite SOFC cathodes, Monatsh. Chem., 2009, 140, 985–999 CrossRef CAS.
- L. W. Tai, M. M. Nasrallah, H. U. Anderson, D. M. Sparlin and S. R. Sehlin, Structure and electrical properties of La1−xSrxCo1−yFeyO3. Part 1. The system La0.8Sr0.2Co1−yFeyO3, Solid State Ionics, 1995, 76, 259–271 CrossRef CAS.
- J. Mizusaki, N. Mori, H. Takai and Y. Yonemura, Oxygen nonstoichiometry and defect equilibrium in the perovskite-type oxides La1−xSrxMnO3+d, Solid State Ionics, 2000, 129, 163–177 CrossRef CAS.
- J. Mizusaki and Y. Miwa, Nonstoichiometry of the Perovskite-Type Oxides La1−xSrxCoO3−d, J. Solid State Chem., 1989, 80, 102–111 CrossRef CAS.
- R. Scurtu, S. Somacescu, J. M. Calderon-Moreno, D. Culita, I. Bulimestru, N. Popa, A. Gulea and P. Osiceanu, Nanocrystalline Sm0.5Sr0.5CoO3−δ synthesized using a chelating route for use in IT-SOFC cathodes: microstructure, surface chemistry and electrical conductivity, J. Solid State Chem., 2014, 210, 53–59 CrossRef CAS.
- C. Sun, R. Hui and J. Roller, Cathode materials for solid oxide fuel cells: a review, J. Solid State Electrochem., 2009, 14, 1125–1144 CrossRef.
- P. Erhart, A. Klein, D. Åberg and B. Sadigh, Efficacy of the DFT+U formalism for modeling hole polarons in perovskite oxides, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 1–8 CrossRef.
- S. Zhang and J. Northrup, Chemical potential dependence of defect formation energies in GaAs: application to Ga self-diffusion, Phys. Rev. Lett., 1991, 67, 2339–2342 CrossRef CAS PubMed.
- H. Raebiger, S. Lany and A. Zunger, Origins of the p-type nature and cation deficiency in Cu2O and related materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 045209 CrossRef.
- T. Tanaka, K. Matsunaga, Y. Ikuhara and T. Yamamoto, First-principles study on structures and energetics of intrinsic vacancies in SrTiO3, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 205213 CrossRef.
- C. G. Van De Walle and J. Neugebauer, First-principles calculations for defects and impurities: applications to III-nitrides, J. Appl. Phys., 2004, 95, 3851–3879 CrossRef CAS.
- P. G. Sundell, M. E. Björketun and G. Wahnström, Thermodynamics of doping and vacancy formation in BaZrO3 perovskite oxide from density functional calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104112 CrossRef.
- A. M. Ritzmann, M. Pavone, A. B. Muñoz-García, J. A. Keith and E. A. Carter, Ab initio DFT+U analysis of oxygen transport in LaCoO3: the effect of Co3+ magnetic states, J. Mater. Chem. A, 2014, 2, 8060–8074 RSC.
- C. Persson, Y. J. Zhao, S. Lany and A. Zunger, n-Type doping of CuInSe2 and CuGaSe2, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 1–14 Search PubMed.
- E. Pawlas-Foryst, K. T. Jacob and K. Fitzner, Thermodynamics of SmMnO3 and SmMn2O5 Phases Determined by the E. M. F. Method, Arch. Metall. Mater., 2006, 51, 253–260 CAS.
- S. C. Parida, V. Venugopal and K. T. Jacob, Thermodynamic properties of SmFeO3(s) and Sm3Fe5O12(s), J. Phase Equilib., 2003, 24, 431–440 CrossRef CAS.
- Q. Li, Y.-X. Deng, Y.-A. Zhu, Y. Li, Z.-J. Sui, D. Chen and W.-K. Yuan, Structural stability of lanthanum-based oxygen-deficient perovskites in redox catalysis: a density functional theory study, Catal. Today, 2018 DOI:10.1016/j.cattod.2018.04.070.
- A. M. Ritzmann and A. B. Muñoz-García, Ab initio DFT+U Analysis of Oxygen Vacancy Formation and Migration in La1−xSrxFeO3−δ (x = 0, 0.25, 0.50), Chem. Mater., 2013, 25, 3011–3019 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Summary of the interatomic potential parameters used for the calculation of thermal expansion coefficients (Table S1), a graphical representation of the different magnetic structures investigated in the main article (Fig. S1), a description on how to obtain chemical potential phase diagrams and link this to the oxygen vacancy formation energy; chemical potential phase diagrams for SmMnO3 and SmFeO3 (Fig. S2); a complete list of all the differences in energy between the different dopant configurations in the individual systems (Table S2); the B–O bond lengths for the most stable structures (Table S3); Bader charges for SmBxCo1−xO3 (Table S4), the magnetic structures calculated for SmBO3 and their relative energies (Table S5); larger DOS (Fig. S3–S7), and electrical conductivities for all systems (Table S6). Additionally, a table with all the oxygen vacancy positions and oxygen vacancy formation energies is included in Table S7, and thermal expansion coefficients in Table S8. See DOI: 10.1039/c9cp00995g |
| This journal is © the Owner Societies 2019 |