Open Access Article
Open Access ArticleBlind spheres of paramagnetic dopants in solid state NMR†
Wenyu
Li
 a,
Qianyun
Zhang
a,
Qianyun
Zhang
 a,
Jonas J.
Joos
a,
Jonas J.
Joos
 b,
Philippe F.
Smet
b,
Philippe F.
Smet
 b and
Jörn
Schmedt auf der Günne
b and
Jörn
Schmedt auf der Günne
 *a
*a
aInorganic Materials Chemistry, University of Siegen, Adolf-Reichwein-Str. 2, 57076 Siegen, Germany. E-mail: gunnej@chemie.uni-siegen.de
bLumiLab, Department of Solid State Sciences, Ghent University, Krijgslaan 281-S1, 9000 Gent, Belgium
First published on 29th April 2019
Abstract
Solid-state NMR on paramagnetically doped crystal structures gives information about the spatial distribution of dopants in the host. Paramagnetic dopants may render NMR active nuclei virtually invisible by relaxation, paramagnetic broadening or shielding. In this contribution blind sphere radii r0 have been reported, which could be extracted through fitting the NMR signal visibility function f(x) = exp(−ar03x) to experimental data obtained on several model compound series: La1−xLnxPO4 (Ln = Nd, Sm, Gd, Dy, Ho, Er, Tm, Yb), Sr1−xEuxGa2S4 and (Zn1−xMnx)3(PO4)2·4H2O. Radii were extracted for 1H, 31P and 71Ga, and dopants like Nd3+, Gd3+, Dy3+, Ho3+, Er3+, Tm3+, Yb3+ and Mn2+. The observed radii determined differed in all cases and covered a range from 5.5 to 13.5 Å. While these radii were obtained from the amount of invisible NMR signal, we also show how to link the visibility function to lineshape parameters. We show under which conditions empirical correlations of linewidth and doping concentration can be used to extract blind sphere radii from second moment or linewidth parameter data. From the second moment analysis of La1−xSmxPO431P MAS NMR spectra for example, a blind sphere size of Sm3+ can be determined, even though the visibility function remains close to 100% over the entire doping range. Dependence of the blind sphere radius r0 on the NMR isotope and on the paramagnetic dopant could be suggested and verified: for different nuclei, r0 shows a 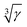 -dependence, γ being the gyromagnetic ratio. The blind sphere radii r0 for different paramagnetic dopants in a lanthanide series could be predicted from the pseudo-contact term.
-dependence, γ being the gyromagnetic ratio. The blind sphere radii r0 for different paramagnetic dopants in a lanthanide series could be predicted from the pseudo-contact term.
Introduction
Nuclear magnetic resonance (NMR) has contributed to the study of paramagnetic systems, such as in structural biology,1–5 battery materials,6–8 characterization of pharmaceutical formulation,9,10 polymers,11,12 chemical shift thermometers13,14 and luminescent materials.15–23 The range of applications of paramagnetic NMR is surprising given that the strong electronic magnetic moment of the paramagnetic species interferes with the NMR measurement in different ways. Nevertheless, paramagnetic NMR may give information about structure,2,12 dynamics8,24 and the distribution of paramagnetic dopants in a host.17–22,25,26 In the latter case different approaches had been used namely relaxation times,19,20,22 linewidths17,18 and observed peaks areas21,25 to relate doping homogeneity to the performance of these luminescent materials.In solid-state NMR a distinction needs to be made between lanthanide atoms and transition metal atoms. The influence transition metal atoms exert on neighbouring NMR nuclei enables studies for example on battery materials6–8 or metal organic framework compounds.27 The computation of the influence on valence electrons is important and progress in the computation of paramagnetic shifts28 has improved significantly in recent years. In contrast, lanthanides with few exceptions show hardly any influence from the valence shell and thus have been used for systematic experimental studies to identify contributions to the paramagnetic spin Hamiltonian.28,29 Paramagnetic NMR of lanthanide containing compounds found various applications to luminescent materials.15–21
A non-trivial problem to paramagnetic NMR is that NMR resonances of paramagnetic compounds may virtually vanish in the dead-time of the NMR spectrometer by relaxation, inhomogeneous broadening mechanisms or anisotropic susceptibility broadening.29 Lineshape analysis as proposed by Van Vleck30 in terms of moment-analysis or NMR line width comes with a visibility caveat. Nevertheless, this approach was proved successful in the characterization of several phosphors,17,18 where it could be shown that, as expected by van Vleck, the linewidth depended linearly on the paramagnetic doping level x at low doping concentration. It should be noted that in the high doping regime a non-trivial dependence due to “exchange narrowing”30–32 may lead to deviations from this simple behaviour. In case of luminescent materials, the doping homogeneity is of major importance to establish an optimal performance.33,34 When luminescent ions are too close, energy can easily be transferred between them, leading to uncontrollable migration of energy in the dopant sublattice that can eventually be non-radiatively dissipated at so-called luminescence killer centres. This effect is usually referred to as concentration quenching35,36 and has been related to the dopant distribution obtained from NMR lineshape analysis in a few cases.17,18 Furthermore, it was evidenced by a microscopic investigation that the thermal quenching behaviour, i.e. the decrease of luminescence quantum yield for increasing temperatures,37 is severely worsened for inhomogeneously doped materials due to areas with a locally more elevated doping concentration.34
Instead of asking for the NMR properties of the visible paramagnetic signals, it may be interesting to ask for the fraction of NMR invisible signal. If a spherical regime around a paramagnetic centre is assumed, from which no NMR signals can be detected, it is possible to relate the signal loss to the size of this sphere of influence which is known under the name blind-sphere38,39 or wipe-out radius.40–42 Such radii are important in solution NMR38,39 where paramagnetic constraints are used for structure solution, and in dynamic nuclear polarization (DNP) to estimate the zone which cannot be accessed by NMR43–45 and for luminescent materials to study doping homogeneity.21
Spectroscopically the blind sphere can be explained by line broadening which leads to undetectable signal by standard experiments,39 or signal shift46 that puts the signal outside of spectral window. The origins of blind sphere may relate to (but are not limited to) the following contributions:39 relaxation which may involve dipolar, Curie, contact and cross relaxation mechanisms, and hyperfine shift which contains contact and pseudo-contact parts.
Reported sizes of blind spheres have been mostly related to the solution NMR, for which Bertini39 and co-workers have laid a foundation. Besides some attempts have been made to quantify the blind sphere radius of DNP polarizing agents.43,47 In solid state, due to anisotropic interactions and more ambiguous estimation of correlation time τc and spectral density function J(ω), blind sphere sizes may differ and questions about the influence that a paramagnetic centre has on its environment remain open. To the best of our knowledge, for solid crystalline samples a systematic study on the sizes of blind spheres of different inorganic dopants has not been published before.
The target of this contribution is to relate the size of blind spheres of solid samples to other physical quantities, for example the gyromagnetic ratio of NMR nuclei and the effective magnetic moment of the paramagnetic ion by studying the blind sphere radii in lanthanide-doped solid solutions. Moreover, given that doping homogeneity of inorganic phosphors can be traced both via the visible signal by lineshape analysis and via the fraction of the invisible signal,21 it is natural to ask whether the blind sphere radius and linewidth or moment analysis can be linked, and if so under which conditions.
Experimental
The La1−xLnxPO4 (Ln = Nd, Sm, Gd, Dy, Er, Ho, Tm, Yb) samples have been synthesized via a co-precipitation method: Ln2O3 (Nd2O3 was bought from chemPUR, the rest from smart elements, the purity is 99.999% for Dy2O3 and 99.99% for the rest) and La2O3 (chemPUR, 99.99%) were dissolved in nitric acid and later on mixed with NH4H2PO4 (VWR chemicals) solution. The resulting precipitates were dried at 80 °C overnight, sintered in corundum crucibles at 1000 °C for 4 h.Sr1−xEuxGa2S4 powders were obtained via a solid state synthesis method. Stoichiometric quantities of SrS (Alfa Aesar, 99.9%), Ga2S3 (Alfa Aesar, 99.99%) and EuF3 (Alfa Aesar, 99.5%) were weighed and mixed in an agate mortar. A small amount (1 weight %) of NH4F (Alfa Aesar, 98+%) was added as a fluxing agent. The mixtures were fired for two hours at 900 °C under a flow of forming gas (90% N2, 10% H2). The obtained powder was again lightly ground.
The (Zn1−xMnx)3(PO4)2·4H2O samples have been synthesized by a co-precipitation method: stoichiometric amounts of MnCl2·4H2O (ACROS organics, 99+%) and Zn(NO3)2·6H2O (chemPUR, 98+%) were dissolved into water and mixed with an excess of NH4H2PO4 (VWR chemicals) in aqueous solution. The precipitates were washed with water and ethanol and dried overnight.
Powder X-ray diffraction (XRD) measurements were performed on a Huber G621 diffractometer with Cu Kα1 radiation (λ = 0.15405931 nm) in transmission geometry. Diffractograms were extracted from the image files, which were obtained by scanning the photostimulable BaBrF:Eu2+ films with an image plate detector (Typhoon FLA 7000, λ = 650 nm), by home-written program ipreader-0.9. The Rietveld analysis was performed via the program TOPAS-Academic (TOtal PAttern Solution, by Coelho Software, V4.1).
The solid state NMR measurements were performed on a Bruker Avance II spectrometer at a magnetic field of 7.05 T. Magic angle spinning (MAS) was done with 4 mm pencil rotors at spinning frequencies of 10 kHz or 12.5 kHz with a home-built McKay probe head. The dead time delay was set to 15 μs. Quantification was assisted by a micro-balance (Sartorius MC5). The deconvolution of peaks and moment analysis were assisted with the program deconv2Dxy48 (version 0.4). The NMR visibility fitting function21 for a homogeneously doped sample is defined as follows.
| f(x) = exp(−ar03x) | (1) |
The wipe-out radius r0 relates to the size of the blind sphere of a paramagnetic centre and the variable a is host-specific number (a = 4πNhostUC/3VUC where NhostUC is the number of “dopable” sites in the unit cell and VUC is the volume of the unit cell). For monazite49 LaPO4 the variable a amounts to 0.055 Å−3. The doping concentration x in this work is defined as the degree of substitution, which is dimensionless. The experimental NMR visibility f was calculated in the following way: first the molar peak areas P = A/n were calculated for all samples in one dopant series (A peak area, n amount of material). The visibility function f(x) and P(x) are related by normalization through the undoped sample, i.e. P(x) = f(x)·P(0). Therefore the experimental P values were fitted with the function P(x) to determine the free parameters r0 and P(0). This approach gives equal weight to all measured points. The diagrams (Fig. 2, 4, 7 and 8) show P(x)/P(0) on the y-axis.
Results and discussion
The target of this contribution is to provide a better understanding of the blind sphere in solids. In order to achieve that, measurements have been performed on three model compounds series, Ln3+ (Ln = Nd, Sm, Gd, Dy, Er, Ho, Tm, Yb) doped monazite LaPO4, Mn2+ doped hopeite Zn3(PO4)2·4H2O and Eu2+ doped SrGa2S4. Lanthanide doped xenotime YPO4 and monazite LaPO4 have been subject to several studies50,51 in terms of a determination of NMR parameters. Lanthanide dopants have the advantage that for a model study chemical interference is reduced to a minimum because of the low lying, unpaired f-shell electrons. To extract the sizes of blind spheres from measured data, approaches which relate the peak area and lineshape to the doping level are investigated. Finally, the obtained sizes are compared to establish relations between blind sphere and physical quantities, for example magnetic moment and gyromagnetic ratio.Peak area and blind sphere
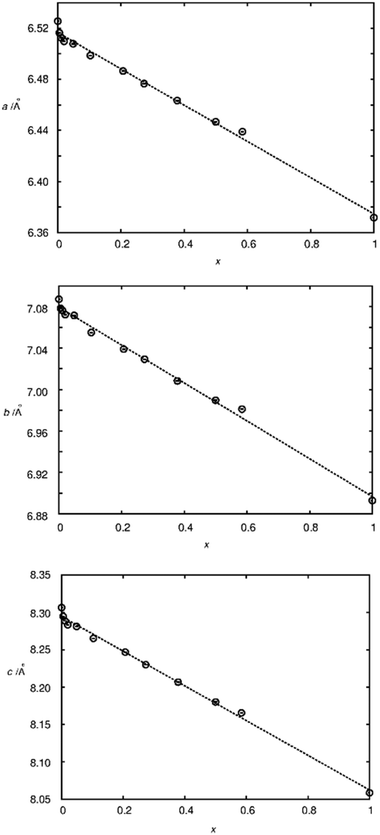
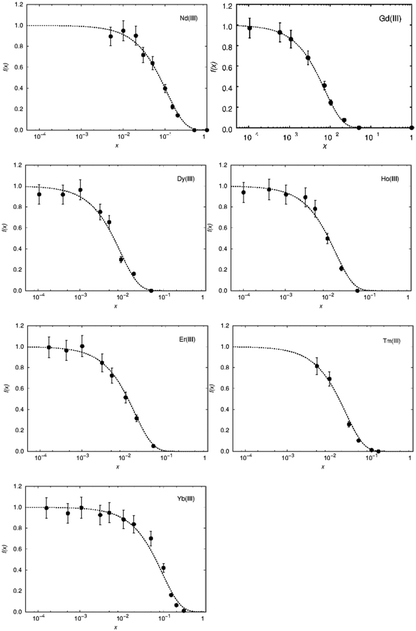
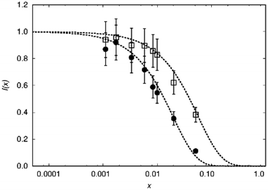
To judge the quality of obtained samples X-ray diffraction was applied. The synthesized samples were phase pure according to X-ray diffraction. Rietveld refinements of the diffraction pattern yielded lattice parameters which followed Vegard's law.52Fig. 1 shows the lattice parameters of La1−xSmxPO4 follow a linear dependence on the doping concentration x as an example. Such a fulfilment of Vegard's law is often considered as evidence for a homogeneously doped phase pure sample in the sense of a solid solution.The single pulse 31P MAS NMR spectra offer information on the change of peak area upon increasing the doping level x. Based on the visibility function21f(x) = exp(−ar03x) blind sphere radii for trivalent dopants Ln3+ (Ln = Nd, Gd, Dy, Er, Ho, Tm, Yb) could be obtained (Fig. 2 and Table 1).
| Dopant ion | r 0/Å | μ eff/μB | N unpaired |
|---|---|---|---|
| Nd3+ | 5.5 | 3.62 | 3 |
| Sm3+ | 0.45* | 1.54 | 5 |
| Gd3+ | 13.5 | 7.95 | 7 |
| Dy3+ | 12.5 | 10.5 | 5 |
| Ho3+ | 10.5 | 10.5 | 4 |
| Er3+ | 10.0 | 9.55 | 3 |
| Tm3+ | 9.0 | 7.5 | 2 |
| Yb3+ | 5.8 | 4.4 | 1 |
While in principle blind sphere radii can be determined from two points only, we fitted the visibility function to all points (experimental part). Because of the discrete nature of the pair distribution function in crystalline materials, radii determined this way become less reliable the smaller the blind-sphere radius (see discussion in ref. 21).
Line shape and blind sphere
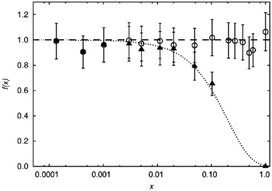
While the visibility function f(x) = exp(−ar03x) proved to be a useful tool for the extraction of blind-sphere radii in the cases above and in case of Sr1−xEuxH2,21 it could not be applied in case of La1−xSmxPO4, because single pulse 31P MAS NMR (Fig. 3) recovers (Fig. 4) signals from all 31P atoms including those of the first coordination sphere around Sm3+, as can be seen from the visibility function (Fig. 4 in circles) which stays close to 100% for all doping concentrations x.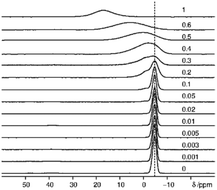 | ||
| Fig. 3 Stack plot of 31P MAS NMR spectra of La1−xSmxPO4 (x values are marked on the corresponding spectra, dashed line indicates the position of the peak of pure LaPO4). | ||
Because of line broadening, precise deconvolution of different environments is difficult for x > 0.1. Despite the large errors from peak deconvolution, an analysis was attempted to relate line width and doping concentration (ESI,† Fig. S1) as previously done on similar systems in literature,17,18 however, a linear dependence could not be found. On the other hand a signal specific 31P visibility function f can be defined, which corresponds only to the area of the peak which has a similar shift and linewidth as the peak of pure host material LaPO4 (Fig. 4, triangles). A radius of 4.5 Å could in principle be obtained this way which as expected covers the P-atoms in the first coordination sphere around the La atom.
A practical approach which works for any kind of lineshape is to calculate the second moment from the lineshape as suggested by Van Vleck30 in the context of dipolar peak broadening on whole spectra, which does not rely on the separation of different environments. This dipolar broadening includes broadening by magnetic dipolar couplings because of the hyperfine coupling. In case of La1−xSmxPO4 the second moment M2/Hz2 follows the doping concentration x in a linear way over a wide range (Fig. 5).
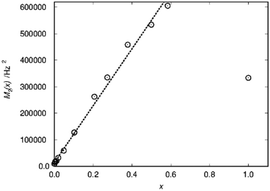 | ||
| Fig. 5 Second moment M2(x) as a function of the substitution degree x in La1−xSmxPO4. The dotted line represents linear fit resulting in M2/Hz2 = 1.4 × 104 + 1.07 × 106·x. | ||
To explain the observed linear relation, a brief discussion of line shape functions and line broadening mechanisms may be helpful. For an idealized free induction decay (FID) of a single nucleus the decay function can be expressed for example as a Gaussian or monoexponentially decaying function. The Fourier transformation of such a FID returns a Gaussian or Lorentzian line shape, respectively. When a resonance is broadened homogeneously, for example by relaxation i.e. by random oscillatory local field components at the Larmor frequency54 or by lifetime broadening,29 then the Lorentzian function is a good basis for the description of the line-shape in the frequency domain. On the other hand, inhomogeneous broadening,55,56 which can be caused for example by magnetic field inhomogeneity, chemical shift anisotropy (CSA) or pseudo-contact term, produces a more complicated, often asymmetric lineshape, for which the description by van Vleck's moment approach is a suitable analysis tool. In van Vleck's moment approach, the dipolarly broadened spectral lineshape is decomposed into a sum of Gaussian functions. Hole-burning57–59 experiments allow to distinguish inhomogeneous from homogeneous broadening.
A simple alternative to the hole-burning experiment is the 2D exchange spectroscopy (EXSY) experiment. EXSY experiments with zero mixing time show a sharp ridge on the diagonal in case of inhomogeneous broadening and a double Lorentzian type lineshape in case of homogeneous broadening. Note that the EXSY looks the same and behaves like the stimulated echo experiment. From the 31P MAS NMR 2D spectra (Fig. 6), it is clear that the 31P 2D NMR signal observed for Sm3+ doped LaPO4 is typical for inhomogeneous broadening, while for Gd3+ homogeneous broadening is observed. The 31P NMR signals for the other measured Ln3+ doped samples, namely Nd3+, Dy3+, Ho3+, Er3+, Tm3+ and Yb3+, all show an inhomogeneous broadening behaviour (ESI,† Fig. S2).
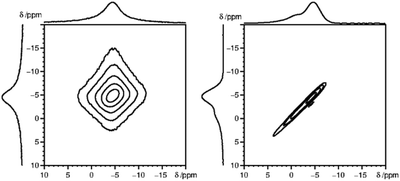 | ||
| Fig. 6 2D 31P MAS EXSY spectra (with zero mixing time) for La0.997Gd0.003PO4 (left) and La0.99Sm0.01PO4 (right), which depicted homogeneous and inhomogeneous type of line broadening, respectively. | ||
In the following, a relation between the blind-sphere radius and the observed line-broadening is developed for simple cases.
The peak area which is the basis of the visibility function f(x) (see above) is related to the intensity of first point of the FID according to the integral theorem of the Fourier transformation.56 Any loss in peak area should then be reflected by the decay of the FID during the dead-time delay tde, either by relaxation or by coherent mechanisms. If spectral line-broadening is assumed to be following a simple Lorentzian or Gaussian function then the decay in the FID needs to be monoexponential or Gaussian, respectively. Thus for simple cases the blind-sphere radius and line-broadening follow simple analytical expressions for a given dead-time delay (see below).
A Gaussian type FID sG(t) of an on-resonance signal is described with a linewidth parameter λG and the amplitude factor sG,0.
sG(t) = sG,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−λG2t2) exp(−λG2t2) | (2) |
The corresponding spectral function IG(ω) is obtained by a single-sided complex Fourier transformation.56
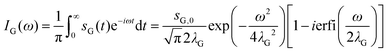 | (3) |
The line width parameter λG is related to the full width half-maximum of the line-shape in Hz as 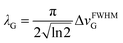 .
.
Given the lineshape of a paramagnetically doped sample can be described with a simple Gaussian function then the peak area AG for a given dead time tde can be predicted on the basis of the integral theorem56 of the Fourier transformation from the decay of the FID.
AG = sG,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−λG2tde2] exp[−λG2tde2] | (4) |
In order to derive the visibility function f(x) in terms of line-broadening λG(x), eqn (4) is plugged into the definition of the visibility function.
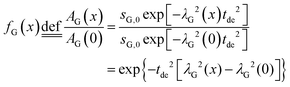 | (5) |
The amplitude factor sG,0 of the doped and the pure host material should the equal, while the line width parameter λG(x) depends on doping concentration. The visibility function can also be expressed in terms of the blind sphere radii r0, the number density parameter a and doping level x (eqn (1)). Therefore, the link between parameter λG and doping level x can be established as follows.
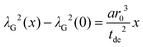 | (6) |
Assuming a negligible frequency difference between signals, the second moment48,56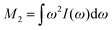 of the Gaussian type function is 2λG2 and the second moment becomes M2(x) = 2λG2(x). Eqn (6) can be rewritten in terms of the second moment.
of the Gaussian type function is 2λG2 and the second moment becomes M2(x) = 2λG2(x). Eqn (6) can be rewritten in terms of the second moment.
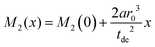 | (7) |
A linear regression of the second moment M2(x) yields the slope 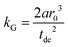 . From the latter the radius of the blind sphere r0 can be estimated via a simple analytical equation.
. From the latter the radius of the blind sphere r0 can be estimated via a simple analytical equation.
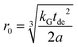 | (8) |
This way the blind-sphere r0 of Sm3+ doped La1−xSmxPO4 was estimated to be 0.45 Å. The La to P and Sm to P distances in the monazite49 structure of LaPO4 and SmPO4 are 3.2 Å and 3.1 Å, respectively, which means that all 31P nuclei are outside of the blind spheres of Sm3+ and thus visible. This is consistent with the observation the signal visibility function f(x) remains close to 100% (Fig. 4). In addition, 19F and 1H NMR signals for SmF360 and SmH361,62 both have been reported to be visible, which supports the found small blind sphere size of Sm3+. Given the estimated blind sphere radius is even smaller than the Shannon radius63 for Sm3+ (around 1 Å) it appears that Sm-compounds in general are good candidates for NMR studies, because no signal loss is expected. The second moment analysis as presented above can provide information on the size of the blind sphere, especially for paramagnetic dopants which have small blind spheres.
For Gd3+, the line broadening is mainly based on the homogeneous broadening mechanism which is relaxation dominated and follows a Lorentzian lineshape. Thus the FID can be described with a monoexponentially decaying function. The line width parameter λL(x) then has a slightly different relation to the blind sphere r0, doping concentration x and deadtime delay tde (see ESI†).
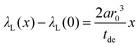 | (9) |
The λL(x) is related to the full width half-maximum in Hz as λL = 2πΔνFWHML.
The relation between the size of blind sphere r0 and the experimental results λL(0) (the line width of non-doped diamagnetic analog) and slope kL value (from the linear fit of λL(x) against x) can be derived in a similar fashion as in the Gaussian case.
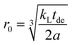 | (10) |
This way the blind sphere r0 for the Gd3+ doped sample becomes 6.7 Å, which is much smaller than the estimated 13.5 Å from signal visibility method. This discrepancy can be explained by the inadequacy of simple functions to describe the FID. In case the spectral lineshape function becomes more complicated it is non-trivial to extract line-width parameters from the spectra and in those cases the visibility function f(x) provides an easier way to determine blind-sphere radii. As shown above line-shape analysis requires knowledge about the decay character of the FID in order to determine the blind sphere radius. The reported17,18 linear relation of doping concentration x and linewidth is only expected in case of Lorentzian type spectral lineshapes. While the derivation of blind-spheres via a line-shape analysis suffers from a number of approximations including the assumption of a sharp transition of the visible to invisible nuclei, we believe that the scaling behaviour of the doping concentration x with respect to second moment and line-width, is the most important insight that is being conveyed by the above analysis.
Blind sphere radius dependence on the gyromagnetic ratio
In order to investigate the size dependence of the blind sphere on the gyromagnetic ratio γ, data obtained from the same paramagnetic ion but different NMR nuclei are compared (Table 2). In the following we assume that Eu2+ and Gd3+ are isoelectronic paramagnetic ions, and thus have equal blind sphere radii. The concept of the blind-sphere is based on the idea that the signals of all atoms inside the sphere vanish in the dead-time delay, i.e. nuclei which are situated on the blind sphere have a critical relaxation rate, a critical amount of line-broadening or paramagnetic shift. Critical relaxation rates R1M and R2M driven by a dipolar coupling mechanism with unpaired electrons or Curie nuclear spin relaxation are then proportional to γ2/r06,39 while critical broadening through the pseudo-contact shift (PCS) relates to γ/r03.39 Given that other influences, like the spectral density, are negligible, it can be concluded that the prefactors which relate to the critical broadening or relaxation rate would feature the same relation of gyromagnetic ratio γ to blind sphere radius r0. In this case the blind sphere radii for different nuclei X and Y in the same compound should feature a cubic root dependence to the gyromagnetic ratio.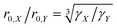 | (11) |
| Host | NMR nucleus | γ/107 rad T−1 s−1 | a/Å−3 | Dopant | r 0/Å | r 0(31P)/Å |
|---|---|---|---|---|---|---|
| SrH2 | 1H | 26.75 | 0.092 | Eu2+ | 1721 | 12.6 |
| SrGa2S4 | 71Ga | 8.18 | 0.025 | Eu2+ | 13 | 14.3 |
| LaPO4 | 31P | 10.84 | 0.055 | Gd3+ | 13.5 | — |
| Zn3(PO4)2·4H2O | 1H | 26.75 | 0.051 | Mn2+ | 10 | 7.4 |
| Zn3(PO4)2·4H2O | 31P | 10.84 | 0.051 | Mn2+ | 7 | — |
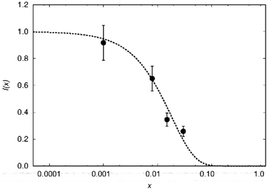
To test this hypothesis we compare blind-sphere radii from different nuclei in the same and in different compounds. The visibility method yielded a blind sphere radius from 71Ga NMR for Eu2+ in Sr1−xEuxGa2S4 (Fig. 7). This may be compared with a blind sphere for Eu2+ in Sr1−xEuxH2 from 1H NMR21 and with one for Gd3+ in La1−xGdxPO4 from 31P NMR (Fig. 2). The values converted to the blind sphere viaeqn (11) of a virtual 31P nucleus are the same (Table 2) within approximated error limits. Given the low number of values in the comparison this is a weak indication that the blind sphere radii of lanthanide dopants may be abstracted from the host structure.
In a second example the sphere radius of Mn2+ is detected by 1H and 31P NMR in hopeite (Zn1−xMnx)3(PO4)2·4H2O (Fig. 8). Again the virtual radius of 31P converted from the radius applying to the 1H nucleus agrees to the observed value within error limits (Table 2). Deviations from this fairly good agreement are expected especially in case of a Fermi-contact contribution64,65 which however does not seem to be relevant here. Another explanation in case of a relaxation dominated blind sphere may be the change of the electronic relaxation mechanism at high doping concentrations which in principle could even lead to an increase visibility in the high concentration regime. In some cases of transition metal doping even at very high dopant concentration64,65 the signal does not vanish. In the presented cases of lanthanide(III) doped monazite the only system where we have an indication of a relaxation dominated blind sphere radius is Gd(III). At 100% doping, i.e. pure GdPO4 no intensity increase can be observed, in line with the presented interpretation.
Blind sphere radius dependence on the effective magnetic moment
In order to test the hypothesis that blind sphere radius depends on the effective magnetic moment, data obtained from the same host LaPO4 and the same NMR nucleus (31P) but different paramagnetic dopants are compared. Relaxation and hyperfine shift are two possible origins of blind spheres, and are discussed resonances in La1−xLnxPO4 are inhomogeneously broadened for all Ln3+ dopants except Gd3+, which indicates that relaxation is dominant in the case of doping by Gd3+ but not as important in case of other paramagnetic Ln3+ as is explained in detail in the following paragraph.Relaxation
Dipolar, Curie-spin and Fermi-contact relaxation are in principle three possible relaxation contributions in paramagnetic systems which lead to homogeneous line broadening. For solid crystalline La1−xLnxPO4, chemical exchange and stochastic reorientation are negligible, only vibrational motions exert efficient influence on the electronic relaxation. Based on the Solomon–Bloembergen–Morgan relaxation model,66,67 the nuclear transverse relaxation time T2 can be described as eqn (12) for lanthanide ions induced paramagnetic relaxation enhancement (PRE). Parameter AFC is the Fermi-contact coupling and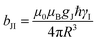 is the spin-dipolar coupling parameter.67T1e and T2e are the longitudinal and transverse electronic relaxation times, respectively, which are used to approximate the corresponding electronic correlation times.67ωI and ωS are the nuclear and electronic Larmor frequencies, respectively. J is the main total angular momentum quantum number. R is the distance between NMR nuclei and the unpaired electrons which belong to the paramagnetic ion and are assumed to be localized on the lanthanide ion (point-dipole approximation). The γI is the nuclear gyromagnetic ratio and gJ is the isotropic Born–Landé g-factor.
is the spin-dipolar coupling parameter.67T1e and T2e are the longitudinal and transverse electronic relaxation times, respectively, which are used to approximate the corresponding electronic correlation times.67ωI and ωS are the nuclear and electronic Larmor frequencies, respectively. J is the main total angular momentum quantum number. R is the distance between NMR nuclei and the unpaired electrons which belong to the paramagnetic ion and are assumed to be localized on the lanthanide ion (point-dipole approximation). The γI is the nuclear gyromagnetic ratio and gJ is the isotropic Born–Landé g-factor.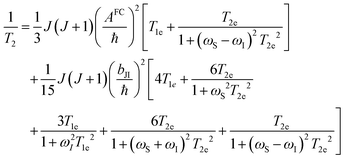 | (12) |
The first term in this equation is caused by Fermi-contact coupling and lacks a simple relation to the blind-sphere radius. The second term, called pseudo-contact term, is caused by a direct dipole–dipole interaction and has a distance dependence of R−6. At the critical relaxation rate (neglecting the Fermi contact contribution) the second term is proportional to bJI2J(J + 1) or expressed with the effective magnetic moment 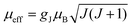 (Landé formula) proportional to μeff2R−6. The electronic relaxation times in solids are driven by vibrational motions and differ by the lanthanide ion. Published ranges39,67 of the electronic relaxation times show only minor differences for lanthanides Ln3+ (Ln = Sm, Nd, Yb, Tm, Er and Ho) with the exception of Gd3+ (see Table 8.6 in ref. 67) for which electronic relaxation rates are several orders of magnitude lower than for the other paramagnetic lanthanide ions, which causes efficient nuclear transversal relaxation and is consistent with the magnitude of the linewidth (few hundreds to kHz) observed from the EXSY (Fig. 6) and single pulse measurements. Note that the EXSY experiment with a very short mixing time behaves like a stimulated echo and provides information about transversal relaxation over the complete linewidth. For the other Ln3+ ions, the observed line broadening (Fig. 6 and ESI,† Fig. S2) is of the order of ten to a hundred Hz. This is much larger than the expected relaxation-induced line broadening which indicates relaxation not to be the predominant source of broadening. This interpretation is in agreement with the observation that the line broadening for Gd3+ is homogeneous while the other Ln3+ dopants generate inhomogeneous line broadening and explains the exceptional role of Gd3+ in the Fig. 9 and 10.
(Landé formula) proportional to μeff2R−6. The electronic relaxation times in solids are driven by vibrational motions and differ by the lanthanide ion. Published ranges39,67 of the electronic relaxation times show only minor differences for lanthanides Ln3+ (Ln = Sm, Nd, Yb, Tm, Er and Ho) with the exception of Gd3+ (see Table 8.6 in ref. 67) for which electronic relaxation rates are several orders of magnitude lower than for the other paramagnetic lanthanide ions, which causes efficient nuclear transversal relaxation and is consistent with the magnitude of the linewidth (few hundreds to kHz) observed from the EXSY (Fig. 6) and single pulse measurements. Note that the EXSY experiment with a very short mixing time behaves like a stimulated echo and provides information about transversal relaxation over the complete linewidth. For the other Ln3+ ions, the observed line broadening (Fig. 6 and ESI,† Fig. S2) is of the order of ten to a hundred Hz. This is much larger than the expected relaxation-induced line broadening which indicates relaxation not to be the predominant source of broadening. This interpretation is in agreement with the observation that the line broadening for Gd3+ is homogeneous while the other Ln3+ dopants generate inhomogeneous line broadening and explains the exceptional role of Gd3+ in the Fig. 9 and 10.
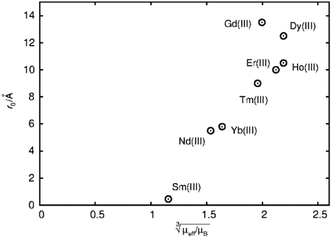 | ||
Fig. 9 Blind sphere radii for Ln(III) dopants of La1−xLnxPO4 series, plotted against 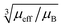 . The μeff and μB refer to effective magnetic moment53 and Bohr magneton, respectively. . The μeff and μB refer to effective magnetic moment53 and Bohr magneton, respectively. | ||
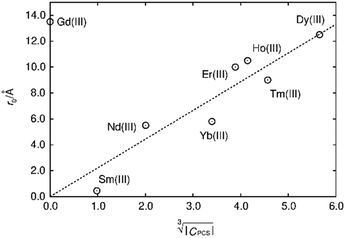 | ||
Fig. 10 Blind sphere radii for Ln(III) dopants of La1−xLnxPO4 series, plotted against 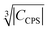 . |CPCS| refers to the magnitude of electronic contribution from pseudo-contact shielding.67,68 The dashed line features the fitting function . |CPCS| refers to the magnitude of electronic contribution from pseudo-contact shielding.67,68 The dashed line features the fitting function 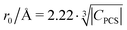 with the coefficient of determination R2 = 0.89. with the coefficient of determination R2 = 0.89. | ||
Paramagnetic shift
Besides relaxation, another possible origin for blind sphere is the paramagnetic shift δparam. The inhomogeneous line-broadening observed on the 31P resonances indicates that the paramagnetic shift is the relevant origin for the blind spheres of LaPO4 doped with Ln3+ (Ln = Nd, Sm, Dy, Er, Ho, Tm, Yb), but not for LaPO4 doped with Gd3+. Different mechanisms may cause a paramagnetic isotropic or anisotropic shift, which have been subject to a recent review.67 In order to compare the relative size of paramagnetic shift in a lanthanide series Bleaney,68 Golding and Halton69 have developed an approach in which they separate the electronic term C from a coupling term. The size of the electronic term can be described by a real number and was tabulated by Pell et al.67 for the contact shift Ccon, the pseudo-contact shift CPCS = g2J(J + 1)(2J − 1)(2J + 3) 〈J||α||J〉67 and the shielding anisotropy CSA (Table 3). Given that a critical broadening or shift exists (see above) which defines the blind-sphere radius r0, it should be possible to obtain a linear relation between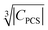 and the blind sphere radius r0. In fact a good correlation is observed (Fig. 10), with the expected exception of Gd3+ (see above). For completeness we have also plotted the blind-sphere radius vs.
and the blind sphere radius r0. In fact a good correlation is observed (Fig. 10), with the expected exception of Gd3+ (see above). For completeness we have also plotted the blind-sphere radius vs.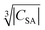 (ESI,† Fig. S3) and
(ESI,† Fig. S3) and 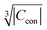 (Fig. S4, ESI†). The observed excellent empirical correlation in case of the contact interaction lacks a good explanation, though. It should not be overinterpreted as it is caused by the drastic change of a single measurement, i.e. on La1−xGdxPO4 for which relaxation is expected to have a big influence.
(Fig. S4, ESI†). The observed excellent empirical correlation in case of the contact interaction lacks a good explanation, though. It should not be overinterpreted as it is caused by the drastic change of a single measurement, i.e. on La1−xGdxPO4 for which relaxation is expected to have a big influence.
| Dopant ion | r A0/Å | |CSA| | |Ccon| | |CPCS| |
|---|---|---|---|---|
| Nd3+ | 5.5 | 13.1 | 4.5 | 8.08 |
| Sm3+ | 0.45 | 0.7 | 0.063 | 0.94 |
| Gd3+ | 13.5 | 63 | 31.5 | 0 |
| Dy3+ | 12.5 | 113.3 | 28.5 | 181 |
| Ho3+ | 10.5 | 112.5 | 22.6 | 71.3 |
| Er3+ | 10.0 | 91.8 | 15.4 | 58.8 |
| Tm3+ | 9.0 | 57.2 | 8.2 | 95.3 |
| Yb3+ | 5.8 | 20.6 | 2.6 | 39.2 |
To sum up, for Ln3+ both relaxation (in case of Gd3+) and the paramagnetic shift (in case of the other presented Ln3+) give an explanation for the origin of the blind sphere. The pseudo-contact term provides a simple explanation for the change of the blind-sphere radius in a lanthanide series and predicts a 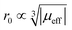 dependence for relaxation and a
dependence for relaxation and a 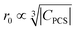 dependence for the paramagnetic shift, of which the latter is confirmed by the experiment.
dependence for the paramagnetic shift, of which the latter is confirmed by the experiment.
Conclusions
In this work, sizes of blind spheres r0 have been determined from NMR spectra by two methods: signal visibility decay function and lineshape analysis. A formula for the blind sphere radius could be derived, that relates the radii of blind sphere to the lineshape for a given dead time of the spectrometer, which allows to estimate blind-sphere radii even when the visibility remains close to 100% over the complete doping range.The dependence of blind sphere radii on the effective magnetic moment of the dopant ions and on the nucleus give insight into processes leading to a blind-sphere and provide estimates for blind sphere radii upon switching the dopant in a lanthanide series or the nucleus. Blind-sphere radii up to 13 Å suggest that a significant amount of material may remain virtually invisible in NMR, while certain paramagnetic ions, like Sm3+, allow the detection of NMR signal even from atoms two bonds away from paramagnetic centre. These results are relevant for evaluating the paramagnetic doping homogeneity of inorganic phosphors and their optical performance and to estimate which nuclei around a paramagnetic centre can directly be observed, for example in dynamic nuclear polarization (DNP) NMR or by direct detection.
Conflicts of interest
There are no conflicts to declare.References
- I. Bertini, P. Turano and A. J. Vila, Chem. Rev., 1993, 93, 2833–2932 CrossRef CAS.
- I. Bertini, C. O. Fernández, B. G. Karlsson, J. Leckner, C. Luchinat, B. G. Malmström, A. M. Nersissian, R. Pierattelli, E. Shipp, J. S. Valentine and A. J. Vila, J. Am. Chem. Soc., 2000, 122, 3701–3707 CrossRef CAS.
- C. Öster, S. Kosol, C. Hartlmüller, J. M. Lamley, D. Iuga, A. Oss, M.-L. Org, K. Vanatalu, A. Samoson, T. Madl and J. R. Lewandowski, J. Am. Chem. Soc., 2017, 139, 12165–12174 CrossRef PubMed.
- E. Ravera, G. Parigi and C. Luchinat, J. Magn. Reson., 2017, 282, 154–169 CrossRef CAS PubMed.
- L. Cerofolini, T. Staderini, S. Giuntini, E. Ravera, M. Fragai, G. Parigi, R. Pierattelli and C. Luchinat, JBIC, J. Biol. Inorg. Chem., 2018, 23, 71–80 CrossRef CAS PubMed.
- J. Kim, D. S. Middlemiss, N. A. Chernova, B. Y. X. Zhu, C. Masquelier and C. P. Grey, J. Am. Chem. Soc., 2010, 132, 16825–16840 CrossRef CAS PubMed.
- L. Zhou, M. Leskes, A. J. Ilott, N. M. Trease and C. P. Grey, J. Magn. Reson., 2013, 234, 44–57 CrossRef CAS PubMed.
- X. Li, M. Tang, X. Feng, I. Hung, A. Rose, P.-H. Chien, Z. Gan and Y.-Y. Hu, Chem. Mater., 2017, 29, 8282–8291 CrossRef CAS.
- C. A. Lepre, J. M. Moore and J. W. Peng, Chem. Rev., 2004, 104, 3641–3676 CrossRef CAS.
- Q. Z. Ni, F. Yang, T. V. Can, I. V. Sergeyev, S. M. D’Addio, S. K. Jawla, Y. Li, M. P. Lipert, W. Xu, R. T. Williamson, A. Leone, R. G. Griffin and Y. Su, J. Phys. Chem. B, 2017, 121, 8132–8141 CrossRef CAS PubMed.
- R. R. Amirov, E. A. Burilova, Y. I. Zhuravleva, A. V. Zakharov and A. B. Ziyatdinova, Polym. Sci., Ser. C, 2017, 59, 133–140 CrossRef CAS.
- N. J. Brownbill, R. S. Sprick, B. Bonillo, S. Pawsey, F. Aussenac, A. J. Fielding, A. I. Cooper and F. Blanc, Macromolecules, 2018, 51, 3088–3096 CrossRef CAS.
- C. S. Zuo, K. R. Metz, Y. Sun and A. D. Sherry, J. Magn. Reson., 1998, 133, 53–60 CrossRef CAS PubMed.
- A. E. Thorarinsdottir, A. I. Gaudette and T. David Harris, Chem. Sci., 2017, 8, 2448–2456 RSC.
- M. Ilibi, T. B. de Queiroz, J. Ren, L. D. Cola, A. S. S. de Camargo and H. Eckert, Dalton Trans., 2014, 43, 8318–8330 RSC.
- M. de Oliveira, T. Uesbeck, T. S. Gonçalves, C. J. Magon, P. S. Pizani, A. S. S. de Camargo and H. Eckert, J. Phys. Chem. C, 2015, 119, 24574–24587 CrossRef CAS.
- T. Harazono, E. Yokota, H. Uchida and T. Watanabe, Bull. Chem. Soc. Jpn., 1998, 71, 2797–2805 CrossRef CAS.
- T. Harazono, E. Yokota, H. Uchida and T. Watanabe, Bull. Chem. Soc. Jpn., 1998, 71, 825–829 CrossRef CAS.
- T. Harazono, R. Adachi, N. Kijima and T. Watanabe, Bull. Chem. Soc. Jpn., 1999, 72, 2655–2664 CrossRef CAS.
- S. Maron, G. Dantelle, T. Gacoin and F. Devreux, Phys. Chem. Chem. Phys., 2014, 16, 18788–18798 RSC.
- W. Li, V. R. Celinski, J. Weber, N. Kunkel, H. Kohlmann and J. Schmedt auf der Günne, Phys. Chem. Chem. Phys., 2016, 18, 9752–9757 RSC.
- S. Maron, N. Ollier, T. Gacoin and G. Dantelle, Phys. Chem. Chem. Phys., 2017, 19, 12175–12184 RSC.
- N. C. George, J. Brgoch, A. J. Pell, C. Cozzan, A. Jaffe, G. Dantelle, A. Llobet, G. Pintacuda, R. Seshadri and B. F. Chmelka, Chem. Mater., 2017, 29, 3538–3546 CrossRef CAS.
- L. Russo, M. Maestre-Martinez, S. Wolff, S. Becker and C. Griesinger, J. Am. Chem. Soc., 2013, 135, 17111–17120 CrossRef CAS PubMed.
- R. J. McCarty and J. F. Stebbins, Solid State Nucl. Magn. Reson., 2016, 79, 11–22 CrossRef CAS PubMed.
- C. P. Grey, C. M. Dobson, A. K. Cheetham and R. J. B. Jakeman, J. Am. Chem. Soc., 1989, 111, 505–511 CrossRef CAS.
- T. Wittmann, A. Mondal, C. B. L. Tschense, J. J. Wittmann, O. Klimm, R. Siegel, B. Corzilius, B. Weber, M. Kaupp and J. Senker, J. Am. Chem. Soc., 2018, 140, 2135–2144 CrossRef CAS PubMed.
- A. Mondal, M. W. Gaultois, A. J. Pell, M. Iannuzzi, C. P. Grey, J. Hutter and M. Kaupp, J. Chem. Theory Comput., 2018, 14, 377–394 CrossRef CAS PubMed.
- A. R. Brough, C. P. Grey and C. M. Dobson, J. Am. Chem. Soc., 1993, 115, 7318–7327 CrossRef CAS.
- J. H. Van Vleck, Phys. Rev., 1948, 74, 1168–1183 CrossRef.
- P. W. Anderson and P. R. Weiss, Rev. Mod. Phys., 1953, 25, 269–276 CrossRef CAS.
- G. W. Parker and F. Lado, Phys. Rev. B: Solid State, 1973, 8, 3081–3092 CrossRef CAS.
- C. Zhang, T. Uchikoshi, L. Liu, B. Dierre, Y. Sakka and N. Hirosaki, Appl. Phys. Lett., 2014, 104, 021914 CrossRef.
- L. I. D. J. Martin, D. Poelman, P. F. Smet and J. J. Joos, ECS J. Solid State Sci. Technol., 2018, 7, R3052–R3056 CrossRef CAS.
- V. Bachmann, C. Ronda, O. Oeckler, W. Schnick and A. Meijerink, Chem. Mater., 2009, 21, 316–325 CrossRef CAS.
- J. J. Joos, K. W. Meert, A. B. Parmentier, D. Poelman and P. F. Smet, Opt. Mater., 2012, 34, 1902–1907 CrossRef CAS.
- V. Bachmann, C. Ronda and A. Meijerink, Chem. Mater., 2009, 21, 2077–2084 CrossRef CAS.
- I. Bertini, C. Luchinat, G. Parigi and R. Pierattelli, ChemBioChem, 2005, 6, 1536–1549 CrossRef CAS PubMed.
- I. Bertini, C. Luchinat, G. Parigi and E. Ravera, NMR of Paramagnetic Molecules: Applications to Metallobiomolecules and Models, Elsevier, 2016 Search PubMed.
- I. J. Lowe and D. Tse, Phys. Rev., 1968, 166, 279–291 CrossRef CAS.
- B. Giovannini, P. Pincus, G. Gladstone and A. J. Heeger, J. Phys., Colloq., 1971, 32, C1-163 CrossRef.
- M. Punkkinen, Phys. Kondens. Mater., 1971, 13, 79–88 CrossRef CAS.
- B. Corzilius, L. B. Andreas, A. A. Smith, Q. Z. Ni and R. G. Griffin, J. Magn. Reson., 2014, 240, 113–123 CrossRef CAS PubMed.
- R. Rogawski, I. V. Sergeyev, Y. Zhang, T. H. Tran, Y. Li, L. Tong and A. E. McDermott, J. Phys. Chem. B, 2017, 121, 10770–10781 CrossRef CAS PubMed.
- T. Wolf, S. Kumar, H. Singh, T. Chakrabarty, F. Aussenac, A. I. Frenkel, D. T. Major and M. Leskes, J. Am. Chem. Soc., 2019, 141, 451–462 CrossRef CAS PubMed.
- A. Bertarello and G. Pintacuda, Paramagnetism in Experimental Biomolecular NMR, 2018, pp. 163–188 Search PubMed.
- S. Lange, A. H. Linden, Ü. Akbey, W. Trent Franks, N. M. Loening, B. J. van Rossum and H. Oschkinat, J. Magn. Reson., 2012, 216, 209–212 CrossRef CAS PubMed.
- D. Jardón-Álvarez and J. Schmedt auf der Günne, Solid State Nucl. Magn. Reson., 2018, 94, 26–30 CrossRef PubMed.
- Y. Ni, J. M. Hughes and A. N. Mariano, Am. Mineral., 1995, 80, 21–26 CAS.
- A. C. Palke, J. F. Stebbins and L. A. Boatner, Inorg. Chem., 2013, 52, 12605–12615 CrossRef CAS PubMed.
- J. F. Stebbins, R. J. McCarty and A. C. Palke, Acta Crystallogr., Sect. C: Struct. Chem., 2017, 73, 128–136 CrossRef CAS.
- L. Vegard, Z. Phys., 1921, 5, 17–26 CrossRef CAS.
- C. H. Evans, Biochemistry of the Lanthanides, Springer Science & Business Media, 2013 Search PubMed.
- G. E. Pake and E. M. Purcell, Phys. Rev., 1948, 74, 1184–1188 CrossRef.
- M. M. Maricq and J. S. Waugh, J. Chem. Phys., 1979, 70, 3300–3316 CrossRef CAS.
- K. Schmidt-Rohr and H. W. Spiess, Multidimensional Solid-State NMR and Polymers, Elsevier, 2012 Search PubMed.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- G. A. Morris and R. Freeman, J. Magn. Reson., 1969, 1978(29), 433–462 Search PubMed.
- P. L. Kuhns and M. S. Conradi, J. Chem. Phys., 1982, 77, 1771–1778 CrossRef CAS.
- A. Y. H. Lo, V. Sudarsan, S. Sivakumar, F. van Veggel and R. W. Schurko, J. Am. Chem. Soc., 2007, 129, 4687–4700 CrossRef CAS PubMed.
- O. J. Żogał, M. Drulis and S. Idziak, Z. Phys. Chem., 1989, 163, 303–308 CrossRef.
- O. J. Żogał, S. Idziak, M. Drulis and K. Niedźwiedź, Phys. Status Solidi B, 1991, 167, K55–K58 CrossRef.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- F. C. Strobridge, D. S. Middlemiss, A. J. Pell, M. Leskes, R. J. Clément, F. Pourpoint, Z. Lu, J. V. Hanna, G. Pintacuda, L. Emsley, A. Samoson and C. P. Grey, J. Mater. Chem. A, 2014, 2, 11948–11957 RSC.
- I. D. Seymour, D. S. Middlemiss, D. M. Halat, N. M. Trease, A. J. Pell and C. P. Grey, J. Am. Chem. Soc., 2016, 138, 9405–9408 CrossRef CAS PubMed.
- N. Bloembergen and L. O. Morgan, J. Chem. Phys., 1961, 34, 842–850 CrossRef CAS.
- A. J. Pell, G. Pintacuda and C. P. Grey, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271 CrossRef CAS.
- B. Bleaney, J. Magn. Reson., 1972, 8, 91–100 CAS.
- R. M. Golding and M. P. Halton, Aust. J. Chem., 1972, 25, 2577–2581 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Numerical for the spectral analysis of LaPO4:Sm, EXSY spectra for LaPO4:Ln, 31P NMR relaxation data for LaPO4:Ln. See DOI: 10.1039/c9cp00953a |
| This journal is © the Owner Societies 2019 |