Prediction of the near-IR spectra of ices by ab initio molecular dynamics

Abstract

A method to predict the near-infrared spectra of amorphous solids by means of ab initio molecular dynamics is presented. These solids can simulate molecular ices. To test the method, mixtures of methane, water and nitrogen are generated as amorphous samples of various concentrations. The full theoretical treatment includes as a first step, the optimization of their geometrical structure for a range of densities, after which, the most stable systems are taken as initial structures for molecular dynamics, performed at 200 K in trajectories of 4 ps duration with a 0.2 fs time step. All the dynamics are carried out using the first principles method, solving the quantum problem for the electrons using density-functional theory (DFT), and integrating the DFT forces, following the Born–Oppenheimer dynamics. After the dynamics, near-IR spectra are predicted by the Fourier transform of the macroscopic polarization autocorrelation function. The calculated spectra are compared with the experimental spectra of ice mixtures of CH₄ and H₂O recorded in our laboratory, and with some spectra recorded by the New Horizons mission on Pluto.

---

Introduction

The near-IR, covering wavelengths from 0.8 to 2.5 μm approximately, corresponds to the absorption of overtones and combination bands of molecular vibrations. This is a particularly interesting IR region for many reasons, one of them being its extended use for the observation of astrophysical ices in the solar system. However, the theoretical simulation of spectra in this zone is a challenging task, especially for amorphous solids formed by a certain number of molecular units. High-level ab initio methods that usually give reasonably accurate results for the description of anharmonic modes of individual molecules or small clusters are not easily applied to systems with several molecules, often linked among them by weak bonding of different types. We explore in this paper the application of ab initio molecular dynamics (AIMD) calculations to predict the spectra of molecular ices in the near-IR region.

There have been some previous experimental investigations on solid mixtures containing CH₄, H₂O, N₂ and other volatiles in various proportions,^1–7 even including the possibility of methane clathrates,⁸ often with the aim of providing information for the analysis of astronomical data. The interest of these systems in the liquid phase goes beyond the astrophysical aspects, since e.g. solutions of CH₄ in H₂O are used in biological environments as a model of hydrophobic interactions relevant in many processes such as protein folding,^9,10 and also in other branches of chemistry as in soft matter. Individual molecular components in this kind of ice formed by water plus non polar molecules are held together mainly by hydrogen bond interactions among the water molecules. They build up a sort of skeleton to which non polar components attach. Weak dispersive forces are responsible for the interactions among the non-polar molecules and among non-polar molecules with water molecules. The very nature of the interactions determines the methodological approach needed to describe the electron structure of the ices in the simulation of the spectra.

From the theoretical point of view, there is also abundant bibliography on the use of molecular dynamics to study molecules or clusters, and sometimes to calculate their vibrational spectra,^11–15 but the specific application of this technique to predict overtone or combination bands, in the near-IR region, has seldom been discussed.¹³ AIMD calculations are not without difficulties, such as the lengthy explorations of the various parameters of the dynamics that must be selected and the choice of the electronic structure method employed to calculate interaction potentials. For the kind of sample that we plan to study here, where polar and non-polar molecules make part of the same structure, this is certainly an important issue.

Some of the most recent exciting results in astrophysics have come from the close observation of Pluto and other Trans-Neptunian Objects (TNO) by the NASA's New Horizons mission. Initial estimates of the surface composition of Pluto by Cruikshank et al.¹⁶ just before the arrival of the New Horizons spacecraft were followed by the publication of astonishingly remarkable spectra of several spots of Pluto's surface taken by the Ralph array of instruments.¹⁷ Later on, many of the results of this observation have been presented in several papers in a special issue of the Icarus journal.¹⁸ It has been found that ices of CH₄, H₂O, N₂, CO and possibly other species are present on Pluto at different concentrations with a widely diverse distribution. Ices formed by mixtures of these species and other molecules, like NH₃, CO₂ or CH₃OH, are also frequently found on other bodies of the solar system and in the interstellar medium.^1,19–21

In this paper we continue previous theoretical studies^3,22–25 on ices of astrophysical relevance, and intend now to theoretically simulate the near-IR spectra of these amorphous solid systems using molecular dynamics. A brief description of the most relevant methodological aspects is included in the next section. We have also recorded in our laboratory the spectra of ice mixtures of CH₄ and H₂O, described in the following one. The Results section presents the application of the method to mixtures of CH₄, H₂O and N₂ in different proportions. Finally, we compare the predicted spectra with those recorded in our lab and with some spectra from different spots on Pluto's surface.

Methodology

The use of molecular dynamics for the prediction of IR spectra has been discussed in a number of previous papers.^{11–15,26–28} and references therein, of which the one by Thomas et al.¹¹ provides a very thorough discussion of the technique. In short, for individual molecules, the IR spectrum can be generated by the Fourier transform of the autocorrelation function of their dipole moment along the trajectory. In classical molecular dynamics simulations, the positions and velocities of the particles within a cell are described by means of force fields of diverse types. These are often based on additive contributions of several terms parameterized according to the interaction between the classically treated nuclei (harmonic terms for the bonds, Lennard-Jones for the interatomic potentials, etc.). Since we were mainly interested in dealing with weak spectral features arising from some 2nd order effects like overtones or combination bands, we chose ab initio molecular dynamics (AIMD) to try to use a better technique to follow the variation of interactions along the dynamics, without the constraint of parameterization. With AIMD, the electronic energies and interatomic forces calculated from the first-principles solution of the quantum problem posed by the electrons and the nuclei are displaced according to the classical trajectory defined by the first-principles forces.

In normal mode calculations of molecules, the IR absorption coefficient S is proportional to the square of the derivatives of the dipole moment μ with respect to the normal coordinates Q:

In AIMD, the dipole moment derivatives are replaced by the dipole time-correlation function, and the Fourier transform is then carried out:

where [small mu, Greek, dot above] represents the time derivative of the dipole moment and ω is the frequency of the Q normal mode, in s⁻¹. Along the dynamics, all vibrational modes are excited simultaneously, and the information contained within the time-correlation function is extracted by its Fourier transform, with some similarity to the space distribution contained in an interferogram in Fourier Transform IR spectroscopy. For bulk solids, the dipole moment operator in eqn (1) and (2) needs to be replaced by the macroscopic polarization of the solid,²⁹ which gives a suitable way to account for all charges within the unit cell.

Our models consisted of cubic cells where different numbers of CH₄, H₂O and N₂ molecules were included generating three-dimensional amorphous periodic structures in a Monte Carlo fashion, by minimizing close contacts between atoms, using the amorphous cell modulus of the Materials Studio package.³⁰ Prior to the dynamics, we performed a geometry optimization of the structures inside the cell for a range of density values, looking for the structure and density which yielded the lowest optimization energy from a set of 10 amorphous structures. Consistency in the optimization was provided by checking that the frequencies of all fundamental vibrational modes were predicted as real numbers, indicating minima in their potential energy surface (PES). The selected structures at the minimum were taken for the dynamics process.

These initial optimizations were performed using the density functional theory (DFT) plane-wave pseudopotential method CASTEP³¹ of the same Materials Studio package.³⁰ We used for these initial structure relaxations the Perdew–Burke–Ernzerhof (PBE) functional with Grimme's D2 dispersion correction,^32,33 with a plane wave basis set cut-off of 750 eV.

All the dynamics calculations were carried out using the Siesta implementation of DFT.^34–36 Basis functions were taken from the literature.³⁷ The Generalized Gradient Approximation (GGA) with revised Perdew–Burke–Ernzerhof (RPBE)³⁸ functionals was chosen. Other parameters of the calculations were a mesh cutoff of 500 Ry giving a converged fine grid in real space for the real-space integrations needed to obtain the matrix elements of the Kohn–Sham Hamiltonian,³⁵ and a k-grid cutoff of 6 Å, defining a sufficiently fine discretization of reciprocal space to approximate integrals over the Brillouin zone.³⁹ The Siesta code was modified to calculate the macroscopic polarization of the samples at a specified number of steps in the dynamics. This was implemented to save computing time because the calculation of the polarization is a lengthy process.⁴⁰ The polarization in a periodic solid up to a quantum of polarization, so that, in order for the results to be homogeneous, all values were referred to as the first quantum. The ensuing steps involved calculating the polarization auto-correlation function (PACF), normalizing the PACF and computing its Fourier transform that yields the IR spectrum.

The dynamics were established as a two-step procedure. First, the equilibration of the initial structure was achieved through an annealing process to a specified target temperature, starting from an initial configuration obtained as described above, and from random velocities corresponding to a Maxwell distribution for the target temperature, and letting it equilibrate following the dynamics of the system under a Berendsen thermostat.⁴¹ The structure at that temperature was selected from the output of geometries and was then taken as the starting point for the full dynamics process.

We chose a constant-volume/constant-energy/constant-composition (NVE) microcanonical ensemble integrated using a time discretization and the Verlet integration algorithm.⁴¹ This implies that our simulation cell was allowed to vary its temperature within reasonable margins, while keeping the cell size and internal energy constant, which allowed a closer reference to the conditions in some astronomical media. The equilibration temperature was 200 K, higher than the estimated value of many astronomical samples, but necessary to excite adequately the very weak vibrational motions that appear in the near-IR region. In practice, we are primarily interested in the relative intensities of spectral features arising from the different components of the sample, mainly methane and water, and not in their absolute intensity, which would require a completely different treatment of the problem, and therefore the choice of 200 K seems justified.

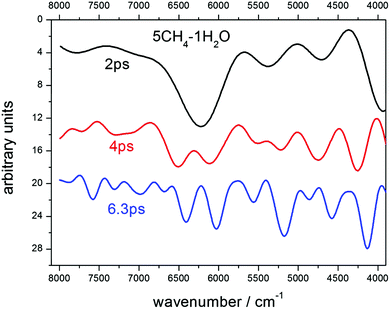
Choosing the time step for the dynamics is a fundamental issue. It's in an inverse ratio to the frequency of the modes that one wants to sample. For the fundamental O–H and C–H stretching modes, which appear at ∼3000 cm⁻¹, or ∼100 THz, time steps of 1 fs or 0.5 fs are usually chosen. Since we were interested in higher frequency modes, we had to reduce the step, but this also increased considerably the computer running time. After checking for 0.2 fs and 0.1 fs, we decided that the gain for the shortest step was not large enough to justify the much longer computing time, so we selected 0.2 fs. In a similar manner, the length of the dynamics fixes the resolution of the spectra. As the resolution of the observed spectra of many astronomical samples is not very large, compared with laboratory measurements, we tried lengths of 2 ps and 4 ps for our trajectories, and finally opted for the second choice for most of our runs, which therefore means dynamics of 20 000 steps. In some particular cases, longer dynamics were performed looking for some increased resolution. For illustration, and to show the consistent behavior of the calculations, we include in Fig. 1 an example of the resolution gain between dynamics of 2 ps and 6.3 ps on the spectra of a sample with 5CH₄ and 1H₂O molecules. The predicted spectra achieve a higher degree of resolution, as can be seen in Fig. 1, where several bands are resolved at each stage. Between 2 ps and 4 ps, the most obvious case is the splitting of the main feature, at ∼6300 cm⁻¹, into two components, at 6100 cm⁻¹ and 6600 cm⁻¹, with other splittings for the bands at 5400 cm⁻¹ and 4100 cm⁻¹. Between 4 ps and 6.3 ps, many individual bands are disclosed in the whole region. The assignments of all these bands will be discussed below. However, the 6.3 ps dynamics conveys a very lengthy computation, so we finally accepted 4 ps as the most adequate length for our purposes.

Fig. 1 Spectra predicted after 3 different dynamics of a sample with 5CH₄–1H₂O molecules. An increase in the length of the run from 2 ps through 6.3 ps allows resolving most of the individual bands. Spectra are offset along the ordinate axis for clarity.

A few considerations must be borne in mind regarding the spectra calculated via molecular dynamics for this near-IR region. First, it is important to stress that the vibrations in this IR window are intrinsically non-linear, inasmuch as they correspond to excitations of two or more normal modes of the same (overtones) or different vibrations (combination bands). The simulation of non-linearity is achieved through the autocorrelation process of the macroscopic polarization that is obtained in a linear calculation. Next, the wavenumber accuracy expected from these calculations cannot be as high as that which can be reached by high level ab initio methods for the fundamental modes of single molecules. To begin with, the basis sets and theoretical parameters used for solving the electronic structure at each stage in our dynamics are chosen to achieve a fast convergence, a constraint that can be waived for non-dynamics ab initio calculations, like those often applied to deal with simple molecules. Moreover, the anharmonicity of the vibrational modes implies wavenumber shifts from the harmonic prediction which are not easy to reproduce. Another important aspect of the spectra concerns the width of the observed lines. All experimental H₂O bands are usually very broad, often spanning more than 200 cm⁻¹, and this is not reproduced in the calculations, where broadening effects induced by H-bonding, for instance, are not specifically taken into account. Finally, the consideration of an amorphous solid as a repetitive unit of a single cell implies in itself some simplifications over the real structure. Taking all this into account, wavenumber predictions with an accuracy of ±100 cm⁻¹ may be considered satisfactory, again for this IR region and this type of vibration.

From the calculation point of view, the inclusion of more molecules within the simulation cell, keeping the CH₄/H₂O ratio, could change the aspect of some vibrations. An example is given in Fig. 2, where a comparison is presented for two dynamics with a CH₄/H₂O ratio of 3/1, namely 3CH₄–1H₂O and 6CH₄–2H₂O samples. In the second case, with 2 water molecules, some wavenumber displacements could be expected, especially for the O–H vibrations where H-bond effects may be important. On the other hand, the CH₄ bands should not shift in the spectrum, but the presence of more molecules in the simulation cell may blur the contour, yielding an apparent loss of resolution. For those samples where very little water is expected, it seems safe to work with models with only one H₂O molecule and a growing number of CH₄ molecules, as discussed below. On the other hand, for the comparison with water-rich samples, models with more H₂O molecules should be used.

Fig. 2 Spectra of two samples with the same ratio of CH₄/H₂O molecules. Some differences can be attributed to shifts in H₂O vibrations involving H-bonding and to broadening of CH₄ bands.

Experimental

Our laboratory is equipped with a high vacuum chamber with a closed-cycle He cryostat, coupled to a Bruker Vertex70 FTIR spectrometer. The setup has been described in detail in a previous article.⁴² Methane and water ice mixtures are grown by vapor deposition on an infrared transparent Si substrate cooled to 30 K. The gases are introduced into the chamber through independent lines, one provided with a Alicat mass flow controller and the other with a needle valve, used for CH₄ and H₂O, respectively. The pressure in the chamber is ∼10⁻⁸ mbar before deposition and increases to 10⁻⁵–10⁻⁴ mbar during the deposits. We grow ice layers between 6 and 15 μm thick at rates that vary from 2 to 5 μm h⁻¹. In order to control the CH₄/H₂O ratio in the mixtures we have calibrated the pressure of each gas in the chamber in the following way. First, we record the spectra of the pure species in the mid-IR and estimate the number of molecules in the sample by reference to literature band strengths of the main bands: A = 1.9 × 10⁻¹⁶ cm per molecule for the H₂O band at 3200 cm⁻¹,⁴ and A = 8.4 × 10⁻¹⁸ cm per molecule for the CH₄ band at 1300 cm⁻¹.⁴³ With these values we can estimate the growing rate of the corresponding ices, and from the growing rates, assuming a sticking coefficient of 1 in agreement with previous literature,⁴⁴ we calculate the gas pressure. In our experiments, we have recorded spectra in the near-IR region using a near-IR lamp with a MCT detector, at 8 cm⁻¹ resolution, adding 300 scans, and covering a spectral range from 8000 to 2000 cm⁻¹.

We have recorded the spectra of samples of pure CH₄, co-deposited CH₄/H₂O mixtures in ratios of 10/1 and 1/1, and pure H₂O ice, at 30 K. The spectra of the pure species are used for comparison and assignments; we present in Fig. 3 the spectra of the mixtures in the region of maximum interest. A baseline with the contour of IR interference fringes has been subtracted from the recorded trace. The CH₄ features are sharp and stand out for both mixtures, whereas the H₂O bands are broad and it is not easy to assert their band center. From the higher water-content sample, we estimate two H₂O band centers at ∼5100 and 6760 cm⁻¹, with a further less obvious feature at 6400 cm⁻¹. Later on in this paper we collect in a table the assignment of the main bands observed in our experiments, together with values from the calculated spectra.

Fig. 3 Laboratory spectra of mixtures of CH₄ and H₂O in ratios of 10/1 (black, above) and 1/1 (red, offset). The absorbance axis has been cut off for a better view of the weaker bands at higher wavenumbers.

Results

We prepared models with a large variation of CH₄ and H₂O ratios, from the individual species themselves to mixtures with different CH₄/H₂O content, plus more samples with N₂ added, to investigate its possible effect on the spectra. We had in mind the possible application of this work to study spectra in astronomical environments. Thus, we chose samples using three strategies: first, with growing CH₄ content, for CH₄/H₂O values from 3/1 to 10/1; then, with growing H₂O content, for values 10/2 (which allowed also direct comparison with the 10/1 case), 3/3, 3/6 and 3/9; and finally, for N₂-containing samples of various compositions. Only spectra that have direct usefulness in the following discussion will be reproduced in the figures of this paper.

For each model, we performed optimization of the geometry for several density values, in the range between 0.45 and 1.0 g cm⁻³. Table 1 collects the results of the lowest-energy structures for some of our samples. It is these structures that were taken as initial values for the dynamics process. We also list in Table 1 the formation energy of the models, calculated as:

ΔE = E(mol.sys.)–m × E(CH₄)–n × E(H₂O)–p × E(N₂) (3)

where E(mol.sys.) is the energy of the fully optimized structure, mCH₄–nH₂O–pN₂, listed in the 4th column of Table 1, and E(CH₄), E(H₂O) and E(N₂) are those of individual CH₄, H₂O and N₂ molecules, respectively, all of them optimized at the same level of theory as the full model. The most interesting result is the largest stabilization achieved when a second H₂O molecule is added to the 10CH₄–1H₂O system, and also when 3H₂O molecules are added to the 3CH₄–3H₂O–6N₂ sample, probably due to the generation of H-bonds among the H₂O molecules.

Table 1 Summary of the results of the most stable samples generated for the molecular mixtures studied in this work. The molecules were contained in cubic cells of side a (2nd column), for which the corresponding density is ρ (3rd column). The listed structures are those that yielded a minimum optimization energy E (4th column). The last column lists the formation energy calculated using eqn (3)

Molecular system	a/Å	ρ/g cm^−3	E/eV	ΔE/eV
3CH4–1H2O	5.53	0.65	−1122.615	−0.587
5CH4–1H2O	6.308	0.65	−1561.997	−0.742
6CH4–2H2O	6.965	0.65	−2245.263	−1.207
10CH4–1H2O	7.696	0.65	−2660.431	−1.108
10CH4–2H2O	7.947	0.65	−3124.476	−1.966
3CH4–3H2O	6.391	0.65	−2049.833	−1.431
3CH4–6H2O	7.363	0.65	−3441.204	−3.241
3CH4–9H2O	8.129	0.65	−4832.555	−5.030
5CH4–1H2O–3N2	6.954	0.90	−3175.189	2.948
3CH4–3H2O–3N2	7.004	0.90	−3667.327	−2.043
3CH4–3H2O–6N2	7.656	1.0	−5284.375	−2.209
3CH4–6H2O–6N2	8.136	1.0	−6675.189	−3.462

---

The analysis of Table 1 allows us to draw some further conclusions. In the first place, it can be seen that the variation of the formation energy of the methane–water mixtures is not exactly linear with an increase in one molecule of either of them. However, the addition of H₂O contributes an amount of energy in the range of 0.4 to 0.8 eV per molecule, which is notably larger than the 0.07–0.08 eV value per molecule for CH₄. For the mixtures containing N₂ in addition to H₂O and CH₄, the individual contribution of N₂ to the energy formation is somewhat more difficult to assess from the data in the table, but it may be close to 0.06 eV per molecule. All this is consistent with the picture of the clusters being formed by a backbone of water molecules linked by H-bond interactions to which the non-polar species are attached.

For the sake of the forthcoming discussion, we reproduce in Fig. 4 the calculated spectrum of the 3CH₄–3H₂O sample. This spectrum is chosen because the most important modes of each species can be seen, which facilitates the comparison with the spectra of samples with higher or lower abundance of either molecule. To summarize this part, Table 2 collects a survey of the main CH₄ and H₂O vibrations in the 4000–8000 cm⁻¹ region, with experimental wavenumbers from the observed spectra in our laboratory together with the calculated wavenumbers reported in this work, taken from the peaks shown in Fig. 4. The quoted assignments are based on previous works (see caption to Table 2). We have indicated with blue arrows in Fig. 4 the peaks assigned to CH₄ and with red arrows those assigned to H₂O.

Fig. 4 Calculated spectrum of a sample with 3CH₄–3H₂O molecules, taken as the basis for the assignments listed in Table 2 and for the discussion on the relative intensities of CH₄ and H₂O spectral features.

Table 2 Main features in the near-IR region of the spectra of CH₄ and H₂O mixtures and tentative assignments. Successive columns display wavenumber values measured from the spectra recorded in our laboratory; tentative assignments for CH₄ and H₂O bands from the indicated references, and wavenumbers calculated in this work, taken from the 3CH₄–3H₂O sample (see Fig. 4)

Lab. observed (this work)/cm^−1	Assignment CH4^a	Assignment H2O^b	Calculated (this work)/cm^−1
a Ref. 5–7. b Ref. 5 and 48. c Tentative assignment. This mode is IR-forbidden, but could be activated in CH4–H2O mixtures. d Br indicates the approximate band origin in broad features. e Unassigned.
4116	ν 2 + 2ν4
4206	ν 1 + ν4		4144
4303	ν 3 + ν4
4530	ν 2 + ν3		4503
5100		ν 1 + ν2, ν2 + ν3	5088
5383	ν 2 + 3ν4
5564	ν 3 + 2ν4		5448
5596	2ν2 + 2ν4
5801	ν 2 + ν3 + ν4		5818
5930	2ν1^c
5993	2ν3		6099
6040	2ν2 + ν3
6400 br^d		ν 1 + 2ν2, ν3 + 2ν2	6448
6760 br		2ν3	6763
7065	2ν1 + ν4;ν2 + ν3 + 2ν4		7133
7124^e
7180	ν 1 + ν2 + ν3
7484	ν 2 + 2ν3		7639

---

Application to the spectra from Pluto

The near-IR spectra recorded by the New Horizons instruments provide a good opportunity to test the validity or usefulness of our method. These spectra have been analyzed in great detail by the members of the New Horizons Science Team^45,46 by means of Principal Component Analysis and the transfer model of Hapke,⁴⁷ in terms of various parameters like the relative concentration of N₂, CH₄, H₂O and CO ices, tholins, grain size and visible dark red material, revealing their complex structure. We therefore do not intend to accurately reproduce them here, but to check how closely we can predict the relative strength of CH₄ and H₂O bands by using our simple model containing various proportions of these molecules, and also to investigate the spectral effects produced by the presence of N₂. In particular, we have focused on two of the spectra presented in Fig. 3 of Grundy et al.,¹⁷ traces a and d, corresponding to Plutos's North Pole and to the area around the Pulfrich crater, respectively.

Fig. 5 displays the spectra of three mixtures with growing CH₄ content, for CH₄/H₂O ratios of 3/1, 5/1 and 10/1. We also include the outline of the spectrum of trace a in Fig. 3 of Grundy et al.,¹⁷ scanned from the original figure and transformed to the linear scale in wavenumber for comparison. None of the calculated spectra matches perfectly the observation, but we can draw some conclusions from a piecewise analysis of the figure. The contour of the experimental spectrum in the lower wavenumber region, between 4000 and 5000 cm⁻¹, is better reproduced in the spectrum of the intermediate sample, with 5CH₄–1H₂O. However, in the 5500–6000 cm⁻¹ and 7000–7500 cm⁻¹ zones, the spectrum of the 10CH₄–1H₂O sample seems to have a closer resemblance to the observed trace than that of the other samples. The match would be even closer if we impose a shift to a higher wavenumber of the order of 100 cm⁻¹ on the calculated results. Such a shift may be acceptable for theoretical calculations of this level of accuracy, involving overtones and combination bands (see Table 2) as indicated above. With respect to the contribution of water bands, it is almost negligible in the experimental spectrum, in contrast to the appearance of strong water features in the two water-rich theoretical samples, top two traces in Fig. 5. Such features are weaker in the bottom trace, although they may still be fairly large for the comparison with the experiment. In conclusion, we estimate that the CH₄ to H₂O ratio in the North Pole of Pluto is probably around 10/1, but values in the 8/1 or 12/1 vicinity cannot be discarded.

Fig. 5 Calculated spectra of three samples with increasing CH₄ proportion, together with the adapted trace a of Fig. 3 of Grundy et al.¹⁷

Going in the opposite direction, we studied the effect of growing H₂O content in the mixture, using as a reference the spectrum of the Pulfrich crater in Pluto, trace d in Fig. 3 of Grundy et al.¹⁷ We present in Fig. 6 the spectra of three samples, with 3CH₄–3H₂O, 3CH₄–6H₂O and 3CH₄–9H₂O molecules. Comparison of the 3/3 and 3/6 spectra (top two traces) is fairly straightforward, with an increase in the intensity of the main H₂O bands, at ∼5100, 6400 and 6740 cm⁻¹, with respect to CH₄ neighboring features. However, interestingly, comparison of the 3/6 and 3/9 spectra is not so obvious. The H₂O bands at the higher wavenumber side grow both in intensity and width, overlapping with nearby CH₄ features with the net effect that the 3/9 spectrum appears as a less resolved trace. The observed spectrum at the Pulfrich crater of Pluto shows very broad H₂O bands with a smaller structure of narrow lines of CH₄ in the 5500–6000 and 7000–7500 cm⁻¹ regions. Keeping in mind the inability of the current method to correctly reproduce the wide H₂O bands observed experimentally, we estimate that the CH₄/H₂O mixing ratio that better resembles that of the Pulfrich crater would be between 1/2 and 1/3.

Fig. 6 Calculated spectra of mixtures with increasing H₂O proportion, in comparison with the spectrum at the Pulfrich crater of Pluto, adapted from trace d of Fig. 3 of Grundy et al.¹⁷

It is worth noting that our estimates for the ratio of CH₄ and H₂O in the cases studied here match reasonably well the results quoted in Table 3 of Protopapa et al.⁴⁶ from their analysis, where their models a and e correspond to the spectra of the Pulfrich crater and North Pole of Pluto, respectively.

Finally, we investigated the effect of adding N₂ molecules on the spectra. Nitrogen is assumed to be abundant in many regions of Pluto, forming N₂-rich/CH₄-rich ices of varying proportions, even giving rise to a weak peak observed in some of the traces of Fig. 3 of Grundy et al.¹⁷ at ∼4650 cm⁻¹, corresponding to the first harmonic of its IR-forbidden fundamental vibration, at ∼2330 cm⁻¹. To check its possible effect on the calculated spectra, we designed further samples based on some of the models described above, with the inclusion of 3N₂ or 6N₂ molecules, which induced a corresponding density increase. The subsequent dynamics yielded the predicted spectra. As an example, we collect in Fig. 7 the spectra of pairs 3CH₄–3H₂O and 3CH₄–3H₂O–6N₂, to discuss the observed effects. The presence of N₂ molecules induces a general blurring of the spectral features, responsible for the apparent intensity gain of the 4500 cm⁻¹ band. This cannot in any case be attributed to the very weak peak experimentally measured at ∼4650 cm⁻¹, as mentioned above, which we could not expect to observe in our simulation, where strong CH₄ and H₂O bands dominate. The blurring could be foreseen as a consequence of the presence of a relatively large number of non-polar species in the simulation cell encountered by the methane or water molecules during their motion, inducing a large inhomogeneity in their environment.

Fig. 7 Comparison of the calculated spectra of two samples with the same CH₄/H₂O content and with and without N₂, namely 3CH₄–3H₂O and 3CH₄–3H₂O–6N₂. The main effect of introducing N₂ molecules in the sample is to blur the total spectrum of the mixture.

Conclusions

We describe in this paper the use of ab initio molecular dynamics as a tool to predict spectra in the near-IR region for molecular solids, with possible application to astronomical ices. The high frequency of this zone compared to mid-IR requires the use of a short time step for the dynamics. On the other hand, the length of the trajectory can be adjusted to achieve a balance between the expected resolution, directly related to the duration of the dynamics, and the computer resources available. For our calculations, we have found that a time step of 0.2 fs over a 4 ps trajectory was a reasonable choice. Although the surface temperature of many astrophysical objects is quite low, we chose to perform our dynamics at an initial temperature of 200 K, because bands in the near-IR region are generally weak and the weaker features would be almost negligible at lower temperatures. All dynamics are performed using a modification of the Siesta code. The Fourier transform of the autocorrelation function of the macroscopic polarization calculated along the trajectory yields the vibrational spectrum.

We have applied this method to the study of ice mixtures of CH₄, H₂O and N₂, species frequently present on astronomical samples. We have built theoretical models of amorphous solids covering a broad range of CH₄ to H₂O ratios, from 10/1 to 3/9. The models consist of simulation cells, where the molecules are introduced, and prior to the dynamics, they are relaxed for a range of density values, looking for a minimum in their PES. Analysis of the formation energies shows an increase in the stabilization of the sample when more than one H₂O molecule is present, probably due to the formation of H-bonds among them. Then, the most stable structures are annealed at 200 K to yield an equilibrated structure, which is subsequently subjected to the dynamics trajectory. From the results of the dynamics, the spectra of our samples in the near-IR region are predicted.

To complement our calculations, we have recorded in our lab the spectra of ices of pure CH₄ and H₂O, and of ice mixtures with ratios of 10/1 and 1/1. We have compared the predictions of our method with our experimental spectra, and with spectra recorded by the New Horizons NASA mission. In particular, for two spots of Pluto's surface which show the largest variation in relative CH₄/H₂O content, we estimate approximate CH₄/H₂O ratios in reasonable agreement with the published results.

Possible extensions of this work may include the addition of more molecules in our samples and the study of mixed amorphous/crystalline species.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The calculations have been carried out at CESGA (CSIC-Xunta de Galicia), Westgrid (Canada) and TCM (Cavendish Laboratory, University of Cambridge). We are particularly grateful to several staff members for their technical support, especially to Michael Rutter (TCM, Cambridge). We are also thankful to M. A. Moreno for assistance with the early dynamics calculations. Funds from the Spanish MINECO FIS2016-77726-C3-1P, MINECO/FEDER CTQ2015-65033-P and MECD Sabbatical PRX17/00126 projects are also acknowledged. R. E. is most grateful to E. Artacho for hospitality during the sabbatical stay at Cambridge.

Notes and references

1. R. Hodyss, P. V. Johnson, J. V. Stern, J. D. Goguen and I. Kanik, Icarus, 2009, 200, 338.
2. C. R. Richey and P. A. Gerakines, Astrophys. J., 2012, 759, 74.
3. V. J. Herrero, O. Gálvez, B. Maté and R. Escribano, Phys. Chem. Chem. Phys., 2010, 12, 3164.
4. R. M. Mastrapa, S. A. Sandford, T. L. Roush, D. P. Cruikshank and C. M. Dalle Ore, Astrophys. J., 2009, 701, 1347.
5. M. P. Bernstein, D. P. Cruikshank and S. A. Sandford, Icarus, 2006, 181, 302.
6. P. A. Gerakines, J. J. Bray, A. Davies and C. R. Richey, Astrophys. J., 2005, 620, 1140.
7. W. M. Grundy, B. Schmitt and E. Quirico, Icarus, 2002, 155, 486.
8. E. Dartois, D. Deboffle and M. Bouzit, Astron. Astrophys., 2010, 514, A49.
9. J.-L. Li, R. Car, C. Tang and N. S. Wingreen, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2626.
10. A. J. Patel, P. Varilly, S. N. Jamadagni, H. Acharya, S. Garde and D. Chandler, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 17678.
11. M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Phys. Chem. Chem. Phys., 2013, 15, 6608.
12. S. D. Ivanov, A. Witt and D. Marx, Phys. Chem. Chem. Phys., 2013, 15, 10270.
13. J.-H. Choi and M. Cho, J. Chem. Theory Comput., 2011, 7, 4097.
14. J. Hornicek, P. Kaprálová and P. Bour, J. Chem. Phys., 2007, 127, 84502.
15. M. Praprotnik and D. Janezic, J. Chem. Phys., 2005, 122, 174103.
16. D. P. Cruikshank, W. M. Grundy, F. E. DeMeo, M. W. Buie, R. P. Binzel, D. E. Jennings, C. B. Olkin, J. W. Parker, D. C. Reuter, J. R. Spencer, S. A. Stern, L. A. Young and H. A. Weaver, Icarus, 2015, 246, 82.
17. W. M. Grundy, et al. , Science, 2016, 351, aad9189.
18. Special issue R. P. Binzel, C. B. Olkin, L. A. Young and P. D. Nicholson, Icarus, 2017, 287, 1-334.
19. A. C. Adwin Boogert, P. A. Gerakines and D. C. B. Whittet, Annu. Rev. Astron. Astrophys., 2015, 53, 541–581.
20. O. Grasset, J. Castillo-Rogez, T. Guillot, L. N. Fletcher and F. Tosi, Space Sci. Rev., 2017, 212, 835.
21. K. I. Öberg, A. C. A. Boogert, K. M. Pontoppidan, G. A. Blake, N. J. Evans, F. Lahuis and E. F. van Dishoeck, Astrophys. J., 2008, 678, 1032.
22. O. Gálvez, B. Maté, V. J. Herrero and R. Escribano, Astrophys. J., 2009, 703, 2101.
23. R. M. Escribano, G. M. Muñoz-Caro, G. A. Cruz-Díaz, Y. Rodríguez-Lazcano and B. Maté, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12899.
24. R. Escribano, E. Artacho, A. Kouchi, T. Hama, Y. Kimura, H. Hidaka and N. Watanabe, Phys. Chem. Chem. Phys., 2017, 19, 7280.
25. P. C. Gómez and R. Escribano, Phys. Chem. Chem. Phys., 2017, 19, 26582.
26. P. D. Dopieralski, Z. Latajk and I. Olovsson, Chem. Phys. Lett., 2009, 476, 223.
27. P. Ghesquière, T. M. Mineva, D. Talbi, P. Theulé, J. A. Noble and T. Chiavassa, Phys. Chem. Chem. Phys., 2015, 17, 11455.
28. P. L. Silvestrelli, M. Bernasconi and M. Parrinello, Chem. Phys. Lett., 1997, 277, 478.
29. R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1651.
30. Materials Studio (http://accelrys.com/products/materials.studio) 2014.
31. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr., 2005, 220(5-6), 567.
32. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
33. E. R. McNellis, J. Meyer and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205414.
34. D. Sánchez-Portal, P. Ordejón and E. Canadell, Struct. Bonding, 2004, 113, 103.
35. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
36. P. Ordejón, E. Artacho and J. M. Soler, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 10441.
37. F. Corsetti, M.-V. Fernández-Serra, J. M. Soler and E. Artacho, J. Phys.: Condens. Matter, 2013, 25, 435504.
38. B. Hammer, L. B. Hansen and J. K. Norskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413.
39. J. Moreno and J. M. Soler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13891.
40. D. Sánchez-Portal, I. Souza and R. M. Martin, AIP Conf. Proc., 2000, 535, 111.
41. D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, 2001.
42. G. Molpeceres, M. A. Satorre, J. Ortigoso, C. Millán, R. Escribano and B. Maté, Astrophys. J., 2016, 825, 156.
43. M. Bouilloud, N. Fray, Y. Benilan, H. Cottin, M.-C. Gazeau and A. Jolly, Mon. Not. R. Astron. Soc., 2015, 451, 2145.
44. J. He, K. Acharyya and G. Vidali, Astrophys. J., 2016, 823, 56.
45. I. B. Schmitt, S. Philippe, W. M. Grundy, D. C. Reuter, R. Côte, E. Quirico, S. Protopapa, L. A. Young, R. P. Binzel, J. C. Cook, D. P. Cruikshank, C. M. Dalle Ore, A. M. Earle, K. Ennico, C. J. A. Howett, D. E. Jennings, I. R. Linscott, A. W. Lunsford, C. B. Olkin, A. H. Parker, J. W. Parker, K. N. Singer, J. R. Spencer, J. A. Stansberry, S. A. Stern, C. C. C. Tsang, A. J. Verbiscer, H. A. Weaver and the New Horizons Science Team, Icarus, 2017, 287, 229.
46. S. Protopapa, W. M. Grundy, D. C. Reuter, D. P. Hamilton, C. M. Dalle Ore, J. C. Cook, D. P. Cruikshank, B. Schmitt, S. Philippe, E. Quirico, R. P. Binzel, A. M. Earle, K. Ennico, C. J. A. Howett, A. W. Lunsford, C. B. Olkin, A. Parker, K. N. Singer, A. Stern, A. J. Verbiscer, H. A. Weaver, L. A. Young and the New Horizons Science Team, Icarus, 2017, 287, 218.
47. B. Hapke, Theory of Reflectance and Emittance Spectroscopy, Topics in Remote Sensing, Cambridge University Press, Cambridge, UK, 1993.
48. R. M. Mastrapa, M. P. Bernstein, S. A. Sandford, T. L. Roush, D. P. Cruikshank and C. M. Dalle Ore, Icarus, 2008, 197, 307.

---