Understanding methane/carbon dioxide partitioning in clay nano- and meso-pores with constant reservoir composition molecular dynamics modeling

Abstract

The interactions among fluid species such as H₂O, CO₂, and CH₄ confined in nano- and meso-pores in shales and other rocks is of central concern to understanding the chemical behavior and transport properties of these species in the earth's subsurface and is of special concern to geological C-sequestration and enhanced production of oil and natural gas. The behavior of CO₂, and CH₄ is less well understood than that of H₂O. This paper presents the results of a computational modeling study of the partitioning of CO₂ and CH₄ between bulk fluid and nano- and meso-pores bounded by the common clay mineral montmorillonite. The calculations were done at 323 K and a total fluid pressure of 124 bars using a novel approach (constant reservoir composition molecular dynamics, CRC-MD) that uses bias forces to maintain a constant composition in the fluid external to the pore. This purely MD approach overcomes the difficulties in making stochastic particle insertion–deletion moves in dense fluids encountered in grand canonical Monte Carlo and related hybrid approaches. The results show that both the basal siloxane surfaces and protonated broken edge surfaces of montmorillonite both prefer CO₂ relative to CH₄ suggesting that methods of enhanced oil and gas production using CO₂ will readily displace CH₄ from such pores. This preference for CO₂ is due to its preferred interaction with the surfaces and extends to approximately 20 Å from them.

---

Introduction

The interactions among fluid species such as water, carbon dioxide and methane confined in nano- and meso-pores in shales and other rocks is of central concern to understanding the chemical behavior and transport properties of these species in the earth's subsurface and is of special concern to geological C-sequestration and enhanced production of oil and natural gas.^1–6 The behavior of water and cations at mineral surfaces and in the interlayer galleries of expandable clays (smectites) has been studied experimentally and computationally for many years,^7–19 and more recently there has been increased interest in carbon dioxide and hydrocarbons.^20–44 The mutual interactions between CO₂ and CH₄ in nano- and meso-scale confinement, however, remain poorly understood. Most simulation studies have focused on single component adsorption in the interlayers of clay minerals. These studies show that the CO₂ is more strongly adsorbed to clay minerals than CH₄.^45–47 Recent Grand Canonical Monte Carlo (GCMC) calculations, for instance, have shown preferential adsorption of CO₂ over CH₄ in the interlayers of dry Na-montmorillonite and other inorganic shale components as functions of temperature (313–373 K) and pressure (0–20 MPa).^47–52 In shales and other sedimentary rocks, pores have a wide range of sizes, and the effects of pore size on CO₂/CH₄ partitioning are poorly understood. This paper presents the results of a computational molecular dynamics (MD) modeling study of the partitioning of CO₂ and CH₄ between bulk fluid and slit-like nano- and meso pores from 4 to 73 Å thick and the structure of the fluid in those pores. In contrast to most computational studies of clays, the montmorillonite substrate model here is of finite size (Fig. 1), allowing study of the fluid interaction with the siloxane basal surfaces and the protonated sites on broken edges of the clay layers. The results show that the partitioning of CO₂ and CH₄ between the bulk fluid (representing fluid in large pores in shales and other rocks) and the nano- and meso-pores is substantially influenced by the pore thickness, with CO₂ being largely preferred in narrow confined pores. CO₂ is also greatly preferred at the protonated edges of broken clay layers.

Fig. 1 Schematic representations of the simulation cells used in the constant reservoir composition molecular dynamics, CRC-MD calculations of CO₂/CH₄ partitioning into pores bounded by montmorillonite basal surfaces. (a) The full simulation cell showing the different regions. Pink arrows represent bias forces. (b) Enlarged image of the silt-like pore and montmorillonite T–O–T layers. Color code: Si – yellow; O – red; Mg – green; Al – pink; H – white; Na – blue; C_CO2 – cyan; C_CH4 – black. Substrate atoms are represented using sticks, and the CO₂/CH₄ fluids and Na⁺ ions are represented in balls. The directions of the X and Z axis are indicated by the arrows on the lower left.

The MD simulations were done using a novel approach that uses self-adjusting bias forces to maintain a constant composition in the fluid external to the pore (constant reservoir composition molecular dynamics, CRC-MD). Such self-adjusting bias forces have been used previously to maintain a constant chemical potential of the fluid species in modelling the growth of urea crystals from solution (constant chemical potential MD)^53,54 and to create a concentration gradient across a membrane for modelling the gas transport and separation of mixtures in membranes (concentration gradient driven MD).⁵⁵ The advantages of using a purely MD approach to maintain the composition of dense fluids rather than using the stochastic particle insertion–deletion moves used in grand canonical Monte Carlo and related hybrid approaches, such as dual control volume grand canonical molecular dynamics,⁵⁶ have been discussed in detail in ref. 55. Inspired by these studies,^53–55 we have implemented the CRC-MD method, which has proven to be an efficient way to evaluate partitioning of fluid species between bulk fluid and nano- and meso-pores and also onto the surfaces of finite size solid substrates.

Methods

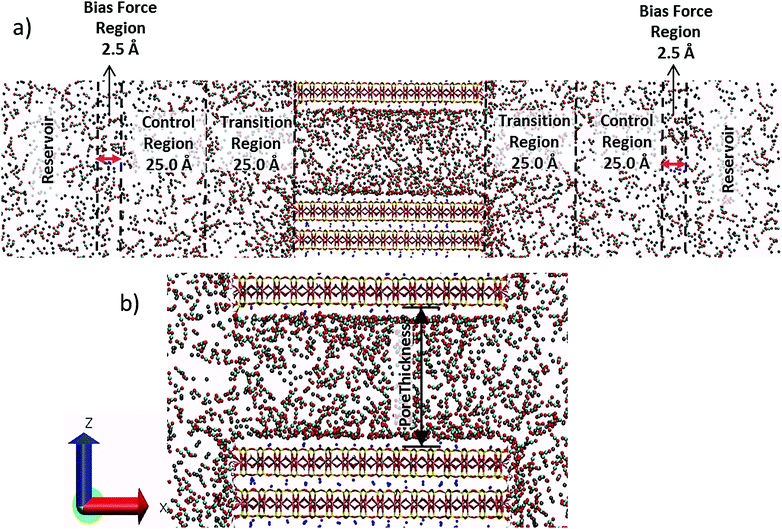
In the CRC-MD method, each simulation cell consists of a bulk fluid reservoir, two bias force regions, two composition control regions, two transition regions, and the substrate (clay) + pore assemblage in the center (Fig. 1a). The concentrations of the fluid species in the control regions are maintained at constant values by forces in the bias force regions. These bias forces act in such a way that if the concentration of a given species in a control region is different than the target concentration molecules of that species are moved into or out of the control region from or to the reservoir. A detailed explanation of the functional forms of the bias forces and how they work can be found elsewhere.⁵⁵

The substrate used in the simulations was the expandable smectite clay mineral, montmorillonite, which develops a permanent negative structural charge by the isomorphic substitution of Al³⁺ for Si⁴⁺ in the tetrahedral sheet and Mg²⁺ for Al³⁺ in the octahedral sheet. The model here has a structural formula of M⁺_0.75(Si_7.75Al_0.25)(Al_3.5Mg_0.5)O₂₀(OH)₄.¹² The distribution of the isomorphic substitutions has a quasi-disordered pattern and was prepared using the “Supercell” program,⁵⁷ which creates substitutions in accordance with an extension of Lowenstein's rule,⁵⁸ which forbids tetrahedral Al–O–Al and octahedral Mg–O–Mg linkages. The simulated montmorillonite particles have lateral dimensions of ∼73.0 Å × 41.4 Å along the a and b crystallographic axes, respectively, with an orthorhombic unit cell. To create a finite size particle, the montmorillonite structure was cleaved along (010), creating broken edge sites on that surface. On the broken edges, the dangling tetrahedral Al³⁺ and Si⁴⁺ sites are saturated by single OH⁻ groups, and most of the dangling octahedral Al³⁺ sites are saturated with 1 OH⁻ and 1 H₂O molecule.⁵⁹ Meanwhile, according to ab initio calculations,⁶⁰ when the octahedral Mg²⁺ sites are saturated with 1 H₂O molecule and 1 OH⁻ group, proton transfer reactions occur with the neighboring octahedral Al³⁺ sites and tetrahedral Si⁴⁺ sites to generate octahedral Mg²⁺ sites saturated with 2 H₂O molecules (as predicted by the crystal growth theory),⁶¹ and a neighboring Al³⁺ site with 2 OH⁻ groups. These coordination environments were used in the clay substrate. Furthermore, the oxygen atoms of the OH⁻ groups of the broken edge sites were assigned a slightly higher negative charge (−0.9659 |e|) compared to the original CLAYFF⁶² value (−0.95 |e|). This was done not only to ensure that the broken edges of the montmorillonite particle are electrostatically neutral, but also because the OH⁻ groups of the edge sites have fewer bond connections compared to those in the interior of the clay structure. Importantly, the two (010) surfaces of this model have different compositions. One contains only unsubstituted tetrahedral Si⁴⁺ and octahedral Al³⁺ sites (left side of the particle in Fig. 1b), whereas the other contains two substituted tetrahedral Al³⁺ and two octahedral Mg²⁺ sites (right side of Fig. 1b).

The modeled montmorillonite particle consists of three T–O–T layers which encompass two anhydrous interlayers and expose two external basal surfaces to the pore (Fig. 1a). Because of the 3-dimensional periodic boundary conditions used, only the broken (010) surfaces and the basal surfaces bounding the pore are exposed to the fluid phase. The lateral dimensions of the simulation cell are 300 Å × 41.4 Å (Fig. 1a). The thickness of the slit-like pore between the external basal surfaces (Fig. 1b) were varied from 4 to 73 Å. For pore thicknesses less than 10 Å, at the start of each simulation the charge compensating Na⁺ ions were placed at the midplane of the pore far from the substitution sites on the external surfaces, thereby allowing the Na⁺ ions to choose their preferred adsorption sites during the course of the simulation. For models with pore thicknesses >10 Å, the Na⁺ ions were initially placed 5 Å from the external basal surface. The CO₂ and CH₄ molecules were initially placed external to the clay particle at distances >∼30 Å from the two broken (010) surfaces. The number of CO₂ and CH₄ molecules in the full simulation cell varies from 3456 to 8063 and increases with increasing pore thickness in order to maintain the desired target densities in the control region. We analyze the CO₂/CH₄ partitioning and density profiles near the clay particle in three different dimensions: (i) normal to the basal surfaces bounding the pore (z direction); (ii) parallel to the broken edges in the transition region (z direction), and (iii) normal to the broken edges in the transition region (x direction). We define the pore thickness as the distance between the centers of the oxygen atoms of the basal surfaces bounding the pore. Similarly, we define the surfaces of the broken edges as the plane containing the centers of the protonated oxygen atoms on the surface. Further details about the analysis methods are described elsewhere.^{10,11,14,15,31–33}

We performed the molecular dynamics simulations in the canonical NVT ensemble at 323 K using the LAMMPS simulation package.⁶³ A Nosé–Hoover thermostat was used to control the temperature.⁶⁴ The interatomic interactions for the montmorillonite were obtained from the CLAYFF⁶² force field, and the parameters for the broken edge sites were obtained from newly developed metal–O–H bending potentials consistent with ClayFF.^65,66 The CO₂ and CH₄ molecules were represented by the EPM2⁶⁷ and TraPPE-UA⁶⁸ models, respectively. Three-dimensional periodic boundary conditions were employed with a cutoff of 14.0 Å for short-range non-electrostatic interactions, and the long-range electrostatic interactions were computed using the particle–particle particle-mesh (PPPM) summation algorithm⁶⁹ with an accuracy of 10⁻⁶. A time step of 1 fs was employed to integrate the equations of motion. Each system was equilibrated for 10 ns followed by another 2 ns of data production with the atomic coordinates recorded every 10 fs. Importantly, we fixed the positions of 18 octahedral atoms (Al³⁺ or Mg²⁺) in the simulated montmorillonite structure (2 left: 2 middle: 2 right per TOT layer) in order to prevent the clay layers from moving with respect to each other.

A modified version of the PLUMED 2.3.0 plugin⁷⁰ was used to apply the bias forces to maintain the fluid composition in the control regions. The target CO₂ and CH₄ densities in the control regions were set to 2 CO₂ and 2 CH₄ molecules per nm³. At 323 K, these densities yield a total fluid pressure of 124 bars, as calculated by using the Peng–Robinson equation of state.⁷¹ These temperature and pressure conditions are relevant to the upper part of the Earth's crust and petroleum reservoirs. The width of the transition regions, control regions and the bias force regions were set to 25 Å, 25 Å and 2.5 Å, respectively. The target composition of the fluid species, i, in the control regions was maintained using the force constants k^L_i = k^R_i = 5000 kJ nm³ mol⁻¹ which are placed at the center of the bias force regions located on the left, L, and right, R, side of the clay particle. The compositions in the control regions were monitored at intervals of 0.5 ps during the entire simulation.

Results and discussion

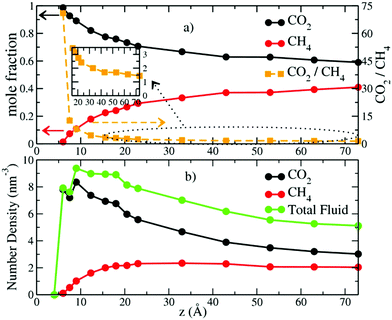
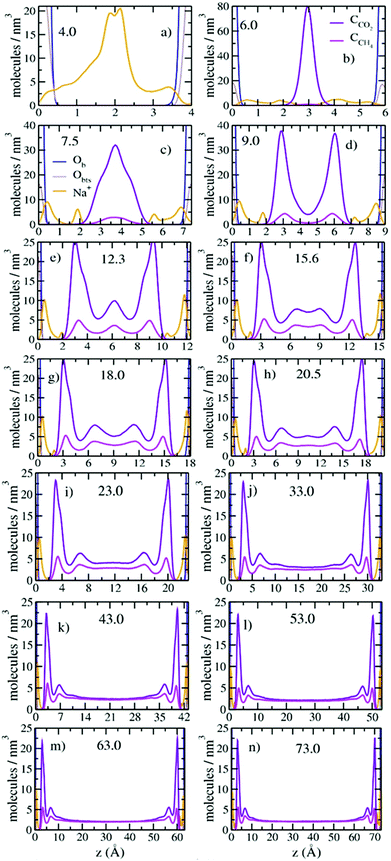
The mole fractions and number densities of CO₂ and CH₄ molecules in the pores vary greatly depending on the pore thickness (Fig. 2a and b). At the smallest thickness studied (4.0 Å), neither CO₂ nor CH₄ enters the pore. At a thickness of 6.0 Å, CO₂ fills the pore and there is only a negligible fraction of CH₄ molecules near the entry points. These results are in good agreement with recent experimental and simulation studies that show that the basal spacing required for CO₂ intercalation in the interlayer galleries of smectite clays is less than for CH₄ due to steric effects.^{6,31,32,38,39} At a pore thicknesses of 7.5 Å some CH₄ enters the pore, and the CO₂/CH₄ ratio decreases rapidly with increasing pore thickness up to 33.0 Å (Fig. 2a). At larger pore thickness, the CO₂/CH₄ ratio decreases less rapidly and slowly approaches the composition in the control regions (2 molecules per nm³), although for the thicknesses studied here it never reaches the control region composition. The number density of CO₂ molecules in the pores is always larger than in the control region, with the highest value of ∼8.2 molecules per nm³ at 9.0 Å and progressively smaller values at larger thicknesses. In contrast, the CH₄ density increases with increasing thickness to 23.0 Å and then decreases with increasing thickness. However, it is never much greater than the value in the control region of 2 molecules per nm³. (Fig. S1, ESI,† shows that the fluid compositions in the control regions were kept at the target values with great accuracy throughout the production runs.) These changes highlight the important conclusion that pores with dimensions of 1 to a few nm bounded by basal clay surfaces preferentially incorporate CO₂ relative to CH₄, with the smallest pores showing the greatest preference (Fig. 2b). These results are in agreement with recent GCMC simulation studies of CO₂/CH₄ adsorption in the interlayers of Na-montmorillonite at 318 K and P_fluid = 0 to 300 bars.⁴⁸ Importantly, the CO₂/CH₄ ratios at small pore sizes (<23.0 Å) are in excellent agreement with the selectivity parameters obtained from recent GCMC simulation studies at similar thermodynamic conditions (323 K and P_fluid = 100 bar).⁴⁹

Fig. 2 (a) Computed mole fractions of CO₂ (black) and CH₄ (red) molecules and the CO₂/CH₄ ratio (gold) as functions of pore thickness. Solid and dashed lines correspond to left and right y axis, respectively. (b) Number density of the fluid species within the pore region bounded by the oxygens of the montmorillonite basal surfaces.

The probability density profiles (PDPs) of CO₂ and CH₄ in the pores perpendicular to their surfaces show that the changes in their concentrations with pore thickness are due to preferential sorption of CO₂ and structuring of the fluid near the pore surfaces (Fig. 3). Significant structuring of the fluid into three discernable layers extends to ∼15.0 Å from each pore surface, with CO₂/CH₄ ratios larger than in the composition control regions extending to ∼20 Å from the surfaces. At a pore thickness of 6.0 Å, the CO₂ molecules are located at the mid-plane of the pore (3.0 Å from each surface), as expected since this thickness corresponds to a clay interlayer with 1 layer of intercalated molecules.³² At a pore thickness of 7.5 Å, the CO₂ begins to form two layers, and the small amount of CH₄ is at the middle of the pore. At 9.0 Å there are two well developed layers of CO₂ and CH₄. At 12.3 Å a third layer of CO₂ and CH₄ begins to develop, and the layer of CO₂ nearest the surfaces develops a shoulder. At 15.6 Å the central layer begins to split into two, and at 20.5 Å a fifth layer begins to develop. By 43.0 Å the fluid structuring near the surfaces is fully developed, and the CO₂ and CH₄ concentrations in the middle of the pore are essentially equal. At 73.0 Å the concentrations in the central region of the pore are close to those in the control volume, 2 molecules per nm³. For all pore thicknesses greater than 33.0 Å the fluid at each surface is structured into three layers of CO₂ and CH₄ with maxima near 3.0, 6.8, and 10.4 Å and peak densities that decrease with increasing distance from the surface. The PDP's are in good agreement with those from GCMC simulation studies of single component adsorption in slit nanopores in Na-montmorillonite at 323 K and P_fluid = 100 bars with a thickness of ∼21.0 Å⁴⁹ and also in interlayers of Na-montmorillonite at 298 K and P_fluid = 40 bars.^45,46 Such three-layer structures commonly occur near surfaces for many fluids, including H₂O.⁷²

Fig. 3 Computed probability density profiles (PDPs) of Na⁺ (orange), C_CO2 (violet) and C_CH4 (magenta) as functions of distance normal to the pore surfaces (montmorillonite basal surface) with varying pore thicknesses. The vertical brown and blue lines represent the positions of oxygen atoms of the montmorillonite basal surface coordinated to tetrahedral Si sites (O_b – blue) and tetrahedral Al sites (O_bts – brown).

The differences in the structure of the CO₂ and CH₄ layers near the pore surfaces are due to the differences in their interaction with the basal surface of the clay. For the CO₂ layer nearest to the surface, the peak at 3.0 Å is due to CO₂ molecules adsorbed with one O_CO2 located above the center of a ditrigonal cavity on the basal surface and the other O_CO2 located above a Si tetrahedron, as observed in earlier simulation studies of smectite interlayers.^25,31,32 The CO₂ molecules at 3.9 Å are located with their C_CO2 closer to a tetrahedral site. This structuring is consistent with the well-known ability of CO₂ to enter smectite clay interlayers.^{6,20–28,31–34,37,38,40} In contrast, the lack of structuring in the CH₄ peak nearest the surface and the equal distances between the three layers suggest that these molecules are interacting much more weakly with the surfaces and behave like hard spheres with the layers packed on one top of each other. This conclusion is consistent with the incorporation of CH₄ into the interlayer galleries of expandable clays occurring by a passive, space filling mechanism with basal spacings similar to 7.5 Å.³⁹

Increasing CO₂ and CH₄ incorporation with increasing pore thickness also greatly effects the coordination of the Na⁺ ions to the pore surfaces (Fig. 3). At 4.0 Å, most of the Na⁺ ions are located at the mid-plane of the pore (near 2.0 Å from each surface) with broad shoulders at 0.5 Å from each surface. Based on previous simulation studies by Greathouse et al.,¹¹ the Na⁺ ions at 0.5 Å are located above the centers of ditrigonal cavities, and those at 2.0 Å are adsorbed near the Si/Al tetrahedra. At 6.0 Å, where CO₂ begins to fill the pore, more Na⁺ occur above the ditrigonal cavities, and as the pore thickness increases progressively more occur on these sites. At larger pore thicknesses (>7.5 Å), the Na⁺ ions located at 2.0 Å from the surfaces are adsorbed only near tetrahedral Al³⁺ sites.

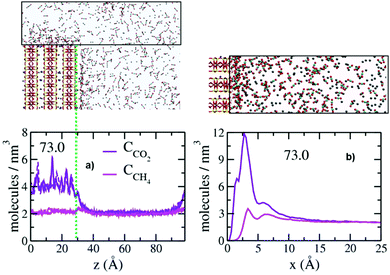
As near the basal surfaces bounding the pores, the concentrations of CO₂ and CH₄ on the surfaces of the broken edges of the clay layers are greater than in the control volumes, and CO₂ is preferentially associated with the surface (Fig. 4). The layered structure of the fluid near the broken edge surfaces is also generally similar to that on the basal surfaces, and concentrations greater than in the control regions extending to ∼20 Å from the surface. The concentrations of CO₂ and CH₄ in the well-defined layers near the broken surfaces are, however, significantly lower than above the basal surfaces (compare values in Fig. 4b with those in Fig. 3), suggesting that both are attracted less strongly to the protonated edge sites than to basal siloxane surfaces. The PDP's show three peaks for CO₂ (1.7 Å, 2.8 Å and 6.3 Å) and two peaks for CH₄ (3.4 Å and 6.7 Å). The positions of the two peaks for CH₄ are the same as above the basal surfaces, again illustrating the weak, non-specific interaction of CH₄ with silicate surfaces. In contrast, the positions of the two peaks for CO₂ are significantly closer to the broken edge surfaces. Recent GCMC simulation studies showed a greater preference for CO₂ relative to CH₄ in hydroxylated pores in quartz, which the authors attributed to stronger interaction of CO₂ with the protonates sites.⁴⁹ The origin of this difference will require substantial additional work, but we note that in the results here the differences between the two broken (010) surfaces with differently substituted octahedral and tetrahedral sites are not significant. Note that in these simulations the structuring of the fluid above the broken surfaces does not depend on pore size, since the broken surfaces face the transition region, for which the thickness is independent of pore size. The PDP's of the fluid species parallel to the broken edges (sum of all molecules within 15.0 Å of the surface) further illustrate the preferential association of CO₂ with the broken edges (Fig. 4a). These plots also demonstrate that the effects of the surface extend only ∼10 Å into the fluid in the transition region above the opening of the pore.

Fig. 4 Computed PDP's of C_CO2 (violet) and C_CH4 (magenta) near the broken and protonated (010) surfaces. (a) Average concentration within 15.0 Å of the surfaces and its extension above the pore (box on the top of the figure) plotted parallel to the surface. (b) PDP normal to the broken edges (box to the right of the surface shown). The solid and dashed lines represent the distributions on the left and right sides of the montmorillonite model which expose differently substituted sites. The differences between these surfaces is not significant. Green dotted lines in (a) represent the plane of basal surface oxygen atoms.

Conclusions

Computational molecular modeling of the partitioning of supercritical CO₂ and CH₄ between bulk fluid and nano- and meso-pores 4 to 73 Å thick bounded by the basal surfaces of the expandable clay mineral montmorillonite show that both species are preferentially incorporated into the pores with the preference for CO₂ much greater than for CH₄. This behavior is due to the association of the fluid species with the clay surface and with a much greater preference of the surface for CO₂ relative to CH₄. Structuring of the fluid extends to ∼15 Å from the surface, and the CO₂/CH₄ ratio is greater than in the control region to ∼20 Å from the surface. The total CO₂/CH₄ ratio in the pores is greatest at a pore thickness of 6 Å, decreases rapidly to 33 Å, and then gradually approaches the bulk value at larger thickness. Even at a pore thickness of 73 Å, however, it has not reached this value. The behavior of CO₂ and CH₄ on protonated, charge-neutral broken (010) edges of the clay layers is broadly similar, but the concentrations of the fluid species near these surfaces are lower than near the basal surfaces, suggesting that they have weaker interactions with protonated edge sites than with siloxane basal surfaces.

The calculations were done at 323 K and a total fluid pressure of 124 bars using a novel approach (constant reservoir composition molecular dynamics, CRC-MD) that maintains a constant composition in the fluid external to the pore. In this method, bias forces are employed to maintain the target composition of the external fluid, here 2 molecules per nm³.^49–51 This purely MD approach overcomes the difficulties in making stochastic particle insertion–deletion moves in dense fluids encountered in grand canonical Monte Carlo and related hybrid approaches. The simulation cell contains a finite size solid substrate, and the approach can be readily applied to many kinds of porous materials such as zeolites, MOFs and C-based materials. It can also be readily applied to pores bounded by non-porous materials, such as silicates and carbonates.

The results here clearly show that nano- and meso-pores in shales bounded by clay minerals have a preference for CO₂ relative to CH₄ and thus methods of enhanced petroleum production such as CO₂ floods or the use of CO₂-based fracking fluids should readily displace CH₄ from such pores. The results are in good agreement with previous experimental and computational, high T and P studies that show that there can be an energetic driving force for CO₂ incorporation in the interlayer galleries of expandable clay minerals, whereas CH₄ enters these spaces by a passive, space filling mechanism.^{6,31,32,38,39,49} The thickness of the surface layer in which the fluid is structured (∼15 Å) is similar to that in which H₂O is structured on oxide and hydroxide surfaces,^72,73 suggesting that computational modeling of geochemically relevant fluids in nano- and meso-pores bounded by such materials need only include pores with thicknesses less than a few nm to capture the essential features of their behavior. The results parallel the preference of other inorganic shale components (e.g., calcite and quartz) for CO₂ relative to CH₄, suggesting that for oxide and oxysalt materials, CH₄ adsorption is relatively weak and its filling of pores bounded by them occurs by a passive, space filling mechanism.^48–52 The organic component of shale known as kerogen is commonly thought to contain much of the CH₄, but recent GCMC studies support the conclusion that although it prefers CO₂ relative to CH₄, the behavior of these species is strongly dependent on the chemical composition, functionality, moisture content and pore structure of the kerogen.^74,75 Overall, the structure, dynamics and energetics of the adsorption environments of CO₂, CH₄, other hydrocarbons, and H₂O in kerogen have not been well explored, and the CRC-MD methods used here can be readily applied to help address these important questions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge computational resources from the UK Materials and Molecular Modelling Hub, which is partially funded by EPSRC (EP/P020194/1), the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under ECARP No. m1649 and the iCER computational facility at Michigan State University. The work in this manuscript was supported by the United States Department of Energy, Office of Science, Office of Basic Energy Science, Chemical Science, Biosciences, and Geosciences division through the sister grants DE-FG02-08ER15929 (Kirkpatrick, P.I. and Yazaydin, co-PI) and DE-FG02-10ER16128 (Bowers, P.I.). A. G. K. and B. F. N. W. acknowledge financial support of the industrial chair “Storage and Disposal of Radioactive Waste” at the IMT-Atlantique, funded by ANDRA, Orano, and EDF, and of the European Union's Horizon 2020 research and innovation program under grant agreements No. 640979 and 764810. We also acknowledge support from the Michigan State University Foundation.

References

1. A. Busch, S. Alles, Y. Gensterblum, D. Prinz, D. N. Dewhurst, D. M. Raven, H. Stanjek and B. M. Krooss, Int. J. Greenhouse Gas Control, 2008, 2, 297–308.
2. B. Cantucci, G. Montegrossi, O. Vaselli, F. Tassi, F. Quattrocchi and H. E. Perkins, Chem. Geol., 2009, 265, 181–197.
3. S. J. Altman, B. Aminzadeh, T. M. Balhoff, P. C. Bennett, S. L. Bryant, M. B. Cardenas, K. Chaudhary, R. T. Cygan, W. Deng, T. Dewers, D. A. DiCarlo, P. Eichhubl, M. A. Hesse, C. Huh, E. N. Matteo, Y. Mehmani, C. M. Tenney and H. Yoon, J. Phys. Chem. C, 2014, 118, 15103–15113.
4. P. Pei, K. G. Ling, J. He and Z. Z. Liu, J. Nat. Gas Sci. Eng., 2015, 26, 1595–1606.
5. A. G. Ilgen, J. E. Heath, I. Y. Akkutlu, L. T. Bryndzia, D. R. Cole, T. J. Kneafsey, K. L. Milliken, L. J. Pyrak-Nolte and R. Suarez-Rivera, Earth-Sci. Rev., 2017, 166, 132–152.
6. H. T. Schaef, N. Loganathan, G. M. Bowers, R. J. Kirkpatrick, A. O. Yazaydin, S. D. Burton, D. W. Hoyt, E. S. Ilton, K. S. Thanthiriwatte, D. A. Dixon, B. P. McGrail, K. M. Rosso, E. S. Ilton and J. S. Loring, ACS Appl. Mater. Interfaces, 2017, 9, 36783–36791.
7. G. M. Bowers, J. W. Singer, D. L. Bish and R. J. Kirkpatrick, J. Phys. Chem. C, 2011, 115, 23395–23407.
8. C. A. Weiss, R. J. Kirkpatrick and S. P. Altaner, Am. Mineral., 1990, 75, 970–982.
9. C. A. Weiss, R. J. Kirkpatrick and S. P. Altaner, Geochim. Cosmochim. Acta, 1990, 54, 1655–1669.
10. C. P. Morrow, A. O. Yazaydin, M. Krishnan, G. M. Bowers, A. G. Kalinichev and R. J. Kirkpatrick, J. Phys. Chem. C, 2013, 117, 5172–5187.
11. J. A. Greathouse, D. B. Hart, G. M. Bowers, R. J. Kirkpatrick and R. T. Cygan, J. Phys. Chem. C, 2015, 119, 17126–17136.
12. B. F. Ngouana Wakou and A. G. Kalinichev, J. Phys. Chem. C, 2014, 118, 12758–12773.
13. R. J. Kirkpatrick, A. G. Kalinichev, G. M. Bowers, A. O. Yazaydin, K. Marimuthu, M. Saharay and C. P. Morrow, Am. Mineral., 2015, 100, 1341–1354.
14. N. Loganathan, A. O. Yazaydin, G. M. Bowers, A. G. Kalinichev and R. J. Kirkpatrick, J. Phys. Chem. C, 2016, 120, 10298–10310.
15. N. Loganathan, A. O. Yazaydin, G. M. Bowers, A. G. Kalinichev and R. J. Kirkpatrick, J. Phys. Chem. C, 2016, 120, 12429–12439.
16. B. Rotenberg, V. Marry, R. Vuilleumier, N. Malikova, C. Simon and P. Turq, Geochim. Cosmochim. Acta, 2007, 71, 5089–5101.
17. S. L. Teich-McGoldrick, J. A. Greathouse, C. F. Colon and R. T. Cygan, J. Phys. Chem. C, 2015, 119, 20880–20891.
18. G. M. Bowers, J. W. Singer, D. L. Bish and R. J. Kirkpatrick, Am. Mineral., 2014, 99, 318–331.
19. U. V. Reddy, G. M. Bowers, N. Loganathan, M. Bowden, A. O. Yazaydin and R. J. Kirkpatrick, J. Phys. Chem. C, 2016, 120, 8863–8876.
20. H. T. Schaef, J. S. Loring, V. A. Glezakou, Q. R. S. Miller, J. Chen, A. T. Owen, M. S. Lee, E. S. Ilton, A. R. Felmy, B. P. McGrail and C. J. Thompson, Geochim. Cosmochim. Acta, 2015, 161, 248–257.
21. J. S. Loring, H. T. Schaef, R. V. F. Turcu, C. J. Thompson, Q. R. Miller, P. F. Martin, J. Hu, D. W. Hoyt, O. Qafoku, E. S. Ilton, A. R. Felmy and K. M. Rosso, Langmuir, 2012, 28, 7125–7128.
22. J. S. Loring, E. S. Ilton, J. Chen, C. J. Thompson, P. F. Martin, P. Benezeth, K. M. Rosso, A. R. Felmy and H. T. Schaef, Langmuir, 2014, 30, 6120–6128.
23. J. S. Loring, H. T. Schaef, C. J. Thompson, R. V. F. Turcu, Q. R. Miller, J. Chen, J. Hu, D. W. Hoyt, P. F. Martin, E. S. Ilton, A. R. Felmy and K. M. Rosso, Energy Procedia, 2013, 37, 5443–5448.
24. E. G. Krukowski, A. Goodman, G. Rother, E. S. Ilton, G. Guthrie and R. J. Bodnar, Appl. Clay Sci., 2015, 114, 61–68.
25. A. Botan, B. Rotenberg, V. Marry, P. Turq and B. Noetinger, J. Phys. Chem. C, 2010, 114, 14962–14969.
26. A. Kadoura, A. K. N. Nair and S. Sun, J. Phys. Chem. C, 2017, 121, 6199–6208.
27. M. Makaremi, K. D. Jordan, G. D. Guthrie and E. M. Myshakin, J. Phys. Chem. C, 2015, 119, 15112–15124.
28. A. Rao and Y. Leng, Langmuir, 2016, 32, 11366–11374.
29. M. M. Sena, C. P. Morrow, R. J. Kirkpatrick and M. Krishnan, Chem. Mater., 2015, 27, 6946–6959.
30. A. O. Yazaydin, G. M. Bowers and R. J. Kirkpatrick, Phys. Chem. Chem. Phys., 2015, 17, 23356–23367.
31. N. Loganathan, A. O. Yazaydin, G. M. Bowers, A. G. Kalinichev and R. J. Kirkpatrick, J. Phys. Chem. C, 2017, 121, 24527–24540.
32. N. Loganathan, G. M. Bowers, A. O. Yazaydin, H. T. Schaef, J. S. Loring, A. G. Kalinichev and R. J. Kirkpatrick, J. Phys. Chem. C, 2018, 122, 4391–4402.
33. N. Loganathan, G. M. Bowers, A. O. Yazaydin, A. G. Kalinichev and R. J. Kirkpatrick, J. Phys. Chem. C, 2018, 122, 23460–23469.
34. D. R. Cole, A. A. Chialvo, G. Rother, L. Vlcek and P. T. Cummings, Philos. Mag., 2010, 90, 2339–2363.
35. D. R. Cole, S. Ok, A. Striolo and A. Phan, Rev. Mineral. Geochem., 2013, 75, 495–545.
36. G. Rother, E. S. Ilton, D. Wallacher, T. Hauss, H. T. Schaef, O. Qafoku, K. M. Rosso, A. R. Felmy, E. G. Krukowski, A. G. Stack, N. Grimm and R. J. Bodnar, Environ. Sci. Technol., 2013, 47, 205–211.
37. E. S. Ilton, H. T. Schaef, O. Qafoku, K. M. Rosso and A. R. Felmy, Environ. Sci. Technol., 2012, 46, 4241–4248.
38. G. M. Bowers, H. T. Schaef, J. S. Loring, D. W. Hoyt, S. D. Burton, E. D. Walter and R. J. Kirkpatrick, J. Phys. Chem. C, 2017, 121, 577–592.
39. G. M. Bowers, J. S. Loring, H. T. Schaef, E. D. Walter, S. D. Burton, D. W. Hoyt, S. S. Cunniff, N. Loganathan and R. J. Kirkpatrick, ACS Earth Space Chem., 2018, 2, 640–652.
40. P. Giesting, S. Guggenheim, A. F. K. van Groos and A. Busch, Int. J. Greenhouse Gas Control, 2012, 8, 73–81.
41. A. Phan, D. R. Cole and A. Striolo, J. Phys. Chem. C, 2014, 118, 4860–4868.
42. A. Phan, D. R. Cole and A. Striolo, Langmuir, 2014, 27, 8066–8077.
43. A. Phan, D. R. Cole, R. G. Weiss, J. Dzubiella and A. Striolo, ACS Nano, 2016, 8, 7646–7656.
44. A. Phan, D. R. Cole and A. Striolo, Philos. Trans. R. Soc., A, 2016, 374, 20150019.
45. Z. Jin and A. Firoozabadi, Fluid Phase Equilib., 2013, 360, 456–465.
46. Z. Jin and A. Firoozabadi, Fluid Phase Equilib., 2014, 382, 10–20.
47. N. Yang, S. Liu and X. Yang, Appl. Surf. Sci., 2015, 356, 1262–1271.
48. Q. Wang and L. Huang, Fuel, 2019, 239, 32–43.
49. H. Sun, H. Zhao, N. Qi, X. Qi, K. Zhang and Y. Li, Mol. Simul., 2017, 43, 1004–1011.
50. H. Sun, H. Zhao, N. Qi, X. Qi, K. Zhang, W. Sun and Y. Li, RSC Adv., 2016, 6, 104456.
51. H. Sun, W. Sun, H. Zhao, Y. Sun, D. Zhang, X. Qi and Y. Li, RSC Adv., 2016, 6, 32770–32778.
52. H. Sun, H. Zhao, N. Qi and Y. Li, Energy Technol., 2017, 5, 2065–2071.
53. C. Perego, M. Salvalaglioa and M. Parrinello, J. Chem. Phys., 2015, 142, 144113.
54. T. Karmakar, P. M. Piaggi, C. Perego and M. Parrinello, J. Chem. Theory Comput., 2018, 14, 2678–2683.
55. A. Ozcan, C. Perego, M. Salvalaglio, M. Parrinello and A. O. Yazaydin, Chem. Sci., 2017, 8, 3858–3865.
56. G. S. Heffelfinger and F. van Swol, J. Chem. Phys., 1994, 100, 7548.
57. K. Okhotnikov, T. Charpentier and S. Cadars, J. Cheminf., 2016, 8, 17.
58. W. Lowenstein, Am. Mineral., 1954, 39, 92–96.
59. S. V. Churakov, J. Phys. Chem. B, 2006, 110, 4135–4146.
60. X. Liu, X. Lu, E. J. Meijer, R. Wang and H. Zhou, Geochim. Cosmochim. Acta, 2012, 81, 56–68.
61. G. N. White and L. W. Zelazny, Clays Clay Miner., 1988, 36, 141–146.
62. R. T. Cygan, J. J. Liang and A. G. Kalinichev, J. Phys. Chem. B, 2004, 108, 1255–1266.
63. S. Plimpton, J. Comp. Physiol., 1995, 117(1), 1–19.
64. W. Shinoda, M. Shiga and M. Mikami, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 134103.
65. M. Pouvreau, J. A. Greathouse, R. T. Cygan and A. G. Kalinichev, J. Phys. Chem. C, 2017, 121, 14757–14771.
66. M. Pouvreau, J. A. Greathouse, R. T. Cygan and A. G. Kalinichev, J. Phys. Chem. C, 2019 DOI:10.1021/acs.jpcc.9b00514.
67. R. T. Cygan, V. N. Romanov and E. M. Myshakin, J. Phys. Chem. C, 2012, 116, 13079–13091.
68. M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577.
69. S. J. Plimpton, R. Pollock and M. J. Stevens, Proceedings of the Eighth SIAM Conference on Parallel Processing for Scientific Computing, Minneapolis, Minnesota, 1997.
70. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
71. D. Y. Peng and D. B. Robinson, Ind. Eng. Chem. Fundam., 1976, 15, 59–64.
72. J. Wang, A. G. Kalinichev and R. J. Kirkpatrick, Geochim. Cosmochim. Acta, 2006, 70, 562–582.
73. S. Gruener, T. Hofmann, D. Wallacher, A. V. Kitky and P. Huber, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 067301.
74. H. Sun, H. Zhao, N. Qi and Y. Li, J. Phys. Chem. C, 2017, 121, 10233–10241.
75. L. Huang, Z. Ning, Q. Wang, W. Zhang, Z. Cheng, X. Wu and H. Qin, Appl. Energy, 2018, 210, 28–43.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp00851a

---