The pseudo-π model of the induced magnetic field: fast and accurate visualization of shielding and deshielding cones in planar conjugated hydrocarbons and spherical fullerenes

Abstract

The induced magnetic fields originating from the π system of planar conjugated polycyclic hydrocarbons and spherical fullerenes are accurately reproduced by their corresponding hydrogen skeletal models (HSMs). Moreover, the individual contribution per molecular orbital is also reproduced unraveling simple symmetry rules related to canonical molecular orbitals. Hence, fast, handy and accurate 3D visualization of shielding and deshielding cones is realized, enabling the interpretation of global and local π aromaticity and antiaromaticity of PAHs and spherical species in a simple and concise manner to facilitate further interpretations of large sized hydrocarbon systems.

---

Introduction

Aromaticity is one of the most fundamental concepts in chemistry providing rationalization of the structure, stability and reactivity of a vast variety of planar, non-planar, belt and spherical species. Magnetic criteria of aromaticity,^1–7 based on the fact that delocalized electrons induce closed ring currents under the effect of an external magnetic field and subsequently induce a secondary magnetic field, have gained a preponderant place among researchers in this field.

The induced magnetic field⁸ (IMF) is accessible from the chemical shielding (CS) tensor according to B^ind_i(r) = −σ_ij(r)B^ext_j (i, j = x, y, z) and is typically visualized as 2D contour maps or 3D isosurfaces of the out-of-plane component B^ind_z. The calculation of CS in 2D and 3D grids for the visual inspection of shielding and deshielding cones induced by the total electronic structure, employing common computational chemistry software, has become a standard method to investigate anti/aromaticity of planar and spherical species.^9–15 The CS tensor embodies contributions from σ and core orbitals which induce significant short and long range effects and obscure the response of delocalized π orbitals. Moreover, CS methods have been questioned for their credibility to appropriately represent the effects of specific π currents.^16–18 However visualizations of the magnetic field induced only from the π subset of orbitals (B^ind_πz) precisely corresponds to the ring current (RC) analysis of monocyclic^12,19,20 and polycyclic²¹ anti/aromatic hydrocarbons and spherical carbon fullerenes.²² Moreover, the dissection of B^ind_πz into contributions from canonical molecular orbitals (CMOs) allows the interpretation of the magnetic response based on relevant chemistry concepts such as symmetry selection rules, orbital overlap and energy gaps.^21,22 Yet, the calculation and visualization of B^ind_πz, apart from the large computational time needed, produces a bulky amount of complex data that requires a custom code to be further processed. Thus, the computational cost of B^ind_πz calculations rapidly increases with the number of electrons and practically restricts the scope of the analysis to small and medium sized molecules.

To overcome similar computational barriers, Fowler proposed in 2002 the pseudo-π model,²³ which was found to produce surprisingly accurate results for the RC analysis^24–27 and multicenter aromaticity bond indices^28–30 in a wide range of large planar and spherical organic molecules at very low computational cost. The pseudo-π model relies on early London findings³¹ that the π orbitals of a cyclic conjugated carbon skeleton can be effectively modelled by σ orbitals of a hydrogen only system with the same geometry and connectivity. Accordingly, in a planar system each π MO of a real conjugated hydrocarbon has a unique counterpart σ MO of the hydrogen skeletal model (HSM). The symmetries of the paired π and σ MOs are related through a symmetry translation operation perpendicular to the molecular plane (Γ_σ = Γ_π × Γ_z), whereas in spherical systems both radial π and σ orbitals have the same symmetry (Γ_σ = Γ_π). Since B^ind_πz is described by the sum of orbital contributions, the B^ind_σz of the hydrogen (or pseudo-π) model should be applicable for the visualization and the analysis of the π induced magnetic field in conjugated carbon species at a relatively low computational cost. In this work we apply the pseudo-π model for the IMF of representative PAHs and spherical fullerenes (Scheme 1), showing that contributions from the overall π system and from each canonical molecular orbital are recovered by minimal models.

Scheme 1 Molecules studied with the pseudo-π method with labelling of unique rings.

Computational methods

The geometry of molecules 1–15 (Scheme 1) was optimized in ADF2017³² with the Becke–Perdew³³ (BP86) exchange–correlation functional using the all electron triple-ζ Slater basis set with two polarization functions (TZ2P). The HSMs were derived from the optimized geometries by keeping the skeletal carbon atoms only and replacing them by hydrogen atoms. Chemical shieldings were calculated in cubic grids ranging from 31³ to 41³ points with a step of 0.3–0.5 Å, using the Perdew–Burke–Ernzerhof³⁴ (PBE) functional. The TZ2P basis set was used for hydrocarbons except for 14 and 15 in which double-ζ DZP was used. The HSMs were calculated with the single-ζ (SZ) Slater basis set. Contributions of the π system of PAHs and σ system of HSMs were derived from the summation of individual contributions of π or σ CMOs. Each CMO contribution was calculated with the GIAO formalism employing the EPR module of ADF and post-processed with custom code as described in previous studies.^20–22 Isosurfaces were visualized with VMD.³⁵

The computational cost of 3D IMF calculations depends on both the size of the molecule and the number of grid points. The grid points can be reduced to one half, one quarter or one eighth of the full grid, depending on the molecular symmetry. Chemical shielding calculations with the pseudo-π method applied on the systems of this study were found to be about 35 times faster on average than the real π calculations. The computational times with or without symmetry of π and pseudo-π calculations with regard to the number of basis functions of molecules 1–15 are given in Chart 1 in a logarithmic scale. The best performance was achieved for 14, in which the computational time involving symmetry was reduced from 532 hours to 11 hours using the pseudo-π method in a 4-core cpu at 4.0 GHz.

Chart 1 Computational cost (hours) of π (TZ2P) and pseudo-π (SZ) methods ordered by increasing number of basis functions of molecules 1–15. Light colored bars correspond to cubic grids of 31³ points and dark colored bars correspond to minimum required sub-grids [number of points: (1 + 30/2)ⁿ × 31³⁻ⁿ, n = 1, 2, 3] according to the molecular symmetry. Computational times were estimated from 31 point scans computed with a 4-core cpu at 4.0 GHz. The computational cost axis is given in a logarithmic scale.

Results and discussion

Due to the intrinsic long range nature of the IMF, it is appropriate to visualize both the long range and the short range topology of the shielding/deshielding cones in order to extract meaningful information about local and global characteristics of the magnetic response. Hence the B^ind_πz of selected benchmark conjugated (poly)cyclic hydrocarbons 1–15 and the pseudo-π B^ind_σz of the corresponding HSMs are visualized with various clipped isosurfaces, ranging from ±2 to ±30 ppm, whereas the short range response is displayed as the full isosurface.

Benzene and cyclobutadiene

From Fig. 1a it is clear that the pseudo-π magnetic response of HSMs (B^ind_σz) of benzene 1 and cyclobutadiene 2 is almost identical to the real π response (B^ind_πz). Both benzene and its HSM display a long range shielding cone, whereas both cyclobutadiene and its HSM display a long range deshielding cone. The pseudo-π model exhibits a slightly contracted response along the z-axis with regard to the real π response, due to the fact that σ orbitals, in contrast to the π orbitals, lie on the molecular plane. However the pseudo-π model is qualitatively accurate to describe the relative differences of aromatic and antiaromatic response, as it correctly predicts that at short-range the deshielding response of 2 is stronger than the shielding response of 1 and inversely, at long range the shielding response of 1 is stronger than the deshielding response of 2.

Fig. 1 (a) Isosurfaces of B^ind_πz (real-π) (up row) and B^ind_σz (pseudo-π) of the corresponding HSMs (down row) of benzene 1 and cyclobutadiene 2. The external field is applied along the z axis. Cyan/blue hues represent diatropicity (shielding) and yellow/red hues paratropicity (deshielding). Isosurface values are at ±2, ±5, ±10, ±20 and ±30 ppm starting from long range down to short range. (b) NICS_zz scan profiles of real-π (black symbols) and pseudo-π (white symbols) contributions above the ring center of benzene (left) and cyclobutadiene (right).

The quantitative features of the pseudo-π model are exposed in the NICS scan profiles of 1 and 2 (Fig. 1b). The pseudo-π method yields larger NICS_πzz values close to the ring until a height of ∼0.6 Å, but decreases with a larger slope with regard to the distance above the ring plane. The quantitative deviation close to the ring is more profound in antiaromatic 2. Hence on the ring center of 1 the pseudo-π method predicts a 5.4 ppm higher NICS_πzz value (−36.3 ppm and −41.7 ppm for real π and pseudo-π respectively), whereas for 2 the pseudo-π value at the ring center (+121.9 ppm) is double the real π value (+58.9 ppm). More specifically, the NICS_πzz profile of 2 shows that the paratropicity of π orbitals increases at close range and presents a maximum at ∼0.6 Å which is characteristic of antiaromatic response, whereas the profile obtained with the pseudo-π method decreases monotonically due to the in-plane overlap of the σ orbitals.

The same quantitative features of the pseudo-π method, with small and large overestimation of the π magnetic response close to the ring plane of aromatic and antiaromatic rings respectively, and a sharper decline above the ring plane as a result of the in-plane overlap of σ orbitals, are also observed in molecules 3–14. NICS(0)_πzz values of molecules 1–14 and relative values taking 1 and 2 as references obtained with the real π and pseudo-π methods are given in Table 1. In general, as it is discussed subsequently, the pseudo-NICS_zz values and profiles correctly reproduce the variations of the π response between rings within the same molecule, as well as among different molecules. Moreover, the pseudo-π values correlate very well with the real π values at various heights (0.0 Å, 0.6 Å and 1.0 Å) above the ring centers (Fig. 2), with the optimum correlation (R² = 0.993) found at 0.6 Å. Hence the pseudo-π method provides an accurate description of the π magnetic response and is suitable for the 3D visualization of the IMF.

Table 1 NICS_zz values (ppm) computed with π (PBE/TZ2P) and pseudo-π (PBE/SZ) methods at the centers of unique rings of molecules 1–14

Molecule	Ring	NICSzz		NICSzz/NICSzz(ref.)^a
		π	Pseudo-π	π	Pseudo-π
a Ref. is 1 for diatropic rings and 2 for paratropic rings.
1		−36.3	−41.7	1.00	1.00
2		58.9	121.9	1.00	1.00
3		−35.8	−40.7	0.99	0.98
4	a	−42.0	−47.4	1.16	1.14
	b	−33.0	−37.4	0.91	0.90
5	a	−42.2	−47.5	1.16	1.14
	b	−30.4	−34.6	0.84	0.83
6	a	−25.9	−27.8	0.71	0.67
	b	−35.9	−41.9	0.99	1.00
7	a	−21.2	−20.1	0.58	0.48
	b	−43.3	−49.6	1.19	1.19
8	a	55.2	108.5	0.94	0.89
	b	−7.2	−4.7	0.20	0.11
9	a	41.9	81.9	0.71	0.67
	b	−13.9	−14.7	0.38	0.35
10	a	−0.9	7.9	0.02	−0.19
	b	53.5	98.9	0.91	0.81
11		80.8	160.8	1.37	1.32
12	a	16.0	26.7	0.27	0.22
	b	45.4	79.6	0.77	0.65
	c	38.6	79.1	0.66	0.65
13	a	−11.0	−0.5	0.30	0.01
	b	−38.6	−42.0	1.06	1.01
14	a	−45.9	−46.7	1.26	1.12
	b	−22.7	−13.4	0.63	0.32
	c	−54.1	−59.9	1.49	1.44
	d	−26.4	−25.4	0.73	0.61

---

Fig. 2 Linear correlation between NICS_πzz and pseudo-NICS_πzz values at the center (grey line and circles), 0.6 Å (dashed line, white circles) and 1 Å (solid line and filled circles) above unique rings of molecules 1–14.

Polyacenes

The real π and pseudo-π isosurfaces of B^ind_z for aromatic polyacenes 3–7 (Fig. 3a) show identical magnetic response with uniform long range shielding cones, representative of planar π aromaticity. The local variations among different rings is revealed at the short range response represented with a full isosurface in Fig. 3a. For naphthalene 3 the −20 ppm isosurfaces of both B^ind_πz and B^ind_σz display a uniform shielding response on the whole molecular structure, which is representative of a global diatropic ring current.^36–39 On the other hand, in linear acenes anthracene 4 and teracene 5 the short range isosurfaces of both π and pseudo-π methods is slightly augmented at the central rings and reduced at the outer rings with regard to 1, in agreement with RC analysis,^38–40 accounting for the superposition of multiple diatropic ring currents at the inner rings.^41,42

Fig. 3 (a) Isosurfaces of B^ind_πz (up row) and pseudo-π B^ind_σz (down row) of naphthalene 3, anthracene 4, tetracene 5, phenanthrene 6 and pyrene 7. (b) NICS_zz scan profiles of real-π (filled symbols) and pseudo-π (white symbols) contributions above the ring centers of 3–7.

The relative difference between inner and outer rings of 4 and 5 is correctly predicted quantitatively by pseudo-NICS_πzz values (Table 1) and scan profiles (Fig. 3b). Specifically, the difference between NICS(0)_πzz of the inner and outer rings of 4 is 9.0 ppm and with the pseudo-π method it is predicted to be 10.0 ppm, whereas the corresponding values for 5 are 11.8 ppm and 12.9 ppm for real π and pseudo-π methods respectively. Accordingly, the relative NICS_πzz with regard to 1 obtained with the real π (pseudo-π) method is 1.16 (1.14) for inner rings and 0.91 (0.90) and 0.84 (0.83) for the outer rings of 4 and 5 respectively (Table 1). Moreover, the pseudo-π NICS_zz scan profiles of 3–7 (Fig. 3b) show the same characteristics with benzene, with small overestimation close to the ring (∼5 ppm) and sharper decline above the ring center.

In contrast to linear acenes, the short range magnetic response of phenanthrene 6 and pyrene 7 illustrates enhanced shielding cones at the outer rings and reduced response at the inner rings (Fig. 3a). In 6 the −20 ppm shielding cone is uniform and gradually contracts towards the inner ring, indicating a global diatropic current that weakens at the inner ring.^40,41 In contrast in 7 the −20 ppm isosurface develops a large shielding cone on the biphenyl moiety with discrete local expansion in each outer ring, a hollow area at the centers of the inner rings, and a moderate shielding area at the outer CC bonds. Hence the inner rings of 7 do not support the formation of a local shielding cone at short range and the diatropicity weakens towards the center of the rings denoting the absence of local contributions. This topology corresponds to a moderate peripheral diatropic current, whereas the outer rings additionally display strong local diatropic contributions, in alignment with RC analysis.^41,43 The relative NICS_πzz values with regard to 1 obtained with the real π (pseudo-π) method are 0.99 (1.00) and 1.19 (1.19) for the outer rings of 6 and 7 respectively, whereas for the inner rings of 6 and 7 they are 0.71 (0.67) and 0.58 (0.48) respectively. The pseudo-π NICS_zz scan profiles of 6 and 7 (Fig. 3b) show that the outer rings follow the same trends observed in molecules 1 and 3–5, but for the less diatropic inner rings the pseudo-π profiles almost coincide with the real π profiles. In summary, the pseudo-π method reproduces accurately and in detail the characteristic features of the π magnetic response in aromatic polyacenes 3–7.

Benzocyclobutadiene, biphenylene and pyracylene

The real and pseudo-π methods applied on benzocyclobutadiene 8, biphenylene 9 and pyracylene 10 (Fig. 4a) also display identical magnetic response inducing strong local deshielding cones on antiaromatic rings and weakened local shielding cones on 6MRs of 8 and 9, whereas the 6MRs of 10 do not support a shielding cone. Particularly for 8 the pseudo-π model accurately predicts a deshielding cone of 4MR with a similar range to that of 2, whereas the 6MR displays a very weak shielding response that forms a cone only at −2 ppm. In 9 the deshielding cone of 4MR is correctly predicted as weaker than those of 2 and 8, while the 6MRs display weak shielding cones, stronger than that of 8 and significantly weaker than that of 1. Lastly, in 10 strong local deshielding cones are induced at the 5MRs with similar range to the 4MR of 8, whereas a weak shielding response (−5 ppm isosurface in Fig. 5) encapsulates the peripheral bonds of 6MRs, denoting the presence of weak diatropic currents on the outer CC bonds.^23,38,39,44

Fig. 4 (a) Isosurfaces of B^ind_πz (up row) and pseudo-π B^ind_σz (down row) of benzocyclobutadiene 8, biphenylene 9 and pyracylene 10. (b) NICS_zz scan profiles of real-π (filled symbols) and pseudo-π (white symbols) contributions above the ring centers of 8–10.

Fig. 5 (a) Isosurfaces of B^ind_πz (up row) and pseudo-π B^ind_σz (down row) of pentalene 11 and bispentalene 12. (b) NICS_zz scan profiles of real-π (filled symbols) and pseudo-π (white symbols) contributions above the ring centers of 11 and 12.

These qualitative remarks derived from the visual inspection of the isosurfaces are also confirmed quantitatively from NICS_πzz values (Table 1) and scan profiles (Fig. 4b). Similar to 2, the pseudo-π method yields nearly double NICS_πzz values at the ring centers of 4MRs and 5MRs with regard to the real π values of 8–10, and overestimate the paratropicity until ∼0.6 Å above the ring center, but correctly predict the relative variation of paratropicity. Hence, the relative NICS(0)_πzz values for antiaromatic rings of 8, 9 and 10 with regard to 2 obtained with the real π (pseudo-π) method are 0.94 (0.89), 0.71 (0.67) and 0.91 (0.81) respectively. Additionally, the weak diatropicity of 6MRs of 8–10 is accurately described by the pseudo-π model, as shown by the scan profiles in Fig. 4b.

Pentalene and bispentalene

In antiaromatic PAHs such as pentalene 11 and bispentalene 12 the pseudo-π model correctly reproduces the characteristics of paratropic magnetic response (Fig. 5). At long range the deshielding cone of 11 is uniform, but at short range the paratropic isosurface of +50 ppm presents local expansion above each 5MR, while retaining significant paratropic contributions at the inner C–C bond, denoting the presence of both global and local strong paratropic currents.^37,45,46 In the pseudo-π method the same local features are more evident closer to the molecular plane. The paratropicity of 11 is 1.37 (1.32) times stronger than that of 2 according to the relative NICS(0)_πzz value obtained using the real π (pseudo-π) method.

In 12 the paratropic response is weaker than that in 11, as shown by its +30 ppm isosurface which is more contracted than the +50 ppm isosurface of 11, in both real π and pseudo-π methods (Fig. 5a). The B^ind_πz isosurfaces of 12 depict in detail the special features of its antiaromatic character. Discrete deshielding cones at +30 ppm are present at each 5MR which unite at the +20 ppm isosurface, retaining however their local augmentation above the 5MRs. This picture accounts for local paratropic currents on each 5MR and a considerably weaker paratropic current on the periphery of the pentalene moiety. The deshielding cone is more extended at the inner 5MR (ring b) with regard to the outer 5MR (ring c), denoting that the paratropic current is somewhat stronger in ring b. Accordingly, the NICS(0)_πzz values for rings b and c are 45.4 ppm and 38.6 ppm respectively. Additionally, the deshielding cone in ring c is not located at the center of the ring but displaced towards the outer carbon atom. Finally, the 6MR (ring a) presents very weak deshielding response (less than +20 ppm) mainly located at the center of the ring and connecting the common CC bonds of 6MR and 5MRs, denoting the presence of a very weak paratropic current in the interior of ring a. The NICS_πzz scan also supports the marginal paratropicity of ring a, starting from +16.0 ppm and presenting a maximum of 17.7 ppm at 0.6 Å above the ring, which is representative of the paratropic response. The pseudo-π method reproduces all the characteristic features of the paratropic response, except for the differentiation between rings b and c, where it predicts equal paratropic response for both 5MRs (pseudo-NICS(0)_πzz values for rings b and c are 79.6 and 79.1 ppm respectively). Additionally, the pseudo-π method predicts a very short ranged spherical deshielding cone at +20 ppm confined in the center of 6MR, representing the weak paratropic current inside the ring a. This interpretation of B^ind_πz of 12 is in agreement with the ring current analysis performed by Sundholm et al. using the GIMIC method.³⁷

Coronene and circumcoronene

A main point of criticism to NICS is its failure to properly describe concurrent hub and rim currents (e.g. in coronene) due to the intrinsic long range effects of IMF. Indeed, the B^ind_πz of coronene 13 and B^ind_σz of its HSM (Fig. 6a) display identical global long range shielding cones. However at short range the local characteristics of the magnetic response are revealed. The −25 ppm isosurface of 13 spreads uniformly on the outer 6MRs representing a global peripheral diatropic current, whereas the central ring is empty denoting the presence of a weak paratropic current that cancels the diatropic effects of the peripheral current in the vicinity of the central ring.

Fig. 6 (a) Isosurfaces of B^ind_πz (up row) and pseudo-π B^ind_σz (down row) of coronene 13 and circumcoronene 14. (b) NICS_zz scan profiles of real-π (filled symbols) and pseudo-π (white symbols) contributions above the ring centers of 13 and 14.

The weak paratropic contributions at the inner ring are indirectly represented in the NICS_πzz scan of 13 (Fig. 6b) which although it is diatropic, its diatropicity decreases close to the ring and displays a local minimum diatropic value at 0.6 Å, representative of paratropic contributions, and then increases as the diatropicity of the peripheral ring dominates. Accordingly the pseudo-NICS_πzz scan profile of the outer ring displays the typical behavior of an aromatic response, with small overestimation of the diatropicity at the center of the ring (NICS_πzz is −38.6 ppm and −42.0 ppm obtained with real π and pseudo-π methods respectively), whereas the pseudo-π profile of the inner ring displays large decrement of diatropicity below 0.6 Å (−11.0 ppm and −0.5 ppm at ring center obtained using real π and pseudo-π methods respectively) which is characteristic of paratropic contributions.

In circumcoronene 14 and its HSM (Fig. 6a) the magnetic response is identical and display a global long range uniform shielding cone. However, at short range (−25 ppm) the magnetic response presents strong local shielding cones accounting for the Clar sextets benzenoid pattern, with strong local diatropic currents within six-membered rings. Additionally, short range shielding areas encapsulate both the inner and the peripheral bonds of the outer non-aromatic rings d without forming a shielding cone. This picture denotes the presence of seven strong local diatropic currents at Clar aromatic rings, a weak global peripheral diatropic current and additionally weak diatropic currents at the inner CC bonds connecting the outer Clar aromatic rings, precisely recovering ring current maps obtained with RC analysis.^47,48

The NICS_πzz scan profiles of 14 (Fig. 6b) support this interpretation. Clar aromatic rings a and c show stronger π diatropicity than benzene (−45.9 ppm, −54.1 ppm and −36.3 ppm at the center of rings a, b and 1 respectively) and typical profiles for local aromatic rings. Ring c is more diatropic at close range until 1.4 Å, but beyond that distance ring a becomes more diatropic due to additive contributions of global and local currents at the central ring. On the other hand, non-aromatic rings b and d are less diatropic (−22.7 ppm and −26.4 ppm at ring centers respectively) and their diatropicity originates from global currents, since they do not support the formation of local shielding cones. The diatropicity of outer ring d originates from single contributions of the outer peripheral global current and decreases gradually above the center. The diatropicity of ring b is weaker at short range and decreases until 0.6 Å denoting the presence of weak local paratropic contributions, but then increases becoming more diatropic than ring d above 1.2 Å and even more diatropic than ring c above 2.4 Å, representing additive contributions from both global and local diatropic currents. The pseudo-π scan profiles reproduce all these characteristics very accurately (Fig. 6b), except for the short range response (<1 Å) of ring b which is significantly less diatropic, indicating the presence of weak local paratropic contributions in ring b. The relative NICS_πzz values with regard to 1 obtained using the real π (pseudo-π) method are 1.26 (1.12), 0.63 (0.32), 1.49 (1.44) and 0.73 (0.61) for rings a, b, c and d of 14 respectively. This picture is in alignment with ring current analysis with the CTOCD method which also predicts peripheral currents.⁴⁷

Spherical fullerenes

For spherical fullerenes the radial features of π orbitals cannot be well reproduced by the σ model and consequently quantitative deviations occur in B^ind_πz and B^ind_σz as observed for isosurfaces of C₆₀ fullerene and its HSM counterpart (Fig. 7a) and their NICS_zz scan profiles (Fig. 7b). However the pseudo-π model correctly recovers the qualitative features of the C₆₀ magnetic response involving core-, σ- and π-electron systems, which is a global short range response with isolated long range deshielding cones located at the 5MRs representing local antiaromatic character and short range shielding response at 6MRs denoting weak local diatropic currents.^22,49 Thus, such effects can be strictly associated with the curved π system, which are not present in planar systems.

Fig. 7 (a) Isosurfaces of B^ind_πz (up row) and pseudo-π B^ind_σz (down row) of C₆₀15 (b) NICS_zz scan profiles of real-π (filled symbols) and pseudo-π (white symbols) contributions from the cage center passing through centers of a pentagon and a hexagon. Cross symbols denote ring centers on the cage surface. (c–e) Pseudo-π B^ind_σz isosurfaces of I_h H₆₀¹⁰⁺, H₆₀⁶⁻ and H₆₀¹²⁻ respectively.

The deviation from the real π response is manifested in the interior of the cage where the +10 ppm isosurface of C₆₀ adopts an augmented spherical shape due to greater overlap of radial π MOs, whereas in the HSM it retains a linear cylindrical shape at both sides of the cage normal to the 5MRs. Likewise, the NICS_zz scan profile along the C₅ rotational axis of H₆₀ shows maximum paratropicity on the center of 5MR and symmetrical response with regard to the cage surface, while it decreases sharply inside the cage to reach a negligible response at the cage center (+2.6 ppm). On the other hand, the real-π profile displays maximum paratropicity in the interior of the cage and retains significant contributions at the cage center (+21.6 ppm) (Fig. 7b). The real π and pseudo-π scan profiles along the C₃ rotational axis show similar weak diatropic response above the 6MR, but diverge significantly inside the cage where the real π profile becomes paratropic due to the contributions of 5MRs, whereas the pseudo-π profile smoothly declines to +2.6 ppm. Overall, the pseudo-π method clearly describes the local antiaromatic character of 5MRs in C₆₀ and its overall non-aromatic character.

Additionally, the pseudo-π model correctly predicts the magnetic response of charged C₆₀^q (q = +10, −6, −12) fullerenes, where C₆₀¹⁰⁺ and C₆₀⁶⁻ display global long range shielding cones representative of spherical aromaticity (the former stronger than the latter), whereas C₆₀¹²⁻ displays strong deshielding response at the 6MRs denoting spherical antiaromatic character (Fig. 7c–e). These results are in complete agreement with reported full DFT calculations of charged fullerenes and their alkali-metal decorated counterparts.²²

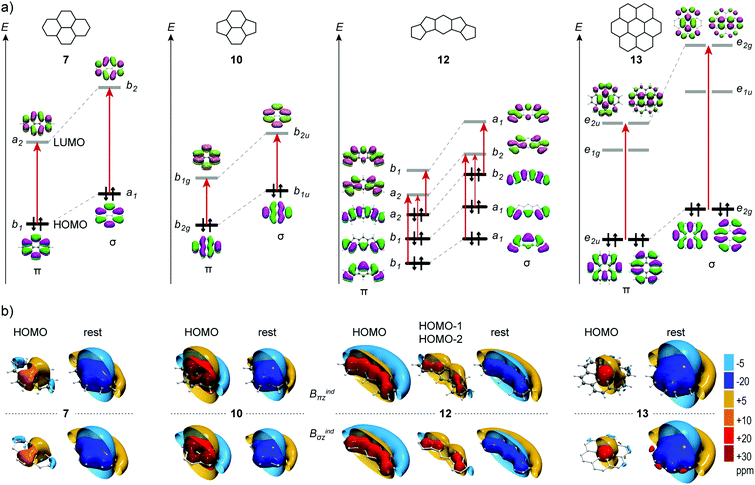
CMO contributions

The IMF can be dissected into contributions of individual canonical molecular orbitals (CMOs), enabling the interpretation of the magnetic response based on simple symmetry selection rules.^20–22 Within the GIAO dissection scheme, the low energy π MOs induce a diatropic response, whereas the overall π response is shaped by the high lying orbitals and especially HOMOs, which induce a paratropic response originating from rotationally allowed π → π* excitations. The strength and the topology of the paratropic response depends on the energy gap and the overlap between the interacting orbitals.^21,50–52 A rotational excitation is symmetry allowed when the direct product of the irreducible representations of occupied and vacant orbitals contains the irreducible representation of the rotation around the axis of the direction of the applied field.

In Fig. 8a the energy levels of frontier orbitals of 7, 10, 12 and 13 and their HSMs are shown together with the rotationally allowed HOMO → π* excitations. The σ orbitals of HSMs have higher energies than the π orbitals, but in all molecules the MO's relative energies and excitation gaps of PAHs are accurately reproduced. The contributions of the HOMOs and the summation of the contributions of the remaining π CMOs (or σ CMOs for HSMs) are given in Fig. 8b. Additionally, the isosurfaces of each CMO contribution of the remaining molecules under study are given in the ESI† (Fig. S1–S7). In all molecules the combined magnetic response for all π MOs (or σ MOs for HSMs) except that of the HOMOs, produces a strong shielding cone uniformly spread on the molecular framework, whereas the total response is shaped mainly by the paratropic response HOMOs. In 7 (and its HSM) the HOMO induces a weak deshielding cone (+10 ppm) located at the naphthalene moiety, which diminishes the diatropicity of these rings excluding any local diatropic contributions. The weak paratropicity originates from the large gap of the HOMO → LUMO excitation with symmetry b₁ → α₂, which for the HSM is transformed through the perpendicular to the molecular plane translation operation (Γ_z = b₁) to α₁ → b₂. Accordingly, in 10 the HOMO → LUMO excitation (b_2g → b_1g for PAH and b_1u → b_2u for HSM) induces a strong paratropic response with large local deshielding cones (+30 ppm) located at the 5MRs that overwhelm the diatropicity of lower MOs, and contracted cones confined in the 6MRs that cancel the diatropicity of lower MOs inside the rings. The strong paratropicity of the HOMO in 10 is due to the small energy gap and it is augmented at the 5MRs because of the greater overlap of the rotated HOMO and LUMO at these rings.

Fig. 8 (a) Relative energy levels of frontier MOs of PAHs 7, 10, 12 and 13 (left columns) and their HSMs (right columns). Red arrows represent rotational excitations of π → π* (left columns) and σ → σ* (right columns) of PAHs and HSMs respectively. (b) CMO contributions to B^ind_πz of PAHs 7, 10, 12 and 13 (up row) and B^ind_σz of their HSMs (down row). For each molecule, the left column depicts the contributions of HOMO and the right column depicts the summation of contributions of the remaining π CMOs of PAHs or σ CMOs of HSMs.

In 12 the HOMO → LUMO excitation is forbidden, but the HOMO → LUMO+1 is allowed (a₂ → b₁ for PAH and b₂ → a₁ for HSM) and has a small energy gap, inducing a strong deshielding cone equally distributed throughout the entire molecular skeleton, canceling the diatropicity induced from lower energy MOs. Additionally, the HOMO−1 → LUMO and HOMO−2 → LUMO excitations are allowed (b₁ → a₂ for PAH and a₁ → b₂ for the HSM) and induce strong deshielding cones located at the 5MRs. Hence in 12 the weak paratropicity of 6MR originates from the HOMO, while the paratropicity of 5MRs is additionally augmented from the contributions of HOMO−1 and HOMO−2.

Finally, in 13 the paratropicity of the central ring is not manifested in the total response due to the contribution from the peripheral rings, but it is well represented in the response of the HOMO, which displays a moderate deshielding cone confined in the central ring, originating from HOMO → LUMO+1 excitation (e_2u → e_2u for PAH and e_2g → e_2g for HSM). This picture accounts well for the observed diatropic currents at the peripheral rings and paratropic currents at the central ring for coronene, as discussed in the literature.⁵³

Hence, the notable resemblance of B^ind_σz to B^ind_πz stems from the practically identical CMO contributions between conjugated hydrocarbons and the HSMs. The σ MOs of the HSMs obey the same symmetry rules that determine the response of π MOs and consequently the pseudo-π model is suitable for the analysis of the magnetic response in terms of CMO contributions, as shown here.

Conclusions

The pseudo-π model proves to be a fast, lightweight and accurate method for the description of the magnetic field induced by π orbitals in planar PAHs and spherical fullerenes. The inspection of the long and short range pseudo-π magnetic response is suitable for the interpretation of global and local π aromaticity and antiaromaticity. Hence, Clar sextet patterns and non-local peripheral currents can be obtained by their short-range nature at large isosurface values (∼−25 ppm). Furthermore, the IMF of hydrogen skeletal models can be reliably analyzed to CMO contributions and paratropic rotational excitations providing insight into the physical origins of the magnetic response of the actual PAHs based on electronic configurations. The compactness and handiness of the pseudo-π method empowers further applications to large planar and spherical conjugated species and nanostructures, enabling a simple and concise manner to facilitate further interpretations.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. R. Gershoni-Poranne and A. Stanger, Chem. Soc. Rev., 2015, 44, 6597–6615.
2. T. Heine, C. Corminboeuf and G. Seifert, Chem. Rev., 2005, 105, 3889–3910.
3. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. von R. Schleyer, Chem. Rev., 2005, 105, 3842–3888.
4. J. A. N. F. Gomes and R. B. Mallion, Chem. Rev., 2001, 101, 1349–1384.
5. P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88.
6. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500.
7. D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678.
8. R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228.
9. P. B. Karadakov and K. E. Horner, J. Phys. Chem. A, 2013, 117, 518–523.
10. A. Muñoz-Castro, Phys. Chem. Chem. Phys., 2017, 19, 12633–12636.
11. E. Kleinpeter, S. Klod and A. Koch, J. Mol. Struct. THEOCHEM, 2007, 811, 45–60.
12. T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309.
13. G. Merino, T. Heine and G. Seifert, Chem. – Eur. J., 2004, 10, 4367–4371.
14. P. B. Karadakov and K. E. Horner, J. Chem. Theory Comput., 2016, 12, 558–563.
15. A. Muñoz-Castro, J. Phys. Chem. C, 2012, 116, 17197–17203.
16. S. Van Damme, G. Acke, R. W. A. Havenith and P. Bultinck, Phys. Chem. Chem. Phys., 2016, 18, 11746–11755.
17. D. Du, D. Sundholm and H. Fliegl, J. Chin. Chem. Soc., 2016, 63, 93–100.
18. S. Pelloni and P. Lazzeretti, J. Phys. Chem. A, 2013, 117, 9083–9092.
19. R. Báez-Grez, L. Ruiz, R. Pino-Rios and W. Tiznado, RSC Adv., 2018, 8, 13446–13453.
20. N. D. Charistos, A. G. Papadopoulos and M. P. Sigalas, J. Phys. Chem. A, 2014, 118, 1113–1122.
21. N. D. Charistos, A. G. Papadopoulos, T. A. Nikopoulos, A. Muñoz-Castro and M. P. Sigalas, J. Comput. Chem., 2017, 38, 2594–2604.
22. N. D. Charistos and A. Muñoz-Castro, J. Phys. Chem. C, 2018, 122, 9688–9698.
23. P. W. Fowler and E. Steiner, Chem. Phys. Lett., 2002, 364, 259–266.
24. A. Soncini, P. W. Fowler and L. W. Jenneskens, Phys. Chem. Chem. Phys., 2004, 6, 277–284.
25. E. Steiner, P. W. Fowler, A. Soncini and L. W. Jenneskens, Faraday Discuss., 2007, 135, 309–323.
26. A. Soncini, R. G. Viglione, R. Zanasi, P. W. Fowler and L. W. Jenneskens, C. R. Chim., 2006, 9, 1085–1093.
27. P. W. Fowler and A. Soncini, Phys. Chem. Chem. Phys., 2011, 13, 20637.
28. P. Bultinck, M. Mandado and R. Mosquera, J. Math. Chem., 2008, 43, 111–118.
29. S. Fias, S. Van Damme and P. Bultinck, J. Comput. Chem., 2008, 29, 358–366.
30. D. W. Szczepanik, Int. J. Quantum Chem., 2018, 118, e25696.
31. F. London, J. Phys. Radium, 1937, 8, 397–409.
32. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
33. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
35. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
36. R. Gershoni-Poranne and A. Stanger, Chem. – Eur. J., 2014, 20, 5673–5688.
37. D. Sundholm, R. J. F. Berger and H. Fliegl, Phys. Chem. Chem. Phys., 2016, 18, 15934–15942.
38. E. Steiner and P. W. Fowler, J. Phys. Chem. A, 2001, 105, 9553–9562.
39. E. Steiner, P. W. Fowler and R. W. A. Havenith, J. Phys. Chem. A, 2002, 106, 7048–7056.
40. A. Ligabue, U. Pincelli, P. Lazzeretti and R. Zanasi, J. Am. Chem. Soc., 1999, 121, 5513–5518.
41. S. Fias, P. W. Fowler, J. L. Delgado, U. Hahn and P. Bultinck, Chem. – Eur. J., 2008, 14, 3093–3099.
42. P. W. Fowler and W. Myrvold, J. Phys. Chem. A, 2011, 115, 13191–13200.
43. E. Steiner, P. W. Fowler, L. W. Jenneskens and R. W. A. Havenith, Eur. J. Org. Chem., 2002, 163–169.
44. J. Poater, M. Solà, R. G. Viglione and R. Zanasi, J. Org. Chem., 2004, 69, 7537–7542.
45. R. W. A. Havenith, J. J. Engelberts, P. W. Fowler, E. Steiner, J. H. van Lenthe and P. Lazzeretti, Phys. Chem. Chem. Phys., 2004, 6, 289–294.
46. I. G. Cuesta, A. Ligabue, A. S. de Merás and P. Lazzeretti, Chem. Phys. Lett., 2005, 401, 282–287.
47. A. Soncini, E. Steiner, P. W. Fowler, R. W. A. Havenith and L. W. Jenneskens, Chem. – Eur. J., 2003, 9, 2974–2981.
48. S. Pelloni and P. Lazzeretti, J. Comput. Chem., 2018, 39, 21–34.
49. E. Kleinpeter, S. Klod and A. Koch, J. Org. Chem., 2008, 73, 1498–1507.
50. R. V. Viesser, L. C. Ducati, C. F. Tormena and J. Autschbach, Chem. Sci., 2017, 8, 6570–6576.
51. I. Pérez-Juste, M. Mandado and L. Carballeira, Chem. Phys. Lett., 2010, 491, 224–229.
52. C. Corminboeuf, R. B. King and P. von R. Schleyer, ChemPhysChem, 2007, 8, 391–398.
53. P. W. Fowler, C. M. Gibson and D. E. Bean, Proc. Math. Phys. Eng. Sci., 2014, 470, 20130617.

---

Footnote

† Electronic supplementary information (ESI) available: CMO contributions to B^ind_z. See DOI: 10.1039/c9cp00836e

---