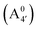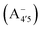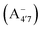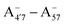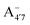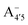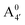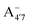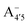Unraveling the molecular mechanisms of color expression in anthocyanins

Abstract

Anthocyanins are a broad family of natural dyes, increasingly finding application as substitutes for artificial colorants in the food industry. In spite of their importance and ubiquity, the molecular principles responsible for their extreme color variability are poorly known. We address these mechanisms by computer simulations and photoabsorption experiments of cyanidin-3-O-glucoside in water solution, as a proxy for more complex members of the family. Experimental results are presented in the range of pH 1–9, accompanied by a comprehensive systematic computational study across relevant charge states and tautomers. The computed spectra are in excellent agreement with the experiments, providing unprecedented insight into the complex behavior underlying color expression in these molecules. Besides confirming the importance of the molecule's charge state, we also unveil the hitherto unrecognized role of internal distortions in the chromophore, which affect its degree of conjugation, modulating the optical gap and in turn the color. This entanglement of structural and electronic traits is also shared by other members of the anthocyanin family (e.g. pelargonidin and delphinidin) highlighting a common mechanism for color expression across this important family of natural dyes.

---

1 Introduction

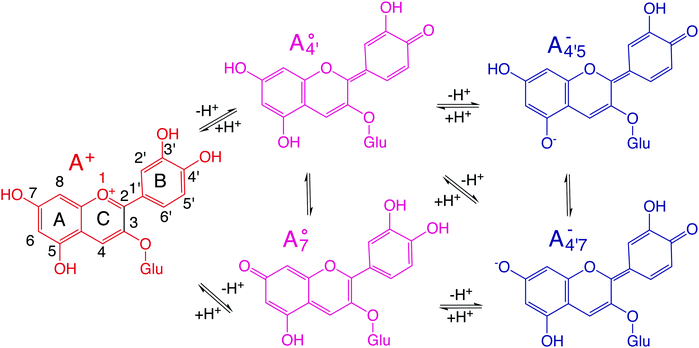
Regulations on colorants are some of the oldest and more rigorous ones in the food industry, with the first list of prohibited additives dating back to 1906.¹ Moreover, nowadays the food industry is experiencing additional mounting pressure from the public to substitute artificial additives with natural alternatives, perceived as healthier and safer. Obvious requirements that natural colorants have to fulfill for use in food applications include non-toxicity, abundance and cost-effectiveness, chemical stability, as well as versatility. While nature provides plenty of options for colors in the red-yellow-green gamut, choices are much more limited in the red-purple-blue range, particularly when it comes to the blue end of the palette.² Anthocyanins are a broad family of dyes responsible for most of the colors in the red-purple-blue gamut found in flowers, fruits, vegetables, leaves, tubers and food products (wines, jams, and syrups) and they account for a large amount of color expression in nature.^2–5

The extreme variety of hues, brightness, and nuances expressed by anthocyanins reflects their chemical variability. Substituents on the A, C and B rings (Fig. 1), including hydroxyl and glycosylic (mostly at positions 3 and 5) will induce a change in color.^2,3 Extra acyl groups connected to the glycosylic units, when bearing phenolic acids, will also modulate the color through both inter- and intra-molecular co-pigmentation. In addition, the optical properties of anthocyanins are highly sensitive to environmental factors such as the pH of the solution or the presence of metal ions.⁶ The red-colored flavylium cation exists at very acidic conditions (pH < 2) while in the pH range of 3–8, flavylium converts into neutral purple-coloring forms, due to the deprotonation of one of its hydroxyls. Upon further pH increase, another hydroxyl will deprotonate, giving rise to the blue-colored anionic quinonoid forms.^3,6

Fig. 1 Scheme of the relevant molecular species of cyanidin-3-glucoside (C3G) in solution at pH 1–9. From left to right, the flavylium cation in red (A⁺), in pink the neutral species deprotonated at either 4′ or 7 (A⁰₇), and in purple two negative species, deprotonated at 4′ and 5 , or at 4′ and 7 .

This variability and complexity of color expression makes the industrial utilization of anthocyanins a challenging endeavor, compared to synthetic dyes which are more stable and predictable. Thus a deep understanding of the mechanisms of color expression in these molecules is still needed, in spite of recent extensive experimental^2,3,5,7,8 and theoretical^9–16 efforts. Moreover, most of the available studies concern the cationic species—responsible for the red hues only—while only few studies have focused so far on the neutral and negative species, which are of striking interest for industrial applications.^2,7

The color expressed by an anthocyanin solution is determined by the optical properties of the solvated molecules, which can be measured experimentally through photoabsorption spectroscopy. Predicting the color using theory and computational methods, however, is not as straightforward.^17,18 Efforts in this direction have comprised quantum chemical calculations performed at various levels of theory, ranging from semiempirical methods,^13–15,19 to post Hartree–Fock¹² and TDDFT,^9,10,16 most of which, however, focused on the cation form only, and did not address charge, tautomerism, and conformation effects, which are expected to be important. Furthermore, the absorption spectrum and perceived color of a solution depend on the different out-of-equilibrium molecular geometries that are experienced by thermal fluctuations, as well as on the interaction with the solvent. Indeed, an accurate modelisation of the optical properties in principle requires taking into account the different molecular states, their possible conformations, thermal fluctuations, and the effects of the solvent. Previous works have gone as far as taking into account thermal fluctuations in the minimum energy conformer,^9,10,20,21 however realistically many conformers will coexist in solution, and each of their contributions to the final color should be taken into account. Such a systematic study is lacking, and the present work intends to be a first step in this direction by applying a multi-scale simulation protocol to the simulation of anthocyanins.

We thus aim to elucidate the relative importance of the aforementioned effects through a combination of computer simulations, performed with a newly introduced multiscale protocol that accounts for each of them at the relevant time/length scale, and photoabsorption experiments, which have been performed for the first time systematically for a glycosylated anthocyanin over an extended (1–9) pH range. Our efforts are focused on cyanidin-3-O-glucoside (C3G, hereafter), chosen as a prototype for singly glycosylated anthocyanins, and which is highly abundant in nature. Fig. 1 shows the relevant molecular states (justified in Section 3.2) and chemical equilibria determining the optical properties of C3G throughout the 1–9 pH range: the flavylium cation (hereafter referred as A⁺), two prototropic tautomeric states (protomers) of the neutral base, deprotonated at either position 4′ or 7 (hereafter referred to as 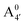and A⁰₇, respectively), and two protomers of the negative base (hereafter referred to as 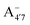and 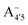, deprotonated at positions 4′ and 7 or 4′ and 5, respectively). Experimentally, controlling the pH is relatively straightforward, however computationally there is no easy correspondence. For this reason, in this study we simulate each of the charge and protomeric states shown in Fig. 1 separately, and compare experimental spectra at a given pH with the computed spectra corresponding to the charge state which is expected to exist in majority at that pH. We have found that each molecular state can also adopt various conformations, whose effects on the optical properties are carefully accounted for in our simulations and discussed in this paper. We define and discuss the elements responsible for the coupling between electronic and structural degrees of freedom, the latter being mainly represented by the torsion in the chromophore between the two conjugated units. The agreement between our theoretical and experimental results is excellent, giving us confidence on the quality of the simulations and their ability to capture the fine details of microscopic mechanisms underlying color expression in this important family of natural dyes.

2 Methods

2.1 Photoabsorption spectroscopy

C3G solutions from pH 1–9 were prepared by adding 1 mL of cyanin stock solution to 20 mL Milli-Q deionized water, adjusting to respective pH using either HCl or NaOH, then completing volume to a total of 24 mL in order to keep the concentration of cyanin constant.

The stock solution of cyanin was prepared by dissolving 11.60 mg cyanin chloride into 25 mL acidified water (0.01% HCl). Cyanin solutions were pH adjusted using various volumes of NaOH and HCl depending on desired final pH. The sodium hydroxide (2.0 M/0.2 M) (sodium hydroxide pellets 99.99% trace metal analysis from Sigma Aldrich – Cat. no. 306576) and HCl (1 M/0.1 M) stock solutions were prepared by dissolving NaOH pellets or diluting concentrated HCl (Hydrochloric Acid TraceMetal Grade from Fisher Scientific – Cat. no. A508-P212), respectively into Milli-Q deionized water (EMD Millipore Milli-Q deionized water). The pH of the final cyanin-pH adjusted solutions were determined by using a Mettler-Toledo SevenEasy pH meter before measuring spectra.

To measure the spectra, an aliquot of pH adjusted cyanin solution was transferred to a 1 cm polystyrene UV visible cuvette (1 cm polystyrene UV visible cuvettes from Fisher Scientific – Cat. no. 14-955-125) on an Agilent 8453 UV visible spectrophotometer. UV visible absorbance data was obtained for wavelength range of 200–700 nm with 1 nm resolution and 0.5 second integration time using Agilent ChemStation software.

2.2 Computer simulations

We have developed a multi-scale computational protocol, enabling us to account for the many effects governing the optical properties of C3G in solution. Firstly, the conformational landscape of each molecular state is sampled using μs-scale enhanced-sampling molecular dynamics (MD).²² Then, each relevant conformer is simulated by means of ab initio MD (AIMD)²³ including explicit solvent, thus accurately accounting for thermal fluctuations and hydrogen bonding effects. The optical spectra of selected statistically independent frames are then computed using time-dependent density functional theory (TDDFT),²⁴ and the final spectrum is obtained as an average of these spectra. The color of the solution is finally estimated using the standard tri-stimulus model.²⁵ While the details of the protocol will be presented and discussed in a future work, its main steps are summarized below.

MD. Classical MD simulations were run using GROMACS 4.5.5,²² upon adequate equilibration with all bonds to hydrogen atoms constrained using LINCS.²⁶ General AMBER Force Field (GAFF)²⁷ parameters were assigned using the antechamber module of AmberTools13, with RESP charges²⁸ at the HF/6-31G* level, calculated on DFT-B3LYP²⁹ optimized geometries, 50/200 Ry basis set.³⁰ For each species of C3G studied, ten replicas were simulated using Hamiltonian replica-exchange MD (HREMD),³¹ as implemented in the PLUMED plugin,³² for a total of 10 μs (1 μs per replica). The molecules were fully solvated in TIP3P water,³³ using cubic cells of 30 Å edge accommodating ∼1000 water molecules, in periodic boundary conditions. The volume was kept fixed, and velocity rescaling was used to keep the average temperature constant (NVT ensemble). In each case only the trajectory of the first replica, at 300 K, was retained for analysis.

Conformational analysis. An advanced clustering algorithm³⁴ was used to identify the most representative conformers, according to the three dihedrals illustrated in Fig. 2. These were selected as they describe distortions of the chromophore, which would in turn affect the color. The statistical weight of each conformer thus identified was evaluated as the normalized ratio between the residence time within each free-energy basin and the total simulation time. In general for each species four main clusters were identified, corresponding to four distinct orientations of θ. The relative orientations of the AC and B rings always deviate from planarity, due to steric hindrance of the substituents on the aromatic rings,³⁵ while the varying position of the sugar results from competition between steric and solvent effects. The parameters used for the clustering algorithm are given in the ESI.†

Fig. 2 θ, α₆ and α₇ dihedral angles are shown in blue, dark and light magenta, respectively, in the specific case of the flavylium cation.

AIMD. Explicit-solvent Car–Parrinello AIMD simulations^23,36 were performed for each one of the four most populated conformers of the five C3G species investigated in this work, using the cp.x module of the Quantum ESPRESSO (QE) distribution.^37,38 Ultrasoft pseudopotentials³⁹ from the QE public repository were used with plane-wave basis sets (25/200 Ry³⁰) and the PBE exchange correlation-functional.⁴⁰ The number of water molecules was reduced to ∼200, so as to fit a simulation cell of linear dimensions ∼20 Å. The NVT ensemble was used, with a Nosé–Hoover thermostat⁴¹ to maintain the temperature at 300 K.

TDDFT. For each relevant conformer, the absorption spectrum was computed using the methodology introduced in ref. 10. Molecular configurations of C3G were selected from the AIMD trajectories every 0.5 ps, ensuring statistical independence. Absorption spectra were computed for each such configuration using the TDDFT-based self-consistent continuum solvation (SCCS) approach,⁴² as implemented in Quantum ESPRESSO^37,38 and using the B3LYP²⁹ XC functional, which was found in ref. 10 and 42 to perform well for the optical properties of anthocyanins, using a 50/200 Ry basis set.³⁰ The solvation model was enhanced by explicitly keeping solvent molecules which are found to be persistently H-bonded to the chromophore (typically, at positions 4′, 3′, 5 and 7: see Table S2, ESI†), thus better accounting for the effects of a protic solvent on the electronic structure of the solute. Finally, for each conformer the spectrum was evaluated as the average of the spectra computed for each selected frame.

Absorption spectra. The overall spectrum for the solution of each species was evaluated by averaging the TDDFT spectra computed for each conformer, weighted by the factors computed in the conformational analysis. The resulting color was finally estimated using the tri-stimulus model,²⁵ as in ref. 10.

Additional quantum-chemical calculations were performed to corroborate some of our results. In particular, QM calculations included in the protocol are performed with QE (with SCCS for solvation), while extra analysis on the orbitals were run using Gaussian09⁴³ (with PCM⁴⁴ for solvation). Further details are reported in the ESI.† Please see: Tables S6 and S7 (ESI†) for bond order calculations; Table S2 (ESI†) for H-bond analysis.

3 Results

3.1 Clustering analysis and molecular conformers

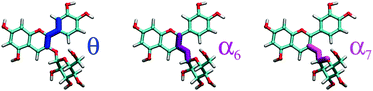
For each molecular state, our HREMD trajectory was analyzed in terms of the three dihedrals θ, α₆, and α₇ (Fig. 2), in order to find representative geometries corresponding to conformers separated by free energy barrier of the order of a few k_BT, impossible to overcome on the timescale accessible to AIMD. Results from this analysis are shown in Fig. 3 for the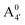 molecular state, and the same clustering procedure was adopted for all the other studied species, giving qualitatively similar results. Conformers are detected as high density clusters in the dihedral space, here visible in the pair-wise distributions, depicted as 2D projections of a 3D density map. The clustering algorithm used in this work³⁴ is based on density and distance cut-off criteria to group the three dimensional data points corresponding to molecular geometries from the MD trajectory. For each cluster a center is defined and the corresponding molecular geometry is selected as the most representative structure (Fig. 3, lower panel). Conformers were identified for each molecular state, as shown in detail in the ESI† (Fig. S2 reports percentages). Only the most populated conformers were then simulated with AIMD, so as to sample more accurately the geometries to be used for spectral computations. From this analysis we found that θ is correlated with the position of the sugar, determined by the values of α₆ and α₇ (Fig. 3 upper panel), and that each species may adopt four main conformations (whose relative population is larger that 10%), corresponding to θ assuming four possible orientations; 180°⁺ (C₁), 0°⁻ (C₂), 0°⁺ (C₃), 180°⁻ (C₄). We remark that the sugar, usually dismissed in studies of the optical properties, as it does not directly participate in the optical transitions on the conjugated core, has nevertheless a major effect on the geometry of the chromophore, thus indirectly but importantly affecting its the optical properties.

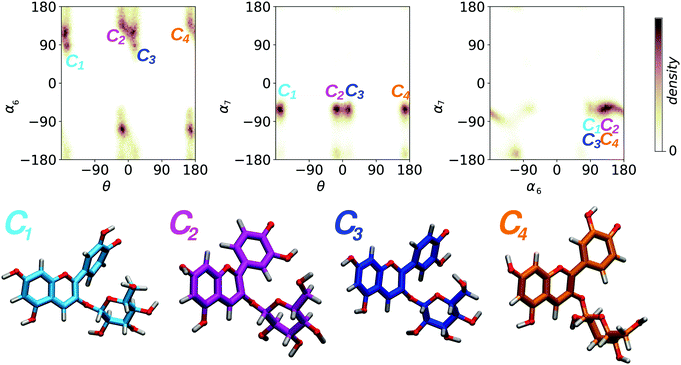Fig. 3 Upper panel: 2D density maps of pairs of dihedral angles (in degrees) resulting from the HREMD trajectory for the 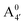state of C3G and used for the cluster analysis performed to select the dominant conformers. Lower panel: geometries of the four most representative conformers of the same 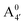. Qualitatively similar results hold for the other molecular states investigated here (see Fig. S1, ESI† for analogous distributions for all species).

3.2 Optical spectra: effects of pH, charge, and protomeric state

Most previous studies have focused on the cationic form of anthocyanins, basically because full protonation lifts any ambiguity as to its tautomeric state and makes it the only relevant species at low pH, thus facilitating the comparison with experiments. In addition, in this work we investigate two out of the three protomers of both the neutral and negative species (excluding A⁰₅ and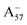 ), selected according to their relative DFT energies (see Table 1). We thus expect C3G in solution to be predominantly a mix of the remaining five charge/protomeric states, whose relative abundance depends on pH.

Table 1 Energy differences of different protomers of C3G, as predicted by energy minimization at the DFT level in implicit solvent (PCM⁴⁴)

	Energy differences (kcal mol^−1)
	−15
	−26
	−5
	−24

---

Our measured and computed spectra are displayed and compared with each other in Fig. 4. The average spectra for each molecular species were computed by weighting the contributions from each conformer (C₁ to C₄) with their relative population (see Fig. S2, ESI†). Experimental spectra at different pH are grouped and compared with those computed for the charge species expected to be prevalent in solution at those pH values, considering the two successive pK_a values of 4 and 7 generally used as a reference for anthocyanins³ indicating that cyanin below pH 4 is expected to be positively charged, while above pH 7 it is expected to be negatively charged. At pHs between 4 and 7 the neutral species are expected to exist. Our predictions are in excellent agreement with experiment, as concerns the position and pH/charge dependence of the maximum absorption wavelength, λ_max. The latter is determined by the S₀ → S₁ transition, which is essentially a single-configuration HOMO → LUMO transition (π → π*, accounting for ∼90% of the total oscillator strength). We also note the existence of a shoulder in the spectra predicted for the neutral and negative species at shorter wavelengths (λ 500 nm) and corresponding mostly to a HOMO − 1 → LUMO transition. This shoulder develops into a full-blown secondary peak in 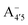, which is remarkably visible in experimental spectra from intermediate to high acidity. This indicates that 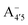is present in solution at room temperature in this pH range, contrary to the higher stability of 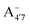predicted by our static computations (see Table 1). Although this discrepancy could be due to the inadequacy of the energy functional or PCM model utilized here, yet unpublished results on the neutral species show that the relative stability of the 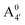and A⁰₇ protomers is in fact reversed once entropic effects are taken into account, indicating that the difference between the minimum energies computed for different protomers in implicit solvent may not accurately reflect the true relative stability of each species, especially when the differences are small. A small entropic contribution to the free-energy difference between 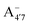and 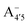could be enough to reverse the stability in this case, making 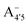dominant, and explaining the prevalence of the two-peak feature in the experimental spectra. We notice that this secondary peak has an outstanding effect on the color expressed, as it subtracts blue components from the light diffused by the solution. We conclude that hindering deprotonation from site 5, e.g. by glycosylation, will likely enhance the blueness of the solution.

Fig. 4 Experimental spectra at different pH values (top) and calculated for the species expected to be relevant for each pH interval.

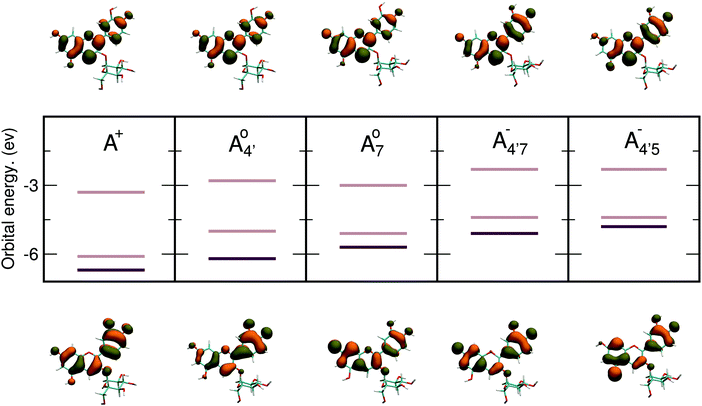
Relevant frontier energy levels (HOMO − 1, HOMO, and LUMO) are shown in Fig. 5, along with a representation of the corresponding molecular orbitals for HOMO and LUMO, for all five molecular states of C3G, calculated in implicit solvent (PCM⁴⁴). Full computational details are given in the ESI.† Energy levels remarkably depend not only on charge state, but also on protonation patterns. These data show that deprotonation lifts the HOMO and LUMO orbital energies, in line with chemical intuition that suggest a decrease of the ionization potential, when increasing the negative charge of the molecule. To a lower extent a similar argument also holds for the LUMO, thus leading to a general decrease of the HOMO–LUMO (HL) gap from the positive to the negative states of C3G. Hence, the overall charge state of the molecule markedly affects the C3G optical properties, consistently with experimental evidence. Isosurfaces of the molecular orbitals are also qualitatively different from each other, and match an alternating distribution of bonding and antibonding characters, reflecting rearrangements of electronic distribution upon (de)protonation at different sites. Both the HOMO and the LUMO lie in the plane of the chromophore and extend over both conjugated moieties (AC and B rings); hence we also expect that distortions in the chromophore might decrease its overall conjugation, and result in a shift of the orbital energies and hence the color of the solution. This is discussed in more detail in the next section.

Fig. 5 HOMO − 1, HOMO and LUMO energy levels for all five molecular states, along with the frontier orbitals HOMO and LUMO. The HOMO–LUMO gap is here the spacing between the light brown lines while the HOMO − 1 level is drawn as a darker line. Energy level position and shapes of the orbitals remarkably differ in each molecular states.

3.3 Conformational effects

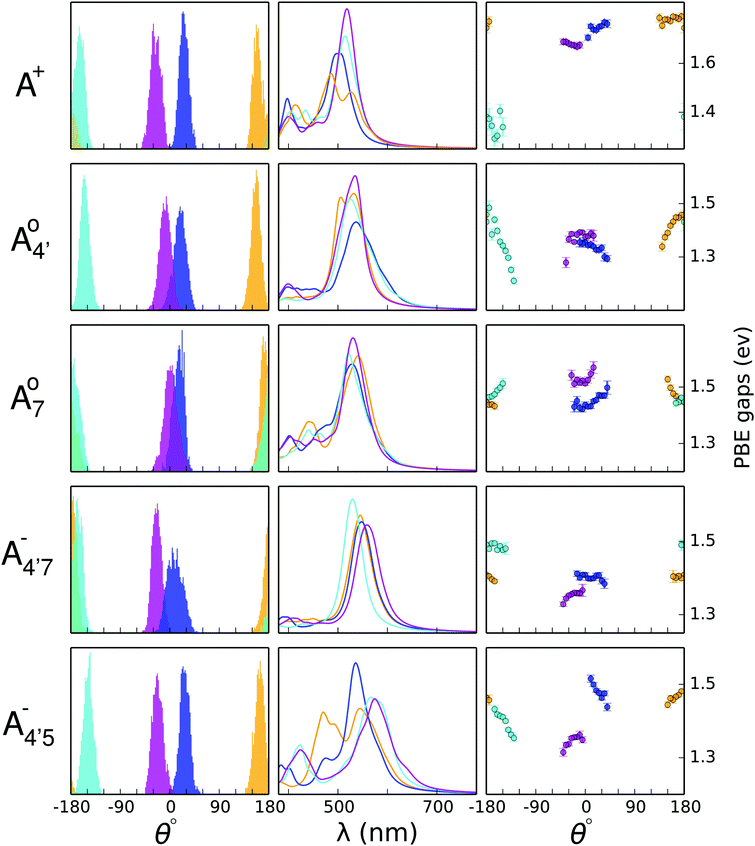
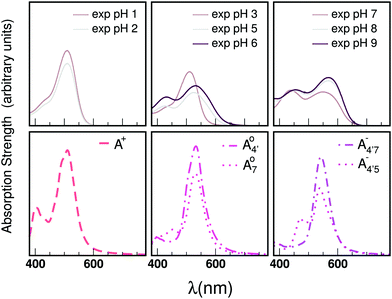
The molecular distortion that mostly affects the optical properties of anthocyanins is the twist between the single (B) and double (AC) rings, described by the dihedral angle θ. In order to ascertain the effects of this distortion on the main absorption peak, we monitor the HL gap using the PBE functional along various AIMD trajectories. Computing these gaps is much less expensive than performing TDDFT excited-state calculations using the B3LYP hybrid functional, while the value of the gap correlates very accurately with the position of the S₀ → S₁ transition, regardless of the functional used (as shown in the ESI;† Section S1 and Fig. S0). The HL gaps were computed with QE in implicit solvent (SCCS) on 1000 geometries extracted from each AIMD trajectory, and were binned according to the θ values of the corresponding structure with a bin-width of 5°. The average gap was computed for each bin with its statistical uncertainty (see Fig. 6, third column).

Fig. 6 Results for A⁺, , A⁰₇, , and species of C3G are reported from top to bottom. Columns from left to right: histograms showing the distribution of the θ dihedral angle for all clusters equilibrated in ab initio MD (AIMD), spectra of each of the conformers, and HOMO–LUMO gaps calculated for frames extracted from AIMD trajectories. All data referring to the C₁, C₂, C₃, and C₄ conformers are reported in cyan, blue, pink and orange, respectively.

In Fig. 6 we show the distribution of the θ dihedral for the five molecular species considered in this work (left panel), along with the average HL gaps recorded within each θ bin for each conformer (right panel). The mid panel reports the average spectra recorded for each conformer. We notice that deviation from planarity induces a variation in the HL gaps, however this variation seems to depend on the molecular species. The nature of the frontier orbitals across the different molecular states is crucial to understand such trends. In order to get further insight, we utilize an indicator, B_π, of the bonding character along the C2–C1′ bond, connecting the AC and B rings, in the various frontier orbitals, defined as:

where c_ix is the projection of the i-th molecular orbital (i = {HOMO,LUMO,…}) over the 2p_z atomic orbital of the x-th C atom (x = {1′,2}). The relative sign of c_i2vs. c_i1′ determines the resulting B_π: B_π ∼ 0 reflects a strong antibonding character, while B_π ∼ 1 corresponds to a fully bonding π orbital. The computed values of B_π for optimized structures of each species are shown in Table 2. This simple quantity is able to explain the behavior of orbital energies upon distortion around the C2–C1′ bond: we expect the energy of a strongly bonding orbital to increase with distortion, whereas an antibonding orbital should be stabilized by distortion. The resulting effect on the gap depends on the relative variation of the HOMO and LUMO energies. 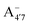From Table 2 we see that , and 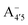have a bonding HOMO (B_π = 0.98 to 0.77) and an antibonding LUMO (B_π = 0.37 to 0.45). Hence we expect to see a strong dependence of the gap on θ, and in particular that the gap should decrease upon distortion. This is indeed what we see in the right panel of Fig. 6. Conversely, A⁰₇ which has a very antibonding HOMO (B_π = 0.08) and slightly bonding LUMO (B_π = 0.65), displays the opposite trend, as the gap increases with higher distortion. Finally, A⁺ is an intermediate case in which the gap does not show a strong dependence on θ, although due to its slightly antibonding HOMO (B_π = 0.44) and bonding LUMO (B_π = 0.67) the trend is nevertheless reversed as in the A⁰₇ case. Following this reasoning, we notice that the behavior of the two negative forms should be very similar to each other, as their B_π values are very close-however the gap's dependence on θ is much more marked in the case of 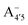than in that of 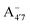. This partial mismatch can be explained by the proximity of the HOMO − 1 and HOMO energy levels in this species (Fig. 5), which is related to the appearance of a second peak in the visible spectrum and partially undermines the single electron–hole pair picture of the optical transitions. We see that the bonding character depends on the protonation pattern more than the charge states—in fact both neutral protomers 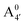and A⁰₇ are at the two extreme in bonding character for both HOMO and LUMO, and indeed the gaps clearly show opposite trends. The molecular orbitals reported in Fig. 5 qualitatively match B_π data. Extra computational details about all these calculations are reported in Section S1 (ESI†).

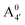Table 2 π-Bonding character parameter B_π(i), with respect to the C–C bond connecting the single and double rings for A⁺, , A⁰₇, 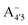and 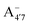of the frontier orbitals of C3G, as defined in eqn (1). The C–C bond order, calculated from the population analysis of natural bond orbitals,⁴⁵ is also shown. As expected, B_π(HOMO) mildly correlates with bond orders – both describing occupied levels

Frontier MO bonding characters Bπ(i) for C2–C1′
	A^+		A^07
HOMO	0.44	0.98	0.08	0.77	0.78
LUMO	0.67	0.37	0.65	0.45	0.45
Bond order	1.17	1.29	1.15	1.24	1.23

---

While the above reasoning explains the dependence of the gap on θ, the behavior of the different conformers within a given species is a consequence of several competing effects, including electronic conjugation, which favors a planar geometry of the chromophore, and glycosylation at position 3, which exerts a torque between the sugar and the ortho (2′ or 6′) hydrogen on the phenyl B ring.³⁵ Each molecular state displays a different degree of conjugation, as shown by the variation in bond orders in Table 2, so that the competition results in a different average value and distribution of θ. The details of such behavior are further discussed in the ESI† (Fig. S4), by explicitly defining other geometrical coordinates which can account for the fine details of the geometrical arrangement of the conjugated and glycosylic units. In addition to all the above, both the average and the spread in the distribution of θ are crucially affected by the solvent. The C₂ and C₃ conformers are characterized by the presence of an H-bonding chain with two water molecules connecting the hydroxyl at position 3′ with the sugar hydroxyls. The presence of these rather persistent water wires locks in the sugar configuration, thus tuning and locking the θ angle. This effect has been confirmed by comparing our explicit-solvent AIMD simulations with similar ones performed in vacuo, as shown in Fig. 7, where results for the C₂ and C₃ conformers are reported in blue and pink, respectively, as in Fig. 6. We notice that water has a restraining effect on α₆, whose values fluctuate more freely in vacuo, thus resulting in wider fluctuations for θ as well. Remarkably, the most likely values of α₆ differ in water and in vacuo. This reveals that water molecules shape the conformational landscape of each cyanin species by creating an ordered solvation shell around the hydrophilic moiety of C3G.

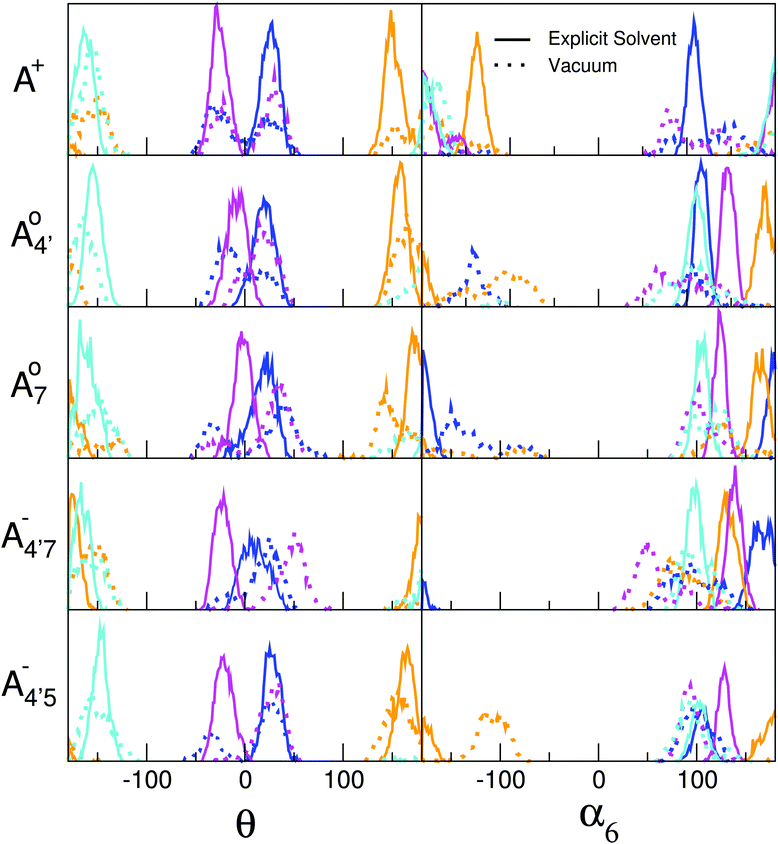Fig. 7 Comparison between the θ and α₆ dihedral-angle distributions resulting from AIMD simulations for C3G in explicit solvent (continuous lines) and in vacuo (dotted lines). The color code refers to different conformers as in Fig. 6. In particular, results for the C₂ and C₃ conformers are reported in blue and pink, respectively.

3.4 Generalization to other anthocyanins

In an attempt at generalizing the relationship between internal distortions and optical properties we have also considered two other anthocyanins, pelargonin and delphinin, which differ from C3G in the number of hydroxyl groups on the B ring. Geometry optimizations of reduced model systems, with constrained values of θ (relaxed scan), reveal that, independently of the charge state and of the protomeric form (Fig. 8), the calculated HL gaps show that delphinidin assumes the bluest nuance, followed by cyanidin and pelargonidin, in line with experimental findings^46,47 and theoretical investigations.¹² Consistently with cyanin, the sensitivity of the HL gap to the θ distortion is confirmed. Indeed, for the same arguments that hold for C3G, a decrease of the gap along with an increased internal distortion is again more pronounced in the neutral quinonoid form deprotonated at 4′ position, and damped when deprotonation occurs at positions 7 or 5. Trends on HL gaps quantitatively expressed above in term of B_π would also explain results reported in Fig. 8. Behaviours are slightly different in because of the already mentioned presence of a close-by second optical transition in the visible, with mixed contributions from (HOMO → LUMO) and (HOMO − 1 → LUMO).

Fig. 8 Trend of the HL gaps with respect to the θ dihedral angle, for a reduced model system of cyanin, pelargonin and delphinin. θ results to be a key internal degree of freedom for all charge states of investigated molecules.

4 Conclusions

In this work we provide the first systematic study of an anthocyanin, notably cyanidin-3-O-glucoside, over a wide (1–9) pH range. Our combination of computer simulations and photo-absorption experiments allow us to shed unprecedented light onto the molecular mechanisms of color expression in this family of natural dyes. Our results, in particular, highlight the prime and hitherto unrecognized role of internal molecular distortions and deprotonation pattern in determining the position of the frontier molecular states, which are in turn responsible for the color optical properties of the dye. The extent of internal distortions is markedly affected by the relative position of the sugar, which critically depends on the H-bond interactions with the water solvent. These findings could be key to guiding industrial efforts to identify natural non-toxic alternatives to some of the artificial colorants currently in use, according to their glycosylation and deprotonation patterns.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Enlightening discussions with Alessandro Laio in the first stages of this work are gratefully acknowledged. This work was supported in part by the European Union through the MaX Center of Excellence for supercomputing applications, grant no. 676598 and 824143, and the HEAD program of the European Social Fund, project no. 2014/2020-25/15, managed by the Italian FVG regional authority, and by Mars Chocolate North America LLC, under the Mars-SISSA collaboration agreement.

Notes and references

1. S. Lehto, M. Buchweitz, A. Klimm, R. Strassburger, C. Bechtold and F. Ulberth, Food Addit. Contam., Part A, 2017, 34, 335–355.
2. K. Yoshida, M. Mori and T. Kondo, Nat. Prod. Rep., 2009, 26(7), 884–915.
3. P. Trouillas, J. C. Sancho-García, V. De Freitas, J. Gierschner, M. Otyepka and O. Dangles, Chem. Rev., 2016, 116(9), 4937–4982.
4. A. Castañeda-Ovando, M. de Lourdes Pacheco-Hernández, M. E. Páez-Hernández, J. A. Rodríguez and C. A. Galán-Vidal, Food Chem., 2009, 113, 859–871.
5. G. T. Sigurdson and M. M. Giusti, J. Agric. Food Chem., 2014, 62(29), 6955–6965.
6. R. Brouillard, in Anthocyanins As Food Colors, ed. P. Markakis, Academic Press, 1982, pp. 1–40.
7. G. Sigurdson, R. Robbins, T. Collins and M. Giusti, Food Chem., 2017, 221, 1088–1095.
8. T. Goto and T. Kondo, Angew. Chem., Int. Ed., 1991, 30, 17–33.
9. X. Ge, I. Timrov, S. Binnie, A. Biancardi, A. Calzolari and S. Baroni, J. Phys. Chem. A, 2015, 119, 3816–3822.
10. I. Timrov, M. Micciarelli, M. Rosa, A. Calzolari and S. Baroni, J. Chem. Theory Comput., 2016, 12, 4423–4429.
11. I. Cacelli, A. Ferretti and G. Prampolini, Theor. Chem. Acc., 2016, 135, 156.
12. K. Sakata, N. Saito and T. Honda, Tetrahedron, 2006, 62, 3721–3731.
13. G. Rastelli, L. Costantino and A. Albasini, THEOCHEM, 1993, 279, 157–166.
14. G. K. Pereira, P. M. Donate and S. E. Galembeck, THEOCHEM, 1997, 392, 169–179.
15. K. Torskangerpoll, K. J. Børve, Ø. M. Andersen and L. J. Sæthre, Spectrochim. Acta, Part A, 1999, 55, 761–771.
16. V. Barone, A. Ferretti and I. Pino, Phys. Chem. Chem. Phys., 2012, 14, 16130–16137.
17. D. Jacquemin, E. A. Perpète, I. Ciofini and C. Adamo, Acc. Chem. Res., 2009, 42, 326–334.
18. C. Adamo and D. Jacquemin, Chem. Soc. Rev., 2013, 42, 845–856.
19. G. K. Pereira and S. E. Galembeck, Spectrochim. Acta, Part A, 1998, 54, 339–348.
20. D. Loco, S. Jurinovich, L. Cupellini, M. F. S. J. Menger and B. Mennucci, Photochem. Photobiol. Sci., 2018, 17, 552–560.
21. E. R. Kjellgren, J. M. Haugaard Olsen and J. Kongsted, J. Chem. Theory Comput., 2018, 14, 4309–4319.
22. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
23. D. Marx and J. Hutter, Ab initio molecular dynamics: basic theory and advanced methods, 2009.
24. E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000.
25. R. W. G. Hunt and M. R. Pointer, Measuring Colour, Wiley, Chichester, 2011.
26. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
27. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
28. U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145.
29. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
30. The notation X/Y Ry indicates a PW basis set up to a kinetic energy cutoff of X Ry for wave functions and Y Ry for charge densities and potentials.
31. G. Bussi, Mol. Phys., 2014, 112, 379–384.
32. M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972.
33. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926.
34. A. Rodriguez and A. Laio, Science, 2014, 344, 1492–1496.
35. F. Pina, M. J. Melo, C. A. T. Laia, A. J. Parola and J. C. Lima, Chem. Soc. Rev., 2012, 41, 869–908.
36. R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474.
37. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
38. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. D. Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, C. E. Kü, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
39. The Quantum ESPRESSO pseudopotential library, http://www.quantum-espresso.org/pseudopotentials, Ultrasoft pseudopotentials: C.pbe-rrkjus.UPF, O.pbe-rrkjus.UPF, H.pbe-rrkjus.UPF; Norm-conserving pseudopotentials: C.blyp-mt.UPF, O.blyp-mt.UPF, H.blyp-vbc.UPF.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
41. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
42. I. Timrov, O. Andreussi, A. Biancardi, N. Marzari and S. Baroni, J. Chem. Phys., 2015, 142, 034111.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian-09 Revision E.01, Gaussian Inc., Wallingford CT, 2009.
44. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
45. A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073.
46. F. Francis, in Anthocyanins As Food Colors, ed. P. Markakis, Academic Press, 1982, pp. 181–207.
47. S. Asen, R. Stewart and K. Norris, Phytochemistry, 1972, 11, 1139–1144.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp00747d

‡ Present address: Institut Rudjer Bošković, Division of Theoretical Physics, Bijenička 54, HR-10000, Croatia.

§ Present address: Dipartimento di Chimica, Università degli Studi di Milano, via C.Golgi 19, 20133 Milano, Italy.

¶ Present address: Dipartimenti di Scienze Chimiche, Università di Padova, Italy.

---