What accounts for the different functions in photolyases and cryptochromes: a computational study of proton transfers to FAD

Abstract

Photolyases (PL) and cryptochromes (CRY) are light-sensitive flavoproteins, respectively, involved in DNA repair and signal transduction. Their activation is triggered by an electron transfer process, which partially or fully reduces the photo-activated FAD cofactor. The full reduction additionally requires a proton transfer to the isoalloxazine ring. In plant CRY, an efficient proton transfer takes place within several μs, enabled by a conserved aspartate working as a proton donor, whereas in E. coli PL a proton transfer occurs in the 4 s timescale without any obvious proton donor, indicating the presence of a long-range proton transfer pathway. Unexpectedly, the insertion of an aspartate as a proton donor in a suitable position for proton transfer in E. coli PL does not initiate a transfer process similar to plant CRY, but even prevents the formation of a protonated FAD. In the present work, thanks to a combination of classical molecular dynamics and state-of-the-art DFTB3/MM simulations, we identify a proton transfer pathway from bulk to FAD in E. coli PL associated with a free energy profile in agreement with the experimental kinetics data. The free energy profiles of the proton transfer between aspartate and FAD show an inversion of the driving force between plant CRY and E. coli PL mutants. In the latter, the proton transfer from the aspartate is faster than in plant CRY but also thermodynamically disfavoured, in agreement with the experimental data. Our results further illustrate the fine tuning of the electrostatic FAD environment and the adaptability of the FAD pocket to ensure the divergent functions of the members of the PL-CRY family.

---

Introduction

Photolyases (PL) and cryptochromes (CRY) constitute a family of flavoproteins, the photolyase/cryptochrome family (PCF), which is present in all kingdoms of life ranging from bacteria to mammals. The structures of both PL and CRY exhibit highly conserved elements such as an electron transfer (ET) pathway consisting of three tryptophans, called the Trp-triad, and a non-covalently bound flavin adenine dinucleotide cofactor (FAD). The photo-reduction of FAD by a cascade of electron transfer reactions (ET) generates the active form of these proteins and enables their biological functions.^1,2

The major role of CRY is in the regulation of diverse biological responses as a signalling molecule. CRY contributes to the entrainment of the circadian rhythm,³ the space orientation by interaction with the Earth's magnetic field^1,2,4,5 (which was especially shown for the avian CRY4⁶), and the regulation of growth or flowering state in plants.^7,8 Therefore, the formation of a radical pair is required and is initiated by an ET reducing FAD_ox to FAD˙⁻. Additionally, further proton transfer (PT) reactions can form FADH˙ in the presence of proton donors. Hence, CRY offers a FAD pocket with an environment supporting FAD to switch between redox states.

The main task of PL is the repair of photo-induced DNA damages by a ET between the photo-activated FADH⁻ and the DNA lesion. Then, a backward ET occurs from the repaired thymines to the FADH˙ semiquinone to close the catalytic cycle. Consistently, the protonated FAD states (FADH˙ semiquinone or FADH⁻ hydroquinone) prevail in PL in vivo,¹ even though the oxidized FAD_ox and its full reduction are obtained in vitro.

This FAD pocket is conserved in most PCF proteins to a large extent,⁹ however, it is still supposed to offer different interaction patterns to enable the different functions. For instance, a FAD˙⁻ or FADH˙ radical needs to be formed in CRY while a FADH⁻ needs to be stabilized in PL. Accordingly, one specific amino acid in a position close to the N₅ of FAD differs between members of the PCF: in most plant CRY, e.g. CRY I from Arabidopsis thaliana (CRYI), an aspartate (Asp) is found in this position,^10,11 but a non-titratable residue is often present, such as a cysteine (Cys) in entomic CRY.¹² In CRY-DASH of a cyanobacterium,¹³ which shows a high similarity in structure and function to the PL, an asparagine (Asn) is found at this position. This homologous Asn is also present in PL, e.g. in PL from E. coli¹⁴ and A. nidulans.¹⁵ The impact of this amino acid has been studied by experimental site-directed mutagenesis, showing that it affects the behaviour of the proteins decisively: in CRYI, the Asp acts as a proton donor to form FADH˙ from a photo-reduced semiquinone FAD˙⁻, whereas a mutation of Asp into Cys, inspired by the entomic CRY, prevents FAD protonation.¹⁶ The mutation into Asn leads to the formation of FADH˙ despite the lack of an obvious proton donor such as Asp, which indicates the presence of an alternative PT pathway. Additionally, in the Asp to Asn mutant, a PL-like DNA repair activity was observed, which in fact requires the stabilization of FADH⁻.¹⁰ Conversely, the presence of Cys in entomic CRY, like in Drosophila melanogaster CRY, inhibits the protonation of FAD˙⁻.^17,18 In this CRY, the mutation of the Cys into Asp, albeit offering a suitable proton donor to FAD, does not lead to the formation of FADH˙.¹⁹ In contrast, a mutation of Cys into Asn leads to stabilization of protonated FADH˙, which does not affect the photoreceptor function.¹⁹

In E. coli and A. nidulans PL, like in the entomic CRY, the mutation of Asn into Asp does not enable a PT to form FADH˙.^20,21 After photo-reduction, the E. coli PL Asn to Asp mutant (PL-N378D) shows a slightly different UV-vis absorption spectrum compared to the spectrum for FAD˙⁻. It is characteristic of the presence of a different FAD state, called FAD^x, and the absence of FADH˙. It was hypothesized that this state indicates a strong hydrogen bond network between Asp and FAD N₅ or a short-lived FADH˙.²⁰ So, the presence of Asp blocks the stabilization of FADH˙ and furthermore inhibits any other PT pathway. Combined spectroscopic and computational studies on E. coli PL (WT-PL) showed that a strong hydrogen bond between FADH⁻ and Asn378 stabilizes the FADH⁻ state, which is essential for the repair activity.^22,23 Further experimental studies investigated the replacement of Asn by Ser in the E. coli PL and a drop of the in vitro DNA repair activity from 50% for WT to less than 1% is observed.²⁴ This underlines the dominant role of Asn in DNA repair, likely by stabilizing the FADH˙ and FADH⁻ states over other redox states.

In summary, the reported observations highlight the fine tuning of the structure of the FAD pocket to stabilize the active form of the protein.²⁵ It appears that the nature of the residue interacting with FAD N₅, which may be Asp, Asn or Cys, is strongly related to the most relevant FAD protonation state in WT, and thus to the biological role of the respective protein. However, a mutation of this residue does not necessarily result in a functional conversion of the mutants. It appears that other structural or dynamical parameters, like the formation of a PT pathway, can influence the protonation/redox state of FAD.

To explore these other parameters, Müller et al. studied the protonation of FAD in WT-PL in vitro by preparing a protein which contained FAD in its fully oxidized state, FAD_ox. The timescale of the ET to form FAD˙⁻ was below 300 ps, and that of the subsequent PT was 4 s (see the mechanism in Fig. 1).²⁰ Since Asn cannot protonate FAD directly, a pathway has to exist, which seems to not involve other acidic residues in the FAD pocket.¹³ Damiani et al. suggested that water molecules can enter the FAD pocket and form a PT pathway from the bulk water to FAD.²¹ The formation of the FAD^x state occurs in 3.3 μs in PL-N378D. Compared to this, spectroscopic studies in CRYI show that the photo-reduction of FAD_ox occurs within 31 ps, the subsequent PT from Asp396 to FAD˙⁻ occurs in 1.7 μs, while the backward transfer is two orders of magnitude slower (690 μs).^26,27 So, the CRYI pocket allows a faster switch between protonated and deprotonated FAD than the PL pocket.

Fig. 1 Comparison of the FAD˙⁻ protonation in E. coli PL-WT, N378 mutant of PL and CRYI. The nature of the proton donor is given wherever identified; otherwise B stands for a generic proton donor. The FAD binding pocket of PL-N378D and CRYI is shown with amino acids colored in white (non-polar), green (polar) and red/blue (acidic/basic). The isoalloxazine ring of FAD and the side chains of Asp378/396 and Glu363 or Met381 are displayed explicitly. Purple dashed lines indicate hydrogen bonds between N₅ of FAD and Asp378/396. Pictures of all the proteins are obtained using VMD.³²

Computational chemistry methods provide a consistent and comparatively cheap approach to investigate the effect of differences at a molecular level between the FAD pockets from CRYI, PL-WT and mutants. In our previous study,²⁸ we computed rate constants for both ET^29–31 and PT²⁸ processes in CRYI in agreement with the experimental results. The aim of the current study is to resolve the mechanism and energetics of the PT processes taking place in PL-WT and PL-N378D, and compare to those in CRYI (see Fig. 1). The combination of QM/MM free energy calculations of the PT and classical MD simulations provide a complete picture of the interplay between the FAD protonation and the structural and dynamical behaviour of the FAD binding pocket.

Methods

Molecular dynamics simulations

The starting structures for MD simulations were adapted from the X-ray crystal structures of E. coli PL (PDB ID 1DNP)³³ and CRY I At. (PDB ID 1U3D)³⁴ by Deisenhofer and coworkers. The protonation states of relevant amino-acid side chains were established on the basis of pK_a calculations performed with PROPKA3.1.^35,36 Since no crystal structure of the N378D mutant of E. coli PL is available, a starting structure of the mutant was created by modifying the WT-PL structure.

For PL-N378D, two different starting structures were created containing different protonation states of Glu363. This residue has a calculated pK_a value of 6 (according to PROPKA3.1 results), which suggests the coexistence of both the protonated and the deprotonated states at physiological pH. The Glu363 side chain can interact with the carboxyl group of Asp378 and the surrounding solvent molecules. Hence, different interaction patterns with the carboxyl group of Asp378 would result from these states: a protonated Glu363 is able to form a strong hydrogen bond with negatively charged Asp378, and a weaker one with neutral Asp378; a deprotonated Glu363, however, leads to the destabilization of the deprotonated Asp378 by electrostatic repulsion. In the PL-WT simulations, this residue is deprotonated.

All of the simulations were performed with the AMBER-SB99-ILDN force field^37,38 using GROMACS 5.0.4.^39,40 The cofactors FAD and MTHF were parameterized with the xLeap module of AmberTools⁴¹ employing the general Amber force field (GAFF).^37,42 The atomic charges of FAD, FAD˙⁻ and FADH˙ were fitted on the electrostatic potential (RESP)^43,44 obtained at the HF/6-31G*^45,46 level of theory with GAUSSIAN09.⁴⁷ The protein was placed in a periodic box sized 96 × 94 × 121 A³ for WT-PL and PL-N378D and 98 × 98 × 98 ų for CRYI. The box was filled with TIP3P water molecules to obtain a density of 1000 kg m⁻³, and an appropriate number of water molecules were substituted by sodium ions to achieve electroneutrality; no extra salt was added. These systems were equilibrated by means of a protocol consisting of a series of energy minimization, NVT (1 ns) and NPT (1 ns), simulations. The eventual production simulations used the Nosé–Hoover thermostat⁴⁸ and the Parrinello–Rahman barostat⁴⁹ to maintain a temperature of 300 K and a pressure of 1 bar, respectively. The simulations employed a leap-frog integrator with a time step of 2 fs. We performed MD simulations containing FAD_ox (100 ns) for the PL-WT, PL-N378D and CRYI. Then, we used the final geometry from these simulations to start 50 ns MD simulations for PL-N378D and CRYI containing FAD˙⁻. Suitable conformations for PT are obtained in a few ns, but we extended these simulations to 200 ns to check the stability of the different interactions. For PL-WT, in order to explore the various structural consequences of FAD photo-reduction, 10 snapshots were extracted from the first simulation with FAD_ox. They were used as the starting points for 50 ns MD simulations with FAD˙⁻. Here, a number of parallel runs are preferred to a single longer simulation because we had no preliminary idea about the PT pathway and we wanted to decrease the probability to sample a system trapped in a deep well where no PT pathway can be formed.

Classical free energy simulations of the rotation of the N378 side chain in PL-WT

The free energies of rotation along the dihedral angle χ ≡ N_δ–C_γ–C_β–C_α of the N378 side chain were obtained with classical well-tempered metadynamics simulations,^50,51 extended to 50 ns using GROMACS interfaced with the Plumed 2.0.1 software,^52,53 which was also used for all the following metadynamics or umbrella sampling (US) simulations. Gaussian-shaped hills of width σ = 20° were added every 500 ps; their initial height was 0.29 kcal mol⁻¹, and the bias factor was 6.

Classical free energy simulations of the formation of a water wire in PL-WT

The free energy profiles of the penetration of water molecules into the FAD binding pocket of PL-WT were generated with classical US simulations. The reaction coordinate for the entrance of the first water molecule was the distance between the centre of mass of the N₅ and O₄ atoms of FAD and the centre of mass of a selected water molecule, originally located in the bulk. The interval of 6.5 Å between the two water molecules was divided into 29 windows. Harmonic biasing potentials with a force constant of 23.9 kcal mol⁻¹ Å⁻² were applied, and each window was simulated for 50 ns. Free energy was obtained applying the weighted histogram analysis method (WHAM).^54,55

QM/MM simulations of proton transfer

Proton transfer reactions were simulated with the quantum chemistry-molecular mechanics (QM/MM) approach employing the third-order tight-binding density functional theory (DFTB3) for the QM part.⁵⁶ In general, DFTB underestimates the barrier for PT because its parameterization is based on a GGA PBE functional.⁵⁷ Nevertheless, DFTB3/3OB⁵⁸ provides a good description of proton affinities, which are relevant for the simulation of PT reactions, as well as PT barriers. The QM/MM simulations were performed with our recent QM/MM implementation of DFTB3 in Gromacs combined with Plumed.⁵⁹ QM/MM boundaries are treated with hydrogen link-atoms.

In PL-WT, the free energy profile of the PT reaction along the water wire in the protein pocket was obtained with an US-DFTB3/MM simulation. The QM region consisted of the isoalloxazine ring of FAD (the D-ribitol tail is replaced by a methyl group), the side chain of Glu106 and five water molecules. The reaction coordinate for the long-range PT in PL-WT involves the N₅ of FAD˙⁻, the atoms of the water wire and the external proton donor, so we used the modified centre of excess charge (mCEC) by König et al.:⁶⁰

here r^H_i are the coordinates of all of the hydrogen atoms possibly taking part in the PT process; r^X_j are the coordinates of the proton acceptors – donors, final acceptors as well as all of the relays, and w^X_j are the numbers of protons bound to each acceptor in the least protonated state (e.g., w = 2 for a water molecule). The last term is a correction of coordinate, which runs over all of the hydrogen atoms and the proton acceptors and it involves a switching function f_sw(d^H_i,X_j) to decide whether each couple of atoms is connected:where r_sw = 1.25 Å and d_sw = 0.04 Å. The coordinate ξ is a vector quantity that expresses the position of the proton being transferred. A scalar reaction coordinate ζ is obtained from ξ aswhere d_ξ,D and d_ξ,A are the distances from the point ξ to the initial proton donor and to the final proton acceptor, respectively. With such a collective variable, the PT reaction proceeds from ζ = 0 for the reactant to ζ = 1 for the product. The distance between the proton acceptor and donor was divided into 57 windows. Harmonic biasing potentials with a force constant of 239 kcal mol⁻¹ Å⁻² were applied, and each simulation was extended to 300 ps with a timestep of 0.5 fs.

In PL-N378D, the free energy profile of the PT reaction between N₅ of FAD and Asp378 was also obtained with a DFTB3/MM using an umbrella sampling approach. The QM region contained the side chain of Asp378 and the isoalloxazine core of FAD. The reaction coordinate for the PT involves the antisymmetric linear combination of the H–O distance of Asp378 and the H–N₅ distance of FAD˙⁻, d_O–H–N. These simulations were performed for the three protein variants involving a protonated Glu363, a deprotonated Glu363 or a methionine in position 363. Harmonic biasing potentials with a force constant of 239 kcal mol⁻¹ Å⁻² were applied, and the simulation at 300 K of each of the 20 windows was extended to 300 ps with a timestep of 0.5 fs. The free energy profile of the PT in CRYI is taken out from a previous study,²⁸ in which the distance between the proton and the N₅ of FAD, d_H–N, was considered as a reaction coordinate.

Rate constants were estimated from the energy barrier heights in the free energy profiles by applying the transition state theory, using the relation⁶¹

where T is the temperature, ΔG^‡ is the barrier height, and k_b and h are Boltzmann's and Planck's constants, respectively. The attempt frequency ν of the transition was estimated aswith k_H–N ≈ 537 kcal mol⁻¹ Ų being the harmonic force constant of the N₅–H bond in the Amber force field and m_H being the mass of a hydrogen atom.

Calculation of Coulomb energy in PL-N378D and CRYI

The GROMACS tool gmx energy was used to evaluate the electrostatic interactions between the groups of atoms defined as follows: the side chain of Asp378, isoalloxazine ring of FAD, solvent and protein (excluding the side chain of Asp378). The classical electrostatic interactions between each pair of groups of atoms were calculated using a cut-off radius of 10 Å along the last 20 ns of the MD trajectories for each protein in the FAD˙⁻ state. Snapshots were extracted every 2 ns to generate 10 starting structures for individual MD simulations containing FADH˙ and deprotonated Asp378/396. Taken together, this leads to a trajectory of an accumulated length of 20 ns, which reflects the immediate structural response of the binding pocket upon the formation of the PT product. We used the structures from the individual trajectories to calculate the corresponding Coulomb energies, E_Coul, between the Asp–FAD complex and the environment. The averaged E_Coul energy of each protonation state is compared according to eqn (6).

ΔE_Coul = E_Coul([ASP⁻–FADH˙]) − E_Coul([ASPH–FAD˙⁻]) (6)

Results

Structural changes after FAD_ox photo-reduction

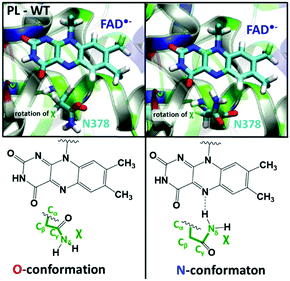
We performed 10 independent 50 ns MD simulations to assess the relaxation of the E. coli PL structure in response to the photo-induced reduction of FAD, starting from several snapshots taken from an MD trajectory containing FAD_ox. The FAD˙⁻ state is represented by means of modified atomic charges on the isoalloxazine ring. In the presence of FAD_ox, the side chain oxygen of Asn378 points towards N₅ of FAD, as illustrated in the so-called O-conformation in Fig. 2. In this conformation, the Asn378 side chain amino group can interact with the Glu363 carboxyl group and several water molecules. In 9 out of 10 simulations with FAD˙⁻, significant structural rearrangements are observed in the area enclosed by FAD, Asn378 and a loop close to the heterocycle of the isoalloxazine ring. These are:

Fig. 2 The different conformations of Asn378 and its closest protein environment. The dihedral angle χ is formed by N_δ, C_γ, C_β and C_α of Asn378. Left: O-conformation: χ = 240°, and the amido oxygen atom of Asn378 forms a hydrogen bond with the protonated FADH˙^/−. Right: N-conformation: χ = 90°, and the amino group of Asn is rotated close to FAD N₅, forming a hydrogen bond.

• The rotation of the Asn378 side chain to face FAD-N₅: in the initial state, the keto group faces N₅, after a rotation of the amino group of Asn (7 occurrences). In this conformation, mentioned as the N-conformation in Fig. 2, no interaction is observed between Asn378 and Glu363. No reverse rotation was observed (more details are provided in Fig. S1 in the ESI†).

• A flow of water molecules into the FAD pocket, also facing the FAD N₅ atom (2 occurrences) while Asn378 stays in the O-conformation (see also Fig. S2 in the ESI†).

In the remaining MD simulation, Asn378 stays in the O-conformation but no water comes into the pocket.

Analogous MD simulations were carried out for PL-N378D and CRYI in the FAD_ox state and then 200 ns MD simulations were carried out in the FAD˙⁻ state. During the MD simulations with FAD_ox, the protonated Asp378/396 backbone carbonyl oxygen faces FAD N5, which prevents any proton transfer. After the switch from FAD_ox to FAD˙⁻, the Asp residue rotates within a few nano-seconds in both proteins: the protonated side chain now faces the O₄ or N₅ of FAD and forms a hydrogen bond (see the ESI,† Fig. S3). This conformation is a prerequisite for a potential PT to FAD˙⁻. The distance between FAD N₅ and the proton of Asp378/396 was measured along the MD trajectories of both PL-N378D and CRYI, as were the distances between FAD and several neighbouring amino acid side chains (shown in Table S1, ESI†).

FAD protonation in E. coli PL-WT

Starting from the structural information obtained with the free MD simulations, we performed various biased sampling simulations to characterize the different steps of the protonation in E. coli PL-WT. Our results are summarized in Fig. 3.

Fig. 3 The different steps for the reduction of FAD_ox to FADH˙ in E. coli PL-WT and their characteristic times obtained from experiments (in black) or computation (red).

Rotation of the Asn378 side chain versus the FAD redox state

The free energy profile of the side chain rotation around the C_β–C_γ bond was quantified by means of metadynamics simulations using the torsion angle N_δ–C_γ–C_β–C_α as the reaction coordinate and considering four different FAD states (FAD_ox, FAD˙⁻, FADH˙ and FADH⁻). The corresponding free energy profiles are given in Fig. 4. FAD_ox, FADH˙ and FADH⁻ favour the O-conformation by 4–5 kcal mol⁻¹. Only the FAD˙⁻ state shows a global minimum at the N-conformation, while the O-conformation is around 3 kcal mol⁻¹ higher and separated by a barrier of 6 kcal mol⁻¹ (for more details, see Table S2, ESI†). The N-conformation can impede the contact between a proton donor (such as a water molecule) and FAD N5, so we consider this rotation of the Asn378 side chain in competition with the formation of a water wire, which was observed in the O-conformation (as described in Fig. 3).

Fig. 4 Free energy profile of the rotation of the side chain of Asn378. The different forms of PL-WT containing FAD_ox (blue), FAD˙⁻ (green), FADH˙ (black) and FADH⁻ (red) were considered. The reaction coordinate χ corresponds to the torsion angle N_δ–C_γ–C_β–C_α; 90° corresponds to the N-conformation, while the O-conformation is found at 240°.

The formation of a water wire

In three of the unbiased MD simulations reported above, Asn378 remains in the O-conformation. In one of these simulations, two water molecules (only one or zero in the other simulations) entered the FAD pocket and engaged in a hydrogen bond network which connects FAD N₅ with the bulk. At the beginning of this simulation, both water molecules are in the bulk solvent, quite far from FAD. After 2.5 ns, one of them enters the pocket and interacts with FAD N₅ (Fig. S2 in ESI†). After 10 ns, the other water molecule also enters, and both of them stay between FAD N₅ and the side chain oxygen of Asn378 for 2.5 ns. Then, the first water molecule is released, and the second water molecule stays in the FAD pocket for the entire remaining simulation time. The entrance of water molecules into the FAD pocket proceeds through a flexible loop composed of Met367 and Leu376. There are multiple other water molecules located in front of the loop which allow the formation of a water wire connecting FAD˙⁻ with the bulk.

To better characterise the kinetics of this event, free energy profiles were computed for the water molecules entering the FAD pocket. We used classical force field simulations in combination with US. To reduce the complexity of the possible reorientations in the pocket, we focused on the free energy barrier for the entrance of two water molecules: (I) the reaction coordinate for the entrance of the first water molecule is the distance of this water molecule from FAD; (II) the reaction coordinate for the second water molecule is the distance of this water molecule from the first water molecule. The resulting free energy profiles are shown in Fig. 5(I) and (II).

Fig. 5 Free energy profiles of the entrance of water molecules into the FAD pocket. I: First molecule enters the FAD pocket. II: An additional water molecule moves into the flexible loop to approach the water molecule already present in the pocket. Reaction coordinates are the distances between FAD and the water molecule (I) and the distance between the first water and the second water molecule (II).

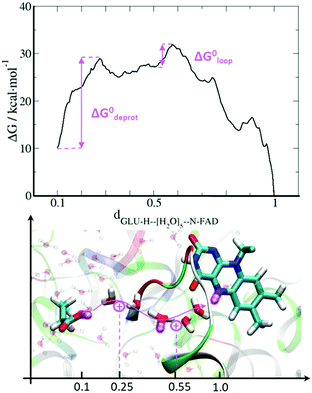
The first water molecule has to overcome a rather low barrier of 3.5 kcal mol⁻¹ corresponding to a rate of k_trans ≈ 18 ns⁻¹, finding a stable minimum in the binding pocket. The second water molecule has to overcome a similar barrier but the final state is not thermodynamically stable, indicating that the formation of this water wire is a transient process. These two water molecules form a path connecting FAD N₅ with a potential proton donor outside the FAD pocket. Inspection of the structure identifies Glu106 as the closest titratable amino acid (Fig. 6). QM/MM US simulations were performed, considering the Glu106 side chain, FAD˙⁻ and the five water molecules as possible proton carriers in the QM region. Since the formation of the water wire is a transient phenomenon, we had to constrain the water position in order to compute the free energy profile for PT from Glu106 to FAD. The resulting free energy profile is shown in Fig. 6.

Fig. 6 Long range PT in PL-WT. Top: Free energy of PT along the water wire. Bottom: View of the PT pathway (purple) between the Glu106 side chain (at 0.1), via water molecules (in the centre), and FAD (at 1.0).

The first barrier of 19 kcal mol⁻¹ is associated with the proton transfer from Glu106 to the water wire. The transfer of the proton to the first water molecule carries an energy penalty of 12.5 kcal mol⁻¹, while moving the proton further to the second water molecule after crossing the first barrier leads to the first stable local minimum. The second step starts with a PT proceeding along the water wire and through the loop, from the third to the fourth water molecule, over another barrier of 7 kcal mol⁻¹. The transfer to the fifth water molecule and then to the N₅ atom of FAD is a downhill process resulting in a product state 10 kcal mol⁻¹ below the reactant state. If we consider a pK_a of 4.2 for Glu106 (pK_a of glutamic acid in solution), this driving force value gives an estimation for the FAD˙⁻ pK_a around 11.5. The rate limiting step is the deprotonation of the donor with a rate constant of 0.13 s⁻¹, which is in agreement with the experimental data.^18,20

FAD protonation in PL-N378D and CRYI

We had previously obtained the free energy profile for the FAD protonation in CRYI.²⁸ To make a comparison possible, we have generated the free energy landscape of the same mechanism in PL-N378D. The now available experimental and computational results for these two proteins are summarised in Fig. 7.

Fig. 7 The individual steps of the FAD protonation by an aspartate in PL-N378D and CRYI and their experimental (black) or computational (red) time constants.

Free energy landscape reveals an endergonic PT in PL-N378D

To study the PT energetics, we computed the one-dimensional free energy landscape of the PT in PL-N378D and compared it to previous results from CRYI (Fig. 8).²⁸ The corresponding reaction and activation free enthalpy values are listed in Table 1. We considered here protonated Glu363 in PL-N378D because it showed the smallest ΔG⁰ for the PT (see the free energy profile of deprotonated Glu363 in the ESI†). The three states labelled I, II and III refer respectively to the reactants with the proton on aspartic acid, the transition state (TS) and the products with the proton on FADH˙. An important difference between the two proteins is clearly apparent in the Gibbs free energy of the PT: while state III (protonated FADH˙) is the global minimum in CRYI with a driving force of 1.4 kcal mol⁻¹ (which corresponds to a more acidic aspartate by the 1 pK_a unit compared to FAD˙⁻), state I (protonated Asp) is favoured in PL-N378D with a driving force of 2.0 kcal mol⁻¹ (so a more acidic FAD˙⁻ than Asp378, by the 1.5 pK_a unit). Therefore, PT is an endergonic reaction in PL-N378D but exothermic in CRYI. Moreover, CRYI shows slow rate constants of 0.02 ns⁻¹ and 0.002 ns⁻¹ for the forward and backward PT respectively.

Fig. 8 Free energy landscape of proton transfer in PL-N378D and in CRYI. The different states are numbered: I reactants, II transition states, and III products. The reaction energies, ΔG⁰, and the barrier heights, ΔG^≠, are indicated by arrows.

Table 1 The free energies and rate constants calculated from the biased QM/MM umbrella sampling of PT in PL-N378D and in CRYI

			PL-N378D	CRYI
ΔG^≠I.→III.	(GII.–GI.)	[kcal mol^−1]	4.9	7.5
ΔG^≠III.→I.	(GII.–GIII.)	[kcal mol^−1]	2.9	8.9
ΔG^0	(GIII.–GI.)	[kcal mol^−1]	2.0	−1.4
ΔG^0PL − ΔG^0CRY		[kcal mol^−1]	3.4
k I.→III.		[ns^−1]	1.6	0.02
k III.→I.		[ns^−1]	47	0.002

---

Our free-energy landscape favouring FADH˙ in CRYI is consistent with the experimentally well-defined FADH˙ spectrum. For PL-N378D, the reported measured spectrum was associated with a state called FAD^x, which mostly overlaps with the FAD˙⁻ spectrum.²⁰ This is in line with the free-energy profile, highlighting an energetically favoured FAD˙⁻ state. Nevertheless, the activation energy for the forward and backward PT is only 4.9 kcal mol⁻¹ and 2.9 kcal mol⁻¹, respectively, which corresponds to rate constants of 1.6 ns⁻¹ and 47 ns⁻¹. So, PT is feasible during the recording time of the spectra, and a weighted superposition of both species may lead to a particular form of the absorption spectrum.

Analysis of the Coulomb interactions between FAD and the pocket

Since the considered PT involves a partial transfer of a negative charge from the large isoalloxazine ring to a small carboxyl group, the electrostatic interactions between the environment and the active site may play an important role in stabilizing the protonation states. To quantify these effects, the electrostatic interaction energies E_coul between the PT complex (isoalloxazine ring and Asp378/396) and the protein or the solvent were calculated for the FADH˙ and the FAD˙⁻ state (see Table S3, ESI†). The difference ΔE_coul between the product and reactant states illustrates the contributions of the individual interactions to the stabilisation of the PT product or the PT reactant.

In CRYI, the FADH˙–Asp378⁻ product is slightly favoured (the sum of ΔE_coul = −3.9 kcal mol⁻¹), while there is no significant preference for either state in PL-N378D (sum of ΔE_coul = +0.6 kcal mol⁻¹). It is interesting to see that the total difference in electrostatic energy of 4.5 kcal mol⁻¹ roughly resembles the difference in the reaction energy shown in Table 1. The analysis of the different contributions (see Table S3, ESI†) shows that the major difference between the proteins is in the interaction between Asp and the environment, while the FAD experiences a similar electrostatic potential.

To obtain further insight, we computed the contributions of the individual amino acid residues to ΔE_coul, visualized in the colouring scheme of Fig. 9 (see also Fig. S4 in the ESI†). The analysis shows three major factors being responsible for the energy difference: the different position of arginine 344/362 close to FAD, the interaction between Asp378 and Glu363 and a different interaction with water molecules.

Fig. 9 Structural view of the FAD binding pocket in CRYI and PL-N378D. Amino acids are coloured in blue, grey and red corresponding to negative, neutral and positive ΔE, respectively. The side chains of all residues with |ΔE_Coul| > 0.25 kcal mol⁻¹ are represented by sticks. Close water molecules are also included and coloured corresponding to the averaged interaction with FAD and Asp378/396 which is −5.58 in CRYI and +7.51 kcal mol⁻¹ in PL-N378D.

No positive value of ΔE_coul larger than +0.3 kcal mol⁻¹, and therefore disfavouring the FADH˙ state, was observed in CRYI. In contrast, in PL-N378D, several positive contributions stand out: +0.3, +0.4 and +2.9 kcal mol⁻¹ for Leu375, Gly381 and Arg344, respectively. Thus, Arg344 (Arg362 in CRYI) interacts differently in PT PL-N378D: while it supports PT in CRYI (−1.74 kcal mol⁻¹), it disfavours it in the PL mutant. The distance between Arg and FAD is on average shorter in PL-N378D (see the ESI,† Table S1), which could explain part of the preference for the negatively charged FAD˙⁻ state.

Furthermore, in PL-N378D, Glu363 is strongly hydrogen-bonded to the negatively charged Asp378 (ΔE_coul = −10.32 kcal mol⁻¹), while in CRYI, the homologous Met381 just slightly interacts with the FAD-Asp complex (ΔE_coul = −1.05 kcal mol⁻¹). At first sight it may seem that this residue is not a good choice for stabilization of FADH˙. However, Met381 shows flexibility allowing water molecules to approach Asp396 resulting in a stabilizing interaction of −5.58 kcal mol⁻¹ with negatively charged Asp. In contrast, the interaction with water molecules is positive (7.51 kcal mol⁻¹) in the PL mutant, destabilizing the product state. We investigated the PL-N378D/E363M double mutant (see Fig. S5 in ESI†); however, no improved stabilization of the PT product was observed.

We also quantified the stabilization of FADH⁻ induced by the pocket after the second photo-reduction. To this end, we calculated the energy of the HOMO of FADH˙⁻ in WT-PL, PL-N378D and CRYI (further details are provided in the ESI†) during a short DFTB/MM calculation. The pocket of PL-WT induces a decrease of the orbital energy of 1.48 eV, i.e. 0.69 eV more than in CRYI (see Fig. S6 in the ESI†).

Discussion

Vital for the function or re-activation of photolyases and cryptochromes, the FAD cofactor takes different redox and protonation states in the different proteins. So, the function of CRYI probably requires the formation of a stable radical pair FAD˙⁻–Trp˙⁺ or FADH˙–Trp˙, which only returns to the resting state FAD_ox on a time scale of seconds. Also here, the de/protonation of FAD is facilitated by a nearby aspartate. In contrast, the biological function of PL requires an FADH⁻ state to repair the DNA damages. The FAD states in PL fluctuate between FADH* and FADH⁻, and there is no proton transfer in the physiological processes in which PL participates. Consequently, the formation and the stabilization of the different FAD redox states in the CRYI or PL play a crucial role in their function.

The protonation of the isoalloxazine ring occurs after its photo-reduction by means of a complex ET through a tryptophan triad. This first step occurs on a subnanosecond timescale, whereas the protonation step is at least four orders of magnitude slower: about 1.7 μs and 4 s in plant CRYI and E. coli PL respectively. Such a timescale difference and the experimental characterization of FAD˙⁻ exclude a coupled electron-proton transfer mechanism (PCET). The environment has time to relax around FAD˙⁻ after the fast photo-reduction. According to our MD simulations, the photo-reduction can lead to some structural rearrangements which consist of prerequisites to PT: the rotation of the PL-Asn378 or the CRYI-Asp396 side chain (close to FAD N5) or the entry of water molecules in the PL FAD pocket. Such observations corroborate the two step formation of the protonated semiquinone FADH˙: the photo-reduction triggers the conformational changes required for a PT, independently of the pH, and then, the basic FAD˙⁻ is protonated.

We first identify a pathway to de/protonate FAD in E. coli PL, and then determine the energetics along this pathway. Unlike CRYI, PL has no close titratable residue that might provide a proton, so a more distant proton donor has to be sought, as has a proton transfer pathway connecting that donor to FAD. Free MD simulations and free energy calculations reveal that the Asn378 side chain plays an important role: its N-orientation is preferred with FAD˙⁻, and it does not allow for any protonation pathway to be formed, whereas the O-conformation is preferred in other states.⁶² Indeed, the N-conformation may be disfavoured by the steric hindrance between H–N₅ of protonated FAD and the Asn378 side chain. Still, Asn378 may remain in the O-conformation for a certain time period after FAD˙⁻ is formed, and we describe how a PT pathway can arise then: two water molecules may enter the FAD binding pocket at a moderate energy cost and these are sufficient to relay a proton from a proton donor like, e.g., the Glu106 side chain, or another external donor. The PT reaction along this pathway is even energetically favourable, meaning that the protonated FADH˙ is stabilized, with a strong basic character (pK_a evaluated at 11.5). Asn378 can contribute to the stabilization of protonated FAD in PL by the formation of a hydrogen bond between the amido oxygen of Asn378 (in the O-conformation) and N₅–H of FADH˙ and FADH⁻ states, as reported before.⁶²

In contrast, in CRYI, Asp396 works as a prolific proton relay and allows switching between protonated and deprotonated semiquinone FAD.²⁸ In addition, we suppose that this residue, in its negative form, impairs the formation of a fully reduced FADH⁻. As expected, the presence of a close negatively charged Asp disfavours the second reduction of FAD compared to a neutral Asn. Then, we like to investigate whether Asp396/Asn378 is really the one residue that is the key to the different de/protonation mechanisms of CRY and PL. To answer this question and mimic previous experiments,²⁰ we study the PL-N378D mutant, which unexpectedly disables the FAD protonation. Reversely, the single point mutation in CRYI-D396N stabilizes protonated FAD states and is able to repair DNA lesions.¹⁰

In contrast to our previous result in CRYI, the free energy profile of PT in the PL-N378D mutant shows that the deprotonated FAD˙⁻ is favoured over FADH˙, in spite of the presence of the proton donor Asp378. The barrier opposing PT is quite low, allowing fast proton exchanges between the isoalloxazine ring and Asp. This result is consistent with the experimental multi-component UV-vis spectrum called FAD_x. The entirely different energetics of PT between CRYI and PL-N378D must have structural causes. A possible explanation comes to light as soon as the electrostatic potentials induced by the protein surroundings are analysed: the combined electrostatic effect of close amino acid residues and water molecules clearly favours the FADH˙–Asp378⁻ state in CRYI, while it slightly stabilizes the reverse state in the PL mutant. Furthermore, a higher flexibility around FAD is observed in our MD simulations of CRYI, in agreement with previous experimental results.^63,64

In the overall picture, it seems that the different protonation propensities of PL and CRYI are caused by multiple effects, based on both structural and dynamical contributions, with a large role played by water molecules transiently present around the FAD pocket. Despite the evident difference between the impacts of Asp and Asn on the favoured FAD redox state, a straightforward substitution of one or two isolated amino acids cannot modify PL to create the PT ability of CRYI in PL.

Conclusions

The different functions of photolyases and cryptochromes are directly linked to the appearance of different FAD oxidation and protonation states. Therefore, an interesting question to be addressed is how these states are stabilized by the respective protein environments. Our computational results underline the strong structure–function relationship around FAD protonation in the PCF: the presence of Asn strongly stabilizes the protonated FAD, highlighted by our exothermic PT in PL-WT, whereas in CRYI, Asp396 ensures fast protonation and deprotonation of FAD during the photocycle,²⁶ and disfavours the photo-reduction of FADH˙. Our simulations highlight the role of dynamic interactions between Asp396 and water molecules in the formation and stabilization of deprotonated aspartate and thus protonated FADH˙ in CRYI. Such interactions are absent in PL-N378D. During the evolution in the PCF family, both the presence of Asp instead of Asn and the gain in flexibility have allowed the switch between FAD redox states, as is required for plant CRY functions. One “drawback” is the inhibition of the second FAD photo-reduction and, consequently, the loss of the DNA repair ability.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

N. Gillet thanks the Alexander von Humboldt Foundation for funding. Computational resources were provided by the state of Baden-Württemberg through bwHPC.

References

1. I. Chaves, R. Pokorny, M. Byrdin, N. Hoang, T. Ritz, K. Brettel, L. O. Essen, G. T. J. van der Horst, A. Batschauer and M. Ahmad, Annu. Rev. Plant Biol., 2011, 62, 335–364.
2. A. Sancar, Chem. Rev., 2003, 103, 2203–2238.
3. P. Emery, W. V. So, M. Kaneko, J. C. Hall and M. Rosbash, Cell, 1998, 95, 669–679.
4. W. Wiltschko, Ethology, 1968, 25, 537–558.
5. H. Mouritsen, U. Janssen-Bienhold, M. Liedvogel, G. Feenders, J. Stalleicken, P. Dirks and R. Weiler, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14294–14299.
6. A. Günther, A. Einwich, E. Sjulstok, R. Feederle, P. Bolte, K.-W. Koch, I. A. Solov’yov and H. Mouritsen, Curr. Biol., 2018, 28, 211–223.
7. M. Chen, J. Chory and C. Fankhauser, Annu. Rev. Genet., 2004, 38, 87–117.
8. C. Lin, Plant Cell, 2002, 14, S207–S225.
9. J. Wang, X. Du, W. Pan, X. Wang and W. Wu, J. Photochem. Photobiol., C, 2015, 22, 84–102.
10. S. Burney, R. Wenzel, T. Kottke, T. Roussel, N. Hoang, J. Bouly, R. Bittl, J. Heberle and M. Ahmad, Angew. Chem., Int. Ed., 2012, 51, 9356–9360.
11. E. N. Worthington, İ. H. Kavakli, G. Berrocal-Tito, B. E. Bondo and A. Sancar, J. Biol. Chem., 2003, 278, 39143–39154.
12. H. Zhu, Q. Yuan, O. Froy, A. Casselman and S. M. Reppert, Curr. Biol., 2005, 15, R953–R954.
13. T. Iwata, Y. Zhang, K. Hitomi, E. D. Getzoff and H. Kandori, Biochemistry, 2010, 49, 8882–8891.
14. H. W. Park, S. T. Kim, A. Sancar and J. Deisenhofer, Science, 1995, 268, 1866–1872.
15. A. Mees, T. Klar, P. Gnau, U. Hennecke, A. P. M. Eker, T. Carell and L.-O. Essen, Science, 2004, 306, 1789–1793.
16. A. Hense, E. Herman, S. Oldemeyer and T. Kottke, J. Biol. Chem., 2015, 290, 1743–1751.
17. A. Berndt, T. Kottke, H. Breitkreuz, R. Dvorsky, S. Hennig, M. Alexander and E. Wolf, J. Biol. Chem., 2007, 282, 13011–13021.
18. B. Paulus, C. Bajzath, F. Melin, L. Heidinger, V. Kromm, C. Herkersdorf, U. Benz, L. Mann, P. Stehle, P. Hellwig, S. Weber and E. Schleicher, FEBS J., 2015, 282, 3175–3189.
19. N. Öztürk, S.-H. Song, C. P. Selby and A. Sancar, J. Biol. Chem., 2008, 283, 3256–3263.
20. P. Müller, K. Brettel, L. Grama, M. Nyitrai and A. Lukacs, ChemPhysChem, 2016, 17, 1329–1340.
21. M. J. Damiani, J. J. Nostedt and M. A. O’Neill, J. Biol. Chem., 2011, 286, 4382–4391.
22. I. A. Solov’yov, T. Domratcheva and K. Schulten, Sci. Rep., 2014, 4, 3845.
23. I. M. M. Wijaya, T. Domratcheva, T. Iwata, E. D. Getzoff and H. Kandori, J. Am. Chem. Soc., 2016, 138, 4368–4376.
24. L. Xu, W. Mu, Y. Ding, Z. Luo, Q. Han, F. Bi, Y. Wang and Q. Song, Biochemistry, 2008, 47, 8736–8743.
25. A. Sancar and C. L. Thompson, Oncogene, 2002, 21, 9043.
26. A. Hense, E. Herman, S. Oldemeyer and T. Kottke, J. Biol. Chem., 2015, 290, 1743–1751.
27. D. Immeln, A. Weigel, T. Kottke and J. L. Pérez Lustres, J. Am. Chem. Soc., 2012, 134, 12536–12546.
28. G. Lüdemann, I. A. Solov’yov, T. Kubař and M. Elstner, J. Am. Chem. Soc., 2015, 137, 1147–1156.
29. P. B. Woiczikowski, T. Steinbrecher, T. Kubař and M. Elstner, J. Phys. Chem. B, 2011, 115, 9846–9863.
30. G. Lüdemann, P. B. Woiczikowski, T. Kubař, M. Elstner and T. B. Steinbrecher, J. Phys. Chem. B, 2013, 117, 10769–10778.
31. D. Holub, H. Ma, N. Krauß, T. Lamparter, M. Elstner and N. Gillet, Chem. Sci., 2018, 9, 1259–1272.
32. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
33. H. W. Park, S. T. Kim, A. Sancar and J. Deisenhofer, Science, 1995, 268, 1866–1872.
34. C. A. Brautigam, B. S. Smith, Z. Ma, M. Palnitkar, D. R. Tomchick, M. Machius and J. Deisenhofer, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 12142–12147.
35. C. R. Søndergaard, M. H. M. Olsson, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 2284–2295.
36. M. H. M. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537.
37. J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260.
38. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725.
39. H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56.
40. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
41. AmberTools 14, available at: http://ambermd.org, 2014.
42. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
43. U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145.
44. B. H. Besler, K. M. Merz and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439.
45. G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218.
46. G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090.
47. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009.
48. D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069.
49. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
50. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.
51. A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603.
52. M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972.
53. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
54. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021.
55. A. Grossfield, “WHAM: the weighted histogram analysis method”, version 2.0.9, http://membrane.urmc.rochester.edu/content/wham.
56. M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931–948.
57. M. Elstner, J. Phys. Chem. A, 2007, 111, 5614–5621.
58. M. Gaus, A. Goez and M. Elstner, J. Chem. Theory Comput., 2013, 9, 338–354.
59. T. Kubar and M. Elstner, J. R. Soc., Interface, 2013, 10, 20130415.
60. P. H. König, N. Ghosh, M. Hoffmann, M. Elstner, E. Tajkhorshid, Th. Frauenheim and Q. Cui, J. Phys. Chem. A, 2006, 110, 548–563.
61. K. F. Herzfeld, Ann. Phys., 1919, 364, 635–667.
62. I. M. M. Wijaya, T. Domratcheva, T. Iwata, E. D. Getzoff and H. Kandori, J. Am. Chem. Soc., 2016, 138, 4368–4376.
63. C. L. Partch, M. W. Clarkson, S. Özgür, A. L. Lee and A. Sancar, Biochemistry, 2005, 44, 3795–3805.
64. Y.-T. Kao, C. Tan, S.-H. Song, N. Oztürk, J. Li, L. Wang, A. Sancar and D. Zhong, J. Am. Chem. Soc., 2008, 130, 7695–7701.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp00694j

---