Absorption shifts of diastereotopically ligated chlorophyll dimers of photosystem I

Abstract

The light-harvesting chlorophyll (Chl) molecules of photosynthetic systems form the basis for light-driven energy conversion. In biological environments, the Chl chromophores occur in two distinct diastereotopic configurations, where the α and β configurations have a magnesium-ligating histidine residue and a 17-propionic acid moiety on the opposite side or on the same side of the Chl ring, respectively. Although β-ligated Chl dimers occupy conserved positions around the reaction center of photosystem I (PSI), the functional relevance of the α/β configuration of the ligation is poorly understood. We employ here correlated ab initio calculations using the algebraic-diagrammatic construction through second order (ADC(2)) and the approximate second-order coupled cluster (CC2) methods in combination with the reduced virtual space (RVS) approach in studies of the intrinsic excited-state properties of α-ligated and β-ligated Chl dimers of PSI. Our ab initio calculations suggest that the absorption of the α-ligated reaction-center Chl dimer of PSI is redshifted by 0.13–0.14 eV in comparison to the β-ligated dimers due to combined excitonic coupling and strain effects. We also show that time-dependent density functional theory (TDDFT) calculations using range-separated density functionals underestimate the absorption shift between the α- and β-ligated dimers. Our findings may provide a molecular starting point for understanding the energy flow in natural photosynthetic systems, as well as a blueprint for developing new molecules that convert sunlight into other forms of energy.

---

Introduction

Photosynthesis evolved on earth more than 3 billion years ago¹ and changed the primordial atmosphere by releasing oxygen. The release of oxygen provided a basis for aerobic respiration, which is an alternative energetic pathway to sustain life.² The capture of sunlight thermodynamically drives the biochemical transformations in which adenosine triphosphate (ATP) is formed. ATP, in turn, serves in all organisms as cellular energy currency for driving endergonic processes.

Harvesting sunlight is the first step in photosynthesis. Light capture is enabled by antenna complexes that are an agglomerate of a large number of chromophores, ensuring a sufficiently large cross section for photon capture. Once excited by light, the chromophore transfers its energy to an energetic sink at the reaction center, where charge separation occurs. Through subsequent electron transfer steps, the hole and the electron of the exciton become separated on opposite sides of the photosynthetic membrane, which couples to the generation of an electrochemical proton gradient that ultimately drives ATP synthesis.^2,3

The antenna complexes are associated with large photosystems that engulf the reaction center. While there is great similarity in the architecture and function of reaction centers, the antennas are adapted to the illumination conditions of the habitat and show a wide variability.⁴ Photosynthetic bacteria living in deep waters have very large antenna systems called chlorosomes, formed by self-assembling bacteriochlorophylls (BChls) that absorb in the near-infrared region of the spectrum.^5,6 Some cyanobacteria use circular light-harvesting systems (LH1 and LH2), which are complex structures formed by self-assembling peptides that ligate two BChl a molecules.⁷ The phycobilisomes used by other cyanobacteria and red algae are constructed from open-chain tetrapyrroles that are embedded into larger and more numerous polypeptides, requiring an additional genetic and synthetic effort.⁸

Photosystem I (PSI, Fig. 1A) and photosystem II (PSII) show the highest level of complexity. In PSI and PSII, different protein subunits regulate the excitation energy transfer and the electron transfer processes. Photosystem I (PSI)⁹ and photosystem II (PSII)¹⁰ have two light-harvesting complexes (LHC) denoted LHCI and LHCII, whereas only PSII is capable of catalyzing the water-splitting reaction.^11–14 Special pigment pairs (P) of chlorophylls (Chls), which absorb light at 700 nm in PSI (P700) and at 680 nm in PSII (P680), are at the heart of the reaction centers. The unique P680 complex of PSII has one of the highest oxidizing potentials found in nature, providing the basis for the water-splitting reaction in PSII.

Fig. 1 (A) The crystal structure of photosystem I (PSI, PDB ID: 1JB0). The studied dimers are shown in the experimental structure. The insets show the studied dimeric models optimized at the DFT level. (B) The α/β nomenclature is used for describing the diastereotopic ligation of tetrapyrroles. The α-configuration has the magnesium ligand below the chiral tetrapyrrolic plane on the opposite side of the substituent at C17, while the β-configuration has the ligand above this plane. The top figure shows the typical chemical formula for Chl a with the rings A–E of the chlorin tetrapyrrole with the IUPAC clockwise atom numbering. Asterisks denote chiral atoms.

Complexation of a Chl molecule with an additional ligand, such as a histidine residue originating from the protein surroundings, leads to an additional stereocenter in Chl-protein complexes.¹⁵ The additional stereocenter is related to the carbon atoms 13², 17, and 18, which are stereogenic with four different substituents. The magnesium ligation by the histidine residue from opposite sides of the Chl macrocycle leads to diastereomeric configurations (Fig. 1B). These diastereomers cannot interconvert in a protein environment due to sterical hindrance. The α configuration is formed if the histidine residue ligates the magnesium from the opposite side of the 17-propionic acid residue esterified with phytol, whereas the β configuration indicates that the histidine residue and the phytyl chain are on the same side of the ring.

The diastereoisomers have different physical properties and chemical reactivities. Interestingly, the ligation of the Chls in PSI is completely conserved between different organisms.¹⁵ In both PSI (Fig. 1A) and PSII, there are two similar β-ligated dimers with a distance of about 30 Å between the magnesium atoms of the proximal chlorophylls.¹⁶ In PSI, the β-ligated dimer in subunit A is ligated by HisA76 and HisA79, whereas the corresponding dimer in subunit B is ligated by HisB49 and HisB52 (Fig. 1A). The distance between the β-ligated dimers and the reaction-center P_A–P_B dimer is suitable for Förster-type excitation energy transfer.^17,18 These findings led Balaban et al.^15,16 to investigate the functional relevance of the diastereotopicity. However, in an ab initio computational study at the approximate second-order coupled cluster (CC2)¹⁹ level, Balaban and co-workers did not find any significant differences in the absorption spectra between monomeric α- and β-ligated Chls.¹⁶ Oba and Tamiaki^20–22 also noted that the α ligation is much more abundant among the 96 Chls in PSI, where only 14 are β-ligated. They found that the α ligation is by about 1 kcal mol⁻¹ more stable than the β ligation. Garcia-Martin et al.²³ noted that hydrogen bonding of the β-ligated BChls may play an important structural role in photosystems. Despite these important insights, the influence of the α/β ligation on the light-absorbing properties of Chl clusters is still unclear.

In this work, we employ large-scale correlated ab initio calculations at the algebraic-diagrammatic construction through second order (ADC(2))^24,25 and the CC2 levels using the reduced virtual space (RVS)^26,27 approach to investigate the excited-state properties of α- and β-ligated Chl dimer models of PSI. We also benchmark the employed computational methods by comparing excitation energies calculated at the different levels of theory. Understanding the intrinsic differences between the light-capturing units in natural photosystems is essential for developing molecular catalysts that efficiently convert solar light into other forms of energy.

Methods

We prepared three dimeric Chl models based on the crystal structure of PSI from Synechococcus elongatus (PDB ID: 1JB0):²⁸ the reaction-center Chl dimer (P_A–P_B), which is doubly α-ligated, and two doubly β-ligated dimers, which are denoted A76–A79 and B49–B52 according to the residue numbers of the ligating histidines (Fig. 1A). The phytyl chains of the models were replaced by methyl groups and the C_α atoms of the histidines were replaced by hydrogens (Fig. 1A). The models comprising 188 atoms were optimized at the BP86-D3/def2-SVP^29–32 level employing the resolution-of-the-identity (RI) approximation. The optimized Cartesian coordinates are given as ESI.† To capture some of the steric constraints imposed by the protein environment, we fixed the magnesium atoms as well as the histidine C_β-atoms in their crystallographic positions during the optimizations, while all other atoms of the cluster models were fully relaxed. The root mean square deviations (RMSD) for the heavy atoms of the Chl rings of the P_A–P_B, A76–A79, and B49–B52 models compared to the ones for PSI crystal structure are 0.33 Å, 0.54 Å, and 0.53 Å, respectively.

Structure optimizations at quantum mechanical levels with the surrounding protein treated at a classical level of theory (QM/MM) yield distorted chlorophylls, whose structure also fluctuates due to the dynamical motion of the protein.^33,34 Ring deformations have been found to cause a small redshift of only 11–17 nm of the chlorophyll Q band,³⁵ which is smaller than the uncertainties of the calculated excitation energies. We considered protein effects by optimizing the same P_A–P_B model at the BP86-D3/def2-SVP level in the presence of point charges. The side-chain atoms of the amino acid residues within 4 Å of the Chl rings taken directly from the crystal structure were represented as point charges after adding missing hydrogen atoms. The partial charges of the 358 point charges were taken from the CHARMM36m force field.³⁶ The obtained P_A–P_B structure has a RMSD for the heavy atoms of the Chl rings of 0.13 Å with respect to the ones of experimental PSI structure.

Vertical excitation energies (VEEs) and oscillator strengths (f) were calculated at the ADC(2)^24,25 and CC2^19,37–39 levels of theory. Since the ADC(2) Hamiltonian is hermitian, the computational cost for ADC(2) calculations of absorption spectra is slightly lower than at the CC2 level. Moreover, the hermiticity of the ADC(2) Hamiltonian allows calculations of charge densities and first-order properties without solving the amplitude equations for the corresponding left states.^39,40

In order to make the correlated ab initio calculations on these large systems tractable, we employed the RVS approach,^26,27 where virtual orbitals with energies higher than 50 eV above the highest occupied molecular orbital (HOMO) are omitted in the ADC(2) and CC2 excited-state calculations. We also calculated VEEs at the ADC(2) and CC2 levels using the Laplace-transformed (LT) scaled opposite-spin (SOS) approximation,^41–44 which reduces the computational scaling to fourth order. We employed the standard SOS scaling factor of 1.3, with the number of integration points n_L = 2 in the LT step, which is found to result in errors in the excitation energies that are smaller than 0.01 eV. In the ADC(2) and CC2 calculations, we employed def2-SVP and def2-TZVP basis sets together with the corresponding auxiliary basis sets.^45–47 We also simulated broadening of the spectral peaks using Gaussian broadening, where the oscillator strength corresponds to the height of the peak.

We also performed calculations at the TDDFT level⁴⁸ using the hybrid functionals B3LYP^49,50 and BHLYP,^30,49,51 as well as the range-separated CAM-B3LYP⁵² and ωB97X⁵³ functionals. In the TDDFT calculations, we employed def2-SVP and def2-TZVP basis sets. All calculations were performed using TURBOMOLE^54,55 versions 6.5–7.2 and ORCA⁵⁶ version 3.0.3.

Results

Monomeric chlorophyll

For an optimized Chl monomer model, without a histidine ligand bound to the magnesium atom, we obtained a bright first excited state at 1.97 eV at the RVS-ADC(2)/def2-TZVP level, which is in good agreement with the experimental gas-phase value of 1.92–1.93 eV.^57,58 Comparing the calculated VEEs for Chl with values calculated for the α-ligated and β-ligated Chl structures (Table 1) shows that complexation with the histidine ligand in the α or β position redshifts the first eight excited states by up to 0.1 eV. The ligating histidine also significantly increases the oscillator strength of the S₂ state in both structures. The difference in VEEs between the α- and β-ligated Chls is small, which was also previously found by Balaban et al.¹⁶ in CC2 calculations on monomeric Chl. The computational results suggest that the differences in the light-absorbing properties caused by the α/β ligation are likely due to the stacking interactions and/or due to structural strain in Chl dimers/multimers.

Table 1 Vertical excitation energies (VEEs, in eV) and oscillator strengths (f) calculated at the RVS-ADC(2)/def2-TZVP level for the ligand-free Chl monomer as well as for α- and β-ligated Chl. The transitions to the first two excited states form the Q bands and the transitions to third and fourth excited states are the most important contributions to the Soret band

VEE	f	VEE	f	VEE	f
Chl		α-Chl		β-Chl
1.97	0.287	1.91	0.194	1.92	0.192
2.11	0.068	2.02	0.142	2.02	0.148
2.95	0.714	2.86	0.536	2.85	0.561
3.06	0.917	2.98	0.805	2.97	0.844
3.15	0.108	3.08	0.080	3.10	0.015
3.20	0.009	3.20	0.010	3.17	0.053
3.26	0.001	3.27	0.006	3.25	0.004
3.55	0.151	3.48	0.168	3.50	0.175

---

The lowest transitions for the dimeric systems

The computational levels employed on the dimeric systems were chosen based on the benchmark calculations (vide infra). The lowest excitation energies of the three dimer models were calculated at the RVS-ADC(2)/def2-TZVP level. The oscillator strengths were obtained in calculations at the RVS-ADC(2)/def2-SVP level.

The VEEs and oscillator strengths calculated at the RVS-ADC(2)/def2-TZVP level for the first two excited states of the studied dimeric systems (P_A–P_B, A76–A79 and B49–B52) are summarized in Table 2. For P_A–P_B, we obtained a bright first excited state at 1.75 eV (708 nm), which is close to the experimental value of 1.77 eV (700 nm). However, as environmental effects due to the surrounding protein and co-factors are not considered in the current models, the agreement with experiment is likely to be partly fortuitous. It is also possible that the protein does not tune the light-absorbing properties by specific interactions in the case of P_A–P_B. The ADC(2) calculations suggest that the second excited state of P_A–P_B at 1.79 eV is a weakly absorbing (dark) state, as indicated by its small oscillator strength. Due to interactions between the monomers, the excitation energy of P_A–P_B is redshifted by 0.16 eV as compared with the corresponding value for the α-ligated Chl monomer. The present calculations thus suggest that the interactions between the Chl monomers account for a large part of the observed redshift in the absorption of the Chl dimer as compared with Chl in the gas phase, which is consistent with the experimental work of Milne et al.⁵⁸

Table 2 The two lowest vertical excitation energies (VEEs) and oscillator strengths (f) for the P_A–P_B, A76–A79, and B49–B52 dimer models calculated at the RVS-ADC(2)/def2-TZVP level. The effect of the histidines on the excitation energies (no His) are also reported. The oscillator strengths (f) for the dimeric systems were calculated using def2-SVP basis sets

VEE	f	VEE	f	VEE	f
PA–PB		A76–A79		B49–B52
1.75	0.332	1.86	0.032	1.84	0.088
1.79	0.011	1.88	0.195	1.89	0.144

---

VEE	f	VEE	f	VEE	f
PA–PB, no His		A76–A79, no His		B49–B52, no His
1.79	0.461	1.90	0.023	1.91	0.051
1.84	0.003	1.95	0.428	1.95	0.403

---

VEE	f	VEE	f	VEE	f
PA–PB-I		A76		B49
1.91	0.199	1.92	0.203	2.15	0.183
2.03	0.132	2.05	0.112	2.26	0.104

---

VEE	f	VEE	f	VEE	f
PA–PB-II		A79		B52
1.91	0.198	2.14	0.185	2.12	0.186
2.03	0.133	2.24	0.110	2.22	0.112

---

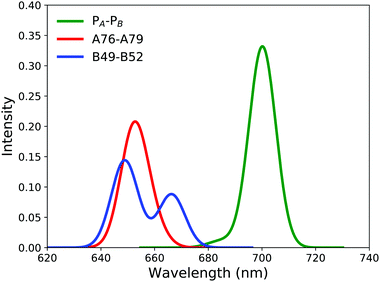
For the A76–A79 dimer, the two lowest VEEs calculated at the RVS-ADC(2)/def2-TZVP level are 1.86 eV and 1.88 eV, whereas for B49–B52, the corresponding energies are 1.84 eV and 1.89 eV. The absorption of the β-ligated dimers is thus blueshifted by 0.13–0.14 eV as compared with P_A–P_B, implying that the β-ligated dimers absorb strongly in the 650 nm region as shown by the red and blue spectra in Fig. 2.

Fig. 2 The absorption spectra for the dimers calculated at the RVS-ADC(2)/def2-TZVP level. The spectra are shifted such that the absorption maximum of P_A–P_B is at the experimental value for P700 of 700 nm. The bandwidth was chosen such that the experimental band shapes are qualitatively reproduced.

The S₁ states of both the A76–A79 and the B49–B52 dimers are weakly absorbing states, whereas the S₂ transition is bright for both of the β-ligated dimers. The transition dipole directions of the chlorophylls in the dimer models shown in Fig. 3 suggest that the S₁ state is bright and the S₂ state is weakly absorbing when the dipole transition moments of the individual dipole moments point in the same direction and the relative position of the monomers is similar for the two models. For the β-ligated dimers, the transition moments point in opposite directions, leading to a weak S₁ state and a bright S₂ state. The direction of the transition moment is determined by the orientation of the chlorophyll moiety with the E ring.

Fig. 3 Transition dipole moment directions of the individual chlorophylls in the dimeric models, where the A76–A79, B49–B52, and P_A–P_B Chl dimer models are introduced in Fig. 1. The strong transitions are marked with boldface text in the figure.

The effect of the ligating histidines on the absorption spectra was investigated by removing them from the models and repeating the excited-state calculations at the RVS-ADC(2)/def2-TZVP level. Comparison of the VEEs calculated with and without the ligands shows that the histidine residue redshifts the absorption energy by 0.04–0.07 eV (Table 2). This suggests that the remaining shift between P_A–P_B and the β-ligated dimers is due to interactions between the Chls or due to structural strain.

For the TDDFT calculations of the dimeric systems, we chose the range-separated ωB97X functional, because it has recently been shown to yield similar excitation energies as ADC(2) for oligothiophene systems.⁵⁹ At the TDDFT level, VEEs and oscillator strengths for the two lowest states were calculated using def2-TZVP basis sets, while in calculations of higher-lying states, def2-SVP basis sets were employed.

The TDDFT calculations performed at the ωB97X/def2-TZVP level yielded excitation energies that are 0.24–0.36 eV larger than those obtained at the ADC(2) level. The excitation energies in Tables 2 and 3 show that the TDDFT calculations yield slightly stronger oscillator strengths and that the same order of the states is obtained at the ADC(2) and ωB97X levels. The excitation energy of the S₁ state of P_A–P_B calculated at the ωB97X level is almost the same as for A76–A79 and B49–B52, whereas at the ADC(2) level, the two lowest excited states of P_A–P_B are redshifted by 0.1 eV relatively to the corresponding states of A76–A79 and B49–B52, suggesting that TDDFT calculations have difficulties in reproducing absorption shifts of excitonically coupled chlorophylls, even when using range-separated functionals.

Table 3 The two lowest vertical excitation energies (VEEs) and oscillator strengths (f) for the P_A–P_B, A76–A79, and B49–B52 dimer models calculated at the ωB97X/def2-TZVP level

PA–PB		A76–A79		B49–B52
VEE	f	VEE	f	VEE	f
2.11	0.448	2.10	0.104	2.10	0.067
2.15	0.052	2.16	0.372	2.16	0.402

---

Steric and electrostatic effects

To decompose the spectral tuning mechanism, we studied how steric effects influence the VEEs of the P_A–P_B dimer by separating the system into two fragments (P_A–P_B-I and P_A–P_B-II) consisting of the Chl monomer and its histidine ligand. At the RVS-ADC(2)/def2-TZVP level, the S₁ energies are 1.91 eV for the unrelaxed structures of both the P_A–P_B-I and P_A–P_B-II fragments (Table 2). The two lowest excited states of the P_A–P_B dimer consist of a bright and a dark combination of the S₁ states of the almost identical monomer fragments. We obtain S₁ VEE values of 1.91 eV for P_A–P_B-I and P_A–P_B-II, which is identical to the VEE of a fully relaxed α-ligated Chl monomer. This suggests that the molecular structures of the two fragments are not significantly strained in the dimer geometry, i.e., the steric effects on the excitation energies are small. Thus, electrostatic and excitonic coupling effects are likely to provide the main effects for the redshifted absorption of the P_A–P_B dimer.

The A76 monomer absorbs at 1.92 eV, which is in close agreement with the value obtained for the fully relaxed β-Chl monomer, suggesting that A76 is almost fully relaxed in the A76–A79 dimer. The A79 monomer of the A76–A79 dimer, however, absorbs at a significantly higher energy of 2.14 eV, showing that A79 is subjected to significant strain. In the B49–B52 dimer, the B49 and B52 monomers absorb at 2.15 eV and 2.12 eV, respectively, implying that both monomers are significantly strained in the B49–B52 dimer.

The large excitation energies for the A79, B49, and B52 monomers due to steric effects are surprising, as the VEEs for the two lowest excited states of the A76–A79 and B49–B52 dimers are in the range of 1.84–1.89 eV. Thus, the large blueshift due to steric effects is compensated by a large redshift caused by the excitonic coupling and the electrostatic interaction between the monomers. Since the electrostatic effects are small in the case of P_A–P_B, excitonic coupling is most likely the main reason for the redshifted absorption.

Calculations of the lowest excitation energies of the P_A–P_B model at the BHLYP/def2-SVP level showed that the point charges had a very small effect of <0.01 eV on the absorption energies. The structural relaxation of the P_A–P_B model in the presence of the nearest protein residues represented by point charges had a larger effect on the excitation energies. The energies of the lowest excited states were redshifted by almost 0.2 eV, which is significantly larger than the structural shift reported by Zucchelli et al.³⁵ The reason for the unexpectedly large structural effect on the excitation energies might be due an overestimated interaction between the point charges and the exterior part of the Chl cluster. After optimization, the distances between the QM and MM parts were somewhat shorter than for the experimental structure.

Higher excited states

To estimate the absorption spectra in the shorter wavelength regime, we calculated VEEs for the ten lowest excited states of the dimeric models at the RVS-LT-SOS-CC2/def2-SVP level. The obtained VEEs and oscillator strengths for the relevant energy range of UV-VIS spectra are reported in Table 4. The ten lowest excitation energies for P_A–P_B were also calculated using the def2-TZVP basis sets. The four lowest states are redshifted by 0.03–0.04 eV when using the triple-ζ quality basis sets and by less than 0.1 eV for the higher excited states. Since qualitatively the same excitation energies were obtained using the two basis sets, the excitation energies of the higher excited states of the A76–A97 and B46–B52 dimers have not been calculated using the larger basis sets.

Table 4 Vertical excitation energies (VEEs) and oscillator strengths (f) calculated for the P_A–P_B, A76–A79, and B49–B52 dimer models at the RVS-LT-SOS-CC2/def2-SVP level. The excitation energies for P_A–P_B in the first column are calculated using the def2-TZVP basis sets

VEE^a	VEE	f	VEE	f	VEE	f
PA–PB			A76–A79		B49–B52
a Calculated using def2-TZVP basis sets.
2.03	2.07	0.363	2.01	0.112	2.02	0.094
2.06	2.09	0.023	2.08	0.205	2.08	0.226
2.23	2.27	0.052	2.28	0.038	2.29	0.043
2.27	2.31	0.052	2.33	0.050	2.34	0.043
2.74	2.85	0.008	3.13	0.003	3.14	0.005
2.82	2.92	0.004	3.23	0.010	3.25	0.009
2.89	2.98	0.041	3.32	1.138	3.32	1.160
2.95	3.03	0.002	3.38	0.380	3.37	0.338
2.98	3.08	0.113	3.42	0.326	3.42	0.402
3.28	3.37	0.058	3.52	1.637	3.55	0.389

---

The lowest excitation energies of the dimer calculated at the SOS-CC2 level are almost the same as obtained for the monomer. The splitting between the S₁ and S₂ states of the dimer is only 0.03 eV. Thus, the excitonic coupling obtained at the SOS-CC2 level is probably too small. Calculations on the monomer show that the SOS approximation introduces a large energy gap between the S₁ and S₂ states, which also leads to a large energy gap between the S₂ and S₃ states of the dimers. The S₁ state is the bright state also at the RVS-LT-SOS-CC2/def2-SVP level. The next bright state of P_A–P_B is the 9th excited state at 3.08 eV (403 nm), which can be assigned to the B band of Gouterman's four-orbital model.⁶⁰ Thus, the P_A–P_B dimer model has four weakly absorbing bands between the Q and B bands that are not related to the monomers, which have no weakly absorbing states between the Q and B bands. The A76–A79 and B49–B52 dimer models have only two weak dimer states between the Q and B bands. The excitonic coupling in P_A–P_B seems to significantly redshift the lowest B band from 3.38 eV in the monomer to 3.08 eV for the dimer. The excitonic splitting of the lowest B band leads to a stronger and a weaker state as for the lowest Q band. In the A76–A79 and B49–B52 dimer models, a much weaker exciton splitting of the Q and B bands is observed. The four highest excited states (S₇–S₁₀) at 3.32–3.55 eV can be identified as the strongly absorbing B bands of the monomers, whose excitation energies are 3.38 eV and 3.57 eV.

The present SOS calculations show that the SOS approximation seems to be unable to properly consider excitonic coupling, leading to a small energy splitting of excited states of the dimer with the same monomer Q band origin. The SOS approximation also leads to a large energy splitting between the Q bands of the chlorophyll monomers and between the corresponding states of the dimer. The computational speed is the main reason for employing the SOS approximation in calculations on chlorophylls.

Benchmarking

The performance of different computational levels was investigated by calculating the four lowest VEEs of an optimized monomeric Chl model using several different methods (Table 5). The studied excited states are well described by single replacements from the Hartree–Fock reference wavefunction. A more comprehensive comparison is given in the ESI.† The ADC(2) excitation energies are systematically redshifted by 0.20–0.22 eV as compared to the CC2 values, which is consistent with previously reported benchmark studies,^44,61,62 where ADC(2) has been found to provide excitation energies of roughly the same accuracy as CC2.

Table 5 Vertical excitation energies (VEEs, in eV) and oscillator strengths (f) of chlorophyll calculated at the ab initio and TDDFT levels using def2-TZVP basis sets

VEE	f	VEE	f	VEE	f	VEE	f
ADC(2)		RVS-ADC(2)		SOS-ADC(2)		LT-SOS-ADC(2)
1.90	0.282	1.97	0.287	1.91	0.253	1.91	0.252
2.04	0.058	2.11	0.068	2.28	0.036	2.29	0.037
2.88	0.719	2.95	0.714	3.16	1.092	3.16	1.092
2.99	0.943	3.06	0.917	3.37	1.108	3.38	1.104

---

VEE	f	VEE	f	VEE	f	VEE	f
CC2		RVS-CC2		SOS-CC2		LT-SOS-CC2
2.12	0.239	2.18	0.259	1.99	0.219	1.99	0.221
2.25	0.061	2.32	0.061	2.31	0.026	2.32	0.026
3.10	0.728	3.17	0.767	3.28	0.919	3.29	0.917
3.20	0.646	3.27	0.613	3.48	0.291	3.48	0.464

---

VEE	f	VEE	f	VEE	f	VEE	f
B3LYP		BHLYP		CAM-B3LYP		ωB97X
2.19	0.285	2.24	0.356	2.20	0.311	2.17	0.295
2.30	0.020	2.53	0.022	2.48	0.027	2.57	0.037
2.90	0.017	3.52	0.074	3.46	0.070	3.61	0.111
3.09	0.018	3.78	1.248	3.71	0.952	3.83	1.377

---

Consistent with previous studies,⁴⁴ employing the RVS approach with a threshold of 50 eV in the ab initio calculations introduces a small blueshift of 0.06–0.07 eV for the first four excited states at the ADC(2) and CC2 levels using def2-TZVP basis sets. The oscillator strengths are not significantly affected by the RVS approximation. The RVS approach that significantly speeds up the calculations has been successfully employed in previous studies of photobiological systems, including chlorophylls.^{26,27,44,63–67}

Comparing the results from the SOS-ADC(2) and SOS-CC2 calculations with the corresponding values calculated at the unscaled CC2 and ADC(2) levels shows that the SOS approximation introduces errors of −0.13 to 0.39 eV for the lowest four excited states of the Chl monomer (Table 5). The oscillator strengths are also affected by the SOS approach. The Laplace-transform step in the LT-SOS-ADC(2) and LT-SOS-CC2 calculations has a negligible effect on the accuracy of the excitation energies (Table 5), while it reduces the computational cost to fourth order with respect to the size of the basis set. The oscillator strength of the fourth excited state calculated using LT algorithm at the CC2 level is 60% larger than when using the standard algorithm, whereas for the rest of the states, the oscillator strengths calculated with and without the LT algorithm agree well. In the present work, we use the RVS-LT-SOS-CC2 method to estimate higher lying VEEs for the dimeric systems to speed up the calculations of the VEEs and oscillator strengths.

We also studied the performance of different density functionals in TDDFT calculations, where we employed the B3LYP, BHLYP, CAM-B3LYP, and ωB97X hybrid functionals. CAM-B3LYP and ωB97X are range-separated functionals with larger amounts of Hartree–Fock exchange at longer interelectronic distances, which is important for an accurate description of e.g., charge-transfer states. At the employed TDDFT levels, the vertical excitation energies of the lowest excited states are systematically blueshifted compared with the values obtained at the ab initio levels (Table 5). The excitation energy and oscillator strength of the third and the fourth excited states depend on the amount of Hartree–Fock exchange in the functional indicating charge-transfer problems.

Conclusions

We have computationally studied the lowest excited singlet states of diastereotopically ligated Chl dimer models of PSI by employing ab initio correlated levels of theory and range-separated TDDFT calculations. Calculations on the P_A–P_B dimer model show that the steric effects on the excitation energies are small, whereas electrostatic and excitonic coupling effects redshift the absorption energy of the Chl dimer. Similar calculations on the A76–A79 and B49–B52 dimers show that molecular strain in the A76, B49 and B52 moieties blueshifts the excitation energies, which is compensated by a redshift due to electrostatic effects and the excitonic coupling. The histidine ligands have a small redshifting effect of 0.04–0.07 eV on the lowest two VEEs of the studied dimers. Comparisons of the shifts calculated at different levels of theory indicates that TDDFT calculations employing the range-separated ωB97X functional have difficulties in accounting for excitonic coupling contributions to the excitation energies of the dimers.

The calculated excitation energies reveal significant differences in the P_A–P_B spectra as compared to the ones for the A76–A79 and B49–B52 dimer models. The first excited state of the P_A–P_B model is a bright state and the S₂ state absorbs more weakly, whereas the S₁ states of the A76–A79 and B49–B52 dimers are weakly absorbing states. The orientation of the E ring moiety determines the direction of the transition dipole moment of the lowest state. When the transition moment are oriented in the same direction, the first excited state of the dimer is the bright state.

P_A–P_B has several weakly absorbing states between the Q and B bands, and the excitonic coupling splits the B band of P_A–P_B, whereas no such splitting is observed in the spectrum of the two other dimers. The present study reveals significant differences in the properties of the excited states of the seemingly similar dimer models.

The ADC(2) calculations suggest that the absorption of the α-ligated Chl dimer of PSI is redshifted by 0.13–0.14 eV in comparison to the doubly β-ligated dimer due to combined excitonic coupling and strain effects. Comparisons of the TDDFT-calculated spectra with those obtained at the ab initio level and with experimental data show that TDDFT calculations have difficulties to provide the correct dimer shifts of the excitation energies, which are needed when aiming at a deeper understanding of the absorption mechanisms in excitonically coupled Chl molecules. The ab initio calculations at the ADC(2) level yield excitation energies that are in close agreement with experimental data, although electrostatic effects from the surrounding protein and the co-factor environment are not considered in the calculations. We also employed the SOS approximation in order to take advantage of the fast LT algorithm, which reduces the computational scaling of the ADC(2) and CC2 methods to fourth order. However, the SOS-ADC(2) calculations yield an energy gap of 0.38 eV between the S₁ and S₂ states of the Chl monomer, leading to a gap of the same size between the S₂ and the S₃ states in the dimer models. Without the SOS approximation, the energy splitting between S₁ and S₂ of the Chl monomer is 0.12 eV at the ADC(2) level. The same trend was obtained in the SOS-CC2 and CC2 calculations of the Chl monomer, with a slightly smaller SOS effect of 0.2 eV. The RVS approximation blueshifts the excitation energies by only 0.03–0.07 eV for the studied states and it significantly speeds up the calculations, rendering computations on the dimeric models using triple-ζ basis sets feasible. At the RVS-ADC(2)/def2-TZVP level, we obtain an excitation energy of 1.97 eV for the S₁ state of Chl, which agrees well with the experimental value of 1.92–1.93 eV. Histidine complexation leads to a small redshift of <0.1 eV and increases the oscillator strength of the S₂ state.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

C.-M. S. has been supported by the Doctoral Programme in Chemistry and Molecular Sciences (CHEMS) at the University of Helsinki, the Swedish Cultural Foundation in Finland, the Sigrid Jusélius Foundation, and the International Human Frontier Science Program (Long-Term Fellowship LT000916-2018-L). This research was also supported by the German Academic Exchange Service-Finnish Academy (287791), Magnus Ehrnrooth Foundation, and the Academy of Finland (275845). CSC – the Finnish IT Center for Science as well as the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533) are acknowledged for computer time. H. F. thanks the Norwegian Research Council through the CoE Hylleraas Centre for Quantum Molecular Sciences (Grant No. 262695 and 231571/F20) for support.

References

1. S. A. Crowe, L. N. Døssing, N. J. Beukes, M. Bau, S. J. Kruger, R. Frei and D. E. Canfield, Nature, 2013, 501, 535–538.
2. R. E. Blankenship, Molecular mechanisms of photosynthesis, John Wiley & Sons, 2013.
3. S. Bahatyrova, R. N. Frese, C. A. Siebert, J. D. Olsen, K. O. van der Werf, R. van Grondelle, R. A. Niederman, P. A. Bullough, C. Otto and C. N. Hunter, Nature, 2004, 430, 1058–1062.
4. T. S. Balaban, Encyclopedia of nanoscience and nanotechnology, American Scientific Publishers, 2004, vol. 4, pp. 505–559.
5. N.-U. Frigaard and D. A. Bryant, Complex intracellular structures in prokaryotes, Springer, 2006, pp. 79–114.
6. G. S. Orf and R. E. Blankenship, Photosynth. Res., 2013, 116, 315–331.
7. A. W. Roszak, T. D. Howard, J. Southall, A. T. Gardiner, C. J. Law, N. W. Isaacs and R. J. Cogdell, Science, 2003, 302, 1969–1972.
8. L. Chang, X. Liu, Y. Li, C.-C. Liu, F. Yang, J. Zhao and S.-F. Sui, Cell Res., 2015, 25, 726–737.
9. A. Amunts, O. Drory and N. Nelson, Nature, 2007, 447, 58–63.
10. X. Wei, X. Su, P. Cao, X. Liu, W. Chang, M. Li, X. Zhang and Z. Liu, Nature, 2016, 534, 69–87.
11. T. Cardona, A. Sedoud, N. Cox and A. W. Rutherford, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 26–43.
12. N. Cox, D. A. Pantazis, F. Neese and W. Lubitz, Acc. Chem. Res., 2013, 46, 1588–1596.
13. P. Joliot, G. Barbieri and R. Chabaud, Photochem. Photobiol., 1969, 10, 309–329.
14. B. Kok, B. Forbush and M. McGloin, Photochem. Photobiol., 1970, 11, 457–475.
15. T. S. Balaban, P. Fromme, A. R. Holzwarth, N. Krauß and V. I. Prokhorenko, Biochim. Biophys. Acta, Bioenerg., 2002, 1556, 197–207.
16. T. S. Balaban, P. Braun, C. Hättig, A. Hellweg, J. Kern, W. Saenger and A. Zouni, Biochim. Biophys. Acta, Bioenerg., 2009, 1787, 1254–1265.
17. T. Förster, Ann. Phys., 1948, 437, 55–75.
18. T. Förster, Radiat. Res., Suppl., 1960, 326–339.
19. O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418.
20. T. Oba and H. Tamiaki, J. Photosci., 2002, 9, 362–363.
21. T. Oba and H. Tamiaki, Photosynth. Res., 2002, 74, 1–10.
22. T. Oba and H. Tamiaki, Bioorg. Med. Chem., 2005, 13, 5733–5739.
23. A. Garcia-Martin, L. G. Kwa, B. Strohmann, B. Robert, A. R. Holzwarth and P. Braun, J. Biol. Chem., 2006, 281, 10626–10634.
24. A. Trofimov and J. Schirmer, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2299–2324.
25. J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416.
26. R. Send, V. R. I. Kaila and D. Sundholm, J. Chem. Phys., 2011, 134, 214114.
27. R. Send, C. Suomivuori, V. R. I. Kaila and D. Sundholm, J. Phys. Chem. B, 2015, 119, 2933–2945.
28. P. Jordan, P. Fromme, H. T. Witt, O. Klukas, W. Saenger and N. Krauß, Nature, 2001, 411, 909–917.
29. J. J. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
30. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
31. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
32. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
33. K. Saito, Y. Umena, K. Kawakami, J.-R. Shen, N. Kamiya and H. Ishikita, Biochemistry, 2012, 51, 4290–4299.
34. S. Vassiliev, A. Mahboob and D. Bruce, Photosynth. Res., 2011, 110, 25–38.
35. G. Zucchelli, D. Brogioli, A. P. Casazza, F. M. Garlaschi and R. C. Jennings, Biophys. J., 2007, 93, 2240–2254.
36. J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. MacKerell Jr, Nat. Methods, 2017, 14, 71–73.
37. C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161.
38. C. Hättig and A. Köhn, J. Chem. Phys., 2002, 117, 6939–6951.
39. C. Hättig, Adv. Quantum Chem., 2005, 50, 37–60.
40. C. Hättig, Computational Nanoscience: Do It Yourself!, NIC series, John von Neumann Institute for Computing, Jülich, 2006, vol. 31, pp. 245–278.
41. Y. M. Rhee, D. Casanova and M. Head-Gordon, J. Phys. Chem. A, 2009, 113, 10564–10576.
42. N. O. C. Winter and C. Hättig, J. Chem. Phys., 2011, 134, 184101.
43. N. O. C. Winter and C. Hättig, Chem. Phys., 2012, 401, 217–227.
44. C.-M. Suomivuori, N. O. C. Winter, C. Hättig, D. Sundholm and V. R. I. Kaila, J. Chem. Theory Comput., 2016, 12, 2644–2651.
45. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
46. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
47. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
48. M. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323.
49. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
50. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
51. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
52. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
53. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
54. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
55. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdisciplinary Reviews: Comput. Mol. Sci., 2014, 4, 91–100.
56. F. Neese, Wiley Interdisciplinary Reviews: Comput. Mol. Sci., 2012, 2, 73–78.
57. N. Shafizadeh, M. Ha-Thi, B. Soep, M. Gaveau, F. Piuzzi and C. Pothier, J. Chem. Phys., 2011, 135, 114303.
58. B. F. Milne, C. Kjær, J. Houmøller, M. H. Stockett, Y. Toker, A. Rubio and S. B. Nielsen, Angew. Chem., Int. Ed., 2016, 55, 6248–6251.
59. H. Li, R. Nieman, A. J. Aquino, H. Lischka and S. Tretiak, J. Chem. Theory Comput., 2014, 10, 3280–3289.
60. M. Gouterman, J. Chem. Phys., 1959, 30, 1139–1161.
61. P. H. P. Harbach, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 064113.
62. D. Jacquemin, J. Chem. Theory Comput., 2018, 14, 1534–1543.
63. V. R. I. Kaila, R. Send and D. Sundholm, J. Phys. Chem. B, 2012, 116, 2249–2258.
64. M. Pabst, D. Sundholm and A. Köhn, J. Phys. Chem. C, 2012, 15203–15217.
65. V. R. I. Kaila, R. Send and D. Sundholm, Phys. Chem. Chem. Phys., 2013, 15, 4491–4495.
66. A. P. Gamiz-Hernandez, I. A. Neycheva, R. Send, D. Sundholm and V. R. I. Kaila, Angew. Chem., Int. Ed., 2015, 54, 11564–11566.
67. C.-M. Suomivuori, A. P. Gamiz-Hernandez, D. Sundholm and V. R. I. Kaila, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7043–7048.

---

Footnotes

† Electronic supplementary information (ESI) available: The Cartesian coordinates of the investigated molecules and comparison of excitation energies of chlorophyll calculated at ab initio and density functional theory levels are compared. See DOI: 10.1039/c9cp00616h

‡ Prof. Teodor Silviu Balaban passed away in the fall of 2016.

---