Open Access Article
Open Access ArticleDelayed feedback control of active particles: a controlled journey towards the destination
S. M. J.
Khadem
 * and
Sabine H. L.
Klapp
* and
Sabine H. L.
Klapp
Institute of Theoretical Physics, Technical University Berlin, Hardenbergstr. 36, 10623 Berlin, Germany. E-mail: jebreiilkhadem@itp.tu-berlin.de
First published on 7th June 2019
Abstract
We explore theoretically the navigation of an active particle based on delayed feedback control. The delayed feedback enters in our expression for the particle orientation which, for an active particle, determines (up to noise) the direction of motion in the next time step. Here we estimate the orientation by comparing the delayed position of the particle with the actual one. This method does not require any real-time monitoring of the particle orientation and may thus be relevant also for controlling sub-micron sized particles, where the imaging process is not easily feasible. We apply the delayed feedback strategy to two experimentally relevant situations, namely, optical trapping and photon nudging. To investigate the performance of our strategy, we calculate the mean arrival time analytically (exploiting a small-delay approximation) and by simulations.
1 Introduction
Navigating the motion of active (self-propelled) particles, which are capable of converting energy from their surrounding environment into directed motion, is a task receiving increasing interest. From an applicational point of view, this problem is relevant, e.g., for targeted active drug delivery1 and in the context of robotics,2 but also for the controlled assembly of microscale systems based on active agents.3 More fundamentally, the question is how to manipulate the motion of an autonomous object subject to random fluctuations, either for an individual agent or for an ensemble. Indeed, even without explicit external control, active particles show a very rich and intriguing collective behavior (see, e.g.,4,5), including formation of spatio-temporal patterns on the mesoscale.6,7Depending on the type of active particle, different mechanisms of (single-particle) control have been proposed involving, e.g., magnetic fields,8 topographical fields (e.g., channels or patterned walls), chemical gradients, and optical and thermophoretic forces (for a review, see ref. 9). Some of these strategies are based on feedback mechanisms, where the propulsion velocity10 or the direction of motion of the particle are continuously adapted depending on its current position and/or orientation. Indeed, feedback control11 is a concept currently gaining growing attention in various areas of colloidal transport, including transport of passive colloids,12–15 (thermophoretic) control of DNA molecules,16 manipulation for biomedical engineering,17 and control of active particles.18,19 An example of feedback control in the area of active colloidal particles is the photon nudging method,19 where the propulsion generated by a weak laser is turned on or off when the swimmer moves towards or away from the target (for a theoretical description, see ref. 20). In the present paper, we propose yet another method of feedback control which, as a crucial new feature, involves a time delay.
Our motivation to do so is as follows. A key ingredient in various of the above-mentioned feedback control strategies (such as, e.g., photon nudging) is the particle orientation as function of time, which determines the direction of motion. Monitoring the particle orientation can, however, be a difficult task, especially for small (sub-micronsize) particles. The purpose of the present paper is to explore, on a theoretical level, a feedback control based on an approximate orientation vector defined as the difference between the actual particle position at time t, r(t), and its position at an earlier time, r(t − δ). Here, δ is the “delay” time. By this approximation, only the position needs to be monitored (which makes the method also applicable to active particles without intrinsic orientation such as active micro-emulsion droplets21). The approximate orientation vector is then used to predict the next step of the translational motion of the particle. Clearly, this approximation requires the delay time to be smaller than the rotational relaxation time, which is one of the key assumptions of our approach. However, given a sufficiently fast imaging device, this assumption should be not too restrictive. The other key assumption is that we can adapt the particle's motility (speed of propulsion) by the intensity of a laser, similar to what has been done in various experimental studies.19,22 We model our control concept mathematically based on suitable Langevin equations, and we discuss, on a theoretical level, two examples of application.
The first example is inspired by the optical trapping method,23 where a particle's position is manipulated by a co-moving laser beam. For real active particles sensitive to light, the laser intensity influences not only the stiffness of the trap, but also the motility.24,25 Within the strategy proposed here, the motility is adapted (through the laser intensity) in response to the approximate orientation vector, i.e., the displacement r(t) − r(t − δ). This introduces a symmetry-breaking of the conventional isotropic translational diffusion. To judge the performance of this strategy we analyze the resulting mean arrival time, which the particle needs to travel from a starting point to a predefined target. To this end we employ both, numerical simulations of the full (delayed) equations of motion and analytical results obtained from a coarse-grained theory.
As a second example of application, we consider theoretically a variant of the photon-nudging method, where the current orientation vector is again estimated on the basis of the displacement r(t) − r(t − δ). We then adapt the motility to perform the navigation.
It should be noted that, due to the usage of the position at an earlier time, our control method falls into the class of delayed feedback control strategies, which are well established in the area of chaos control,26,27e.g. in laser systems28,29 and in chemical reaction networks.30–32 On a theoretical level, time delay considerably complicates the mathematical treatment since the underlying stochastic equations become non-Markovian in character. This leads, e.g., to an non-trivial (hierarchical) Fokker–Planck equation already in the single-particle case.33 Here we circumvent this problem by assuming the delay to be small, allowing for an effectively Markovian treatment similar to that employed in an earlier study on the use of (sensorial) delay for autonomous agents.34,35
The remainder of this work is structured as follows: in Section 2, we discuss those types of active particles for which our method seems applicable, and we briefly introduce active Brownian particles as a suitable mathematical model. In Section 3.1, we propose a delayed feedback strategy within the optical trapping method and analyze the proposed equations of motion by theory and numerical simulation. For our analytical treatment, we focus on small delay times and introduce coarse-grained equations of motion focusing solely on the translational dynamics, following closely an approach suggested in ref. 34. Based on this theory we then calculate the mean arrival time, which turns out to agree very well with corresponding results from numerical simulations. In Section 3.2, we combine the concepts of delayed feedback method and the photon nudging method, and investigate its applicability numerically. We also compare our results with corresponding numerical results from “standard” photon nudging based on the true particle orientation. Finally, a summary and outlook is given in Section 4.
2 Systems of interest and model
In contrast to passive Brownian particles, active particles display a directed motion on timescales which are much longer than the diffusion time of a passive particle of the same size. Such a motion may be generated, for instance, through a chemical reaction of the particle with the surrounding environment (examples being gold-platinum and gold-nickel microrods in hydrogen peroxide solutions36,37) or by an external field. Examples of the latter kind are chiral magnetic objects driven by a magnetic field38 or metallic microrods driven by an acoustic field.39Regardless of the origin of activity in these systems, photon-based control methods such as optical trapping and photon nudging are clearly applicable only if the motion of the particle can be actuated by means of photon induction. This actuation may occur via the thermophoretic effect, or by photophoretic or radiation-pressure forces.40 For instance, it has been demonstrated that metal-coated Janus particles show activity due to thermophoresis when they are illuminated with a strong laser light.25 Another example are Janus particles of the same type immersed in a binary solution with lower critical point. This allows for local phase separation and, consequently, diffusiophoretic motion with much lower laser intensities.41 In the present work, we focus on those active particles which can be controlled by laser light.
A simple model for the real particles of interest are so-called active Brownian particles. An active Brownian particle moves with constant velocity v0 (motility), where the direction of this velocity changes in course of time due to rotational noise. Most of the calculations in the present study are based on a fully two-dimensional version of an active Brownian particle where both, the translations and the rotations, are restricted to say, the x−y plane. The Langevin equations for this “disk-like” active particle are given by
 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin
ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ)T relative to the x-axis. Further, U(x,y) is the external potential, DT and ξT,x(t), ξT,y(t) are the translational diffusion constant and noise terms, respectively, and DR and ξR(t) relate to rotational diffusion. All noise terms here are independent, and each is considered to be Gaussian white noise with zero mean, i.e. 〈ξ(t)〉 = 0, and 〈ξ(t1)ξ(t2)〉 = δ(t1 − t2). In Section 3.1.4 we additionally consider a “spherical” active Brownian particles whose translational motion is still restricted to the x–y-plane (e.g., by some sort of confinement) whereas the noisy rotational motion is three-dimensional.
ϕ)T relative to the x-axis. Further, U(x,y) is the external potential, DT and ξT,x(t), ξT,y(t) are the translational diffusion constant and noise terms, respectively, and DR and ξR(t) relate to rotational diffusion. All noise terms here are independent, and each is considered to be Gaussian white noise with zero mean, i.e. 〈ξ(t)〉 = 0, and 〈ξ(t1)ξ(t2)〉 = δ(t1 − t2). In Section 3.1.4 we additionally consider a “spherical” active Brownian particles whose translational motion is still restricted to the x–y-plane (e.g., by some sort of confinement) whereas the noisy rotational motion is three-dimensional.
An equivalent representation of the two-dimensional model in eqn (1) is given by the Smoluchowski equation42
| ∂tψ = {∇·(∇U − v0ê(t) + DT∇) + ∂ϕ2}ψ, | (2) |
Calculating from eqn (2) the mean position of the active particle with the initial conditions x(0) = 0, y(0) = 0 and ϕ(0) = 0, one obtains
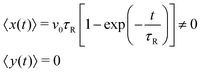 | (3) |
3 Delayed feedback control
In this section we propose a delayed feedback control strategy for steering an active particle in the framework of two methods based on laser light.3.1 Optical trapping
The conventional optical trapping method without feedback control23 is based on a strong laser beam which acts like a “tweezer”. This laser tweezer restricts the random motion due thermal fluctuations by introducing a confining potential. Apart from particle localization, the tweezer provides the possibility to move the particle by moving the laser beam. However, tuning the laser intensity is not trivial: if the laser beam is not sufficiently strong to sharply localize the particle, there is the possibility of losing the particle while translating the laser beam position. This has to be balanced with the fact that a too strong intensity can damage the particle. While these considerations apply already to passive particles, trapping of active particles can be even more involved since, upon switching on the laser beam, they can transform the received energy into directional motion.However, when the laser beam is much larger than the particle size, the trapping effect becomes significant only when then particle reaches the border of laser spot. Within the spot, the motion of the particle consists of large free displacements due to the activity of the particles. Experimentally, it has been demonstrated that such a set-up could be provided by a defocused laser beam.24 The mean squared displacement (MSD) of particles in a defocused laser beam has been experimentally shown to have a ballistic regime due to the directed motions of ABPs followed by a crossover to normal diffusion at times longer than the rotational relaxation time. Only at very long times, the MSD reaches a plateau due to the trapping effect in the laser beam.
In what follows we propose a delayed feedback control which could be coupled to the aforementioned optical trapping method in order to localize and steer an active particle.
We recall that the irradiation of a laser beam has two different impacts on the motion of a (photo-sensitive) active particle. On the one hand, it increases the mobility by creating a temperature gradient around the particle (self-thermophoresis).24 On the other hand, it leads to a two-dimensional trapping of the particle.43 Here we aim at combining these two effects in order to restrict the two-dimensional random motion of the particle with its three degrees of freedom (i.e., x, y, ϕ) to a quasi-one dimensional motion with a preferred direction. Our proposal for such a control process consists of two steps: first, restricting the motion in quasi-one dimension by an optical trap and second, breaking the symmetry of motion by adapting the intensity.
In order to restrict the particle motion along one dimension, say x, one needs to enhance the trapping effect in y-axis. At the same time, the particle should be able to freely move in x-direction. This could be realized with a laser beam (with a waist being a few times the particle size to allow for limited free motion), whose center moves with the particle, yet only along the x-axis.
Let us now construct the corresponding potential: in general, a particle at position r = (x,y) in an optical trap located at r0 = (x0,y0) experiences an approximately harmonic potential of the form
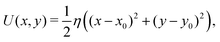 | (4) |
We recall that we want the particle to move from rA = (xA,0) to rB = (xB,0). We therefore set the y-component of the trap position r0 to zero. Further we assume that there is a delay time δ between monitoring the position of particle at time t and driving the laser along the x-axis. The “control” potential then has the form
 | (5) |
For small delay times (and thus, small differences x(t) − x(t − δ)), the trapping effect in x-direction is therefore much weaker than that in y-direction, and for δ → 0, the particle feels no trapping in x-direction at all.
From eqn (5), the control force acting on the particle follows as
| Fc(t) = −∇Uc(x,y,t) = −η[(x(t) − x(t − δ))î + y(t)ĵ], | (6) |
To this end, the next step of our control strategy is to break the symmetry of the quasi-one dimensional motion along the x-axis in favor of our desired direction. For this, we propose to modify the intensity of the applied laser intensity depending on the previous position of the particle (see Fig. 1 for a sketch). This idea is based on the fact that the laser intensity determines both, the motility (v0) of the active particle and the stiffness (η) of the harmonic (optical) trap.
 | ||
| Fig. 1 Schematic explanation of the control strategy involving optical trapping from a theoretical perspective. The intensity of the laser beam, which controls the motility of the particle, is a function of its displacement during the delay time (see eqn (7)). If the particles is heading towards its destination, i.e., in positive x-direction, the intensity is enhanced as indicated by the deeper red color. | ||
Consider the difference between the particle's position in x-direction at time t, x(t), and the corresponding position at the earlier time t − δ. If the displacement x(t) − x(t − δ) is positive, the particle is most likely heading in the desired direction towards its destination at point B (with xB > xA). Under this condition, we increase the intensity in order to increase the motility. Likewise, for negative x(t) − x(t − δ) we decrease the intensity such that particle motion in the “wrong” direction is hindered. Specifically, we assume a linear modification of the laser intensity described by
| I(t,δ) =I(x(t) − x(t − δ)) = I0(1 + β(x(t) − x(t − δ))), | (7) |
We now consider the resulting effect on the motility. Experimental reports indicate a linear relationship between motility and the laser intensity,19v(t) ∝ I(t), for moderate intensities. Combining this with the above ansatz for the intensity, eqn (7), the motility at time t for a given δ becomes
| v(t,δ) = v0(1 + β(x(t) − x(t − δ))), | (8) |
| η(t,δ) = η0(1 +β(x(t) − x(t − δ))). | (9) |
One may note that the above considerations do not take into account a spatial dependency of the intensity and thus, the motility and stiffness, inside the trap. We have indeed neglected such a dependency assuming that the laser beam is much bigger than the particle size (“defocused laser beam”). In this situation, the particle displacement during the delay time is so small that one may safely assume the intensity at any point in the optical trap to be equal. This assumption, however, is not crucial for our approach; one could easily include a spatial dependence as well.
We are now in the position to construct the equation of motion in presence of delayed feedback. To this end we start from the conventional equations of motion for an active Brownian particle, eqn (1). First, we replace the constant motility v0 by the time-dependent motility given in eqn (8). Second, we replace the derivative of the potential U(x,y) by the control force given in eqn (6), where the spring constant is now given by eqn (9). With these steps we arrive at
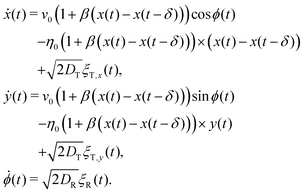 | (10) |
From a mathematical perspective, eqn (10) represent a set of coupled stochastic delay-differential equations. Treating such systems is generally a challenging task: For example, the delay can induce new dynamical features such as spontaneous oscillations45,46 not seen in the Markovian case. Moreover, the transition towards a Fokker–Planck description is significantly more involved (see, e.g.,33).
In the present study we proceed with the theoretical description by assuming that the delay time, δ, is much shorter than the rotational relaxation time, τR. In other words, there is only a very small displacement of the particle during the delay time. This assumption justifies a Taylor expansion of x(t − δ) around δ = 0, i.e., x(t − δ) ≃ x(t) − δẋ(t) + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (δ2). Substituting the Taylor expansion into eqn (10), neglecting all terms in δ beyond the linear one and solving the resulting equations with respect to ẋ and ẏ, we obtain the non-delayed (and thus, Markovian) equations
(δ2). Substituting the Taylor expansion into eqn (10), neglecting all terms in δ beyond the linear one and solving the resulting equations with respect to ẋ and ẏ, we obtain the non-delayed (and thus, Markovian) equations
 | (11) |
We recall our argumentation in the previous section (after eqn (7)) regarding the limitation in choosing the value of β. This restriction can now be formulated more precisely. Applying the small delay approximation to the right side of eqn (7), one obtains the condition βδẋ(t) > −1, which relates the β to the delay time δ. This implies that to keep the intensity positive, and noting that the sign of ẋ(t) can become negative, large values of β require small values of δ.
Our coarse-graining procedure closely follows that proposed by Mijialkov et al.34 and Leyman et al.35 (see the Appendices of these references for details). We start by considering the limiting case of eqn (11), where the rotational relaxation time τR and the delay time δ are both very small, but their ratio is finite and tends to zero, i.e., δ/τR → 0. Formally, this is done by introducing a small parameter ε such that δ = cε and τR = kε, with c and k being constants and ε → 0. In order to keep the particle displacement significant for small τR, we define  . Inserting these definitions into eqn (11) and keeping only the leading forms i.e., those of order ε−1/2 and unity, we obtain
. Inserting these definitions into eqn (11) and keeping only the leading forms i.e., those of order ε−1/2 and unity, we obtain
 | (12) |
The PDF ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (r,ϕ,t) corresponding to eqn (12) (i.e., the rescaled Langevin equations in small-delay approximation) obeys the backward Kolmogorov equation
(r,ϕ,t) corresponding to eqn (12) (i.e., the rescaled Langevin equations in small-delay approximation) obeys the backward Kolmogorov equation
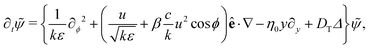 | (13) |
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) in powers of
in powers of  as
as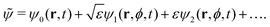 | (14) |
We further note that eqn (13) may be written as
 | (15) |
 | (16) |
Inserting the ansatz (14) into eqn (15) and sorting the terms according to their order in  , we obtain in order
, we obtain in order 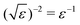
 | (17) |
 we find
we find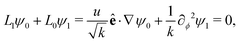 | (18) |
 ,
,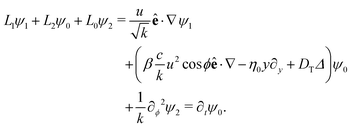 | (19) |
Eqn (17) allows for a solution ψ0 which contains a linear term in ϕ and a constant. Here we select the constant solution since the coarse-grained PDF should not depend on ϕ, i.e., ψ0 = ψ0(x,y,t). Further, eqn (18) implies that  where we have used the fact that ê = (cos
where we have used the fact that ê = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin
ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ). Finally, eqn (19) can be rewritten as L0ψ2 = ∂tψ0 − L1ψ1 − L2ψ0. Formally (see ref. 47 for a more mathematical discussion) this implies that the function u(r,ϕ,t) = ∂tψ0 − L1ψ1 − L2ψ0 is in the range of the operator L0, where L0 is an operator in ϕ and u is considered as a function slowly varying in ϕ. As a consequence,47u has to be orthogonal to the null space (kernel) of the adjoint operator L0* (where the null space is the set of functions ρ for which L0*(ρ) = 0). Here, L0 is a self-adjoint operator, i.e., L0* = L0, and the null space corresponds to a constant function in ϕ, as argued already at the beginning of this paragraph. This yields the orthogonality relation
ϕ). Finally, eqn (19) can be rewritten as L0ψ2 = ∂tψ0 − L1ψ1 − L2ψ0. Formally (see ref. 47 for a more mathematical discussion) this implies that the function u(r,ϕ,t) = ∂tψ0 − L1ψ1 − L2ψ0 is in the range of the operator L0, where L0 is an operator in ϕ and u is considered as a function slowly varying in ϕ. As a consequence,47u has to be orthogonal to the null space (kernel) of the adjoint operator L0* (where the null space is the set of functions ρ for which L0*(ρ) = 0). Here, L0 is a self-adjoint operator, i.e., L0* = L0, and the null space corresponds to a constant function in ϕ, as argued already at the beginning of this paragraph. This yields the orthogonality relation
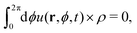 | (20) |
 | (21) |
Substituting  , as obtained above, in the integral and performing the integration, one reaches to the desired backwarded Kolmogorov equation for the coarse-grained PDF ψ0, that is,
, as obtained above, in the integral and performing the integration, one reaches to the desired backwarded Kolmogorov equation for the coarse-grained PDF ψ0, that is,
 | (22) |
As a last step of our coarse-graining strategy, we note that eqn (22) corresponds to the following set of (Markovian) Langevin equations for the variables x and y,
 | (23) |
A “pedestrian” proof of the drift term in the equation for ẋ and the friction term in the equation for ẏ in equations above can be done by looking at the long time asymptotic behavior of each term in eqn (11) or (12). At very long times, the particle visits all the orientations with the same probability, that is the angular probability density is a constant 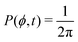 . This corresponds to a unweighted average over ϕ. Thus, terms linear in sin
. This corresponds to a unweighted average over ϕ. Thus, terms linear in sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ and cos
ϕ and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ will not effectively drive the particle. The term cos2
ϕ will not effectively drive the particle. The term cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ in the equation for ẋ will, however, remain positive and its average of 1/2 leads to a drift term as βδv02/2. In the equation for the y component, the −η0y term is independent of the particle orientation. This leads to the friction term.
ϕ in the equation for ẋ will, however, remain positive and its average of 1/2 leads to a drift term as βδv02/2. In the equation for the y component, the −η0y term is independent of the particle orientation. This leads to the friction term.
In conclusion, inspecting the first member of the coarse-grained Langevin eqn (23), we find that the active particle effectively feels a constant driving force of magnitude βδv02/2 in positive x-direction, i.e., towards its destination. As a consequence, the average position in x-direction at time t is given by 〈x(t)〉 = βδv02/2t. We recall that the separation between the target position xB and the initial position xA is given by L. From this, we obtain the mean arrival time
 | (24) |
The y-component of the particle position (see the second member of eqn (23)) is, however, described by an Ornstein–Uhlenbeck process. From this one can calculate the mean y-position,
| 〈y(t) 〉 = 0 | (25) |
and the mean squared displacement in y-direction,
 | (26) |
In Fig. 2 and 3 we present exemplary particles trajectories, first, in the x–y plane (Fig. 2) and second, in x-direction as function of time (Fig. 3). The particle moves from the starting point at rA = (0,y0) to the target position rB = (1000σ,y0), where the different values of y0 are solely used to separate different trajectories. The shown trajectories differ by the parameter βσ, where we recall that β (which has the dimension of an inverse length) controls the strength of symmetry breaking in x-direction. For better visibility, we focus on the range y > −200σ.
 | ||
| Fig. 2 Exemplary particle trajectories in the x–y plane according to eqn (10) for βσ = 0 (brown), 5 (black), 10 (red), 15 (green) and 20 (blue). For better visibility, the data corresponding to different βσ are shifted by ΔyA/σ = 80. The other parameters are set to τR = 65δ, v0 = 1σ/δ, and η0 = 0.1σδ−2. | ||
 | ||
| Fig. 3 The x-component of the particle position as function of time according to eqn (10) for βσ = 0 (brown), 5 (black), 10 (red), 15 (green) and 20 (blue). The other parameter are chosen as in Fig. 2. | ||
We start by considering the case βσ = 0. In this case, the laser intensity and thus, the motility and stiffness are always constant (see eqn (7)–(9)) and there is no symmetry breaking in x-direction. The impact of the control then reduces to the trapping in y-direction. The latter effect is clearly visible from Fig. 2, where the trajectory for βσ = 0 appears like a densely filled “stripe”. However, this shape of the trajectory also implies that the particle moves randomly to the right and left, that is, there is no bias. The latter point is even better seen in Fig. 3, which shows the x-position as function of time. Clearly, for βσ = 0 there is no preference for negative or positive values of x.
Increasing the parameter βσ from zero, the trapping in y-direction continues to be effective. This is seen from Fig. 2, illustrating that the area explored by the particle in y-direction stays essentially constant compared to βσ = 0. Importantly, however, the motion in x-direction becomes more and more directed towards positive values. In more detail, at the lowest nonzero value considered (βσ = 5), particle motion in negative direction is still significant. Closer inspection reveals that the trajectory (in x–y-plane) here consists of large loops which slowly move towards positive x-values. For larger values of βσ the symmetry breaking is more significant and displacements in negative x direction become progressively shorter (see, e.g., the case βσ = 20).
These effects are even better visible in Fig. 3, showing clearly the importance of the symmetry breaking in x-direction to push the particle into the right direction. From a mathematical point of view, this becomes understandable when we take a look at the first member of eqn (23). For small values of β, the effective noise described by the last term competes with the drift term, the latter being proportional to β. Consequently, the particle experiences significant fluctuations im x-direction. These fluctuations become more and more restricted when the drift term is enhanced by increasing β.
We now turn to the mean arrival time, which the particle requires to reach its target. To obtain numerical results, we have performed 103 simulation runs for each value of βσ. The averaged numerical data are shown in Fig. 4, which also includes the analytical prediction from the coarse-grained theory (see eqn (24)).
 | ||
| Fig. 4 Mean arrival time of the particle as a function of the distance between starting point and target for βσ = 5 (black), 10 (red), 15 (green) and 20 (blue). Symbols correspond to averaged numerical results from eqn (10), whereas black lines represent plots of eqn (24). | ||
At the smallest value considered, βσ = 5, we observe small deviations between theory and simulation data. The reason is that in this weakly controlled situation, fluctuations in x-direction are non-negligible, as already explained above. In contrast, we observe excellent agreement between theory and simulations at larger values of βσ. This agreement is due to the fact that, within our analytical theory, larger values of β correspond to a larger drift term in the (coarse-grained) equation for the x-component, see eqn (23). The impact of the noise term (second term) then becomes negligible. One should note, however, that even in the numerical simulations the control parameter β cannot be chosen arbitrarily large: the reason is that the intensity, which depends on β and on the displacement (see eqn (7)), has always to remain positive, yielding the condition 1 + β(x(t) − x(t − δ)) ≥ 0. For negative displacements, this imposes an upper limit for β.
Finally, it is worth to note that essentially the same efficiency of our control strategy (quantified through the mean arrival time) could be achieved if we kept the stiffness of the trap, η, constant. Indeed the main effect of a constant stiffness is that the width of the channel in y-direction becomes constant. However, test calculations showed that this is essentially irrelevant for the resulting mean arrival time. The underlying reason can be seen from the original (delayed) equations of motion, eqn (10). These equations reflect that the stiffness enters the dynamics of the x-coordinate only to second order in the displacement (in contrast, the dynamics of the y-coordinate is affected already in linear order). Therefore, the mean arrival time for steered motion in x-direction (for which our proposal has been formulated), is only weakly affected by the time dependence of the stiffness. If we considered more refined measures of efficiency, such as the degree of fluctuations in perpendicular (y-) direction, these would certainly be more sensitive.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin
ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,cos
ϕ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), with ϕ and θ being the polar and azimuthal angle, respectively. We refer to this model henceforth as “3d”, where d is the dimension of rotational motion. From a physical point of view, this 3d model describes, e.g., an active colloid which is resting on the bottom of a container, or a confined particle which motion in z-direction is restricted by walls.20,48,49 Assuming again a two-dimensional self-propulsion of the form v0(ex,ey), the corresponding Langevin equations read
θ), with ϕ and θ being the polar and azimuthal angle, respectively. We refer to this model henceforth as “3d”, where d is the dimension of rotational motion. From a physical point of view, this 3d model describes, e.g., an active colloid which is resting on the bottom of a container, or a confined particle which motion in z-direction is restricted by walls.20,48,49 Assuming again a two-dimensional self-propulsion of the form v0(ex,ey), the corresponding Langevin equations read | (27) |
In analogy to our procedure for the 2d model (see Section 3.1), we now replace the constant motility v0 by the time-dependent motility given in eqn (8), and the derivative of the potential U(x,y) eqn (6), utilizing eqn (9) for the spring constant. This yields the delayed Langevin equations
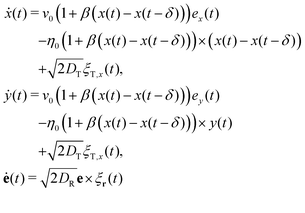 | (28) |
To study the impact of the different character of rotational noise (as compared to the 2d model considered before), we have performed a set of numerical simulations similar to those described in the previous section, for control parameters βσ = 5, 10, 15 and 20. Results for the mean time which a particles needs to move over a distance L on the x-axis are plotted in Fig. 5. The data indicate again a linear dependence of the arrival time of the distance, consistent with what we have seen in the case of two-dimensional rotational motion, see Fig. 4. However, closer inspection shows that (within the errors arising from the noise terms in the equations of motion) the mean arrival times in the case of 3d rotational noise are larger by almost fifty percent. This implies, in particular, that the prediction for τarr of our coarse-grained model, eqn (24), which gave a very good estimate for the 2d situation (see Fig. 4), does not properly describe the 3d case.
 | ||
| Fig. 5 Mean arrival time of a confined active particle with three-dimensional rotational noise as function of the distance between starting point and target for βσ = 5 (black), 10 (red), 15 (green) and 20 (blue). Symbols correspond to averaged numerical results from eqn (28), whereas black lines represent plots of the function τ3darr defined in eqn (29). | ||
To this end, it is helpful to have a closer look on the implications of the definition of the orientation vector. In the 3d case, the x and y components are given as ex = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ and ey = sin
ϕ and ey = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, where the factor sin
ϕ, where the factor sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ makes the difference to the 2d case. From eqn (27) or (28) it can be seen that this factor may also be regarded as a prefactor of the motility, v0, suggesting the definition of a modified motility ν0′ = ν0
θ makes the difference to the 2d case. From eqn (27) or (28) it can be seen that this factor may also be regarded as a prefactor of the motility, v0, suggesting the definition of a modified motility ν0′ = ν0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. With this modified motility, eqn (28) for ẋ(t) and ẏ(t) become identical to those in the 2d case, see eqn (10). We now turn back to our earlier prediction of the mean arrival time, eqn (24), which involves an inverse quadratic dependence on the motility. To apply this to the 3d case, we suggest to replace v02 by
θ. With this modified motility, eqn (28) for ẋ(t) and ẏ(t) become identical to those in the 2d case, see eqn (10). We now turn back to our earlier prediction of the mean arrival time, eqn (24), which involves an inverse quadratic dependence on the motility. To apply this to the 3d case, we suggest to replace v02 by  . To estimate the average we use a similar argument as we did within our “pedestrian proof” below eqn (23): At long times (i.e., large distances to the starting point), the angle θ explores all values in the interval [0,π], with a weight being given by the (normalized) distribution is P(θ) = 2−1
. To estimate the average we use a similar argument as we did within our “pedestrian proof” below eqn (23): At long times (i.e., large distances to the starting point), the angle θ explores all values in the interval [0,π], with a weight being given by the (normalized) distribution is P(θ) = 2−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (corresponding to a uniform sampling of the unit sphere). The average is therefore given as
θ (corresponding to a uniform sampling of the unit sphere). The average is therefore given as  . Inserting this expression into eqn (24), we obtain
. Inserting this expression into eqn (24), we obtain
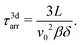 | (29) |
Comparing the resulting data for the mean arrival times with the numerical ones, see Fig. 5, we find that the agreement is again remarkably good, similar as it was in the 2d case. Of course, one reason for the simple relation between the analytical results for the mean arrival time in the 2d and 3d case is that, even for the 3d situation, we still consider a motion along the x-axis. An analytical treatment for a path in two or three spatial dimensions would be much more involved. Also, our treatment of the 3d case neglects any frictional forces, which might be present for a real spherical particle confined by a wall in z-direction.
3.2 Photon nudging: control strategy
While optical trapping has, generally, a wide range of applications, it also has drawbacks (e.g., destruction) and limitations in complex systems such as biological environment,51 even at low laser intensity. This motivated us to examine the proposed idea to approximate the particle orientation in the context of the photon nudging method, where the laser intensity is typically even smaller and the laser is not continuously active.More specifically, within the photon nudging method,19 a focused laser beam of moderate intensity pushes the active particle along its heading direction. Physically, the propulsion process is based on two mechanisms which occur simultaneously, that is, radiation-pressure52,53 and photophoresis.23 In order to navigate the particle, the propulsion becomes active, that is, the laser is switched on only when the particle orientation ê(t) has the desired direction19 given by the connection vector between the particle and the target. This clearly requires monitoring ê(t) in real time.
Here we propose an alternative strategy where the particle orientation is estimated via the difference between the actual and delayed position. This is similar in spirit to what we have proposed within the optical trapping strategy (see, e.g., eqn (6)), with the difference that we now require two delayed coordinates instead of only one (due to the absence of a confinement in y-direction). Specifically, the estimated orientation vector is written as
| p(t) = (x(t) − x(t − δ))î + (y(t) − y(t − δ))ĵ, | (30) |
To quantify the deviation between the particle orientation and the desired direction of motion, we introduce the (dimensionless) angle α(t) defined as
 | (31) |
| rT(t) = (L − x(t))î − y(t)ĵ. | (32) |
An illustration of these quantities is given in Fig. 6. The central idea of control is to adapt the laser intensity I based on the actual value of α(t).
Let us now turn to the formulation of the equations of the motion. Similar to our approach for optical trapping (see, in particular, eqn (7) and (8)), we assume a linear relationship between the laser intensity (and thus, the motility) and the control parameter, in this case α. In the optimal case, α should be zero (i.e., p(t) is directed towards the target). In order to prevent considerable motion in the direction opposite to the target, we define a cut-off angle α0 above which the intensity (and thus the motility) is reset to a constant small value. With these considerations in mind, we make the following ansatz for the motility:
 | (33) |
In eqn (33), the dimensionless function f(α) is set to zero for α(t) > α0 and to a constant positive value f0 when α(t) < α0. The resulting motility becomes maximal (v(t) = vmax = v0(1 + f0)) if α(t) = 0, as it should be.
To summarize, we now have two control parameters (contrary to our optical trapping strategy): First, the parameter f0 which determines how fast the particle moves when it has the proper orientation. Second, the cut-off angle α0 which, as we will see from the numerical results presented below, plays a crucial in the control process.
The Langevin equations of such a controlled motion then read
 | (34) |
To this end we have performed calculations for different values of the cut-off angle α0 at fixed f0 = 7, v0 = 0.1σ/δ and τR = 65δ. Exemplary trajectories in the x–y plane are shown in Fig. 7. The particle starts at rA = (0,0) and is supposed to move to rB = (L,0). The data reveal several effects. For small cut-off values (e.g., α0 = 15) the trajectory involves significant portions in the wrong (i.e., negative x-)direction. This changes upon increase of α0, indicating that higher values of the cut-off parameter provide a faster steering process. Finally, the full trajectories presented in the inset of Fig. 7 show that the particle reaches its destination for all values of α0 considered. This indicates that our control based on the estimated particle orientation is indeed successful and robust against changes of α0.
To compare the method proposed here with the “conventional” strategy based on the true orientation vector ê(t), we calculated the mean arrival time. Results for different α0 are presented in Fig. 8. We find that the present method yields essentially the same results as the conventional method; indeed, deviations are visible only for the smallest value of α0 (black data). The results also confirm our earlier observation, namely, that higher values of the cut-off parameter lead to faster steering.
 | ||
| Fig. 8 Mean arrival times as function of distance to the target and different values of the cut-off parameter: α0 = 15 (black), 30 (red), and 45 (green). The data labeled by circles have been obtained by the present method based on the estimated particle orientation, while those labeled by the blue asterisks are calculated by the conventional method based on the true orientation. The remaining parameters are set as in Fig. 7. | ||
Finally, we mention one conceptual difference between the strategy proposed here and the conventional one: in our case, the laser intensity should not never be zero. The underlying reason is that our strategy uses the displacements at earlier times to predict the orientation of the particle at a given time (see eqn (30)). Whenever the so-obtained heading vector is oriented in the wrong direction, the particle will still slightly move. The corresponding displacement must be detectable (for a camera) in order to allow for corrections at later time. This requires a certain minimum motility v0 and thus, intensity I0. On the other hand, I0 should be as small as possible to avoiding significant motion in unwanted direction. For small cut-off values α0, this fact could make a non-negligible difference in efficiency compared to the conventional method, since the particle spends more time in the state where the laser would be off in the conventional method.
4 Summary
In this work, we have explored methods to navigate an active particles through its approximate orientation vector determining the direction of its motion. The approximation involves the difference between the actual particle position at time t and that a somewhat earlier (“delayed”) time, t − δ. This approximation is inspired by the idea that, especially for small particles, real-time monitoring of the true orientation can be experimentally very difficult or even impossible. In contrast, positional control can given achieved via fluorescence spectroscopy even for small particle sizes on the nanoscale.We have applied (on a theoretical and numerical level) the idea of using the delayed position for navigation of the particle, first, in the context of optical trapping. By following the particle with a laser trap along the direction towards the target, we confine its motion effectively into a channel. Navigation in the channel is achieved by introduced an asymmetry in motion based on the approximate orientation. The resulting set-up drives the particle efficiently into the desired direction, as we have shown by numerical simulations of the full (delayed) equations of motion and by analytical theory. The latter is based on a coarse-graining approach for the limit of small delay times, yielding explicit results for the effective force acting on the particle and the mean arrival time. The agreement between theory and simulation is excellent. In this context, we also note an interesting effect of the dimension of rotational noise. Indeed, most of our results refer to a completely two-dimensional situation, where the active particle is spatially confined to a plane and rotates only in this plane. In Section 3.1.4 we have additionally explored the situation that the confined particle can rotationally explore all directions on the unit sphere. It turns out that the mean arrival time increases, as one might expect. Interestingly, this effect can still be captured by a coarse-grained theory as long as the translational motion remains one-dimensional.
As a second application we have considered a variant of the photon nudging method where, instead of the true particle orientation, the approximate one is used. We have provided numerical results for different values of the cut-off parameter used to adapt the (laser) intensity. The data indicate a very good performance of the approximation.
We note that, although we have assumed the delay to be small, it is clearly a crucial ingredient: without delay, our approximation for the particle orientation breaks down. In this sense, our approach provides an example of a feedback-controlled system in which time delay has a constructive effect. Indeed, in many studies of feedback-control, delay is rather considered as a disturbance, whose role is therefore neglected. Here, not only we do not neglect the delay, but also utilize it.
Of course, it would be very important and interesting to see the performance of our proposal in a real experiment. In this context, we also mention that there are some ingredients of our proposal which could be applied to a passive particle as well. In particular, trapping a passive particle by a laser beam is nowadays a standard method (optical tweezer),54,55 and also moving traps are quite common.56–58 Furthermore, the approximation of the particle's velocity (which, for our active particle model, equals the orientation vector) through its displacement vector related to a given time interval between t and t − τ could also be applied to a passive particle. One should note, however, that the typical diffusion time scale of a passive particle is smaller than that of an active one, which might render the approximation more severe. Moreover, for a light-sensitive active particle, changing the intensity of the laser beam has an impact on the motility, and we have used this fact both, in the optical trapping part and within the photon-nudging part. For a passive particle, this effect is obviously absent, and one would need another mechanism to drive the particle.
The present work may be considered as a contribution to ongoing efforts to understand and put forward the role of feedback control for stochastic Langevin systems, in this case self-propelled particles. There are many intriguing open questions, such as thermodynamical implications, which proves to be particularly challenging in presence of time delay.59 Moreover, from the physical (and applicational) side there is strong interest in navigating the motion not only of single self-propelled objects, but also of larger ensemble which can display complex collective behavior already in the absence of any control. In these contexts, time delay may again play a significant role, as first studies indicate.34
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge discussion with R. Klages and F. Cichos. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Projektnummer 163436311 – SFB 910.References
- W. Wang, W. Duan, S. Ahmed, T. E. Mallouk and A. Sen, Nano Today, 2013, 8, 531 CrossRef CAS.
- M. Brambilla, E. Ferrante, M. Birattari and M. Dorigo, Swarm Intelligence, 2013, 7, 1 CrossRef.
- S.-H. Kim, S. Y. Lee, S.-M. Yang and G.-R. Yi, NPG Asia Mater., 2011, 3, 25 CrossRef CAS.
- J. Stenhammar, R. Wittkowski, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2015, 114, 018301 CrossRef PubMed.
- R. Golestanian, Phys. Rev. Lett., 2012, 108, 038303 CrossRef PubMed.
- H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308 CrossRef CAS PubMed.
- S. Heidenreich, J. Dunkel, S. H. L. Klapp and M. Bär, Phys. Rev. E, 2016, 94, 020601 CrossRef PubMed.
- P. Tierno, R. Golestanian, I. Pagonabarraga and F. Sagués, Phys. Rev. Lett., 2008, 101, 218304 CrossRef PubMed.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- D. F. Haeufle, T. Bäuerle, J. Steiner, L. Bremicker, S. Schmitt and C. Bechinger, Phys. Rev. E, 2016, 94, 012617 CrossRef PubMed.
- J. Bechhoefer, Rev. Mod. Phys., 2005, 77, 783 CrossRef.
- R. Gernert, S. A. Loos, K. Lichtner and S. H. L. Klapp, Feedback control of colloidal transport, in Control of Self-Organizing Nonlinear Systems, Springer, 2016, p. 375 Search PubMed.
- A. E. Cohen, Phys. Rev. Lett., 2005, 94, 118102 CrossRef PubMed.
- Y. Jun and J. Bechhoefer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 061106 CrossRef PubMed.
- J. Gieseler, L. Novotny, C. Moritz and C. Dellago, New J. Phys., 2015, 17, 045011 CrossRef.
- M. Braun, A. P. Bregulla, K. Günther, M. Mertig and F. Cichos, Nano Lett., 2015, 15, 5499 CrossRef CAS PubMed.
- J. Fisher, J. Cummings, K. Desai, L. Vicci, B. Wilde, K. Keller, C. Weigle, G. Bishop, R. Taylor and C. Davis, et al. , Rev. Sci. Instrum., 2005, 76, 053711 CrossRef.
- M. Braun, A. Würger and F. Cichos, Phys. Chem. Chem. Phys., 2014, 16, 15207 RSC.
- A. P. Bregulla, H. Yang and F. Cichos, ACS Nano, 2014, 8, 6542 CrossRef CAS PubMed.
- M. Selmke, U. Khadka, A. P. Bregulla, F. Cichos and H. Yang, Phys. Chem. Chem. Phys., 2018, 20, 10502 RSC.
- C. C. Maass, C. Krüger, S. Herminghaus and C. Bahr, Annu. Rev. Condens. Matter Phys., 2016, 7, 171–193 CrossRef CAS.
- B. Qian, D. Montiel, A. Bregulla, F. Cichos and H. Yang, Chem. Sci., 2013, 4, 1420 RSC.
- A. Ashkin, J. M. Dziedzic, J. Bjorkholm and S. Chu, Opt. Lett., 1986, 11, 288 CrossRef CAS.
- H.-R. Jiang, N. Yoshinaga and M. Sano, Phys. Rev. Lett., 2010, 105, 268302 CrossRef PubMed.
- H.-R. Jiang, H. Wada, N. Yoshinaga and M. Sano, Phys. Rev. Lett., 2009, 102, 208301 CrossRef PubMed.
- E. Schöll and H. G. Schuster, Handbook of chaos control, John Wiley & Sons, 2008 Search PubMed.
- F. M. Atay, Complex time-delay systems: theory and applications, Springer, 2010 Search PubMed.
- F. Marino and G. Giacomelli, Chaos, 2017, 27, 114302 CrossRef PubMed.
- T. Schemmelmann, F. Tabbert, A. Pimenov, A. G. Vladimirov and S. V. Gurevich, Chaos, 2017, 27, 114304 CrossRef CAS PubMed.
- D. Yu and J. Gomm, Control Eng. Pract., 2003, 11, 1315 CrossRef.
- A. A. Pogodaev, A. S. Wong and W. T. Huck, J. Am. Chem. Soc., 2017, 139, 15296 CrossRef CAS PubMed.
- V. H. Thanh, R. Zunino and C. Priami, J. Chem. Phys., 2017, 146, 084107 CrossRef PubMed.
- S. A. Loos and S. H. L. Klapp, Phys. Rev. E, 2017, 96, 012106 CrossRef PubMed.
- M. Mijalkov, A. McDaniel, J. Wehr and G. Volpe, Phys. Rev. X, 2016, 6, 011008 Search PubMed.
- M. Leyman, F. Ogemark, J. Wehr and G. Volpe, Phys. Rev. E, 2018, 98, 052606 CrossRef.
- W. F. Paxton, K. C. Kistler, C. C. Olmeda, A. Sen, S. K. St. Angelo, Y. Cao, T. E. Mallouk, P. E. Lammert and V. H. Crespi, J. Am. Chem. Soc., 2004, 126, 13424 CrossRef CAS PubMed.
- S. Fournier-Bidoz, A. C. Arsenault, I. Manners and G. A. Ozin, Chem. Commun., 2005, 441 RSC.
- A. Ghosh and P. Fischer, Nano Lett., 2009, 9, 2243 CrossRef CAS PubMed.
- W. Wang, L. A. Castro, M. Hoyos and T. E. Mallouk, ACS Nano, 2012, 6, 6122 CrossRef CAS.
- A. Ashkin, Phys. Rev. Lett., 1970, 24, 156 CrossRef CAS.
- G. Volpe, I. Buttinoni, D. Vogt, H.-J. Kümmerer and C. Bechinger, Soft Matter, 2011, 7, 8810 RSC.
- F. J. Sevilla and M. Sandoval, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 052150 CrossRef PubMed.
- S. Sato, Y. Harada and Y. Waseda, Opt. Lett., 1994, 19, 1807 CrossRef CAS PubMed.
- V. R. Rodrigues, A. Mondal, J. A. Dharmadhikari, S. Panigrahi, D. Mathur and A. K. Dharmadhikari, PLoS One, 2013, 8, e61310 CrossRef CAS PubMed.
- L. Tsimring and A. Pikovsky, Phys. Rev. Lett., 2001, 87, 250602 CrossRef CAS PubMed.
- H. Hong, G. S. Jeon and M. Choi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 026208 CrossRef CAS PubMed.
- G. Pavliotis and A. Stuart, Multiscale methods: averaging and homogenization, Springer Science & Business Media, 2008 Search PubMed.
- F. J. Schwarzendahl and M. G. Mazza, arXiv preprint arXiv:1812.06687, 2018.
- A. Zöttl and H. Stark, J. Phys.: Condens. Matter, 2016, 28, 253001 CrossRef.
- J. K. Dhont, An introduction to dynamics of colloids, Elsevier, 1996, vol. 2 Search PubMed.
- K. C. Neuman and A. Nagy, Nat. Methods, 2008, 5, 491 CrossRef CAS PubMed.
- V. Barkas, Philos. Mag., 1926, 2, 1019 Search PubMed.
- F. Ehrenhaft, Ann. Phys., 1918, 361, 81 CrossRef.
- A. Ashkin, Optical trapping and manipulation of neutral particles using lasers: a reprint volume with commentaries, World Scientific, 2006 Search PubMed.
- M. Dienerowitz, M. Mazilu and K. Dholakia, J. Nanophotonics, 2008, 2, 021875 CrossRef.
- R. M. Simmons, J. T. Finer, S. Chu and J. A. Spudich, Biophys. J., 1996, 70, 1813–1822 CrossRef CAS PubMed.
- M. Daly, M. Sergides and S. Nic Chormaic, Laser Photonics Rev., 2015, 9, 309–329 CrossRef CAS.
- D. Gao, W. Ding, M. Nieto-Vesperinas, X. Ding, M. Rahman, T. Zhang, C. Lim and C.-W. Qiu, Light: Sci. Appl., 2017, 6, e17039 CrossRef CAS PubMed.
- S. A. Loos and S. H. L. Klapp, Sci. Rep., 2019, 9, 2491 CrossRef PubMed.
| This journal is © the Owner Societies 2019 |