Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Strained hydrogen bonding in imidazole trimer: a combined infrared, Raman, and theory study†
Thomas
Forsting
 ,
Julia
Zischang
,
Martin A.
Suhm
,
Julia
Zischang
,
Martin A.
Suhm
 *,
Marco
Eckhoff
*,
Marco
Eckhoff
 ,
Benjamin
Schröder
and
Ricardo A.
Mata
*
,
Benjamin
Schröder
and
Ricardo A.
Mata
*
Institut für Physikalische Chemie, Universität Göttingen, Tammannstr. 6, 37077 Göttingen, Germany. E-mail: msuhm@gwdg.de; rmata@gwdg.de
First published on 25th February 2019
Abstract
In this work, a careful analysis of anharmonic couplings in NH and some CH stretch modes of imidazole is carried out. This includes IR and Raman spectra of the isolated molecule and aggregates up to the trimer, together with two different theoretical approaches to the calculation of anharmonic shifts and absolute band positions. The imidazole dimer is vibrationally characterized for the first time in vacuum isolation under supersonic jet conditions, showing substantial shifts from previous helium droplet experiments and evidence for Fermi resonance for the hydrogen-bonded NH stretch. The most stable imidazole trimer structure is unambiguously shown to be cyclic with three non-equivalent, highly strained hydrogen bonds. This contrasts the helium droplet observation of a chain trimer involving two unstrained hydrogen bonds. These experimental conclusions are strongly corroborated by theory, including vibrational perturbation theory and anharmonic normal mode analysis. Systematic error compensation in some of these methods is emphasized. Intramolecular anharmonic coupling constants from perturbation theory are validated by Raman hot band jet spectroscopy of the monomer. Imidazole aggregation is shown to provide valuable benchmarking opportunities for electronic structure and in particular for anharmonic vibrational methods, covering the field of strong and strongly distorted hydrogen bonding.
1 Introduction
The aggregation of imidazole has frequently served to benchmark theoretical predictions of non-covalent interactions,1–9 certainly motivated by its role as a building block for histidine and purine interactions. It involves a hydrogen bond donor and a hydrogen bond acceptor pointing away from each other due to their 1,3-placement in the heteroaromatic pentacycle. Small ambivalent solvent molecules have a choice between in plane solvation sites of the donor or the acceptor,4 besides secondary C–H contacts.10,11 Aromatic donors and acceptors can optimize secondary interactions by variation of the tilt angle in V- or T-shaped arrangements.6,12 In contrast to the isomeric heterocycle pyrazole13 with more aligned donor and acceptor groups, the homodimer of imidazole cannot realize both hydrogen bond functionalities at the same time and thus involves a single, unstrained hydrogen bond. This dimer has been characterized vibrationally in helium droplets14,15 and rotationally in the gas phase, using microwave spectroscopy.16 Argon matrix isolation was less conclusive, and what was denoted as a dimer signal1 around 3000 cm−1 is more likely due to large clusters. The imidazole trimer as the first cluster size capable of forming a concerted hydrogen bond cycle has been postulated and calculated before,17 but its vibrational spectrum in the gas phase has remained unassigned. In conflict with this proposed cyclic structure, the trimer spectrum in helium droplets displays a free NH stretch. This has been explained by a non-cyclic, chain-like structure18 which persists in the hydrate,19 in agreement with an earlier B3LYP prediction,20 at the time without London dispersion corrections.21 The previous B3LYP prediction of a cyclic structure17 was not discussed, but it was mentioned that the chain-like structure may be kinetically controlled.18 This non-cyclic structure was adopted in later work as the prototypical imidazole trimer aggregation pattern22 and the original cyclic structure proposal was not revisited. The present study explores different computational strategies to predict the vibrational spectrum of imidazole clusters and compares them to experimental IR and Raman spectra in supersonic jets, which suffer less from kinetic control than helium droplet pickup experiments.4 It concludes that the preferred trimer structure is indeed cyclic, but highly strained. Furthermore, it revisits the imidazole dimer in the NH/CH-stretching manifold. Although none of the investigated species has inversion symmetry, the complementarity of infrared and Raman spectroscopy in terms of NH/CH transition moments turns out to be very useful for the structural and dynamical characterization of imidazole clusters, in particular when supported by electronic structure and vibrational calculations. Furthermore, the observation of monomer hot bands in the Raman spectra directly helps to validate coupling constant predictions from vibrational perturbation theory.For benchmarking purposes, it is important that theory and experiment are compared on the same or at least a similar footing. Anharmonic predictions are best compared to gas phase spectra,23 although the shifts observed in helium droplets are often small enough to allow for a useful comparison14,15 and substantially smaller than in conventional rare gas matrices,24 let alone the bulk solid.25 Harmonic predictions for hydride stretching fundamentals based on density functionals often match anharmonic experiment better than their anharmonic counterparts,26 obviously for the wrong reason. For vibrational shifts induced by complexation, the harmonic approximation may appear better justified due to the compensation of leading anharmonic terms, but cancellation between diagonal and off-diagonal anharmonicity contributions cannot be relied upon in a quantitative fashion, either.27 By carrying out high level variational calculations in stretching subspaces and lower level vibrational perturbation theory calculations in full vibrational space, we shed light onto the evolution of some anharmonic effects with cluster size.
2 Experimental techniques
The infrared absorption measurements for imidazole (99%, Alfa Aesar, used as supplied) in a supersonic slit jet expansion are described in detail in ref. 4 and 28. Helium was saturated with the vapor over an imidazole-coated molecular sieve sample kept at a sample temperature ϑs (between 110 and 130 °C) and expanded through a double-slit nozzle heated to ϑn = ϑs + 20 °C. The expansion pulses were synchronized to FTIR scans at 2 cm−1 resolution and the spectra were compared with those obtained immediately before the pulse to obtain an absorbance spectrum in the NH/CH stretching range. The IR spectra alone4 (typically from 300 averaged scans) did not provide a fully conclusive assignment28 and led to the recording of Raman spectra.The setup used for Raman scattering measurements in a continuous single slit jet expansion is described in detail in ref. 29 and 30. The nozzle was kept at ϑn = 100–120 °C as the supersonic jet expansion was probed 3 mm downstream of the nozzle with a focused cw-laser beam (Spectra Physics Millennia eV 25 W, 532 nm). Comparison between theoretical and experimental Raman scattering signals is only done on a relative scale and involves a number of corrections.29,31 The helium carrier gas was enriched with imidazole (99%, abcr chemicals, used without further purification) in a heated saturator at ϑs ≈ 80–100 °C. Here, the He partial pressure is set to 1.0–1.2 bar and maintained as the stagnation pressure of the jet expansion. Every Raman spectrum consists of a minimum of 12 scans of 300 s exposure time each, which were averaged after automated removal of cosmic ray artifacts. A detailed listing of the experimental properties of each spectrum can be found in the ESI.†
Monomer vibrations are labelled νk where the index is sorted from high to low wavenumber without symmetry blocking. For dimers, a d or a label for hydrogen bond donor or acceptor is added, where needed. Trimer vibrations are differentiated by 1–3 primes (′).
3 Computational techniques
Geometry optimizations and harmonic calculations were performed at the B3LYP/def2-TZVP32,33 level of approximation including two-body dispersion corrections with Becke–Johnson damping (D3(BJ)34). Concurrently, B2PLYP calculations with the larger def2-QZVP basis33 were carried out to obtain a potentially improved estimate of the fundamental harmonic frequencies. BSSE corrections were not applied.Vibrational pertubation theory calculations (VPT2)23,35,36 were performed on top of a B3LYP-D3(BJ)/def2-TZVP harmonic frequency analysis with geometries optimized at the same level. Results with the cc-pVTZ basis set are also available for the imidazole monomer and lowest energy dimer, but these are only reported in the ESI,† because they agree very well with the smaller basis set results. Also included in the ESI,† is an analysis of the importance of intermolecular mode couplings. All B3LYP calculations were done with the Gaussian 09 (Rev. E.01) program package.37 The geometries were optimized to a RMS force value of 1 × 10−5 a.u. (opt = tight), while making use of a DFT integration grid with 150 radial shells and 974 points per shell for each atom (int = SuperFine). Raman activities were obtained additionally for all harmonic frequency calculations. Presented Raman cross-sections were calculated from these Raman activities as explained in ref. 31.
As an alternative method to compute anharmonic vibrational corrections, the B2PLYP/def2-QZVP38,39 optimized geometries and harmonic analysis were used to carry out 1D potential scans along the NH stretch modes. The latter served to obtain dominant anharmonic (diagonal) corrections. The scans were performed at the same level of theory as used for the structures (B2PLYP/def2-QZVP) and for comparison at the DLPNO-CCSD(T)/cc-pVTZ level.40–42 Since the aim of the work was to discuss structures from the monomer up to the trimer, the computational cost of harmonic calculations at the DLPNO-CCSD(T) was, unfortunately, too prohibitive. Based on the energy scans, it is possible to derive an harmonic estimate for the higher-level method, but the latter values have little relation to the actual wavenumbers computed on optimised geometries. Comparisons are available in the ESI.† The latter results will be later signalled in the text as CCSD(T). All of the latter calculations were performed with the ORCA program package (version 3.0.3).43
4 Experimental assignments
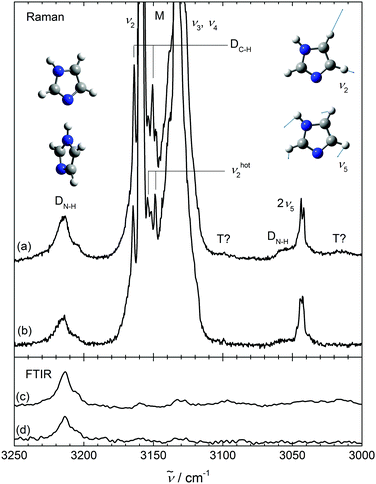
Fig. 1 shows the NH stretching region (ν1) of imidazole expansions as a Raman (upper) and IR (lower) trace under conditions where less than about 10% of the molecules are aggregated. The Raman spectrum is dominated by the sharp Q-branch at 3518 cm−1. Superimposed on the broader ΔJ ≠ 0 transitions and to lower wavenumbers, there are sharp bands which scale like the main transition upon increasing the stagnation pressure, confirming their monomer origin. They are due to NH stretching transitions out of excited low frequency states νk (νhot1), and their shift from the fundamental immediately provides the anharmonic coupling constant x1,k. The strongest of these ((ν1 + ν21) −ν21) is shifted by −21 cm−1 and very likely belongs to the NH out-of-plane bend24ν21 near 513 cm−1. Its intensity amounts to ≈14% of the main Q-branch (I21/I1 = 0.14 in Table 2 below). Assuming that the NH stretching transition moment is not affected by bending motion, the intensity ratio corresponds to an effective vibrational temperature close to the nozzle temperature of 370 K. The other hot bands with shifts of −9 and −39 cm−1 are an order of magnitude weaker and must be due to vibrations at about twice the ν21 wavenumber, if a uniform Boltzmann distribution with a similar vibrational temperature applies. An obvious candidate for the most downshifted hot band is 2ν21. The other one (marked νhot1) is difficult to assign without theoretical anharmonicity constants.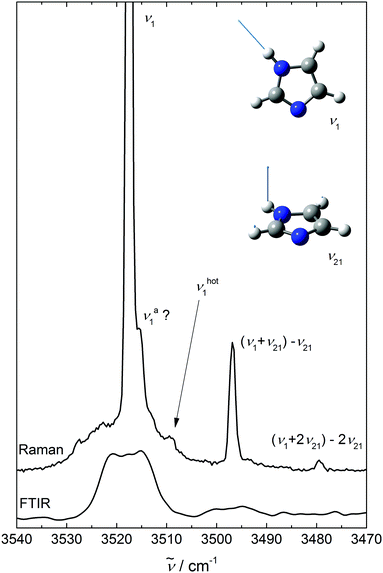 | ||
| Fig. 1 NH stretching spectra of imidazole monomers (insets illustrating the ν1 and ν21 modes) using Raman (upper, ϑn = 100 °C) and IR spectroscopy (lower, ϑn = 150 °C). | ||
The IR spectrum has a poorer S/N ratio for monomers than the Raman spectrum due to the extensive rotational structure and small dipole derivative. It thus only reveals the hot band building on ν21 with a similar rotational PQR structure as the ν1 fundamental. This rotational structure is about 6 times more narrow than in a 473 K gas phase spectrum,24 consistent with a rotational temperature of 10–15 K and enabling the separation of the IR hot band from the cold band center. The hot-to-cold band intensity ratio of ≈0.1 is consistent with a vibrational temperature of roughly 320 K, somewhat lower than the nozzle temperature of 420 K but much higher than the rotational temperature. The differences in IR and Raman vibrational temperatures are barely significant and may in part be due to focussed Raman probing 3 mm downstream the nozzle vs. IR probing at more than 10 mm2 cross section downstream and in between two parallel slit nozzles. The acceptor NH stretching vibration of the dimer νa1 as a minor constituent under the chosen expansion conditions overlaps with the monomer signal in the IR and Raman cases. Comparison to a He droplet experiment14 suggests a downshift of 2 cm−1, which may be tentatively associated with a low-frequency shoulder visible in the Raman Q-branch signal. However, this feature could also be due to a monomer hot band caused by another low frequency mode. Such contributions are somewhat difficult to disentangle on top of the strong monomer band.
In Fig. 2, we turn to the CH stretching range, which is dominated in the Raman spectrum by the in-phase CH stretching mode ν2 of the two neighboring CH bonds. Some of its intensity is transferred to the overtone of the in-plane HCCH bending mode ν5, which also involves other CH and NH in plane bending motion and therefore may be aggregation-sensitive. Indeed, there are significant differences between Raman spectra which only differ in imidazole concentration (top two traces, the upper one having a larger cluster fraction). The four bands marked D roughly double after scaling the spectra to the ν2 monomer intensity. As the first of these (DN−H), slightly above 3200 cm−1, matches reasonably well with a helium droplet band at 3200 cm−1 assigned to imidazole dimer14 and the helium environment is expected to induce a small downshift, it is plausible to assign all four D bands to dimers. Most of the other signal in this spectral window has monomer origin (M), although there are some weak features near 3100 and 3020 cm−1 (tentatively marked T?) which may be due to trimers or even larger clusters, as spectra at intermediate concentrations suggest. The IR spectrum is much less sensitive to CH stretching modes due to the small dipole transition moment as opposed to the polarizability change relevant for the Raman signal. This allows for a clear separation of CH stretching from hydrogen-bonded NH vibrational character due to the linearity of both employed techniques. The bottom two traces of Fig. 2 (FTIR) are also scaled to roughly equal (very weak) ν2 intensity and the relative Raman/IR scaling is chosen such that the strong dimer signals above 3200 cm−1 match approximately for the more diluted expansion. Because resonance between bright and dark states transfers fractional intensity independent on transition moments, this immediately shows that the two intermediate D bands in the Raman spectrum (DC–H) have mostly CH character, whereas the tentative T? bands and perhaps also the rightmost DN–H band near 3054 cm−1 may profit from some NH intensity transfer. The three CH stretching monomer fundamentals ν2, ν3, ν4, which are off-scale in the Raman traces, are seen as weak bands in the IR spectra. The NH stretching band of the dimer is strong in the IR, but any signal of the rightmost dimer band (DN–H) is at best very weak. Therefore, it remains unclear whether this band profits from NH intensity stealing (which would explain its width) or is a pure CH bending overtone shifted from the monomer, as long as no improved S/N-ratio in the IR is available. We can still provide an approximate upper limit of the dimer donor Fermi resonance coupling constant Wd1,5,5 between the modes 2ν5 and ν1 giving rise to the DN–H bands in Fig. 2, based on a conservative intensity ratio of <0.3, when taking into account band overlap in both cases. From their energetic splitting ΔE ≈ 160 cm−1, the effective stretch-bend coupling constant Wd1,5,5 has to be smaller than ≈67 cm−1, even if the bending overtone carries no zeroth order intensity.44 An improved IR spectrum would be needed to assess this zeroth order intensity.
Turning back to the Raman CH stretching region and in close analogy to the monomer NH stretching case in Fig. 1, two downshifted satellites (by 6 and 11 cm−1) of the ν2 band may be identified as monomer hot bands (νhot2), whereas the ν3,4 pattern is too congested to allow for hot band separations in the Raman spectrum. The intensity ratio of the two monomer hot bands and the ν2 fundamental is difficult to assess quantitatively due to severe overlap, but it appears to be consistent with higher frequency carrier modes than ν21. This encodes valuable monomer anharmonicity information which is completely lost in a regular gas phase spectrum24 and can be retrieved by comparison to theory. The two CH satellites marked DC–H must be due to the ν2 mode in the donor (νd2) and acceptor (νa2) units of the hydrogen-bonded dimer and it is a useful test of quantum-chemical calculations to predict which one is upshifted and which one is downshifted from the monomer value. The upshifted one may have somewhat more NH stretching character due to its closer proximity to the dimer NH stretch and a somewhat higher intensity.
The relatively large discrepancy between the helium droplet (3200 cm−1) and jet value (3214 cm−1 with a shoulder at 3206 cm−1) of the dimer NH donor band deserves some discussion. Two effects may contribute. On one hand, the jet cooling is not perfect, as illustrated above. Residual torsional motion around the hydrogen bond (although believed to be cooled almost as well as overall rotation) and out-of-plane bending (shown above to be cooled poorly) may weaken it and partially reduce the downshift. On the other hand, the helium droplet environment is close to a true low temperature equilibrium value, but it is empirically established45 that helium solvation has some caging effect on hydrogen-bonded complexes and that the solvation downshift is roughly proportional to the hydrogen bond-induced downshift. A hydrogen bond shift of 300 cm−1 implies a solvation downshift of 13 cm−1, although this already corresponds to a slight extrapolation of the empirical relationship.45 This extrapolated solvation shift matches the observed value of 14 cm−1 very well, such that residual thermal excitation in the jet does not have to be invoked as a major source of band shifting. The shifted dimer NH stretching band in helium droplets displays a similar, but less-pronounced asymmetry as in the jet.14 The nature of this low-frequency shoulder is not completely clear. Tunneling splitting between the two enantiomeric forms of imidazole dimer, torsional excitation around the hydrogen bond and Fermi resonance with dark states13 are among the possibilities. The former two explanations are not very compatible with the persistence of the effect in cold helium droplets. The latter explanation appears more likely and fits the larger width of this dimer donor band as evidence for fast intracluster vibrational redistribution. IR/Raman correspondence as a signature of resonance-induced wavefunction mixing is indeed very pronounced for the 3206 cm−1 shoulder. It would correspond to an anharmonic coupling constant Wd ≈ 3 cm−1, much smaller than Wd1,5,5. Given the complex NH stretching spectrum of condensed imidazole,25 it is to be expected that vibrational resonances of different strength appear already in the cluster spectra. As shown for pyrazole,13 this is largely due to the shift of the NH stretching fundamental into a region with strongly coupled framework modes. In summary, the isolated dimer donor NH stretching band is at 3214 ± 4 cm−1, but there may be weaker contributions at 3206 ± 4 cm−1 and tentatively at 3054 ± 8 cm−1 due to resonances with dark states.
After having understood the experimental monomer and dimer spectrum of imidazole, we can turn to the trimer. If it involves linear hydrogen bonds like the dimer, cooperativity should lead to further downshifts, besides one dangling NH group with negligible shift. While the latter cannot be rigorously excluded due to monomer overlap, there are only weak indications for further downshifted NH signals, marked T? in Fig. 2. Instead, we find two sizeable trimer signals between the monomer and dimer regions at 3381 ± 2 cm−1 and 3322 ± 4 cm−1, as shown in Fig. 3, which extends Fig. 2 into the higher frequency range. Their concentration scaling is clearly different from that of the dimer band, supporting a trimer assignment. A third band (T?) may be located right underneath the main dimer peak or with similar likelihood on its high-frequency slope. A contribution to the low frequency shoulder is less likely based on the band profile evolution with concentration, such that we estimate the trimer band center at 3220 ± 10 cm−1. The bandwidth of the trimer contributions increases progressively with downshift, indicative of an increasing coupling of the NH mode to bath modes. However, the trimer appears to be free of pronounced resonances due to its small frequency shift from the monomer,13 unless some resonance is hidden under the dimer signal or the bands marked T? in Fig. 2 also belong to the cyclic trimer.
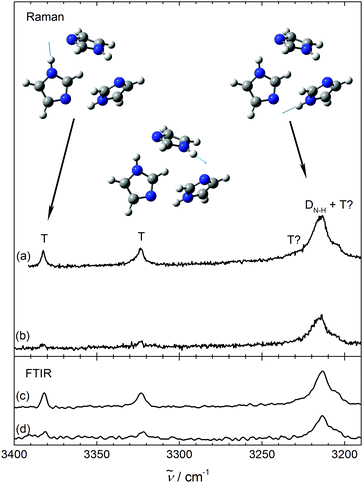 | ||
| Fig. 3 NH stretching spectra of imidazole dimers (D) and trimers (T,T?) using Raman (upper pair (a and b), ϑn = 120 °C, higher concentration on top) and IR spectroscopy (lower pair (c and d), ϑn = 150/130 °C, higher concentration on top), scaled as in Fig. 2. | ||
A reduced downshift with increasing cluster size is the signature of hydrogen bond strain.29 The trimer intensity pattern is very similar in the IR and Raman traces (see Fig. 3), pointing at the lack of (approximate) symmetry in this cluster. If the three imidazole units were symmetrically connected like in pyrrole or in pyrazole or in (one isomer of) N-methyl acetamide trimer,22,29 more complementarity between Raman and IR spectra would be expected.46 Therefore, the only consistent experimental assignment of the major spectral oligomer contribution (T) is to an unsymmetrical, highly strained, cyclic trimer, as proposed before.17 The chain-like trimer that was prepared in helium droplets,18 possibly under kinetic control, is at best present in minor quantities.
5 Theoretical results and comparison to experiment
Comparison of theoretical predictions with the experimental spectra reported and assigned in the previous section is useful at several different levels. This may provide critical tests to the accuracy of the underlying electronic structure method and/or the approximations used for the vibrational Hamiltonian.Harmonic predictions can be compared to experiment after applying a uniform shift or scaling due to the diagonal anharmonicity of the NH and CH oscillators.28 This is the standard approach which we critically extend in the present work. Vibrational perturbation theory is useful to predict hot band shifts and perhaps also to refine the harmonic high frequency mode pattern, including IR intensities.47 Finally, variational calculations along individual normal modes allow to identify major diagonal anharmonic contributions in an independent and potentially more rigorous way.48,49
Vibrational calculations crucially depend on an accurate description of the molecular structure. The level of computation chosen to conduct the bulk of the calculations (B3LYP-D3(BJ)/def2-TZVP) seems to be at least adequate for the structure optimizations. This is analyzed in Table 1 by comparison to experiment for the monomer50 and the dimer16 in two different ways. One is to allow for an up to ≈1% decrease in the rotational constants upon vibrational averaging.51,52 Rewardingly, the B3LYP minimum energy structures fit this window in all cases. The largest deviation by 1.0% involves the A constant for the dimer, which carries a large experimental uncertainty of 0.5%. The other, more explicit way is to directly compare VPT2-corrected rotational constants to experimental values. Now, the deviations are always smaller than 0.4% except for the dimer A value, where the deviation by +0.8% might again be blamed on the larger experimental uncertainty. For comparison, we also include in the same table values calculated from the B2PLYP/def2-QZVP computed structures (which are later used for 1D normal mode analysis). The pattern is more or less the same, albeit an even larger error in the dimer A value.
| e | B2PLYP | B3LYP-D3 | |||||
|---|---|---|---|---|---|---|---|
| m | Δm–e/% | m | Δm–e/% | VPT2 | Δpt–e/% | ||
| Monomer50 | |||||||
| A | 9.725 | 9.800 | +0.7 | 9.765 | +0.4 | 9.688 | −0.4 |
| B | 9.374 | 9.473 | +1.1 | 9.463 | +0.9 | 9.387 | +0.1 |
| C | 4.772 | 4.817 | +0.9 | 4.806 | +0.7 | 4.766 | −0.1 |
| Dimer16 | |||||||
| A | 4.800 | 4.884 | +1.8 | 4.849 | +1.0 | 4.841 | +0.8 |
| B | 0.458 | 0.460 | +0.4 | 0.462 | +0.9 | 0.457 | −0.2 |
| C | 0.456 | 0.458 | +0.4 | 0.460 | +0.9 | 0.455 | −0.2 |
| Average | +0.8 | 0.0 | |||||
For the monomer, comparison to higher level theoretical equilibrium structures is possible. In the Table S1 of ref. 16, a CCSD(T)-F12C/cc-pVDZ-F12 structure is presented (although from the text in the article, it is not completely unambiguous whether it is a full CCSD(T) optimization). Its three equilibrium rotational constants uniformly deviate from experiment by 0.5%. If we add the equally uniform −0.8% VPT2 anharmonic correction from the B3LYP calculation (Table 1), a systematic deviation of the anharmonically corrected CCSD(T) prediction from experiment by −0.3% for all three rotational constants may be estimated. This deviation is slightly larger, but of the same magnitude as the corresponding B2PLYP and B3LYP values and possibly within the error margins of the VPT2 treatment. For completeness we also include a comparison of internal coordinates between the different methods in the ESI.†
The hot band structure of the monomer modes νi from populated low frequency modes νk can only be predicted anharmonically. Table 2 summarizes the predictions of a standard VPT2 calculation at B3LYP-D3(BJ)/def2-TZVP level in comparison to some sufficiently separated experimental (νi + νk) −νk band positions ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i+k −
i+k − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) k in terms of anharmonic constants xi,k = (
k in terms of anharmonic constants xi,k = (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i+k −
i+k − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) k) −
k) − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i. The performance is very good, with a matching band for every predicted large downshift. For hot bands building on NH, the intensity is consistent with the predicted anharmonic (or harmonic) excitation wavenumbers in combination with a vibrational temperature below or around the nozzle temperature. For hot bands building on the CH stretch, experiment only provides a lower bound for the intensity due to strong overlap with a broad spectral background from rotational structure. A vibrational temperature cannot be reliably extracted in these cases.
i. The performance is very good, with a matching band for every predicted large downshift. For hot bands building on NH, the intensity is consistent with the predicted anharmonic (or harmonic) excitation wavenumbers in combination with a vibrational temperature below or around the nozzle temperature. For hot bands building on the CH stretch, experiment only provides a lower bound for the intensity due to strong overlap with a broad spectral background from rotational structure. A vibrational temperature cannot be reliably extracted in these cases.
| i | k |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) VPT2
k
/cm−1
VPT2
k
/cm−1 |
x VPT2 i,k/cm−1 | x exp i,k/cm−1 | I k /Ii |
|---|---|---|---|---|---|
| a Higher than the corresponding harmonic wavenumber. b From spectrum in Fig. 1. c Lower bounds from spectrum (a) in Fig. 2 due to overlap. | |||||
| 1 | 12 | 1071 | −8 | −9 | 0.01b |
| 1 | 21 | 531a | −20 | −21 | 0.14b |
| 1 | 2 × 21 | 1087a | −40 | −39 | 0.01b |
| 2 | 13 | 1056 | −8 | −6 | ≥0.005c |
| 2 | 16 | 869 | −5 | −6 | |
| 2 | 18 | 731 | −13 | −11 | ≥0.01c |
VPT2 at this hybrid density functional level can also be used to predict anharmonic shifts of the fundamentals relative to the harmonic approximation, which can later be combined with higher level harmonic predictions. The shifts are listed in Table 3 for the monomer and the dimer.
| Mode | i | 2xi,i | Δ(νi) | 2xai,i | Δ(νai) | 2xdi,i | Δ(νdi) |
|---|---|---|---|---|---|---|---|
| NH | 1 | −140 | −166 | −139 | −158 | −238 | −155 |
| CHs | 2 | −92 | −134 | −87 | −135 | −93 | −136 |
| CHa | 3 | −51 | −135 | −56 | −139 | −73 | −136 |
| CHa | 4 | −59 | −136 | −74 | −139 | −85 | −137 |
Superficially, the anharmonic corrections for the NH stretching fundamental Δ(ν1) are quite well-behaved. For the monomer and the dimer acceptor, the total anharmonic correction is −(158 to 166) cm−1 and for the dimer donor, it is still rather similar with −155 cm−1. This suggests that simple harmonic scaling can be quite successful in reproducing experiment. However, the diagonal contribution x1,1 increases by >70% from the acceptor to the donor, which is more than compensated by off-diagonal contributions, in particular due to NH stretch-bend couplings. Although VPT2 is certainly not reliable for the soft torsion around the hydrogen bond of the dimer and B3LYP-D3 probably overestimates anharmonic effects, this VPT2 prediction indicates that harmonic scaling and even variational calculations within the stretching subspace may give the right answer for the wrong reason. For the CH stretching modes, the situation is more complex with large variations in the diagonal anharmonicity due to extensive mode coupling, but again the net anharmonicity correction falls in the potentially misleading narrow range of −(134 to 139) cm−1.
In order to obtain further insight into the anharmonic shifts of the relevant NH bands, we have carried out a decomposition and analysis of the latter. The anharmonic fundamental band position can be calculated as a composite value
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = ω + Δ(d) + Δoff + ΔF, = ω + Δ(d) + Δoff + ΔF, | (1) |
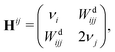 | (2) |
As an alternative to VPT2, and given the high computational cost associated with trimer calculations, we opted for a 1D normal mode analysis. From energy scans along the NH stretch normal coordinate it is possible to compute an approximation to the diagonal correction. Considering a transition νi, the latter correction is given by53
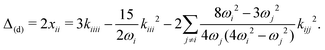 | (3) |
Table 4 collects all values, both for the B3LYP-D3(BJ)/def2-TZVP VPT2 calculations and the normal mode analysis. The latter calculations were carried out on B2PLYP/def2-QZVP optimized geometries and normal modes. The 1D scans were also repeated at the coupled cluster level and values for Δ1M(d) and ΔF are available at this level of theory. Other combinations of basis sets (as well as local coupled cluster variants) were tested, varying the reference geometry. The results of this analysis are provided in the ESI.† They show that the computed values are relatively stable, with the largest variations observed in the harmonic ω values.
| Method | ω | Δ1M(d) | ΔMM(d) | Δoff | ΔF |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif)
|
|---|---|---|---|---|---|---|
| a B3LYP-D3(BJ)/def2-TZVP VPT2. b B2PLYP/def2-QZVP optimisation, harmonic wavenumber + normal mode 1D calculation. c DLPNO-CCSD(T)/cc-pVTZ normal mode 1D calculation based on the B2PLYP structure and normal modes. | ||||||
| Monomer ν1 | ||||||
| B3LYP-D3(BJ)a | 3649 | −140 | 0 | −26 | 3483 | |
| B2PLYPb | 3683 | −139 | 3518 | |||
| DLPNO-CCSD(T)c | −138 | 3519 | ||||
| Exp. | 3518 | |||||
| Dimer νa1 | ||||||
| B3LYP-D3(BJ)a | 3648 | −138 | −1 | −19 | 3490 | |
| B2PLYPb | 3680 | −138 | 3522 | |||
| DLPNO-CCSD(T)c | −134 | 3526 | ||||
| Exp. | 3516 ± 2 | |||||
| Dimer νd1 | ||||||
| B3LYP-D3(BJ)a | 3304 | −201 | −37 | +51 | +31 | 3149 |
| B2PLYPb | 3343 | −218 | +25 | 3164 | ||
| DLPNO-CCSD(T)c | −215 | +25 | 3167 | |||
| Exp. | 3214 ± 4 | |||||
| Trimer ν1′ | ||||||
| B3LYP-D3(BJ)a | 3527 | −152 | −32 | −6 | 3337 | |
| B2PLYPb | 3559 | −152 | 3369 | |||
| DLPNO-CCSD(T)c | −144 | 3377 | ||||
| Exp. | 3381 ± 2 | |||||
| Trimer ν1′′ | ||||||
| B3LYP-D3(BJ)a | 3459 | −166 | −36 | +12 | 3269 | |
| B2PLYPb | 3494 | −168 | 3302 | |||
| DLPNO-CCSD(T)c | −163 | 3307 | ||||
| Exp. | 3322 ± 4 | |||||
| Trimer ν1′′′ | ||||||
| B3LYP-D3(BJ)a | 3358 | −180 | −86 | +59 | 3151 | |
| B2PLYPb | 3384 | −185 | 3172 | |||
| DLPNO-CCSD(T)c | −181 | 3176 | ||||
| Exp. | 3220 ± 10 | |||||
Returning to the results provided in Table 4, a few comments should be made about the anharmonic fundamental values ν provided. In the case of B3LYP, the ν value is obtained directly from the VPT2 calculation. For the other methods, it is a composite value. For B2PLYP, the missing terms from eqn (1) were taken from B3LYP VPT2 (ΔMM(d) and Δoff). ΔF is computed through the matrix of eqn (2), with the composite B2LYP values for the diagonal terms and the B3LYP VPT2 off-diagonal coupling values. In the case of DLPNO-CCSD(T) the same corrections were used and the harmonic fundamental used was taken from B2PLYP, consistent with the normal mode used for the scan.
The best composite values we obtained (B2PLYP fundamentals, combining the DLPNO-CCSD(T) dominant diagonal anharmonic corrections plus B3LYP VPT2 terms) are found in general good agreement with the measured IR bands, particularly for small shifts. We start by discussing the monomer values. The pure VPT2 results, as previously observed, show a deviation from experiment of 35 cm−1, which is drastically reduced when the harmonic value computed from B2PLYP is applied. Comparing the diagonal single-mode anharmonic contributions from all three methods, one finds a striking agreement (variations of only 2 cm−1). This is a strong indication that there should be little error compensation at work. The only other significant corrections are from off-diagonal terms, which were already observed to be well captured by VPT2.
We now turn to the dimer, where the largest deviations are found between our composite values and the experimental wavenumbers (donor NH νd1, ≈50 cm−1). There are several possible reasons behind this discrepancy. First of all, the same type of agreement observed in the monomer for the Δ1M(d) term is not repeated here (deviations of up to 17 cm−1). This raises the uncertainty in the remaining anharmonic corrections. The Fermi resonance, given its sensitivity to the computation details and the relative position of the unperturbed transitions, is also an important factor. Our results do seem to show a consistent shift of 25–31 cm−1. Given that the coupling constant is always the same (B3LYP) one can at least state that the difference between the diagonal elements has little impact on the computed ΔF. But ultimately it could also boil down to the description of the harmonic normal mode, the strongest hydrogen bond featured in this study.
The νa1 band in the dimer is, as previously noted, quite close to the monomer band and all methods are able to reproduce the absolute value quite well. However, closer inspection reveals a clear deficiency. While harmonically all methods reproduce the qualitative trend of a slight downshift from the monomer, all anharmonic treatments predict a small upshift. Apparently, such small shifts are within the noise of VPT2 treatments for floppy systems, which involves long sums of small terms with different signs.
Regarding the trimers, the overall picture does not change much. The deviation between computed values and experiment seems to be correlated to the downshift of these bands. Nonetheless, the diagonal anharmonic corrections appear to be quite stable across all three different methods (in the ESI,† one can observe that these values are relatively straightforward to converge).
Overall, the systematically smaller CCSD(T) Δ1M(d) correction for the more strongly downshifted modes indicates a stiffer CCSD(T) oscillator, which may also affect the harmonic values and potentially reduce the gap between theory and experiment which opens up for the more downshifted NH stretch modes.
The best composite method from Table 4 shows deviations of +10, −47, −4, −15, and −44 cm−1 when compared to the five experimentally assigned NH stretching modes of imidazole clusters. This may be compared to +1, −29, +19, +13, and +17 cm−1 when a traditional monomer-matching uniform scaling factor (0.9641) is applied to harmonic B3LYP predictions. Formally, the simple scaling procedure looks superior, and if one corrects for the Fermi resonance in the dimer donor vibration which a scaling procedure cannot capture, even the single outlier disappears. However, the scaling implies that all contributions become smaller with increasing downshift, whereas Table 4 shows that the opposite is true for the diagonal anharmonicity and to some extent also for the off-diagonal contributions. Only the sum of all anharmonic contributions is reasonably constant from the monomer to the trimer modes and this explains the apparent success of harmonic scaling in the imidazole case.
We come back to the prediction of the dimerization splitting of ν2 (CH stretch), which was observed to be +5/−8 cm−1 relative to the free monomer value. Although the B3LYP VPT2 treatment suffers from an almost perfect accidental degeneracy between νa2 and νd1 (both at 3149 cm−1), the splitting is predicted quite closely at +7/−7 cm−1. The calculation provides an assignment of νa2 for the higher and νd2 for the lower frequency mode.
Finally, we address the energy difference between chain and cyclic forms of the imidazole trimer (Table 5). Reliable anharmonic VPT2 ZPVE corrections are not available, because even the cyclic form suffers from instabilities in some of the low frequency modes. However, the situation is sufficiently clear-cut to use the harmonic approximation of the ZPVE. At B3LYP/def2-TZVP level, the cyclic trimer is higher in energy by 10.5 kJ mol−1 without D3 correction and lower by 12.1 kJ mol−1 with D3(BJ) correction (Table 5). Using the cc-VTZ basis sets, the numbers change to 9 kJ mol−1 and 14 kJ mol−1, respectively. At the B2PLYP/def2-QZVP level, the electronic energy advantage of the cyclic trimer is virtually the same as at B3LYP/def2-TZVP level. Evidently, cyclization in imidazole trimer is a strongly dispersion-driven process, which introduces strain in the hydrogen bonds and lowers their typical polarization-induced cooperativity, such that the trimer NH stretch spectrum is actually less downshifted than the dimer spectrum.
| Method | D | T cyclic | T linear | T cyclic–Tlinear |
|---|---|---|---|---|
| a Carried out with the Gaussian 09 program package.37 b Carried out with the Orca program package.43 | ||||
| B3LYP/def2-TZVPa | −17.8 | −23.3 | −26.3 | 9.0 |
| −15.8 | −20.2 | −23.8 | 10.5 | |
| B3LYP-D3(BJ)/def2-TZVPa | −21.6 | −36.8 | −31.7 | −15.2 |
| −19.6 | −33.1 | −29.1 | −12.1 | |
| SCS-MP2/def2-TZVPb | −19.8 | −34.7 | −29.0 | −17.2 |
| −18.2 | −31.4 | −26.7 | −14.3 | |
| B2PLYP/def2-QZVPb | −20.9 | −35.6 | −30.6 | −15.1 |
| −19.1 | −32.2 | −28.1 | −12.3 | |
6 Conclusions
The combined infrared and Raman study of supersonic jet expansions of imidazole in helium has allowed to assign several bands in the NH/CH stretching fundamental region to monomers, dimers, and trimers of imidazole. The trimer is shown to be cyclic with severe strain and asymmetry, at variance with earlier assumptions and helium nanodroplet evidence. Its vibrational dynamics appears to be quite regular, whereas evidence for Fermi resonance in the linear dimer is presented. For the monomer, limited vibrational cooling of some strongly coupling modes in the hydride stretching region is detected in the Raman spectra for heated nozzles. This could be developed into a systematic tool for the elucidation of anharmonic coupling constants in medium-sized molecules which are difficult to resolve rotationally.The second part of this work explores how well vibrational treatments from harmonic over perturbational to variational are able to predict the NH stretch spectra. The best results are obtained for a composite approach which uses diagonal anharmonicity at CCSD(T) level and adds anharmonic couplings at B3LYP VPT2 level. The agreement degrades with increasing hydrogen-bond induced downshift. The best affordable level for the structure optimization and harmonic frequency calculations was B2PLYP/def2-QZVP, but it is anticipated that analogous CCSD(T) input would further improve the agreement for large downshifts. Our analysis shows that the traditional scaling of low level B3LYP harmonic frequencies to monomer values may appear to be quite successful, but for the wrong reasons. This is reminiscent of the methanol dimer case.27
As shown in this work, imidazole trimer is one of the ambivalent supramolecular structures whose correct hydrogen bond topology depends crucially on whether London dispersion correction is applied to density functional treatments.29 Cyclic imidazole trimer units as organizational units of spatially close histidine amino acids are unlikely to occur in natural peptides because of comparative histidine scarcity and the limited flexibility of the peptide backbone. However, they may play a role in more flexible design variants, such as in γ-peptide foldamers,54 where even amide cycles29 can be realized.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We greatly acknowledge financial support by the German Research Foundation (DFG, Su 121/5 with project identifier 271107160 and Su 121/6 with project identifier 298754033) that enabled important sensitivity improvements of the jet spectrometers employed in this study.Notes and references
- M. K. Van Bael, J. Smets, K. Schoone, L. Houben, W. McCarthy, L. Adamowicz, M. J. Nowak and G. Maes, J. Phys. Chem. A, 1997, 101, 2397–2413 CrossRef CAS.
- P. R. Rablen, J. W. Lockman and W. L. Jorgensen, J. Phys. Chem. A, 1998, 102, 3782–3797 CrossRef CAS.
- F. O. Talbot and J. P. Simons, Eur. Phys. J. D, 2002, 20, 389–398 CrossRef CAS.
- J. Zischang, J. J. Lee and M. A. Suhm, J. Chem. Phys., 2011, 135, 061102 CrossRef PubMed.
- A. Bhattacherjee and S. Wategaonkar, Phys. Chem. Chem. Phys., 2015, 17, 20080–20092 RSC.
- M. A. Trachsel, P. Ottiger, H.-M. Frey, C. Pfaffen, A. Bihlmeier, W. Klopper and S. Leutwyler, J. Phys. Chem. B, 2015, 119, 7778–7790 CrossRef CAS PubMed.
- D. E. Taylor, J. G. Ángyán, G. Galli, C. Zhang, F. Gygi, K. Hirao, J. W. Song, K. Rahul, O. A. von Lilienfeld, R. Podeszwa, I. W. Bulik, T. M. Henderson, G. E. Scuseria, J. Toulouse, R. Peverati, D. G. Truhlar and K. Szalewicz, J. Chem. Phys., 2016, 145, 124105 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 145, 186101 CrossRef PubMed.
- M. Gatchell, M. Goulart, L. Kranabetter, M. Kuhn, P. Martini, B. Rasul and P. Scheier, Phys. Chem. Chem. Phys., 2018, 20, 7739–7745 RSC.
- S. Scheiner, T. Kar and J. Pattanayak, J. Am. Chem. Soc., 2002, 124, 13257–13264 CrossRef CAS PubMed.
- A. Bhattacherjee and S. Wategaonkar, J. Phys. Chem. A, 2017, 121, 4283–4295 CrossRef CAS PubMed.
- S. Kumar, A. Mukherjee and A. Das, J. Phys. Chem. A, 2012, 116, 11573–11580 CrossRef CAS PubMed.
- T. N. Wassermann, C. A. Rice, M. A. Suhm and D. Luckhaus, J. Chem. Phys., 2007, 127, 234309 CrossRef CAS PubMed.
- M. Y. Choi and R. E. Miller, J. Phys. Chem. A, 2006, 110, 9344–9351 CrossRef CAS PubMed.
- M. Y. Choi and R. E. Miller, Chem. Phys. Lett., 2009, 477, 276–280 CrossRef CAS.
- J. C. Mullaney, D. P. Zaleski, D. P. Tew, N. R. Walker and A. C. Legon, ChemPhysChem, 2016, 17, 1154–1158 CrossRef CAS PubMed.
- V. Poterya, V. Profant, M. Fárník, L. Šištík, P. Slavíček and U. Buck, J. Phys. Chem. A, 2009, 113, 14583 CrossRef CAS PubMed.
- S. Lee, S. J. Lee, A. Ahn, Y. Kim, A. Min, M. Y. Choi and R. E. Miller, Bull. Korean Chem. Soc., 2011, 32, 885–888 CrossRef CAS.
- A. Ahn, S. J. Lee, S. Lee, A. Min, Y. Kim, H. J. Jung, S. M. Hong, J.-H. Lee, M. Y. Choi and R. E. Miller, Bull. Korean Chem. Soc., 2011, 32, 1407–1410 CrossRef CAS.
- M. Torrent, D. G. Musaev, K. Morokuma, S.-C. Ke and K. Warncke, J. Phys. Chem. B, 1999, 103, 8618–8627 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. Slavíček and M. Fárník, Phys. Chem. Chem. Phys., 2011, 13, 12123–12137 RSC.
- V. Barone, M. Biczysko and J. Bloino, Phys. Chem. Chem. Phys., 2014, 16, 1759–1787 RSC.
- S. T. King, J. Phys. Chem., 1970, 74, 2133–2138 CrossRef CAS.
- M. J. Wójcik, J. Kwiendacz, M. Boczar, Ł. Boda and Y. Ozaki, Chem. Phys., 2010, 372, 72–81 CrossRef.
- G. M. Chaban and R. B. Gerber, Theor. Chem. Acc., 2008, 120, 273–279 Search PubMed.
- M. Heger, M. A. Suhm and R. A. Mata, J. Chem. Phys., 2014, 141, 101105 CrossRef PubMed.
- J. Zischang, PhD thesis, Georg-August Universität, Göttingen, 2014.
- T. Forsting, H. C. Gottschalk, B. Hartwig, M. Mons and M. A. Suhm, Phys. Chem. Chem. Phys., 2017, 19, 10727–10737 RSC.
- T. Forsting and M. A. Suhm, Curry-Jet SETUP, 2019, https://figshare.com/articles/Curry-Jet_SETUP/6395840/1.
- N. O. B. Lüttschwager and M. A. Suhm, Soft Matter, 2014, 10, 4885–4901 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- V. Barone, J. Chem. Phys., 2004, 120, 3059–3065 CrossRef CAS PubMed.
- V. Barone, J. Chem. Phys., 2005, 122, 14108 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, 2009 Search PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- E. R. Davidson, Chem. Phys. Lett., 1996, 260, 514–518 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- S. J. Daunt and H. F. Shurvell, J. Mol. Spectrosc., 1976, 62, 373–395 CrossRef CAS.
- M. Y. Choi, G. E. Douberly, T. M. Falconer, W. K. Lewis, C. M. Lindsay, J. M. Merritt, P. L. Stiles and R. E. Miller, Int. Rev. Phys. Chem., 2006, 25, 15–75 Search PubMed.
- I. Dauster, C. A. Rice, P. Zielke and M. A. Suhm, Phys. Chem. Chem. Phys., 2008, 10, 2827–2835 RSC.
- J. Bloino and V. Barone, J. Chem. Phys., 2012, 136, 124108 CrossRef PubMed.
- D. Luckhaus, M. Quack, U. Schmitt and M. A. Suhm, Ber. Bunsen-Ges., 1995, 99, 457–468 CrossRef CAS.
- P. Botschwina, Chem. Phys., 1982, 68, 41 CrossRef CAS.
- D. Christen, J. H. Griffiths and J. Sheridan, Z. Naturforsch., A: Phys. Sci., 1981, 36, 1378–1385 Search PubMed.
- C. Puzzarini, M. Heckert and J. Gauss, J. Chem. Phys., 2008, 128, 194108 CrossRef PubMed.
- T. Risthaus, M. Steinmetz and S. Grimme, J. Comput. Chem., 2014, 35, 1509–1516 CrossRef CAS PubMed.
- H. H. Nielsen, Encyclopedia of Physics, ATOMS III – MOLECULES I, Springer, Berlin, 1959, vol. XXXVII/1, p. 173 Search PubMed.
- W. H. James, E. G. Buchanan, C. W. Müller, J. C. Dean, D. Kosenkov, L. V. Slipchenko, L. Guo, A. G. Reidenbach, S. H. Gellman and T. S. Zwier, J. Phys. Chem. A, 2011, 115, 13783–13798 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed experimental measurements, tabulated Raman and IR vibrational transitions with assignments, anharmonic shifts and diagonal contributions to NH stretch bands as well as 1D normal mode NH stretch scan results at different levels of theory, cartesian coordinates of the presented molecular structures. See DOI: 10.1039/c9cp00399a |
| This journal is © the Owner Societies 2019 |