Open Access Article
Open Access ArticleCompetition between folded and extended structures of alanylalanine (Ala-Ala) in a molecular beam†
Vasyl
Yatsyna
 ab,
Ranim
Mallat
ab,
Ranim
Mallat
 a,
Tim
Gorn
c,
Michael
Schmitt
a,
Tim
Gorn
c,
Michael
Schmitt
 c,
Raimund
Feifel
c,
Raimund
Feifel
 a,
Anouk M.
Rijs
a,
Anouk M.
Rijs
 *b and
Vitali
Zhaunerchyk
*b and
Vitali
Zhaunerchyk
 *a
*a
aUniversity of Gothenburg, Department of Physics, 412 96 Gotheburg, Sweden. E-mail: vitali.zhaunerchyk@physics.gu.se; Tel: +46-317869150
bRadboud University, Institute for Molecules and Materials, FELIX Laboratory, Toernoovield 7-c, 6525 ED Nijmegen, The Netherlands. E-mail: a.rijs@science.ru.nl; Tel: +31-243653940
cHeinrich-Heine-Universität, Institut für Physikalische Chemie I, D-40225 Düsseldorf, Germany
First published on 6th March 2019
Abstract
We report the gas phase conformational preferences of laser desorbed Ala-Ala dipeptides probed by action spectroscopy using the IRMPD-VUV method. The molecules were internally cooled through collisional cooling in a supersonic jet environment. An IR spectrum was obtained experimentally in the spectral range of 700–1850 cm−1, and subsequently interpreted with the help of quantum chemical calculations. Although theory predicts that folded structures have lower electronic energies and, thus, are more stable at low temperatures compared to their extended (β-strand-like) counterparts, analysis of the experimental data concluded the extended conformer to be the most dominant. An explanation to this observation is discussed in this paper and rationalized in terms of collisional conformer relaxation processes occurring in the supersonic jet molecular beam.
1 Introduction
Proteins perform important biological functions in living organisms. As there is an intimate relation between the protein functioning and its three-dimensional structure assumed upon folding, investigating protein structures at the atomic level is of great importance. Insight into fundamental interactions that are responsible for protein structure stabilization can typically be obtained by studying amino acids and small peptides, which are protein building blocks.1–4 In order to investigate stabilization effects associated solely with intra-molecular interactions, the molecules of interest should preferably be isolated from neighboring counterparts. The molecular beam environment provides nearly perfect molecular isolation conditions. Furthermore, these isolated molecules are amenable to advanced quantum chemical calculations.Gas-phase infrared (IR) spectroscopy is a powerful tool to derive structures of molecules,5–9 especially when combined with quantum chemical calculations. A conventional method to measure IR spectra of neutral cold gas-phase molecules is IR–UV ion-dip action spectroscopy.10,11 This method is based on resonant absorption of a single IR photon and resonant-enhanced UV multi-photon ionization (REMPI). The advantage of this technique is that it is conformer-specific, though it can only be implemented for molecules possessing an aromatic UV-absorption chromophore such as a phenyl ring. This fact significantly limits the scope of molecules that can be studied with this technique. To overcome this limitation, the IRMPD-VUV method (IR multiple photon dissociation) was recently demonstrated.12 Although this method is not conformer-specific, structural information on various molecular conformers can be successfully derived from the experimental IR spectra with the help of quantum chemical calculations.13
To circumvent the issue related to thermal broadening of IR bands, molecules are seeded in a supersonic jet, where due to collisions with a carrier gas they are efficiently cooled down to 15 K.14 However, populations of molecular conformers upon supersonic jet cooling can be different compared to that expected from equilibrium thermal populations at 15 K.15,16 In particular it was shown that conformers with high barriers to interconversion (>800 cm−1) do not undergo any efficient conformer relaxation17–19 and their structures stay essentially frozen in the supersonic jet. Another factor which determines conformer conversion efficiency is the choice of carrier gas. Argon, for example, is more efficient for conformer relaxation than He and Ne.17 Collisional relaxation was found to be particularly important in our recent investigations into the gas-phase conformational preferences of laser desorbed, supersonic-jet cooled glycylglycine (Gly-Gly) with the IRMPD-VUV method.13 Despite its relative simplicity, Gly-Gly has a very rich conformational landscape with many stable low-energy conformers. Among various conformers populated upon laser desorption, only C5-trans (extended) was conclusively observed in a cold molecular beam.
In this work we report experimental results of an alanylalanine (Ala-Ala) IRMPD-VUV spectroscopy study combined with advanced quantum chemical calculations. The previous gas-phase studies on relatively small neutral Ala peptides have mostly been limited to aromatic ring containing species.20–22 The recently demonstrated IRMPD-VUV method does not possess such a limitation and can be applied to gas-phase IR spectroscopy of chromophore-free peptides. In this work we take advantage of this IRMPD-VUV method to identify IR signatures of the Ala-Ala peptide and explore the conformational preferences and interconversion processes in the gas phase. Similar to Gly-Gly,13 it is expected that Ala-Ala can adopt both extended and folded structures. Previous studies on peptides adopting such structures have indicated that competition between them can occur due to entropy stabilization effects.21,23 The folded and extended structures of Ala-Ala are expected to have similar electronic energies but different entropy contributions to the free energy, which can potentially lead to competition. Therefore, the study of Ala-Ala conformational preferences with respect to conformational temperature is particularly appealing.
2 Methods
The experimental procedure for the measurements reported in this work is similar to that employed by us previously for IRMPD-VUV spectroscopy of Gly-Gly13 and, therefore, it is described briefly here. The experiment was performed at the FELIX laboratory facility utilizing the FELIX-2 free electron laser (FEL) as an IR source. The Ala-Ala sample was obtained commercially from Sigma-Aldrich and used without any purification. The sample was sublimated with a laser desorption technique and the desorbed molecules were delivered to the interaction region by a supersonic flow of Ar carrier gas. In the supersonic Ar flow molecules underwent numerous collisions which resulted in efficient cooling of their translational and internal degrees-of-freedom down to 15 K.14 Collisions in the supersonic jet also had consequences on conformer populations, which will be discussed in detail below. In the interaction region the Ala-Ala molecules were exposed to the intense IR FELIX pulses and 10.5 eV VUV light. The IR wavelength was scanned in the range of 700–1850 cm−1. When the IR photon energy was resonant with a vibrational transition in Ala-Ala, the IRMPD process occurred. The resulting fragments were ionized with the VUV pulses and subsequently mass analyzed with a reflectron-type mass spectrometer. We observed only one type of fragments produced upon IRMPD of Ala-Ala, which is NH2CHCH3+ (m/z = 44). The VUV mass spectra measured without FELIX IR pulses also contained the m/z = 44 peak implying that the VUV photon energy of 10.5 eV was sufficiently high to fragment Ala-Ala upon ionization. These NH2CHCH3+ fragments interfered with the IRMPD-VUV products. A similar tendency was observed in our previous Gly-Gly measurements.13 In order to account for such background “IR off” charged fragments, the relative IR absorption intensity was found as13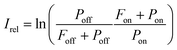 | (1) |
To predict Ala-Ala conformational preferences in the gas phase under our experimental conditions and to assign experimental IR bands, quantum chemical calculations have been carried out with the Gaussian software.24 A set of 235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Ala-Ala structures with random torsional angles, covering a large extent of the Ala-Ala conformational landscape, were pre-optimized with the computationally cheap PM6-D3H4 method using MOPAC.25 The most stable structures were then fully optimized with the ωB97X-D/6-311++G(d,p) method.26 To obtain insight into possible conformer relaxation pathways, barriers for interconversion were found as transition states (TS) connecting the two conformers employing the QST2 approach,27 or QST3 when QST2 failed. The structures of the TSs were optimized at the ωB97X-D/6-311++G(d,p) level of theory. The vibrational modes with imaginary frequencies of the optimized TS structures were checked for consistency with conformer interconversion coordinates. Finally, G4MP2 single point calculations28,29 were performed for the ωB97X-D/6-311++G(d,p) optimized structures to obtain highly accurate electronic energies, Eel, and Gibbs free energies, G. For calculating frequencies of the vibrational transitions the harmonic and VPT2 anharmonic analyses30–32 were performed with the B3LYP/N07D method including the D3BJ empirical dispersion.33,34
000 Ala-Ala structures with random torsional angles, covering a large extent of the Ala-Ala conformational landscape, were pre-optimized with the computationally cheap PM6-D3H4 method using MOPAC.25 The most stable structures were then fully optimized with the ωB97X-D/6-311++G(d,p) method.26 To obtain insight into possible conformer relaxation pathways, barriers for interconversion were found as transition states (TS) connecting the two conformers employing the QST2 approach,27 or QST3 when QST2 failed. The structures of the TSs were optimized at the ωB97X-D/6-311++G(d,p) level of theory. The vibrational modes with imaginary frequencies of the optimized TS structures were checked for consistency with conformer interconversion coordinates. Finally, G4MP2 single point calculations28,29 were performed for the ωB97X-D/6-311++G(d,p) optimized structures to obtain highly accurate electronic energies, Eel, and Gibbs free energies, G. For calculating frequencies of the vibrational transitions the harmonic and VPT2 anharmonic analyses30–32 were performed with the B3LYP/N07D method including the D3BJ empirical dispersion.33,34
3 Results and discussion
3.1 Ala-Ala conformers and their collisional relaxation
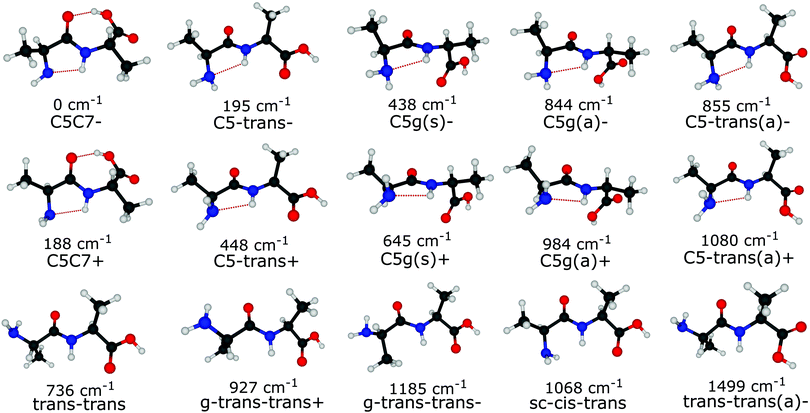
Out of the large number of stable Ala-Ala conformers found with the conformational search, only those with relative Gibbs free energies below 1500 cm−1 in the temperature range of T < 500 K are considered for further analysis. T ≈ 500 K is the upper limit for a conformational temperature prior cooling which is expected upon laser desorption with the laser source employed by us21,35 and such conformers can potentially be populated in our experiment. The conformers are presented in Fig. 2. The notation of the structures is based on the backbone dihedral angles starting from N-terminus (see Fig. 1): ψ1 ≈ ±180° and ≈ 0° are denoted with trans and cis, respectively, and ϕ2 ≈ ±180° and ≈ ±90° are denoted with trans and gauche, respectively. The COOH group rotation for the gauche structures is represented by the ψT dihedral angle being either in syn-coplanar (s), ψT ≈ 0°, or anti-coplanar (a), ψT ≈ ±180°, configurations. In the structures with relatively strong hydrogen bonds, the notation is based on the size of the ring formed by the hydrogen bond: C5 and C7 correspond to five and seven atoms in the rings, correspondingly. The structures denoted with either “+” or “−” symbols have comparable absolute values but opposite signs for backbone dihedral angles.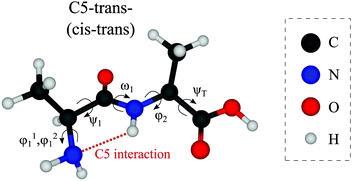 | ||
| Fig. 1 Structure of the Ala-Ala molecule in the cis–trans backbone configuration at the N- and C-termini, respectively (ψ1 close to 0° and ϕ2 close to 180°). | ||
Despite the large variety of conformers that can exist under laser desorption conditions, those with sufficiently low barriers to interconversion will relax to lower energy conformers.17–19,36–38 It was shown that relaxation is efficient if the interconversion barrier height is lower than a critical value, which depends on many factors such as type of carrier gas, initial temperature, gas stagnation pressure and the molecular size.39 In the case of supersonic jets of Ar the reported critical barrier heights17–19 range from 400 to 800 cm−1. Our experimental conditions in terms of laser desorption temperate and supersonic-jet expansion are quite similar to those of glycine, alanine and histamine studies,18,19 for which the critical barrier was found to be ≈700–800 cm−1. Therefore, in this study we assume the critical barrier to be in the range of 700–800 cm−1.
The different relaxation pathways and the corresponding barriers obtained for Ala-Ala conformers with the G4MP2 method are listed in Table 1. We note that the ΔG barrier for the C5C7+ → C5C7− transition is listed for a temperature of 100 K instead of 15 K. The reason is that the C5C7+ and C5C7− structures are quite similar and have a very low barrier to relaxation. The barrier at 15 K is so low that it lies within the inaccuracy range of the G4MP2 method. We also note that the C5C7− → C5-trans− and trans–trans → C5-trans− transitions include more than one dihedral angle rotation and, thus, they proceed in two steps involving an intermediate stable state. For example, sc–cis–trans is the intermediate state for trans–trans → C5-trans−. The barrier heights for the two-step transitions presented in Table 1 refer to the interconversion barriers for the first step.
| Relaxation pathway | ΔG (15 K) | ΔEel |
|---|---|---|
| a ΔG is presented for T = 100 K. | ||
| C5-trans(a)− → C5g(a)− | 150.34 | 123.56 |
| C5g(a)− → C5g(s)− | 295.41 | 299.58 |
| C5g(s)− → C5-trans− | 101.18 | 109.74 |
| g–trans–trans− → trans–trans | 76.60 | 206.96 |
| g–trans–trans+ → trans–trans | 293.22 | 311.87 |
| sc–cis–trans → trans–trans | 454.75 | 480.21 |
| sc–cis–trans → C5-trans− | 192.92 | 291.90 |
| trans–trans(a)− → trans–trans | 313.85 | 295.85 |
| g–trans–trans− → C5-trans− | 321.97 | 341.94 |
| g–trans–trans+ → C5-trans− | 329.21 | 327.68 |
| C5-trans(a)+ → C5-trans(a)− | 7.24 | 97.23 |
| C5C7+ → C5C7− | 9.88a | 30.95 |
| C5-trans+ → C5-trans− | 13.61 | 101.62 |
| C5g(s)+ → C5g(s)− | 47.41 | 127.08 |
| C5g(a)+ → C5g(a)− | 75.94 | 149.46 |
| trans–trans → C5-trans− | 786.60 | 840.37 |
| C5C7− → C5-trans− | 2070.08 | 2280.56 |
Under the assumption that interconversion from a higher energy conformer to a lower energy one prevails,18,19,36,38 the results presented in Table 1 suggest that the following chains of conformer relaxation pathways will efficiently occur:
| C5-trans(a)− → C5g(a)− → C5g(s)− → C5-trans− | (2) |
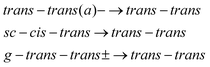 | (3) |
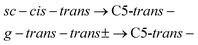 | (4) |
| X+ → X−, | (5) |
3.2 IRMPD-VUV spectroscopy of Ala-Ala
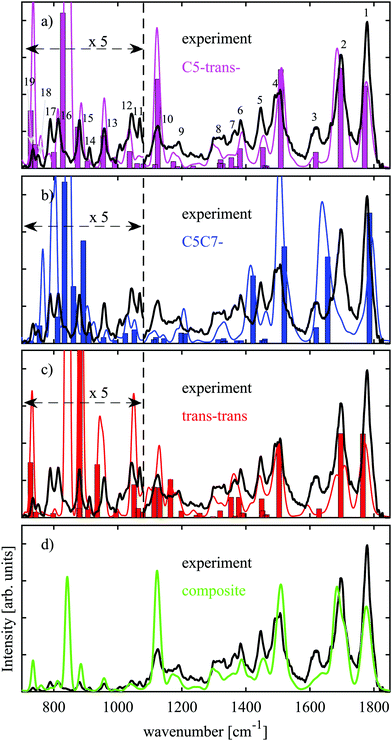
In the previous section we have argued that only three conformers, C5-trans−, C5C7−, and trans–trans are expected to be present under our experimental conditions. Relative abundances of these conformers can be inferred from comparison of their theoretical IR spectra with the experimental one. We have performed harmonic and VPT2 anharmonic analysis at the B3LYP-D3BJ/N07D level of theory, the results of which are presented in Fig. 3(a)–(c) together with our experimental data. The harmonic frequencies are scaled by 0.975 factor to partially account for anharmonicity, while no scaling is required for the VPT2 anharmonic frequencies. The theoretical absorption bands obtained with the anharmonic VPT2 analysis were convoluted with Gaussian functions with a relative bandwidth of 1.5% (FWHM) to fit the width of the IR peaks in the experimental spectrum. The experimental and theoretical spectra in Fig. 3(a)–(c) below 1080 cm−1 are magnified 5 times as the bands are relatively weak for this spectral region. The most prominent experimental peaks are numbered between 1 and 19 in Fig. 3(a). The first three peaks, peak 1–peak 3, can readily be assigned based on the IR spectroscopy data available in the literature. Peak 1 and peak 2 are associated with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching at the C-terminus and C
O stretching at the C-terminus and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching at the peptide link, respectively. The latter is commonly designated as the amide I band. The absorption band denoted as peak 3 in Fig. 3(a) originates from the NH2 scissoring motion.
O stretching at the peptide link, respectively. The latter is commonly designated as the amide I band. The absorption band denoted as peak 3 in Fig. 3(a) originates from the NH2 scissoring motion.
The amide I band in the case of Ala-Ala is particularly useful for assignment of folded or extended structures. Upon formation of the C7-ring, which implies hydrogen bonding between oxygen of the peptide link and hydrogen of the carboxylic group, this band will be red-shifted. Such a tendency is well reflected in the C5C7− theoretical spectrum (Fig. 3(b)) when compared to those of the extended C5-trans− (Fig. 3(a)) and trans–trans structures (Fig. 3(c)). Both harmonic and anharmonic analysis performed for C5C7− do not reproduce experimental peak 2 (Fig. 3(b)), which enables us to draw the conclusion that the C5C7− conformer is not the most dominant species.
The theoretically predicted IR bands for C5-trans− and trans–trans within the harmonic approximation (bars in Fig. 3(a)–(c)) are quite similar, though they exhibit some differences. The VPT2 anharmonic analysis predicts peak 3 for the trans–trans structure to be red-shifted. The fact that harmonic and anharmonic analyses give different results for this band implies that the NH2 scissoring motion is anharmonic. It is not so surprising that the anharmonic vibrational analysis predicts the NH2 scissoring band to be different for the C5-trans− and trans–trans structures, as these structures differ in orientation of the amino group. Another dissimilarity between the theoretical spectra of these conformers is that experimental peaks 16 and 17 are not reproduced by trans–trans. According to our assignment for C5-trans−, these bands are associated with NH2 wagging. Similar to NH2 scissoring, these bands are also conformer-specific. NH2 wagging is known to be anharmonic31,40 and the VPT2 analysis of these NH2 wagging modes indeed improves the agreement with the experimental IR spectrum (Fig. 3(a)). The analysis of the NH2 associated vibrations enables us to rule out trans–trans as the most prominent conformer and finally conclude that the C5-trans− conformer is the most abundant. Table 2 lists the vibrational assignment of the absorption bands observed in the experimental spectrum based on the analysis performed for the C5-trans− conformer.
| Peak | Center frequency, cm−1 | Signature |
|---|---|---|
| 1 | 1779 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching (carboxylic group) O stretching (carboxylic group) |
| 2 | 1697 | Amide I: C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching (peptide link) O stretching (peptide link) |
| 3 | 1615 | NH2 scissoring |
| 4 | 1501 | Amide II: NH in-plane bending & CN stretching (peptide link) |
| 5 | 1447 | CH3 deformations |
| 6 | 1383 | CH3 umbrella & CC stretching (C-terminus) |
| 7 | 1365 | CH3 umbrella & CC stretching (C-terminus) |
| 8 | 1313 | Contribution from several modes associated with CH wagging |
| 9 | 1191 | (a) CN & CO stretching (C-terminus); |
| (b) Amide III: NH in-plane bending & CN stretching (peptide link) | ||
| 10 | 1125 | COH bending & CO, CN stretching (C-terminus) |
| 11 | 1069 | CCH bending (C-terminus) |
| 12 | 1043 | CCH bending (N-terminus) |
| 13 | 953 | CC stretching & CCH bending (entire molecule) |
| 14 | 911 | CC,CN stretching & CCH bending (C-terminus) |
| 15 | 879 | OCN in-plane bending & CC,CN stretching (N-terminus) |
| 16 | 813 | NH2 wagging & CN stretching (N-terminus) |
| 17 | 789 | NH2 wagging & CC stretching (backbone) & CCH bending (CH3 at C-terminus) |
| 18 | 751 | Amide IV: NC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O out of plane bending & NH wagging (peptide link) O out of plane bending & NH wagging (peptide link) |
| 19 | 735 | NC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, OC O, OC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O out of plane bending & COH wagging O out of plane bending & COH wagging |
3.3 Conformer populations
The conclusion drawn from the theoretical analysis of the experimental IR spectrum that the C5-trans− conformer is the most abundant and a contribution from the C5C7− conformer is negligible might be somewhat surprising, as C5C7− has a lower electronic energy (see energies in Fig. 2). In order to resolve this seeming contradiction, the initial temperature of the molecules upon laser desorption needs to be taken into account. The relative abundances of the C5-trans−, C5C7−, and trans–trans conformers in the interaction region can be estimated with a Boltzmann distribution under the assumption of a thermal equilibrium upon the laser desorption, as well as complete relaxation through the pathways presented in eqn (2), (3) and (5). A similar approach has successfully been used to model conformer abundances in supersonic jet molecular beams.18,19,21,38 For these purposes we have calculated Gibbs free energies for all conformers shown in Fig. 2 in the temperature range of 15–600 K. The Gibbs free energies of conformers and their corresponding relative abundances at different temperatures can be found in Tables TS1 and TS2 of ESI,† respectively. The data shows that at very low temperatures only the folded C5C7− conformer is expected to be populated, which reflects the fact that this conformer has the lowest electronic energy. As the temperature increases, C5C7− gets less stable, and its population becomes lower than that of the extended C5-trans− conformer for T > 250 K. Such a temperature dependence reflects the fact that the entropy contribution at higher temperatures becomes more prominent and, since the folded C5C7− structure has a lower entropy compared to that of C5-trans−, the relative Gibbs free energy of C5C7− drops slower with increasing temperature. Such a property of Ala-Ala provides a sensitive tool to probe conformational temperature from conformer relative abundances.Assuming the full relaxation of the conformers through the pathways presented in eqn (2), (3) and (5), temperature dependent abundances of the C5C7−, C5-trans−, and trans–trans conformers are presented in Fig. 4. We note that the temperature presented in Fig. 4 should be considered as a conformational temperature of Ala-Ala upon the laser desorption, while the relative abundances concern final populations of supersonic-jet cooled Ala-Ala in the interaction region. Taking into account that the conformational temperature upon laser desorption under our experimental conditions can be estimated to be in the range of 350–500 K,21,35 the relative abundances of C5-trans−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C5C7−
C5C7−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) trans–trans in the interaction region are predicted to be ≈75%
trans–trans in the interaction region are predicted to be ≈75%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16%
16%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9% (Fig. 4). If the sc–cis–trans and g–trans–trans relaxation pathways presented in eqn (4) are more efficient than those from eqn (3), then the final trans–trans contribution will be few percents lower and the C5-trans− population will increase accordingly. These relative abundances of C5-trans−, C5C7−, and trans–trans derived from the Boltzmann distribution are in line with the conclusion drawn in Section 3.2 that C5-trans− is the most abundant species.
9% (Fig. 4). If the sc–cis–trans and g–trans–trans relaxation pathways presented in eqn (4) are more efficient than those from eqn (3), then the final trans–trans contribution will be few percents lower and the C5-trans− population will increase accordingly. These relative abundances of C5-trans−, C5C7−, and trans–trans derived from the Boltzmann distribution are in line with the conclusion drawn in Section 3.2 that C5-trans− is the most abundant species.
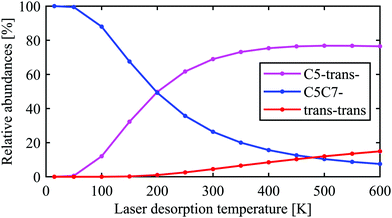 | ||
| Fig. 4 Relative abundances of the C5-trans−, C5C7−, and trans–trans conformers expected in the interaction region as a function of conformational temperature upon laser desorption. The abundances were estimated assuming complete relaxation through the pathways presented in eqn (2), (3) and (5) as well as assuming a Boltzmann distribution upon the laser desorption, ∝ exp(−ΔG(T)/kT), where ΔG(T) is the relative Gibbs free energy and T is the laser desorption temperature. | ||
Fig. 3(d) demonstrates a comparison between the experimental IR spectrum and a composite IR spectrum obtained from the VPT2 anharmonic analysis with relative abundances of ≈75%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16%
16%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9% for C5-trans−
9% for C5-trans−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C5C7−
C5C7−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) trans–trans, respectively. The theoretical spectrum does not match well to the NH2 scissoring band at 1615 cm−1. The fact that this band is adequately reproduced only by C5-trans− (Fig. 3(a)–(c)) points towards even greater abundance of this conformer than 75%.
trans–trans, respectively. The theoretical spectrum does not match well to the NH2 scissoring band at 1615 cm−1. The fact that this band is adequately reproduced only by C5-trans− (Fig. 3(a)–(c)) points towards even greater abundance of this conformer than 75%.
4 Conclusions
Ala-Ala is the simplest homo-dipeptide after Gly-Gly. Similar to Gly-Gly, it is a floppy molecule with a rich conformational space. The current work investigates this conformational space under laser desorption and supersonic-jet expansion conditions using our IRMPD-VUV method. The conformational search has revealed a large number of stable Ala-Ala structures, from which we considered the 15 lowest energy conformers. Quantum chemical calculations performed for these stable structures and transition states indicated that all conformers, apart from C5C7− (folded), C5-trans− (extended) and trans–trans (extended) underwent efficient conformer relaxation in numerous collisions occurring in the supersonic jet molecular beam. In the experimental IR spectrum only the C5-trans− was conclusively observed. Accordingly, the most prominent experimental vibrational bands were assigned with the help of the theoretical vibrational analysis performed for the C5-trans− structure.The relative abundances between the extended and folded conformers vary substantially with conformational temperature. Such a competition can be rationalized in terms of entropy stabilization effects. The folded structures have lower entropy, as they are more rigid. If the conformational temperature was determined solely by the temperature achieved upon the supersonic jet cooling, namely 15 K, then C5C7− would only be populated. However, this is in strong contrast with our conclusions drawn from the theoretical analysis of the experimental IR data that the C5-trans− was the most abundant species. Furthermore, the predominance of the C5-trans− was verified by taking into account possible collisional relaxation pathways and predicted Boltzmann populations with 350–500 K laser desorption temperature.
It is interesting to note that, although Gly-Gly has a more flexible structure than Ala-Ala due to the simpler side chain, the conformational preferences of Gly-Gly are very similar to those of Ala-Ala: in both molecules C5-trans is the most dominant conformer while contributions of C5C7 and trans–trans are too small to be conclusively detected by IRMPD-VUV spectroscopy. The difference between these two systems is that the methyl side chains in Ala-Ala result in increased steric hindrance in the C5-trans− structure with respect to C5C7−, which makes C5C7− more stable in terms of electronic energy. This results in the C5C7− conformer of Ala-Ala being favored at low temperatures (<200 K). Nevertheless, high energy barrier to interconversion between C5C7− and C5-trans− as well as relatively hot laser desorption conditions lead to a low abundance of C5C7 in a cold molecular beam of Ala-Ala, similarly to the case of Gly-Gly.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Swedish Research Council (VR), the Knut and Alice Wallenberg Foundation (Sweden) and the NWO Physical Sciences (Netherlands) for financial support. The research leading to these results has received funding from LASERLAB-EUROPE (grant agreement no. 654148, European Union's Horizon 2020 research and innovation programme). The authors highly appreciate the skillful assistance of the staff at the FELIX laboratory. Calculations were performed on resources at the Chalmers Centre for Computational Science and Engineering (C3SE) provided by the Swedish National Infrastructure for Computing (SNIC).References
- M. S. de Vries and P. Hobza, Annu. Rev. Phys. Chem., 2007, 58, 585–612 CrossRef CAS.
- Gas-Phase IR Spectroscopy and Structure of Biological Molecules, ed. A. M. Rijs and J. Oomens, Top. Curr. Chem., 2015, vol. 364, pp. 1–406, and references therein Search PubMed.
- C. Cabezas, M. A. T. Robben, A. M. Rijs, I. Pena and J. L. Alonso, Phys. Chem. Chem. Phys., 2015, 17, 20274–20280 RSC.
- E. M. Neeman, I. Leon, E. R. Alonso, L. Kolesnikova, S. Mata and J. L. Alonso, Phys. Chem. Chem. Phys., 2018, 20, 29159–29165 RSC.
- W. Chin, F. Piuzzi, I. Dimicoli and M. Mons, Phys. Chem. Chem. Phys., 2006, 8, 1033–1048 RSC.
- R. Chaudret, B. de Courcy, J. Contreras-Garcia, E. Gloaguen, A. Zehnacker-Rentien, M. Mons and J.-P. Piquemal, Phys. Chem. Chem. Phys., 2014, 16, 9876–9891 RSC.
- K. Schwing and M. Gerhards, Int. Rev. Phys. Chem., 2016, 35, 569–677 Search PubMed.
- N. S. Nagornova, T. R. Rizzo and O. V. Boyarkin, Science, 2012, 336, 320–323 CrossRef CAS.
- E. Garand, M. Z. Kamrath, P. A. Jordan, A. B. Wolk, C. M. Leavitt, A. B. McCoy, S. J. Miller and M. A. Johnson, Science, 2012, 335, 694–698 CrossRef CAS.
- R. H. Page, Y. R. Shen and Y. T. Lee, J. Chem. Phys., 1988, 88, 4621–4636 CrossRef CAS.
- A. M. Rijs and J. Oomens, in IR Spectroscopic Techniques to Study Isolated Biomolecules, ed. A. M. Rijs and J. Oomens, Springer International Publishing, Cham, 2015, pp. 1–42 Search PubMed.
- V. Yatsyna, D. J. Bakker, P. Salen, R. Feifel, A. M. Rijs and V. Zhaunerchyk, Phys. Rev. Lett., 2016, 117, 118101 CrossRef.
- V. Yatsyna, R. Mallat, T. Gorn, M. Schmitt, R. Feifel, A. M. Rijs and V. Zhaunerchyk, J. Phys. Chem. A, 2019, 123, 862–872 CrossRef CAS.
- G. Meijer, M. S. de Vries, H. E. Hunziker and H. R. Wendt, Appl. Phys. B: Photophys. Laser Chem., 1990, 51, 395–403 CrossRef.
- J. D. Rodriguez and J. M. Lisy, Int. J. Mass Spectrom., 2009, 283, 135–139 CrossRef CAS.
- O. Rodriguez and J. M. Lisy, J. Phys. Chem. Lett., 2011, 2, 1444–1448 CrossRef CAS.
- R. S. Ruoff, T. D. Klots, T. Emilsson and H. S. Gutowsky, J. Chem. Phys., 1990, 93, 3142–3150 CrossRef CAS.
- P. D. Godfrey, R. D. Brown and F. M. Rodgers, J. Mol. Struct., 1996, 376, 65–81 CrossRef CAS.
- P. D. Godfrey and R. D. Brown, J. Am. Chem. Soc., 1998, 120, 10724–10732 CrossRef CAS.
- E. Gloaguen, B. de Courcy, J.-P. Piquemal, J. Pilmé, O. Parisel, R. Pollet, H. S. Biswal, F. Piuzzi, B. Tardivel, M. Broquier and M. Mons, J. Am. Chem. Soc., 2010, 132, 11860–11863 CrossRef CAS.
- R. J. Plowright, E. Gloaguen and M. Mons, ChemPhysChem, 2012, 12, 1889–1899 CrossRef.
- E. Gloaguen, R. Pollet, F. Piuzzi, B. Tardivel and M. Mons, Phys. Chem. Chem. Phys., 2009, 11, 11385–11388 RSC.
- V. A. Shubert, E. E. Baquero, J. R. Clarkson, W. H. James III, J. A. Turk, A. A. Hare, K. Worrel, M. A. Lipton, D. P. Schofield, K. D. Jordan and T. S. Zwier, J. Chem. Phys., 2007, 127, 234315 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- J. Rezac and P. Hobza, J. Chem. Theory Comput., 2012, 8, 141–151 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- C. Peng and H. Bernhard Schlegel, Isr. J. Chem., 1993, 33, 449–454 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 127, 124105 CrossRef.
- Y. K. Kang and H. S. Park, Chem. Phys. Lett., 2014, 600, 112–117 CrossRef CAS.
- V. Barone, M. Biczysko and J. Bloino, Phys. Chem. Chem. Phys., 2014, 16, 1759–1787 RSC.
- V. Yatsyna, D. J. Bakker, R. Feifel, A. M. Rijs and V. Zhaunerchyk, Phys. Chem. Chem. Phys., 2016, 18, 6275–6283 RSC.
- V. Yatsyna, D. J. Bakker, R. Feifel, A. M. Rijs and V. Zhaunerchyk, J. Chem. Phys., 2016, 145, 104309 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- M. Handschuh, S. Nettesheim and R. Zenobi, J. Phys. Chem. B, 1999, 103, 1719–1726 CrossRef CAS.
- U. Erlekam, M. Frankowski, G. von Helden and G. Meijer, Phys. Chem. Chem. Phys., 2007, 9, 3786–3789 RSC.
- T. F. Miller III, D. C. Clary and A. J. H. M. Meijer, J. Chem. Phys., 2005, 122, 244323 CrossRef.
- B. Yang, S. Liu and Z. Lin, Sci. Rep., 2017, 7, 15869 CrossRef.
- P. Felder and H. Günthard, Chem. Phys., 1982, 71, 9–25 CrossRef CAS.
- R. A. Kydd and P. J. Krueger, J. Chem. Phys., 1978, 69, 827–832 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Gibbs free energies and relative abundances of Ala-Ala conformers at different temperatures. See DOI: 10.1039/c9cp00140a |
| This journal is © the Owner Societies 2019 |