Macroscopic defects upon decomposition of CO₂ clathrate hydrate crystals

Abstract

Micrometer- and submicrometer-sized pores and macroscopic defects like cracks and tubular channels can be found in a variety of clathrate hydrates (hydrates for short) during formation and decomposition. Their origin, their evolution in time, and their effect on hydrate decomposition kinetics are unclear. We used time-lapse micro computed tomography (μCT) in combination with temperature control and pressure monitoring to study the formation and evolution of pores and macroscopic defects in decomposing CO₂ hydrates at subzero (Celsius) temperature. Our results suggest that the decomposition of hydrates is always accompanied by the formation of pores and an increase of the apparent hydrate volume by more than 3%. Hydrate decomposition often starts with the formation of cracks inside the hydrate and not necessarily at the free surface of the hydrate, which frequently remains intact for a long period and seems to be self-preserved in some regions. Decomposition spreads out from these cracks in a uniform fashion yielding a variety of macroscopic features. In some cases, the propagating decomposition front seems to get blocked by planar barriers inside the hydrate yielding regions with high resistance against decomposition. This, together with a generally heterogeneous distribution of decomposition resistant regions, challenges the shrinking core model of hydrate decomposition as well as the popular ice-rind theory used to explain the effect of self-preservation.

---

1 Introduction

Clathrate hydrates, or hydrates for short, are crystalline, ice-like solids comprising water and small-sized guest molecules, most prominently light hydrocarbons or carbon dioxide.^1–3 Their structure is determined by a hydrogen-bonded network of water molecules that form polyhedra (or cavities) which are stabilized by the guest molecules. In the case of CO₂ as the guest molecule, six large polyhedra (truncated hexagonal trapezohedra) and two small polyhedra (pentagonal dodecahedra) form a unit cell of the cubic structure termed sI.⁴

Hydrates are generally non-stoichiometric compounds, meaning that not all polyhedra have to be occupied by a guest molecule. However, in the ideal stoichiometric case all cavities of a CO₂ hydrate are occupied by exactly one guest molecule. That gives a ratio of 8 guest molecules per 46 water molecules or CO₂·5.75H₂O. Combined with a theoretical stoichiometric density¹ of 1.13 g cm⁻³ this yields 7.7 kilomoles of CO₂ per cubic meter of hydrate. Thus, at standard temperature and pressure (STP) conditions 174 volumes of gaseous CO₂ are stored in one volume of CO₂ hydrate. For comparison, dry ice accumulates approximately 796 volumes of gas (STP) per volume of solid.

This high density of CO₂ combined with stability at moderate pressures and medium temperatures (e.g. 1.2 MPa at 273 K)¹ makes CO₂ hydrate an interesting material for several industrial applications. The food industry has tried to produce carbonated ice (i.e., CO₂ hydrate) as a means for home production of soft drinks since the 1950s.⁵ Although a real product is still hard to find, their efforts have continued also in recent years.⁶ Hatakeyama et al.⁷ showed that CO₂ hydrate can be effectively used for fire fighting. The large heat of hydrate dissociation (∼60 kJ mol⁻¹)⁸ cools down the flame while the released non-flammable gas reduces the supply of oxygen. Another application making use of the large enthalpy of hydrate dissociation is in refrigeration systems where a CO₂ hydrate slurry is the two-phase refrigerant with minimal impact on the environment.^9,10 The largest field of possible future application is the sequestration of CO₂ from pre- and post-combustion gas in hydrate form combined with subsequent long term storage in deep geological formations or the deep ocean. Although this carbon capture technology is currently too energy intensive for industrial use, this may change due to the development of hybrid technologies or new additives, which can significantly reduce the hydrate formation pressures.^11–15

Besides artificially formed CO₂ hydrate, there are also natural occurrences. On Earth, they have been found at the sea floor in hydrothermal fields where CO₂ rich gas bubbles are emitted from volcanic sources.¹⁶ Though direct evidence is still missing, extraterrestrial occurrences of CO₂ hydrate on icy moons (e.g. Europa,¹⁷ and the satellites of Saturn^18,19), comets,^20,21 and on Mars²² are assumed mainly based on the existence of both CO₂ and water together with temperature conditions which prevent the hydrate from dissociation.

Although phase equilibrium data are well established over a wide range of temperatures,¹ the processes involved in nucleation, formation, and decomposition of hydrates remain unclear even with a large amount of experimental work using a variety of techniques.²³ For instance, hydrate gas release and dissociation rates are determined using both macroscopic pVT-work^24–30 and time-resolved diffraction measurements.^31–36 In the case of neutron diffraction in situ experiments were done even at elevated pressures,^37,38 revealing phase fractions of hydrate and ice and identifying metastable intermediate phases like cubic ice (ice Ic). Micro-computed X-ray tomography (μCT) can be used to capture the three-dimensional structure of hydrate samples.^39,40 Phase-shift information is added in diffraction-enhanced X-ray imaging (DEI) to overcome the common problem of poor contrast between hydrate and ice/water in conventional attenuation-based μCT.^41,42 Optical microscopy and visual observations of hydrates are used to investigate changes of the surface texture during decomposition.^27,28,43 More detailed information on the surface microstructure on the micrometer and submicrometer scale is collected using cryo scanning electron microscopy (SEM).^{25,26,29,37,38,43} The local interaction between guest and host molecules is usually examined using Raman or infrared spectrometry.^44,45

Focusing on decomposition, the difficulty until today is mainly finding a meaningful relation between dissociation kinetics and thermodynamic state variables. Clathrate hydrates of guests which are gaseous at STP conditions decompose into gas and ice (T < 273.2 K) or gas and water (T > 273.2 K) when they are placed outside their stability region by either superheating (T > T_eq.) or under-pressurizing (p < p_eq.). The assumption that the stronger the driving force (i.e., the chemical potential difference associated with superheating or under-pressurizing), the higher the dissociation rate does not hold in general. In fact, some hydrates (CH₄, CO₂, Kr, Ar, O₂, N₂ and others³³) show very small rates of dissociation outside the stability field, but both at lower and higher temperatures, rates are significantly larger. Davidson et al.⁴⁶ first observed this phenomenon in calorimetry experiments with natural gas and methane hydrates at 240 < T < 273 K while Handa et al.⁴⁷ reported the same for Kr hydrates at 225 < T < 273 K shortly after. They argued that the ice produced in the initial period of decomposition protects the remaining hydrate from further dissociation by forming an impenetrable coating. This effect was later termed “self-preservation” by Yakushev and Istomin⁴⁸ and since then has been observed many times by numerous researchers.^{24,25,29–31,38,49–51}

The abrupt change in dissociation rates at the onset temperature of the self-preservation effect, as well as two distinct minima within the self-preservation regime,^24,52,53 made the development of a working hypothesis for hydrate decomposition difficult. Today it seems established that ice as a hydrate decomposition product is a crucial factor in hydrate decomposition and self-preservation in particular. This is also the foundation of two popular hypotheses: (1) Kuhs et al.³⁷ found that the ice formed during decomposition is generally defective and stacking-faulty up to T ≈ 240 K. They concluded that below 240 K the ice cannot act as an efficient diffusion barrier, while above 240 K annealing turns it into a rather dense and impermeable shield of hexagonal ice (ice Ih). Later, Falenty and Kuhs³⁸ suggested that the annealing of defective ice combined with a variety of microstructures found on freshly formed ice might lead to various decomposition paths including one with a very pronounced effect of preservation. (2) In several studies Melnikov et al.^27,28,54 showed that liquid water formation during hydrate dissociation is possible in the temperature range from 253 K to 273 K. Furthermore they showed that due to a high energy barrier, the solid–solid transformation of hydrate to ice is unlikely in a metastable region bounded by the three phase equilibrium curves of ice–hydrate–gas and water–hydrate–gas extended to temperatures below 273.2 K. Since supercooled liquid water can exist in the temperature range from 233 K to 273 K at 0.1 MPa, they proposed a relation between supercooled liquid water formation and the effect of self-preservation and suggested that freezing of a layer of supercooled water generates the gas-impermeable ice shell.

Additionally, pores and macroscopic defects like cracks and tubes on the micrometer and submicrometer scale have been found in several studies on natural and synthetic hydrates during both formation and decomposition.^{37,42,55–61} Although pores seem to be characteristic of hydrates, to our knowledge, no serious attempts have been made so far to study the influence of pores on the decomposition behavior. The same is true for cracks, which seem to act as nucleation sites for hydrate decomposition.^42,60,61

We use time-resolved attenuation-based μCT to study the formation and evolution of pores and macroscopic defects in decomposing CO₂ hydrates at different conditions inside and outside the self-preservation regime (from 240 K to 273 K). The samples were produced using vapor co-deposition of water and CO₂.⁶² The three-dimensional images are combined with pT-data collected from our in situ setup described in ref. 63. The pressure data are used to correlate the volume of decomposed hydrate with the amount of gas released. Although submicrometer-sized pores are too small to be detected directly with the resolution used (a voxel edge length of 6 μm), we can still infer their existence. This is because the formation of pores in decomposing hydrate is accompanied by a significant change in apparent density when compared to hexagonal ice. The unique setup used herein offers a combination of non-destructive long-term observation, accurate mass balance due to a closed system, and highly controlled sample history. It is applied to understand the role of pores, cracks and other macroscopic defects in the decomposition process of hydrates and self-preservation in particular.

2 Experimental

Sample preparation, the tomographic setup, and the experimental procedures used are briefly described in this section. Details on μCT settings, temperature and mass calibration, leakage, the non-uniform temperature field, and segmentation error are discussed in the ESI† provided with this document.

2.1 Sample preparation

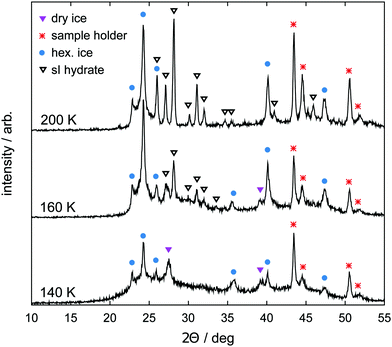
Samples are prepared using a vapor co-deposition technique as described in ref. 62, 64 and 65. Water vapor is deposited as amorphous solid water (ASW) together with CO₂ on a copper sample holder cooled to 77 K in a vacuum system. The co-deposition is done for 12 h at partial pressures p(H₂O) = 0.20 mbar and p(CO₂) = 0.02 mbar. The base pressure of the high vacuum chamber is 10⁻⁴ mbar. Subsequent warming of the deposit to 140 K in the vacuum causes the ASW to sinter and to efficiently capture CO₂ in the pore space of the ASW. Additionally, it causes the desorption of CO₂ adsorbed on external surfaces. This hydrate precursor material is then cooled back to 77 K, recovered after venting with dry nitrogen and stored in liquid nitrogen until needed in the experiments.

Samples of the hydrate precursor material are characterized by powder X-ray diffraction (PXRD). To this end, the samples are powdered under liquid nitrogen and transferred to the sample holder using a cryospoon. The sample holder is made from nickel-plated copper, precooled to about 80 K and allows for the powder to remain in a horizontal position for the whole measurement. The sample holder is part of the low temperature chamber TTK450 from Anton Paar GmbH. PXRD measurements are done on a Siemens D5000 instrument equipped with a Cu Kα1 X-ray source (wavelength 1.5406 Å) operated at 40 kV and 40 mA in θ/2θ scanning mode in the 2θ range from 10° to 55° (step width 0.02°). Installation of a Göbel mirror for parallel beam optics allows for measurement of undistorted Bragg peaks even for small amounts of powdered sample. For measurement, the chamber is evacuated to below 1 mbar, where the valve to the pump system is closed for the measurement itself (“static vacuum”). The temperature is regulated by controlling resistive heaters at the sample holder as well as the liquid nitrogen flow through the TTK450 chamber using a needle valve and a temperature controller (LakeShore, model CI330). As shown in Fig. 1, the precursor material transforms to CO₂ hydrate and hexagonal ice during the loading procedure as the temperature reaches 200 K.

Fig. 1 Powder X-ray diffraction (PXRD) patterns obtained from the sample precursor material at three different temperatures upon heating. At 140 K the halo of amorphous solid water (ASW) is visible together with a few Bragg peaks of hexagonal ice and crystalline CO₂ (dry ice). Bragg peaks of sI hydrate start to become visible at 160 K. They become more intense at 200 K where no Bragg peaks of crystalline CO₂ can be found anymore. The PXRD pattern at 200 K corresponds to the starting material of our experiments.

2.2 Tomographic setup

A lab-scale GE nanotom-m μCT system is used to perform full rotation scans of the samples. All scans are done using a tube voltage of 70 kV and a geometrical magnification factor of 16.7 resulting in a voxel edge length of 6 μm.

The manipulator of the μCT is equipped with a slightly improved version of the custom-built cryo stage designed for our recent study.⁶³ The stage (cf.Fig. 2) is cooled by a stack of thermoelectric Peltier elements (QC-31-1.0-3.9MS and QC-17-1.4-3.7MS, Quick-Ohm Germany) as well as a flow of cold gaseous nitrogen (N₂(g)). N₂(g) is produced from liquid nitrogen within the closed X-ray cabin using two independent custom-built evaporators ensuring a controlled flow of N₂(g).

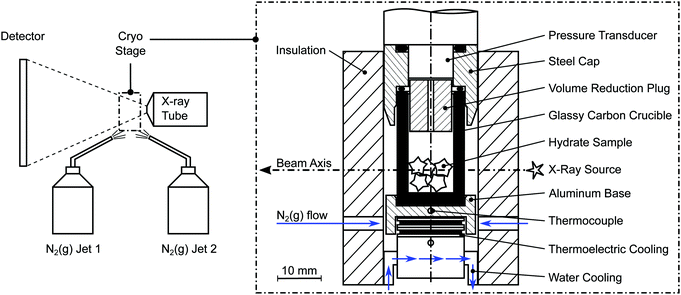Fig. 2 Schematic of the tomographic setup (left) together with a cross sectional view of the cryo stage (right).

The pressure vessel of the cryo stage consists of a glassy carbon crucible (SIGRADUR G, HTW Germany) and a steel cap fitted together using a two-component epoxy adhesive. It is referred to as the cell for the rest of this manuscript. Glassy carbon is chosen as the cell wall material since it is highly transparent to X-rays, impermeable to gases and liquids, extremely resistant to thermal shocks, and strong enough to withstand high pressures in a wide range of temperatures. An aluminum base, in good thermal contact with the glassy carbon crucible, is cooled using both N₂(g) flow and thermoelectric cooling. The latter is primarily used to avoid temperature fluctuation. The sample temperature is measured with an accuracy of 1 K by a calibrated thermocouple (K-type, d = 1 mm) positioned in the center of the aluminum base. A pressure transducer (PXM459, OMEGA Germany) with an accuracy of 6 mbar is connected to the steel cap of the cell. Due to the small cell volume (1.90 mL) even minor amounts of gas release can be registered with an accuracy of 1 μg. The experiment is monitored, controlled, and logged at a frequency of 1 Hz using a commercial data acquisition system (NI cRIO-9022, National Instruments USA). The setup has been tested to 10 MPa and can be used to cool samples down to 180 K.

The temperature gradient in the setup and the sample, a unique feature of our setup, is a direct consequence of space limitations in the μCT cabin and our requirements of (1) the highest possible magnification in the μCT, (2) maximal pressure resolution, and (3) accessibility of a wide range of temperatures and pressures.

2.3 Image processing

Radiograms collected during the μCT measurements are used by GE's phoenix datos|x reconstruction software (GE Sensing & Inspection Technologies, Germany) to compute the three-dimensional raster image of the sample with a voxel edge length of 6 μm. The image data is filtered with a three dimensional median filter with a kernel size of 7 voxels in order to enhance the signal to noise ratio. The random walk segmentation algorithm of Grady⁶⁶ is applied subsequently to segment the image data into gas, hydrate, and decomposed hydrate/ice phases. In this segmentation algorithm each voxel of the image data is classified based on its gray scale value and that of the neighboring voxels. It is particularly useful in preserving the connectedness of regions even in the presence of unwanted image noise. The process is shown in Fig. S6 (ESI†) together with further details about the individual steps and a brief discussion on segmentation error.

2.4 Procedure

Three different pathways, namely a temperature stepping one (cf.Fig. 3) and two isothermal (cf.Fig. 4) ones, are used in our experiments. The idea consists of the following loop: stable state → structure capture via μCT → destabilization → decomposition and pressure rise → stabilization at the vapor–ice–hydrate (V–I–H) equilibrium pressure → stable state. In the case of the temperature stepping pathway the hydrate is destabilized by overheating with respect to the stability temperatures. In experiments following the isothermal pathway, the destabilization is triggered by rapid depressurization from the stability pressures.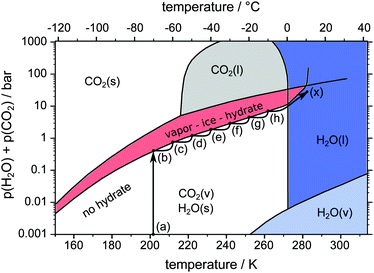

Fig. 3 pT-pathway of the temperature stepping procedure. After loading the sample at point (a) the equilibrium pressure is achieved at point (b). Starting from there the temperature is raised in steps of 10 K (b–h) leading to new equilibrium pressures. Eventually the sample is heated across the melting point (h–x). The phase diagram of the two-component system H₂O–CO₂ is based on data and theoretical predictions from ref. 1.

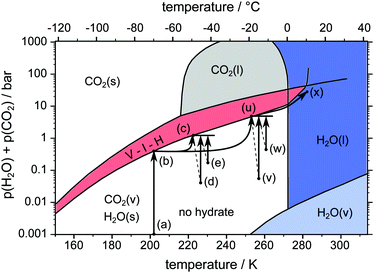Fig. 4 pT-pathway of the isothermal procedures. After loading the sample at point (a) the equilibrium pressure is achieved at point (b). Subsequently the temperature is rapidly raised to the isothermal set point temperature accompanied by new equilibrium pressures (point (c) or (u)). Rapid depressurization to points (d), (e), (v) and (w) results in further gas release until equilibrium pressures are restored. Eventually, the samples are heated across the melting point towards point (x). The phase diagram of the two-component system H₂O–CO₂ is based on data and theoretical predictions from ref. 1. Note that pressures at points (d), (e), (v) and (w) are not to scale. An explanation for differing pressures after rapid depressurization is given in the text. Points (d), (e), (v), and (w) are shifted in temperature for reasons of readability only.

In all pathways, loading is done by transferring the sample from the liquid nitrogen dewar directly into the precooled (203 K) cell. The cell is tightly closed immediately after the transfer. This is accompanied by a very sharp increase of pressure due to the evaporation of liquid nitrogen. In order to release the evaporated nitrogen the cell is opened once or twice after loading. Within less than one minute no further evaporation is observed and the experiment is started with the cell containing mainly N₂(g). After loading, the sample is outside the stability region at point (a) so the decomposition starts with a release of gas, resulting in an increase of pressure in the closed cell. The pressure continues to rise until it reaches the V–I–H equilibrium pressure of 0.43 bar¹ at point (b). There, the first μCT scan is done 15 min after the pressure stabilizes.

In the temperature stepping experiment (cf.Fig. 3) the temperature is repeatedly raised by 10 K at a rate of 2 K min⁻¹ following the path (b–h). Every step in temperature causes further decomposition, release of gas, and pressure increase. At every step, a μCT scan is done once the new equilibrium pressure is reached after some time. Eventually, the sample is brought to full decomposition by heating (1 K min⁻¹) across the melting point of ice.

Two different isothermal experiments are depicted as pathways (a-b-c-d-c-e-c-x) and (a-b-u-v-u-w-u-x) in Fig. 4. After an initial scan at point (b) the temperature is rapidly raised by 10 K min⁻¹ to either 228 K at point (c) or 253 K at point (u). Again, the new equilibrium pressure is reached and a μCT scan is started. After the scan is completed, the cell is rapidly depressurized to point (d) or (v) at constant temperature by opening and closing. This destabilizes the hydrate and decomposition continues. When point (c) or (u) is attained once more, the current state of the hydrate structure is captured with another scan. The rapid depressurization procedure is repeated several times provided that the amount of remaining hydrate is enough to restore point (c) or (u) after one more depressurization. Note that the term “isothermal” here refers to parts (c-d-c-e-c) and (u-v-u-w-u) of the pathway, where the cell is kept at constant temperature for a long time. The isentropic cooling of the cell gas due to rapid depressurization is neglected in this description. Similar to temperature stepping, the isothermal experiments are terminated by heating the sample across the melting point of ice. The sum of partial pressures of CO₂ and H₂O immediately after rapid depressurization (points (d), (e), (v), and (w)) is below 1 atm (see Fig. 4). The difference to 1 atm refers to the partial pressure of the undetermined amount of N₂(g) gas in the system. With every opening event this difference decreases due to escaping N₂(g).

In both temperature stepping and isothermal experiments the total amount of water in the system is obtained based on the reconstructed volume from the last scan at point (x).

In all procedures, N₂(g) as an additional component in the gas composition allows the investigation of CO₂ hydrates at sub-atmospheric pressures without the use of a vacuum pump, which would have made the loading procedure severely more complicated. Besides, the self-preservation phenomenon in CO₂ hydrate occurs at a variety of atmospheric conditions, including mixtures of CO₂ and N₂.³⁶ Moreover, the formation pressure of N₂ hydrate (e.g. 16 MPa at 273 K)¹ is considerably larger than the maximal N₂(g) partial pressure in our experiments (0.1 MPa). Additionally, the statistical thermodynamic modeling predictions of CSMGem¹ point towards a neglectable amount of N₂ in the sI hydrate phase at the conditions investigated. Therefore, we assume that no N₂ is taken up in the CO₂ hydrates of our experiments. Thus, the amount of nitrogen in the cell gas remains constant over the course of the experiment, provided that the cell is not opened. The absolute pressure and CO₂ concentration, reflected as the CO₂ partial pressure, influence the decomposition at the hydrate–gas interface. Here, it is supposed that pressure effects at the hydrate–gas interface are subordinate to concentration effects. As a consequence, we assume that the initial amount of nitrogen gas shifts the vapor–ice–hydrate (V–I–H) equilibrium pressures of the two component system CO₂–H₂O by a constant pressure offset.

2.5 Determination of the mass, composition, and temperature

The combination of accurate volume and pressure data enables us to determine the sample mass and sample composition. The mass of water m(H₂O) in the sample is determined from the volume of liquid water V_Liquid measured at 283 K at the end of the experiment and a liquid water density of 0.9997 g cm⁻³. The gas mass m_CO2(t) released from the hydrate from the beginning of the experiment until time t is derived from the pressure signal using a fitted model equation for the mass–pressure relation (cf. ESI†). Gas leakage and dissolution of CO₂ in water are neglected in the computation of m_CO2. While the accuracy of m(H₂O) is 1%, larger uncertainties are associated with the computation of m_CO2 due to the unknown amount of N₂(g) in the cell. To account for that, we use the subscripts min and max to refer to an initial N₂(g) partial pressure of 1 atm and 0 atm, respectively. For instance, m_min,CO2 and m_max,CO2 denote the lower and upper bounds of m_CO2 depending on the initial amount of N₂(g) in the cell. Both m_min,CO2 and m_max,CO2 are accurate to within 1.5%. The largest pressure value observed immediately after the full decomposition of the hydrate at time t* (i.e., when all CO₂ is in the gas phase) yields m_min(CO₂) := m_min,CO2(t*) and m_max(CO₂) := m_max,CO2(t*), the lower and upper bounds of the total mass of CO₂ in the sample. Since the maximal pressure is usually found at temperatures slightly below 273 K the effect of dissolved CO₂ on m_min(CO₂) and m_max(CO₂) is neglected. The knowledge of the water and guest gas mass allows the determination of the sample composition, i.e., the determination of n in CO₂·nH₂O. However, in cases of n > 5.75, this number cannot be used to differentiate between excess water in ice form and that in empty hydrate cages. From the powder X-ray diffraction (PXRD) patterns of Fig. 1 it is clear though that a small amount of ice is present in our samples. While the cell pressure and the sample volume can be measured directly, direct determination of the sample temperature is possible only in the lowest region of the sample (temperature of T_low, cf. ESI†). Further above the bottom of the cell, temperatures are higher due to the temperature gradient along the cell axis (cf. ESI†). The temperature gradient reduces linearly from about 2.5 K mm⁻¹ at T_low = 203 K to approximately 0.5 K mm⁻¹ at T_low = 273 K. The highest temperature that the sample is exposed to is denoted as T_high. Since in our setup T_high cannot be determined directly, we use the settled experimental pressure to obtain a range T_high,min < T_high < T_high,max of possible values (cf. ESI†). For simplicity all temperatures in the text refer to T_low if not specified differently.

3 Results and discussion

For clarity reasons, the results are presented in four subsections. First, a correlation between hydrate gas release and mesostructural change is established. Second, mesostructural changes between isothermal experiments at 228 K and 253 K are compared. Third, the evolution of macroscopic defects and pores is tracked. Fourth, close-up views of the initial phase of decomposition expressed by gas release rates are presented. Important key data of all experiments are summarized in Table 1.

Table 1 Key data of all experiments as derived from the pressure signal and the μCT scans

Experiment	m(H2O) (mg)	m min(CO2) (mg)	m max(CO2) (mg)	CO2·nH2O (−)	V Sample,initial (mm^3)	V Sample,end (mm^3)	V Liquid (mm^3)
Temp. stepping	90.0	23.4	27.3	8.0 < n < 9.4	120.1	127.1	90.0
Isothermal 228 K	155.7	47.2	—	n < 8.0	205.9	213.2	155.7
Isothermal 253 K	134.6	45.9	—	n < 7.2	209.8	216.2	134.6

---

3.1 Temperature stepping

Two ice particles are added to a hydrate sample in a temperature stepping experiment in order to serve as a well determined reference for the ice phase. The mass of the ice particles is 19 mg and the total amount of water in the cell is 109 mg. Fig. 5 shows T_low, the gauge pressure, and the released CO₂ mass m_min,CO2 over the course of the experiment. μCT scans done at eight different temperatures are labeled with Roman numerals and tagged as blue dots on the temperature signal. The dotted line shows the theoretical value of the V–I–H equilibrium pressure corresponding to T_low. Differences between measured and equilibrium pressures are caused by the non-uniform temperature field (cf. ESI†) and the initial amount of N₂(g) introduced during the loading procedure.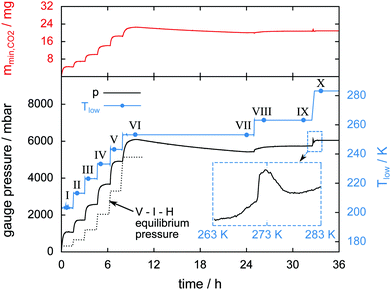

Fig. 5 Gauge pressure, temperature T_low, and m_min,CO2 (mass of the released CO₂) as a function of time. Blue dots denote the start of a μCT scan labeled with Roman numerals. The inset shows the gauge pressure as a function of temperature during melting of the hydrate at a heating rate of 1 K min⁻¹. The dotted line shows the theoretical V–I–H equilibrium pressure at the corresponding temperature as predicted by the software CSMGem.¹

During the initial period of the experiment every increase in the sample temperature results in a period of significant gas release until the pressure settles at a new V–I–H equilibrium. This is observed until scan VI is done at 253 K after 10 h experiment time. In the period between 10 h and 24 h experiment time, the full halt of gas release leads to a small decrease of pressure caused by leakage. Remarkably, after scan VIII at 263 K, the pressure remains constant for more than 6 h. This implies that the leak of gas is now compensated by the gas release from the hydrate. The sample melting is shown in the inset of Fig. 5. Here, the gauge pressure is depicted as a function of temperature during heating at a rate of 1 K min⁻¹. The jump in pressure at 271 K is caused by the complete decomposition of the hydrate. This abrupt release of all remaining gas slightly below the melting point of pure ice has also been found by other researchers.^24–26 Subsequently, a decrease in pressure caused by the contraction of the sample due to melting and the dissolution of CO₂ in water is visible from 273 K to 279 K. The relative mass of hydrate which is preserved until melting is only 3.5%. The preservation of such small amounts of hydrate for a very long time is observed in many of our own experiments and has also been reported in previous studies.^{24,25,29,34,38,53}

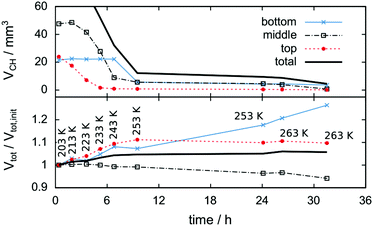
Fig. 6 shows tomograms of the sample at four different scan times at identical coordinates. The assignment of the different materials (hydrate, ice, or gas) to shades of gray is deduced empirically. Because of their respective theoretical densities and elemental compositions, among these materials, the hydrate should attenuate X-rays the strongest, followed by the ice, and finally, the gas. In general, the stronger the attenuation of X-rays, the brighter the gray scale values in our tomograms. Thus, dark shades of gray are assigned to gas, which attenuates the X-rays only weakly. The ice particles, produced by freezing water droplets in liquid nitrogen, are easily identifiable by their spherical shape and stability over time. The remaining shades of gray can be hydrate and decomposed hydrate only. Since the decomposed hydrate lacks CO₂, it attenuates X-rays less than the intact hydrate does. In addition, regions of decomposed hydrate grow during the decomposition while regions of hydrate shrink. Histograms of regions r1, r2, and r3 (cf.Fig. 6, scan III) corresponding to decomposed hydrate, ice, and hydrate, respectively, and a line profile across all phases (cf.Fig. 6, line A-B-C-D, scan III) are shown in Fig. 7. Two important findings are apparent: (1) phases of ice, hydrate, decomposed hydrate, and gas are distinguishable by different gray scale values. Particularly, hydrate and decomposed hydrate show almost no overlap in their gray scale histograms. (2) The decomposed hydrate phase is slightly darker than the ice phase. Since both phases contain water molecules only, this implies that the apparent density of the decomposed hydrate is smaller than that of ice, i.e., the decomposed hydrate is porous. This rather good contrast helps with the segmentation of the raster image data, which in turn yields accurate volume information. While the accuracy and reliability of the volume information usually have to be estimated based on the image data alone, here we can make use of the independent pressure signal to verify our phase assignment. Fig. 8 displays the volume of decomposed hydrate as a function of m_min,CO2. The linear correlation between volume and mass is evident. The small offset of 0.6 mm³ in the fitting function V(m) = 0.6 + 5.1·m to the experimental data corresponds to the initial volume of hydrate, which decomposes during the loading procedure. All data points deviate from the linear fit by less than 4 mm³ (i.e., about 3% of the sample volume). This good correlation is found in all experiments of this work (cf. ESI†) and implies that our assignment of phases in the tomographic data is correct. Moreover, it justifies a more detailed local inspection of the sample based on the image data alone. This is done to examine the effect of the inhomogeneous temperature field on the hydrate stability. The volume containing the sample is subdivided into bottom, middle, and top regions. Each region has a height of 3 mm. The hydrate volume for each region is displayed as a function of time in the upper part of Fig. 9 together with the total hydrate volume. The top region of the hydrate decomposes within the first 5 h. During the same period, approximately 50% of the hydrate in the middle region decomposes while the bottom region shows no decomposition at all. Between 5 h and 10 h the hydrate in both the middle and the bottom regions decomposes almost completely. Only approximately 5 mm³ of hydrate remains in each of the two regions until the temperature is increased to 263 K. After 5 h at 263 K the rest of the hydrate of the middle region decomposes as well. The 5 mm³ of hydrate in the bottom region remains until the sample melts. The extraordinary stability of the bottom region during the first 7 h of the experiment can be explained using the non-uniform temperature field and its effects on the sample upon heating (cf. ESI,† Fig. S3). Table 2 provides the pair T_low and T_high,min as well as their difference ΔT. A comparison between the conditions at the start and end of each heating step (values in two successive lines in Table 2) shows that T_low after heating is smaller than T_high,min at the beginning of heating until T_low is roughly 253 K. That implies that for T_low < 253 K the coldest region of the sample (i.e., the bottom region) can never leave the hydrate stability region. The negative value for ΔT at T_low = 263 K implies that the settled pressure (corresponding to T_high,min) is below the V–I–H equilibrium pressure corresponding to T_low. Since any temperature the sample is exposed to is above or equal to T_low this means either that there is no hydrate left or that the absence or low rate of gas release prevented the attainment of the equilibrium pressure.

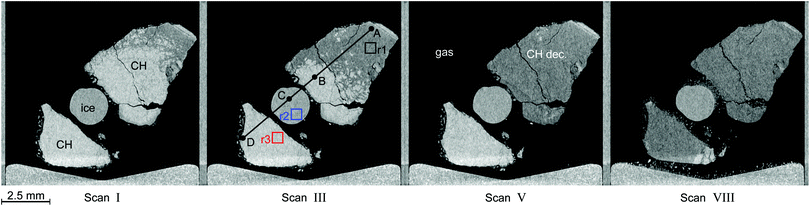Fig. 6 Tomograms of the sample configuration at four different times in a temperature stepping experiment. Roman numerals refer to the μCT scan number as in Fig. 5. In descending order of brightness the different regions are: clathrate hydrate (CH, white), ice (gray), decomposed hydrate (CH dec., dark gray), and gas (black). The squares in black (r1), blue (r2), and red (r3) in the tomogram of scan III denote regions used for the computation of histograms. They are depicted in Fig. 7 together with a line profile along the path from A to D. The wedge-shaped bright area at the bottom of the images is the cell base.

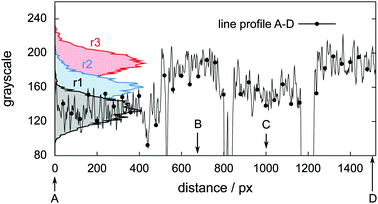Fig. 7 Histograms and line profile of gray scale values obtained from the tomogram of scan III shown in Fig. 6. The line profile starts in the decomposed hydrate region (point A), intersects with the hydrate region first (point B), the ice region afterwards (point C), and eventually ends in the hydrate region (point D).

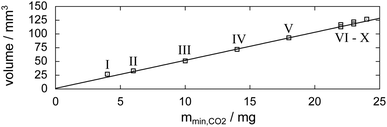Fig. 8 Relation between μCT image data and released gas mass m_min,CO2 (derived from the pressure signal). Markers denote the volume of the decomposed hydrate at the individual scan times (labeled by Roman numerals; cf.Fig. 5) as a function of the mass of released hydrate gas. The fitting function to the experimental data is V(m) = 0.6 + 5.1·m.

Fig. 9 Change of hydrate volume over the experiment time in absolute numbers (top) and change of total particle volume (i.e., decomposed plus preserved hydrate volume) relative to the initial condition after loading (bottom). Data are shown for the entire volume investigated (black solid line) as well as separated into the bottom, middle, and top thirds (markers). Note the relative growth of approximately 5% in the total particle volume. The temperature program is indicated by T_low labels.

Table 2 Comparison of the lowest and highest sample temperature during the temperature stepping experiment

T low (K)	T high,min (K)	ΔT = Thigh,min − Tlow (K)
203	220.5	17.5
213	229.5	16.5
223	237.8	14.8
233	245.7	12.7
243	252.3	9.3
253	257.6	4.6
263	256.2	−6.8

---

The lower part of Fig. 9 tracks the sum of the hydrate and decomposed hydrate volumes over the experimental time relative to its value at the beginning of the experiment. A comparison between the total volume at the end and the beginning of the experiment yields a volumetric expansion of approximately 5% during hydrate decomposition. It is shown that the bottom region of the hydrate gains significantly more volume than the middle and top regions. The middle region is even losing some of its initial volume, although no displacement of the sample is observed. This can be explained by mass transport of water via the sublimation–diffusion–resublimation mechanism known from snow metamorphosis.^67–70 Distinct indications for this are the needle like ice crystals growing in the interstices between the hydrate and the ice particles over the course of the experiment (cf.Fig. 6, scan VIII).

Eventually, during melting, the sum of the hydrate and decomposed hydrate volumes drops by 29% from solid to liquid. That is significantly larger than the volume reduction of pure ice during melting (9%). Similarly, a comparison of the volume of liquid water with the initial volume of the hydrate sample yields a volume reduction of 25%.

3.2 Isothermal experiments

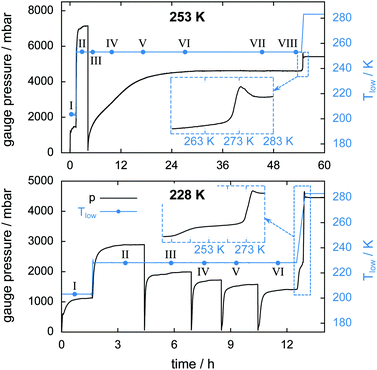
Two isothermal experiments, as described in Section 2.4 and Fig. 4, are carried out at T_low = 228 K and T_low = 253 K. The important key features of the experiments are listed in Table 1. An estimation of m_max(CO₂) is omitted here due to the unknown amount of guest gas escaping the cell at rapid depressurization events. The pT-conditions during the experiments are displayed in Fig. 10 together with the starting times of the μCT scans. Four successive rapid depressurization events are triggered in the 228 K experiment while only one event is initiated at 253 K due to the small amount of hydrate left after the first opening. Due to very low dissociation rates in the 253 K experiment, μCT scans are possible even during decomposition (i.e., volume and phase changes over a 60 min long scan are negligible). A comparison between the pressure signals of the two isothermal experiments after the rapid depressurization procedure shows a distinct difference in the dissociation behaviour. While at 228 K the pressure settles within about 1 h after rapid depressurization it takes about 18 h to reach equilibrium at 253 K. This reduced rate of gas release at 253 K (with respect to 228 K) indicates that at 253 K the hydrate is self-preserved.

Fig. 10 Gauge pressure and temperature T_low as a function of time for the isothermal experiment at 253 K (top) and at 228 K (bottom). Blue dots denote the start of a μCT scan labeled with Roman numerals. The insets show the gauge pressure as a function of temperature during melting of the hydrate at a heating rate of 2 K min⁻¹.

Table 3 lists upper and lower bounds for the warmest sample temperature T_high at the beginning and at the end of the isothermal phase of the experiment. It is assumed that initially the N₂(g) partial pressure is 1 atm. With every cell opening event the N₂(g) partial pressure is reduced. Hence, at the beginning of the experiment T_high ≈ T_high,min while at the end T_high ≈ T_high,max (cf. ESI†). A comparison between the sample temperature conditions (i.e., T_low and T_high) of the two isothermal experiments shows that for the 228 K experiment the temperature in the cell is nowhere above 253 K. Additionally, the temperature data indicate that the isothermal experiment at 253 K is done completely inside the self-preservation region (240 K < T < 273 K) while at 228 K the majority of the sample lies outside that region.

Table 3 Highest sample temperature during the isothermal experiments

Experiment	Scan no.	T high,min (K)	T high,max (K)
Isothermal 253 K	II	262	265
Isothermal 253 K	VI–VIII	251	256
Isothermal 228 K	II	240	247
Isothermal 228 K	VI	225	236

---

The insets of Fig. 10 show the gauge pressure as a function of temperature during the final temperature ramp (2 K min⁻¹) which leads to the complete decomposition of the hydrate samples. The characteristic pressure signal upon melting, already seen in Fig. 5, recurs. In both isothermal experiments the remaining gas is released shortly before melting of the ice starts. Notably, a flattening of the pressure curve is observed from about 240 K to 271 K in the 228 K isothermal experiment. Since a large amount of CO₂ is released only upon melting this flattening is probably caused by the onset of self-preservation during heating.

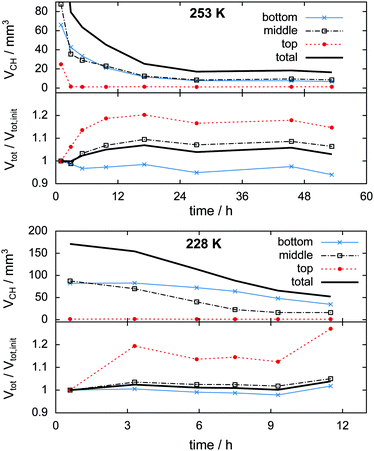
In the 253 K isothermal experiment (cf.Fig. 11, top) the top region of the sample decomposes almost completely before the cell is opened for pressure relief. A significant fraction of hydrate, totalling 20 mm³ or 10% of the initial sample volume, outlasts the rapid depressurization procedure in the middle and bottom regions. In contrast to the temperature stepping experiment, the hydrate volume in the middle and bottom regions here changes in an almost identical fashion after the cell opening event. This implies that rates of dissociation are similarly low in both regions. The first 17 h of decomposition are accompanied by a steady expansion of the sample region. The degree of expansion correlates with the ratio of decomposed to remaining hydrate. That means in relative numbers the top region grows more than the middle region, which grows more than the bottom region. Furthermore, the growth in the top region is observed mainly after 3 h when only a minute amount of hydrate is left. This implies that the expansion takes place primarily after decomposition. Subsequent to the period of expansion, the measured volumes stabilize and start to even shrink slightly. This can be explained using the growth of pores. Once pore sizes become big enough (>15 μm), void space becomes clearly distinguishable from solid phases, which results in a reduction of the measured solid volume.

Fig. 11 Change of hydrate volume over the experiment time in absolute numbers (top half of graphs) and change of total particle volume (i.e., decomposed plus preserved hydrate volume) relative to the initial condition after loading (bottom half of graphs) obtained from the isothermal experiments at 228 K and 253 K. Data are shown for the entire volume investigated (black solid line) as well as separated into the bottom, middle, and top thirds (markers).

In the isothermal experiment at 228 K (cf.Fig. 11, bottom) a similar behaviour is found in terms of expansion. The top region decomposes completely before the first scan is done and expands by 20% until the time of the second scan. The middle and bottom regions show almost no expansion during the first 9 h. Only at the end of the experiment does a total volumetric expansion of 3.6% become apparent. A reduction of the sample volume at advanced experimental time, as observed in the 253 K case, is missing here due to the much shorter duration of the experiment. Both the middle and the bottom regions contain an almost identical initial amount of approximately 85 mm³ hydrate. Contrary to the result of the isothermal experiment at 253 K, here the hydrate decomposes significantly faster in the middle region than in the bottom region. This behaviour reflects higher rates of dissociation attributed to the higher temperatures in the middle region.

3.3 Macroscopic defects and pore formation

In this section the focus is set on the macroscopic defects observed in the tomograms obtained from the μCT scans. No differences between the results obtained from the temperature stepping and the two isothermal experiments are found. Instead, a few common features, presented in Fig. 12–15, are observed in all three experiments. More views of μCT scans are provided in the ESI.†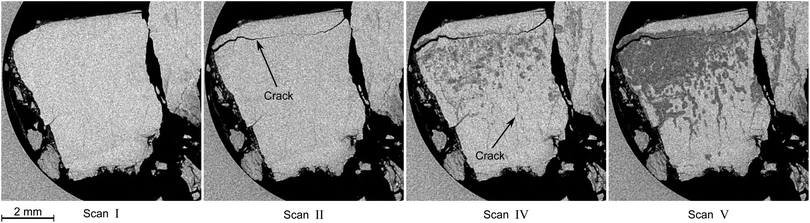

Fig. 12 Typical degradation pattern as observed in horizontal tomograms obtained during the isothermal experiment at 228 K. Roman numerals refer to the scan numbers as labeled in Fig. 10. Hydrate is the bright, decomposed hydrate the dark gray, and gas the black phase. The circular region at the left side of the slices is the glassy carbon crucible. Note the appearance of a large crack in the tomogram of scan II and the subsequent advent of decomposition, which seems to start from the big crack initially and from smaller cracks at later times.

Fig. 13 3D illustration of decomposing hydrate at four different stages of decomposition. The views are obtained from tomograms collected during the isothermal experiment at 228 K. Roman numerals refer to the scan numbers as labeled in Fig. 10. Regions of bright color represent hydrate and red regions correspond to already decomposed hydrate.

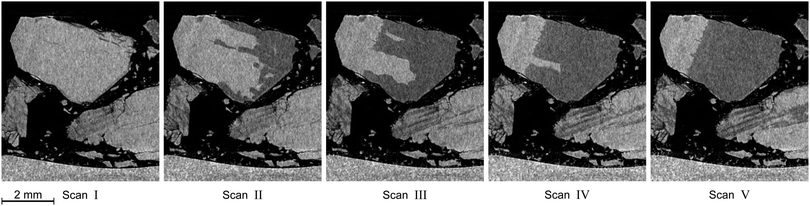Fig. 14 Distinctive degradation pattern as observed in vertical tomograms obtained during the isothermal experiment at 228 K. Roman numerals refer to the scan numbers marked in Fig. 10. Note how decomposition starts from the right side of the particle and stops at a plane which acts as a barrier for further decomposition. The blocking effect of that plane persists over the whole course of the experiment.

Fig. 15 Horizontal tomograms, showing the process of pore formation taking place during the decomposition of a hydrate particle. The tomograms are obtained from the isothermal experiment at 253 K and labeled with Roman numerals according to the labeling in Fig. 10. Note how the particle expands as it decomposes (from left to right). The double headed arrow is provided as a visual aid for comparison.

Cracks. Hydrate decomposition is found to be accompanied by the formation of cracks. The formation of a particularly large crack is observed in the 228 K experiment and shown in Fig. 12. The crack forms during the temperature increase from 203 K to 228 K. No signs of decomposition are visible in the vicinity of the crack at the time of scan II. At later times (scan IV and later) smaller cracks become visible mainly because of hydrate decomposition along crack surfaces. Surprisingly, only minor signs of decomposition are found at the exposed free surface of the sample. To support our observations, three-dimensional renderings of the same sample are presented in Fig. 13. The regions colored in red correspond to already decomposed hydrate while intact hydrate is colored gray. The large crack seen in Fig. 12 and many small cracks on the surface of the hydrate particle are visible in the rendering of scan II of Fig. 13. Likewise, decomposition along the surface of small cracks is also evident in the isothermal experiment at 253 K (cf. scans II and IV of Fig. 15). In general, it seems that decomposition often starts at the surface of cracks or in the vicinity of cracks.

Similar observations were made by Takey et al.^42,60 and Mimachi et al.⁶¹ in nondestructive studies of natural gas and methane hydrate pellets using phase contrast X-ray imaging. The authors speculated that differences in the thermal expansion between hexagonal ice (ice Ih) and hydrate (at 200 K the coefficient of linear expansion is a = 56 × 10⁻⁶ K⁻¹ and c = 57 × 10⁻⁶ K⁻¹ for hexagonal ice and 77 × 10⁻⁶ K⁻¹ for sI hydrate)⁷¹ form thermal cracks upon cooling or heating of the hydrate. Note that the difference between the coefficients of thermal expansion of sI hydrate and ice Ih remains roughly the same at higher temperatures.⁷² The cracks are assumed to act as nucleation sites for hydrate decomposition. It is suggested that nucleation and the accompanying induction times at the crack are the rate-determining processes for hydrate decomposition after the initial step of dissociation at the free surface of the hydrate.⁶⁰ In the present study, in most cases no sign of decomposition can be found in the vicinity of the crack at the time of crack appearance. Many cracks seem to form during the initial heating period from 203 K to the set point temperature. Additionally, in the samples used here roughly 20 wt% to 40 wt% of the water is presumably ice. Hence, differences in thermal expansion between ice and hydrate seem to be a plausible cause for the formation of cracks in this study as well. Nevertheless, mechanical stress caused by hydrate gas release or by a change in volume upon the hydrate–ice phase transformation can be an additional factor.

Decomposition barriers. A completely different decomposition feature is illustrated in Fig. 14. Here, decomposition starts at the upper right corner of the hydrate particle and along a crack in the center. During the course of the experiment the decomposed region extends to the left side of the particle. However, a planar barrier seems to hinder further propagation of the decomposed region towards the upper left corner. As a result a big portion (∼6 mm³) of the hydrate particle remains intact until the very end of the experiment while the other portion decomposes completely. The pressure data support that this region, resistant to decomposition, is hydrate. Additionally, homogeneous gray scale values in the hydrate particle (cf. scan I of Fig. 14) point towards a homogeneous phase. An accumulation of ice in that region would result in a marked contrast to the hydrate phase. The planar character of the decomposition barrier seen in Fig. 14 is better assessed in the three-dimensional renderings of Fig. 13 (cf. upper right corner of scan II) or in the renderings provided with the ESI† (cf. Fig. S8–S10). More of these planar barriers to decomposition are found across the particles in both isothermal experiments (see for instance scan IV of Fig. 13). The surface area of the barrier planes is on the order of 1 mm². Although the sample preparation method produces polycrystalline hydrate, the planes seem to be too big to be grain boundaries or crystallographic planes. The barrier planes are also unlikely to be cracks. Otherwise, and corresponding to the results above, we would expect decomposition to start from these planes and not to stop there. It is unlikely but conceivable that the barrier planes are thin layers of dense ice with a thickness below the detectability limit of our μCT (roughly 10 μm). This layer, together with a similarly thin layer of dense ice at the free surface of the decomposition resistant region, could form a gas tight ice shield around the remaining hydrate. In the popular self-preservation hypothesis, such an ice shield is assumed to protect the encapsulated hydrate from decomposition. However, it is unclear why such a thin layer of ice is either absent or dysfunctional at the free surface of the decomposing region.

Decomposition resistant regions. Fig. 15 shows a feature found in all three experiments: of all hydrate regions outlasting the whole experiment many of them are found at the outer exposed surface of the hydrate particle while most of the inner part of the hydrate particle decomposes completely. In the temperature stepping experiment a small fraction of the hydrate (<5 wt%) outlasts the experiment even at unstable conditions until the sample is melted. Similarly small parts of hydrate have been found to persist until premelting or melting in various other studies.^{24,25,29,34,38,53} This is usually not attributed to the self-preservation phenomenon. Instead it is explained by gas or hydrate becoming trapped within ice grain interiors or along ice grain boundaries in a thick layer of product ice which formed during decomposition from the surface to the core of the hydrate particle.^24,25,53 This implies the remaining gas or hydrate is dispersed homogeneously across the ice. We cannot confirm this explanation, since in many of our experiments the preserved hydrate seems to be concentrated in connected regions at the free surface of the particle. Again, it is unknown whether these regions are coated with a layer of dense ice with a thickness below roughly 10 μm. Then the question remains why only some exposed regions of hydrate outlast the temperature–pressure program while everywhere else the hydrate decomposes completely.

Pores. The structural evolution of a decomposing hydrate sample over a period of 50 h is shown in Fig. 15. With time, pores start to become visible at the resolution of our measurements. Particularly, the tomogram of scan VIII shows a network of pores with sizes of several tens of micrometers. This growth of pores is observed at temperatures above 250 K and reflects the tendency to minimize the surface energy. It is unclear whether the mass transport involved with pore growth is due to ice creep or snow metamorphism (i.e., transport over sublimation, diffusion, and resublimation of water).^67–70 Nevertheless, the effect of snow metamorphism is visible at the exposed surface of the sample, where ice crystals grow from water vapor.

On the basis of Fig. 15 alone, we conclude that the macroscopic pores grow either from a network of pores already present in the hydrate samples or from pores produced during the decomposition process. In either case, the pore size of the initial pore network is well below the resolution limit of our μCT. However, porosities for our hydrate samples derived from the initial hydrate volume, hydrate composition and liquid water volume range from 4% to 24%. This implies that the hydrate samples are already porous after synthesis. Our data are in good agreement with the results of Kuhs et al.,⁵⁵ who reported porosities ranging from 10% to 20% and pores with size ranging from 20 nm to 100 nm in CO₂ hydrates produced by subjecting ice powder to pressurized gas. Even higher porosities of 44% were found by Circone et al.²⁶ in CO₂ hydrates produced from ice powder using a more complex temperature–pressure program. In general, the results from various studies show that hydrates of both natural and synthetic origin exhibit guest gas specific porosities, which are further correlated to the crystal structure, formation environment, and progress of decomposition.^{56–59,73–75} Here, the pores at the initial stage of the experiments are presumably a direct consequence of the sample preparation process involving ASW, which is known to be microporous.^64,65,76

An increase of the apparent volume by more than 3% is found during hydrate decomposition in all of our μCT measurements and also observed in Fig. 15, where the diagonal of a hydrate particle grows by approximately 3% during decomposition. Melting at the end of the experiments leads to volume reductions between the solid and the liquid in the range of 27% to 38%. This is significantly larger than the volume reduction of dense ice during melting (9%). Additionally, during the phase transition from sI hydrate to ice, the water density increases from 0.79 g cm⁻³ (assuming a lattice constant of 12.0 Å) to 0.92 g cm⁻³. The growth of the apparent volume and the increase in the density of water together result in the occurrence of voids in the sample, which in turn leads to the large reduction of the apparent volume during melting. Since our results show only homogeneous regions of decomposed hydrate, no significant accumulation of void space or mass takes place during decomposition. Therefore, a homogeneous network of pores must have formed during decomposition. This agrees well with the SEM results of Stern et al.²⁵ who reported an aerated appearance of ice as a hydrate dissociation product. Similarly, microstructures resembling Swiss cheese were found in decomposed natural gas⁷⁵ and CO₂³⁸ hydrates. Moreover, Takeya et al.^31,49 reported extraordinarily large diffusivities of guest gas across the ice produced from hydrate decomposition and inferred diffusion across pores and along grain boundaries as a cause.

In this work, microporous regions of decomposed hydrate, once formed, grow during decomposition and spread out into the hydrate volume. The propagation front of decomposing regions differs widely and is found to be smooth in some and highly irregular in other cases. These characteristics of the propagation front are likely determined by the microstructure before decomposition.

The thickness of porous ice as a decomposition product is of minor importance with respect to its ability to form an efficient diffusion barrier, especially if the pore network is permeable. On the other hand, it is conceivable that water vapor generated by decomposing hydrates can under certain conditions plug such a network of pores by deposition at the pore walls. No matter whether the pore network is connected or not, due to the small pore size, plugging could eventually yield a highly pressure resistant structure that can explain how a rather thin layer of ice can withstand the pressures developing in self-preserved hydrates far outside their stability region.

3.4 Rapid depressurization events

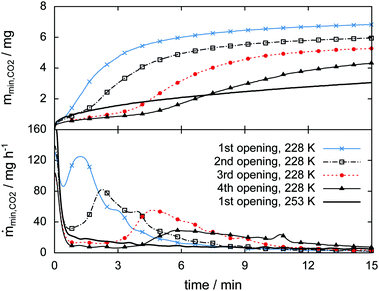
The high sampling rate of the pT-data acquisition combined with the high accuracy of the pressure signal is used for a detailed analysis of the rapid depressurization events. Fig. 16 shows the mass of the gas released and its rate as a function of time immediately after the cell is closed. In the isothermal experiment at 253 K the gas release seems to follow a two-step process. The first step is characterized by a vigorous release of gas at a release rate of 170 mg h⁻¹. Within one minute after rapid depressurization the gas release rate drops to below 20 mg h⁻¹ and decreases steadily henceforth. This low rate of gas release marks the second step of the process. Both steps were also reported by Handa⁴⁷ and verified in various studies later on.^31,33,49,77

Fig. 16 Released guest gas mass (top) and mass release rate (bottom) as a function of time right after opening events (i.e., rapid depressurization) as observed in the isothermal experiments at 228 K and 253 K. Note the retarded 2nd jump in the gas release rate only observed in the case of the isothermal experiment at 228 K. Data are recorded at a frequency of 1 Hz. Markers are plotted every 50 s.

Similarly high gas release rates of more than 100 mg h⁻¹ and a subsequent drop of rates are also observed every time after rapid depressurization in the 228 K isothermal experiment. However, at 228 K a third step, characterized by a pronounced period of gas release, is observed at later times. With an increasing number of rapid depressurization events this third step happens at later times and with decreasing strength.

Since this behavior is unexpected, this part of the experiment is repeated several times using additional samples. The focus is set on rapid depressurization events at 228 K and 253 K only. μCT scans are used to determine volume and phase information. The two-step process of gas release observed at 253 K recurs in all of six additional rapid depressurization events performed with three samples. Remarkably, the third step of gas release is confirmed in only one out of 14 additional rapid depressurization events accomplished using four different samples at 228 K. Agreement is found in the case of a sample with a molar ratio CO₂·nH₂O of n = 13.3. In the remaining 13 events the hydrate is of even lower quality (n > 13.7). Notably, all of these 13 events show some degree of self-preservation (even at 228 K), expressed by remarkably low gas release rates. This is most pronounced in the case of maximal molar water content (n = 30) and is shown in Fig. S11 of the ESI.†

It is remarkable that the initial two steps of hydrate decomposition are the same for the self-preserved (228 K) and the non-preserved (253 K) hydrate. Nevertheless, it is unclear what causes this second phase (i.e., the third step) of strong gas release. A possible explanation is the sudden occurrence of new decomposition sites. These could be produced by the formation of new cracks or the bursting of existing decomposition barriers. For now, our results are not able to confirm or exclude any of these suggestions.

4 Conclusions

Establishing a predictive model for the decomposition of clathrate hydrates is a worthwhile but difficult task. It is worthwhile because such a model will eventually help with the estimation of the applicability of hydrate technologies. It is difficult because such a model has to combine thermodynamics, decomposition kinetics, heat and mass transport mechanisms as well as micro- and macroscopic features of the bulk and surface. Similarly, the isolation of a single parameter of decomposition is very challenging in experiments. Thus, until today there is no comprehensive model which can be used to explain the decomposition behavior of hydrates in its entirety.

In this work, we studied the influence of micro- and macroscopic features on the decomposition behavior of clathrate hydrates. Particularly, the role of cracks and pores is addressed using μCT in combination with accurate temperature control and pressure monitoring. The good contrast between hydrate and decomposed hydrate is used to segment the tomographic data set into regions of different phases. The assignment of these phases is very accurate, as verified using released gas mass data obtained from the pressure signal. This cross-correlation, which is shown for the first time, allows for a detailed study of the structural information obtained from μCT. So far, the experimental setup used is not capable of resolving either thin layers (<10 μm) of ice or small density differences between supercooled liquid water and ice. Hence, the direct examination of popular self-preservation hypotheses, such as a thin diffusion limiting ice-shield^37,38 or liquid water as an intermediate decomposition product,^27,28,54 is difficult. Nevertheless, the observations made here add new perspectives to the understanding of decomposition and self-preservation of CO₂ hydrates. Besides a homogeneous network of pores, additional features like cracks and decomposition barriers form in our samples during hydrate decomposition.

Since the apparent particle volume does not reduce during hydrate decomposition, the formation of porous ice must be a consequence of the increase in water density from hydrate (0.79 g cm⁻³) to ice (0.92 g cm⁻³). Depending on the pore size distribution and the pore connectivity, a network of pores can offer many possible pathways for the gas to escape. In the extreme cases, this can range from a gas-tight layer of closed pores to a permeable network of open pores.

Although the formation of cracks during hydrate decomposition has been observed earlier,^42,60,61 their role in the decomposition process of hydrates is rarely discussed. Since our results show that cracks form very often and always act as a precursor for hydrate decomposition, their role seems to be important for macroscopic samples like ours. It is furthermore conceivable that cracks, or actually, the absence of cracks, are an important ingredient regarding the phenomenon of self-preservation. That is because any formation of cracks will result in new decomposition sites resulting in the release of gas. While mechanical stress induced by hydrate decomposition can cause the formation of cracks, our observations also support the notion that the formation of cracks is related to differences between the thermal expansion of ice and hydrate. Local changes in temperature at interfaces between hydrate and ice, caused by either endothermic cooling upon decomposition or external heat, can lead to small cracks and the formation of new decomposition sites. The gas released from these sites can in turn result in mechanical stress and the enlargement of the cracks. This process can be used to explain the second phase of strong gas release observed in our rapid depressurization experiments at 228 K.

Decomposition barriers, a complex and irregular decomposition front, and seemingly resistant regions to decomposition at the exposed sample surface are found at temperatures inside and outside the self-preservation regime. These results do not match the shrinking-core model of hydrate decomposition in which decomposition is assumed to start from the exposed hydrate surface, proceeding inward.^31,49 Similarly, our results do not support the theory of an ice-shield protecting the hydrate from further decomposition, as is often assumed to explain the phenomenon of self-preservation. However, our observations that some connected regions of the hydrate (in contact with the free surface) decompose while similar regions remain intact point towards a local cause of the decomposition process. Since a non-uniform distribution of the hydration number is a natural consequence of the gas-phase deposition process used to make such samples, we infer that the local distribution of guest molecules and ice, i.e., the hydration number, plays an important role in the decomposition process.

Altogether our results show a variety of phenomena associated with hydrate decomposition in macroscopically-sized samples. Further analysis is needed to study the role of sample preparation as well as the influence of parameters like temperature, pressure, particle size, and ice content on the cracks and barriers on both micro- and macroscopic scales. Nevertheless, it is established that pores, cracks, and decomposition barriers are important factors in hydrate decomposition and the self-preservation phenomenon.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Stefan Arzbacher, Nima Rahmatian, and Jörg Petrasch thank the Austrian Research Promotion Agency (FFG) for financial support (TomoFuma project, no. 839070). Thomas Loerting received funding from the Austrian Science Fund (FWF) within the project no. I-1392.

References

1. E. D. Sloan and C. Koh, Clathrate Hydrates of Natural Gases, CRC Press, 3rd edn, 2007.
2. Gas Hydrates 1: Fundamentals, Characterization and Modeling, ed. D. Broseta, L. Ruffine and A. Desmedt, ISTE Ltd/John Wiley and Sons Inc, Hoboken, NJ, 2017.
3. Gas Hydrates 2: Geoscience Issues and Potential Industrial Applications, ed. L. Ruffine, D. Broseta and A. Desmedt, ISTE Ltd/John Wiley and Sons Inc, Hoboken, NJ, 2018.
4. M. von Stackelberg and H. R. Müller, Z. Electrochem., 1954, 58, 25–39.
5. H. M. Barnes, L. N. Kremzner and W. A. Mitchell, US Pat., US2975603A, General Foods Corp., 1958.
6. A. Aldred, R. D. Bee, V. S. E. Evans and M. Trycholik-Kinavuidi, WO Pat., WO2017093084A1, Unilever Plc, 2015.
7. T. Hatakeyama, E. Aida, T. Yokomori, R. Ohmura and T. Ueda, Ind. Eng. Chem. Res., 2009, 48, 4083–4087.
8. G. K. Anderson, J. Chem. Thermodyn., 2003, 35, 1171–1183.
9. L. Fournaison, A. Delahaye, I. Chatti and J.-P. Petitet, Ind. Eng. Chem. Res., 2004, 43, 6521–6526.
10. W. Zhang, Y. Wang, X. Lang and S. Fan, Energy Convers. Manage., 2017, 146, 43–51.
11. Z. Ma, P. Zhang, H. Bao and S. Deng, Renewable Sustainable Energy Rev., 2016, 53, 1273–1302.
12. D. M. D'Alessandro, B. Smit and J. R. Long, Angew. Chem., Int. Ed., 2010, 49, 6058–6082.
13. P. Babu, P. Linga, R. Kumar and P. Englezos, Energy, 2015, 85, 261–279.
14. H. Dashti, L. Zhehao Yew and X. Lou, J. Nat. Gas Sci. Eng., 2015, 23, 195–207.
15. S. M. Benson and F. M. Orr, MRS Bull., 2008, 33, 303–305.
16. H. Sakai, T. Gamo, E.-S. Kim, M. Tsutsumi, T. Tanaka, J. Ishibashi, H. Wakita, M. Yamano and T. Oomori, Science, 1990, 248, 1093–1096.
17. O. Prieto-Ballesteros, J. S. Kargel, M. Fernandez-Sampedro, F. Selsis, E. S. Martinez and D. L. Hogenboom, Icarus, 2005, 177, 491–505.
18. S. W. Kieffer, X. Lu, C. M. Bethke, J. R. Spencer, S. Marshak and A. Navrotsky, Science, 2006, 314, 1764–1766.
19. D. P. Cruikshank, A. W. Meyer, R. H. Brown, R. N. Clark, R. Jaumann, K. Stephan, C. A. Hibbitts, S. A. Sandford, R. M. Mastrapa, G. Filacchione, C. M. D. Ore, P. D. Nicholson, B. J. Buratti, T. B. McCord, R. M. Nelson, J. B. Dalton, K. H. Baines and D. L. Matson, Icarus, 2010, 206, 561–572.
20. A.-H. Delsemme and P. Swings, Ann. Astrophys., 1952, 15, 1–6.
21. S. L. Miller, Proc. Natl. Acad. Sci. U. S. A., 1961, 47, 1798–1808.
22. S. L. Miller and W. D. Smythe, Science, 1970, 170, 531–533.
23. J. A. Ripmeester and S. Alavi, Curr. Opin. Solid State Mater. Sci., 2016, 20, 344–351.
24. L. A. Stern, S. Circone, S. H. Kirby and W. B. Durham, J. Phys. Chem. B, 2001, 105, 1756–1762.
25. L. A. Stern, S. Circone, S. H. Kirby and W. B. Durham, Can. J. Phys., 2003, 81, 271–283.
26. S. Circone, L. A. Stern, S. H. Kirby, W. B. Durham, B. C. Chakoumakos, C. J. Rawn, A. J. Rondinone and Y. Ishii, J. Phys. Chem. B, 2003, 107, 5529–5539.
27. V. Melnikov, A. Nesterov, A. Reshetnikov and A. Zavodovsky, Chem. Eng. Sci., 2009, 64, 1160–1166.
28. V. Melnikov, A. Nesterov, A. Reshetnikov, V. Istomin and V. Kwon, Chem. Eng. Sci., 2010, 65, 906–914.
29. A. Falenty, W. F. Kuhs, M. Glockzin and G. Rehder, Energy Fuels, 2014, 28, 6275–6283.
30. A. S. Stoporev, A. Y. Manakov, L. K. Altunina, A. V. Bogoslovsky, L. A. Strelets and E. Y. Aladko, Energy Fuels, 2014, 28, 794–802.
31. S. Takeya, T. Ebinuma, T. Uchida, J. Nagao and H. Narita, J. Cryst. Growth, 2002, 237–239, 379–382.
32. S. Takeya, T. Uchida, J. Nagao, R. Ohmura, W. Shimada, Y. Kamata, T. Ebinuma and H. Narita, Chem. Eng. Sci., 2005, 60, 1383–1387.
33. S. Takeya and J. A. Ripmeester, Angew. Chem., Int. Ed., 2008, 120, 1296–1299.
34. S. Takeya and J. A. Ripmeester, ChemPhysChem, 2010, 11, 70–73.
35. H. Mimachi, S. Takeya, A. Yoneyama, K. Hyodo, T. Takeda, Y. Gotoh and T. Murayama, Chem. Eng. Sci., 2014, 118, 208–213.
36. S. Takeya, S. Muromachi, Y. Yamamoto, H. Umeda and S. Matsuo, Fluid Phase Equilib., 2016, 413, 137–141.
37. W. F. Kuhs, G. Genov, D. K. Staykova and T. Hansen, Phys. Chem. Chem. Phys., 2004, 6, 4917–4920.
38. A. Falenty and W. F. Kuhs, J. Phys. Chem. B, 2009, 113, 15975–15988.
39. H. Ohno, H. Narita and J. Nagao, J. Phys. Chem. Lett., 2011, 2, 201–205.
40. L. Yang, A. Falenty, M. Chaouachi, D. Haberthür and W. F. Kuhs, Geochem., Geophys., Geosyst., 2016, 3717–3732.
41. S. Takeya, K. Honda, Y. Gotoh, A. Yoneyama, K. Ueda, A. Miyamoto, T. Hondoh, A. Hori, D. Sun, R. Ohmura, K. Hyodo and T. Takeda, J. Synchrotron Radiat., 2012, 19, 1038–1042.
42. S. Takeya, A. Yoneyama, K. Ueda, K. Hyodo, T. Takeda, H. Mimachi, M. Takahashi, T. Iwasaki, K. Sano, H. Yamawaki and Y. Gotoh, J. Phys. Chem. C, 2011, 115, 16193–16199.
43. W. Shimada, S. Takeya, Y. Kamata, T. Uchida, J. Nagao, T. Ebinuma and H. Narita, J. Phys. Chem. B, 2005, 109, 5802–5807.
44. V. Buch, J. P. Devlin, I. A. Monreal, B. Jagoda-Cwiklik, N. Uras-Aytemiz and L. Cwiklik, Phys. Chem. Chem. Phys., 2009, 11, 10245–10265.
45. J.-R. Zhong, X.-Y. Zeng, F.-H. Zhou, Q.-D. Ran, C.-Y. Sun, R.-Q. Zhong, L.-Y. Yang, G.-J. Chen and C. A. Koh, Sci. Rep., 2016, 6, 38855.
46. D. Davidson, S. Garg, S. Gough, Y. Handa, C. Ratcliffe, J. Ripmeester, J. Tse and W. Lawson, Geochim. Cosmochim. Acta, 1986, 50, 619–623.
47. Y. Handa, J. Chem. Thermodyn., 1986, 18, 891–902.
48. V. S. Yakushev and V. Istomin, Physics and Chemistry of Ice, Sapporo, Japan, 1992, pp. 136–140.
49. S. Takeya, W. Shimada, Y. Kamata, T. Ebinuma, T. Uchida, J. Nagao and H. Narita, J. Phys. Chem. A, 2001, 105, 9756–9759.
50. V. A. Istomin, V. S. Yakushev, N. A. Makhonina, V. G. Kwon and E. M. Chuvilin, Gas Ind. Russ., 2006, 4, 16–27.
51. V. P. Melnikov, L. S. Podenko, A. N. Nesterov, A. O. Drachuk, N. S. Molokitina and A. M. Reshetnikov, Dokl. Chem., 2016, 466, 53–56.
52. J. W. Wilder and D. H. Smith, J. Phys. Chem. B, 2002, 106, 226–227.
53. L. A. Stern, S. Circone, S. H. Kirby and W. B. Durham, J. Phys. Chem. B, 2002, 106, 228–230.
54. V. Melnikov, A. Nesterov, A. Reshetnikov and V. Istomin, Chem. Eng. Sci., 2011, 66, 73–77.
55. W. F. Kuhs, A. Klapproth, F. Gotthardt, K. Techmer and T. Heinrichs, Geophys. Res. Lett., 2000, 27, 2929–2932.
56. L. A. Stern, S. H. Kirby, S. Circone and W. B. Durham, Am. Mineral., 2004, 89, 1162–1175.
57. G. Bohrmann, W. F. Kuhs, S. A. Klapp, K. S. Techmer, H. Klein, M. M. Murshed and F. Abegg, Mar. Geol., 2007, 244, 1–14.
58. S. A. Klapp, G. Bohrmann, W. F. Kuhs, M. M. Murshed, T. Pape, H. Klein, K. S. Techmer, K. U. Heeschen and F. Abegg, Mar. Pet. Geol., 2010, 27, 116–125.
59. S. A. Klapp, F. Enzmann, P. Walz, T. Huthwelker, J. Tuckermann, J.-O. Schwarz, T. Pape, E. T. Peltzer, R. Mokso, D. Wangner, F. Marone, M. Kersten, G. Bohrmann, W. F. Kuhs, M. Stampanoni and P. G. Brewer, Geo-Mar. Lett., 2012, 32, 555–562.
60. S. Takeya, A. Yoneyama, K. Ueda, H. Mimachi, M. Takahashi, K. Sano, K. Hyodo, T. Takeda and Y. Gotoh, J. Phys. Chem. C, 2012, 116, 13842–13848.
61. H. Mimachi, M. Takahashi, S. Takeya, Y. Gotoh, A. Yoneyama, K. Hyodo, T. Takeda and T. Murayama, Energy Fuels, 2015, 29, 4827–4834.
62. C. Mitterdorfer, M. Bauer and T. Loerting, Phys. Chem. Chem. Phys., 2011, 13, 19765.
63. S. Arzbacher, J. Petrasch, A. Ostermann and T. Loerting, Materials, 2016, 9, 668.
64. E. Mayer and A. Hallbrucker, J. Chem. Soc., Chem. Commun., 1989, 749–751.
65. A. Hallbrucker and E. Mayer, J. Chem. Soc., Faraday Trans., 1990, 86, 3785–3792.
66. L. Grady, IEEE Trans. Pattern Anal. Mach. Intell., 2006, 28, 1768–1783.
67. Z. Yosida, H. Oura, D. Kuroiwa, T. Huzioka, K. Kojima, S.-I. Aoki and S. Kinosita, Contributions from the Institute of Low Temperature Science, 1955, vol. 7, pp. 19–74.
68. B. R. Pinzer, M. Schneebeli and T. U. Kaempfer, The Cryosphere, 2012, 6, 1141–1155.
69. K. Hammonds, R. Lieb-Lappen, I. Baker and X. Wang, Cold Reg. Sci. Technol., 2015, 120, 157–167.
70. K. Hammonds and I. Baker, Cold Reg. Sci. Technol., 2016, 125, 12–20.
71. J. S. Tse, J. Inclusion Phenom. Mol. Recognit. Chem., 1990, 8, 25–32.
72. K. C. Hester, Z. Huo, A. L. Ballard, C. A. Koh, K. T. Miller and E. D. Sloan, J. Phys. Chem. B, 2007, 111, 8830–8835.
73. D. K. Staykova, W. F. Kuhs, A. N. Salamatin and T. Hansen, J. Phys. Chem. B, 2003, 107, 10299–10311.
74. G. Genov, W. F. Kuhs, D. K. Staykova, E. Goreshnik and A. N. Salamatin, Am. Mineral., 2004, 89, 1228–1239.
75. W. F. Kuhs, G. Genov, E. Goreshnik, A. Zeller, K. S. Techmer and G. Bohrmann, Int. J. Offshore Polar Eng., 2004, 14, 305–309.
76. C. R. Hill, C. Mitterdorfer, T. G. A. Youngs, D. T. Bowron, H. J. Fraser and T. Loerting, Phys. Rev. Lett., 2016, 116, 215501.
77. S. Takeya and J. A. Ripmeester, Proceedings of the 7th International Conference on Gas Hydrates (ICGH 2011), Edinburgh, Scotland, UK, 2011.

---

Footnote

† Electronic supplementary information (ESI) available: Section 1: Tomographic setup. Section 2: Temperature calibration. Section 3: Temperature field. Section 4: Leakage. Section 5: Mass calibration. Section 6: Image processing. Section 7: 3D illustrations of CT results and pressure–temperature data of a verification experiment. See DOI: 10.1039/c8cp07871h

---