Competition of individual domain folding with inter-domain interaction in WW domain engineered repeat proteins†
Abstract
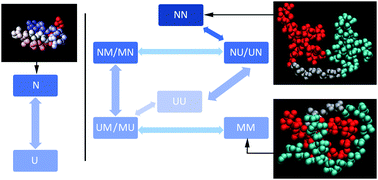
Engineered repeat proteins have proven to be a fertile ground for studying the competition between folding, misfolding and transient aggregation of tethered protein domains. We examine the interplay between folding and inter-domain interactions of engineered FiP35 WW domain repeat proteins with n = 1 through 5 repeats. We characterize protein expression, thermal and guanidium melts, as well as laser T-jump kinetics. All experimental data is fitted by a global fitting model with two states per domain (U, N), plus a third state M to account for non-native states due to domain interactions present in all but the monomer. A detailed structural model is provided by coarse-grained simulated annealing using the AWSEM Hamiltonian. Tethered FiP35 WW domains with n = 2 and 3 domains are just slightly less stable than the monomer. The n = 4 oligomer is yet less stable, its expression yield is much lower than the monomer's, and depends on the purification tag used. The n = 5 plasmid did not express at all, indicating the sudden onset of aggregation past n = 4. Thus, tethered FiP35 has a critical nucleus size for inter-domain aggregation of n ≈ 4. According to our simulations, misfolded structures become increasingly prevalent as one proceeds from monomer to pentamer, with extended inter-domain beta sheets appearing first, then multi-sheet ‘intramolecular amyloid’ structures, and finally novel motifs containing alpha helices. We discuss the implications of our results for oligomeric aggregate formation and structure, transient aggregation of proteins whilst folding, as well as for protein evolution that starts with repeat proteins.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...