Impact of confinement in multimolecular inclusion compounds of melamine and cyanuric acid†
Abstract
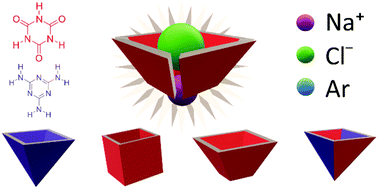
Supramolecular cavities can be found in clathrates and self-assembling capsules. In these computational experiments, we studied the effect of folding planar hydrogen-bonded supramolecules of melamine (M) and cyanuric acid (CA) into stable cage-like quartets. Based on dispersion-corrected density functional theory calculations at the ωB97XD/6-311++G(d,p) level, we show the flexibility of M and CA molecules to form free confined spaces. Our bonding analysis indicates that only CA can form a cage, which is more stable than its planar systems. We then studied the capacity of the complexes to host ionic and neutral monoatomic species like Na+, Cl− and Ar. The encapsulation energies range from −2 to −65 kcal mol−1. A detailed energy decomposition analysis (EDA) supports the fact that the triazine ring of CA is superior to the M one for capturing chloride ions. In addition, the EDA and the topology of the electron density, by means of the Atoms in Molecules (AIM) theory and electrostatic potential maps, reveal the nature of the host–guest interactions in the confined space. The CA cluster appears to be the best multimolecular inclusion compound because it can host the three species and keep its cage structure, and therefore it could also act as a dual receptor of the ionic pair Na+Cl−. We think these findings could inspire the design of new heteromolecular inclusion compounds based on triazines and hydrogen bonds.


 Please wait while we load your content...
Please wait while we load your content...