Influence of microscopic precipitate structures on macroscopic pattern formation in reactive flows in a confined geometry

Abstract

Thanks to the coupling between chemical precipitation reactions and hydrodynamics, new dynamic phenomena may be obtained and new types of materials can be synthesized. Here we experimentally investigate how the characteristic microscopic crystal properties affect the macroscopic pattern obtained. To shed light on such interactions, different reactant solutions are radially injected into a calcium chloride solution at different volumetric flow rates in a confined geometry. Depending on the reactants used and the flow conditions, deformed precipitate membranes have been observed due to reaction-driven viscous fingering. In such cases we show that upon injection a large number of small particles is produced in situ by the reaction at the miscible interface between the two reactant solutions. Therefore, a colloidal gel composed of those tiny particles is pushed forward by the injected aqueous solution giving rise to a viscosity gradient-driven hydrodynamic instability.

---

1 Introduction

Flow conditions have recently been shown to be able to affect the yield of precipitation reactions^1,2 as well as the spatio-temporal distribution of the solid phase produced.^1–9 Experiments consisting of injecting a solution of a given reactant of a precipitation reaction into a confined geometry containing a solution of the other reactant have indeed made it possible to show that, depending on the concentrations of the chemicals and the injection flow rate, various precipitation patterns can be obtained. The resulting structures depend not only on the cohesion of the solid phase produced by the reaction but also on possible hydrodynamic instabilities.

Regarding the nature of the chemicals, Haudin et al. have shown that chemical garden patterns obtained in confined geometries under flow conditions were globally robust with regard to changes in the nature of the metallic cation used provided that sodium silicate displaced the solution.⁵ A comparison between calcium and barium carbonate precipitate structures produced in similar geometries with injection has further shown that in some range of concentrations and flow rates the patterns are the same while they may differ in other zones of the parameter space.⁸ Applying low reactant concentrations and flow rates typically leads to similar, more or less radially symmetric patterns. Also, membrane-like patterns were obtained in both systems using high reactant concentrations and flow rates independently of the injected solution. For intermediate values of parameters however, significantly different patterns formed. This has been interpreted as the CaCO₃ and BaCO₃ crystals are of different shape and size and thus have different cohesion properties which can manifest only under appropriate circumstances. This points to the coupling of hydrodynamics and microscopic properties of the crystals which may influence the macroscopic precipitation structure. It was shown in these previous experiments that the viscosity ratio of the reactant solutions is not sufficiently high (at the flow rate applied) to trigger viscous fingering. However, no attention has been paid to viscosity changes possibly emerging in the reaction–injection system.

In parallel, hydrodynamic instabilities triggered by gradients of density,^10,11 viscosity⁶ or permeability^12,13 can affect the spatiotemporal distribution of macroscopic precipitation patterns as well. Buoyancy-driven stripes¹⁰ can for instance shape needle-like solid structures during injection¹¹ while changes in permeability can trigger fingering patterns.^12,13 On the other hand, the injection of a cobalt solution in a concentrated viscous solution of silicate can induce flower-like patterns influenced by a viscous fingering instability due to the fact that the injected aqueous solution of cobalt is less viscous than the silicate one.^3,6 The change in viscosity is here however not induced by the reaction but by a difference in physical properties of the reactant solutions. In situ reaction-driven changes in viscosities have been shown to be able to trigger fingering instabilities^14,15 but in systems without any precipitation.

In this context, we analyze here experimentally the interplay between a precipitation reaction and in situ reaction-driven viscosity changes and precipitate membrane formation on solid precipitate structures under flow conditions. We show that depending on the nature of a reactant solution injected into a solution of calcium chloride in a confined geometry, different crystals are produced at the microscopic scale resulting in different macroscopic precipitate structures. In the case where the reaction yields a product in the form of very small particles, a colloidal gel can be obtained which locally increases the viscosity and generates a membrane in the reaction zone between the two solutions. Because of the large gradients of viscosity, a viscous fingering instability can take place that shapes the precipitation pattern. In contrast, if a low number of large particles is produced, the local permeability is affected which induces a coarse-grained macroscopic pattern. These results show that the very nature of the reactants and of the crystals generated by the reaction can influence the properties of the flow which in turn shapes the macroscopic form of the precipitation structure.

2 Experimental conditions

To investigate how different precipitation reactions affect pattern formation in confined geometries, experiments have been performed via radially injecting one reactant solution into the other one in a modified Hele-Shaw cell described elsewhere.^1,2 In this set-up, a 2 M calcium chloride solution (prepared from CaCl₂·2H₂O) is initially filling a horizontal (0.5 mm thick) gap confined by an upper and a lower Plexiglas plate. The calcium chloride solution is displaced radially by injecting a sodium salt solution through an inlet port in the center of the lower Plexiglas plate. The injected solution (1 M concentration in each case) was varied as sodium dihydrogen phosphate (NaH₂PO₄·2H₂O), sodium sulfate (Na₂SO₄·10H₂O), sodium carbonate (Na₂CO₃), or sodium silicate (Na₂O(SiO₂)_x·xH₂O). In the mixing zone between the displaced and injected solutions, a precipitation reaction takes place whereby a sparingly soluble calcium salt appearing as solid precipitate particles is produced by the reaction of the displaced Ca²⁺ ion with the respective anion of the injected solution. The concentrations mentioned above correspond to experiments targeting macroscopic pattern visualization. For microscopic precipitate characterization, different concentrations were used as will be indicated for the corresponding cases. All solutions were prepared by dissolving the respective powders in water with the exception of the silicate solution which was diluted from a commercially available 6 M solution (∼27% SiO₂ in 14% NaOH, Sigma Aldrich). The hydrodynamically relevant solution properties were measured with a DMA 500 density meter and a Brookfield LVDV-II+P viscometer and are listed in Table 1. The injection was performed by a syringe pump (KDS Legato 101) applying different flow rates (Q = 0.1, 1.0, and 5.0 mL min⁻¹) for the separate experiments. The dynamic macroscopic precipitate patterns were recorded in top view by a digital camera (Adimec-2000m).

Table 1 List of the solutions used and their properties: molar concentration (c), pH, density (ρ), and dynamic viscosity (μ)

Chemicals	c (M)	pH	ρ (g cm^−3)	μ (cP)
CaCl2	1.0	6.24	1.0852	0.94
	2.0	6.00	1.1683	1.12
NaH2PO4	0.5	4.30	1.0403	1.14
	1.0	4.10	1.0809	1.31
Na2SO4	0.5	5.77	1.0631	1.16
	1.0	6.30	1.1328	1.53
Na2CO3	0.5	11.09	1.0490	1.18
	1.0	11.85	1.0982	1.67
Na2O(SiO2)x	0.5	11.09	1.0344	1.43
	1.0	11.43	1.0738	1.54

---

A similar set of experiments was carried out under an optical microscope (Nikon Eclipse Ts2R coupled with a digital camera) to shed light on the link between the precipitate micro- and macro-structures. Since the patterns are fragile and cannot be directly sampled from the gap of the Hele-Shaw cell, time and space dependent particle characterization was performed in situ with the aid of a positionable sample holder. For these experiments, a circular Hele-Shaw cell was created and placed on movable rails. Sliding the rails and rotating around the cell allowed us to easily access the microscopic pattern characteristics (shape, size, and spatial distribution) within ≈10 cm radius of the injection port in the horizontal plane. The reactant concentrations used to study the macroscopic patterns were sufficiently large to produce a large amount of precipitate able to affect the flow. However, such a high particle concentration cannot be investigated by optical microscopy. Therefore, to maintain sufficiently lower reactant concentrations, 0.5 M solutions were injected into 1 M CaCl₂ solution at 1.0 mL min⁻¹ flow rate with the exception of the phosphate solution for which the original concentrations (1 M NaH₂PO₄ and 2 M CaCl₂) were appropriate to obtain well visible particles.

When precipitate particles form and grow in a flowing liquid layer, the entire hydrodynamics may be modified depending on the interaction between the solid and the liquid phases. Therefore, to monitor the temporal evolution of the patterns, we additionally performed the same set of experiments in a shadowgraph optical system as already used to study e.g. Marangoni instabilities.^16,17 This technique is sensitive towards the second derivative (Laplacian) of the refractive index field.¹⁸ It thus can visualize structures in the concentration field of the solutions since the solutes change the refractive index of the fluid. The concentration field is influenced both by the flow and by the concentration changes due to the precipitation reaction.^19,20 Furthermore, the shadowgraph optics is able to image precipitate membranes which may appear transparent in the direct camera records.

3 Results and discussion

3.1 Macroscopic precipitation patterns

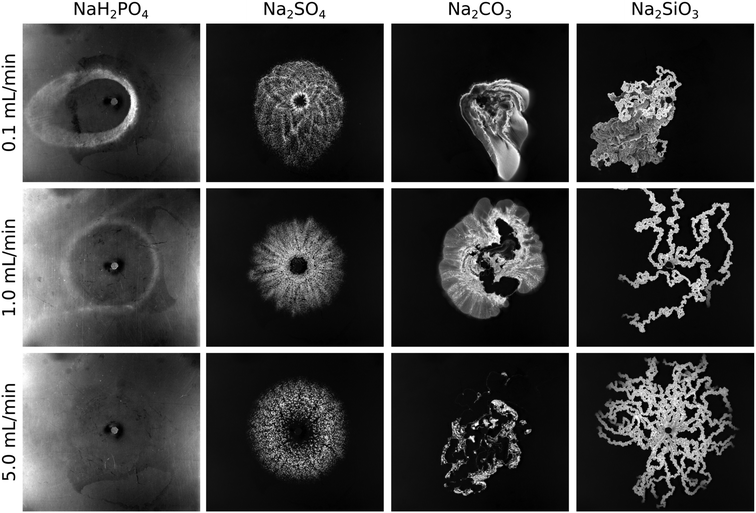
Precipitation reactions under flow conditions in a confined domain lead to different patterns depending on the chemical reactant used even if other experimental parameters (flow rate, gap width, reactant concentration, etc.) are constant (see Fig. 1). In the case where a NaH₂PO₄ solution is radially injected into a CaCl₂ solution at a low flow rate (Q = 0.1 mL min⁻¹), a precipitate ring distorted by flow imperfections is obtained. At this low flow rate (where the driving force is reduced compared to higher flow rates), we could not reach a perfect circle even when repeating the experiment several times (top left pattern of Fig. 1). This suggests that the pattern is composed of small and separated particles whose motion is already affected by the flow. We also see that increasing the injection rate reduces the amount of product. This is documented by the observation that the precipitate ring first becomes less visible (1.0 mL min⁻¹), then undetectable for a sufficiently large flow rate (5.0 mL min⁻¹) even if the contrast of the image was increased to enhance the sensitivity (resulting in a brighter background compared to the other cases). This is in good agreement with the fact that the amount of product formed during injection may be tuned by the flow rate in radial systems because the injection rate modifies the in situ concentration profiles as already demonstrated for the case of calcium carbonate.² However, we highlight that the flow rate applied here is significantly higher than the one used in this former work where the precipitate was not flushed away. In addition, considering the kinetic and hydrodynamic time scales, the formation of a calcium phosphate precipitate is slow while that of calcium carbonate is fast compared to the flow rate applied. Therefore, in the present case of a calcium phosphate precipitate, the amount of product decreases with increasing flow rate because precipitation takes place on a significantly longer time scale than that of injection.

Fig. 1 Precipitation patterns observed when solutions (5 mL) of different sodium salts displaced a calcium chloride solution at various flow rates. Field of view: 19.6 cm × 17.5 cm. The contrast of the patterns in the first column is increased for better visualization which results in reflections at the edges.

When the inflowing solution is changed to Na₂SO₄, we observe a different pattern compared to NaH₂PO₄. First of all, calcium sulfate precipitates faster than calcium phosphate, and thus no precipitate-less inner circle is seen at lower flow rates (patterns of Fig. 1 corresponding to 0.1 and 1.0 mL min⁻¹ flow rates). The radial symmetry is more pronounced for each flow rate and the particles form well visible aggregates. This suggests that the larger precipitate particles are to a lesser extent advected by the flow. However, the preserved radial symmetry also indicates a weak interaction between hydrodynamics and precipitate formation, since the injected solution keeps spreading radially on the macroscopic scale despite the presence of precipitate obstacles.

In the case of Na₂CO₃ as inflowing solution, the situation significantly changes. The calcium carbonate pattern misses any radial symmetry already at the lowest flow rate (Fig. 1; 0.1 mL min⁻¹ flow rate). Here we highlight that the fluid properties of the reactant solutions listed in Table 1 preclude viscous fingering at the injection rates used. The pattern is fully covered with precipitate although its distribution is inhomogeneous, i.e., less and more populated regions are present. Hence, an increasing interaction between flow and precipitation can be expected in comparison to the previous cases (calcium phosphate and sulfate systems). When Q is increased to 1 mL min⁻¹, the coupling is even more pronounced since a precipitate-less region filled with the inflowing solution appears in the middle of the pattern which is bounded by a short, membrane-like precipitate wall on the bottom part. Such precipitate wall is typically short and appears at random places upon reproducing the experiment because the experimental conditions are such that the transition from separated particles to cohesive structure can be observed. The cohesive precipitate wall behaves like a membrane in the sense of allowing the transport of certain components while others are held back. Increasing the flow rate even further results in a pattern mainly characterized by this membrane behavior. Those membranes appear at sufficiently high flow rate and reactant concentrations which locally leads to the formation of a large amount of precipitate in the mixing zone.⁸ In total, the amount of product sharply drops at the largest flow rate since those membranes separate the inflowing and displaced reactants during the injection. However, we also see that the membrane is slightly permeable, thus some secondary precipitation takes place proceeding from the membrane towards the bulk of the calcium solution. This exclusive direction is determined by the effective diffusion coefficient of the chemical species present.^21,22

Finally, the last set of experiments was performed by injecting a Na₂SiO₃ solution into CaCl₂. In this case, precipitation modifies the flow even stronger. Despite the radial injection system, the calcium silicate pattern depicts pronounced directionality and forms precipitate tubes (3-dimensional membranes) already at the lowest flow rate (see Fig. 1). Again, we highlight that the viscosity ratio of the reactant solutions is not large enough for viscous fingering (Table 1). Numerous elongated tubes appear with increasing flow rate (Q = 1 mL min⁻¹). Applying the highest flow rate leads to the formation of even more tubes. The precipitate wall does not sustain the interior pressure and breaks up at certain points (close to the inlet) where new tubes originate. Once the interior pressure decreases sufficiently due to the large number of tubes (i.e. the stream in the tubes splits and thus becomes weaker), the tubes rather grow forward instead of splitting. The growth dynamics resembles that of filaments in confined chemical gardens^3,4,23 which was found to be nearly ballistic and fully self-avoiding. In addition, no secondary precipitation is seen during the injection unlike in the case of calcium carbonate which suggests that calcium silicate membranes are less permeable. Such chemical character dependent tube permeability was also reported elsewhere for the comparison of copper phosphate and silicate chemical gardens.²⁴

To wrap up the macroscopic pattern characteristics, we conclude that significantly different patterns can be obtained even when applying the same experimental conditions (reactant concentrations, flow rate, gap width, etc.) if the chemical composition of the injected reactant solution is varied. In addition, by considering the relevant solubility products²⁵ (pK_sp) of the expected precipitated sparingly soluble salts (pK_sp,CaSO4 = 4.62, pK_{sp,CaHPO4·2H2O} = 6.58, pK_sp,CaSiO3 = 7.2, pK_sp,Ca2P2O4 = 7.9, pK_sp,CaCO3 = 8.35), we can see that the highest thermodynamic tendency to form a precipitate (i.e., highest pK_sp) not necessarily results in the most pronounced coupling between hydrodynamics and precipitation. For example, calcium sulphate having a lower pK_sp than calcium phosphate yields much more precipitate in our flow-driven system during the time scale of injection. Also, calcium silicate forms more pronounced precipitate membranes than calcium carbonate despite its lower pK_sp. It is worth mentioning that each presented reaction can lead to precipitate particles with varying chemical composition (i.e., corresponding to different pK_sp values). However, the investigation of crystal structures is beyond the scope of the present work. The flow conditions being the same, the significant difference seen in the patterns must be related to the microscopic properties of the solid particles formed. Therefore, to understand the pattern selection depending on the injected anion, we next investigate the microscale structure of the respective precipitates.

3.2 Microscopic precipitate characteristics

The macroscopic patterns obtained within the confinement (0.5 mm gap width) are composed of solid particles whose degree of dispersion (i.e., the typical mean distance between particles) strongly depends on the reactants. In our study, we avoided an invasive sampling of the precipitate for particle characterization. Removing the cover lid results in a meniscus at the wedge between both plates which indeed mixes the solution and accumulates the liquid phase on a small area. This completely changes the concentration distribution of the solutions and destroys most of the patterns (with the exception of silicate tubes). Therefore, to visualize the precipitate microstructure, we repeated our experiments under an optical microscope. Characteristic images of the different precipitates are shown in Fig. 2.

Fig. 2 Optical microscope images of the different precipitates (calcium phosphate (a), sulphate (b), carbonate (c), and silicate (d)) produced under flow conditions in a confined geometry. Images are taken at 30 s after the end of injection (3 mL).

In the case of calcium phosphate (Fig. 2a), two different particle types have developed at the end of the injection. On one hand, small (≈5–10 μm length) and separated precipitate particles of an irregular structure cover the field of view. Besides them, a low number of much larger crystals can be found. This microscopic observation confirms the ring-shaped pattern presented for 1.0 mL min⁻¹ in Fig. 1. The well-dispersed state (no sign of aggregation) and the low number density of the particles (number of particles per unit volume) despite the high concentrations used (1 M NaH₂PO₄ and 2 M CaCl₂) allow a direct advection by the radial flow.

The reactant concentrations of the other precipitation systems are halved to reduce the number density of the particles for the microscopic visualization. In the case of calcium sulphate, star-like aggregates composed of elongated primary particles are observed. We highlight here that these aggregates are much larger compared to those of the three other systems, so that a significantly lower magnification had to be used (see the scale bar in Fig. 2b). Here again the microscopic characteristics of the calcium sulphate agree well with the patterns observed in Fig. 1. In addition to the higher reaction rate noted in the previous section, the larger aggregates sediment quickly. Thus the radial pattern is filled with precipitate instead of producing a ring of advected small size particles in the periphery. A small precipitate-free region in the center is only obtained at 5.0 mL min⁻¹ flow rate (Fig. 1). At this flow rate, aggregation is further enhanced by the advection of smaller particles which attach to the existing larger ones resulting in a coarse-grained precipitation pattern.

When the Na₂CO₃ solution is injected into CaCl₂, three different particle types are formed (Fig. 2c). There are several larger crystals (≈15 μm) either of rhombohedral or spherical (multicrystalline) shape most probably corresponding to calcite and vaterite polymorphs of calcium carbonate.⁷ The larger crystals are surrounded by regions where very fine particles are present in high number density. Their particle size cannot be precisely determined by the optical microscope due to the resolution limit. Images recorded at the highest magnification (not shown here) suggest a characteristic size in the submicron range which is in line with laser diffraction measurements on precipitated calcium carbonate particles.²⁶

Finally, experiments performed to produce calcium silicate precipitate result in an even higher number density of submicron particles (Fig. 2d). In this case, coarse particles are absent in our microscope images and submicron particles are significantly smaller than those for calcium carbonate.

To further investigate the dynamics of the particle formation and reorganization processes, which probably influence the coupling of hydrodynamics and precipitation, we estimated the growth rate of the different calcium precipitates. To do so, consecutive images were taken in time (see a selection in Fig. 3) and the projected area of the particles was measured once the injection stopped and the particles no longer followed the flow. This method assumes that the growth rate under flow conditions is similar to that in a quiescent solution layer. Although this assumption might not be always valid, it allows us to estimate the trends. In addition, the particles moving together with the flow both in horizontal and vertical directions cannot be tracked in time and space because they move out of focus. The analysis was not performed for the silicate system because the particle size falls below the resolution limit of the optical microscope. For the other systems, a linear relationship is found between the projected particle area and the time elapsed. Comparing the results of the different precipitates, calcium carbonate grows at the lowest rate which in fact slightly depends on the type of the polymorph as well: (0.25 ± 0.03) μm² s⁻¹ for calcite and (0.33 ± 0.05) μm² s⁻¹ for vaterite. In addition, the small particles originally surrounding the larger calcite and vaterite crystals dissolve while calcite and vaterite ones grow due to Ostwald ripening (Fig. 3c and d). This phenomenon was not observed in the other systems where the growth is caused by the ongoing precipitation reaction. Calcium phosphate grows one order of magnitude faster ((7.5 ± 2.0) μm² s⁻¹) and calcium sulphate even greatly exceeds this value ((2500 ± 380) μm² s⁻¹). This tendency agrees well with the typical crystal sizes reached during the injection (see Fig. 2), which may confirm that the growth speed measured shortly after the injection is also a reasonable approximation during the flow.

Fig. 3 Optical microscope images illustrating the growth of calcium sulphate (upper row) and carbonate (lower row) crystals. Images are taken at (a) 30 s, (b) 80 s, (c) 30 s, and (d) 200 s after the end of injection (3 mL).

Therefore, we can conclude that the most striking interaction between hydrodynamics and precipitation is seen in the systems where very fine particles are produced in a high number density (like in the case of silicate). Upon mixing, a tremendous amount of fine particles appear which cannot significantly grow further because of the depletion zones of the reactants around them. In these systems, where nucleation is more favoured than crystal growth, precipitate membranes consisting of a colloidal gel are formed.^26–28 The gel results from attractive particle interactions like van der Waals forces linking the particles to form a three dimensional network at sufficiently large number density. Due to the high ionic strength of the non-precipitating Na⁺ and Cl⁻ ions, the electrical double layer around the particles is compressed so that repulsive particle interactions are strongly reduced²⁹ and the total interaction becomes attractive. The formed gel membranes sustain the interior pressure caused by the continuing injection and lead to the distinct patterns shown in Fig. 1 for carbonate and silicate at the highest flow rate, as explained in the next section. The stability of the gel is determined by the number density of particles, the magnitude of the attractive interactions and the reorganization processes as can be seen from comparing the calcium carbonate and silicate patterns. The calcium silicate tubes are less permeable, long-lasting (no sign of secondary precipitation) and even survive the removal of the cover lid of the Hele-Shaw cell. By contrast, in the calcium carbonate system, the reorganization and crystal growth processes degenerate the gel in time; thus, no membrane structure develops at the lowest flow rates. When fewer but larger particles are produced (i.e., crystal growth is more favoured than nucleation, e.g., in the sulphate system), circular precipitation patterns are obtained instead of the membrane structures. The solid particles simply settle down and the further injected solution penetrates between them.

3.3 Hydrodynamic background of the patterns

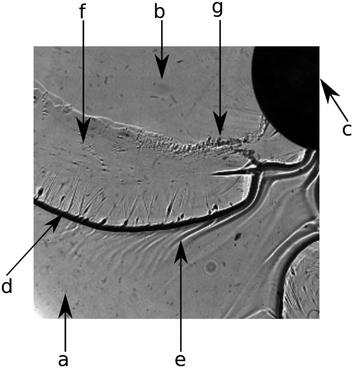
In the previous section, we discussed how the precipitate micro-structure influences the macroscopic pattern. By shadowgraph visualization, we now focus on the temporal evolution of the flow leading to the different patterns observed in Fig. 1. In Fig. 4, details of a typical shadowgraph image are shown to explain the prominent regions of the patterns.

Fig. 4 Shadowgraph image showing the different regions present while a finger-like pattern of CaCO₃ precipitate grows. (a) Displaced CaCl₂ solution; (b) inflowing Na₂CO₃ solution; (c) injection port; (d) gel front; (e) pattern due to the concentration distribution in the mixing zone of the two reactants; (f) thin gel film remaining on the Plexiglas plates; (g) zone of transition from colloidal gel to larger precipitate crystals.

Initially, the entire setup is filled with CaCl₂ solution (Fig. 4a). The inflowing solution of Na₂CO₃ (Fig. 4b) is injected through the inlet (Fig. 4c) and mixes with the displaced solution. In the mixing zone, fine CaCO₃ particles appear in a large amount (as shown in Fig. 2c) leading to the formation of a colloidal gel. Due to its different refractive index, the gel front is visible as a black line in the shadowgraph (Fig. 4d). The gel displays a strongly increased viscosity compared to the educt solutions.²⁶ This rheological change is further confirmed in the literature in the case of silicate.³⁰ However, to estimate how pronounced the viscosity change might be, 2 M CaCl₂ and 1 M Na₂SiO₃ solutions have been mixed in 1 : 1 volume ratio and the viscosity of the resulted precipitate containing suspension has been measured (Brookfield LVDV-II+P viscometer) at low rotation speed (3 rpm). It has been found that the suspension has ≈40× larger viscosity (70 cP) than that for any of the reactant solutions (see Table 1). Although the rheological properties of such suspensions depend on shear rate, particle size and shape, etc., a large viscosity change is clearly present in the system. Therefore, the inflowing aqueous solution pushes a more viscous gel layer giving rise to viscous fingering effects^6,31 as discussed later. Such viscosity measurements have been performed with calcium-sulphate and calcium-carbonate systems as well. In the case of sulphate, precipitate particles settled quickly which coincides with fast crystal growth presented earlier. Therefore, no viscosity corresponding to a homogeneous mixture could be obtained. Upon mixing calcium and carbonate reactants in a beaker, the product formed with a gel-like structure. During rheological measurement, such gel-like texture diminished which again coincides with a recrystallization process seen in Fig. 3c and d, thus the viscosity of the gel-like material could not be measured. Right before the precipitation front, Schlieren patterns (light inhomogeneities) can be seen in the shadowgraph image (Fig. 4e) which are caused by the concentration changes in the mixing zone leading to buoyancy effects.¹⁰ Behind the precipitation front, a thin gel film remains on the Plexiglas plates (Fig. 4f). Over time, the transition from the gel state to larger particles by reorganization and crystal growth takes place (Fig. 4g).

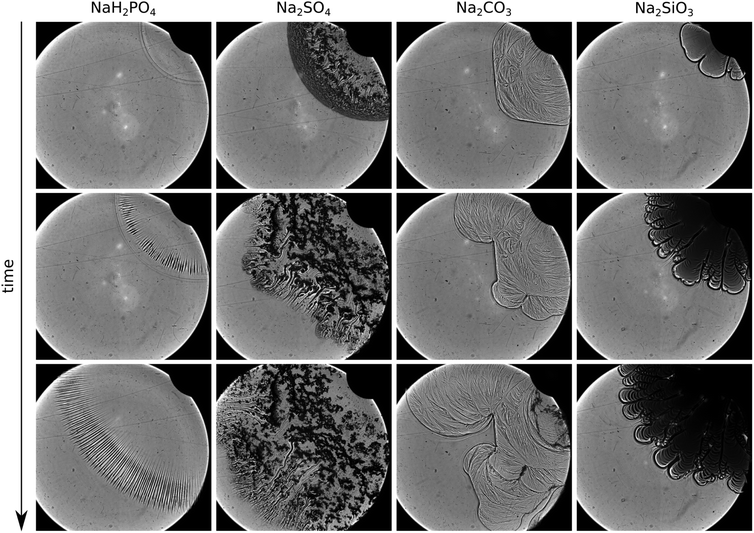
Since most of this information cannot be obtained by the direct camera records (Fig. 1), we repeated a selection of our experiments in the shadowgraph optics. In the case of NaH₂PO₄ injected at Q = 5 mL min⁻¹, no precipitate is found because, as discussed earlier, the reaction is slow and the solid phase appears only later. However, in the shadowgraph images in Fig. 5, a striped pattern becomes visible at the edge of the expanding circle of the injected solution. These stripes are due to a buoyancy-driven instability caused by the density difference between the mixing solutions. Such a buoyancy-driven pattern is known and well-described in the literature.^10,11

Fig. 5 Temporal image sequence of confined precipitation patterns recorded using a shadowgraph technique. For concentrations see Section 2; the flow rate is Q = 5.0 mL min⁻¹. Injection port placed in the top right corner. Field of view: 4 cm × 3.8 cm.

In the sulfate system, the interior part of the pattern is covered with precipitate particles (see Fig. 5). These particles are large and their number density is low. Therefore, they cannot link into a three dimensional gel network as expected from the absence of the black front seen in Fig. 4d. Instead, isolated solid aggregates are formed. The proceeding growth of the aggregates observed in the microscopy experiment is also visible in the shadowgraph image sequence. These aggregates settle down when the radially spreading flow becomes sufficiently weak, so that the injected solution flows between the obstacles and forms finger-like channels, clearly seen as curved schlieren, in the later stage due to local changes in the permeability.¹²

We see a significantly different behavior when the carbonate solution is injected into the calcium one. A thin black front is present at the rim of the injected solution which persists over time (third column of Fig. 5) indicating the formation of a gel front. Due to the changed rheological properties of that layer, pattern formation is initiated bearing analogy to viscous fingering. However, our system obviously is more complex than the injection of a low-viscous Newtonian fluid into a high-viscous one (see Table 1 for viscosity values). The gel front is a relatively thin layer between the two low-viscosity reactant solutions. During injection, the gel front bulges until it breaks up initiating further precipitation and hence a regeneration of the front. The viscoelastic properties of the gel are visible in the thin film of gel remaining at the plexiglass plates. Due to the deformation by the continuing flow, this film wrinkles producing stripes of varying thickness as visible in the shadowgraph image (third column of Fig. 5). The ensuing transition into macroscopic precipitate particles can be seen in the top right part of the image at the latest stage of the injection. To further support the idea that the patterns are caused by a viscous fingering-like effect due to the in situ formation of the gel membrane, we refer to the literature where the existence of critical parameters (reactant concentration and flow rate) to obtain precipitate fingers is proven.⁸ In that study comparing calcium- and barium-carbonate patterns, the increase of reactant concentrations leads to membrane formation in both cases. This effect is caused since at higher reactant concentrations precipitate nuclei evolve in a larger number resulting in a fast depletion in the surroundings; hence particles barely grow (the large number of small particles is also seen in Fig. 2c). We highlight here, as the apparent flow rate is also a critical parameter, that patterns obtained upon radial injection are transient since the flow velocity decays with increasing radius. To avoid such effect, one may use a rectilinear system.

Finally, when the silicate solution is used for the experiments, fingers bounded by a pronounced colloidal gel layer (thick black line) are present from the beginning of the injection (last column of Fig. 5). In this system, the nucleation step is more favourable than crystal growth, and thus a vast amount of small particles is produced (i.e., high nucleation rate restricts mass flux to individual nuclei, hence their growth). The high particle density leads to the formation of an extremely dense and stable gel network. Analogous to viscous fingering, this manifests in a smaller wavelength and accordingly a higher number of fingers. Unlike the calcium carbonate, the silicate precipitation does not produce a thin, transparent gel film at the Plexiglas plates but robust, opaque precipitate tube-like membranes. These membranes are stable independently of the applied flow rate, i.e., the duration of the experiment, since no notable particle coarsening occurs in this time frame.

4 Conclusions

Flow-driven precipitation experiments have been performed in a confined geometry by injecting one reactant solution of a sodium salt into a solution of calcium chloride. The nature of the precipitating anion of the injected solution affects the precipitation patterns even if all other experimental conditions are kept constant. The pattern selection has been investigated and explained based on the coupling of hydrodynamics and precipitate formation. It is found that the formation of a low number of large particles influences the flow due to the local permeability decrease in the confinement, while precipitation of a large amount of small colloidal particles forms a gel front resulting in flow-driven pattern formation influenced by viscous fingering. Therefore, more enhanced coupling of chemistry and hydrodynamics may be reached with precipitants leading to high nucleation rate and restricted mass flux and thus producing a vast amount of fine particles.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Research, Development and Innovation Office (K119795 and PD121010), the GINOP-2.3.2-15-2016-00013 project, the German Helmholtz Association; and by the EU-MaSNEC M-ERA-NET programme. We thank Dr F. Babick for fruitful discussions.

References

1. G. Schuszter, F. Brau and A. De Wit, Flow-Driven Control of Calcium Carbonate Precipitation Patterns in Confined Geometry, Phys. Chem. Chem. Phys., 2016, 18, 25592.
2. F. Brau, G. Schuszter and A. De Wit, Flow Control of A + B → C Fronts by Radial Injection, Phys. Rev. Lett., 2017, 118, 134101.
3. F. Haudin, J. H. E. Cartwright, F. Brau and A. De Wit, Spiral Precipitation Patterns in Confined Chemical Gardens, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(49), 17363–17367.
4. F. Haudin, J. H. E. Cartwright and A. De Wit, Direct and Reverse Chemical Garden Patterns Grown upon Injection in Confined Geometries, J. Phys. Chem. C, 2015, 119, 15067–15076.
5. F. Haudin, V. Brasiliense, J. H. E. Cartwright, F. Brau and A. De Wit, Genericity of Confined Chemical Garden Patterns with Regard to Changes in the Reactants, Phys. Chem. Chem. Phys., 2015, 17, 12804.
6. F. Haudin and A. De Wit, Patterns Due to an Interplay Between Viscous and Precipitation-driven Fingering, Phys. Fluids, 2015, 27, 113101.
7. B. Bohner, G. Schuszter, D. Horváth and Á. Tóth, Morphology Control by Flow-driven Self-organizing Precipitation, Chem. Phys. Lett., 2015, 631–632, 114–117.
8. G. Schuszter and A. De Wit, Comparison of Flow-controlled Calcium and Barium Carbonate Precipitation Patterns, J. Chem. Phys., 2016, 145, 224201.
9. S. Wagatsuma, T. Higashi, Y. Sumino and A. Achiwa, Pattern of a Confined Chemical Garden Controlled by Injection Speed, Phys. Rev. E, 2017, 95, 052220.
10. F. Haudin, L. A. Riolfo, B. Knaepen, G. M. Homsy and A. De Wit, Experimental Study of Buoyancy-driven Instability of Miscible Horizontal Displacement in a Hele-Shaw Cell, Phys. Fluids, 2014, 26, 044102.
11. A. Baker, Á. Tóth, D. Horváth, J. Walkush, A. S. Ali, W. Kukovecz, J. J. Pantaleone and J. Maselko, Precipitation Pattern Formation in the Copper(ii) Oxalate System with Gravity Flow and Axial Symmetry, J. Phys. Chem. A, 2009, 113(29), 8243–8248.
12. Y. Nagatsu, Y. Ishii, Y. Tada and A. De Wit, Hydrodynamic Fingering Instability Induced by a Precipitation Reaction, Phys. Rev. Lett., 2014, 113, 024502.
13. P. Shukla and A. De Wit, Fingering Dynamics Driven by a Precipitation Reaction: Nonlinear Simulations, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 016202.
14. T. Podgorski, M. C. Sostarecz, S. Zorman and A. Belmonte, Fingering Instabilities of a Reactive Micellar Interface, Phys. Rev. E, 2016, 93, 023103.
15. L. A. Riolfo, Y. Nagatsu, S. Iwata, R. Maes, P. M. J. Trevelyan and A. De Wit, Experimental Evidence of Reaction-driven Miscible Viscous Fingering, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 015304(R).
16. K. Eckert, M. Acker, R. Tadmouri and V. Pimienta, Chemo-Marangoni Convection driven by an Interfacial Reaction: Pattern Formation and Kinetics, Chaos, 2012, 22(3), 0371112.
17. T. Köllner, K. Schwarzenberger, K. Eckert and T. Boeck, Multiscale structures in solutal Marangoni Convection: Three-dimensional Simulations and Supporting Experiments, Phys. Fluids, 2013, 25(9), 092109.
18. W. Merzkirch, Flow Visualization, Academic Press, 1987.
19. P. Bunton, B. Dice, J. A. Pojman, A. De Wit and F. Brau, Reconstruction by Fluorescence Imaging of the Spatio-temporal Evolution of the Viscosity Field in Hele-Shaw Flows, Phys. Fluids, 2014, 26, 114106.
20. P. Bunton, D. Martin, S. Stewart, E. Meiburg and A. De Wit, Schlieren Imaging of Viscous Fingering in a Horizontal Hele-Shaw Cell, Exp. Fluids, 2016, 57, 28.
21. B. C. Batista and O. Steinbock, Growing Inorganic Membranes in Microfluidic Devices: Chemical Gardens Reduced to Linear Walls, J. Phys. Chem. C, 2015, 119(48), 27045–27052.
22. Q. Wang, M. R. Bentley and O. Steinbock, Self-Organization of Layered Inorganic Membranes in Microfluidic Devices, J. Phys. Chem. C, 2017, 121, 14120–14127.
23. F. Brau, F. Haudin, S. Thouvenel-Romans, A. De Wit, O. Steinbock, S. S. S. Cardoso and J. H. E. Cartwright, Filament Dynamics in Confined Chemical Gardens and in Filiform Corrosion, Phys. Chem. Chem. Phys., 2018, 20, 784–793.
24. E. Rauscher, G. Schuszter, B. Bohner, Á. Tóth and D. Horváth, Osmotic Contribution to the Flow-driven Tube Formation of Copper–Phosphate and Copper–Silicate Chemical Gardens, Phys. Chem. Chem. Phys., 2018, 20, 5766–5770.
25. S. Kotrlý and L. Šucha, Handbook of Chemical Equilibria in Analytical Chemistry, Ellis Horwood Limited, England, 1985.
26. J. Schlomach, K. Quarch and M. Kind, Investigation of Precipitation of Calcium Carbonate at High Supersaturations, Chem. Eng. Technol., 2006, 29, 2.
27. R. D. Coatman, N. L. Thomas and D. D. Double, Studies of the Growth of Silicate Gardens and Related Phenomena, J. Mater. Sci., 1980, 15, 2017–2026.
28. J. H. Cartwright, B. Escribano, S. Khokhlov and C. I. Sainz-Díaz, Chemical Gardens from Silicates and Cations of Group 2: a Comparative Study of Composition, Morphology and Microstructure, Phys. Chem. Chem. Phys., 2011, 13, 1030–1036.
29. R. J. Hunter, Foundations of Colloid Science, Oxford University Press, 2009.
30. J. Schlomach and M. Kind, Investigations on the Semi-batch Precipitation of Silica, J. Colloid Interface Sci., 2004, 277, 316.
31. G. M. Homsy, Viscous Fingering in Porous Media, Annu. Rev. Fluid Mech., 1987, 19, 271–311.

---

Footnote

† Authors contributed equally to the work.

---