Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fundamental limitations of the time-dependent Stokes shift for investigating protein hydration dynamics
Esther
Heid
 *a and
Daniel
Braun
*a and
Daniel
Braun
 *ab
*ab
aDepartment of Computational Biological Chemistry, Faculty of Chemistry, University of Vienna, Währingerstr. 17, 1090 Vienna, Austria. E-mail: esther.heid@univie.ac.at; daniel.braun@univie.ac.at
bDepartment of Structural and Computational Biology, Max F. Perutz Laboratories, University of Vienna, Campus Vienna Biocenter 5, 1030 Vienna, Austria
First published on 1st February 2019
Abstract
The time-dependent Stokes shift (TDSS) has attracted increasing interest for measuring hydration dynamics around biomolecules during the last decades. Its ability to report on hydration dynamics around proteins, however, was questioned recently since the experimental signal stems from both water and protein motion with an unknown ratio of contribution. Using large-scale computer simulations, we examine the ability of the TDSS to capture local hydration dynamics at nine different sites around the protein ubiquitin. By computationally constraining protein motion, it is shown that the remaining water component is meaningful and in line with the picture of a heterogeneous yet overall mobile hydration layer. However, protein contributions are excessively large and cannot be removed in an experimental context, thus obscuring the water component. Consequently, we conclude that the experimental TDSS may not be suitable for the investigation of hydration dynamics around proteins.
1 Introduction
The dynamics of water in the vicinity of proteins and other biomolecules differs from bulk water dynamics. Despite general consensus about the importance of this behavior in biological processes, its characterization is still not conclusive, largely owing to the multitude of different approaches, contradictory interpretations and, therefore, a seeming inconsistency.Both 17O nuclear quadrupole relaxation (NQR)1–5 experiments and multiple independent molecular dynamics (MD) simulations6–12 report on a highly heterogeneous yet overall mobile hydration layer. More precisely, depending on the surface topology of the protein, few water molecules experience strong retardation, but the majority (>90%) of water molecules in the first hydration shell is slowed down mildly compared to bulk water, with a retardation factor (RF) of only 2–3. At first glance, dielectric relaxation spectroscopy (DRS) seems to offer a different point of view: the collective modes in this experiment show very slow dynamics compared to bulk water, and they were mistakenly suspected to stem from a large number of rigid water molecules surrounding the protein.13–15 It is now clear that these modes are unique to the collective nature of the dielectric experiment16–19 and, apart from one slightly retarded peak (RF < 2), cannot be associated with the motion of individual water molecules.18,19 During the last decades, however, fluorescence spectroscopy in protein systems has gained increased attention, and the appearance of very long relaxation times has again challenged the picture of an overall mobile hydration layer.20–26
Fluorescence spectroscopy uses a molecular probe to indirectly measure the collective relaxation of its surroundings. This probe can be a chromophore that is introduced into the system or one that is naturally present, e.g., tryptophan in proteins. The time-dependent Stokes shift (TDSS) is recorded by electronic excitation of the chromophore and subsequent measurement of the emitted fluorescence frequencies.27–31 Analogous to the Frank–Condon principle, immediately after excitation, the nuclear positions of the surroundings still correspond to the unexcited state of the chromophore and, at the same time, an energetically unfavorable conformation in the context of the excited state. Over time, the surroundings adapt to the altered electrostatic potential of the chromophore, thus lowering its emitted fluorescence frequencies. Therefore, these time-dependent frequencies represent the relaxation of the surroundings in response to a change in the chromophore's charge distribution.
A fundamental property of TDSS is that it measures the collective response of the system,31–33i.e., the sum of all electrostatic interactions with the excited group. Besides the components of interest (here, local water molecules), irrelevant parts of the surroundings can contribute to the signal. This becomes especially important in proteins, where a substantial fraction of the chromophore's surroundings can be the protein itself.33–37 Apart from direct contribution of protein motion to the TDSS, the protein introduces long relaxation times also via coupled protein–water motions.38–40 Furthermore, due to its collective nature, the TDSS experiment is practically insensitive to exchange processes of solvent molecules.34,36 In other words, the event of a solvent molecule leaving a particular site and being replaced by another one hardly affects the TDSS, particularly not the relaxation on time scales longer than the exchange process itself.
The overall aim of this study is an in-depth analysis of the origin and nature of TDSS relaxation mechanisms at sites which are known to have differing hydration dynamics, furthermore, an assessment with respect to other experiments and finally, a discussion of the consequent limitations of the TDSS for investigating protein hydration dynamics.
We investigate our system with respect to linear response theory (LRT), which is assumed to be applicable when inferring equilibrium properties from the nonequilibrium TDSS experiment (and vice versa in many simulation studies). Next, we present the total (experimentally obtainable) TDSS of nine different sites on the surface of the protein ubiquitin (UBQ). Furthermore, we provide a full decomposition into protein and water contributions and also an estimate of the influence of coupled protein–water motions, based on MD simulations where protein motion is constrained. All results are discussed in the context of three previously analyzed experiments: NQR10 and DRS19 (see above) and, in particular, the protein–water nuclear Overhauser effect (NOE), since it reflects local water residence times at the protein surface and, therefore, is able to provide the distribution of heterogeneous water dynamics in the protein hydration layer.11 Notably, these previous analyses are all based on the very same simulation system as the current study, ensuring the consistency of all calculated observables. This approach realizes a previous proposition of analyzing multiple experiments within a single computational and theoretical framework in order to resolve inconsistencies in the field of biomolecular dynamics41 and is essential in the evaluation of TDSS and its limitations in the context of protein hydration.
2 Theory
The time-dependent Stokes shift (TDSS) shows the time-evolution of the fluorescence energy, i.e., the change of the energy gap between ground and excited state caused by changes in the interaction energy ΔU(t) of the chromophore with its surroundings, which, in polar media, is defined as the sum of Coulomb interactions.31,42 Since TDSS is, in principle, a nonequilibrium property, it is best reflected by nonequilibrium simulations, where the solvent-chromophore equilibrium is perturbed by a sudden change of the chromophore's charge distribution corresponding to its excited state. The absolute time-resolved Stokes shift from nonequilibrium simulation shifted to zero at the instance of excitation (t = 0) then is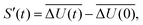 | (1) |
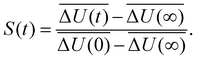 | (2) |
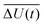 with the fluctuations of the interaction energy δΔU(t) = ΔU(t) − 〈ΔU〉 observed in the equilibrated system. Then, the correlation function
with the fluctuations of the interaction energy δΔU(t) = ΔU(t) − 〈ΔU〉 observed in the equilibrated system. Then, the correlation function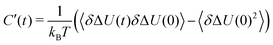 | (3) |
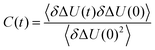 | (4) |
| S(t) = Swater(t) + Sprotein(t) + Sion(t) | (5) |
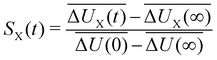 | (6) |
| C(t) = Cwater(t) + Cprotein(t) + Cion(t) | (7) |
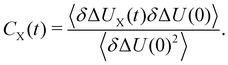 | (8) |
3 Methods
Molecular dynamics simulations were performed on the protein ubiquitin (UBQ), solvated in 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules and 150 NaCl ion pairs, where the CHARMM36 force field45 was employed to describe the proteins and ions, and the SPC/E force field46 to model water. To ensure comparability, system parameters were chosen in line with three previous studies investigating hydration dynamics in the context of NQR, NOE and DRS.10,11,19 The large number of water molecules in the simulation system was chosen to assess possible long-range effects in the studied experimental observables. Additionally, it was recently shown that meaningful simulations of biomolecular systems might require a much larger number of water molecules than previously thought.47 The SPC/E water model was chosen due to its accurate description of experimental properties, in particular dielectric properties48–51 and TDSS timescales around proteins.37–39 Moreover, SPC/E has been shown to combine well with the CHARMM protein force field.52
000 water molecules and 150 NaCl ion pairs, where the CHARMM36 force field45 was employed to describe the proteins and ions, and the SPC/E force field46 to model water. To ensure comparability, system parameters were chosen in line with three previous studies investigating hydration dynamics in the context of NQR, NOE and DRS.10,11,19 The large number of water molecules in the simulation system was chosen to assess possible long-range effects in the studied experimental observables. Additionally, it was recently shown that meaningful simulations of biomolecular systems might require a much larger number of water molecules than previously thought.47 The SPC/E water model was chosen due to its accurate description of experimental properties, in particular dielectric properties48–51 and TDSS timescales around proteins.37–39 Moreover, SPC/E has been shown to combine well with the CHARMM protein force field.52
All MD simulations were conducted with the program DOMDEC CHARMM,53,54 using the leapfrog integrator55 with a 2 fs timestep, an nVT ensemble kept at an average of 300 K with a Nosé–Hoover thermostat56,57 with a coupling constant of 1000 kcal mol−1 ps2 and periodic boundary conditions. The particle mesh Ewald method58,59 (grid spacing 1 Å, 6th-order cubic splines, and κ = 0.41 Å−1) was employed to calculate electrostatic interactions. van der Waals interactions were turned off at 12 Å, with a smooth switching function between 10 and 12 Å. Bonds containing hydrogen atoms were kept fixed using the SHAKE algorithm.60 The different simulation setups (trajectory length, number of replicas, write-out frequency, free or constrained protein motion, presence of an actual excitation) are described in the following. In total, 3.85 μs of trajectories were produced (disregarding equilibration periods), which, to the best of our knowledge, is the largest atomistic computer simulation study of the TDSS around proteins. Therefore, this work is a significant step-up with regard to most current studies, where the much shorter trajectories and deficient sampling of phase space render a detailed analysis difficult. For an overview of all simulations please refer to Table 1.
| EQ/NEQ | UBQ motion | Write-out | Length | Replicas |
|---|---|---|---|---|
| EQ | Free | 1 ps | 200 ns | 5 |
| EQ | Free | 20 fs | 10 ns | 3 |
| EQ | Constrained | 1 ps | 5 ns | 200 |
| EQ | Constrained | 20 fs | 100 ps | 200 |
| NEQ | Free | 2 fs–2 ps | 500 ps | 9 × 200 |
| NEQ | Constrained | 2 fs–2 ps | 500 ps | 9 × 200 |
Equilibrium trajectories with a total length of 1 μs (cf. line 1 in Table 1) already used for the analysis of NQR, NOE and DRS10,11,19 were reused for the calculation of the TDSS in this study. They were calculated from 5 independent starting configurations, which were generated with the program PACKMOL,61 using the 1UBQ62 structure from the RCSB Protein Data Bank and a cubic box.63 After energy minimization with the steepest descent method, a box side length of 110.9 Å was determined in the nPT ensemble. The first 5 ns in the nVT ensemble were then discarded previous to production runs of the 5 replicas.
The starting configurations for 2.85 μs of additional equilibrium and nonequilibrium trajectories (with or without constrained protein motion, cf. lines 2–6 in Table 1), which were necessary for an in-depth analysis of the TDSS, were taken randomly from the initial 1 μs trajectory. Namely, three equilibrium trajectories with an increased write-out frequency were conducted to describe the subpicosecond portion of the TDSS. Furthermore, 200 replicas of constrained equilibrium simulations with different lengths and write-out frequencies were conducted, where a harmonic potential with a force constant of 200 kcal mol−1 Å−2 was imposed on each protein atom relative to its starting configuration.
We furthermore calculated nonequilibrium simulations which mimic the TDSS experimental setup, where the partial charge distribution of a chromophore is changed abruptly (in contrast to equilibrium simulations, which solely comprise equilibrated ground-state trajectories). For each of the nonequilibrium simulations, the partial charge distribution of either tyrosine, histidine or seven different lysine residues was changed at t = 0 according to Fig. 1. Coordinates were saved for 0.5 ns at non-uniform time intervals starting with 2 fs intervals right after the excitation and increasing up to 2 ps. For each of the nine excitations, 200 replicas with free protein motions, as well as 200 replicas with constrained protein motion were calculated.
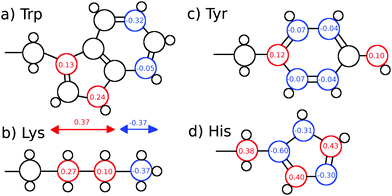 | ||
| Fig. 1 (a) Tryptophan excitation by Halle and Nilsson,34 (b) artificial lysine excitation, (c) tyrosine excitation and (d) histidine excitation used in this study. The lysine excitation is purely artificial, whereas the tyrosine and histidine excitations were derived from quantum-mechanical calculations of p-cresol and 5-methylimidazole. | ||
We chose tyrosine, histidine and lysine as chromophores. Tyrosine and histidine are natural chromophores, and are thus an obvious choice. The partial charge changes (CHelpG) of tyrosine and histidine were derived from quantum-mechanical calculations with the program Gaussian0964 of p-cresol and 5-methylimidazolium. More precisely, we calculated the ground state using DFT and the first excited (singlet) state using TD-DFT with the ωB97xD functional,65 the aug-cc-pVTZ basis set and the polarizable continuum model65 (PCM) to account for solvent effects of water. The geometries were optimized in the ground state using the 6-311++G(2d,2p) basis set and PCM. The respective functional and basis sets were shown to work well for the calculation of chromophore excitations.44,66,67 Partial charge changes were summed into the respective non-hydrogen atom.
Since UBQ has no tryptophan, and only one tyrosine and one histidine, we furthermore chose to artificially excite lysine, which is not photoactive but abundant in UBQ, to examine the site-specificity of the TDSS. Computationally, any change in charge distribution can be used to calculate a TDSS. For example, Golosov and Karplus used an artificial threonine excitation to probe polar solvation dynamics around the B1 domain of protein G.35 Analogously, we excite lysine by changing the partial charge distribution of its sidechain, where the δ carbon gains 0.27 e, the ε carbon gains 0.1 e and the nitrogen loses 0.37 e upon excitation. This artificial excitation remotely resembles the changes in partial charge distribution of tryptophan in ref. 34 (cf.Fig. 1).
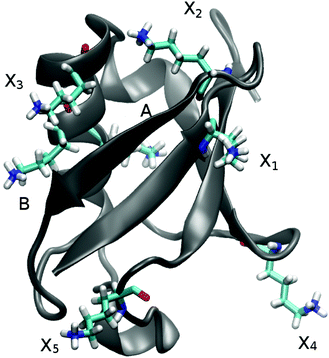
In UBQ, lysine occurs seven times at locations with differing hydration dynamics at the protein surface (cf.Fig. 2). Lysines A and B (residue numbers 27 and 29, respectively) are in close proximity to known retarded sites that, in a previous study,11 were identified from a trajectory also used here (line 1, Table 1) and in another independent study.68 Moreover, lysine A is located in a surface pocket of UBQ well-known for the presence of a water molecule in the crystal structure.1,62 Sites named Xn are not in close proximity to any retarded site, with X1 corresponding to residue number 6, X2 to 11, X3 to 33, X4 to 48 and X5 to 63.
For comparison of the TDSS to other observables, we use the TDSS of the seven lysine residues and NQR,10 NOE11 and DRS19 previously calculated from trajectories also used in this work (line 1 in Table 1). Particularly, the protein–water NOE converted to residence times (τm.RES in the ESI of ref. 11) is an appropriate measure since it provides site-resolved quantities. For this, we take the average of τm.RES of the terminal hydrogens in each lysine sidechain (named HZ) and calculate a retardation factor with respect to the shortest observed τm.RES (21 ps) at the protein surface (referred to as RFτres). Please note that lysines A and B are situated not directly in but only in close proximity to sites with retarded protein hydration dynamics. For this reason, RFτres of lysine A is 46 instead of ∼95 in the actual retarded site, and RFτres of lysine B is 14 instead of ∼52. In ref. 11, a third retarded site is found in UBQ, which does not have any close lysine residue and thus is not included in the current study.
4 Results and discussion
As a first step, in Fig. 3 we present the TDSS at nine different sites in UBQ (cf.Fig. 2). Besides the total TDSS, which can be obtained experimentally, we provide a decomposition into water and protein contributions for each signal, as well as the TDSS from separate simulations, where protein motion is constrained, in order to assess the influence of protein–water coupling.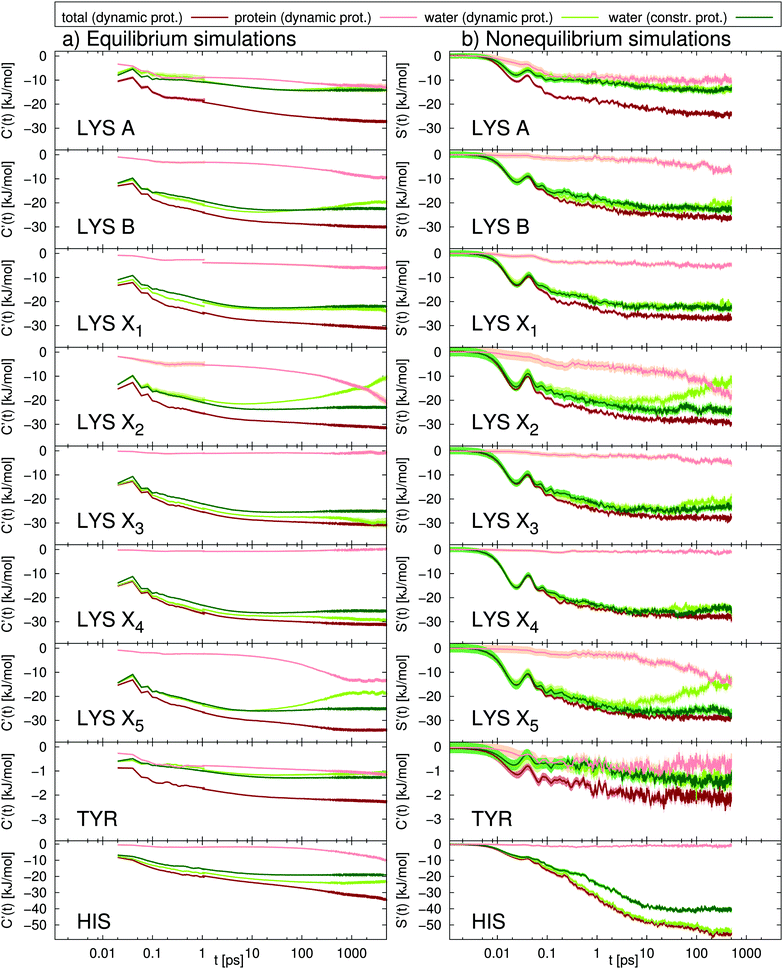 | ||
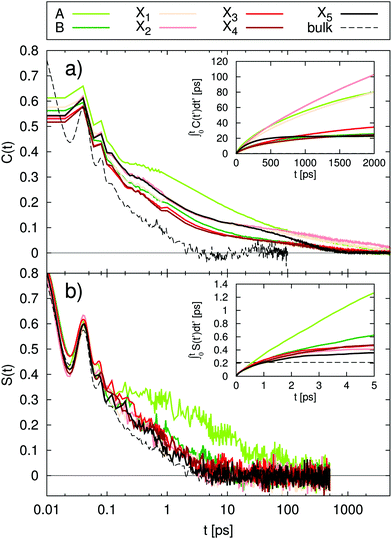
Fig. 3 Absolute TDSS of the seven lysine residues as well as tyrosine and histidine in UBQ obtained from (a) equilibrium and (b) nonequilibrium simulations. Contributions from protein (light red), water (light green) as well as the response of a system with constrained protein motion (dark green). All curves include standard errors as shaded areas 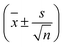 , which are smaller than the line width if not visible. The equilibrium simulations consist of two different sets of trajectories with different length and write-out-frequency (cf.Table 1) and are thus broken at 1 ps. , which are smaller than the line width if not visible. The equilibrium simulations consist of two different sets of trajectories with different length and write-out-frequency (cf.Table 1) and are thus broken at 1 ps. | ||
The comparison of equilibrium simulations (Fig. 3a) and nonequilibrium simulation (Fig. 3b) indicates that LRT is applicable to the TDSS of all lysine residues, as well as tyrosine, i.e., that the correlation functions obtained from equilibrium simulations correspond to the true nonequilibrium responses. This is favorable for three reasons. First, usually one is interested in the equilibrated state of the system. With LRT being applicable, the equilibrium properties can be probed by the nonequilibrium TDSS experiment. Second, from a computational perspective, equilibrium simulations are computationally less demanding than nonequilibrium simulations, so that conducting only equilibrium simulations and relying on LRT potentially reduces the workload for future investigations. Third, equilibrium simulations used in this work (line 1, Table 1) were already employed to calculate NQR, NOE and DRS properties as well as local residence times.10,11,19 The TDSS can thus be directly compared to the respective observables, without errors due to different system parameters.
A different picture arises for histidine, which undergoes very large charge changes (cf.Fig. 1). Here, the TDSS obtained from equilibrium and nonequilibrium simulations differs in magnitude and also to some extent in timescale. We therefore recommend to check for LRT applicability whenever large charge changes occur in a chromophore.
Next, we proceed to the analysis of water and protein contributions to the total TDSS. In Fig. 3, the protein (light-red line) contributes to the total response (dark-red line) at all sites, with the least influence at X3 and X4 but a considerable influence at all other sites. Tyrosine, in particular, being less flexible than lysine and undergoing very small charge changes, shows large protein contributions about half the size of the total TDSS. As can be seen in Fig. 3, not only long but also short timescales are affected, so that not even the subpicosecond response can be attributed to water dynamics alone. It should be noted that we do not find a simple explanation for the influence of the protein on the total TDSS. For example, neither the local RMSF (root mean square fluctuation) around the respective side chain nor its exposure to water are sufficient to estimate the amount of protein contribution. Therefore, it cannot be removed in an experimental context and drastically reduces the potential of the TDSS to report on hydration dynamics.
Besides the direct contribution of protein motion, in some cases, also coupling between protein and water motion has a significant influence on the TDSS, visible in the disagreement between the water contribution with a dynamic (light-green line) or constrained protein (dark-green line). Nearly no coupling occurs for lysines A and X1 and tyrosine (nearly no differences in the light and dark-green lines), medium coupling for lysines B, X3 and X4 as well as histidine (visible, but small differences in the light and dark-green lines) and strong coupling for lysines X2 and X5 (large deviations of the light-green from the dark-green line). Thus, we observe that the amount of coupling can vary strongly between different sites in the same protein. On top of that, coupled water motion compensates the influence of the protein to a varying degree, especially at long timescales. Just like direct protein motion, this coupling effect cannot be removed in an experimental context and thus further hinders the ability of the TDSS to reflect hydration dynamics.
In summary, at all sites, we observe relaxation at long timescales. Decomposition of the computational TDSS, as described above, reveals that these relaxation processes at long timescales solely stem from protein motion, either directly or via coupling to water, which is visible in the disagreement of the water contribution in the constrained system (dark-green line in Fig. 3) and the total TDSS (dark-red line in Fig. 3). These observations, i.e., the attribution of long TDSS relaxation times to protein motion, have been reported in simulation studies of various systems.34–39 Furthermore, the appearance of long relaxation times is in accordance with TDSS experiments. For example, Zewail and coworkers report on decay times of 0.8 ps and 38 ps for the subtilisin Carlsberg protein, measured via an intrinsic tryptophan probe after subtraction of a 2.8 ns long time decay component and normalization at 200 ps, as well as 1.5 ps and a small shift at 40 ps for the same protein, measured via an extrinsic dansyl probe bonded to lysine and arginine after subtraction of a 4.8 ns long time decay and normalization at 200 ps.22 TDSS measurements of the sweet protein Monellin conducted by the same group yielded decay times of 2 ps and 16 ps after subtraction of a long time component of 2.1 ns and normalization at 120 ps.69 In contrast, the TDSS of tryptophan in solution shows a bimodal decay with 0.18 ps and 1.1 ps, which corresponds to a relaxation time in the subpicosecond regime.22 Thus, the experimental TDSS shows retardation factors of one to two orders of magnitude, even with normalization prior to complete equilibration of the excited state.
In order to calculate integral relaxation times in our system, we normalize the total TDSS curves of the lysine residues from equilibrium simulations according to eqn (4), as is done with experimental data. The corresponding functions in Fig. 4a show relaxation up to many nanoseconds, with integral relaxation times τtot of tens to hundreds of picoseconds (corresponding to t = ∞ in the inset of Fig. 4a). As discussed above, experimental decay times of 38 ps and 16 ps where reported for other proteins employing a tryptophan excitation and normalizing (setting the shift to zero) at 120 ps or 200 ps, which reduces the relaxation times.22,69 Bhattacharyya and coworkers even found timescales up to ten nanoseconds for the solvation dynamics of an external chromophore in an aqueous solution of human serum albumin.20 The observed integral relaxation times are thus well within experimental TDSS timescales. The computational retardation factors (RF) in this study with respect to the relaxation time of free lysine in water (τbulk = 0.21 ps) are all above 100 (cf.Table 2), grossly inconsistent with the moderate RF (∼2–3) observed via NQR experiments1–5 and MD simulations6–12 as well as the relevant peak in DRS.18,19
| Site | TDSS | NOE | |
|---|---|---|---|
| RFτtot | RFτcons | RFτres | |
| A | 733 | 46 | 19 |
| B | 123 | 3.4 | 14 |
| X1 | 757 | 1.9 | 1.6 |
| X2 | 1214 | 1.8 | 2.6 |
| X3 | 286 | 2.1 | 1.7 |
| X4 | 119 | 2.2 | 2.3 |
| X5 | 104 | 1.5 | 1.5 |
Fig. 4b shows the normalized TDSS with constrained protein motion. Here, all relaxation processes converge much faster than in the unconstrained case and within the length of nonequilibrium simulations (0.5 ns). Since equilibrium and nonequilibrium simulations are practically identical (cf.Fig. 3), but the short-time behavior is more accurately described by nonequilibrium simulations, they are used for the normalization (cf.eqn (2)). Commensurate with the much faster convergence, the integral relaxation times τcons are also drastically lower than in the unconstrained case (cf. inset of Fig. 4b) and most of them are even of similar magnitude as τbulk. In fact, all lysines Xn show a mere ∼2-fold retardation, and also for lysines A and B retardation is more moderate (cf.Table 2). Overall, these values fit the picture of protein hydration dynamics as reported by a range of experiments and simulations much better than the total TDSS.1–12,18,19 Furthermore, please note that the correlation between τcons and τtot is insignificant (R < 0.25). In other words, the character of local hydration dynamics is obscured by the influence of protein motion and is thus not reflected in the total TDSS.
Finally, for a site-resolved comparison to other observables, we use the residence times τres calculated from the protein–water NOE11 based on the same simulation system as this work (for more details, please refer to the Method section). Starting out with τcons, which is not accessible by experiment but represents the hydration component of TDSS, all lysines Xn agree well with τres, showing a retardation factor of ∼2 for both observables (cf.Table 2). Moreover, the higher retardation at lysines A and B is also visible in both observables. However, while rather high retardation is observed in both sites for τres, it is not reflected as much in τcons for lysine B. This can be explained by the fact that long residence times do not necessarily entail a low in-place mobility of water, where, by its nature, TDSS is only sensitive to the latter, but not to the former. This is supported by the well-known presence of a water molecule in the crystal structure of UBQ in site A,1,62 indicating lower in-place mobility of water as compared to site B.
As expected, the correlation between τtot and τres is non-existent (R < 0.05). This reflects the above analysis, which implies that a comparison of the total TDSS with observables of hydration dynamics is devoid of meaning.
5 Conclusion
We conducted large-scale computer simulations of the TDSS at nine different sites of the protein ubiquitin in water, where both equilibrium and nonequilibrium simulations with either free or constrained protein motion were calculated. We found that LRT is applicable to all sites except histidine, both to the total response and the respective water and protein contributions. Therefore, equilibrium properties are reflected well by the nonequilibrium TDSS for the lysine and tyrosine excitations. For future studies, this means a potential decrease of computational effort, if only equilibrium simulations are employed.It is well-known that the ability of the TDSS to reflect protein hydration dynamics can be hampered by direct and indirect contributions of protein motion. These contributions can be artificially set to zero by constraining protein motion, so that the computed TDSS only reports on water dynamics. Employing this approach, we found a low retardation factor of ∼2 at five out of seven lysine sites (all Xn). This is in good agreement with the protein–water NOE, NQR and the relevant peak in DRS.10,11,19 Sites which are known to have higher retardation (lysine A and B) partly reproduce this behavior in the TDSS calculated from simulations with constrained protein motion. While site B had a retardation factor of 3.4, site A showed a nearly 50-fold retardation. Such a large retardation without protein contribution has not been observed before, but was predicted by Singer and coworkers a decade ago to be possible near protein surface pockets.39 Indeed, site A is in a surface pocket, which, in fact, holds a water molecule in the crystal structure of ubiquitin,1,62 attesting the low in-place mobility of water at site A. This is not the case for site B, where the in-place mobility of water is higher, despite long residence times as observed via NOE.
Since protein motion cannot be suppressed within the experimental TDSS, results obtained from constrained simulations are, in fact, secondary. In the total TDSS, we observed very slow relaxation processes at all sites, specifically stemming either from the protein directly or from coupling of protein motion to water. Identifying these processes with the hydration dynamics, as done in a number of experimental studies,20–26 would result in retardation factors that are all above 100, which, obviously, does not represent the actual character of hydration water, as discussed above.
Summing up, despite the meaningfulness of the computationally accessible hydration component, the ability of the experimental TDSS to report on protein hydration dynamics is severely limited by the direct and indirect contributions of protein motion at all timescales. Even for the least impaired sites, the influence of the protein is overwhelming, and hydration dynamics get overshadowed. As a consequence, we conclude that the TDSS may be an unsuitable tool to examine hydration dynamics, which, in fact, mostly reports on the dynamics of the protein itself. In light of this, we support the view that the term “solvation/hydration dynamics” is inappropriate for the TDSS in a protein context.34 At the same time, the current study eliminates doubts about the picture of a heterogeneous yet overall mobile hydration layer,1–12,18,19 which were raised by a number of previous TDSS studies.20–26
Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. H. is recipient of a DOC Fellowship of the Austrian Academy of Sciences at the Institute of Computational Biological Chemistry. We thankfully acknowledge the provided resources at the Institute of Computational Biological Chemistry at the University of Vienna.References
- V. P. Denisov and B. Halle, J. Mol. Biol., 1995, 245, 682–697 CrossRef CAS PubMed.
- B. Halle, in Hydration Processes in Biology: Theoretical and Experimental Approaches, ed. M. Bellissent-Funel, IOS Press, 1999, vol. 305, p. 233 Search PubMed.
- B. Halle, Philos. Trans. R. Soc., B, 2004, 359, 1207–1224 CrossRef CAS PubMed.
- C. Mattea, J. Qvist and B. Halle, Biophys. J., 2008, 95, 2951–2963 CrossRef CAS PubMed.
- J. Qvist, E. Persson, C. Mattea and B. Halle, Faraday Discuss., 2009, 141, 131–144 RSC.
- R. Abseher, H. Schreiber and O. Steinhauser, Proteins, 1996, 25, 366–378 CrossRef CAS.
- F. Sterpone, M. Ceccarelli and M. Marchi, J. Mol. Biol., 2001, 311, 409–419 CrossRef CAS PubMed.
- R. H. Henchman and J. A. McCammon, Protein Sci., 2002, 11, 2080–2090 CrossRef CAS PubMed.
- A. C. Fogarty and D. Laage, J. Phys. Chem. B, 2014, 118, 7715–7729 CrossRef CAS PubMed.
- D. Braun, M. Schmollngruber and O. Steinhauser, Phys. Chem. Chem. Phys., 2016, 18, 24620 RSC.
- D. Braun, M. Schmollngruber and O. Steinhauser, J. Phys. Chem. Lett., 2017, 8, 3421 CrossRef CAS PubMed.
- F. Persson, P. Söderhjelm and B. Halle, J. Chem. Phys., 2018, 148, 215103 CrossRef PubMed.
- E. H. Grant, B. G. Mitton, G. P. South and R. J. Sheppard, Biochem. J., 1974, 139, 375–380 CrossRef CAS PubMed.
- E. Dachwitz, F. Parak and M. Stockhausen, Ber. Bunsenges. Phys. Chem., 1989, 93, 1454 CrossRef CAS.
- R. Pethig, Annu. Rev. Phys. Chem., 1992, 43, 177–205 CrossRef CAS PubMed.
- G. Löffler, H. Schreiber and O. Steinhauser, J. Mol. Biol., 1997, 270, 520 CrossRef PubMed.
- S. Boresch, P. Höchtl and O. Steinhauser, J. Phys. Chem. B, 2000, 104, 8743 CrossRef CAS.
- A. Oleinikova, P. Sasisanker and H. Weingärtner, J. Phys. Chem. B, 2004, 108, 8467 CrossRef CAS.
- D. Braun, M. Schmollngruber and O. Steinhauser, Phys. Chem. Chem. Phys., 2017, 19, 26980 RSC.
- S. K. Pal, D. Mandal, D. Sukul, S. Sen and K. Bhattacharyya, J. Phys. Chem. B, 2001, 105, 1438–1441 CrossRef CAS.
- S. K. Pal, J. Peon and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 15297 CrossRef CAS PubMed.
- S. K. Pal, J. Peon and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 1763–1768 CrossRef CAS PubMed.
- S. K. Pal, J. Peon, B. Bagchi and A. H. Zewail, J. Phys. Chem. B, 2002, 106, 12376–12395 CrossRef CAS.
- S. M. Bhattacharyya, Z.-G. Wang and A. H. Zewail, J. Phys. Chem. B, 2003, 107, 13218–13228 CrossRef CAS.
- S. K. Pal and A. H. Zewail, Chem. Rev., 2004, 104, 2099–2124 CrossRef CAS PubMed.
- D. Zhong, S. K. Pal and A. H. Zewail, Chem. Phys. Lett., 2011, 503, 1–11 CrossRef CAS.
- M. Maroncelli and G. R. Fleming, J. Chem. Phys., 1987, 86, 6221 CrossRef CAS.
- S. Vajda, R. Jimenez, S. J. Rosenthal, V. Fidler, G. R. Fleming and E. W. Castner, Jr., J. Chem. Soc., Faraday Trans., 1995, 91, 867 RSC.
- R. Jimenez, G. R. Fleming, P. V. Kumar and M. Maroncelli, Nature, 1994, 369, 471 CrossRef CAS.
- E. L. Mertz, V. A. Tikhomirov and L. I. Krishtalik, J. Phys. Chem. A, 1997, 101, 3433 CrossRef CAS.
- M. Maroncelli, J. Mol. Liq., 1993, 57, 1 CrossRef CAS.
- M. Maroncelli and G. R. Fleming, J. Chem. Phys., 1988, 89, 5044 CrossRef CAS.
- D. Laage, T. Elsaesser and J. T. Hynes, Chem. Rev., 2017, 117, 10694–10725 CrossRef CAS PubMed.
- L. Nilsson and B. Halle, PNAS, 2005, 102, 13867 CrossRef CAS PubMed.
- A. A. Golosov and M. Karplus, J. Phys. Chem. B, 2007, 111, 1482 CrossRef CAS PubMed.
- B. Halle and L. Nilsson, J. Phys. Chem. B, 2009, 113, 8210–8213 CrossRef CAS PubMed.
- S. Mondal, S. Mukherjee and B. Bagchi, Chem. Phys. Lett., 2017, 683, 29–37 CrossRef CAS.
- T. Li, A. A. Hassanali, Y.-T. Kao, D. Zhong and S. J. Singer, J. Am. Chem. Soc., 2007, 129, 3376 CrossRef CAS PubMed.
- T. Li, A. A. Hassanali and S. J. Singer, J. Phys. Chem. B, 2008, 112, 16121 CrossRef CAS PubMed.
- L. Zhang, Y. Yang, Y.-T. Kao, L. Wang and D. Zhong, J. Am. Chem. Soc., 2009, 131, 10677–10691 CrossRef CAS PubMed.
- D. M. Leitner, M. Havenith and M. Gruebele, Int. Rev. Phys. Chem., 2006, 25, 553–582 Search PubMed.
- P. V. Kumar and M. Maroncelli, J. Chem. Phys., 1995, 103, 3038–3060 CrossRef CAS.
- M. Schmollngruber, D. Braun and O. Steinhauser, Phys. Chem. Chem. Phys., 2016, 18, 30954 RSC.
- E. Heid and C. Schröder, Phys. Chem. Chem. Phys., 2018, 20, 5246 RSC.
- R. B. Best, X. Zhu, J. Shim, P. E. M. Lopes, J. Mittal, M. Feig and A. D. MacKerell, Jr., J. Chem. Theory Comput., 2012, 8, 3257 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. R. Grigers and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269 CrossRef CAS.
- K. El Hage, F. Hédin, P. K. Gupta, M. Meuwly and M. Karplus, eLife, 2018, 7, e35560 CrossRef PubMed.
- M. Sega and C. Schröder, J. Phys. Chem. A, 2015, 119, 1539 CrossRef CAS PubMed.
- D. Braun, S. Boresch and O. Steinhauser, J. Chem. Phys., 2014, 140, 064107 CrossRef PubMed.
- M. Tarek and D. J. Tobias, Biophys. J., 2000, 79, 3244–3257 CrossRef CAS PubMed.
- M. Marchi, F. Sterpone and M. Ceccarelli, J. Am. Chem. Soc., 2002, 124, 6787–6791 CrossRef CAS PubMed.
- G. Schirò, Y. Fichou, F.-X. Gallat, K. Wood, F. Gabel, M. Moulin, M. Härtlein, M. Heyden, J.-P. Colletier and A. Orecchini, et al. , Nat. Commun., 2015, 6, 6490 CrossRef PubMed.
- A.-P. Hynninen and M. F. Crowley, J. Comput. Chem., 2014, 35, 406 CrossRef CAS PubMed.
- B. R. Brooks, C. L. Brooks III, A. D. MacKerell Jr., L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- R. W. Hockney, Methods Comput. Phys., 1970, 9, 135–211 Search PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 102, 8577 CrossRef.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327 CrossRef CAS.
- L. Martínez, R. Andrade, G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- S. Vijay-Kumar, C. E. Bugg and W. J. Cook, J. Mol. Biol., 1987, 194, 531–544 CrossRef CAS PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Wallingford CT, 2009 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- E. Heid, S. Harringer and C. Schröder, J. Chem. Phys., 2016, 145, 164506 CrossRef PubMed.
- E. Heid and C. Schröder, J. Phys. Chem. B, 2017, 121, 9639–9646 CrossRef CAS PubMed.
- J. Tian and A. E. Garca, J. Chem. Phys., 2011, 134, 06B603 CrossRef PubMed.
- J. Peon, S. K. Pal and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 10964–10969 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2019 |