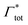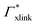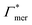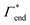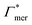Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cross-linker effect on solute adsorption in swollen thermoresponsive polymer networks
Sebastian
Milster
 abc,
Richard
Chudoba
abc,
Richard
Chudoba
 abc,
Matej
Kanduč
abc,
Matej
Kanduč
 ad and
Joachim
Dzubiella
ad and
Joachim
Dzubiella
 *ac
*ac
aResearch Group for Simulations of Energy Materials, Helmholtz-Zentrum Berlin für Materialien und Energie, Hahn-Meitner-Platz 1, D-14109 Berlin, Germany. E-mail: joachim.dzubiella@physik.uni-freiburg.de
bInstitut für Physik, Humboldt-Universität zu Berlin, Newtonstr. 15, D-12489 Berlin, Germany
cApplied Theoretical Physics – Computational Physics, Physikalisches Institut, Albert-Ludwigs-Universität Freiburg, Hermann-Herder Str. 3, D-79104 Freiburg, Germany
dJožef Stefan Institute, Jamova 39, SI-1000, Ljubljana, Slovenia
First published on 7th March 2019
Abstract
The selective solute partitioning within a polymeric network is of key importance to applications in which controlled release or uptake of solutes in a responsive hydrogel is required. In this work we investigate the impact of cross-links on solute adsorption in a swollen polymer network by means of all-atom, explicit-water molecular dynamics simulations. We focus on a representative network subunit consisting of poly(N-isopropylacrylamide) (PNIPAM) and N,N′-methylenebisacrylamide (BIS/MBA) cross-linker types. Our studied system consists of one BIS-linker with four atactic PNIPAM chains attached in a tetrahedral geometry. The adsorption of several representative solutes of different polarity in the low concentration limit at the linker region is examined. We subdivide the solute adsorption regions and distinguish between contributions stemming from polymer chains and cross-link parts. In comparison to a single polymer chain, we observe that the adsorption of the solutes to the cross-link region can significantly differ, with details depending on the specific compounds’ size and polarity. In particular, for solutes that have already a relatively large affinity to PNIPAM chains the dense cross-link region (where many-body attractions are at play) amplifies the local adsorption by an order of magnitude. We also find that the cross-link region can serve as a seed for the aggregation of mutually attractive solutes at higher solute concentrations. Utilizing the microscopic adsorption coefficients in a mean-field model of an idealized macroscopic polymer network, we extrapolate these results to the global solute partitioning in a swollen hydrogel and predict that these adsorption features may lead to non-monotonic partition ratios as a function of the cross-link density.
1 Introduction
Responsive polymers have increasingly gained attention in many research fields due to their ability to reversibly adapt to external stimuli such as temperature, osmotic pressure, or pH. Various types and shapes at different length scales have been designed, providing various possibilities for applications,1,2 such as solute uptake, transport3 and release,4,5 sensors,6 intelligent coatings, switchable catalysis,7,8etc. To structurally stabilize and fine-tune properties and function, polymer architectures are often equipped with chemical cross-linkers covalently interconnecting the chains,9 which are then referred to as hydrogels. Typical responsive hydrogels in most studies barely exceed a molar cross-linker density of twenty percent, since greater values increase the rigidity of the gel and reduce the swelling properties due to the denser polymer network structure.8,10In the zoo of constituents, thermoresponsive hydrogels based on poly(N-isopropylacrylamide) (PNIPAM) are among the most intensively investigated systems, since their volume phase transition at about room temperature as well as a high water content promise good biocompatibility5,11 and make them convenient to handle. Pure PNIPAM was found to have the lower critical solution temperature (LCST) at roughly 304 K as reported by Heskins and Guilett in 1968.12 A frequently utilized cross-linker for PNIPAM gels, used in radical polymerization, is N,N′-methylenebisacrylamide, often abbreviated as BIS or MBA. BIS has chemical similarity to PNIPAM (compare Fig. 1), is non-degradable, has a very high reactivity, and retains PNIPAM's LCST.13–17
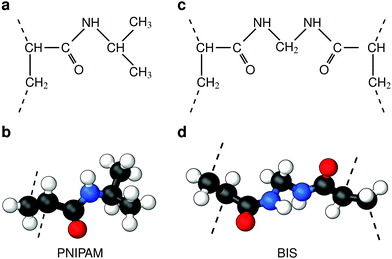 | ||
| Fig. 1 Chemical structures (top) and corresponding ball-and-stick representations (bottom) of poly(N-isopropylacrylamide) [PNIPAM] (panels a and b), and the cross-linker N,N′-methylenebisacrylamide [BIS] (panels c and d). Dashed lines represent possible bonds to neighboring PNIPAM monomers or BIS. Associated carbon atoms are referred to as the polymer backbone. PNIPAM's amide group and isopropyl group form side chains. The amide groups and BIS’ central methylene bridge are hydrophilic, potentially forming hydrogen bonds45 with the surrounding. The backbone and isopropyl group have a hydrophobic character. | ||
Besides these morphological properties, the degree of cross-linking influences solute uptake and partitioning. The partition ratio is the ratio of the solute concentrations inside and outside the gel and is therefore a crucial parameter controlling device functionality especially for drug delivery or catalytic systems. For the latter, for instance, metal nanoparticles inside hydrogels catalyze reactions and the effective reaction rates depend crucially on the concentration of the reactants in the permeable polymer matrix.7,8,18,19 The partition ratio may be affected by generic as well as specific cross-linker effects. The cross-linker density first of all simply changes the packing fraction and with that the overall steric exclusion by the polymer mesh.11 Furthermore, it has become clear that more complex, e.g., local attractive and/or electrostatic interactions can lead to complex and even cooperative effects in the partitioning.20–23 In particular, a ‘vertex trapping’ effect due to many-body attractions in the dense cross-link region has been reported in generic coarse-grained simulations of polymer networks.24–28 More specific chemical effects should also play a role, as indicated by all-atom molecular dynamics (MD) computer simulations of bare PNIPAM chains,29–31 peptide-like chains,32–34 these in combination with solutes with various polarity35–40 as well as by simulations revealing the influence of cross-links to polymer networks solvation and structural properties.41–44
The aim of this work is to investigate the effects of cross-linking on solute adsorption in swollen hydrogels made up of PNIPAM and BIS (below the volume phase transition temperature (VPTT)) by utilizing all-atom, explicit water MD simulations of a minimal polymer network setup. In order to do this, we consider one BIS cross-linker with four atactic PNIPAM chains restrained in a tetrahedral geometry. In our analysis, we subdivide the solute adsorption regions and systematically distinguish between contributions stemming from polymer chains and cross-linker parts. We probe solutes of various polarity, representing typical chemical compounds, in the highly diluted regime. We finally demonstrate in a simple model, how these contributions affect the global solute partitioning in large hydrogels as accessible by experiments.
2 Methods
2.1 Hydrogel building blocks: PNIPAM and BIS
Constructing covalently cross-linked polymeric networks for our computer simulations requires two types of building blocks: chain monomers and the cross-linker (see Fig. 1). The former provides two binding sites and builds up the chains. The latter has four binding sites and thus interconnects four chains. We have chosen poly(N-isopropylacrylamide) (PNIPAM) and N,N′-methylenebisacrylamide (BIS) for the chains and the cross-linker unit respectively (see Fig. 1).We employ the OPLS-QM2 force field recently developed by Palivec et al.31 for the PNIPAM monomers. Compared to the standard OPLS-AA46 parameters, this force field features a reparametrization of the partial charges retrieved from ab initio calculations and further manual fine-tuning to reproduce the experimental LCST of PNIPAM. Due to the chemical similarity of BIS and PNIPAM, we adopt the very same partial charges for the cross-linker. These were confirmed by our own quantum mechanical calculations using the Gaussian 09 software.47 More details on the force field parameters are provided in Appendix A.
2.2 Setup
The actual polymerization procedure in experiments is subjected to randomness leading to different possible network topologies. Looking at the very local structure inside a hydrogel, the following sources for inhomogeneities are possible: dangling chains, entangled chains, and loops.48 This work, however, focuses on generic subunits of a defect-free network architecture of a swollen hydrogel,22,49 namely the cross-linker and its four adjacent chains. Our setup consists of one BIS-linker connected with four PNIPAM chains (Fig. 2a), each composed of 12 monomers, i.e., 48 monomers in total. The terminal backbone carbon atoms of each chain are position-restrained in order to sustain a tetrahedral structure. It further facilitates a clear analysis and the results can be to some extent generalized, which will be discussed later in this work.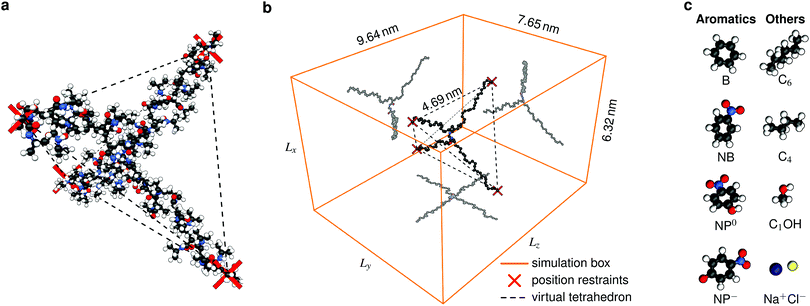 | ||
Fig. 2 Simulation snapshots of the studied polymeric molecule, consisting of one BIS-linker and four PNIPAM chains, at T = 290 K and relative chain extension λ = 0.83 in (a) all-atom ball-and-stick representation and (b) showing only backbone and heavy BIS atoms inside the simulations box ( ) and in addition as 2D projections. Terminal backbone carbons are position-restrained (marked as ) and in addition as 2D projections. Terminal backbone carbons are position-restrained (marked as  ) in the corners of a virtual tetrahedron (- - -), which has an edge length of 4.69 nm and a vertex-to-centroid distance of L = 2.87 nm. For the sake of clarity, water molecules are not shown. (c) Probe solutes. Atoms are color-coded by element, i.e., black carbon, red oxygen, blue nitrogen, and white hydrogen atoms. See Table 1 for the full simulation specifications. ) in the corners of a virtual tetrahedron (- - -), which has an edge length of 4.69 nm and a vertex-to-centroid distance of L = 2.87 nm. For the sake of clarity, water molecules are not shown. (c) Probe solutes. Atoms are color-coded by element, i.e., black carbon, red oxygen, blue nitrogen, and white hydrogen atoms. See Table 1 for the full simulation specifications. | ||
The corners of the tetrahedron, generated by the position restraints, are L = 2.87 nm distant to its centroid and the edge length accounts to 4.69 nm (Fig. 2b). We have chosen this size to ensure a relative chain stretch λ between 0.75 and 0.85, which is expected in swollen hydrogels.38 The relative chain stretch λ is defined as the ratio of the mean end-to-end distance and the contour length
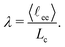 | (1) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ee〉 = 2.65 nm, where the brackets 〈⋯〉 denote ensemble average. The distance
ee〉 = 2.65 nm, where the brackets 〈⋯〉 denote ensemble average. The distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ee was measured from the cross-linker contact backbone atom to the chain's terminal backbone atoms during the NpT-simulation. The contour length per monomer ΔLc in an atactic PNIPAM chain is approximately 0.265 nm, and when multiplied by 12, one obtains the contour length of a single chain. Eventually, the average relative stretch in all simulations is λ = 0.83.
ee was measured from the cross-linker contact backbone atom to the chain's terminal backbone atoms during the NpT-simulation. The contour length per monomer ΔLc in an atactic PNIPAM chain is approximately 0.265 nm, and when multiplied by 12, one obtains the contour length of a single chain. Eventually, the average relative stretch in all simulations is λ = 0.83.
Generating such a setup starts by placing the BIS-linker in the center of the box, which is the centroid of the virtual tetrahedron. At each backbone binding site, indicated by dashed lines in Fig. 1, PNIPAM monomers with random tacticity are attached in a head-to-tail manner with the backbone axis pointing towards the desired coordinates of the position restraint. PNIPAM's backbone bonds are squeezed to match the size of the tetrahedron and were allowed to relax during the first steps (energy minimization and equilibration) of the simulation.
The edge lengths of the rectangular simulation box are chosen large enough (6.32 nm × 7.65 nm × 9.64 nm on average) in order to ensure that the position-restrained backbone terminals of different periodic images are separated by at least 3 nm in x- and y-, and 5 nm in z-direction (Fig. 2b). Thus, we avoid interactions between chain ends across the box boundaries and can locate a (water/solute) bulk phase in peripheral box regions.
The solutes are subsequently inserted at random positions in the simulation box, which is finally filled with more than 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 SPC/E50 water molecules. Details are listed in Table 1.
000 SPC/E50 water molecules. Details are listed in Table 1.
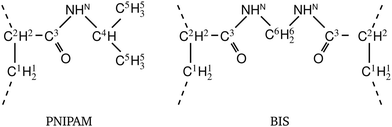
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules, one solute (30 molecules and three pairs in the case of C1OH and Na+/Cl−, respectively) and analyzed within a simulation time of tsim. Nitro-aromatics were further tested with Nsolute = 20 molecules and we added Na+ counterions for charged NP−. Note the differences in the simulation time, e.g., the simulations with Nsolute = 1 were carried out approximately ten times as long as with 20 individuals in order to reach sufficient sampling quality. Adsorption coefficients Γ* = Γ/ρ0 are split into contributions as described by eqn (5) and (7) and are normalized by solute bulk concentration ρ0 (details are provided in the main text). For the NP−/Na+ pairs, only results for NP− are presented. The ions Na+ and Cl− were simulated together but analyzed separately. Both types yield very similar results. The most relevant results, the adsorption coefficients
000 water molecules, one solute (30 molecules and three pairs in the case of C1OH and Na+/Cl−, respectively) and analyzed within a simulation time of tsim. Nitro-aromatics were further tested with Nsolute = 20 molecules and we added Na+ counterions for charged NP−. Note the differences in the simulation time, e.g., the simulations with Nsolute = 1 were carried out approximately ten times as long as with 20 individuals in order to reach sufficient sampling quality. Adsorption coefficients Γ* = Γ/ρ0 are split into contributions as described by eqn (5) and (7) and are normalized by solute bulk concentration ρ0 (details are provided in the main text). For the NP−/Na+ pairs, only results for NP− are presented. The ions Na+ and Cl− were simulated together but analyzed separately. Both types yield very similar results. The most relevant results, the adsorption coefficients 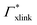 and
and 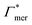 to the cross-linkers and monomers, respectively, are visualized in Fig. 5
to the cross-linkers and monomers, respectively, are visualized in Fig. 5
| Simulation specifications | Results | |||||||
|---|---|---|---|---|---|---|---|---|
| Aromatics | N solute | t sim [μs] | ρ 0 [mM] | |||||
| B | Benzene | 1 | 12.6 | 3.2 ± 0.1 | 54 ± 3 | −2 ± 2 | 1.0 ± 0.1 | 7 ± 3 |
| NB | Nitrobenzene | 1 | 11.9 | 2.8 ± 0.1 | 124 ± 6 | 5 ± 2 | 2.3 ± 0.2 | 10 ± 6 |
| NB | Nitrobenzene | 20 | 1.1 | 28.0 ± 2.0 | 720 ± 220 | 70 ± 20 | 16.0 ± 2.0 | −140 ± 220 |
| NP0 | 4-Nitrophenol | 1 | 12.3 | 2.8 ± 0.1 | 121 ± 17 | 21 ± 3 | 2.1 ± 0.2 | −2 ± 7 |
| NP0 | 4-Nitrophenol | 20 | 1.2 | 42.1 ± 2.0 | 280 ± 60 | 100 ± 20 | 4.6 ± 0.5 | −40 ± 60 |
| NP− | 4-Nitrophenolate | 1 | 8.4 | 2.3 ± 0.1 | 270 ± 20 | 43 ± 8 | 4.5 ± 0.4 | 10 ± 20 |
| NP−/Na+ | 4-Nitrophenolate + sodium | 20 pairs | 1.1 | 63.0 ± 1.0 | 67 ± 3 | 14 ± 2 | 1.3 ± 0.1 | −11 ± 3 |
| Others | ||||||||
| C6 | Hexane | 1 | 11.2 | 3.3 ± 0.1 | 33 ± 5 | −2 ± 4 | 0.8 ± 0.1 | −1 ± 5 |
| C4 | Butane | 1 | 7.4 | 3.4 ± 0.1 | 25 ± 2 | −1 ± 2 | 0.44 ± 0.05 | 5 ± 2 |
| C1OH | Methanol | 30 | 3.5 | 107.3 ± 1.0 | −2 ± 1 | 0 ± 4 | −0.05 ± 0.05 | 1 ± 1 |
| Na+/Cl− | Sodium chloride | 3 pairs | 8.4 | 11.5 ± 0.1 | −33 ± 2 | 5 ± 1 | −0.65 ± 0.02 | −6 ± 2 |
2.3 Probe molecules
We analyze the adsorption properties of several types of molecules covering different sizes and polarity. We focus on some aromatic compounds due to their application as model reactants in catalytic experiments18,51 and since aromatic rings are found in numerous drugs,52–54e.g., common painkillers. Precisely, these compounds are benzene (B), nitrobenzene (NB), (uncharged) 4-nitrophenol (NP0), and (charged) deprotonated 4-nitrophenolate (NP−).We further probe two alkanes, namely hexane (C6) and butane (C4), sodium chloride (Na+/Cl−), and methanol (C1OH). All compounds are visualized in Fig. 2c. If not stated otherwise, we insert one probe molecule into the system to analyze the infinite dilution limit. To estimate finite concentration effects of aromatic compounds we perform simulations with 20 solutes. List of solutes and the simulation setups are listed in the summary Table 1. The standard OPLS-AA46 force field was utilized except for the charged nitrophenolate NP−, for which the excess charge was distributed among the molecule due to the mesomeric effect,38 leading to higher polarity of the nitro group.
2.4 Simulation details
We employed all-atom, explicit-water molecular dynamics (MD) simulations to study the polymer–solute interactions. The simulations were performed using the Gromacs 5.1 software55–57 utilizing force fields mentioned above.All covalent bonds of hydrogens were constrained with the LINCS58 algorithm. The cut-off distance for Lennard-Jones and short-range electrostatic interactions was set to 1.0 nm while long range electrostatics was accounted for by the Particle Mesh Ewald (PME) method with cubic interpolation and a grid spacing of 0.12 nm.59
Periodic boundary conditions in all three directions were used and the simulations were carried out under constant temperature and pressure, which were controlled by the velocity-rescale thermostat (at T = 290 K, τT = 0.1 ps) and the Berendsen barostat (at p = 1 bar, τp = 1 ps), respectively.60,61
After the initial energy minimization (steepest descent), the system was equilibrated in the NVT ensemble for 2 ns and in the NpT ensemble for another 10 ns. The integration step of the leap-frog integrator was set to 2 fs and data were collected every 10 ps. The total simulation time tsim per solute is summarized in Table 1.
3 Analysis and discussion
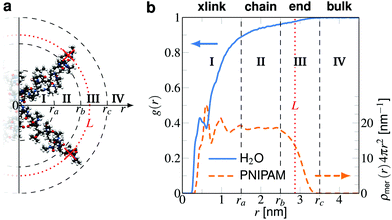
From the trajectories we calculate the center of mass (COM) positions of the cross-linker and the structure of the chain monomers, the solute(s) and water molecules around it. The distances r between the COM of the cross-linker and the COM of molecules is used to obtain the normalized radial density distributions g(r) = ρ(r)/ρ0 for BIS–water and BIS–solute. The bulk phase concentration ρ0 (see Fig. 3 and Table 1) is obtained from simulations by calculating the number density along the z-axis and averaged in the region 1.5 nm distant to the restrained polymer atoms.For the 20 NP−/Na+ pairs, we only analyzed the nitrophenolate trajectories. In the case of the Na+/Cl− simulation, each ion type was analyzed individually. The results for sodium and chloride ions are very similar and yield the same results within the range of our precision and thus are presented for either type in Table 1.
Further, the PNIPAM monomer density distribution ρmer(r) is retrieved, which helps us to distinguish between different polymer adsorption domains (Fig. 3). The solutes' distributions are the basis for calculating the solute–polymer adsorption in our setup as detailed below. We demonstrate how the splitting of the adsorption into the chain and the cross-linker contributions is achieved and how this can be used to estimate partition ratios of an entire hydrogel.
3.1 Polymer distribution
The position restraints restrict the movement of the PNIPAM monomers and the cross-linker. The COM of the cross-linker in this setup fluctuates around the simulation box center with a mean displacement of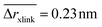 . The PNIPAM distribution for each monomer has been evaluated with respect to the COM of BIS. The closest monomers to the cross-linker distribute in a bimodal fashion, stemming from multiple possible side-chain–side-chain and cross-linker–side-chain interactions. This effect averages out for chain monomers further distant from the linker resulting in Gaussian distributions. The distances of two adjacent monomers is roughly 0.25 nm. The distribution of all monomers together (i.e., averaged over a spherical shell ∝ρmer(r)4πr2dr including all chains) shows a plateau region between 1.5 and 2.5 nm, see Fig. 3b. In this range we find an almost constant monomer number, which can be used to evaluate the intrinsic adsorption per chain monomer. We thus define the number of monomers in an interval [r1,r2] as
. The PNIPAM distribution for each monomer has been evaluated with respect to the COM of BIS. The closest monomers to the cross-linker distribute in a bimodal fashion, stemming from multiple possible side-chain–side-chain and cross-linker–side-chain interactions. This effect averages out for chain monomers further distant from the linker resulting in Gaussian distributions. The distances of two adjacent monomers is roughly 0.25 nm. The distribution of all monomers together (i.e., averaged over a spherical shell ∝ρmer(r)4πr2dr including all chains) shows a plateau region between 1.5 and 2.5 nm, see Fig. 3b. In this range we find an almost constant monomer number, which can be used to evaluate the intrinsic adsorption per chain monomer. We thus define the number of monomers in an interval [r1,r2] as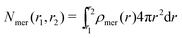 | (2) |
3.2 Solute adsorption in high dilution
The adsorption of solute inside the hydrogel of volume Vgel (including the containing water) can be calculated from the radial distribution as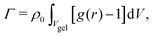 | (3) |
Transferring this concept to our setup (Fig. 2), for which radial density profiles g(r) of the solutes (Fig. 4a and b) are measured from the COM of BIS, we define the partial adsorption Γ(r1,r2) counting excess solutes in the interval [r1,r2], reading
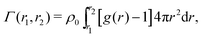 | (4) |
| Γtot = Γxlink + Γchain + Γend. | (5) |
The equilibrium bulk concentration ρ0 depends on the simulation box size and the binding affinity. It is convenient to define an infinite-dilution solute-specific adsorption coefficient that does not depend on concentration via
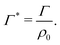 | (6) |
| Γchain = NmerΓmer | (7) |
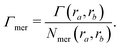 | (8) |
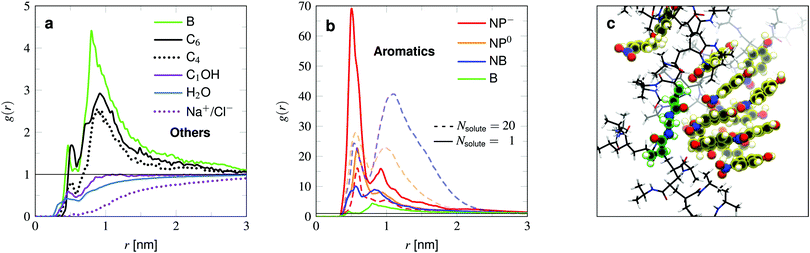
We now compare the adsorption of the solutes to the PNIPAM chain, listed in Table 1 and visualized in Fig. 5. The results can further be compared with the density profiles (Fig. 4a and b). We start with the examination of the rather weakly adsorbing species (Fig. 4a). Methanol is the smallest probe molecule tested and is highly soluble in water and shows a rather low binding propensity. It is in fact slightly attracted to the polymer, but this cannot compensate the volume exclusion effect of PNIPAM and thus its adsorption coefficient is of negative value. Methanol's preferential adsorption has already been reported in experiments64 and other simulations,65–68 studying primarily the cononsolvency of PNIPAM in water–methanol mixtures.
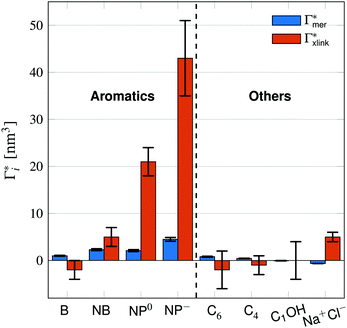 | ||
Fig. 5 Adsorption coefficients (Γ* = Γ/ρ0) quantifying the binding affinities of different solutes to one PNIPAM monomer  and the cross-linker and the cross-linker  in the infinite dilution regime, as summarized in Table 1. The adsorption to the monomers increases with size, e.g., compare C4 → C6. The aromatic molecules show the highest adsorption, which is magnified by increasing polarity B → NB → NP0 → NP−, coinciding with a cross-linker-enhanced binding affinity. in the infinite dilution regime, as summarized in Table 1. The adsorption to the monomers increases with size, e.g., compare C4 → C6. The aromatic molecules show the highest adsorption, which is magnified by increasing polarity B → NB → NP0 → NP−, coinciding with a cross-linker-enhanced binding affinity. | ||
Sodium and chloride have the lowest binding affinity to the hydrogel, which has already been shown in previous simulations of isolated chains.35,38 As expected, simple well-hydrated ions are repelled from low dielectric (less polar) regions.
The two probed alkanes, butane and hexane, have very similar profiles. The bigger hexane shows slightly higher adsorption than butane owing to the larger surface area, which facilitates hydrophobic interactions with apolar groups of the polymer chains. The very same argument does not hold when comparing with benzene. Benzene has about the same size as the alkanes, but shows higher binding affinity than the larger hexane. On the molecular level, the adsorption mechanism looks similar. Benzene and hexane tend to preferentially make contact with hydrophobic parts of the polymer.
Comparing the aromatic compounds, which are roughly of equal size, we find the adsorption generally increases with the polarity of their substituents. The order according to their polarity, starting with the apolar benzene, is B → NB → NP0 → NP−, cf.Fig. 4b. All of them own a hydrophobic aromatic ring, interacting with the hydrogel described as in the benzene case. With one polar substituent for benzene, namely the nitrobenzene, the adsorption is more than doubled. This stems from additional hydrogen bonding45 between the nitro-oxygens and the polymer's amide hydrogens. The very same interaction mechanism applies to NP0 and NP−. The extra hydroxy tail in the case of nitrophenol (NP0) does not lead to a significant change of the adsorption to PNIPAM. On the one hand, the OH group can interact with the polymer's amide group and on the other hand, increases the water solubility. These two effects seem to compensate for NP0 adsorption to the chains, such that the adsorption is similar to the one for NB.
The deprotonated and hence charged NP− is the best adsorbing compound tested. The deprotonation leads to a redistribution of the electronic density, increasing the polarity of the whole molecule. The higher charging of the nitro-oxygens as well as the O− tail stabilize the contacts with PNIPAM's amide hydrogens, resulting in a roughly two times higher adsorption coefficient compared to NB and NP0.
| Γxlink = Γ(0,ra) − ΓmerNmer(0,ra). | (9) |
Note that in comparison to PNIPAM monomers, BIS has two amide groups and no isopropyl groups, thus creating a more hydrophilic environment than the chains. The apolar compounds, B, C4, and C6 show a slightly negative binding affinity in the cross-link region. In contrast, see again Table 1 and Fig. 5, the solute adsorption 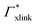 increases with polarity, where nitro-aromatic solutes are especially attracted. Nitrobenzene shows a more than doubled adsorption to the cross-link region when compared to bare chain monomers. The NP0 and NP− adsorption per cross-linker is even tenfold higher. The binding mechanism is similar to the single chain adsorption. The numerous amide hydrogen combinations make it very probable for the nitro-oxygens to find binding partners.
increases with polarity, where nitro-aromatic solutes are especially attracted. Nitrobenzene shows a more than doubled adsorption to the cross-link region when compared to bare chain monomers. The NP0 and NP− adsorption per cross-linker is even tenfold higher. The binding mechanism is similar to the single chain adsorption. The numerous amide hydrogen combinations make it very probable for the nitro-oxygens to find binding partners.
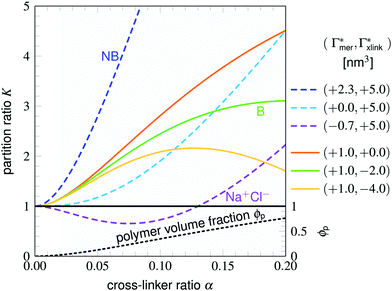
As already stated for the chain adsorption, NP− has the most polar nitro group resulting in the strongest adsorption coefficients in this study. Examining the simulation trajectories, we repeatedly found NP− in the location shown in Fig. 6. One or both of the nitro-oxygens couple (forming hydrogen bonds) with two to three hydrogens from the amide groups: one from BIS and one or two from the PNIPAM monomers. Additionally, the hydrophobic isopropyl groups or the backbone of PNIPAM can contact, almost embed, the aromatic ring, enhancing the stability of such an adsorbed state. The same mechanism has been observed for NB and NP0, but the higher partial charges of NP− promote the binding.
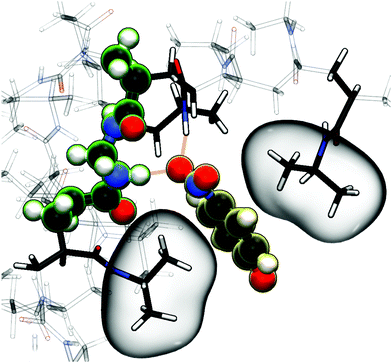 | ||
| Fig. 6 Simulation snapshot of NP− (illuminated yellow) benefiting from several possible interaction sites in the BIS-linker (illuminated green) proximity, serving as an illustrative explanation for the strong adsorption amplification due to the cross-linker (see Table 1 and Fig. 5). Nitro-oxygens of NP− can form hydrogen bonds (dashed orange lines depict potential hydrogen bond formation in this configuration) with numerous amide hydrogens, whereas the non-polar aromatic ring is surrounded by hydrophobic environment, i.e., isopropyl groups, (highlighted by bubbles) of the flexible PNIPAM side-chains. An aromatic ring–backbone contact has been observed but less frequently than the presented scenario. NP− can stay in such a conformation (with interchanging binding sites) for several tens of nanoseconds. | ||
The least polar compound among them, nitrobenzene, shows the most substantial amplification of binding to the cross-linker at higher concentrations. NB is known to form NB–NB pairs and stacks of the aromatic rings,69 resulting thus in positive cooperativity for local adsorption (refer to earlier work38 for further explanation). Note that the bulk concentration of ρ0 = (28 ± 2) mM might have exceeded the solubility of nitrobenzene in water. At 298 K the experimental value is 16 mM, but computer simulations can overestimate the solubility (115 mM).70
NP0 also performs stacking (Fig. 4c), but due to its additional OH-tail, it has a higher water solubility and is thus less probable to aggregate. In stark contrast, the NP− adsorption to the whole network unit drastically drops at higher concentrations due to their electrostatic repulsion. This is an example of strong negative cooperativity of adsorption at higher concentrations. Note that a real hydrogel may change in size (in particular close to its VPTT) because of the solute–polymer interactions and that solutes may occupy a non-negligible volume, which in return limit the solute adsorption.20,35,71,72
3.3 Partitioning in a hydrogel
The adsorption coefficients retrieved in this work can be used to estimate the resulting solute partition ratios in swollen PNIPAM–BIS hydrogels, which will be compared with experimental data in this section. To this end, we extrapolate our results using an idealized, mean-field model of a large network.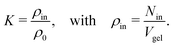 | (10) |
The number of particles Nin inside the gel can be assessed using the total solute adsorption as
| Nin = Γtot + ρ0Vgel. | (11) |
| Γtot = NmerΓmer + NxlinkΓxlink, | (12) |
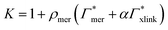 | (13) |
Considering now a defect-free diamond lattice network architecture22,49 of the hydrogel, we can deduce the functional form of the monomer concentration vs. the cross-linker ratio, i.e., ρmer → ρmer(α), see Appendix B. For different adsorption coefficient pairs (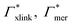 ) and in dependence on the cross-linker ratio, K is visualized in Fig. 7. We find that K and α can have a non-linear relation and even a non-monotonic behavior. The reason is that higher cross-linker ratios directly enhance the influence of
) and in dependence on the cross-linker ratio, K is visualized in Fig. 7. We find that K and α can have a non-linear relation and even a non-monotonic behavior. The reason is that higher cross-linker ratios directly enhance the influence of 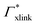 , and additionally, as already discussed, increase the PNIPAM concentration ρmer(α), promoting the influence of
, and additionally, as already discussed, increase the PNIPAM concentration ρmer(α), promoting the influence of 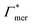 . If now
. If now 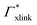 and
and 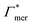 have even different signs, i.e., a solute, for example, is preferentially desorbed from the polymer but adsorbed by cross-linker then naturally non-monotonic behavior must occur.
have even different signs, i.e., a solute, for example, is preferentially desorbed from the polymer but adsorbed by cross-linker then naturally non-monotonic behavior must occur.
 | ||
| Fig. 8 Chemical structures of PNIPAM and BIS. The superscript indices differentiate atoms regarding their partial charges, shown in Table 2. | ||
Typical values for cross-linker ratios in experiments range from roughly 0.02 to 0.2. In our model (see Appendix B), this corresponds to volume fractions ranging from approximately 0.03 to 0.75 with an almost linear relation to α in this interval. Thus the plotted region in Fig. 7 is quite reasonable for demonstrating the non-linear and non-monotonous α-dependencies of the partition ratio. In particular, with positive adsorption coefficients, like all nitro-aromatics have, we find that the partition ratio monotonically increases with larger cross-linker ratios, exemplified by nitrobenzene in Fig. 7.
Selective solute–cross-linker binding affinities are not solely responsible for an increasing partition ratio when increasing the cross-link ratio. As an illustration, we show scenarios of hypothetical solutes that have either zero adsorption to cross-linkers or zero adsorption to the chains. For small values of α, the coefficient 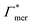 has greater impact on partitioning increase than
has greater impact on partitioning increase than 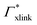 . In the case of benzene (similarly hexane and butane), where we find a positive chain adsorption, but repulsion from the cross-linker, the partitioning reaches a plateau at α = 0.2. Weaker chain adsorption, or stronger cross-linker repulsion can lead to a maximum in the plotted range, which is exemplified by the hypothetical solute with
. In the case of benzene (similarly hexane and butane), where we find a positive chain adsorption, but repulsion from the cross-linker, the partitioning reaches a plateau at α = 0.2. Weaker chain adsorption, or stronger cross-linker repulsion can lead to a maximum in the plotted range, which is exemplified by the hypothetical solute with 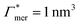 and
and 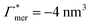 . The very opposite case, i.e., cross-linker affinity in combination with chain avoidance, as we find for the tested ion pair Na+/Cl−, exhibits a minimum.
. The very opposite case, i.e., cross-linker affinity in combination with chain avoidance, as we find for the tested ion pair Na+/Cl−, exhibits a minimum.
Summing up, the adsorption coefficients 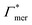 and
and 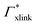 determine the gradient and concavity of the solute partitioning in dependence on the cross-linker ratio, assuming homogeneous and diamond lattice-like network structure. We conclude that partitioning vs. the cross-linker ratio may be complex and non-monotonous, exhibiting minima and maxima and intercepting the K = 1 line.
determine the gradient and concavity of the solute partitioning in dependence on the cross-linker ratio, assuming homogeneous and diamond lattice-like network structure. We conclude that partitioning vs. the cross-linker ratio may be complex and non-monotonous, exhibiting minima and maxima and intercepting the K = 1 line.
Our investigation focuses on very low solute concentrations, though the response of the polymer to the penetrants might not be negligible. From experiments71,72,75 it is known, that solutes may change the hydrogel's VPTT, which has additionally been demonstrated in computer simulations.20,35
Nevertheless, our idealized approach tackling the partitioning does allow for an indirect comparison to experimental data. One experiment on the rate of the nitrobenzene reduction in an (N-isopropylacrylamide-co-acrylic-acid (PNIPAM-co-AAc)) nanoreactor76 shows an increase in the reduction rate with increasing cross-link (BIS) density, which is attributed to the higher nitrobenzene concentration inside the hydrogel. Parasuraman et al.77 used a very similar hydrogel (PNIPAM-co-AAc-BIS) and proved the increased dye uptake (Orange II) with increasing cross-link ratio. Both studies qualitatively support our findings. They, however, have in common that the initial increase of the reduction rate and the dye uptake, respectively, apparently saturates for higher cross-link degrees. This effect is not captured by our model and might result from steric hindrances, i.e., undersized pore/mesh size of the polymer architecture and already occupied adsorption sites for higher solute concentrations.
After qualitatively confirming the impact of the cross-link ratio on the partitioning of the aromatic compounds, we will now assess the comparison in terms of absolute values. Experimentally, partition ratios have been reported for several molecules containing aromatic rings. A study by Molina et al.52 retrieved K in PNIPAM–BIS-hydrogels (α = 2%) for probe drugs (tryptophan, propranolol chloride, dansyl chloride, methyl orange, riboflavin, and ruthenium-tris(2,2′-bipyridyl)dichloride), which contain two to six aromatic rings as well as polar and/or charged residues. The partition ratio, depending on the compound, ranges from roughly 4.6 to 10.
Comparing to our perfect network model, the much smaller NB and NP− show partition ratios of approximately 1.3 and 1.8, respectively, at α = 2%, and 2.7 and 5.7 at α = 5% in the low dilution limit (Nsolute = 1). For Nsolute = 20, K is about 3.7 at α = 2% for NB. It is expected that larger molecules at higher concentrations, as established in the mentioned experiments, will lead to higher partition ratios78 and can thus be regarded as supportive of our results. Furthermore, the adsorption increase due to positive cooperativity (e.g., NB) has been shown for methylene blue in a superabsorbent hydrogel.79
The salt partition ratios in 1% cross-linked PNIPAM–BIS gels at room temperature have been reported80 and amount to KLiCl = 0.97 ± 0.05, KKCl = 0.91 ± 0.05 and KNaCl ≈ 0.95, i.e., just below unity as in our prediction for sodium chloride.
However, the non-monotonicity of the partition ratio in dependence on the cross-link ratio predicted by our model has not been reported by experimentalists so far and is yet to be tested.
4 Concluding remarks
We investigated the effects of cross-linking on solute adsorption in swollen PNIPAM hydrogels by means of explicit-water MD simulations at T = 290 K, i.e., below the PNIPAM collapse transition temperature. We considered a generic hydrogel subunit consisting of one BIS-linker and four PNIPAM chains, which was kept in tetrahedral geometry by position-restrained backbone terminals. By subdividing the radial distance from the central cross-linker, we classified four different adsorption regions according to the polymer's prevalent features, namely the cross-linker region, the linear chain region, the chain terminal region, and the bulk solvent domain. We evaluated the adsorption of different solutes, representing typical charged, polar and nonpolar molecular compounds.Comparing the cross-linker and monomer effects on adsorption, we find different scenarios. Apolar species show small attraction to chain monomers and slight repulsion from the cross-linker region. Sodium chloride behaves the opposite, it has negative chain adsorption but is attracted towards the cross-linker. The strongest adsorbing solutes, the nitro-aromatics, adsorb to all parts of the polymer and show the highest binding affinity, which is promoted by hydrophobic interactions between the aromatic ring and PNIPAM's isopropyl groups as well as by hydrogen bonds between the nitro-oxygens and the amide groups. The adsorption at the cross-linker relative to a single PNIPAM monomer adsorption, spans from Γxlink/Γmer ≈ 2 (NB) to Γxlink/Γmer ≈ 10 (NP0, NP−). This indicates that the cross-linker can significantly enhance the overall adsorption to the network unit. Hence, for solutes that have a significant affinity to PNIPAM chains already, the dense cross-linker region, where many-body attractions are at play, amplifies the local adsorption by even an order of magnitude. Thereby we confirm the ‘vertex trapping’ effect that has been first reported in generic coarse-grained simulations of polymer networks.24–28
In the case of the nitro-aromatics, we furthermore performed simulations with higher solute concentrations to estimate cooperative adsorption effects. Nitrobenzene shows enhanced aromatic stacking at the cross-linker and the adsorption is elevated in a superlinear fashion with increasing concentration. Nitrophenol shows similar, positive cooperativity but a less pronounced behavior. For both NB and NP0 the cross-linker promotes higher positive cooperation effects than single chains. In contrast, in the case of the negatively charged nitrophenolate, we observe less adsorption at higher concentrations due to negative cooperativity stemming from the electrostatic repulsion.
The adsorption coefficients for cross-linker and chain monomers in the low concentration regime were used to estimate partition ratios of the solutes within an idealized, homogeneous diamond-lattice macrogel, which allowed a comparison with experimental findings. In our model, we found that highly adsorbing substances like nitro-aromatics have a partition ratio ranging from 2 to 5 at a cross-linker concentration of 5%. Solutes with adsorption coefficients of opposite signs may show non-monotonic behavior as a function of the cross-linker ratio: positive/negative chain adsorption and negative/positive cross-linker adsorption leads to a maximum/minimum in the partition ratio. These yet poorly known features should be considered in future experiments and modeling of hydrogels as they play an important role for the fine-tuning of solute uptake within the needs of the desired function and application.
Conflicts of interest
There are no conflicts of interest to declare.Appendix
A Force field parameters
From our ab initio calculations with the Gaussian 09 software,47 we obtain partial charges for the cross-linker and monomers, which are very similar and in good agreement with the OPLS-QM2 force field.31 Due to the chemical similarity of BIS and PNIPAM, we apply the PNIPAM's partial charges of the OPLS-QM2 force field for BIS atoms as well. The partial charges from the original OPLS-AA46 and OPLS-QM2 force fields as well as our results are shown in Table 2. The standard OPLS force field is used for all remaining parameters like potentials, masses, etc. The hitherto undefined N–C–N angle and C–N–C–N dihedral potentials for the cross-linker were adopted from the OPLS C–C–C angle and C–N–C–C dihedral parameters, respectively.| OPLS-AA46 | HF-6-31G(d) | OPLS-QM231 | Charges used in this work | ||
|---|---|---|---|---|---|
| BIS | PNIPAM | PNIPAM | |||
| C1 | −0.12 | −0.22 | −0.20 | −0.18 | −0.18 |
| H1 | 0.06 | 0.07 | 0.08 | 0.09 | 0.09 |
| C2 | −0.06 | −0.13 | −0.07 | 0.00 | 0.00 |
| H2 | 0.06 | 0.06 | 0.05 | 0.05 | 0.05 |
| C3 | 0.50 | 0.81 | 0.80 | 0.50 | 0.50 |
| O | −0.50 | −0.61 | −0.65 | −0.57 | −0.57 |
| N | −0.50 | −0.69 | −0.84 | −0.57 | −0.57 |
| HN | 0.30 | 0.39 | 0.39 | 0.33 | 0.33 |
| C4 | 0.14 | — | 0.64 | 0.36 | 0.36 |
| H4 | 0.06 | — | −0.01 | 0.06 | 0.06 |
| C5 | −0.18 | — | −0.52 | −0.32 | −0.32 |
| H5 | 0.06 | — | 0.12 | 0.08 | 0.08 |
| C6 | — | 0.06 | — | — | 0.40 |
| H6 | 0.06 | 0.14 | — | — | 0.06 |
Recapturing the results for the adsorptions around single chains reported by our group before,38 the reader may compare the standard OPLS-AA force field for PNIPAM polymers with the further optimized OPLS-QM2 version31 employed in this work. The qualitative trends, i.e., size and polarity dependence as well as the strong nitro aromatic binding affinity remain. However, comparing absolute numbers for aromatic compounds, the standard force field38 shows a roughly twice as high adsorption coefficient to the chain monomers. We attribute this effect to more polar amide groups in the OPLS-QM2 force field and hence to more hydrophilic behavior. Moreover, the adsorption of NP− to PNIPAM (in the OPLS-QM2 version) is significantly larger owing to its polar nitro group.
B Defect-free PNIPAM–BIS hydrogels
We assume a homogeneous network with cross-linkers arranged in a perfect diamond lattice and thus connected with chains of an equal number of monomers. Given this perfect lattice, we can simply deduce from the geometry the monomer concentration as a function of the cross-linker ratio, ρmer(α) = nmer(α)/vgel(α). We can also assess the network's unit cell volume vgel(α) and its PNIPAM monomer content nmer(α). Such a unit cell contains eight cross-linkers and 16 chains, hence nmer(α) = 8/α, and the number of monomers between two associated cross-linkers is nchain(α) = 1/(2α). The distance between two cross-linkers is then given by![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) xx(α) = xx(α) = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) xlink + nchain(α)λΔLc, xlink + nchain(α)λΔLc, | (14) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) xlink = 0.22 nm, the effective length contribution of one BIS-linker, which is an average value retrieved from simulations solving L =
xlink = 0.22 nm, the effective length contribution of one BIS-linker, which is an average value retrieved from simulations solving L = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) xlink/2 +
xlink/2 + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ee. The unit cell volume reads
ee. The unit cell volume reads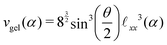 | (15) |
By knowing nmer(α), we can further approximate the polymer volume fraction, which allows us to identify physically meaningful values of α and K. Using the water profile (Fig. 3) we extract the excluded volume per monomer as Vex,mer = 0.167 nm3 and assume the BIS’ volume to scale with the number of heavy atoms (without hydrogens) compared to a PNIPAM monomer (11 vs. 8), yielding Vex,xlink = 0.230 nm3. The excluded volume in one unit cell is then vex = 8Vex,xlink + nmer(α)Vex,mer and the polymer volume fraction for different values of α is obtained as ϕp = vex/vgel (Fig. 7).
Acknowledgements
The authors would like to thank Won Kyu ‘Q’ Kim and the whole ERC team for fruitful discussions. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 646659). M. K. acknowledges the financial support from the Slovenian Research Agency (research core funding no. P1-0055). The simulations were performed with resources provided by the North-German Supercomputing Alliance (HLRN). The authors acknowledge support by the state of Baden-Württemberg through bwHPC.References
- M. A. C. Stuart, W. T. S. Huck, J. Genzer, M. Müller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk, M. Urban, F. Winnik, S. Zauscher, I. Luzinov and S. Minko, Nat. Mater., 2010, 9, 101–113 CrossRef PubMed.
- A. Fernandez-Nieves, H. Wyss, J. Mattsson and D. A. Weitz, Microgel suspensions: fundamentals and applications, John Wiley & Sons, 2011 Search PubMed.
- Y. H. Bae, T. Okano and S. W. Kim, Pharm. Res., 1991, 8, 531–537 CrossRef CAS.
- M. Motornov, Y. Roiter, I. Tokarev and S. Minko, Prog. Polym. Sci., 2010, 35, 174–211 CrossRef CAS.
- H. G. Schild, Prog. Polym. Sci., 1992, 17, 163–249 CrossRef CAS.
- G. R. Hendrickson and L. A. Lyon, Soft Matter, 2009, 5, 29–35 RSC.
- R. Roa, W. K. Kim, M. Kanduč, J. Dzubiella and S. Angioletti-Uberti, ACS Catal., 2017, 7, 5604–5611 CrossRef CAS PubMed.
- S. Carregal-Romero, N. J. Buurma, J. Pérez-Juste, L. M. Liz-Marzán and P. Hervés, Chem. Mater., 2010, 22, 3051–3059 CrossRef CAS.
- W. E. Hennink and C. F. van Nostrum, Adv. Drug Delivery Rev., 2002, 54, 13–36 CrossRef CAS PubMed.
- X. Zhu, X. Gu, L. Zhang and X.-Z. Kong, Nanoscale Res. Lett., 2012, 7, 519 CrossRef PubMed.
- S. H. Gehrke, J. P. Fisher, M. Palasis and M. E. Lund, Ann. N. Y. Acad. Sci., 1997, 831, 179–207 CrossRef CAS PubMed.
- M. Heskins and J. E. Guillet, J. Macromol. Sci., Part A: Pure Appl. Chem., 1968, 2, 1441–1455 CrossRef CAS.
- N. Sanson and J. Rieger, Polym. Chem., 2010, 1, 965–977 RSC.
- T. Still, K. Chen, A. M. Alsayed, K. B. Aptowicz and A. Yodh, J. Colloid Interface Sci., 2013, 405, 96–102 CrossRef CAS PubMed.
- N. Nagaoka, A. Safranj, M. Yoshida, H. Omichi, H. Kubota and R. Katakait, Macromolecules, 1993, 26, 7386–7388 CrossRef CAS.
- Y. Hirokawa and T. Tanaka, J. Chem. Phys., 1984, 81, 6379 CrossRef.
- H. Senff and W. Richtering, Colloid Polym. Sci., 2000, 278, 830–840 CrossRef CAS.
- P. Hervés, M. Pérez-Lorenzo, L. M. Liz-Marzán, J. Dzubiella, Y. Lu and M. Ballauff, Chem. Soc. Rev., 2012, 41, 5577–5587 RSC.
- Y. Lu and M. Ballauff, Prog. Polym. Sci., 2011, 36, 767–792 CrossRef CAS.
- W. K. Kim, A. Moncho-Jordá, R. Roa, M. Kanduč and J. Dzubiella, Macromolecules, 2017, 50, 6227–6237 CrossRef CAS.
- I. Adroher-Bentez, S. Ahualli, A. Martn-Molina, M. Quesada-Pérez and A. Moncho-Jord, Macromolecules, 2015, 48, 4645–4656 CrossRef.
- L. Pérez-Mas, A. Martn-Molina, M. Quesada-Pérez and A. Moncho-Jordá, Phys. Chem. Chem. Phys., 2018, 20, 2814–2825 RSC.
- A. Vagias, K. Sergelen, K. Koynov, P. Košovan, J. Dostalek, U. Jonas, W. Knoll and G. Fytas, Macromolecules, 2017, 50, 4770–4779 CrossRef CAS.
- X. Zhang, J. Hansing, R. R. Netz and J. E. Derouchey, Biophys. J., 2015, 108, 530–539 CrossRef CAS PubMed.
- J. Hansing, C. Ciemer, W. K. Kim, X. Zhang, J. E. DeRouchey and R. R. Netz, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 53 CrossRef PubMed.
- J. Hansing and R. R. Netz, Macromolecules, 2018, 51, 7608–7620 CrossRef CAS.
- J. Hansing and R. R. Netz, Biophys. J., 2018, 114, 2653–2664 CrossRef CAS PubMed.
- J. Hansing, J. R. Duke III, E. B. Fryman, J. E. DeRouchey and R. R. Netz, Nano Lett., 2018, 18, 5248–5256 CrossRef CAS PubMed.
- M. Alaghemandi and E. Spohr, Macromol. Theory Simul., 2012, 21, 106–112 CrossRef CAS.
- S. A. Deshmukh, S. K. Sankaranarayanan, K. Suthar and D. C. Mancini, J. Phys. Chem. B, 2012, 116, 2651–2663 CrossRef CAS PubMed.
- V. Palivec, D. Zadrazil and J. Heyda, 2018, arXiv:1806.05592.
- N. Schwierz, D. Horinek, S. Liese, T. Pirzer, B. N. Balzer, T. Hugel and R. R. Netz, J. Am. Chem. Soc., 2012, 134, 19628–19638 CrossRef CAS PubMed.
- N. Schwierz, S. Krysiak, T. Hugel and M. Zacharias, Langmuir, 2016, 32, 810–821 CrossRef CAS PubMed.
- S. Kienle, S. Liese, N. Schwierz, R. R. Netz and T. Hugel, ChemPhysChem, 2012, 13, 982–989 CrossRef CAS PubMed.
- H. Du, R. Wickramasinghe and X. Qian, J. Phys. Chem. B, 2010, 114, 16594–16604 CrossRef CAS PubMed.
- D. Horinek and R. R. Netz, J. Phys. Chem. A, 2011, 115, 6125–6136 CrossRef CAS PubMed.
- F. Rodrguez-Ropero and N. F. van der Vegt, Phys. Chem. Chem. Phys., 2015, 17, 8491–8498 RSC.
- M. Kanduč, R. Chudoba, K. Palczynski, W. K. Kim, R. Roa and J. Dzubiella, Phys. Chem. Chem. Phys., 2017, 19, 5906–5916 RSC.
- M. Kanduč, W. K. Kim, R. Roa and J. Dzubiella, Macromolecules, 2018, 51, 4853–4864 CrossRef.
- D. Nayar, A. Folberth and N. F. van der Vegt, Phys. Chem. Chem. Phys., 2017, 19, 18156–18161 RSC.
- T. Tönsing and C. Oldiges, Phys. Chem. Chem. Phys., 2001, 3, 5542–5549 RSC.
- S. Deshmukh, D. A. Mooney, T. McDermott, S. Kulkarni and J. D. MacElroy, Soft Matter, 2009, 5, 1514–1521 RSC.
- S. Deshmukh, D. A. Mooney and J. M. D. D. MacElroy, Mol. Simul., 2011, 37, 846–854 CrossRef CAS.
- P. Košovan, T. Richter and C. Holm, Intelligent Hydrogels, Springer, 2013, pp. 205–221 Search PubMed.
- A. Luzar and D. Chandler, Nature, 1996, 379, 55 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- F. Ikkai and M. Shibayama, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 617–628 CrossRef CAS.
- S. Schneider and P. Linse, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 8, 457–460 CrossRef CAS PubMed.
- H. Berendsen, J. Grigera and T. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- S. Wu, J. Dzubiella, J. Kaiser, M. Drechsler, X. Guo, M. Ballauff and Y. Lu, Angew. Chem., Int. Ed., 2012, 51, 2229–2233 CrossRef CAS PubMed.
- M. Molina, C. Rivarola and C. Barbero, Polymer, 2012, 53, 445–453 CrossRef CAS.
- T. Hoare and R. Pelton, Langmuir, 2008, 24, 1005–1012 CrossRef CAS PubMed.
- T. J. Ritchie and S. J. Macdonald, Drug Discovery Today, 2009, 14, 1011–1020 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1-2, 19–25 CrossRef.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 14101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1951, 19, 774–777 CrossRef CAS.
- A. Ben-Nairn, Molecular Theory of Water and Aqueous Solutions: Part I: Understanding Water, World Scientific, 2009 Search PubMed.
- F. M. Winnik, M. F. Ottaviani, S. H. Bossmann, M. Garcia-Garibay and N. J. Turro, Macromolecules, 1992, 25, 6007–6017 CrossRef CAS.
- C. Dalgicdir, F. Rodriguez-Ropero and N. F. van der Vegt, J. Phys. Chem. B, 2017, 121, 7741–7748 CrossRef CAS PubMed.
- D. Mukherji, M. Wagner, M. D. Watson, S. Winzen, T. E. de Oliveira, C. M. Marques and K. Kremer, Soft Matter, 2016, 12, 7995–8003 RSC.
- J. Pang, H. Yang, J. Ma and R. Cheng, J. Phys. Chem. B, 2010, 114, 8652–8658 CrossRef CAS PubMed.
- F. Rodrguez-Ropero, T. Hajari and N. F. van der Vegt, J. Phys. Chem., 2015, 119, 15780–15788 CrossRef PubMed.
- C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Chem. Soc., Perkin Trans. 2, 2001, 651–669 RSC.
- W. L. Jorgensen and E. M. Duffy, Bioorg. Med. Chem. Lett., 2000, 10, 1155–1158 CrossRef CAS PubMed.
- C. H. Hofmann and M. Schönhoff, Colloid Polym. Sci., 2012, 290, 689–698 CrossRef CAS.
- D. Coughlan and O. Corrigan, Int. J. Pharm., 2006, 313, 163–174 CrossRef CAS PubMed.
- R. Acciaro, T. Gilanyi and I. Varga, Langmuir, 2011, 27, 7917–7925 CrossRef CAS PubMed.
- S. Meyer and W. Richtering, Macromolecules, 2005, 38, 1517–1519 CrossRef CAS.
- H. Kawasaki, S. Sasaki, H. Maeda, S. Mihara, M. Tokita and T. Komai, J. Phys. Chem., 1996, 100, 16282–16284 CrossRef CAS.
- Z. H. Farooqi, S. R. Khan, R. Begum, T. Hussain and N. Batool, Walailak J. Sci. Tech., 2015, 12, 1147–1156 Search PubMed.
- D. Parasuraman, A. K. Sarker and M. J. Serpe, Chem. Phys. Chem., 2012, 13, 2507–2515 CrossRef CAS PubMed.
- M. Kanduč, W. K. Kim, R. Roa and J. Dzubiella, J. Phys. Chem. B, 2019, 123, 720–728 CrossRef PubMed.
- A. T. Paulino, M. R. Guilherme, A. V. Reis, G. M. Campese, E. C. Muniz and J. Nozaki, J. Colloid Interface Sci., 2006, 301, 55–62 CrossRef CAS PubMed.
- H. Kawasaki, T. Mitou, S. Sasaki and H. Maeda, Langmuir, 2000, 16, 1444–1446 CrossRef CAS.
| This journal is © the Owner Societies 2019 |