The opposing effect of butanol and butyric acid on the abundance of bromide and iodide at the aqueous solution–air interface

Abstract

The efficient oxidation of iodide and bromide at the aqueous solution–air interface of the ocean or of sea spray aerosol particles had been suggested to be related to their surface propensity. The ubiquitous presence of organic material at the ocean surface calls for an assessment of the impact of often surface-active organic compounds on the interfacial density of halide ions. We used in situ X-ray photoelectron spectroscopy with a liquid micro-jet to obtain chemical composition information at aqueous solution–vapor interfaces from mixed aqueous solutions containing bromide or iodide and 1-butanol or butyric acid as organic surfactants. Core level spectra of Br 3d, Na 2s, C 1s and O 1s at ca. 160 eV kinetic energy and core level spectra of I 4d and O 1s at ca. 400 eV kinetic energy are compared for solutions with 1-butanol and butyric acid as a function of organic concentration. A simple model was developed to account for the attenuation of photoelectrons by the aliphatic carbon layer of the surfactants and for changing local density of bromide and iodide in response to the presence of the surfactants. We observed that 1-butanol increases the interfacial density of bromide by 25%, while butyric acid reduces it by 40%, both in comparison to the pure aqueous halide solution. Qualitatively similar behavior was observed for the case of iodide. Classical molecular dynamics simulations failed to reproduce the details of the response of the halide ions to the presence of the two organics. This is attributed to the lack of correct monovalent ion parameters at low concentration possibly leading to an overestimation of the halide ion concentration at the interface in absence of organics. The results clearly demonstrate that organic surfactants change the electrostatic interactions near the interface with headgroup specific effects. This has implications for halogen activation processes specifically when oxidants interact with halide ions at the aqueous solution–air interfaces of the ocean surface or sea spray aerosol particles.

---

Introduction

The ozone budget in the marine boundary layer has remained a hot topic in the atmospheric chemistry community.^1,2 The oxidation of bromide (Br⁻) and iodide (I⁻) at the aqueous solution–air interface by atmospheric oxidants, such as ozone (O₃) or hydroxyl OH radical, has been found critical in initiating halogen cycling reactions in marine air and particularly important for the global budgets of bromine and iodine and also the O₃ budget.^2–7 While halogen chemistry directly represents several tens of percent of the global tropospheric O₃ sink and is thus undoubtedly important, it also has substantial effects on the biogeochemical cycling of other species, such as mercury, with implications for the marine food-web.^8,9 Due to the fact that O₃ acts as a greenhouse gas in the upper troposphere, halogen chemistry has also an impact on the radiative balance and the climate.⁵

The halide oxidation reactions mentioned above have been suggested to be enhanced at the aqueous solution–air interface.^10–14 For the case of oxidation of bromide by ozone (O₃), a recent study has identified the bromide ozonide intermediate of this reaction to exhibit high propensity for the aqueous solution–air interface.¹⁵ Aqueous NaBr and NaI solutions exhibit positive surface tension change with increasing bulk mole fraction^16,17 and thus negative surface excess, i.e., depletion from the interface due to charge repulsion. Though, NaI shows the least positive slope, followed by NaBr, NaCl and NaF. This had been attributed to polarizability increasing with size in the halide ion series, and thus increasing propensity for the interface, which may partially counteract the electrostatic repulsion, as suggested by past experimental and theoretical studies.^18–28 Initially, the interfacial density of halide ions was suggested to be strongly enhanced and also suggested to be at the origin of the surface catalysis of the oxidation reactions mentioned above.^10,12 This has initiated many spectroscopic,^19,29–33 theory^{25,26,34–36} and kinetic experiments^13–15,37 on the one side and also atmospheric modelling studies on the other side^4,9 to assess the environmental implications. Though, the absolute extent of the relative enhancement of the halide anions has not been finally quantified.^34,38

Recently, the fact that the ocean surface carries a layer consisting of a wealth of organic compounds deriving from marine biota has received a lot of attention.^39–42 Insight into the response of the halide ions especially also at mixed aqueous liquid surfaces to the presence of often surface active organics is crucial for understanding the chemistry of marine aerosols, brines associated with arctic sea ice and snow packs, which are more complex than just halide solutions, and for assessing the general implications of halogen chemistry.

X-ray photoelectron spectroscopy (XPS) has been the key technique to unravel the halide ion enhancements at the surface of concentrated aqueous solutions.¹⁹ XPS experiments have also provided first indications for the entanglement of iodide anions, potassium cations and the headgroup of an alcohol surfactant for such solutions.⁴³ XPS provides important information for this purpose via its high surface sensitivity, typically in the nm range, which arises from the short inelastic mean free path (IMFP) of electrons in condensed matter,⁴⁴ and also in aqueous solution.^34,45–47 Liquid micro-jet (LJ) XPS enables electron spectroscopy of volatile liquids.^48–51 Such experiments have become possible recently with the advent of differentially pumped electrostatic lens systems that allow focussing photoelectrons from a small acceptance volume of a few hundred μm at pressures up to the mbar range into an electron analyser kept in ultrahigh vacuum. The liquid jet provides a continuously renewed interface that moves fast enough to avoid radiation induced build-up of radicals that would lead to chemical alteration of labile species and fast enough to avoid deposition of carbonaceous impurities, a common occurrence in XPS experiments with static samples. Our recent study showed a correlation between the solute photoemission signals of aqueous solutions of C1 to C4 alcohols and carboxylic acids with the surface excess derived from surface tension measurements, thus nicely demonstrating that XPS probes a locally equilibrated interface with respect to bulk – surface equilibrium.⁵² Therefore, LJ-XPS is the ideal tool for furthering our understanding of the halide ions co-existing with organic matter at the aqueous solution–vapor interface.

In a recent study,⁵³ we have made an attempt to assess the impact of citric acid, a proxy for highly oxidized organic compounds in the atmosphere, on the abundance of bromide at the aqueous solution–gas interface. Together with other studies,^54–59 it has become apparent that subtle effects control the impact of organic species on the ion profiles. While bromide was observed to be displaced from the interface by citric acid, sodium seemed to be rather attracted further towards the interface in presence of citric acid, which has three carboxylic groups and one alcohol group.⁵³ Therefore, a more systematic approach into the interplay of both ions with different functional groups at the interface is warranted. In this study, we address the difference between an alcohol and carboxylic acid headgroup of a monofunctional surfactant on the abundance of Na⁺, Br⁻, and I⁻ at the interface within the probe depth using LJ-XPS.⁴⁸ The surfactants chosen were 1-butanol and butyric acid, which exhibit well characterized surface excess for the concentration range used in our experiments.^60,61 We also document and discuss the use of classical molecular dynamics simulations that turned out to be unable to explain the experimental results.

Methods

We made use of the NAPP endstation with the liquid microjet setup at the SIM beamline of the SLS at PSI.⁴⁸ The electron analyzer uses a three-stage differentially pumped electrostatic lens system and a hemispherical analyzer to collect photoelectrons from samples in chamber pressures up to a few mbar. For the present experiments, a quartz nozzle, forming a liquid microjet with a diameter of 26 μm, was used to deliver a liquid sample into the vacuum chamber. The liquid was cooled to 279 K immediately before entry into the ionization chamber, and a flow rate of 0.35 mL min⁻¹ was used. The chamber pressure with the jet running was between 1.0 × 10⁻³ and 1.0 × 10⁻⁴ mbar. The photoelectrons from the liquid surface entered the analyzer through an orifice (skimmer) with a diameter of 500 μm. The working distance between the liquid jet and this orifice was 500 μm.

A complete description of the equilibrated nature of a liquid microjet under the conditions of photoemission experiments has been given in the literature previously.^49,62 In the context of interest in this study, it is important that the surface active organic species (1-butanol and butyric acid) can reach their equilibrium concentration at the surface until the jet is hit by the X-ray beam, at 100 μs. For the 0.1 M/0.002 mole fraction solution range relevant for this study, the diffusional time scale for the formation of a monolayer equivalent on the surface is less than 1 μs.^52,53,62,63

For bromide containing solutions, spectra for obtaining core-level spectra of Br 3d, Na 2s, C 1s and O 1s at about the same kinetic energy were not taken each one after the other with setting the beamline energy to the appropriate energy value in between. We set the primary photon energy for the detection of Br 3d and Na 2s to 229 eV, resulting in a photoelectron KE of ca. 155 eV and 160 eV, respectively, as in our previous study.⁵³ We made use of the ca. 10% of photon flux associated with 2nd order light, which simultaneously passes the monochromator with photon energies of 458 eV, to ionize the C 1s orbital for a KE of 163–168 eV. The even smaller amounts of 3rd order light at 687 eV were used to excite the O 1s orbital for a KE of 148.9 eV for liquid water. This procedure⁶⁴ allowed determining photoemission signals for each element within one sweep of the electron analyzer in a relatively narrow kinetic energy range. 50 sweeps were averaged to create one spectrum.

For spectroscopic reasons, this was not possible with the iodide solutions. In that case, we have measured the Na 2s and I 4d at a KE of ca. 382 and 395 eV, respectively, with a primary photon energy of 450 eV, and oxygen 1s at ca. 362 eV KE excited by the 2nd order light at 900 eV. The core level C 1s was assessed from separate spectra measured at the same photon energy with KE around 150 eV. 50 sweeps were averaged to create one spectrum.

In order to optimize photoemission signal intensities for all configurations combined and maintain consistent beamline settings, the linear polarization was kept at 0°, rather than at the magic angle of 54.7°. We thereby neglect possibly occurring changes to the angular distribution of photoelectrons upon adding surfactants at the interface.

A constant concentration (0.12 mole L⁻¹, corresponding to 0.002 mole fraction) of sodium bromide (NaBr, BioXtra ≥99.0%, Sigma-Aldrich) and sodium Iodide (NaI, ACS reagent ≥99.5%, Sigma-Aldrich) in 0.001, 0.002, 0.004, and 0.008 mole fraction 1-butanol (Bu-ol, 99.9%, Sigma-Aldrich) and butyric acid (Bu-acid, ≥99+%, Alfa Aesar), respectively, were prepared for analysis. The solutions were prepared by adding stock solutions of NaBr and the organics to Milli-Q water (Millipore, 18.2 MΩ cm at 25 °C). The solutions were kept at their native pH. In absence of organics, the NaBr and NaI solutions had a pH of 6.9 and 6.7, respectively. In mixtures with butanol, the pH was 6.8 and 6.4, respectively. In mixtures with butyric acid, the pH varied from 3.2 to 2.7 and from 3.0 to 2.6, respectively, for the butyric acid mole fraction range from 0.001 to 0.008, for NaBr and NaI solutions. Thus, the degree of dissociation of butyric acid (pK_a = 4.8) remained at around 10⁻² and below.

The classical molecular dynamics simulations are described in the ESI.†

Results and discussion

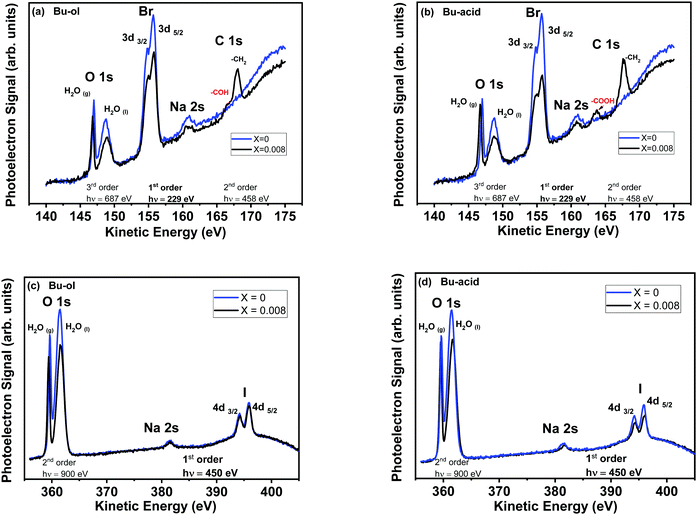
Fig. 1(a and b) shows exemplary combined O 1s, Br 3d, Na 2s, and C 1s photoelectron spectra from 0.002 mole fraction NaBr aqueous solutions as a function of the Bu-ol (a) and Bu-acid (b) mole fraction (0–0.008) taken at the nominal photon energy of 229 eV and making use of the higher order light components to obtain C 1s and O 1s in the same kinetic energy (KE) window as described above.⁵³ This obviously goes at the expense of signal-to-noise ratio for O 1s and C 1s, but has the advantage to provide photoemission signals for all four elements within one sweep of the electron analyzer and thereby allows keeping track of variations induced by small movements of the liquid jet. This allows normalizing Br 3d, I 4d and Na 2s photoemission intensities reliably to O 1s intensities, thus providing access to local ion concentrations and not only halide anion to cation ratios as in most previous XPS studies. Higher signal-to-noise spectra were obtained separately for each core level region measured with standard first order light to obtain proper constraints on the fits of the former spectra. The spin–orbit split bromine levels Br 3d_3/2,5/2 appear at a photoelectron KE of about 155 eV. Na 2s is observed at 160.7 eV KE. C 1s, excited by photons at around 458 eV, appears in the spectrum at photoelectron KEs of 164.4 eV (carboxyl C of Bu-acid), 166.6 eV (alcohol C from Bu-ol) and 168.2 eV (aliphatic C for both organics).^43,65 Note that for the present solutions, Bu-acid remained almost entirely protonated, and thus the corresponding carboxylate ion is not becoming apparent in the spectra. O 1s was excited at a photon energy of 687 eV. The lower KE peak (147.1 eV) with smaller full width at half maximum (FWHM) is assigned to gas phase water molecules.⁶⁶ Within the broader condensed phase O 1s peak two components should be present: oxygen present in solvent water at ∼55 M and oxygen present in the functional group of the two organic solutes at 0.5 M. Due to the strong overlap of these, we are, however, unable to resolve the individual contributions (water dominates) and fit the condensed phase O 1s region with a single component. Apparently, the condensed phase O 1s, the Br 3d and Na 2s peaks were found to decrease with the presence of organic, which may be expected qualitatively due to electron attenuation by the additional density of mostly carbon atoms at the interface. Correspondingly, the C 1s peaks were found to increase with the presence of organic for either Bu-ol or Bu-acid. Note that the signal intensity attributed to gas phase water vapor remains unchanged, since the presence of 0.008 mole fraction of organic does not significantly alter the water vapor pressure or the evaporation rate, so that the amount of gas phase water molecules excited by the X-rays remains the same.

Fig. 1 (a) Exemplary photoelectron spectra from aqueous solutions containing 0.002 mole fraction NaBr and varying mole fraction (X) of Bu-ol (X = 0, blue; X = 0.001, black) excited by X-rays with a nominal photon energy of 229 eV. (b) The same experiments as in (a) but with Bu-acid. (c) Exemplary photoelectron spectra from aqueous solutions containing 0.002 mole fraction NaI and varying amounts of Bu-ol (0, blue; X = 0.008, black) excited by X-rays with a nominal photon energy of 450 eV. (d) The same experiments as in (c) but with Bu-acid.

Fig. 1(c and d) shows exemplary combined O 1s, Na 2s, and I 4d PE spectra from 0.002 mole fraction NaI aqueous solutions as a function of the Bu-ol (c) and Bu-acid (d) concentration (at mole fractions 0 and 0.008) taken at a nominal photon energy of 450 eV and making use of the 2nd order light components to obtain O 1s in the same kinetic energy (KE) window. The change in Na 2s and I 4d signals with increasing organic mole fraction is comparable to that for the corresponding bromide solutions. However, note that due to the larger kinetic energy, the effects are less pronounced due to the larger probe depth.

At the photon energy used in the present experiments, 229 eV and 450 eV, the photoionization cross section for the excitation of the Na 2s core level is relatively low, so that the analysis of the Na 2s photoemission peak is affected by a lower signal to noise ratio.⁶⁷

It becomes already apparent from the spectra shown in Fig. 1 that in presence of Bu-ol, the Br 3d and I 4d signal intensities decrease by a smaller amount than that of O 1s, while they decrease markedly more strongly in presence of Bu-acid.

In Fig. 2, the C 1s PE signal (left axis) of the same NaBr and NaI solutions, each mixed with Bu-ol or Bu-acid in the mole fraction range from 0.001 to 0.008, are shown. The equilibrium concentration of such organics at the surface is expressed by the surface excess, Γ, which can be derived from surface tension data. Amphiphilic organics tend to minimize solvation of the hydrophobic tails and orient themselves in a way that the butyl chains reside above the interface while hydrating the hydrophilic head group.^52,68,69 The surface excess was derived from surface tension data reported by Granados et al. (2006) for Bu-acid and by Donaldson and Anderson⁶⁰ for Bu-ol, as described previously,⁵² in both cases for solutions not containing halide salts. This allows us to calculate the photoemission signal with a simple model. We assume that the solution is covered by a thin layer of carbon. The thickness of this layer, d, is estimated from the number of carbon and hydrogen atoms in the aliphatic portion of the Bu-ol and Bu-acid molecule assumed to reside above the surface from the surface excess (the functional group carbons and oxygens are considered part of the aqueous solution underneath):

d = Γm_CHx/ρ (1)

where m_CHx denotes the mass (g) of the aliphatic carbon chain, composed of –(CH₂)–(CH₂)–CH₃, i.e., a molar mass of 43 g mole⁻¹. The density of this layer, ρ, is assumed to be that of liquid Bu-ol and Bu-acid, 0.81 g cm⁻³ and 0.96 g cm⁻³, respectively. Maximum values of d based on eqn (1) are 0.28 nm and 0.21 nm for Bu-ol and Bu-acid, respectively.

Fig. 2 Functional group C 1s PE signals of Bu-ol (black) and Bu-acid (red) as a function of their mole fraction for aqueous solutions of 0.002 mole fraction NaBr (squares) and of 0.002 mole fraction NaI (triangles) (left axis), taken at a photon energy of 458 eV. Solid lines represent calculated photoemission signals based on surface excess for aqueous solutions of Bu-ol/Bu-acid derived from surface tension as described in the text, with dashed lines representing estimated error bounds. Each data set is shown on its own relative scale.

While this layer does not reflect the detailed strongly fluctuating arrangement of the molecules at the interface, it roughly captures the average number of atoms that photoelectrons encounter on their trajectory out of the sample in addition to those from the aqueous solution. To first approximation, the treatment following below is not sensitive to the choice of density assumed. But the choice of the density of liquid Bu-ol and Bu-acid allows assuming the IMFP within this layer being similar to that of water; a lower density but thicker layer would result in similar attenuation. Since in Fig. 2 we show the headgroup carbon C 1s signal, the C 1s photoemission signal from the molecules constituting the surface excess is then obtained by assuming attenuation by the aliphatic overlayer:

I_C1s,surface = AΓe^−d/λ (2)

A denotes a factor accounting for photon flux, ionization cross section and detection efficiency, and λ is the inelastic mean free path (1.2 nm) at 170 eV kinetic energy.⁴⁶ This simple photoelectron attenuation law neglects elastic scattering effects, which are likely too small to become relevant in view of the uncertainty of all parameters involved, as also discussed further below. Note that for values of d/λ ≪ 1, the expression on the right hand side approaches AΓ, which corresponds to the case where all photoelectrons from carbon atoms from molecules constituting Γ are detected without attenuation, as assumed in our previous study by Lee et al.,⁵² which seemed a reasonable approximation as d/λ doesn’t exceed 0.25 for C1 to C4 organics. For the cases in this study, the difference to eqn (2) is around up to 15%.

The contribution by Bu-ol and Bu-acid in the bulk with a constant density n_b (molecule cm⁻³) is then obtained by integrating over the solution from d onwards:

The overall signal intensity is then given by:

I_C1s = I_C1s,surface + I_C1s,bulk = A(Γe^−d/λ + λn_be^−2d/λ)n_b (4)

For low surface coverage (small d ≪ λ), attenuation by the overlayer could also be neglected, so that eqn (4) simplifies to the expression used by Lee et al.:⁵²

I_C1s ≈ A(Γ + n_bλ) (5)

Eqn (4) was used to calculate I_C1s in this work, plotted as a function of the mole fraction of organic in Fig. 2 (right axis). The surface excess data indicate that both surface active organic compounds exhibit saturated surface excess above 0.002 mole fraction, which is confirmed by the XPS measurements. Note that since the bulk number density, n_b, increases with the bulk mole fraction, the photoemission signal increases even if the surface coverage levels off, as apparent from eqn (4). Within uncertainty, the shape of the calculated photoemission signal is consistent with the measured data. No fit is involved in the application of eqn (5). Each data set is shown on its own relative scale, thus in normalized form, since the purpose is to compare the relative shape of the increase in signal with eqn (4), rather than the absolute photoemission intensities. Thus, the absolute value of A is not relevant here. For the relatively low bromide and iodide concentrations, salting out effects seem not strong enough to become apparent within the uncertainty of our measurement and that of the surface tension measurement. When comparing our results to the Krisch et al. study,⁴³ their surface excess derived from their surface tension measurements of Bu-ol solutions in presence of nearly saturated (thus high molarity) KI concentrations, a significant salting out effect by KI was observed. It exhibited saturated surface excess below 0.001 mole fraction in the presence of KI. The agreement between simulated and measured data indicates that the simple model adopted here represents the relative contributions from the bulk and the surface well. It is also more precise than the method used by Lee et al. The systematic uncertainty captured in the error range in Fig. 2 reflects the uncertainty of the effective electron scattering cross section by the aliphatic carbon chains.

Fig. 3(a and b) shows the relative departure of the bromide Br 3d, Na 2s and O 1s photoemission signals from their value for the neat bromide solutions as a function of mole fraction of Bu-ol (a) and Bu-acid (b). The signals (measured at 150–170 eV kinetic energy) are proportional to the amount of bromide anions, sodium cations and water, respectively, within a characteristic depth of about 1.1 nm from the surface.⁴⁶ The O 1s signal decrease is due to the increasing attenuation by the aliphatic carbons of Bu-ol and Bu-acid accumulating on the surface, as seen from the C 1s signals discussed above. Similar to eqn (3), we calculate the photoemission signal contribution of O atoms, assumed to be homogeneously distributed over the bulk up to below the aliphatic carbon layer, which is not containing oxygen:

The proportionality factor B is now different from A above, because of the different photoionization cross section of O 1s from that of C 1s. λ is 1.1 nm for the O 1s measurement at 150 eV kinetic energy. As obvious from Fig. 3a and b, the O 1s signal follows eqn (6) well. It does not include a fit parameter, and thus eqn (4) and (6) consistently explain the C 1s and O 1s signal intensities within the same assumptions of the attenuation model as a function of surface excess. Note that the absolute value of B is not relevant in eqn (6), since we only plot the relative change, normalized to the intensity measured for the pure NaBr solution.

Fig. 3 (a and b) Relative change of O 1s (black circles), Br 3d (blue triangles) and Na 2s (green diamonds) PE signals as a function of Bu-ol (a) and Bu-acid (b) mole fraction for aqueous solutions of 0.002 mole fraction NaBr. (c and d) Relative change of Br/O (blue triangles), Na/O (green diamonds) and Br/Na (red circles) signal intensity ratios as a function of organic mole fraction for aqueous solutions of 0.002 mole fraction M NaBr. Lines are calculated signals and ratios based on the model described in the text. Error bars in (a and b) are estimated based on standard deviation of replicate measurements and taking into account uncertainties in the peak fitting procedure and propagated for the ratios in (c and d).

While the Na 2s signal follows that of oxygen (water) fairly closely, the Br 3d signal decreases less strongly in the presence of Bu-ol but more strongly in the presence of Bu-acid, as already mentioned above in relation to Fig. 2. This suggests that more bromide is present in the interfacial region underneath the Bu-ol monolayer in presence of Bu-ol than on the neat NaBr solution, while bromide behaves in the opposite manner in presence of Bu-acid. This is also apparent from the Br/O, Na/O and Br/Na signal intensity ratios shown in Fig. 3c and d. Due to the relatively large uncertainty associated with the Na signal, further below we only quantitatively interpret the Br/O ratio. As mentioned above, our analysis neglects effects by elastic scattering and the anisotropic distribution of photoelectrons and their changes upon adding the organic surfactants. Olivieri et al.³⁴ have recently assessed the impact of elastic scattering at 65 eV KE to affect I/Na signal ratios from 1 M solutions at 10%. In view of the higher kinetic energies used here (155 eV and 390 eV for bromide and iodide solutions, respectively) the potential impacts are beyond the uncertainties of our measurements.

Similar trends are observed for the iodide solution results summarized in Fig. 4a–d, however they are just at the edge of being significant, because of the larger kinetic energy (360–400 eV), corresponding to an electron inelastic mean free path of around 1.9 nm,⁴⁶ used to probe the O 1s, Na 2s and I 4d levels. This explains the much smaller decrease of the O 1s signal with the organic mole fraction by less than 25% (Fig. 4a), compared to the 40% reduction observed at 0.008 mole fraction organic for the bromide solutions (Fig. 3a) observed at lower kinetic energy, in line with eqn (6). Still, within these constraints, we may cautiously and qualitatively conclude that also iodide ions tend to be attracted towards the Bu-ol covered interface, while rather being repelled from the Bu-acid covered interface.

Fig. 4 (a and b) Relative change of O 1s (black circles), I 4d (blue squares) and Na 2s (green diamonds) PE signals as a function of Bu-ol (a) and Bu-acid (b) mole fraction for aqueous solutions of 0.002 mole fraction NaI. (c and d) Relative change of I/O (blue squares), Na/O (green diamonds) and I/Na (red circles) signal intensity ratios as a function of organic mole fraction for aqueous solutions of 0.002 mole fraction M NaI. Lines are calculated signals and ratios based on the model described in the text. Error bars in (a and b) are estimated based on standard deviation of replicate measurements and taking into account uncertainties in the peak fitting procedure and propagated for the ratios in (c and d).

In an attempt to interpret the relative changes of the Br 3d and I 4d photoemission signal intensities further, we refined the model used above. We introduced an additional layer of thickness Δ, just below the aliphatic carbon layer at depth d, within the aqueous solution. In this layer, the halide ion density is set different from that of the bulk density by a factor, f, i.e., fn_b, while the density of the organic is equal to that in the bulk. f is a function of the surface excess of organic, Γ_org. In the simple terms of this model and in absence of organic f = f₀ is related to the surface excess of the halide ions, Γ_X−, via:

Γ_X− = n_bΔ(1 − f₀) (7)

The Br 3d (and I 4d) photoemission signal intensity is then obtained from the following integration:As further above for A and B, C is accounting for photon flux, ionization cross section and detection efficiency. Ideally, we would derive the local density of bromide or iodide, fn_b, from molecular dynamics (MD) simulations. Previous MD simulations of halide solutions feature strong variations of the density profiles of halide anions and the alkali cations within the topmost nanometer.^26,34,38,59 In terms of calculating photoemission intensity from these density profiles, further complications arise from strong dynamic effects of a rapidly fluctuating interface, where on average the instantaneous H₂O density profile experienced by an outgoing electron originating from a halide ion is different from the smooth averaged density profile.^34,38 In addition, the density profiles of halide ions turned out to be very sensitive to the ionic concentration and force field parameters.^{28,38,70–72} The force-field optimization usually fails to reproduce the structure and thermodynamics of ions in low ionic concentration even for simple ionic solutions since at high salt concentration the cation–anion interactions dominate the solution thermodynamics.⁷³ In spite of the relatively high interfacial halide ion densities derived based on MD simulations with polarizable force fields, Jungwirth and Tobias²⁶ pointed out that since the enhanced concentration of halide ions in the outermost interfacial layer is followed by a depletion layer, their density profile could still be reconciled with an overall depleted interfacial region derived from surface tension measurements, which exhibit increasing surface tension with bromide activity. We have therefore also attempted to obtain density profiles for bromide and sodium in presence and absence of Bu-ol and Bu-acid by molecular dynamics simulations as described in the ESI.† The results clearly demonstrate that the photoemission signals estimated from those density profiles are not in agreement with the XPS measurements presented above, especially not the striking difference in the Br/O signal intensity ratios shown in Fig. 3c and d. This is possibly related to the fact that the bromide enhancement at the interface of the solution in absence of either of the organic is overestimated due to the choice of the force-field as described in the ESI.† Testing other force field options was beyond the scope of this work.

Instead of density profiles from MD simulations, we continue with the more semi-quantitative attenuation model introduced above. We use a simple approximation to estimate fn_b, the bromide density in the near surface layer of thickness Δ introduced above. Also, the present experiments were not designed to obtain absolute Br/O atomic ratios or to resolve this ratio at varying probe depth, but to emphasize the change to this ratio as a function of the mole fraction of Bu-ol and Bu-acid. In absence of organic, choosing Δ as 1 nm and f₀ as 0.5 leads to Γ_Br⁻ ≈ −3 × 10¹² molecule cm⁻² from eqn (7), consistent with surface tension measurements.¹⁶ Obviously, the choice of Δ and f₀ bear substantial uncertainty, and it must remain the purpose of future studies to constrain these parameters further by kinetic energy dependent experiments. Eqn (8) is only little sensitive to the width of the layer depleted or enriched by f₀, but more to what degree f changes with mole fraction of organic, while Δ as such was considered constant. In a simple approach, we assumed

with Γ_org,max set to 3.2 × 10⁻¹⁴ molecule cm⁻² and 3.6 × 10⁻¹⁴ molecule cm⁻² for Bu-ol and Bu-acid, respectively (from the surface excess data already used for Fig. 2). The blue lines in Fig. 3a and b show the calculated relative change in the Br 3d photoemission signal as a function of mole fraction of organic with a = 0.25 for Bu-ol and a = −0.40 for Bu-acid, meaning that at saturating organic concentration Bu-ol enhances the bromide concentration within the layer of width Δ by 25%, while Bu-acid has the opposite effect of reducing the apparent bromide density in this layer by 40%. On a surface area basis, this means that ca. 8 × 10¹² ion cm⁻² are additionally drawn towards the surface in presence of Bu-ol or ca. 1 × 10¹² ion cm⁻² are moved away from the surface in presence of Bu-acid. The parameter a was chosen such that the calculated intensity and intensity ratio matched the measured ones, especially for the highest mole fractions. Clearly, the calculated Br 3d signal and also the ratio to the O 1s signal underestimates those measured at low Bu-ol mole fraction and overestimates that at low Bu-acid mole fraction. Apart from general uncertainty of the measurement and also of the surface excess, the response of the interfacial bromide density must not be linear with respect to the organic surface excess. These aspects must be elucidated by molecular simulations in the future.

Since the uncertainty for the iodide case is much larger due to the larger kinetic energy used, as discussed above, we applied exactly the same parameters to calculate signal intensities and ratios shown in Fig. 4. This indicates that Bu-ol and Bu-acid have a qualitatively similar effect on the density of iodide ions in the interfacial region as on that of bromide ions.

The uncertainty of the measured Na 2s signal intensity is relatively large in this work as mentioned upfront. Fig. 3c and d qualitatively indicate that the Na/O ratio rather shows opposite behavior from that of bromide in the case of Bu-ol. This suggests that the observed enrichment of bromide in presence of Bu-ol is not necessarily mediated by Na⁺. Earlier photoelectron spectroscopy experiments with a static saturated salt solution surface and related MD simulations proposed that cations may closely associate with the alcohol head group.^43,59 In turn, second harmonic spectroscopy (SHG) experiments for the water–dodecanol interface⁵⁶ indicated that dodecanol may change the solvation shell of interfacial bromide to increase its propensity for the interface. Huang et al.⁵⁴ further argue that this is in line with the smaller increase in NaBr–glycerol surface tension than in corresponding aqueous solutions. Close proximity of the strongly chaotropic thiocyanate anion at the interface of a long-chain alcohol and water was also reported by Onorato et al.⁵⁶ Also Wen et al.⁷⁴ found both iodide and chloride to reside more closely to the alcohol covered interface than the Na cations. Therefore, our present finding of bromide being attracted towards an alcohol surfactant covered interface is consistent with other recent evidence. The case of carboxylic acid is less straightforward. The Na 2s to O 1s signal intensity ratios do not show significant deviation of the behavior of the Na cations from that of bromide in presence of Bu-acid. Interactions between cations and the carboxylic acid headgroups of surfactant monolayers have been discussed, including the possibility of partial deprotonation.^57,75,76 Since detailed and more precise analysis of the abundance of Na ions was not within the scope of the present study, we refrain from a more detailed discussion of possible cation specific effects for this case.

Conclusions

The photoelectron spectroscopic investigation of ternary solutions by LJ-XPS demonstrates that 1-butanol and butyric acid exhibit surfactant behavior in line with known surface excess. Taking into account attenuation of photoelectrons by the aliphatic carbon overlayer established by the organic monolayer expressed by the surface excess allows quantifying the relative effect of 1-butanol and butyric acid on the relative abundance of bromide and iodide in the interfacial region. 1-Butanol increases the local density of both halide ions by about 25% above that of neat aqueous halide solutions. In turn, a saturated butyric acid monolayer led to reduction of the interfacial halide ion density by about 40%. Thus, the detailed headgroup properties of surfactants have a strong impact on the interfacial ion distribution. This has important implications for halogen activation processes, for which the availability of halide ions to atmospheric oxidants at the air–water interface is crucial.⁷⁷ The two examples also show that these effects may strongly vary, and further surfactant systems should be studied for a more detailed assessment of these effects for complex environmental conditions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was performed at the SIM beamline of the Swiss Light Source, Paul Scherrer Institute. The NAPP spectrometer is co-funded by PSI FoKo and SNF R’Equip programs. Inga Jordan and Hans Jakob Wörner are acknowledged for their technical support. This work was supported by the Swiss National Science Foundation (grants no. 149492 and 169176).

References

1. J. P. D. Abbatt, J. L. Thomas, K. Abrahamsson, C. Boxe, A. Granfors, A. E. Jones, M. D. King, A. Saiz-Lopez, P. B. Shepson, J. Sodeau, D. W. Toohey, C. Toubin, R. von Glasow, S. N. Wren and X. Yang, Atmos. Chem. Phys., 2012, 12, 6237–6271.
2. W. R. Simpson, S. S. Brown, A. Saiz-Lopez, J. A. Thornton and R. v. Glasow, Chem. Rev., 2015, 115, 4035–4062.
3. L. J. Carpenter, S. M. MacDonald, M. D. Shaw, R. Kumar, R. W. Saunders, R. Parthipan, J. Wilson and J. M. C. Plane, Nat. Geosci., 2013, 6, 108–111.
4. J. A. Schmidt, D. J. Jacob, H. M. Horowitz, L. Hu, T. Sherwen, M. J. Evans, Q. Liang, R. M. Suleiman, D. E. Oram, M. Le Breton, C. J. Percival, S. Wang, B. Dix and R. Volkamer, J. Geophys. Res., 2016, 121, 11819–11835.
5. T. Sherwen, M. J. Evans, L. J. Carpenter, J. A. Schmidt and L. J. Mickley, Atmos. Chem. Phys., 2017, 17, 1557–1569.
6. T. Sherwen, J. A. Schmidt, M. J. Evans, L. J. Carpenter, K. Großmann, S. D. Eastham, D. J. Jacob, B. Dix, T. K. Koenig, R. Sinreich, I. Ortega, R. Volkamer, A. Saiz-Lopez, C. Prados-Roman, A. S. Mahajan and C. Ordóñez, Atmos. Chem. Phys., 2016, 16, 12239–12271.
7. S. Wang, J. A. Schmidt, S. Baidar, S. Coburn, B. Dix, T. K. Koenig, E. Apel, D. Bowdalo, T. L. Campos, E. Eloranta, M. J. Evans, J. P. DiGangi, M. A. Zondlo, R.-S. Gao, J. A. Haggerty, S. R. Hall, R. S. Hornbrook, D. Jacob, B. Morley, B. Pierce, M. Reeves, P. Romashkin, A. ter Schure and R. Volkamer, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 9281–9286,  DOI:10.1073/pnas.1505142112.
8. L. J. Carpenter and P. D. Nightingale, Chem. Rev., 2015, 115, 4015–4034.
9. A. Saiz-Lopez and R. von Glasow, Chem. Soc. Rev., 2012, 41, 6448–6472.
10. K. W. Oum, M. J. Lakin, D. O. DeHaan, T. Brauers and B. J. Finlayson-Pitts, Science, 1998, 279, 74–77.
11. K. W. Oum, M. J. Lakin and B. J. Finlayson-Pitts, Geophys. Res. Lett., 1998, 25, 3923–3926.
12. S. W. Hunt, M. Roeselova, W. Wang, L. M. Wingen, E. M. Knipping, D. J. Tobias, D. Dabdub and B. J. Finlayson-Pitts, J. Phys. Chem. A, 2004, 108, 11559–11572.
13. D. Clifford and D. J. Donaldson, J. Phys. Chem. A, 2007, 111, 9809–9814.
14. N. W. Oldridge and J. P. D. Abbatt, J. Phys. Chem. A, 2011, 115, 2590–2598.
15. L. Artiglia, J. Edebeli, F. Orlando, S. Chen, M.-T. Lee, P. Corral Arroyo, A. Gilgen, T. Bartels-Rausch, A. Kleibert, M. Vazdar, M. Andres Carignano, J. S. Francisco, P. B. Shepson, I. Gladich and M. Ammann, Nat. Commun., 2017, 8, 700.
16. A.-u.-H. A. Shah, K. Ali and S. Bilal, Colloids Surf., A, 2013, 417, 183–190.
17. P. K. Weissenborn and R. J. Pugh, J. Colloid Interface Sci., 1996, 184, 550–563.
18. M. A. Brown, R. D'Auria, I. F. W. Kuo, M. J. Krisch, D. E. Starr, H. Bluhm, D. J. Tobias and J. C. Hemminger, Phys. Chem. Chem. Phys., 2008, 10, 4778–4784.
19. S. Ghosal, J. C. Hemminger, H. Bluhm, B. S. Mun, E. L. D. Hebenstreit, G. Ketteler, D. F. Ogletree, F. G. Requejo and M. Salmeron, Science, 2005, 307, 563–566.
20. C. Caleman, J. S. Hub, P. J. van Maaren and D. van der Spoel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6838–6842.
21. T. M. Chang and L. X. Dang, Chem. Rev., 2006, 106, 1305–1322.
22. L. X. Dang and T. M. Chang, J. Phys. Chem. B, 2002, 106, 235–238.
23. D. Horinek, A. Herz, L. Vrbka, F. Sedlmeier, S. I. Mamatkulov and R. R. Netz, Chem. Phys. Lett., 2009, 479, 173–183.
24. T. Ishiyama and A. Morita, J. Phys. Chem. C, 2007, 111, 721–737.
25. P. Jungwirth and D. J. Tobias, J. Phys. Chem. B, 2001, 105, 10468–10472.
26. P. Jungwirth and D. J. Tobias, Chem. Rev., 2006, 106, 1259–1281.
27. P. B. Petersen and R. J. Saykally, Annu. Rev. Phys. Chem., 2006, 57, 333–364.
28. M. Vazdar, E. Pluharova, P. E. Mason, R. Vacha and P. Jungwirth, J. Phys. Chem. Lett., 2012, 3, 2087–2091.
29. H. C. Allen, N. N. Casillas-Ituarte, M. R. Sierra-Hernandez, X. Chen and C. Y. Tang, Phys. Chem. Chem. Phys., 2009, 11, 5538–5549.
30. N. N. Casillas-Ituarte, K. M. Callahan, C. Y. Tang, X. Chen, M. Roeselová, D. J. Tobias and H. C. Allen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6616–6621.
31. S. Ghosal, M. A. Brown, H. Bluhm, M. J. Krisch, M. Salmeron, P. Jungwirth and J. C. Hemminger, J. Phys. Chem. A, 2008, 112, 12378–12384.
32. S. Gopalakrishnan, D. Liu, H. C. Allen, M. Kuo and M. J. Shultz, Chem. Rev., 2006, 106, 1155–1175.
33. N. Ottosson, L. Cwiklik, J. Söderstrom, O. Björneholm, G. Öhrwall and P. Jungwirth, J. Phys. Chem. Lett., 2011, 2, 972–976.
34. G. Olivieri, K. M. Parry, C. J. Powell, D. J. Tobias and M. A. Brown, J. Chem. Phys., 2016, 144, 154704.
35. I. Gladich, P. Shepson, I. Szleifer and M. Carignano, Chem. Phys. Lett., 2010, 489, 113–117.
36. I. Gladich, P. B. Shepson, M. A. Carignano and I. Szleifer, J. Phys. Chem. A, 2011, 115, 5895–5899.
37. Y. Sakamoto, M. Goda and J. Hirokawa, J. Phys. Chem. A, 2018, 122, 2723–2731.
38. G. Olivieri, K. M. Parry, R. D’Auria, D. J. Tobias and M. A. Brown, J. Phys. Chem. B, 2018, 122, 910–918.
39. D. J. Donaldson and C. George, Environ. Sci. Technol., 2012, 46, 10385–10389.
40. P. A. Alpert, R. Ciuraru, S. Rossignol, M. Passananti, L. Tinel, S. Perrier, Y. Dupart, S. S. Steimer, M. Ammann, D. J. Donaldson and C. George, Sci. Rep., 2017, 7, 12693.
41. R. Chiu, L. Tinel, L. Gonzalez, R. Ciuraru, F. Bernard, C. George and R. Volkamer, Geophys. Res. Lett., 2017, 44, 1079–1087.
42. L. Tinel, S. Dumas and C. George, C. R. Chim., 2014, 17, 801–807.
43. M. J. Krisch, R. D'Auria, M. A. Brown, D. J. Tobias, J. C. Hemminger, M. Ammann, D. E. Starr and H. Bluhm, J. Phys. Chem. C, 2007, 111, 13497–13509.
44. M. P. Seah and W. A. Dench, Surf. Interface Anal., 1979, 1, 2–11.
45. N. Ottosson, M. Faubel, S. E. Bradforth, P. Jungwirth and B. Winter, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 60–70.
46. H. Shinotsuka, B. Da, S. Tanuma, H. Yoshikawa, C. J. Powell and D. R. Penn, Surf. Interface Anal., 2017, 49, 238–252.
47. S. Thürmer, R. Seidel, M. Faubel, W. Eberhardt, J. C. Hemminger, S. E. Bradforth and B. Winter, Phys. Rev. Lett., 2013, 111, 173005.
48. M. A. Brown, A. B. Redondo, I. Jordan, N. Duyckaerts, M.-T. Lee, M. Ammann, F. Nolting, A. Kleibert, T. Huthwelker, J.-P. Maechler, M. Birrer, J. Honegger, R. Wetter, H. J. Woerner and J. A. van Bokhoven, Rev. Sci. Instrum., 2013, 84, 073904.
49. M. A. Brown, M. Faubel and B. Winter, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2009, 105, 174.
50. B. Winter, Nucl. Instr. Meth., 2009, 601, 139–150.
51. G. Olivieri, J. B. Giorgi, R. G. Green and M. A. Brown, J. Electron Spectrosc. Relat. Phenom., 2017, 216, 1–16.
52. M.-T. Lee, F. Orlando, L. Artiglia, S. Chen and M. Ammann, J. Phys. Chem. A, 2016, 120, 9749–9758.
53. M.-T. Lee, M. A. Brown, S. Kato, A. Kleibert, A. Tuerler and M. Ammann, J. Phys. Chem. A, 2015, 119, 4600–4608.
54. Z. Huang, W. Hua, D. Verreault and H. C. Allen, J. Phys. Chem. A, 2013, 117, 6346–6353.
55. Z. Huang, W. Hua, D. Verreault and H. C. Allen, J. Phys. Chem. A, 2013, 117, 13412–13418.
56. R. M. Onorato, D. E. Otten and R. J. Saykally, J. Phys. Chem. C, 2010, 114, 13746–13751.
57. C. Y. Tang and H. C. Allen, J. Phys. Chem. A, 2009, 113, 7383–7393.
58. H. I. Okur, J. Kherb and P. S. Cremer, J. Am. Chem. Soc., 2013, 135, 5062–5067.
59. D. J. Tobias and J. C. Hemminger, Science, 2008, 319, 1197–1198.
60. D. J. Donaldson and D. Anderson, J. Phys. Chem. A, 1999, 103, 871–876.
61. K. Granados, J. Gracia-Fadrique, A. Amigo and R. Bravo, J. Chem. Eng. Data, 2006, 51, 1356–1360.
62. M. Faubel, B. Steiner and J. P. Toennies, J. Chem. Phys., 1997, 106, 9013–9031.
63. J. G. Pruyne, M.-T. Lee, C. Fábri, A. Beloqui Redondo, A. Kleibert, M. Ammann, M. A. Brown and M. J. Krisch, J. Phys. Chem. C, 2014, 118, 29350–29360.
64. G. Olivieri, A. Goel, A. Kleibert and M. A. Brown, J. Synchrotron Radiat., 2015, 22, 1528–1530.
65. G. Ketteler, P. Ashby, B. S. Mun, I. Ratera, H. Bluhm, B. Kasemo and M. Salmeron, J. Phys.: Condens. Matter, 2008, 20, 184024.
66. M. A. Brown, F. Vila, M. Sterrer, S. Thuermer, B. Winter, M. Ammann, J. J. Rehr and J. A. van Bokhoven, J. Phys. Chem. Lett., 2012, 3, 1754–1759.
67. J. J. Yeh and I. Lindau, At. Data Nucl. Data Tables, 1985, 32, 1–155.
68. M. M. Walz, C. Caleman, J. Werner, V. Ekholm, D. Lundberg, N. L. Prisle, G. Öhrwall and O. Björneholm, Phys. Chem. Chem. Phys., 2015, 17, 14036–14044.
69. M. M. Walz, J. Werner, V. Ekholm, N. L. Prisle, G. Öhrwall and O. Björneholm, Phys. Chem. Chem. Phys., 2016, 18, 6648–6656.
70. M. Fyta and R. R. Netz, J. Chem. Phys., 2012, 136, 124103.
71. J. Li and F. Wang, J. Chem. Phys., 2015, 143, 194505.
72. M. D. Baer and C. J. Mundy, J. Phys. Chem. Lett., 2011, 2, 1088–1093.
73. B. Hess, C. Holm and N. van der Vegt, Phys. Rev. Lett., 2006, 96, 147801.
74. Y.-C. Wen, S. Zha, C. Tian and Y. R. Shen, J. Phys. Chem. C, 2016, 120, 15224–15229.
75. E. F. Aziz, N. Ottosson, S. Eisebitt, W. Eberhardt, B. Jagoda-Cwiklik, R. Vácha, P. Jungwirth and B. Winter, J. Phys. Chem. B, 2008, 112, 12567–12570.
76. J. S. Uejio, C. P. Schwartz, A. M. Duffin, W. S. Drisdell, R. C. Cohen and R. J. Saykally, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 6809–6812.
77. C. G. Moreno, O. Gálvez, V. López-Arza Moreno, E. M. Espildora-García and M. T. Baeza-Romero, Phys. Chem. Chem. Phys., 2018, 20, 27571–27584.

---

Footnotes

† Electronic supplementary information (ESI) available: Description of molecular dynamics simulations, their results and comparison to experimental data. See DOI: 10.1039/c8cp07448h

‡ Now at: Dept. of Chemistry – Ångström Laboratory, Lägerhyddsvägen 1, Polacksbacken, 751 21 Uppsala, Sweden.

§ Passed away.

---