Spectroscopic characterisation of centropolyindanes

Abstract

A highly promising class of three-dimensional polyaromatic hydrocarbons comprises the centropolyindanes. The characteristic feature of these compounds is the mutual fusion of several molecules of indane along the saturated C–C bonds of their cyclopentane rings. Among the polycyclic aromatic hydrocarbons, the centropolyindanes are special because of the saturated core of sp³-hybridised carbon atoms embedded in a three-dimensional environment of aromatic building blocks. While the centropolyindanes and their numerous derivatives have been studied in detail by NMR spectroscopy, mass spectrometry and X-ray diffraction, investigation of their vibrational features, and especially those of the neopentane core present in most cases, have not been performed so far. In the present paper, we report the first systematic study of a set of centropolyindanes by vibrational spectroscopy, using inelastic neutron scattering (INS), infrared and Raman spectroscopies.

---

Introduction

In the past decades, the combination of the fundamental structural tool-kit of organic chemistry with geometrically strict motifs has led to an enormous expansion of non-natural molecular architecture that represents a classical field of chemical research.¹ This holds true in particular for ideally two-dimensional carbon frameworks based on hexagonal benzene building blocks^2,3 as well as for the distorted variants, most of which contain non-hexagonal, such as five-, seven- and eight-membered ring elements,^4–9 and includes tube-like¹⁰ and fully globular carbon networks.¹¹ Other albeit less variable molecular motifs comprise linear, acetylene- and cumulene-based carbon chains.¹² Strictly three-dimensional carbon-based constructs have remained relatively scarce but have started to gain increasing attention.^13–17 In this context, a highly promising class of novel three-dimensional molecular motifs comprises the centropolyindanes.¹⁸

The characteristic feature of the centropolyindane hydrocarbons is the mutual fusion of several molecules of indane (1, Chart 1) along the saturated C–C bonds of their five-membered (cyclopentane) rings. For example, several centrotriindanes are known, such as triptindane, 2 (a tribenzo[3.3.3]propellane or “monofuso-centrotriindane”),^13,19,20 the angularly fused difuso-centrotriindane 4,²¹ and tribenzotriquinacene 3 (a trifuso-centrotriindane).^22,23 Fenestrindane, 6,²⁴ represents one of the two possible regular centrotetraindanes.¹⁸ As an extreme, six indane units can be merged about a common neopentane core, generating centrohexaindane, which has been addressed as a “Cartesian” hydrocarbon due to the strictly orthogonal orientation of its six benzene units in space.²⁵ In recent years, decisive progress has been made to merge the particular structural motifs of tribenzotriquinacene (3) and fenestrindane (6) with genuine benzenoid frameworks.^26,27

Chart 1 Structures of the compounds studied. Below the sample numbers, the chemical name, the empirical formula and the molecular point group are given. If the solid-state structure has been determined, the space group, followed by the Cambridge Structural Database²⁹ refcode and the reference to the structure are also presented. Ball-and-stick representations of the structures are given in Fig. S1–S6, S13, S15, S17 and S19 of the ESI.†

Among the polycyclic aromatic hydrocarbons, the centropolyindanes are special because of the saturated, sp³-hybridised core embedded in a three-dimensional environment of aromatic building blocks. While these three-dimensional hydrocarbons and their numerous derivatives have been studied in detail by NMR spectroscopy, mass spectrometry and X-ray diffraction,²⁸ investigation of their vibrational features, and especially those of the neopentane core, have not been performed so far. In the present paper, we report the first systematic study of a set of centropolyindanes by vibrational spectroscopy, using inelastic neutron scattering (INS), infrared and Raman spectroscopies. The nine centropolyindanes, 2–10, investigated here are displayed in Chart 1, along with their structural parent hydrocarbon, indane (1).

Experimental

Materials

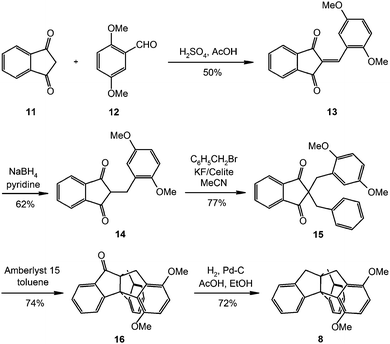
Indane (Aldrich, 95%) was used as received. Triptindane (2),²⁰ tribenzotriquinacene (3),²² difuso-centrotriindane (4),²¹ tribenzo[5.5.5.5]fenestrene (5),²⁴ fenestrindane (6),²⁴ triptindan-9-one (7),²⁰ 12d-methyltribenzotriquinacene (9)²¹ and 4b,8b,12b,12d-tetramethyltribenzotriquinacene (10)³⁰ were synthesised as described in the literature.¹⁸ The synthesis of 1,4-dimethoxytriptindane (8) was performed as shown in Scheme 1. The details are given in the ESI.†

Scheme 1 Synthesis of 1,4-dimethoxytriptindane (8).

Vibrational spectroscopy

Inelastic neutron scattering (INS) spectra were recorded at less than 20 K using TOSCA³¹ at ISIS (http://www.isis.stfc.ac.uk/). The spectra are available at the INS database: http://wwwisis2.isis.rl.ac.uk/INSdatabase/. Infrared spectra were recorded using a Bruker Vertex70 FTIR spectrometer, over the range 100 to 4000 cm⁻¹ at 4 cm⁻¹ resolution with a DLaTGS detector using 64 scans and the Bruker Diamond ATR. Variable temperature infrared spectra were recorded for some samples using a Specac Golden Gate accessory. The use of the ultra-wide range beam splitter enabled the entire spectral range to be recorded without the need to change beam splitters. The spectra have been corrected for the wavelength-dependent variation in path length using the Bruker software. FT-Raman spectra were recorded with a Bruker MultiRam spectrometer using 1064 nm excitation, 4 cm⁻¹ resolution, 500 mW laser power and 64 scans. Variable temperature Raman spectra were recorded using 785 nm excitation and a Renishaw InVia spectrometer that has been previously described.³² For both Raman instruments, the low wavenumber limit was ∼50 cm⁻¹, as determined by the laser line rejection filter.

Computational studies

Isolated molecule calculations were carried out with Gaussian 03 and Gaussian 09.³³ In both cases, the 6-311G(d) basis set was used with the B3LYP hybrid functional. Solid state calculations used the plane wave pseudopotential-based program CASTEP^34,35 with the inclusion of the Tkatchenko and Scheffler³⁶ dispersion correction for the calculation of the vibrational transition energies and their intensities. The generalized gradient approximation Perdew–Burke–Ernzerhof functional was used in conjunction with optimized norm-conserving pseudopotentials. All of the calculations were converged to better than |0.0035| eV Å⁻¹. After geometry optimization, the vibrational spectra were calculated in the harmonic approximation using density functional perturbation theory. Both Gaussian and CASTEP generate the vibrational eigenvalues and eigenvectors, which allows visualization of the modes within GaussView³⁷ and Materials Studio (http://accelrys.com/products/collaborative-science/biovia-materials-studio/) respectively. It is also the information needed to calculate the INS spectrum using the program ACLIMAX.³⁸ Infrared and Raman spectra were generated from the Gaussian output using either GaussView or GaussSum.³⁹ We emphasize that the transition energies have not been scaled.

Results and discussion

The structures of the compounds studied are shown in Chart 1. Ball-and-stick representations are given in Fig. S1–S6, S13, S15, S17 and S19 of the ESI.† For some of the compounds, the structure is known from X-ray crystallography (2,⁴⁰3,⁴¹6²⁴ and 9^30,41), the remainder have been characterised by solution NMR spectroscopy and mass spectrometry. This group of compounds was chosen so as to examine: (i) how the progressive addition of indane (1) sub-units to the core (2, 3, 4, 5, 6) and (ii) substitution of the indane framework (2, 7, 8) and substitution at the central carbons (3, 9, 10) modifies the spectra.

Fig. 1–3 show the INS, infrared and FT-Raman spectra of a series of compounds in order of increasing complexity (1, 2, 3, 4, 5, 6). The three types of spectra for each compound are shown in Fig. S1–S6 (ESI†).

Fig. 1 INS spectra from top to bottom of: solid indane (1), triptindane (2), tribenzotriquinacene (3), difuso-centrotriindane (4), tribenzo[5.5.5.5]fenestrene (5) and fenestrindane (6).

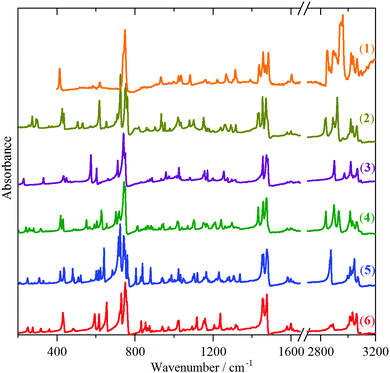Fig. 2 Infrared spectra from top to bottom of: solid indane (1), triptindane (2), tribenzotriquinacene (3), difuso-centrotriindane (4), tribenzo[5.5.5.5]fenestrene (5) and fenestrindane (6).

Fig. 3 FT-Raman spectra from top to bottom of: solid indane (1), triptindane (2), tribenzotriquinacene (3), difuso-centrotriindane (4), tribenzo[5.5.5.5]fenestrene (5) and fenestrindane (6). The right-hand side set of spectra (500–3200 cm⁻¹) are ×2, ×3, ×4, ×5, ×4, ×4 respectively, ordinate expanded relative to the left-hand side set (50–500 cm⁻¹).

While the spectra are clearly very rich, each technique shows a remarkable similarity between the different molecules. In the INS spectra (Fig. 1), the overall pattern is similar in the 400–1600 cm⁻¹ range, in the infrared spectra (Fig. 2), strong bands are seen at ∼450, 750 and 1480 cm⁻¹, and in the Raman spectra (Fig. 3), strong modes occur at ∼150, 750, 1020 and 1600 cm⁻¹. This suggests that the vibrational spectra are largely characteristic of indane. While it is perhaps unsurprising that the aromatic modes are largely unchanged, the very different central framework of the molecules might have been expected to be reflected in the spectra. The approach that has been adopted was to carry out a detailed assignment of the parent molecule, indane (1), and then to examine the differences between the systems.

Indane (1)

Indane (1) has two possible conformations of the C5 ring: planar (C_2v) and buckled (C_s). It is formally a cyclopentene derivative and the parent molecule is known to be puckered,^42,43i.e., to have C_s symmetry. Further, while the crystal structure of indane itself is not known, that of many of its derivatives are known and these all exhibit a puckered C5 ring. For example, in 4- and 5-nitroindane⁴⁴ the CH₂ group is 5.0° and 12.7° out of the ring and in trans,trans-1,2,3-triphenylindane⁴⁵ it is 16.9° out of the ring. An isolated molecule, i.e. gas phase, calculation of the planar C_2v structure found one imaginary mode that corresponded to movement of the CH₂ group out-of-the plane. Comparison of the calculated isolated molecule buckled (C_s) structure with the gas phase structure⁴⁶ shows good agreement.

Fig. 4 compares the experimental solid state INS spectrum and the calculated isolated (i.e. gas phase) molecule INS spectrum of indane. The isolated molecule does not include the lattice modes (the intense broad band centered at ∼100 cm⁻¹ in Fig. 4a) but in the internal mode region above 150 cm⁻¹, it can be seen that the agreement is excellent. Fig. S7 (ESI†) shows similarly good agreement for the infrared spectra, with the exception of the C–H stretch modes which are, as is the usual case, calculated at too high an energy. This is because the calculation assumes a harmonic potential and the real system is anharmonic.⁴⁷

Fig. 4 Comparison of INS spectra of indane (1): (a) experimental in the solid state and (b) calculated for the isolated molecule. The bands below 150 cm⁻¹ in (a) are the lattice modes and are outside of the scope of the calculation shown in (b).

Spectroscopic studies of indane have been dominated by attempts to determine the puckering potential in the gas phase.^48–50 The infrared and Raman spectra and their assignment for the liquid phase have been reported;⁵¹ there are no data for the solid state. Table S1 (ESI†) lists the observed and calculated transition energies and their assignment. These are largely in agreement with the only previous work,⁵¹ which was based on an empirical force field. The disagreements are mainly in the low energy region, <500 cm⁻¹, where the infrared and Raman bands are weak, whereas the deformations result in large amplitude motions of the hydrogen atoms and hence strong INS modes. It is noteworthy that the transition energies of the phenylene (C₆H₄) modes are typical of those found for ortho-disubstituted benzenes.^52,53

Comparison of the spectra

As crystal structures are not available for the whole set of the compounds, we anticipated that in the absence of significant intermolecular interactions, the isolated molecule approximation should provide a good description of the vibrational spectra. To enable comparisons, this was used for all of the molecules. Tribenzotriquinacene (3) is the simplest of the centropolyindanes studied here, consisting of three fused indane sub-units, sharing the common apical carbon of the five-membered rings. This provides a test of this assumption as the crystal structure is known.⁴¹ It consists of stacks of molecules aligned along the c-axis, with the closest intermolecular distance being H⋯H contacts at 2.220 Å. Fig. 5 compares the experimental INS spectrum with those calculated using the isolated molecule approximation (Gaussian) and the full periodic calculation (CASTEP). It can be seen that both methods are in good agreement with the data and while the CASTEP calculation produces a better overall match, the differences are small, justifying the use of isolated molecule calculations.

Fig. 5 Comparison of INS spectra of tribenzotriquinacene (3): experimental spectrum (middle) and those calculated using the isolated molecule approximation (bottom, Gaussian) and from a full periodic calculation (top, CASTEP).

For molecular solids such as these it might be expected that inclusion of long-range interactions would be required to obtain good agreement between experiment and theory. We have investigated this possibility for both intermolecular and intramolecular consequences. As explained further in the ESI,† the effect of the inclusion of the long-range interactions via the Tkatchenko and Scheffler³⁶ (TS) correction is very small for the systems studied here.

Fig. S8–S12 (ESI†) compare the calculated and observed INS and infrared spectra for the centropolyindanes 2–6. In all cases the agreement is acceptable and enables assignments to be made. As suggested by the comparison with indane, the strong infrared features at 450, 750 and 1480 cm⁻¹ are assigned as phenylene modes (the Wilson⁵² labelling of the parent benzene modes is given in brackets): out-of-plane ring deformation (16b), C–H out-of-plane bend (11) and C–C stretch (19a), respectively. Similarly, for the Raman spectra, the strong mode at ∼1020 cm⁻¹ is the phenylene C–H in-plane bend (18b). All of the centropolyindanes have a very strong Raman mode (note the difference in ordinate scales between the left and right sides of Fig. 3) at ∼100 cm⁻¹, and compounds 2, 4, 5 and 6, but neither indane (1) nor tribenzotriquinacene (3) have a strong mode at ∼150 cm⁻¹. (The same modes are also seen in the INS spectra.) Visualisation of the modes shows that the 100 cm⁻¹ mode is related to the indane mode at ∼160 cm⁻¹, (C9–C1 + C4–C3 in-phase torsion), that has shifted down in energy because of the replacement of hydrogen atoms by the heavier indane moieties. This fragment is common to all the molecules and thus appears in all their spectra. In contrast, the ∼150 cm⁻¹ mode involves the central neopentane core and is formally derived from one component of ν₁₉, a triply degenerate C–C–C bending motion.⁵⁴ This explains why it is only seen in compounds 2, 4, 5 and 6: only these have the fully developed neopentane core. The modes are shown in Fig. 6 for fenestrindane (6), together with a comparison of the calculated spectra for the isolated molecule (Z = 1) and the primitive cell (Z = 2). It can be seen that for these very low energy modes there is a small, but significant, influence of the intermolecular interactions.

Fig. 6 Comparison of Raman spectra of fenestrindane (6) in the low energy region: experimental (FT-R) spectrum and that calculated using the isolated molecule approximation (Z = 1) and from a full periodic calculation (Z = 2). The top part shows the torsional mode and the lower part the neopentane-derived mode. Note the different displacements of the indane rings.

At the opposite end of the spectra, the C–H stretch region is remarkably simple (Fig. 7). In the aromatic region, >3000 cm⁻¹, for both the Raman and the infrared spectra the pattern found for indane is largely replicated, consisting of two and three bands, respectively. This indicates that, in all the samples, the phenylene groups of the indane residues behave as independent entities, there is little or no coupling between them. The aliphatic region shows more variety, but this is understandable because of the different types of C–H groups present. Thus indane (1) has three methylene groups, which, as the spectra indicate, are coupled (since there are more than the two modes expected for isolated oscillators: the symmetric, ∼2850 cm⁻¹, and asymmetric, ∼2940 cm⁻¹, H–C–H stretch modes). Triptindane (2) also has three methylene groups, but these are separated from each other by the central carbon atom. Nonetheless, the spectrum resembles that of indane. Compounds 3, 5 and 6 each contain four bridgehead methine groups but only show a single band at ∼2890 cm⁻¹, in both the Raman and infrared spectra. Difuso-centrotriindane 4 bears two methine groups and two methylene groups; thus the spectrum shows the methylene doublet at 2840 and 2930 cm⁻¹, and the methine band at 2900 cm⁻¹.

Fig. 7 Raman (left) and infrared (right) spectra in the C–H stretch region, from top to bottom, of: solid indane (1), triptindane (2), tribenzotriquinacene (3), difuso-centrotriindane (4), tribenzo[5.5.5.5]fenestrene (5) and fenestrindane (6).

The C–C stretch modes

Potentially, the most interesting modes are those that involve carbon atoms that are common to two or more indane sub-units because these reflect the strength of the bonding between the indane sub-units. However, as we have already seen, the spectra are dominated by the ortho-phenylene modes and the aliphatic framework does not contribute strong modes (except for the low energy deformation mode described previously). The DFT-calculated INS spectra provide a means to access the aliphatic C–C stretch modes. By setting the cross sections of all the atoms to zero except those of interest, the resulting “pseudo-spectra” only contain modes where the atom(s) of interest have significant motion. Fig. 8 shows the results of this exercise where only the carbon atom that is common to the most indane sub-units has a non-zero cross section. Thus for compounds 2, 3, 4 and 5 the common carbon atom links three indane sub-units and for compound 6 it links four indane sub-units. For tribenzotriquinacene (3) this is a tertiary carbon atom, for the hydrocarbons 2, 4, 5 and 6 it is a quaternary carbon atom.

Fig. 8 INS pseudo-spectra generated from the DFT calculations showing only the modes that involve motion of the central carbon atom(s). From top to bottom: triptindane (2), tribenzotriquinacene (3), difuso-centrotriindane (4), tribenzo[5.5.5.5]fenestrene (5) and fenestrindane (6).

From Fig. 8, it can be seen that there are three regions where there is significant motion of the atom of interest: 450–650 cm⁻¹, 1000–1150 cm⁻¹ and 1250–1400 cm⁻¹. Note that the pseudo-spectra only report modes where there is motion of the atom, not whether it is the driving force of the mode. Visualisation of the modes shows that the intensity in the 1250–1400 cm⁻¹ region is a consequence of the requirement for a normal mode that the centre of mass is invariant, thus atoms can move simply to satisfy this criterion, even though there is no change in bond lengths or angles that involve the atoms. A similar situation is found for the modes at 450–650 cm⁻¹, although in the case of compounds 2 and 3 the mode around 550 cm⁻¹ does include contributions from C–C–C bending modes involving the atom of interest. The modes at 1000–1150 cm⁻¹ do have large components of motion that contain C–C stretch modes of the central carbon atom. In triptindane (2), the C–C stretch of the central carbon atoms (the two common to all three indane sub-units) is calculated at 1047 cm⁻¹ (1036 cm⁻¹ observed). The similarity of the transition energy in all cases indicates that the bonding is also of similar strength; the additional indane unit makes little difference to the transition energy for fenestrindane (6). What is apparent is that the local symmetry around the carbon atom is important: for compounds 2 and 3 it is trigonal (C_3v) and this gives two modes, for compounds 4, 5 and 6 it is tetrahedral (T_d). This results in a triply degenerate asymmetric stretch mode (T₂) and a non-degenerate symmetric (A₁) C–C stretch mode. While the local symmetry is T_d, the molecular symmetry is lower and this lifts the degeneracy of the T₂ mode, so for 6, the mode at 1065 cm⁻¹ actually consists of three components, calculated at 1063, 1069 and 1070 cm⁻¹. For 4, 5 and 6 the A₁ mode is found at 671, 661 and 657 cm⁻¹ respectively. This is either very weak or absent from the spectra in Fig. 8 because in T_d symmetry the mode does not involve displacement of the central atom. For comparison, in neopentane⁵⁴ the C–C stretch modes occur at 924 (T₂) and 733 cm⁻¹ (A₁).

The effect of substitution

The compounds investigated also enable insights into how substitution of the indane framework (2, 7 and 8) and substitution at the central carbons (3, 9 and 10) modifies the spectra.

Substitution of the indane framework. Fig. 9 shows the infrared spectra of triptindane (2), triptindan-9-one (7) and 1,4-dimethoxytriptindane (8). For the derivatives 7 and 8, the corresponding INS and FT-Raman spectra and their comparison to the calculated spectra are shown in Fig. S13–S16 (ESI†). In compounds 7 and 8 only one and two carbon atoms, respectively, of 23 in the parent triptindane (2) are substituted; therefore, the overall effect on the spectra might be expected to be small. The profiles in all three cases are broadly similar, again reflecting that the spectra are largely determined by the aromatic rings. However, the substituents are clearly present, as evidenced by the strong carbonyl band at 1706 cm⁻¹ in ketone 7 and the strong peaks at 1077, 1089, 1251 cm⁻¹ and the increased width of the modes at ∼1450 cm⁻¹ in the dimethoxy compound 8.

Fig. 9 Infrared spectra of triptindane (2), triptindan-9-one (7) and 1,4-dimethoxytriptindane (8).

The carbonyl peak position in 7 is unusual: in cyclopentanone it occurs at 1746 cm⁻¹, well above the usual range of 1710–1720 cm⁻¹ for dialkyl ketones; the difference is ascribed to the effects of ring strain.⁵³ More generally, alkyl–aryl ketones show C=O stretch bands in the range 1680–1690 cm⁻¹.⁵⁵ Thus aryl substitution decreases the carbonyl transition energy by ∼30 cm⁻¹, which is consistent with the carbonyl transition energy of 1-indanone being 1715 cm⁻¹. The further small decrease must be the result of a long-range interaction with the two other indane rings, since in benzophenone the carbonyl transition energy is 1660 cm⁻¹. That this is an electronic effect and not a ring strain effect is demonstrated by the C–C(=O)–C angles in cyclopentanone,⁵⁶ 1-indanone⁵⁷ and triptindan-9-one (7) being 108.3/109.1° (there are two independent molecules in the unit cell), 107.5° and 107.3° (calculated) respectively, i.e. essentially the same, but showing a 40 cm⁻¹ difference in transition energy.

The new peaks at 1077, 1089, 1251 cm⁻¹ and the increased width of the modes at ∼1450 cm⁻¹ in 1,4-dimethoxytriptindane (8) are all associated with the aryl–O–CH₃ functionality. They are assigned as: the O–CH₃ stretches (1077, 1089 cm⁻¹), the aryl–O stretch (1251 cm⁻¹) and the symmetric and asymmetric methyl deformations (1435–1470 cm⁻¹).⁵⁵

The C–H stretch region of ketone 7 is very similar to that of the parent hydrocarbon 2 apart from a general weakening of the bands. For the dimethoxy compound 8, this region is made more complex by the addition of the symmetric and asymmetric methyl C–H stretch modes at the usual positions (∼2880 and 2980 cm⁻¹).⁵⁵

Substitution at the central carbon atoms. Fig. 10 shows the low energy part of the INS spectra and the C–H stretch region of the FT-Raman spectra of the tribenzotriquinacenes 3, 9 and 10. (The complete INS, infrared and Raman spectra of the derivatives 9 and 10 and their comparison to the calculated spectra are shown in Fig. S17–S20, ESI†). The most striking changes in the INS spectra occur in the low-energy region, which is where the torsional modes occur. These are usually only easily seen in the INS spectrum. Comparison of the spectra shown in Fig. 10 demonstrates that the intensities of the tribenzotriquinacene framework modes, e.g. at 350, 425 and 575 cm⁻¹, are similar in all three cases. (Note that the spectra are normalised to one mole of sample and are plotted on the same scale, so the intensities are directly comparable between the samples.) The most striking feature in the spectrum of 12d-methyltribenzotriquinacene 9 in Fig. 10 is the enormously strong mode at 296 cm⁻¹. This is assigned to the methyl torsion (and confirmed by DFT), whereas the strong mode at 252 cm⁻¹ is attributed to the doubly degenerate framework-CH₃ bending mode. The methyl torsion seen here is anomalously high in energy; the methyl torsions in the n-alkanes all occur at ∼250 cm⁻¹.^58,59 The unusually high energy does not appear to be a consequence of the crystal packing:^30,41 the closest contacts are at 2.6 Å and do not involve the methyl group.

Fig. 10 Spectra of tribenzotriquinacene (3), 12d-methyltribenzotriquinacene (9) and 4b,8b,12b,12d-tetramethyltribenzotriquinacene (10). Left: INS spectra in the low energy region. Note that the INS spectra are normalised to one mole of sample and are plotted on the same ordinate scale (they are vertically displaced for clarity) so the intensities are directly comparable between the samples. Right: FT-Raman spectra in the C–H stretch region.

It might be expected that the addition of more methyl groups in the fully methylated tribenzotriquinacene 10 would simply result in a corresponding number of very intense torsional modes. This is not the case; rather, a complex manifold of modes is observed (Fig. 10). The DFT calculations show that the four methyl torsions occur at: 239 (265), 277 (293) and 392 (387) cm⁻¹ (experimental values in brackets). Visualisation of the modes provides two surprises: firstly, although the 293 cm⁻¹ mode in the tetramethyl derivative 10 is at the same transition energy as for the monomethyl analogue 9, it does not involve the central methyl group, only the peripheral ones. It is a doubly degenerate mode, so its intensity is doubled, otherwise all of the modes would have comparable intensity. Secondly, the central methyl's torsion occurs at 387 cm⁻¹ and, in contrast to the other torsional modes (which are almost pure torsions), it is highly mixed with the tribenzotriquinacene framework modes. A methyl torsion at this energy is completely unprecedented.

In the C–H stretch region, the aromatic modes above 3000 cm⁻¹ are very similar for all three tribenzotriquinacenes 3, 9 and 10. For the parent material, 3, with four methine C–H groups, the classical methine stretch at 2901 cm⁻¹ is seen, involving all four methines. In addition there is a band at 2976 cm⁻¹ which is almost a pure C–H stretch of the central methine group. On substitution by the methyl group in hydrocarbon 9, this vanishes and is replaced by weak modes at 2863 cm⁻¹ (CH₃ symmetric stretch) and 2924/2959 cm⁻¹ (CH₃ asymmetric stretch). Complete substitution of the methine hydrogens in compound 10 by methyl groups results in the disappearance of the 2901 cm⁻¹ band and the appearance of a cluster of bands in the regions expected for the symmetric and asymmetric methyl stretch modes.⁵⁵

Conclusions

The vibrational spectra of a set of various centropolyindanes has provided insights into the bonding present and some surprises. The spectra clearly show that the ortho-phenylene rings of the indane sub-units largely behave as independent entities. There is no evidence for any significant coupling between them, as demonstrated by the similarity of the spectra, both to each other and to the parent molecule, indane (1). The C–C stretch modes of the carbon atoms that are common to two or more indane sub-units occur in the usual range associated with sp³ C–C bonds, suggesting that these are conventional bonds.

The surprises occur on substitution of the molecules. Thus the carbonyl stretch mode of triptindan-9-one (7) is lower than would be expected. This is not a ring strain effect, but appears to be a longer-range effect of the additional ortho-phenylene rings. Methyl substitution in the tribenzotriquinacene derivatives 9 and 10 produces methyl torsional modes that are the highest known. The assignments provided here are a reference for future studies of these unusual hydrocarbons.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The STFC Rutherford Appleton Laboratory is thanked for access to neutron beam facilities. Computing resources (time on the SCARF compute cluster for the CASTEP and Gaussian calculations) was provided by STFC's e-Science facility. This research has been performed with the aid of facilities at the Research Complex at Harwell (RCaH), including the FT-Raman spectrometer. The authors would like to thank the Research Complex for access and support to these facilities and equipment.

Notes and references

1. H. Hopf, Classics in Hydrocarbon Chemistry, Wiley-VCH, Weinheim, 2000.
2. A. Narita, X.-Y. Wang, X. Feng and K. Müllen, Chem. Soc. Rev., 2015, 44, 6616–6643.
3. E. L. Spitler, C. A. Johnson II and M. M. Haley, Chem. Rev., 2006, 106, 5344–5386.
4. V. M. Tsefrikas and L. T. Scott, Chem. Rev., 2006, 106, 4868–4884.
5. T.-Y. Wu and J. S. Siegel, Chem. Rev., 2006, 106, 4843–4867.
6. Y. Segawa, A. Yagi, K. Matsui and K. Itami, Angew. Chem., 2016, 128, 5222–5245 ( Angew. Chem., Int. Ed. , 2016 , 55 , 5136–5158 ).
7. K. Y. Cheung, X. Xu and Q. Miao, J. Am. Chem. Soc., 2015, 137, 3910–3914.
8. J.-W. Han, X. Li and H. N. C. Wong, Chem. Rec., 2015, 15, 107–131.
9. K. Ikemoto, J. Lin, R. Kobayashi, S. Sato and H. Isobe, Angew. Chem., 2018, 130, 8691–8695 ( Angew. Chem., Int. Ed. , 2018 , 57 , 8555–8559 ).
10. Fragments of Fullerenes and Carbon Nanotubes, ed. M. A. Petrukhina and L. T. Scott, Wiley, Hoboken, 2012.
11. C. Thilgen and F. Diederich, Chem. Rev., 2006, 106, 5049–5135.
12. D. Wendinger and R. R. Tykwinski, Acc. Chem. Res., 2017, 50, 1468–1479.
13. P. Gund and T. M. Gund, J. Am. Chem. Soc., 1981, 103, 4458–4465.
14. Diamond and Related Nanostructures, Vol. 6 of Carbon Materials: Chemistry and Physics (F. Cataldo and P. Milani, Series Eds.), ed. M. V. Diudea and C. L. Nagy, Springer, Dordrecht, 2013.
15. M. Mastalerz, Acc. Chem. Res., 2018, 51, 2411–2422.
16. F. Beuerle and B. Gole, Angew. Chem., 2018, 130, 4942–4972 ( Angew. Chem., Int. Ed. , 2018 , 57 , 4850–4878 ).
17. X. Shen, D. M. Ho and R. A. Pascal Jr., Org. Lett., 2003, 5, 369–371.
18. D. Kuck, Chem. Rev., 2006, 106, 4885–4925.
19. H. W. Thompson, J. Org. Chem., 1968, 33, 621–625.
20. B. Paisdor and D. Kuck, J. Org. Chem., 1991, 56, 4753–4759.
21. D. Kuck, Angew. Chem., 1984, 23, 508–509 ( Angew. Chem., Int. Ed. Engl. , 1984 , 96 , 515–516 ).
22. D. Kuck, T. Lindenthal and A. Schuster, Chem. Ber., 1992, 125, 1449–1460.
23. G. Markopoulos, L. Henneicke, J. Shen, Y. Okamoto, P. G. Jones and H. Hopf, Angew. Chem., 2012, 124, 13057–13060 ( Angew. Chem., Int. Ed. , 2012 , 51 , 12884 ).
24. D. Kuck and H. Bögge, J. Am. Chem. Soc., 1986, 108, 8107–8109.
25. D. Kuck and A. Schuster, Angew. Chem., 1988, 100, 1222–1224 ( Angew. Chem., Int. Ed. Engl. , 1988 , 27 , 1192–1194 ).
26. H.-W. Ip, C.-F. Ng, H.-F. Chow and D. Kuck, J. Am. Chem. Soc., 2016, 138, 13778–13781.
27. W.-S. Wong, C.-F. Ng, D. Kuck and H.-F. Chow, Angew. Chem., 2017, 129, 12528–12532 ( Angew. Chem., Int. Ed. , 2017 , 56 , 12356–12360 ).
28. For example, see: D. Kuck, J. Linke, L. C. Teichmann, D. Barth, J. Tellenbröker, D. Gestmann, B. Neumann, H.-G. Stammler and H. Bögge, Phys. Chem. Chem. Phys., 2016, 18, 11722–11737.
29. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, B72, 171–179.
30. D. Kuck, A. Schuster, R. A. Krause, J. Tellenbröker, C. P. Exner, M. Penk, H. Bögge and A. Müller, Tetrahedron, 2001, 57, 3587–3613.
31. S. F. Parker, F. Fernandez-Alonso, A. J. Ramirez-Cuesta, J. Tomkinson, S. Rudić, R. S. Pinna, G. Gorini and J. Fernández Castañon, J. Phys.: Conf. Ser., 2014, 554, 012003.
32. M. A. Adams, S. F. Parker, F. Fernandez-Alonso, D. J. Cutler, C. Hodges and A. King, Appl. Spectrosc., 2009, 63, 727–732.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.02, Gaussian, Inc., Wallingford CT, 2016.
34. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
35. K. Refson, P. R. Tulip and S. J. Clark, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155114.
36. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
37. R. Dennington, T. A. Keith and J. M. Millam, GaussView, Version 5.0.9, Semichem Inc., Shawnee Mission, KS, 2016.
38. A. J. Ramirez-Cuesta, Comput. Phys. Commun., 2004, 157, 226–238.
39. N. M. O'Boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845.
40. M. Harig, B. Neumann, H.-G. Stammler and D. Kuck, ChemPlusChem, 2017, 82, 1078–1095 , see ref. 76 cited therein.
41. J. G. Brandenburg, S. Grimme, P. G. Jones, G. Markopoulos, H. Hopf, M. K. Cyranski and D. Kuck, Chem. – Eur. J., 2013, 19, 9930–9938.
42. M. I. Davis and T. W. Muecke, J. Phys. Chem., 1970, 74, 1104–1108.
43. S. F. Parker, D. Siegel, N. G. Hamilton, J. Kapitán, L. Hecht and D. Lennon, J. Phys. Chem. A, 2012, 116, 333–346.
44. J. F. Fuller and E. J. Valente, J. Chem. Crystallogr., 1996, 26, 815–821.
45. Y. Li, L. Zhang, Z. Zhang, J. Xu, Y. Pan, C. Xu, L. Liu, Z. Li, Z. Yu, H. Li and L. Xu, Adv. Synth. Catal., 2016, 358, 2148–2155.
46. L. B. Favero, W. X. Li, G. Spadini and W. Caminati, J. Mol. Spectrosc., 2015, 316, 45–48.
47. A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513.
48. T. L. Smithson, J. A. Duckett and H. Wieser, J. Phys. Chem., 1984, 88, 1102–1109.
49. K. H. Hassan and J. M. Hollas, J. Mol. Spectrosc., 1991, 147, 100–113.
50. Z. Arp, N. Meinander, J. Choo and J. Laane, J. Chem. Phys., 2002, 116, 6648–6655.
51. L. Bardet, G. Fleury, R. Granger and C. Sablayrolles, J. Mol. Struct., 1968, 2, 397–408.
52. G. Varsanyi, Assignments for vibrational spectra of 700 benzene derivatives, Akadémiai Kiadó, Budapest, 1973.
53. F. R. Dollish, W. G. Fateley and F. F. Bentley, Characteristic Raman frequencies of organic compounds, John Wiley & Sons, New York, 1974.
54. H. Jobic, S. Sportouch and A. Renouprez, J. Mol. Spectrosc., 1983, 99, 47–55.
55. D. Lin-Vien, N. B. Colthup, W. G. Fateley and J. G. Grasselli, The handbook of infrared and Raman characteristic frequencies of organic molecules, Academic Press, Boston, 1991.
56. D. S. Yufit and J. A. K. Howard, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2011, 67, o104–o106.
57. T. P. Ruiz, M. Fernandez-Gomez, J. J. L. Gonzalez, A. E. Koziol and J. M. G. Roldan, J. Mol. Struct., 2004, 707, 33–46.
58. D. A. Braden, S. F. Parker, J. Tomkinson and B. S. Hudson, J. Chem. Phys., 1999, 111, 429–437.
59. J. Tomkinson, S. F. Parker, D. A. Braden and B. S. Hudson, Phys. Chem. Chem. Phys., 2002, 4, 716–721.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis of compound 8, structure and spectra of compounds 1–10, comparisons of observed and calculated infrared and INS spectra. See DOI: 10.1039/c8cp07311b

---