Deep core photoionization of iodine in CH₃I and CF₃I molecules: how deep down does the chemical shift reach?

Abstract

Hard X-ray electron spectroscopic study of iodine 1s and 2s photoionization of iodomethane (CH₃I) and trifluoroiodomethane (CF₃I) molecules is presented. The experiment was carried out at the SPring-8 synchrotron radiation facility in Japan. The results are analyzed with the aid of relativistic molecular and atomic calculations. It is shown that charge redistribution within the molecule is experimentally observable even for very deep levels and is a function of the number of electron vacancies. We also show that the analysis of Auger spectra subsequent to hard X-ray photoionization can be used to provide insight into charge distribution in molecules and highlight the necessity of quantum electrodynamics corrections in the prediction of core shell binding energies in molecules that contain heavy atoms.

---

1 Introduction

Electron spectroscopy for chemical analysis (ESCA) in the VUV to the soft X-ray photon energy region (∼50–1500 eV) has been for decades one of the most influential tools in materials science for the research on element-specific material ranging from isolated atoms to surface science.^1–4 Lack of suitable instrumentation has, however, hindered for a long time a direct investigation of deep core levels of heavy atoms with photoelectron and Auger spectroscopy. Until very recently, no photoemission spectra of deep core ionization of heavy atoms have been reported, at least for ionization energies in the range of 30–40 keV. A novel major development in this direction has taken place at the synchrotron radiation facility SPring-8 in Japan, where two hard X-ray beam lines equipped with end stations capable of measuring gas-phase samples have recently come into operation.⁵ Exploiting this new instrumental opportunity, a pioneering paper by us on the 1s ionization of xenon (ionization energy ∼35 keV) has not only shown the feasibility of this kind of experiment, but has also shed light on the novel information that can be extracted. In particular, a core-hole lifetime in the attosecond range was derived, together with direct evidence of the relative weight of radiative (photon emission) versus nonradiative (Auger) decay following K-edge ionization of Xe.⁶ Following that first groundbreaking work, here we extend this research field to small polyatomic molecules, namely 1s core ionization of iodine in two representative systems, iodomethane (CH₃I) and trifluoroiodomethane (CF₃I).

The main aim of the present work is to investigate whether the molecular environment plays a role in such deep ionization processes, and to assess whether widespread concepts such as electronegativity and charge distribution inside a molecule extend down to very deep levels, or should the levels be considered purely atomic in nature.

Photoelectron spectra of the 1s and 2s core levels of both molecules have been measured, and compared with Dirac–Fock theoretical calculations. Core-hole lifetimes have been extracted, and compared with previously reported values based on fluorescence measurements. To complement the information from photoelectron spectra, Auger LMX spectra have also been measured. As in the previous work on Kr⁵ and Xe,⁶ the comparison of the LMX decay above and below the K-edge is informative about the importance of radiative versus nonradiative decay.

A key point in the theoretical description we use has been to perform calculations for the molecular systems, for the iodine isolated atom, and for the iodine negative ion (isoelectronic with xenon). The rationale is to assess the importance of charge redistribution within the molecule even for deep core excitation and relaxation processes.

As results we show that there are measurable chemical shifts for both 1s and 2s ionization energies between the two molecules (0.7 eV for the 1s level and 1.3 eV for the 2s level). To our knowledge, this is the first time that chemical shift is observed in the ionization of such deep levels. An interesting result of the theoretical simulations including a neutral iodine atom and a Xe-like iodine negative ion is that the best agreement with the experimental ionization energies is obtained when the neutral atom is considered. A charge distribution analysis indicates that while the difference in charge withdrawing by the fluorine atoms compared to the hydrogen atoms is strong, this effect is compensated by charge redistribution on the carbon site, so that the iodine atom is neutral in both cases. At variance with this result, in the analysis of the Auger spectra we show that the negative charge on the iodine site increases significantly when the total charge is 2. In other words, charge redistribution within the molecule is a function of the number and of the depth of the electron vacancies.

2 Experiment

The measurements were carried out at the BL19LXU⁷ beamline of the SPring-8 synchrotron radiation facility in Japan. The spectra were recorded using two photon energy values: 35.5 keV to ionize iodine from the 1s orbital and 10 keV to ionize the 2s orbital. The electron spectra were measured using a hemispherical electron energy analyzer SES-2002 with a gas cell GC-50 (Scienta Omicron). The target gas pressure was maintained at about 1.20 × 10⁻⁵ mbar outside the cell. The acceptance axis of the electron energy analyzer was oriented parallel with respect to the polarization vector of the horizontally linearly polarized photon beam.

The energy resolution of the analyzer was 781 meV and 313 meV for the two pass energies, 500 eV and 200 eV, used in the high and low photon energy measurements, respectively. The photon energy bandwidth was estimated to be 4.83 eV at 35.46 keV and 1.30 eV at 10.0 keV. The energy scale of the photon beam at 35.5 keV was calibrated by using the 1s photoelectron line of Xe⁶ and at 10.0 keV using the 2s and 2p photoelectron lines of Xe atoms.⁸ The kinetic energy scale of the spectrometer was calibrated with the aid of the well-known KLX Auger electron spectrum of Ar⁹ and LMM spectrum of Xe.^10,11

3 Calculations

The molecular calculations were carried out with two codes; ORCA (4.0.0.2)¹² and DIRAC (16.0).¹³ The molecular geometries of CH₃I and CF₃I were optimized with ORCA at coupled-cluster (CC) SD(T) calculations¹⁴ including MP2¹⁵ and zeroth order regular approximation^16,17 corrections with all-electron def2-TZVPP¹⁸ basis sets. The obtained bond lengths; r_CH = 1.083 Å, r_CI = 2.108 Å, and r_CF = 1.332 Å, r_CI = 2.112 Å for CH₃I and CF₃I, respectively, are in reasonable agreement with the experimentally determined values r_CH = 1.120(3) Å, r_CI = 2.11(3) Å,¹⁹ and r_CF = 1.3285(23) Å, r_CI = 2.1438(27) Å.²⁰

The molecular states were further studied by calculating the partial charges at different sites. This was done by performing a natural population analysis (NPA)²¹ with the JANPA²² package using the CCSD molecular orbitals from the ORCA calculations. Partial charges were calculated using the NPA method due to its reliability in the case of bonds with high ionic character.²¹

The DIRAC code was used to obtain the absolute 1s and 2s ionization energies of I in CH₃I, CF₃I, I and I⁻ forms within the Δ-SCF framework using the geometries obtained from ORCA calculations. For these calculations the Dyall's triple-ζ basis set²³ was adopted. The calculations were carried out at two levels, using the bare Dirac–Coulomb Hamiltonian and including the Gaunt interaction.^24,25

In addition to molecular calculations, single-atom configuration interaction Dirac–Fock simulations were performed. The results are used to check the quality of the molecular calculations, to obtain quantum electrodynamics (QED) corrections not present in the molecular codes and to analyze the experimental LMX Auger spectra subsequent to K and L photoionization, and KL fluorescence decay in the binding energy region of the iodine K-shell of CH₃I and CF₃I molecules. The atomic wave functions were calculated using the relativistic GRASP2K²⁶ program. The configurations included for the calculation of the Auger decay spectra were selected by the same procedure as presented in ref. 10. The Auger spectra and photoionization cross sections were modeled by using the RATIP²⁷ package, and fluorescence decay rates were obtained from the REOS²⁸ program using a length gauge.

4 Results and discussion

4.1 Iodine 1s and 2s photoelectron spectra

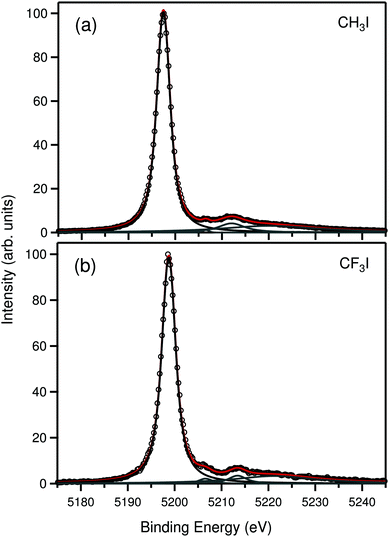
We begin the discussion from the iodine 2s photoelectron spectrum of CH₃I and CF₃I molecules, shown in panels (a) and (b) of Fig. 1. The spectra are composed of an intense main peak at about 5200 eV in binding energy, which arises from direct ionization of the 2s orbital of iodine, and a broad satellite structure that extends from about 5205 eV to 5240 eV. The fit of the main peak is shown in black color, the satellites are in gray and the total least-squares minimized sum is shown in red. All individual fitting profiles are Voigt functions with a fixed Gaussian width of 1.54 eV, representing experimental broadening. The complete satellite structure consists of a huge number of transitions that extend far beyond the 2s-valence double ionization threshold. The satellite structure was fitted with four Voigt profiles that was the minimum amount required to cover the whole feature with sufficient accuracy. For the present article the knowledge of the 2s satellites becomes relevant for extracting the 1s binding energies, as will be discussed below.

Fig. 1 Experimental iodine 2s photoelectron spectrum of CH₃I (a) and CF₃I (b). Black circles show the experimental data points. Black and gray solid lines show the individual fitting profiles, and the red line shows their sum.

From the fits we extracted lifetime broadening of the iodine 2s core–hole states in CH₃I and CF₃I molecules. The values are 2.71 ± 0.13 eV, and 2.85 ± 0.14 eV, respectively, which corresponds to the lifetimes of 241.1 ± 11 as and 230.6 ± 10 as. The values differ considerably from the value of 3.46 eV²⁹ reported for solid iodine, obtained using X-ray fluorescence measurements. The values are also notably smaller than those of the calculated widths using GRASP2K in the present work for atomic iodine (3.24 eV) and the Xe-like iodine anion (3.26 eV), which also indicates that the chemical environment should not affect the lifetime of the 2s hole of iodine considerably. It is emphasized that in the present measurement the total full width at half-maximum (FWHM) of the 2s lines were about 3.4 eV, which combined with the known photon bandpass of about 1.3 eV and analyzer broadening of about 0.8 eV means that the discrepancy cannot be explained solely by fitting uncertainties. The reason for this observed anomaly, however, remained unknown. We assume that the maximum of the peak corresponds to the GS → I 2s⁻¹(ν₀ = 0) transition and it is noted that the same discrepancy is also observed in the case of 2s ionization of atomic Xe, which means that the anomaly does not arise from molecular effects.

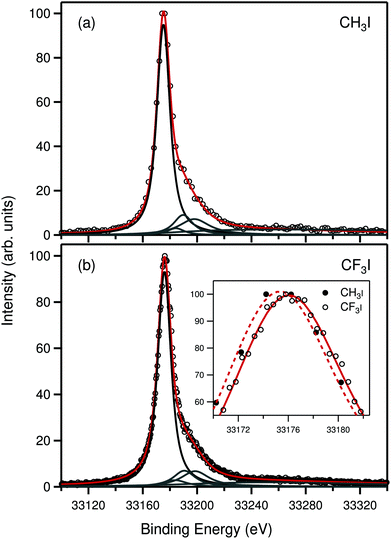
Fig. 2 presents the 1s photoelectron spectra of CH₃I and CF₃I measured at the photon energy of 35440 ± 5 eV. The spectra consist of a single line that corresponds to the direct 1s ionization of iodine and a satellite region at higher binding energy. In comparison to the 2s case, due to the larger lifetime broadening and photon bandpass, the satellite features are now seen as an asymmetric shoulder on the right-hand side of the main line. Due to the overlap and lack of precise knowledge about the shape of the satellite part, fitting of the 1s spectrum is somewhat complicated. In the present work the fitting was carried out by making an approximation that the relative position of the satellite spectrum with respect to the main line does not change between 1s and 2s ionization. The approximation can be justified by the fact that both 1s and 2s holes are very deep in the system and therefore relaxation of the valence orbitals in the final state is practically the same in both cases. Therefore the shoulders in the 1s spectra were fitted by fixing the relative positions of the four profiles obtained from the fit of the better resolved satellite part of the 2s spectrum. In addition a fifth profile centered at about 33 260 eV was added to cover the far extending tail of the satellite part.

Fig. 2 Experimental iodine 1s photoelectron spectrum of CH₃I (a) and CF₃I (b). Black circles show the experimental data points. Black and gray solid lines show the individual fitting profiles, and red line shows their sum. To highlight the chemical shift, inset in panel (b) shows the highest region of the two spectra in the same scale.

The shapes of the iodine 1s spectra of CH₃I and CF₃I are similar to the 1s spectrum of atomic Xe.^5,6 The main line is accompanied by a satellite shoulder and a very broad tail that extends about 140 eV above the main line. Such similarity is expected since the iodine 1s ionized state of CH₃I and CF₃I is not dissociative and the large lifetime broadening smears out vibrational and rotational effects. However, after a careful analysis it is possible to gain information from the spectra, as will be discussed in the following.

The 1s main lines in Fig. 2 have FWHM of about 11.63 eV for CH₃I and 11.69 eV for CF₃I. Taking into account the experimental contribution of 4.84 eV, we are able to deduce the iodine 1s lifetime broadening to be 9.5 ± 0.6 eV for CH₃I and 9.6 ± 0.6 eV for CF₃I, corresponding to the lifetimes of 69 ± 4 as and 68 ± 4 as, respectively. The values are the same as those⁵ measured with a slightly different photon energy and well in line with the lifetime broadening of 9.6 ± 0.2 eV (68 ± 2 as) of the 1s ionized state of Xe.⁶ Interestingly, however, similar to the 2s case the lifetime broadening values obtained from the present experiment are smaller than the value of 10.6 eV obtained from fluorescence measurements of solid iodine,²⁹ thus showing the same trend as seen in the case of 1s ionization of Xe.⁶ Comparison to the calculated broadening value of 10.3 eV using GRASP2K for atomic and Xe-like iodine also shows the same behavior as in the 2s case that the theory overestimates the width against the present measurement, but agrees well with the fluorescence data from ref. 29.

The results for the experimental 1s and 2s binding energies of iodine in CH₃I and CF₃I molecules are summarized in Table 1. The table also contains the results from theoretical calculations for I in the studied molecules, as well as in atomic neutral and Xe-like forms. The atomic calculations were carried out to monitor the quality of the chosen basis set for molecular calculations and to obtain estimates for QED corrections that, to our knowledge, are not currently implemented in commonly available molecular codes, namely Breit interaction, vacuum polarization and self energy, which make an important contribution to deep core binding energies of heavy atoms (see, e.g., ref. 30–32 and references therein).

Table 1 Experimental and calculated K and L₁-shell binding energies of I in CH₃I and CF₃I molecules (in eV). The theoretical results are shown for bare Dirac–Coulomb Hamiltonian (D–C) with further corrections. G stands for Gaunt interaction from the DIRAC program. B, VP and SE are full Breit interaction, vacuum polarization and self energy from atomic calculations using the GRASP2K program, respectively. See text for further details

Iodine 1s^−1	CH3I	CF3I	I	I^−
a Corrections from atomic calculations. b Value for solid iodine from ref. 8.
DIRAC
D–C	33293.7	33295.0	33295.2	33286.2
+G	33210.1	33211.4	33211.6	33202.4
+B, VP, SE^a	33177.0	33178.3	33178.5	33169.5
GRASP2K
D–C	—	—	33295.4	33286.2
+B	—	—	33217.8	33208.5
+B, VP, SE	—	—	33178.7	33169.5
Experiment	33175.2	33175.9	—	33169.69(89)^b

---

Iodine 2s^−1	CH3I	CF3I	I	I^−
DIRAC
D–C	5214.3	5215.7	5215.9	5206.7
+G	5206.6	5207.9	5208.1	5199.0
+B, VP, SE^a	5202.0	5203.4	5203.6	5194.4
GRASP2K
D–C	—	—	5215.8	5206.6
+B	—	—	5208.6	5199.4
+B, VP, SE	—	—	5203.5	5194.3
Experiment	5197.47	5198.75	—	5188.38(81)^b

---

Comparison of the atomic calculations with bare Dirac–Coulomb Hamiltonian (lines D–C) between DIRAC and GRASP2K codes shows a remarkably good agreement. The results for both I and I⁻ are within a maximum of 0.2 eV from each other, which shows that the selected basis set (Dyall's triple-ζ) is of sufficient quality for the present task. Comparing the addition of Gaunt correction in DIRAC against the full Breit interaction (lines +G and +B) in GRASP2K shows that in the case of 2s ionization the two differ by 0.5 eV, but the difference increases drastically to 6.1 eV in the case of 1s ionization. We thus arrive at the conclusion, which is the same as the example in ref. 33, that even though the magnetic part (i.e. Gaunt) dominates the Breit interaction, the retardation term needs to be included in the calculation of core ionization energies of heavy atoms. The Dirac–Coulomb–Breit Hamiltonian is, however, still not sufficient, because the QED terms vacuum polarization and especially self energy become significant (see, e.g.ref. 6, 30 and 33). In the present case for 2s the combined effect of the two terms is about 5.1 eV and for 1s it is 39.1 eV, which are far above the experimental resolution. As already mentioned, the considered QED terms are not available even in the relativistic DIRAC code. Therefore we made an assumption that the terms do not change much when moving from an atomic to molecular environment, which is justified by the fact that the corrections are practically the same between I and I⁻. The results of this approximation are summarized in line “+B, VP, SE” of Table 1, where the total shift arising from full Breit interaction, vacuum polarization and self energy is taken from the atomic calculation to correct the bare Dirac–Coulomb result of the DIRAC calculations. This provides theoretical binding energies that are remarkably close to the experimental binding energies, in the case of 1s the difference is about 2 eV and in the case of 2s about 4.5 eV. These results are notably better than the ones obtained directly from DIRAC with a Gaunt correction that deviates only for 1s and 2s by about 35 eV and 9 eV from the experimental values, respectively. We may thus conclude that even though it seems that one may transfer the leading QED corrections from atomic to molecular calculations, there is a clear future need to implement them directly into the relativistic molecular codes.

The experiment shows that the chemical shift between CH₃I and CF₃I is from the 2s spectra −1.3 ± 0.05 eV and from the 1s spectra −0.7 ± 0.6 eV, when the calculation gives −1.4 eV for 2s and −1.3 eV for 1s. Deviation between the experiment and theory in the 1s case is in the region of error bars due to the large width of the photoelectron line and overlapping satellite region. Nevertheless, it is notable that the chemical shift is observed in the 1s case, which to the best of our knowledge makes the present data the highest energy photoelectron spectroscopic measurement where a molecular chemical shift is observed. We emphasize that the knowledge of the chemical shifts transferred all the way to the deepest orbitals of heavy atoms can prove to be useful in the site-specific study of complex systems that contain light and heavy atoms. This is because the photon energy required to ionize iodine 1s is so far above all thresholds of the second row elements that materials containing mainly these elements are almost transparent to hard X-rays.

Comparison of the chemical shifts between CH₃I, CF₃I, I and I⁻ shows that the molecular values are surprisingly close to I rather than I⁻ and that the chemical shift between CH₃I and CF₃I is fairly small, only about 1.3 eV, despite the fact that H atoms are electropositive and F atoms are highly electronegative. Also since iodine is electronegative, one might intuitively assume that in a molecular environment the atom would appear as a Xe-like anion. The reason for the behavior can be, however, understood from the distribution of partial charges in the molecule.

Table 2 shows the results of natural population analysis carried out for the molecules in the original state and by increasing the nuclear charge of iodine by one and two, which mimics the effect of removal of one or two core electrons, which will be discussed in the next chapter. In the present work, the neutral case, i.e. column “I(Z = 53)”, shows that, as expected, there is a huge difference in the partial charges in the H and F-sites. However, the charge is compensated by a change of partial charge in the C-site so that in CF₃I the carbon loses almost a unit charge whereas in CH₃I the carbon gains charge. The change is, however, not reflected in the I atoms because the CH₃ and CF₃ units as a whole are almost neutral. The small chemical shift between the two molecules can be understood by considering the C bridge acting as a charge buffer, which nullifies most of the effect arising from the change of H atoms to F atoms. This can also be seen from the calculated 1s binding energies of carbon which are 291.58 eV in CH₃I and 299.46 eV in CF₃I, thus giving a chemical shift of 7.9 eV. We notice that a comparably small chemical shift (1.05 eV) has been reported in the literature between the I 4d_3/2 levels for the same two molecules,³⁴ confirming our overall interpretation based on charge distribution. It also indicates that even though in the present case the iodine 1s and 2s chemical shifts are quite small, it should not be considered as a general rule.

Table 2 Difference in total electronic charge at different molecular sites with respect to neutral atoms from natural population analysis in charge neutral, and Z + 1 and Z + 2 approximations. The sites are marked by underlines

	I(Z = 53)	I(Z = 54)	I(Z = 55)
C̲H3I	−0.67	−0.50	−0.36
CH̲3I	0.20	0.25	0.30
CH3I̲	0.08	−0.24	−0.54
C̲F3I	0.95	1.06	1.13
CF̲3I	−0.36	−0.29	−0.20
CF3I̲	0.13	−0.18	−0.52

---

4.2 Iodine LMX Auger decay

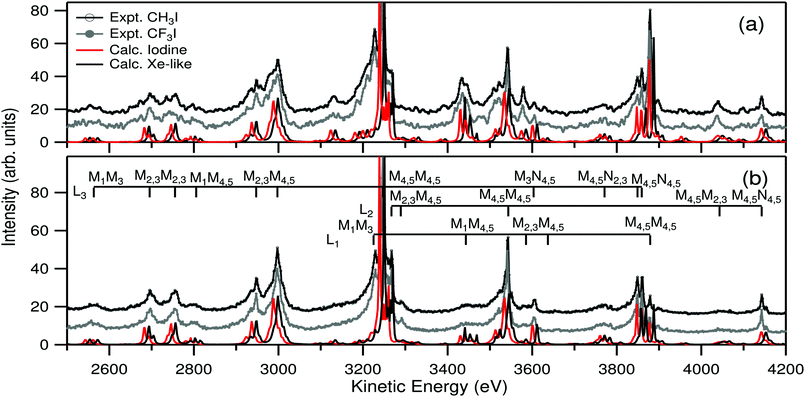
Fig. 3 depicts the experimental LMM and LMN Auger decay spectrum of iodine in CH₃I and CF₃I molecules. Panel 3(a) shows the spectrum measured using a photon energy below the 1s ionization threshold and panel 3(b) above the 1s threshold. In addition the panels show the corresponding theoretical calculations for bare atomic iodine and Xe-like iodine atom using the GRASP2K package (for details, see Theory section).

Fig. 3 Experimental CH₃I and CF₃I, and calculated atomic iodine and Xe-like iodine LMX Auger spectra at (a) below and (b) above the 1s ionization threshold, at photon energies of 31 960 eV and 35 460 eV, respectively. For visibility the baselines of the experimental spectra are lifted. All spectra are normalized so that the highest peak at 3247 eV is 100. The combs in panel (b) show the most prominent decay Auger channels in the case of three initial states.

The observed changes in the intensities between above and below the 1s threshold are highly similar to the same case in atomic xenon, discussed recently in ref. 6. The variations can be understood by the fact that below the 1s threshold the population of the initial states of the Auger decay is simply governed by the branching ratio of the 2s, 2p_1/2 and 2p_3/2 photoionization cross sections at the selected photon energy, but above the 1s threshold, population of 2p hole states increases dramatically because of dominant KL_2,3 fluorescence decay. The consequence of this can be seen as an increase in the intensity of the L_2,3MX Auger lines with respect to L₁MX lines.

As expected, also the overall shapes of the measured Auger spectra are very similar to atomic Xe studied in ref. 6 and 10. In comparison to Xe, the whole spectrum is shifted by about 150 eV to smaller kinetic energy, but otherwise one can locate precisely the same spectral features and roughly the same relative intensities. The reason is that the decay takes place between very deep atomic-like orbitals, and photoionization does not directly affect the valence structure of the systems. Therefore the initial and final states of the decay remain as the bonding state. Moreover, due to the large lifetime broadening, all vibrational effects smear out. Since the LMX Auger spectrum of Xe has been recently analyzed in ref. 10, we do not repeat line identifications here. An interested reader can easily label the spectral features using the Xe case in Fig. 1 of ref. 10.

Comparison of the experimental Auger spectra of CH₃I and CF₃I molecules in Fig. 3 shows remarkable similarity. Line positions and intensities show no statistically significant differences in the present experimental resolution and noise level. The difficulty in finding differences is at least partly due to large natural width combined with considerable line overlap, which makes the study of individual Auger decay lines challenging. However, even the most isolated lines in the spectra appear to be almost identical in both molecules.

Comparison of the experimental spectra against the theory shows an interesting behavior. The intensities of both calculations, Xe-like and pure iodine, are in very good agreement with the experiment. However, the calculated line positions are found to be located in such a way that the pure iodine spectrum is at lower and Xe-like spectrum at higher kinetic energy, and the experimental spectrum is roughly in the center between the two cases. It should be noted that it is not likely that the behavior arises from computational uncertainties because in ref. 6 and 10 it was shown that in the case of atomic Xe the method predicts the positions of all line groups of the spectrum exceptionally well. The observation is in clear contrast to the photoionization results presented in Table 1, where in both molecules it is seen that the iodine site appears to be almost charge neutral “iodine-like” in the ground state. As in the case of photoionization, the behavior can be qualitatively understood by studying the partial charges in the molecules. The two rightmost columns of Table 2 show that in singly and doubly core ionized cases the iodine site gains a charge of about −0.2 e and −0.5 e, respectively. It thus means that when the core of the iodine site becomes more positive, it is able to attract more negative charge from the rest of the molecule and the chemical environment in the valence region of the site becomes more Xe-like, which in turn is reflected in the kinetic energies of the Auger lines. The values from Table 2 are well in line with the atomic calculations in Fig. 3 showing that core ionization changes the valence charge distribution in the molecule significantly, but even doubly core ionized core is not sufficient to make the site completely Xe-like in valence.

5 Conclusions

Experimental and theoretical data are reported for deep core ionization and LMX Auger decay in two iodine-containing molecules, CH₃I and CF₃I. Ionization energies for the 1s and 2s iodine deep core levels are compared, and chemical shifts of 0.7 eV for the 1s ionization and 1.3 eV for the 2s one are derived. To our knowledge, this is the first time that chemical shifts are obtained for such inner-shell levels.

Theoretical calculations have been performed for the molecules, atomic iodine and Xe-like I⁻ (negatively charged iodine). We show that for the 1s and 2s ionization energies the experimental values are in better agreement with theory when atomic iodine is considered, implying that the charge transfer from the CX₃ moiety to the iodine center is negligible for deep core ionization. At variance with this result, the calculated energy values for the Auger transitions are in-between atomic iodine and Xe-like iodine. This in turn indicates that the charge distribution inside the molecules, and namely the capability of the electronegative iodine atom to draw charge from the rest of the molecule, is a detectable effect when the species are doubly charged (as in Auger decay) even for levels as deep as the ones involved in the LMX Auger transitions. This conclusion is supported by calculated charge distributions within the molecules.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The synchrotron radiation experiments were performed at BL19LXU of SPring-8 with the approval of RIKEN SPring-8 Center (Proposal No. 20170028). The authors are grateful to the members of the Engineering Team of the RIKEN SPring-8 Center for their technical assistance. We would like to thank TOSO F-TECH, Inc, for providing CF₃I samples, and we are grateful for the financial support by the European Union's Horizon 2020 research and innovation programme under the Marie Skoldowska-Curie grant agreement (No. 713606).

References

1. D. R. Penn, J. Electron Spectrosc. Relat. Phenom., 1976, 9, 29–40.
2. C. Wagner, Surf. Interface Anal., 1981, 3, 211.
3. H. Siegbahn, J. Phys. Chem., 1985, 89, 897–909.
4. K. Siegbahn, C. Nordling, G. Johansson, J. Hedman, P. Heden, K. Hamrin, U. Gelius and T. Bergmark, L. O. Werme, R. Manne and Y. Baer, ESCA applied to free molecules, 1969.
5. M. Oura, K. Nagaya, T. Gejo, Y. Kohmura, K. Tamasaku, L. Journel, M. N. Piancastelli and M. Simon, New J. Phys., accepted.
6. M. N. Piancastelli, K. Jänkälä, L. Journel, T. Gejo, Y. Kohmura, M. Huttula, M. Simon and M. Oura, Phys. Rev. A, 2017, 95, 061402.
7. M. Yabashi, T. Mochizuki, H. Yamazaki, S. Goto, H. Ohashi, K. Takeshita, T. Ohata, T. Matsushita, K. Tamasaku, Y. Tanaka and T. Ishikawa, Nucl. Instrum. Methods Phys. Res., Sect. A, 2001, 467–468, 678–681.
8. R. D. Deslattes, E. G. Kessler, P. Indelicato, L. de Billy, E. Lindroth and J. Anton, Rev. Mod. Phys., 2003, 75, 35–99.
9. L. Asplund, P. Kelfve, B. Blomster, H. Siegbahn and K. Siegbahn, Phys. Scr., 1977, 16, 268.
10. R. Püttner, K. Jänkälä, R. Kushawaha, T. Marchenko, G. Goldsztejn, O. Travnikova, R. Guillemin, L. Journel, I. Ismail and B. C. de Miranda, et al. , Phys. Rev. A, 2017, 96, 022501.
11. G. B. Armen, T. Åberg, J. C. Levin, B. Crasemann, M. H. Chen, G. E. Ice and G. S. Brown, Phys. Rev. Lett., 1985, 54, 1142.
12. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
13. H. J. Aa. Jensen, R. Bast, T. Saue, and L. Visscher, with contributions from V. Bakken, K. G. Dyall, S. Dubillard, U. Ekström, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, A. S. P. Gomes, T. Helgaker, J. Henriksson, M. Iliaš, Ch. R. Jacob, S. Knecht, S. Komorovský, O. Kullie, J. K. Lærdahl, C. V. Larsen, Y. S. Lee, H. S. Nataraj, M. K. Nayak, P. Norman, G. Olejniczak, J. Olsen, Y. C. Park, J. K. Pedersen, M. Pernpointner, R. di Remigio, K. Ruud, P. Sałek, B. Schimmelpfennig, A. Shee, J. Sikkema, A. J. Thorvaldsen, J. Thyssen, J. van Stralen, S. Villaume, O. Visser, T. Winther and S. Yamamoto, DIRAC, a relativistic ab initio electronic structure program, Release DIRAC16, 2016, see http://www.diracprogram.org.
14. G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918.
15. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618.
16. E. v. Lenthe, E.-J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
17. E. van Lenthe, E.-J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792.
18. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
19. I. J. McNaught, J. Chem. Educ., 1982, 59, 879.
20. A. P. Cox, G. Duxbury, J. A. Hardy and Y. Kawashima, J. Chem. Soc., Faraday Trans. 2, 1980, 76, 339–350.
21. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
22. T. Y. Nikolaienko, L. A. Bulavin and D. M. Hovorun, Comput. Theor. Chem., 2014, 1050, 15–22.
23. K. G. Dyall, Theor. Chem. Acc., 2006, 115, 441–447.
24. J. A. Gaunt, Philos. Trans. R. Soc., A, 1929, 228, 151–196.
25. J. B. Mann, Phys. Rev. A: At., Mol., Opt. Phys., 1971, 4, 41.
26. P. Jönsson, X. He, C. F. Fischer and I. Grant, Comput. Phys. Commun., 2007, 177, 597–622.
27. S. Fritzsche, Comput. Phys. Commun., 2012, 183, 1525–1559.
28. S. Fritzsche and C. F. Fischer, Comput. Phys. Commun., 1997, 99, 323–334.
29. M. O. Krause, J. Phys. Chem. Ref. Data, 1979, 8, 307–327.
30. J. Niskanen, K. Jänkälä, M. Huttula and A. Föhlisch, J. Chem. Phys., 2017, 146, 144312.
31. J. Niskanen, P. Norman, H. Aksela and H. Ågren, J. Chem. Phys., 2011, 135, 054310.
32. K. Kozioł and G. A. Aucar, J. Chem. Phys., 2018, 148, 134101.
33. K. Kozioł, C. A. Giménez and G. A. Aucar, J. Chem. Phys., 2018, 148, 044113.
34. J. Cutler, G. Bancroft and K. Tan, J. Chem. Phys., 1992, 97, 7932–7943.

---