Open Access Article
Open Access ArticleSpatial confinement – rapid 2D F− diffusion in micro- and nanocrystalline RbSn2F5†
Maria
Gombotz
*a,
Sarah
Lunghammer
a,
Stefan
Breuer
 a,
Ilie
Hanzu
a,
Ilie
Hanzu
 ab,
Florian
Preishuber-Pflügl‡
a and
H. Martin R.
Wilkening
ab,
Florian
Preishuber-Pflügl‡
a and
H. Martin R.
Wilkening
 *ab
*ab
aChristian Doppler Laboratory for Lithium Batteries, and Institute for Chemistry and Technology of Materials, Graz University of Technology (NAWI Graz), Stremayrgasse 9, 8010 Graz, Austria. E-mail: wilkening@tugraz.at; gombotz@tugraz.at; Fax: +43 316 873 32332; Tel: +43 316 873 32330
bAlistore-ERI European Research Institute, 33 rue Saint Leu, 80039 Amiens, France
First published on 9th January 2019
Abstract
Diffusion of small ions in materials with confined space for translational dynamics can be quite different to isotropic (3D) diffusion, which is found in the majority of solids. Finding credible indications for 2D diffusion is not as easy as it looks at first glance, especially if only powder samples are available. Here we chose the ternary fluoride RbSn2F5 as a new model system to seek out low-dimensional anion diffusion in a nanocrystalline material. We prepared RbSn2F5via mechanochemically-assisted solid state synthesis and used both ac conductivity spectroscopy and spin-lock NMR relaxation measurements to find evidence that the fluorine ions preferably diffuse between the Rb-rich layers. In both cases the diffusion induced spin-lock NMR rates are only consistent with conductivity data if they are analyzed with the semi-empirical spectral density function for 2D jump diffusion as introduced by P. M. Richards [Solid State Commun., 1978, 25, 1019].
1 Introduction
Solid-state ionic conductors represent an essential component in microelectronics and devices to electrochemically store electricity.1–4 In the last ten years, quite a number of new compounds with exceptionally fast ion transport have been presented.5–12 In particular, highly conducting Li-bearing and Na-containing materials were developed to serve as non-flammable electrolytes in ion batteries.12–15 Also cation-mixed fluorides,16,17 such as La1−xBaxF3−x, see ref. 18–21, and Ba1−xCaxF2 (0 < x < 1), see ref. 22, re-entered the scientific stage as they might be used as solid electrolytes in fluorine-based energy storage systems.23,24 Such ternary fluorides are anticipated to take a leap forward in batteries with high energy densities.Besides such application-oriented challenges, fluorine ion conductors offer attractive model systems to study ultra-rapid jump processes8,25 from a fundamental point of view. To develop new functional materials we need to improve our understanding about the influence of crystal structure and morphology on ion transport. The highly reversible insertion and de-insertion processes in rocking-chair batteries, relying on insertion compounds, take advantage of layered materials that offer fast 2D diffusion pathways. From an atomic scale point of view it is, if only powder samples are available, a challenge to undoubtedly show that 2D diffusion prevails.26–29 The same troubles hold for 1D diffusion taking place along or inside the channels.30,31 Intrachannel and intralayer hopping processes may water the reasoning for 1D or 2D diffusion down.
Only few examples have been presented in literature26,27 for which rapid 2D diffusion of Li, Na or F ions has either unequivocally been shown or at least strongly anticipated. These examples include Na-beta′′-alumina,33–35 cathode materials based on LiyCoO2 (y ≤ 1) and LiFePO4,36,37 Li containing transition metal sulfides (or selenides), such as LixTiS2 (0 < x ≤ 1)38–41 or LizNbS2 (0 < z ≤ 1),29 hexagonal LiBH4,27 polycrystalline ZrBe2H1.4,26,42 and the ternary fluorides PbSnF4, see ref. 43 and 44, and BaSnF4.45 In some of these examples only a multi-method approach turned out to be successful to show that low-dimensional diffusion is present. For LixMS2 (M = Ti, Nb) and ZrBe2H1.4 the use of variable-frequency nuclear magnetic resonance (NMR) relaxation measurements turned out to be successful to prove low-dimensional diffusion as the main motional process. For instance, McDowell et al.26 impressively showed via variable-frequency 1H NMR spin–lattice relaxation measurements that the protons in the metal-hydride ZrBe2H1.4 are indeed subjected to 2D diffusion.
For many cathode materials, which are used in insertion batteries,37,46–48 the NMR technique will, however, be of very limited use as paramagnetic centers cause short relaxation times which drastically narrow the time window needed for dimensionality analyses. In addition, strong spin-electron interactions govern the NMR relaxation rates rather than diffusive motions. Focussing here on rapid anion dynamics, ternary fluorides provide some very encouraging materials useful as model substance to test NMR relaxation models proposed for 2D diffusion.49–51
Here, RbSn2F5 attracted our attention. It belongs to the family of the pseudo-binary system MF-SnF2 where M is a monovalent cation such as Rb+, K+, Na+ or Cs+.52 Within this family RbSn2F5 offers the highest ion conductivity53 followed by KSn2F5 and NaSn2F5.54,55 Up to now it has only been prepared by solid-state reaction52 or hydrothermal synthesis in aqueous solution as first reported by Donaldson and O'Donoghue in 1964.56 In 1987 the structure of KSn2F5, to which RbSn2F5 is isomorphous, was resolved as being trigonal, i.e., crystallizing with the space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) .57 Later structure refinement was also carried out by Yamada et al.32 In Fig. 1 the crystal structure of RbSn2F5 is illustrated, which clearly shows the two-dimensional nature of this compound. In 1991 Hirokawa et al.58 suggested to interpret NMR data by using a 2D spectral density. Later, in 2004, Yamada et al.32 pointed out that also conductivity isotherms are in line with low-dimensional transport. A direct comparison of results from both NMR and conductivity spectroscopy is, however, still missing. While earlier studies focussed on coarse-grained polycrystalline samples with μm-sized crystallites, F self-diffusion in nanocrystalline RbSn2F5 has not been reported yet. Thus, the present study also aims at discussing possible effects on 2D diffusion in RbSn2F5 when the mean crystallite size is reduced to ca. 20 nm.
.57 Later structure refinement was also carried out by Yamada et al.32 In Fig. 1 the crystal structure of RbSn2F5 is illustrated, which clearly shows the two-dimensional nature of this compound. In 1991 Hirokawa et al.58 suggested to interpret NMR data by using a 2D spectral density. Later, in 2004, Yamada et al.32 pointed out that also conductivity isotherms are in line with low-dimensional transport. A direct comparison of results from both NMR and conductivity spectroscopy is, however, still missing. While earlier studies focussed on coarse-grained polycrystalline samples with μm-sized crystallites, F self-diffusion in nanocrystalline RbSn2F5 has not been reported yet. Thus, the present study also aims at discussing possible effects on 2D diffusion in RbSn2F5 when the mean crystallite size is reduced to ca. 20 nm.
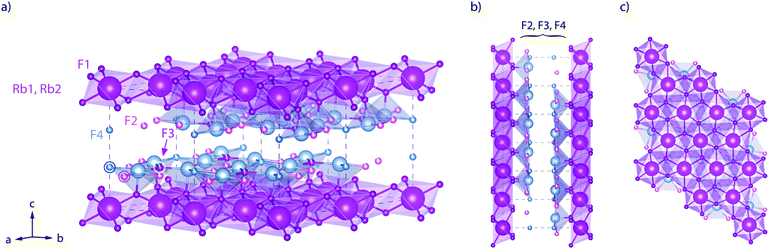 | ||
Fig. 1 Crystal structure of RbSn2F5 below the phase transition at approximately T = 368 K. The illustration shows the arrangement of atoms according to the structure refinement of Yamada et al.32 (space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , no. (147); a = 7.3857(4) Å, c = 10.104(1) Å, Z = 3.) (a) view to illustrate the fluorine ions in the Sn-rich layers. (b) View along the b-axis. (c) View along the b-axis to visualise the hexagonal arrangement of the Rb+ cations. The F sites between the Rb-rich layers (labelled F2, F3, and F4) are only filled by 90%; F1 sites are fully occupied. , no. (147); a = 7.3857(4) Å, c = 10.104(1) Å, Z = 3.) (a) view to illustrate the fluorine ions in the Sn-rich layers. (b) View along the b-axis. (c) View along the b-axis to visualise the hexagonal arrangement of the Rb+ cations. The F sites between the Rb-rich layers (labelled F2, F3, and F4) are only filled by 90%; F1 sites are fully occupied. | ||
For this purpose, that is, to compare F diffusion in microcrystalline RbSn2F5 with that in the nanocrystalline form, we synthesized the layer-structured fluoride employing a mechanochemically-assisted ceramic route. Using a one pot synthesis, nanocrystalline RbSn2F5 was directly obtained after high-energy ball milling59 the binary starting materials RbF and SnF2. Through soft annealing we converted the as-prepared material into a microcrystalline sample. Spin-lock 19F NMR60 instead of ordinary spin–lattice relaxation NMR61 was used to record purely diffusion-controlled relaxation rates. For non-nanocrystalline RbSn2F5 the NMR rates are consistent with results from conductivity measurements only if we analyse the NMR rate peak with the model of Richards49,62 introduced for 2D jump diffusion. This result is also consistent with the electrical responses seen by conductivity spectroscopy. These findings, being in close agreement to results from literature,32 build the basis for the analysis of F anion dynamics in nanocrystalline RbSn2F5.
2 Experiment
Mechanochemical synthesis59,63 of nanocrystalline RbSn2F5 was carried out in ZrO2 cups (45 ml) loaded with ZrO2 balls (5 mm diameter) and the corresponding educts. We made use of a high-energy planetary mill (Fritsch Pulverisette 7 premium line) to form the ternary fluoride. To guarantee moisture free reaction conditions the educts (RbF (Sigma Aldrich 99.8%), SnF2 (Sigma Aldrich 99%)) were dried in vacuum over night. Handling of the milling cups, i.e., filling and emptying of the beakers was carried out in an Ar-filled glovebox (H2O and O2 < 0.5 ppm). We milled the starting materials at a rotation speed of 600 rpm for 10 h according to the following procedure: 15 min milling followed by 15 min cooling of the beakers. Subsequently, the powders were annealed at 373, 423 and 473 K for 4 or 8 h in a tube furnace under vacuum or Ar atmosphere. For this annealing step 100 mg of the milled sample was pressed to pellets with a diameter of 5 mm using a hand press and by applying a force of 0.5 tons for 2 minutes. Annealing caused grain growth of the RbSn2F5 crystallites and densified the powder.The milled and annealed samples were characterised by X-ray diffraction (XRD) under atmospheric pressure and at room temperature. A Bruker D8 Advance diffractometer with Bragg Brentano geometry and CuKα radiation (1.5406 Å) was used to collect the diffractograms. Data points were recorded from 10 to 100° 2θ with a stepsize of 0.02° 2θ; the measuring time for each step was 1 second. Rietveld Refinement was performed with X-PertHighScorePlus (PANalytical).
Magic angle spinning (MAS) NMR was carried out on a Bruker Avance III 500 spectrometer at a nominal magnetic field of 11.7 T. This external magnetic field translates in resonance frequencies of 186.40 MHz for 119Sn, 470.30 MHz for 19F and 163.60 MHz for 87Rb. We used a Bruker MAS probe designed for 2.5 mm rotors (ZrO2) to acquire free induction decays (FIDs) at a spinning speed of 25 kHz (target gas flow: 400 L h−1, frame cooling: 35% of target gas flow). The bearing gas temperature was 293 K.
Spectra were obtained after Fourier transformation of the FIDs and referenced to the isotropic chemical shifts δiso of LiF (δiso(19F) = −204.3 ppm), SnO2 (δiso(119Sn) = −604.3 ppm) and RbNO3 (δiso(87Rb) = −30 ppm site 3), respectively. The relaxation rates 1/T1 and 1/T1ρ were determined with a Bruker Avance III 300 NMR spectrometer at a magnetic field of 7.04 T, i.e., at a 19F NMR resonance frequency of 281.79 MHz. Prior to the relaxation measurements the powder sample was fire-sealed in a glass cylinder with a length of approximately 3 cm and 4 mm in diameter. The rates were recorded with the saturation recovery pulse sequence where at first a train of 10 closely spaced 90° pulses destroys any longitudinal magnetization Mz before its recovery as a function of delay time td was then detected with a single 90° pulse. The transients Mz(td) were analyzed with stretched exponentials Mz(td) ∝ 1 − exp(−(t/T1ρ)γ) with 0 < γ ≤ 1. While T1 NMR is sensitive to fast F anion dynamics, slower motional processes were measured with the spin-lock technique introduced by Slichter and Ailion64–66 utilizing the pulse sequence 90°(tlock) − acq.67–70 The locking frequency ω1 was set to ω1/2π ≈ 100 kHz and the duration of the locking pulse tlock was varied from 100 μs to 10 ms. Note that the recycle delay for the spin-lock experiments was at least 5 × T1 to ensure complete longitudinal relaxation between each scan. Once again, stretched exponentials served to parameterize the spin-lock transients Mρ(tlock) ∝ exp(−(tlock/T1ρ)γρ) (0 < γρ ≤ 1) to extract T1ρ(1/T).
To carry out the impedance spectroscopy measurements, approximately 60 mg of the sample powder was pressed to cylindrical pellets with a final diameter of 5 mm, using a hand press. As for the annealing step, we applied a uniaxial pressure of 0.5 t for 2 min. Au electrodes, which block ion transport, with a thickness of 100 nm were sputtered onto both sides of the pellets using a Leica sputter device (EM SCD050).
Alternating current (ac) impedance measurement were then performed with a broadband spectrometer (Novocontrol, Concept 80) in combination with an active BDS 1200 cell and a ZGS interface.71 The temperature was varied from 173 K to 473 K controlled by a QUATRO cryosystem. Our conductivity measurements covered a frequency range from 10−2 Hz to 107 Hz. All experiments were performed under a constant flow of dry, freshly evaporated N2 gas. ZView (Princeton Applied Research) and IGOR Pro (Wavemetrics) software were used to analyze the data.
For Hebb–Wagner-type polarisation measurements under N2 atmosphere we used pellets with 5 mm in diameter and employed a Parstat MC potentiostat (Princeton Applied Research) equipped with a low-current option. All preparation steps, including the metallisation, were carried out in Ar filled gloveboxes with an O2 and H2O content of less than 1 ppm.
3 Results and discussion
3.1 X-ray diffraction
The phase purity of mechanosynthesized RbSn2F5 before and after the annealing steps was studied by XRD, the corresponding diffractograms are shown in Fig. 2. Directly after milling a diffractogram is obtained that is composed of relatively broad reflections due to both small, nm-sized crystallites and lattice strain. It already resembles that of the low-temperature modification of Rb2SnF5 showing that the ternary fluoride is directly obtained via this one-pot mechanochemical synthesis.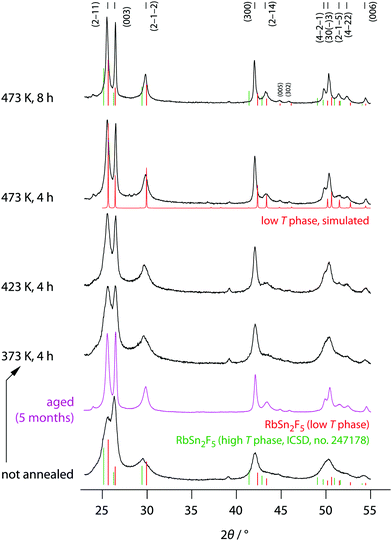 | ||
| Fig. 2 X-ray diffractograms of all RbSn2F5 samples prepared. XRD patterns were recorded at room temperature before and after the annealing steps indicated. The vertical bars shows the expected positions of the reflections for the low-T and high-T modification, respectively. While the reflections for the phase being stable above 368 K were taken from literature (ICSD no. 247178, recorded at 538 K); those for the low-T modification were constructed according to the structure model proposed by Yamada et al.32 | ||
Soft annealing, i.e., holding the sample for 8 h at 473 K under dry, oxygen-free inert gas atmosphere, clearly narrows the reflections because of crystallite growth and/or the release of strain. Lower annealing temperatures also lead to narrow reflections but the narrowing turned out to be less pronounced. Worth noting, if we simply store the ball-milled sample for several month in dry Ar atmosphere, we recognize a significant growth in average grain size. Therefore, crystallization also takes place under ambient conditions. At his temperature the crystallization kinetics are, of course, much slower than at high T. Obviously, crystal growth is driven by the high F anion conductivity of the samples. For comparison, at 293 K the ionic conductivity σdc is 6.24 × 10−5 S cm−1, see below.
The final reflections seen after soft annealing are in agreement with the structure refinement proposed by Yamada et al.32 assuming P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry and vacancies on the F1, F2 and F3 positions, see also Fig. 1. In Fig. 2 the positions of the main reflections of both the high-T and low-T phase of RbSn2F5 are indicated by vertical lines. We also included a simulation of the XRD pattern of the low-T form of RbSn2F5.
symmetry and vacancies on the F1, F2 and F3 positions, see also Fig. 1. In Fig. 2 the positions of the main reflections of both the high-T and low-T phase of RbSn2F5 are indicated by vertical lines. We also included a simulation of the XRD pattern of the low-T form of RbSn2F5.
Annealing the samples at temperatures higher than 473 K, e.g., at 568 K for several hours, causes decomposition of the ternary fluoride. Light microscopy revealed small regions that shine metallic. We assume that, due to disproportionation of Sn4+, metallic tin is formed at sufficiently high T; cf. also Fig. S1 (see ESI†). Scanning electron microscopy showed a mixture of needle-like crystallites and rectangular tubes with a length of up to 20 μm, see also Fig. S1 (ESI†).
Below 368 K the ternary fluoride crystallizes with P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry (Z = 3); at higher temperatures RbSn2F5 reversibly transforms to P
symmetry (Z = 3); at higher temperatures RbSn2F5 reversibly transforms to P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) with Z = 1. The same transition has been reported for K2SnF5.57 Yamada et al. investigated this contraction along the c-axis. The contraction is accompanied by an expansion along the ab-axis.32 Defect disorder in the vacancy-rich (F1, F2, F3)-sublattices, caused by the phase transition, leads to an easily measurable increase in F anion conductivity. This increase is also seen here; we used broadband conductivity spectroscopy to study electrical responses over a wide range of temperature and a broad frequency region.
with Z = 1. The same transition has been reported for K2SnF5.57 Yamada et al. investigated this contraction along the c-axis. The contraction is accompanied by an expansion along the ab-axis.32 Defect disorder in the vacancy-rich (F1, F2, F3)-sublattices, caused by the phase transition, leads to an easily measurable increase in F anion conductivity. This increase is also seen here; we used broadband conductivity spectroscopy to study electrical responses over a wide range of temperature and a broad frequency region.
3.2 F anion transport in RbSn2F5
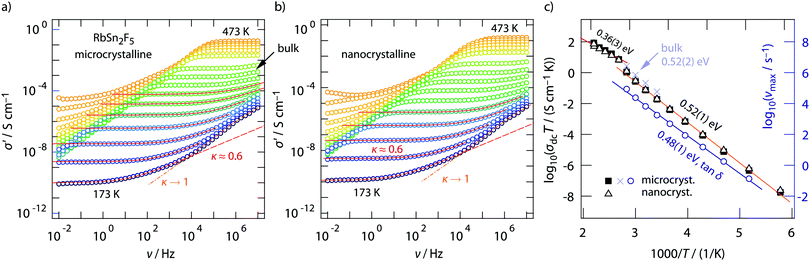
Conductivity isotherms of annealed RbSn2F5 are shown in Fig. 3a. If we look at data recorded up to 107 Hz distinct frequency-independent (direct current, dc) plateaus are visible that merge into dispersive regimes. At first glance, these regimes can be approximated with a Jonscher power law, σ′ ∝ νκ. Here, the exponent turned out to depend only slightly on temperature and amounts to κ ≈ 0.6. While for 3D ionic conductors κ usually shows values ranging from 0.65 to 0.85; 2D ionic transport is assumed to be characterized by exponents of approximately 0.55. As pointed out by Sidebottom,72 for 1D ion transport even lower values of 0.3 are expected. The latter has recently been found for channel-like ion transport in BaMgF4.73 Considering κ extracted from the fits shown in Fig. 3, the shape of the dispersive regions provides indications that 2D ion dynamics prevails in RbSn2F5.We will see later on that this view is supported by diffusion-induced nuclear spin relaxation. It is also in line with earlier reports on 2D ionic conduction in coarse-grained RbSn2F5 investigated by both impedance spectroscopy and NMR.32,58
A closer look at the data, especially if we include conductivity data recorded up to the GHz range, reveals that the situation is, however, more complex than can be recognized at first glance. At very low temperatures the isotherms, irrespective if we look at those from micro- or nanocrystalline RbSn2F5 (see Fig. 3a and b) deviate from the σ′ ∝ ν0.6 behaviour. Instead the dispersive regimes merge into a classical nearly constant loss (NCL) regime,74,75 being characterized by κ → 1. At sufficiently low T it is thus difficult to separate the two contributions from each other. On the other hand, at high temperatures, i.e., before the phase transformation of RbSn2F5 occurs, we can recognize that σ′ passes into a second dc plateau at frequencies above 106 Hz, see the arrow in Fig. 3a.
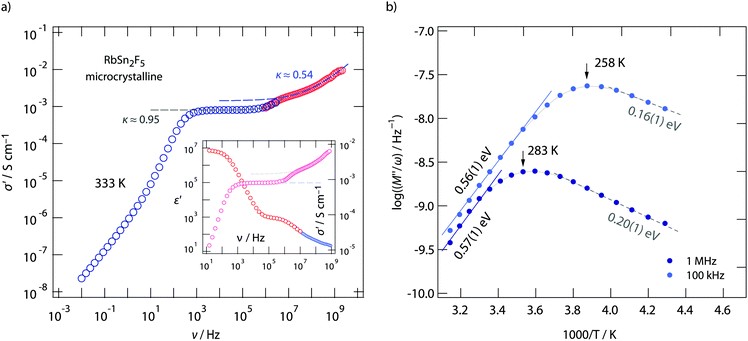
To clarify this feature we extended our measurements to frequencies in the GHz range. Fig. 4 shows the conductivity isotherm recorded at 333 K. It is clearly composed of two dc plateaus, the one occurring at high frequencies definitely belongs to bulk ion dynamics, while the one extending over a large frequency range at lower ν might also be influenced by grain boundary contributions. Importantly, the dispersive regime of the bulk plateau, whose conductivities obey an Arrhenius law with a very similar activation energy as σdc (see Fig. 3c) (0.52 eV), is characterised by κ = 0.54. This value is even closer to what we expect for 2D ionic conduction.72
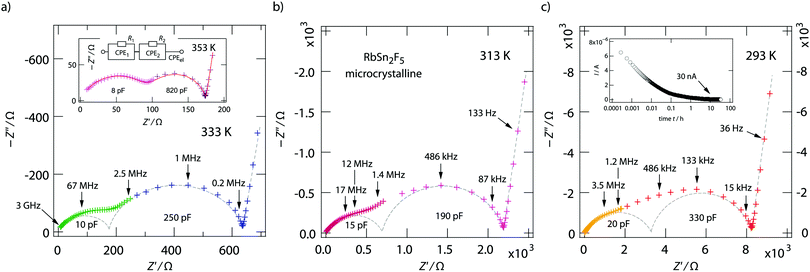
The two contributions to the overall electrical response of σ′ can also be distinguished in the Nyquist plots of Fig. 5, where the imaginary part −Z′′ of the complex impedance Ẑ is plotted versus its real part Z′. The higher the temperature the better the separation; at low T the two semicircles merge into each other. Together with the NCL-type response, showing up at even lower T, they cannot be separately analyzed at T ≪ 293 K.
We analyzed the complex impedance data by using suitable equivalent circuits consisting of individual resistances R and constant phase elements (CPEs) representing the responses from bulk, grain-boundaries (g.b.) and electrodes. The complex impedance ẐCPE of a constant phase element can be simply expressed by
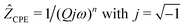 | (1) |
| C = R(1−n)/nQ1/n | (2) |
The two electrical relaxation processes are also seen in permittivity spectra. Whereas isotherms recorded at high T are less suitable to separate them (see the inset of Fig. 4a), at low T the real part, ε′, of the complex permittivity ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) clearly reveals two contributions, see ESI† (Fig. S2). We attribute these two processes to electrical relaxation in the bulk and caused by g.b. regions. Similar features are also seen for the nanocrystalline sample, for which σdc almost coincides with that of the annealed sample, see Fig. 3c. In both cases, below 370 K the product σdcT follows an Arrhenius line characterized by 0.52 eV. This activation energy perfectly agrees with that published by Yamada et al.32 and Hirokawa et al.,58 both studies report on an activation energy of 0.54 eV.
clearly reveals two contributions, see ESI† (Fig. S2). We attribute these two processes to electrical relaxation in the bulk and caused by g.b. regions. Similar features are also seen for the nanocrystalline sample, for which σdc almost coincides with that of the annealed sample, see Fig. 3c. In both cases, below 370 K the product σdcT follows an Arrhenius line characterized by 0.52 eV. This activation energy perfectly agrees with that published by Yamada et al.32 and Hirokawa et al.,58 both studies report on an activation energy of 0.54 eV.
Almost the same activation energy is obtained if we analyze tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peaks (0.48 eV, see Fig. 3c, right axis) or electric modulus peaks M′′ (0.49 eV), not shown here for the sake of brevity. The slight increase from 0.48 eV to 0.52 eV, which is seen when we compare the temperature behaviour of σdcT with that of νmax from tan
δ peaks (0.48 eV, see Fig. 3c, right axis) or electric modulus peaks M′′ (0.49 eV), not shown here for the sake of brevity. The slight increase from 0.48 eV to 0.52 eV, which is seen when we compare the temperature behaviour of σdcT with that of νmax from tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, points to a very slight increase of the charge carrier concentration N with increasing temperature. For comparison, Yamada et al. reported that N did not change much with T.32
δ, points to a very slight increase of the charge carrier concentration N with increasing temperature. For comparison, Yamada et al. reported that N did not change much with T.32
If we look at electrical properties recorded at fixed frequency but variable temperature further information about the energy landscape the F anions sense can be extracted. In Fig. 4b the temperature dependence of the resistivity, expressed as M′′/ω, is shown for two frequencies, viz. ν = 100 kHz and ν = 1 MHz. Asymmetric relaxation peaks are obtained with the high-T flanks yielding 0.56 eV in very good agreement with σdcT(1/T). Importantly, the low-T flank is characterized by a much smaller value of approximately 0.2 eV. According to Ngai's coupling concept of ionic transport,75–77 such values can be identified as the activation barriers characterising short-range ion hopping processes. By using 19F spin–lattice relaxation NMR we extracted very similar values, see below. Comparing results from conductivity spectroscopy with those from NMR will help us to describe the shape of the underlying motional correlation function that governs the electrical and nuclear magnetic responses of 2D dynamics in RbSn2F5.
3.3 Local structures and F anion diffusivity in RbSn2F5 as seen by NMR
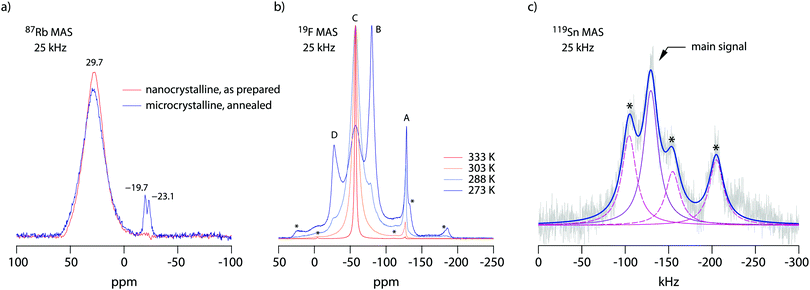
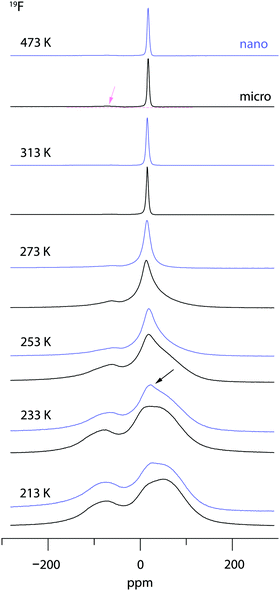
19F NMR provides insights into both local structure and dynamics of solids. In Fig. 619F, 119Sn and 87Rb MAS NMR spectra are shown, which were recorded to characterize the annealed sample. 119Sn MAS NMR, carried out at 25 kHz spinning speed, reveals a single, anisotropically broadened line in agreement with the layered crystal structure. The chemical shift anisotropy turned out to be −1850 ppm. The 87Rb NMR spectrum shows a broad resonance at 695 ppm, when referenced to SnO2 (0 ppm). At a spinning speed of 25 kHz we were not able to resolve the two Rb positions of RbSn2F5. Either they show very similar chemical shifts or (local) structural disorder, even for the annealed sample, leads to a wide distribution of magnetic and quadrupolar electric interactions causing broad resonances. At low temperatures the 19F MAS NMR spectrum reveals several, at least 4, lines with distinct chemical shifts and intensities (labelled A, B, C and D, see Fig. 6b). This result is expected when we remember the various magnetically inequivalent F sites in the structure of RbSn2F5. With increasing temperature the lines coalesce yielding a single line (see line C) in the center of gravity of the spectrum. This line already shows up at 243 K. Thus, even lower temperatures are needed to completely freeze F anion exchange in RbSn2F5 illustrating its fast ion dynamics with respect to the NMR time scale.Variable-temperature 19F NMR spectra recorded under static conditions also reveal this coalescence, see Fig. 7. In the rigid-lattice regime, which is reached at sufficiently low T, we deal with a dipolarly broadened signal composed of several contributions as expected from MAS NMR. With increasing T dipole–dipole interactions are averaged; in the extreme narrowing regime, i.e., above 313 K, a single line governs the spectra, once again showing that nearly all F anions participate in fast self-diffusion processes. Only the very shallow signal at −75 ppm reveals some F anions that do not contribute to the coalesced signal, see the arrow in Fig. 7.
Comparing the spectra for microcrystalline RbSn2F5 with those of nanocrystalline RbSn2F5 we see that heterogeneous motional narrowing starts at slighter lower T for the nanocrystalline sample, see Fig. 7. While the ionic conductivity of microcrystalline and nanocrystalline RbSn2F5 reveals no significant difference, in defect-rich ball-milled RbSn2F5 (local) structural disorder slightly increases ionic motion – at least on the length scale to which NMR line shapes are sensitive. Obviously, the defect structure of nano-RbSn2F5 is not of detrimental nature for long-range ion transport. Ions at the grain boundary or interfacial regions might benefit from such disorder, while those having access to long-range 2D pathways along the inner surfaces already participate in fast exchange processes. However, in contrast to other systems the enhancement seen for nanocrystalline RbSn2F5 turned out to be marginal. For comparison, for poorly conducting oxides with 3D pathways, the introduction of defects usually leads to an enhancement in ion dynamics by several orders of magnitude.78–80 As an example, this behaviour has also been observed for nanocrystalline LiNbO3 and LiTaO3 prepared by high-energy ball milling.78,79
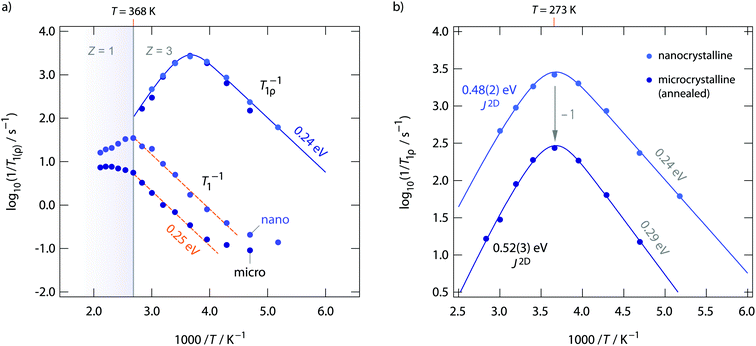
Diffusion-induced 19F NMR spin–lattice relaxation rates R1(ρ) for both annealed and as-prepared RbSn2F5 are shown in Fig. 8. Whereas spin–lattice relaxation in the laboratory frame (R1), i.e., being measured at Larmor frequencies in the MHz range, is sensitive to short-range F motions on the angstrom scale, with the rates recorded at locking frequencies in the kHz range (R1ρ) we sense long-range ion transport. Below 220 K the rates R1 are dominated by non-diffusion induced processes. 19F spins couple to phonons or paramagnetic impurities. Above 220 K spin–lattice relaxation gets increasingly controlled by F motional processes. The flanks seen in Fig. 8a result in activation energies of ca. 0.25 eV. This value agrees well with those seen on the low-T flank of the M′′/ω-curves shown in Fig. 4b. As RbSn2F5 reversibly transforms into a different crystal structure at 368 K, the R1 rates show deviations from Arrhenius behaviour at this temperature. Spin–lattice relaxation in nanocrystalline (ball-milled) RbSn2F5 is faster by approximately 1 order of magnitude if we compare R1 rates measured at 330 K. Obviously, local F dynamics is somewhat faster in the non-annealed form; this increase in local diffusivity, however, does not affect long-range ion transport in RbSn2F5 as σdc is the same for the two samples.
The behaviour of σdc is also seen in R1ρ. Obviously, R1ρ measurements are able to detect the same long-range ion dynamics as is sensed by σdc. The R1ρ rates of annealed and non-annealed RbSn2F5 almost coincide and follow the expected behaviour for a diffusion-induced relaxation processes when R1ρ is plotted vs. 1/T. In general, R1ρ (and R1) will pass through a diffusion-induced rate peak whose maximum shows up when the jump rate τ−1 reaches the order of the locking (or Larmor) frequency: ω1(0)τ−1. While in the limit ω1τ ≫ 1 the flank of the R1ρ(1/T) peak is influenced by correlation effects and structural disorder, the flank in the regime ω1τ ≪ 1 should sense dynamic parameters being comparable to long-range ion dynamics. Here, the low-T flanks yield 0.29 eV and 0.24 eV, respectively. Once again, these values agree well with those obtained from R1 measurements and the analysis of M′′ω. The high-T flank, however, results in 0.39 eV for nano-RbSn2F5 and 0.41 eV for micro-RbSn2F5. These activation energies are clearly smaller than those seen by σdc. Obviously, simply analyzing the high-T flanks of the 19F NMR relaxation peaks, which does not take into account any effects from low-dimensional diffusion, yields activation energies being inconsistent with that seen by conductivity spectroscopy. Ea extracted from the slope of high-T flanks is only of use when 3D diffusion processes are to be analyzed.
If we take into account 2D diffusion and use the semi-empirical relaxation model introduced by Richards49,62 to analyze the R1ρ(1/T) NMR peaks we obtain a different result. The solid lines in Fig. 8a show fits with spectral density functions J(ω1)2D ∝ R1ρ that include a logarithmic frequency dependence of the R1ρ rates in the limit ω1τ ≪ 1. This dependence is characteristic for 2D diffusion. J(ω1)2D, for uncorrelated motion, results in an asymmetric rate peak with the high-T slope being smaller than that in the low-T regime. For correlated motion, instead, the low-T flank is lower than that expected for 3D diffusion. Correlation effects are taken into account by the factor β in the following expression for J(ω1)2D
J(ω1)2D ∝ τc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 + 1/(2ω1τc)β) ∝ R1ρ ln(1 + 1/(2ω1τc)β) ∝ R1ρ | (3) |
| J(ω1)3D ∝ τc/(1 + (2ω1τc)β) | (4) |
It is valid for homonuclear 19F–19F spin fluctuations; here we restricted ourselves to a single term for a good approximation of the rates measured. The limiting cases of eqn (3) for the high- and low-T slopes of the corresponding R1ρ(1/T) relaxation peak are the following ones:82
J(ω1)2D ∝ τc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1/(2ω1τc)), for ω1τc ≪ 1 ln(1/(2ω1τc)), for ω1τc ≪ 1 | (5) |
| J(ω1)2D ∝ τc1−β(2ω1)−β, for ω1τc ≫ 1 | (6) |
For β = 2, eqn (5) is identical with the result for 3D uncorrelated motion. τc−1 is expected to be identical with the jump rate τ−1 within a factor of 2–3. τ−1 is assumed to be thermally activated according to an Arrhenius law:
τ−1 = τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/(kBT)) exp(−Ea/(kBT)) | (7) |
Using J(ω1)2D, see eqn (3), to analyse the rate peaks of Fig. 8, yields fits that properly agree with the temperature behaviour of the rates measured, see the solid lines in Fig. 8. The activation energies for micro- and nanocrystalline RbSn2F5 turn out to be 0.52 eV and 0.48 eV, respectively. Especially the value for micro-RbSn2F5 perfectly agrees with that from conductivity measurements (0.52 eV). In contrast, eqn (4), i.e., using a 3D diffusion model, yields 0.39 eV (almost the same value is obtained if only the high-T slope is analyzed, as mentioned above). Although the quality of the two types of fits are very similar, only the spectral density of Richards developed for 2D diffusion is in agreement with the expectation that Ea from this model equals that deduced from σdc.
Here, as mentioned above, we have restricted J(ω1)iD (with i = 2, 3) to a single term. Including higher-order terms does not change the quality of the fits and has no effect on Ea and τ0−1. The pre-factors τ0−1 of the fits shown in Fig. 8b are in the order of 2 × 1015 s−1. Such a value is relatively high but in agreement with similar observations for surface diffusion.83 Obviously, F diffusion along the buried or inner planes84 of RbSn2F5 resembles ion dynamics on surfaces.
In both cases, i.e., for nanocrystalline and microcrystalline RbSn2F5, the correlation factor β turned out to be 1.51 (nano) and 1.57 (micro), respectively. β directly influences the slope on the low-T side, the smaller value of 1.45 leads to a slightly smaller slope for nano-RbSn2F5 as seen in Fig. 8b. Considering the frequency limits of J(ω1)3D (R1 ∝ τc and R1 ∝ τc1−βω0−β) we see that the activation energies on the low-T and high-T side are connected to each other via
| Elow-Ta = (β − 1)Ehigh-Ta | (8) |
For 2D ionic motion essentially the same equation holds true, we have, however, to replace Ea(high-T) with the activation energy from the fit with J(ω1)2D.29 If we simply take the slope of the R1(ρ)(1/T) peak we must consider that E2Da is related to E3Da = Ea(high-T) via E3Da = 3/4E2Da;49 with the values obtained here we have 0.39 eV = 3/4 × 0.52 eV. With β = 1.57 the relationship E2Da(low-T) = (β − 1)E2Da is also fulfilled as we indeed have found 0.29 eV ≈ 0.57 × 0.52 eV. The same also holds for nanocrystalline RbSn2F5 with β − 1 ≈ 0.5 and E2Da(low-T) = 1/2E2Da.
In summary, while long-range ion transport in microcrystalline RbSn2F5 is characterized by 0.52 eV, short-range motions, taking into account correlation effects such as strictly confined hopping processes, local disorder and Coulomb interactions are best described by an activation energy of 0.29 eV. For nanocrystalline RbSn2F5 this value is somewhat reduced to 0.24 eV; this slight change is also reflected in 19F NMR line narrowing, see above. This view on ion transport is also in agreement with the model introduced by Ngai. Independent of any dimensionality effects in Ngai's coupling concept dispersive regions in σ′(ν) would be expected that follow a νn=β−1 behaviour, which is fulfilled in the present case.
To further compare results from NMR with those from conductivity spectroscopy, we can use the rate R1ρ(1/T) peak to estimate a self-diffusion coefficient for F− hopping in RbSn2F5. At the peak maximum, which is seen at 273 K, the condition ω1τc ≈ 0.5 is valid; here, we have 1/τc = 2.5 × 106 s−1. Using the Einstein–Smoluchowski equation85,86D = a2/(2dτ) with d = 2 for 2D diffusion we obtain D = 2.8 × 10−14 m2 s−1 if we insert a mean jump distance of a ≈ 3 Å. The jump distances of the F anions labelled F2, F3 and F4 (see Fig. 1) range from 2.89 to 2.97 Å. The distance from F1 to F2 is 2.95 Å. For comparison, at 273 K the bulk ionic conductivity is in the order of 1.4 × 10−5 S cm−1. This value translates, according to the Nernst–Einstein equation87,88 using a charge carrier density of 3 × 1027 m3, into a solid-state diffusion coefficient Dσ of 6.7 × 10−14 m2 s−1. Thus, as the two diffusion coefficients only differ by a factor of 2, 19F NMR spin–lattice relaxation, if the maximum of the rate peak is used to estimate D, and conductivity spectroscopy sense the same motional process in layer-structured RbSn2F5.
Finally, we shall discuss the change in ion dynamics when going from microcrystalline RbSn2F5 to its structurally disordered, nanocrystalline form. Many studies, dedicated to comparing diffusion properties of nanocrystalline ceramics with those from coarse-grained materials of the same chemical composition, report on huge differences at least if poorly conducting oxides or fluorides are considered, see above.17,59,78–80 For materials with rapid ion dynamics from the start, the influence of structural disorder or size effects on ion transport is expected to be moderate or marginal if not without any positive effect on ion transport. If we consider layered materials structural disorder might even slow down ionic transport rather than increase it. For nanocrystalline LixTiS2 (0 < x ≤ 1), crystallizing with a layered structure, Winter and Heitjans did not found any large increase in Li diffusivity when compared to its coarse-grained form.89,90 Li diffusion in the TiS2 host is governed by very similar activation energies for the two forms. The incorporation of Rb for Ba in the fast 2D ionic conductor BaSnF4 increases ionic conductivity;59 most likely aliovalent doping affects, however, the slower interlayer exchange process rather than fast intralayer diffusion.59,91 For the layer-structured form of LiBH4,27,92 crystallizing with hexagonal symmetry and showing 2D diffusion, downsizing the mean crystallite diameter through ball-milling has only small effect on Li ion conductivity.92 On the other hand, the poorly conducting orthorhombic form of LiBH4 with 3D diffusion, clearly benefits from nanostructuring. In such a sample, NMR relaxation measurements clearly revealed a subset of rapidly diffusing Li ions.93
Here, the nanocrystalline form of RbSn2F5 does not reveal strongly enhanced ion dynamics as compared to the annealed material with sharpened X-ray reflections. Conductivity spectroscopy clearly shows that ionic conductivities are the same for the two morphologies. On the contrary, one might even expect a slight decrease if defects disturb the fast 2D diffusion pathways that are already equipped with a large number fraction of vacant F anion sites. While we cannot recognize any strong effect on long-range ion transport from conductivity measurements, 19F NMR line shapes point to slightly faster ion dynamics in the nanocrystalline form as seen by the motionally averaged line emerging at lower temperatures for non-annealed RbSn2F5. Presumably, disordered grain-boundary structures act as hosts for these mobile ions being able to contribute to dipole–dipole averaging already at slightly lower temperatures. This observation is consistent with enhanced R1 relaxation rates of nano-RbSn2F5 if compared to those of microcrystalline RbSn2F5. Moreover, the corresponding activation energy on the low-T side of the spin-lock NMR peak is reduced from 0.29 eV to 0.24 eV.
Although the effects are small, on the short-range or angstrom length scale we see enhanced dynamics for the as-prepared form. Also magnetic field fluctuations of spatially confined jump processes might contribute to faster relaxation processes communicated to other 19F spins via spin-diffusion. At least, the F anions residing near the defect sites do not become trapped. Such trapping effects could easily explain any decrease in overall ion transport of layer-structured materials.
In other cases, fast localized dynamics are able to trigger through-going macroscopic transport.25 These dynamic processes might be involved in also causing the huge increase in conductivity seen for the aforementioned nanocrystalline oxides, fluorides and carbonates prepared by milling.91,94 Prominent examples include, for example, LiXO3 (X = Ta, Nb),78,79 LiAlO2,80 BaF2,95 CaF217,96,97 and Li2CO3,94 as mentioned above. Here, the subtle changes when going from the micro scale to nm-sized crystallites are, however, hardly comparable with the boosts in 3D ionic conductivity seen for the disordered systems. To sum up, for the fast 2D ionic conductor RbSn2F5 site disorder is of limited help to further enhance the already rapid long-range ion transport along the internal or buried interfaces.
4 Conclusions and outlook
Layer-structured RbSn2F5 has been prepared by a one-pot mechanochemical approach in a nanocrystalline form. We softly annealed the as-prepared sample in inert gas atmosphere to obtain microcrystalline RbSn2F5 with a mean crystallite diameter in the μm range. Annealing temperatures have to be adjusted carefully to avoid decomposition of the product. Also storing the as-prepared nanocrystalline material in Ar atmosphere for several months lead to grain growth as seen by sharp X-ray reflections. Obviously, the crystallization behaviour is triggered by fast F− diffusion in the ternary fluoride. Indeed, conductivity spectroscopy and 19F NMR relaxation show rapid F ion dynamics.Careful analysis of both the conductivity isotherms and variable-temperature Nyquist curves, which are composed of bulk and grain boundary regions, revealed indications that F dynamics in RbSn2F5 is of 2D nature. Importantly, only if analyzed with a spectral density formalism which was developed for 2D diffusion the 19F NMR data are consistent with dynamic parameters from conductivity spectroscopy. NMR relaxation measurements point to highly correlated F− exchange processes for both the nanocrystalline and microcrystalline form. Local jump processes in micro-RbSn2F5 are to be characterized by an average activation energy as low as 0.24 eV; an even lower value of only 0.16 eV can be inferred from dielectric spectroscopy. An activation energy of 0.52 eV, on the other hand, determines long-range ion transport.
By comparing our results on microcrystalline and nanocrystalline RbSn2F5 we see that structural site disorder does not lead to any drastic enhancement of ion dynamics as it has been recognized for other ionic conductors. Obviously, for layer-structured materials, as it is also known for LiCoO2 used as cathodes in lithium-ion batteries, the structurally perfect layers guiding the ions along the internal interfaces. This guidance is crucial to ensure long-range ion transport being fast enough that additional disorder does not lead to any further enhancement. Quite the contrary, one might also expect the opposite behaviour. Against this background, it seems worth considering the effect of dimensionality as a design principle for fast ion conductors.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by the Deutsche Forschungsgemeinschaft (DFG Research Unit 1277, grant no. WI 3600 4-1 5-2, WI3600/2-1(4-1) and WI3600/5-2 (SPP 1415)) as well as by the Austrian Federal Ministry of Science, Research and Economy, and the Austrian National Foundation for Research, Technology and Development (Christian Doppler Laboratory of Lithium Batteries: Ageing Effects, Technology and New Materials) is greatly appreciated.References
- P. Knauth, Solid State Ionics, 2009, 180, 911 CrossRef CAS
.
- P. Knauth and H. Tuller, J. Am. Ceram. Soc., 2002, 85, 1654 CrossRef CAS
.
- K. Funke, Sci. Technol. Adv. Mater., 2013, 14, 043502 CrossRef PubMed
.
- P. Heitjans and S. Indris, J. Phys.: Condens. Matter, 2003, 15, R1257 CrossRef CAS
.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682 CrossRef CAS PubMed
.
- S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16303 Search PubMed
.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778 CrossRef CAS PubMed
.
- V. Epp, O. Gün, H.-J. Deiseroth and M. Wilkening, J. Phys. Chem. Lett., 2013, 4, 2118–2123 CrossRef CAS
.
- A. Hayashi and M. Tatsumisago, Electron. Mater. Lett., 2012, 8, 199 CrossRef CAS
.
- A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Nat. Commun., 2012, 3, 856 CrossRef PubMed
.
- S. Narayanan, V. Epp, M. Wilkening and V. Thangadurai, RSC Adv., 2012, 2, 2553 RSC
.
- V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714–4727 RSC
.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed
.
- J. Lau, R. H. DeBlock, D. M. Butts, D. S. Ashby, C. S. Choi and B. S. Dunn, Adv. Energy Storage Mater., 2018, 8, 1800933 CrossRef
.
- Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier, M. Armand and L. Chen, Energy Environ. Sci., 2018, 11, 1945–1976 RSC
.
- S. Breuer, S. Lunghammer, A. Kiesl and M. Wilkening, J. Mater. Sci., 2018, 53, 13669–13681 CrossRef CAS
.
- A. Düvel, B. Ruprecht, P. Heitjans and M. Wilkening, J. Phys. Chem. C, 2011, 115, 23784–23789 CrossRef
.
- C. Rongeat, M. Reddy, R. Witter and M. Fichtner, J. Phys. Chem. C, 2013, 117, 4943–4950 CrossRef CAS
.
- C. Rongeat, M. Anji Reddy, R. Witter and M. Fichtner, ACS Appl. Mater. Interfaces, 2014, 6, 2103–2110 CrossRef CAS PubMed
.
- F. Preishuber-Pflügl, P. Bottke, V. Pregartner, B. Bitschnau and M. Wilkening, Phys. Chem. Chem. Phys., 2014, 16, 9580–9590 RSC
.
- S. Breuer, M. Gombotz, V. Pregartner, I. Hanzu and M. Wilkening, Energy Storage Mater., 2019, 16, 481–490 CrossRef
.
- S. Breuer and M. Wilkening, Dalton Trans., 2018, 47, 4105–4117 RSC
.
- M. Anji Reddy and M. Fichtner, J. Mater. Chem., 2011, 21, 17059–17062 RSC
.
- I. Mohammad, R. Witter, M. Fichtner and M. Anji Reddy, ACS Appl. Energy Mater., 2018, 1, 4766–4775 CrossRef CAS
.
- S. Lunghammer, D. Prutsch, S. Breuer, D. Rettenwander, I. Hanzu, Q. Ma, F. Tietz and H. Wilkening, Sci. Rep., 2018, 8, 11970 CrossRef CAS PubMed
.
- A. F. McDowell, C. F. Mendelsohn, M. S. Conradi, R. C. Bowman and A. J. Maeland, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 6336 CrossRef CAS
.
- V. Epp and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 020301 CrossRef
.
- V. Epp, S. Nakhal, M. Lerch and M. Wilkening, J. Phys.: Condens. Matter, 2013, 25, 195402 CrossRef CAS PubMed
.
- B. Stanje, V. Epp, S. Nakhal, M. Lerch and M. Wilkening, ACS Appl. Mater. Interfaces, 2015, 7, 4089–4099 CrossRef CAS PubMed
.
- A. Kuhn, P. Sreeraj, R. Pöttgen, H.-D. Wiemhöfer, M. Wilkening and P. Heitjans, J. Am. Chem. Soc., 2011, 133, 11018 CrossRef CAS PubMed
.
- D. Prutsch, B. Gadermaier, H. Brandstätter, V. Pregartner, B. Stanje, D. Wohlmuth, V. Epp, D. Rettenwander, I. Hanzu and H. M. R. Wilkening, Chem. Mater., 2018, 30, 7575–7586 CrossRef CAS
.
- K. Yamada, M. M. Ahmad, Y. Ogiso, T. Okuda, J. Chikami, G. Miehe, H. Ehrenberg and H. Fuess, Eur. Phys. J. B, 2004, 40, 167–176 CrossRef CAS
.
- G. C. Farrington and J. L. Briant, Science, 1979, 204, 1371 CrossRef CAS PubMed
.
- J. L. Bjorkstam, P. Ferloni and M. Villa, J. Chem. Phys., 1980, 73, 2932–2936 CrossRef CAS
.
- J. L. Bjorkstam and M. Villa, J. Phys., 1981, 42, 345–351 CrossRef CAS
.
- J. Li, W. Yao, S. Martin and D. Vaknin, Solid State Ionics, 2008, 179, 2016–2019 CrossRef CAS
.
- B. L. Ellis, K. T. Lee and L. F. Nazar, Chem. Mater., 2010, 22, 691–714 CrossRef CAS
.
- M. Wilkening, W. Küchler and P. Heitjans, Phys. Rev. Lett., 2006, 97, 065901 CrossRef CAS PubMed
.
- M. Wilkening and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 024311 CrossRef
.
- W. Küchler, P. Heitjans, A. Payer and R. Schöllhorn, Solid State Ionics, 1994, 70/71, 434 CrossRef
.
- J. R. Dahn, W. R. McKinnon, R. R. Haering, W. J. L. Buyers and B. M. Powell, Can. J. Phys., 1980, 58, 207–213 CrossRef CAS
.
- F. Kimmerle, G. Majer, U. Kaess, A. J. Maeland, M. S. Conradi and A. F. McDowell, J. Alloys Compd., 1998, 264, 63–70 CrossRef CAS
.
- E. Murray, D. F. Brougham, J. Stankovic and I. Abrahams, J. Phys. Chem. C, 2008, 112, 5672–5678 CrossRef CAS
.
- M. Castiglione, P. A. Madden, P. Berastegui and S. Hull, J. Phys.: Condens. Matter, 2005, 17, 845 CrossRef CAS
.
- S. Chaudhuri, F. Wang and C. P. Grey, J. Am. Chem. Soc., 2002, 124, 11746–11757 CrossRef CAS PubMed
.
- M. S. Whittingham, Chem. Rev., 2004, 104, 4271 CrossRef CAS PubMed
.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587 CrossRef CAS
.
- B. L. Ellis and L. F. Nazar, Curr. Opin. Solid State Mater. Sci., 2012, 16, 168 CrossRef CAS
.
-
P. M. Richards, in Topics in Current Physics, ed. M. B. Salamon, Springer, Berlin, 1979, vol. 15 Search PubMed
.
-
P. Heitjans, A. Schirmer and S. Indris, in Diffusion in Condensed Matter, ed. P. Heitjans and J. Kärger, Springer, 2005, ch. 9, p. 367 Search PubMed
.
- K. Volgmann, V. Epp, J. Langer, B. Stanje, J. Heine, S. Nakhal, M. Lerch, M. Wilkening and P. Heitjans, Z. Phys. Chem., 2017, 231, 1215–1241 CAS
.
- S. Vilminot, R. Bachmann and H. Schulz, Solid State Ionics, 1983, 9-10, 559–562 CrossRef CAS
.
- M. Ahmad, K. Yamada and T. Okuda, Solid State Commun., 2002, 123, 185–189 CrossRef CAS
.
- M. M. Ahmad, K. Yamada and T. Okuda, Phys. B, 2003, 339, 94–100 CrossRef CAS
.
- L. N. Patro and K. Hariharan, Mater. Sci. Eng., B, 2009, 162, 173–178 CrossRef CAS
.
- J. D. Donaldson and J. D. O'Donoghue, J. Chem. Soc., 1964, 271–275 RSC
.
- J. Battut, J. Dupuis, S. Soudani, W. Granier, S. Vilminot and H. Wahbi, Solid State Ionics, 1987, 22, 247–252 CrossRef CAS
.
- K. Hirokawa, H. Kitahara, Y. Furukawa and D. Nakamura, Ber. Bunsenges. Phys. Chem., 1991, 95, 651–658 CrossRef CAS
.
- F. Preishuber-Pflügl and M. Wilkening, Dalton Trans., 2016, 45, 8675–8687 RSC
.
- A. Kuhn, S. Narayanan, L. Spencer, G. Goward, V. Thangadurai and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 094302 CrossRef
.
- R. Bertermann and W. Müller-Warmuth, Z. Naturforsch., A: Phys. Sci., 1998, 53, 863 CAS
.
- P. M. Richards, Solid State Commun., 1978, 25, 1019 CrossRef
.
- V. Ŝepelák, A. Düvel, M. Wilkening, K.-D. Becker and P. Heitjans, Chem. Soc. Rev., 2013, 42, 7507–7520 RSC
.
- D. Ailion and C. P. Slichter, Phys. Rev. Lett., 1964, 12, 168 CrossRef CAS
.
- C. P. Slichter and D. Ailion, Phys. Rev., 1964, 135, A1099 CrossRef
.
- D. C. Ailion and C. P. Slichter, Phys. Rev., 1965, 137, A235 CrossRef
.
- D. C. Look and I. J. Lowe, J. Chem. Phys., 1966, 44, 2995 CrossRef CAS
.
- T. J. Rowland and F. Y. Fradin, Phys. Rev., 1969, 182, 760 CrossRef CAS
.
- D. Wolf, Phys. Rev. B: Solid State, 1974, 10, 2724 CrossRef CAS
.
-
E. Fukushima and S. B. W. Roeder, ExperimentalPulse NMR: A Nuts and Bolts Approach, Addison-Wesley Pub. Co., Advanced Book Program, Reading, Mass., 1981 Search PubMed
.
- S. Lunghammer, Q. Ma, D. Rettenwander, I. Hanzu, F. Tietz and H. Wilkening, Chem. Phys. Lett., 2018, 701, 147–150 CrossRef CAS
.
- D. L. Sidebottom, Rev. Mod. Phys., 2009, 81, 999 CrossRef
.
- F. Preishuber-Pflügl and M. Wilkening, Dalton Trans., 2014, 43, 9901–9908 RSC
.
-
K. Funke, C. Cramer and D. Wilmer, in Diffusion in Condensed Matter - Methods, Materials, Models, ed. P. Heitjans and J. Kärger, Springer, Berlin, 2nd edn, 2005, ch. 21, pp. 857–893 Search PubMed
.
-
K. L. Ngai, Relaxation and Diffusion in Complex Systems, Springer, New York, 2011 Search PubMed
.
- C. Leon, J. Habasaki and K. L. Ngai, Z. Phys. Chem., 2009, 223, 1311 CrossRef CAS
.
- K. Ngai, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13481 CrossRef CAS
.
- M. Wilkening, V. Epp, A. Feldhoff and P. Heitjans, J. Phys. Chem. C, 2008, 112, 9291 CrossRef CAS
.
- P. Heitjans, M. Masoud, A. Feldhoff and M. Wilkening, Faraday Discuss., 2007, 134, 67 RSC
.
- D. Wohlmuth, V. Epp, P. Bottke, I. Hanzu, B. Bitschnau, I. Letofsky-Papst, M. Kriechbaum, H. Amenitsch, F. Hofer and M. Wilkening, J. Mater. Chem. A, 2014, 2, 20295–20306 RSC
.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679 CrossRef CAS
.
- M. Uitz, V. Epp, P. Bottke and M. Wilkening, J. Electroceram., 2017, 38, 142–156 CrossRef CAS
.
- J. Hinterberg, A. Adams, B. Blümich, P. Heitjans, S. Kim, Z. A. Munir and M. Martin, Phys. Chem. Chem. Phys., 2013, 15, 19825–19830 RSC
.
- P. Heitjans and M. Wilkening, Mater. Res. Bull., 2009, 34, 915 CrossRef CAS
.
- A. Einstein, Ann. Phys., 1905, 14, 182–193 CrossRef
.
- M. von Smoluchowski, Ann. Phys., 1906, 326, 756–780 CrossRef
.
- R. McKee, Solid State Ionics, 1981, 5, 133–136 CrossRef CAS
.
-
H. Mehrer, Diffusion in Solids., Springer, Berlin, 2006 Search PubMed
.
- R. Winter and P. Heitjans, J. Phys. Chem. B, 2001, 105, 6108 CrossRef CAS
.
- R. Winter and P. Heitjans, J. Non-Cryst. Solids, 2001, 293, 19 CrossRef
.
- M. Wilkening, A. Düvel, F. Preishuber-Pflügl, K. Da Silva, S. Breuer, V. Ŝepelák and P. Heitjans, Z. Kristallogr. – Cryst. Mater., 2017, 232, 107–127 CAS
.
- V. Epp and M. Wilkening, ChemPhysChem, 2013, 14, 3706–3713 CrossRef CAS PubMed
.
- S. Breuer, M. Uitz and H. M. R. Wilkening, J. Phys. Chem. Lett., 2018, 9, 2093–2097 CrossRef CAS PubMed
.
- D. Prutsch, S. Breuer, M. Uitz, P. Bottke, J. Langer, S. Lunghammer, M. Philipp, P. Posch, V. Pregartner, B. Stanje, A. Dunst, D. Wohlmuth, H. Brandstätter, W. Schmidt, V. Epp, A. Chadwick, I. Hanzu and M. Wilkening, Z. Phys. Chem., 2017, 231, 1361–1405 CAS
.
- B. Ruprecht, M. Wilkening, R. Uecker and P. Heitjans, Phys. Chem. Chem. Phys., 2012, 14, 11974 RSC
.
- W. Puin, S. Rodewald, R. Ramlau, P. Heitjans and J. Maier, Solid State Ionics, 2000, 131, 159–164 CrossRef CAS
.
- W. Puin and P. Heitjans, Nanostruct. Mater., 1995, 6, 885–888 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available: Further NMR spectra and conductivity data. See DOI: 10.1039/c8cp07206j |
| ‡ Present address: Schunk Carbon Technology GmbH, Au 62, 4822 Bad Goisern, Austria. |
| This journal is © the Owner Societies 2019 |