Computational microscopy study of the granular structure and pH dependence of PEDOT:PSS

Abstract

Computational microscopy based on Martini coarse grained molecular dynamics (MD) simulations of a doped conducting polymer poly(3,4-ethylenedioxythiophene)polystyrene sulfonate (best known as PEDOT:PSS) was performed focussing on the formation of the granular structure and PEDOT crystallites, and the effect of pH on the material morphology. The PEDOT:PSS morphology is shown to be sensitive to the initial distribution of PEDOT and PSS in the solution, and the results of the modelling suggest that the experimentally observed granular structure of PEDOT:PSS can be only obtained if the PEDOT/PSS solution is in the dispersive state in the initial crystallization stages. Variation of the pH is demonstrated to strongly affect the morphology of PEDOT:PSS films, altering their structure between granular-type and homogeneous. It also affects the size of crystallites and the relative arrangement of PEDOT and PSS chains. It is shown that the crystallites in PEDOT:PSS are smaller than those in PEDOT with molecular counterions such as PEDOT:tosylate, which is consistent with the available experimental data. The predicted changes of the PEDOT:PSS morphology with variation of the pH can be tested experimentally, and the calculated atomistic picture of PEDOT:PSS films (not accessible by conventional experimental techniques) is instrumental for understanding the material structure and building realistic models of PEDOT:PSS morphology.

---

1 Introduction

Poly(3,4-ethylenedioxythiophene) polymerized in the presence of polystyrene sulfonate (PEDOT:PSS) is one of the most technologically important conducting polymers.^1,2 In contrast to many other conducting polymers, PEDOT:PSS is thermally and chemically stable and is thus used as an active element in various technological applications including flexible and printable electronic and optical devices, as well as energy storage devices.^3–9

A massive number of experimental studies have been devoted to investigation of various aspects of the morphology of PEDOT:PSS (for reviews see e.g.ref. 10–12). The experimental techniques include electron microscopy such as high-resolution transmission electron microscopy (HR-TEM), scanning electron microscopy (SEM), and atomic force microscopy (AFM);^13–15 diffraction scattering such as grazing incidence wide-angle X-ray scattering (GIWAXS) and grazing-incidence small-angle X-ray scattering (GISAXS);^16–18 and photo-electron spectroscopy such as X-ray photoelectron spectroscopy (XPS) and ultraviolet photoelectron spectroscopy (UPS).^19,20 The morphology and electrical conductivity of PEDOT:PSS are strongly dependent on the fabrication process, pH,^21–25 PSS composition ratio,²⁶ and additive concentration.^26–28 In its pristine (as polymerized) form, the electrical conductivity of PEDOT:PSS is rather low ∼1 S cm⁻¹,¹² which is attributed to the formation of an insulating layer of PSS around conducting PEDOT cores. PSS is used in an excess weight ratio, keeping the whole polymer in a dispersed state, and does not contribute to the conductivity. The treatment of pristine PEDOT:PSS with small amounts of high boiling solvents like dimethyl-sulfoxide (DMSO), ethylene glycol and glycerol causes phase separation, enhancement of the formation of the lamellar structure and improvement of the interchain coupling of PEDOT,²⁹ leading to more organized PEDOT:PSS films. Washing the treated film with water removes the excess of insulating separated PSS and enhances the conductivity up to ∼5000 S cm⁻¹, approaching the conductivities of transparent electrodes such as indium tin oxide.^12,28–33

Changing the pH-value through acidic and basic treatment modifies the optical properties, film morphology (roughness), thermoelectric properties and electrical conductivity.^{22–25,27,34–36} The suggested mechanism for electrical conductivity enhancement by acidic treatment is the formation of PSS-H. For example, the conductivity enhancement was related to the transformation of non-conductive PSS chains into PSS-H form,³⁴ phase separation between PEDOT and PSS-H,³⁷ phase separation between PEDOT and PSS and enhanced π–π stacking between PEDOT chains³⁶ and removing PSS domains and enhanced inter-chain coupling.³⁵ X-ray photoelectron spectroscopy also shows the change in the chemical environment of PSS and reducing the PSS weight ratio after acidic treatment.^22,38–41

The morphology of PEDOT:PSS shows a very complex character and depends on various factors as outlined above. It should be stressed however that that are several major features that are repeatedly reported in many studies. They include (a) formation of small crystallites consisting of several π–π stacking PEDOT chains,^{15,17,42–46} and (b) granular structure featuring PEDOT-rich and PSS-rich regions (micellar) of characteristic sizes of 20–30 nm.^{13–15,26–28,35,46–49} Based on the available experimental observations, there are many morphological pictures for PEDOT:PSS proposed in various studies.^{23,25,27,40,48,50–61} Some representative pictures are summarized in Fig. 1. It is apparent from Fig. 1 that not all of these pictures are consistent with each other. Also, some of the suggested morphologies are difficult to reconcile with the experimental observations. For example, the morphology of Fig. 1(d) (ref. 16) does not feature the granular structure, whereas the morphologies shown in Fig. 1(c, b and g) (ref. 25, 29 and 43, respectively) are not consistent with the high conductance of thin films requiring a percolative network of π–π coupled PEDOT chains extending over the entire film.⁶²

Fig. 1 A brief overview of representative morphological pictures of PEDOT:PSS. The presented morphological pictures are based on (a) Nardes et al.⁴⁷ (reproduced with permission from John Wiley and Sons), (b) Kim et al.²⁹ (reproduced with permission from American Physical Society), (c) Tanaka et al.⁴³ (reproduced with permission from American Chemical Society), (d) Wei et al.¹⁶ (reproduced with permission from John Wiley and Sons), (e) Rivney et al.⁴⁸ (reproduced under a creative commons license), (f) Palumbiny et al.⁴⁴ (reproduced with permission from John Wiley and Sons), (g) Pang et al.²⁵ (reproduced with permission from Elsevier) and (h) Volkov et al.⁴⁶ (reproduced with permission from John Wiley and Sons).

The conflicting reports on the morphological picture of PEDOT:PSS mentioned above can be attributed in part to a lack of theoretical understanding of its complex morphology. Note that various aspects of morphology and transport in PEDOT doped with molecular counterions (as opposed to PSS, which is a poly-anion) were recently studied by the present authors using all atomistic and coarse-grained molecular dynamics simulations (CG MD), addressing the effect of crystallite formation,⁶³ the chain length,⁶² various counterions and oxidation levels,¹⁸ ion diffusion,⁶⁴ and the effect of the substrate on the morphology and conductivity.⁶⁵ At the same time, theoretical studies of realistic PEDOT:PSS capturing the essential features of the PEDOT:PSS morphology such as π–π stacking and granular structure formation are practically missing. This is remarkable, taking into account the fact that the number of experimental papers on PEDOT:PSS far exceeds 1000 per year and is growing.^11,12 Modeling of a realistic PEDOT:PSS morphology represents a challenging task as compared to PEDOT with molecular counterions, because it requires computation on a length scale exceeding ∼20 nm in order to describe a granular structure of PEDOT:PSS. This therefore requires coarse grained MD approaches, because all-atomistic MD simulations would be prohibitively expensive to reproduce the realistic PEDOT:PSS morphology on this length scale. At the same time, coarse grained approaches should be sufficiently detailed to be able to reproduce the π–π stacking and crystallite formation, which is essential for the formation of the percolative conductance paths through PEDOT.⁶² (It should be noted that several all-atomistic MD studies of PEDOT:PSS have been reported recently.^66–68 They however did not address the morphological features discussed above such as π–π stacking formation and granular structure of PEDOT:PSS.)

In the present paper we, based on CG MD simulations, report computational microscopy of realistic PEDOT:PSS thin films focussing on the formation of PEDOT- and PSS-rich grains and crystallite structure and especially on the effect of pH on the thin film morphology. We used the Martini coarse-grained model for the description of PEDOT, PSS, ions and polarizable-water molecules. The Martini force-field improves the speed, accuracy, and versatility of CG simulations and provides a platform for long-time MD simulation of a large enough simulation box.^69–71 We demonstrate that the PEDOT:PSS morphology is sensitive to the initial distribution of PEDOT and PSS in the solution, and the results of our modelling suggest that in the initial stage of crystallization the PEDOT/PSS solution must have a dispersive character. We also demonstrate that variation of the pH strongly affects the morphology of PEDOT:PSS films, changing their structure between granular-type and homogeneous ones, which can be tested experimentally. We believe that our computational microscopy study provides a detailed atomistic view not accessible by conventional experimental means, which can help to build realistic models of PEDOT:PSS morphology. Our findings, revealing the effect of the pH on molecular packing, will lead to better understanding of this complex material and hopefully inspire further experimental studies of the effect of pH on the material morphology.

2 Model and computational details

2.1 The system under investigation

We investigate the morphology of PEDOT:PSS at different pH values using Martini coarse-grained molecular dynamics simulations. The PEDOT to PSS weight ratio is set to 1 : 2.5, which is equivalent to the well-known Clevios PH¹ commercial samples. The computational box contains 500 PEDOT chains and 230 PSS chains of length 12 and 50 monomer units respectively. The chemical structure of PEDOT and PSS and details of the simulation model are provided in Fig. 2. In all simulations the oxidation level of PEDOT is set to C_ox = 33.3% (corresponding to pristine PEDOT:PSS), which is modeled by equally distributed charges +0.333e on virtual sites.⁶⁴ In the simulation we consider PSS chains with different deprotonation level α defined aswhere [SO₃H] and [SO₃⁻] are the concentrations of the undissociated acid and acid conjugate base which are randomly distributed in a PSS chain. (From this expression, α = 0 corresponds to full protonation, whereas α = 1 corresponds to full deprotonation.) The distribution of the deprotonated groups remains fixed during the whole simulation. By performing calculations with different initial distributions, we verified that our computational system is large enough such that different initial distributions of the deprotonated groups always lead to the (statistically) same final configuration for all α. The pH of the solution is determined by the protonation ratio of the sulphonate group using the Henderson Hasselbalch equation,where pK_a = 2.9 is the logarithmic dissociation constant of PSS.⁷²Fig. 2(c) shows a relation between the PSS protonation level α and the pH calculated according to eqn (2). In this study we present results for three representative cases α = 0, 0.2, and 1, which respectively correspond to pH → 0, pH ≈ 2.5, and pH ≳ 5 (results for more values of α can be found in the Appendix). In order to maintain charge neutrality negative Cl⁻ ions (positive Na⁺ ions) are added to the system for the high (low) protonation level as outlined in Fig. 2(c).

Fig. 2 (a) The Martini CG model for PEDOT and PSS chains. (b) The content of simulation boxes for different protonation levels α = 0, 0.2, and 1. (c) The relation between pH and the protonation level α as defined by eqn (1) and (2). (d) The evolution of the simulation box during evaporation from a hydrated solution (Hy = 70%) to a dry film (Hy = 10%). PSS chains, PEDOT chains, and SO₃H, SO₃⁻, Na⁺ and Cl⁻ ions are represented by green, blue, purple, cyan, silver and red colors respectively.

The initial solutions were prepared with a water weight ratio (hydration level) Hy = 70%, and the size of the initial simulation box is 30 nm × 30 nm × 20 nm, see Fig. 2(d). Then the solvent (water) is gradually removed from the solution to reach a dry phase of the polymer film. This way to reach the final dry film from the initial solution corresponds to the experimental procedure used by Palumbiny at al.,⁴⁴ and was utilized in our previous studies.^{18,63–65,73} During evaporation we fix the x- and y-dimensions of the simulation box to mimic the drop-casting process used in the experimental fabrication of polymer thin films. The final size of the computational box is 30 nm × 30 nm × 5 nm for a dry film at Hy = 10%, see Fig. 2(d). (Note that nominally “dry” PEDOT:PSS films usually still contain some water of 5–15 wt%, and therefore in what follows we will refer to the films with Hy = 10% as nominally dry. In nominally dry experimental samples the presence of water is related to the content of water in the solvents used during the synthesis protocol and drop casting process and/or to the water uptake from the air humidity and environment.)

2.2 Martini coarse grained simulations

Fig. 2(a) shows the schematic of the Martini CG models for PEDOT and PSS chains used in the simulations. For PEDOT chains we utilize a Martini model recently developed by us.⁶⁴ For polarizable water we use a model reported in ref. 74 and 75, and for PSS⁻ we use a model of ref. 76. To determine the bead for the protonated sylphonate group SO₃H, we performed all atomistic MD calculations for the hydrogenated PSS-H, and compared the radius of gyration and end-to-end distance with the corresponding results of the CG model using different beads, see Table S1 in the ESI.† We find that the Martini bead P5 gives the best agreement with the AA MD calculations, and we thus use this bead to model the protonated sulfonate group SO₃H in PSS, see Fig. 2(a).

As the initial configuration we consider two kinds of starting assemblies: a homogeneous solution and a dispersive mixture of PEDOT and PSS/PSS-H molecules. For the homogeneous solution, PEDOT and PSS chains are initially distributed uniformly (randomly) in the simulation box. For the dispersive initial conditions, PEDOT chains are brought together in a dense core in the center of the simulation box surrounded by PSS chains. Both homogeneous and dispersive initial simulation boxes are shown in Fig. 3 and 4, respectively. For both simulations the Na⁺ and Cl⁻ ions are distributed randomly to keep the charge neutrality (from the experimental point of view, the addition of an acid and/or base is the source of these ions). The long range Coulomb interaction between charged beads is truncated using the Particle Mesh Ewald (PME) method.⁷⁷ For the starting configuration the energy is minimized with the steepest descent algorithm. Water molecules are equilibrated for 100 ns in the NPT ensemble with position restraints on PEDOT and PSS chains by using the Berendsen thermostat and barostat⁷⁸ (T = 300 K and P = 1 bar). The production run for the initial solution was performed in the NPT ensemble for 300 ns and allowing polymer chains to move. The temperature is set to T = 300 K with velocity rescaling temperature coupling. The duration of the production run is chosen to ensure that the total energy, and also the root-mean-square deviation of PEDOT and PSS backbones, saturates as shown in Fig. S1 and S2 (ESI†). Additional confirmation that the equilibrium is achieved is obtained using simulated annealing calculations as described in Section S2 (ESI†). To reach the dry film, water molecules are evaporated (taken away from the box) randomly with a rate of 1.25% w/w in nearly 50 evaporation steps. In each evaporation step, the system is equilibrated in two stages as follows: firstly, water equilibration for 4 ns with PEDOT-PSS backbones restrained and secondly, PEDOT-PSS is un-restrained to produce an 8 ns MD run. Both stages are performed with a 20 fs time step and in the NPT ensemble with velocity rescaling temperature coupling⁷⁹ (T = 300 K) and the Parrinello–Rahman barostat⁸⁰ (P = 1 bar). A similar protocol for water evaporation is used with a different evaporation speed for Martini CG study of a poly(3-hexyl-thiophene) and phenyl-C61-butyric acid methyl ester mixture.⁸¹ All the MD calculations are performed by using the Gromacs-V5 package.^82–84

Fig. 3 Morphology of PEDOT:PSS films for an initial homogeneous solution for deprotonation levels α = 0 (a–d), 0.2 (e–h), and 1.0 (i–l). Left panels: Initial configuration; right panels: final morphology of dry films at the hydration level Hy = 10%. Insets show zoomed images. In figures (d, h and l) some PEDOT π–π stacks are highlighted to outline the formation of crystallites. PSS chains, PEDOT chains, and SO₃H, SSO₃⁻, Na⁺ and Cl⁻ ions are represented by green, blue, purple, cyan, silver and red colors respectively.

Fig. 4 Morphology of PEDOT:PSS films for an initial dispersive solution for deprotonation levels α = 0 (a–h), 0.2 (i–p), and 1.0 (q–x). Left panels: Initial configuration; right panels: final morphology of dry films at the hydration level Hy = 10%. Insets show zoomed images; for clarification in the side view (f, n and v) and zoom in the center (g, o and w) we just consider the backbone of PEDOT and PSS with ions. PSS chains, PEDOT chains, and SO₃H, SO₃⁻, Na⁺ and Cl⁻ ions are represented by green, blue, purple, cyan, silver and red colors respectively.

3 Results and discussion

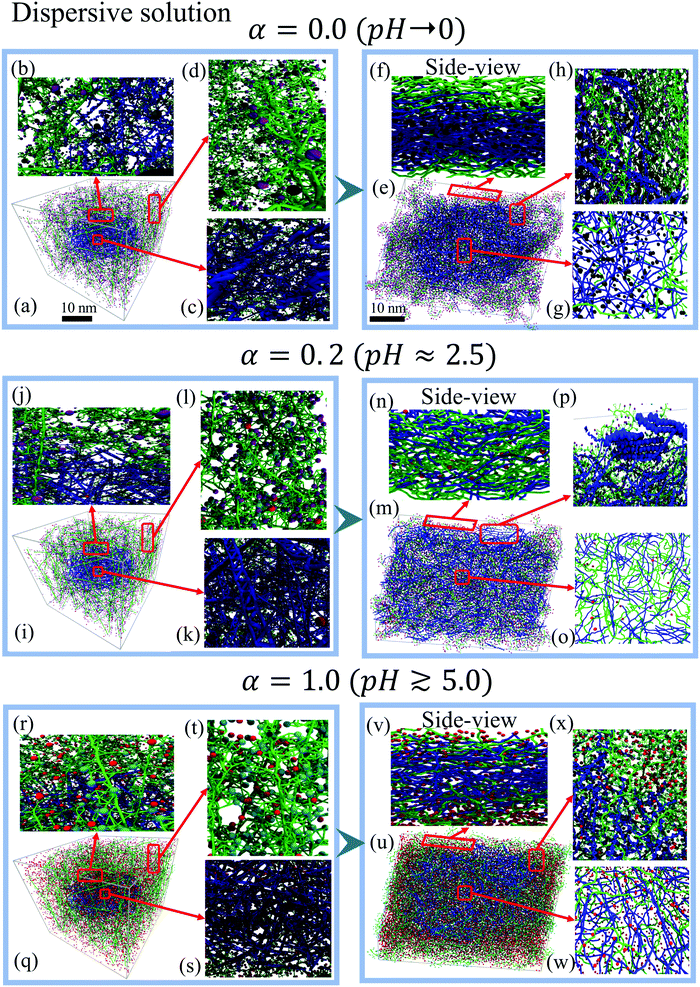
In this section we study and characterize the morphology of PEDOT:PSS nominally dried films for two cases of the initial distributions, namely a homogeneous (random) distribution, and a dispersive distribution. For each of these distributions we consider three representative deprotonation levels α = 0, 0.2, and 1 (corresponding to pH → 0, pH ≈ 2.5, and pH ≳ 5 respectively). The morphologies of PEDOT:PSS films for more deprotonation levels α = 0.1, 0.5, and 0.8 are provided in Fig. S4 (ESI†).

3.1 Initial homogeneous solution

Fig. 3(a, e and i) along with zoomed images Fig. 3(b, f and j) show the initial random distribution of PEDOT and PSS chains and Na⁺ and Cl⁻ ions in the simulation box at different deprotonation levels α. The right panels of Fig. 3 show the final morphology of PEDOT:PSS films with Hy = 10% after nearly 700 ns molecular dynamics simulation of the water evaporation process. Snapshots of the structure demonstrate that small PEDOT crystallites consisting of several π–π stacked PEDOT chains are formed in the film, see Fig. 3(c, g and k). (Some representative PEDOT chains in π–π stacking are highlighted in Fig. 3(d, h and l).) The PEDOT crystallites are well separated by PSS chains. The distinguished feature of all morphologies is that the initial homogeneous solution always leads to a uniform distribution of PEDOT chains in the PSS matrix. As discussed in the Introduction, PEDOT:PSS films typically show well defined PEDOT- and PSS-rich regions. Thus, the obtained homogeneous morphology does not reproduce a generally accepted morphological picture of PEDOT:PSS. Hence, we conclude that formation of PEDOT:PSS films does not start from a homogeneous mix of PEDOT and PSS chains. In the next subsection we therefore explore the PEDOT:PSS morphology starting from a dispersive PEDOT/PSS solution.

3.2 Initial dispersive solution

3.2.1 Distribution of PEDOT and PSS in thin films. We model the dispersed PEDOT in PSS solution by considering a dense PEDOT core with a surrounding PSS shell like a PEDOT-PSS micelle as shown in Fig. 4(a, i and q). In these simulations we start with an initial size of 15–20 nm for the PEDOT-rich region, which is in the range of the experimental PEDOT:PSS grain size.^{13–15,26–28,35,46–49,85,86}Fig. 4(a, i and q) are the initial solutions with a PEDOT core in the center of box. Zoomed images in Fig. 4(b, j and r), (d, l and t) and (c, k and s) represent the initial configuration at the interface between PEDOT and PSS, the outer PSS shell, and the inner PEDOT core respectively.

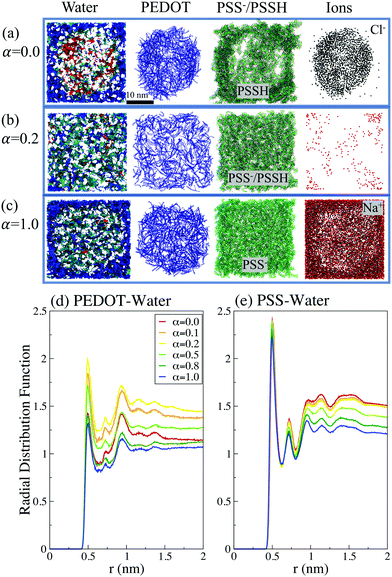
The calculations show that for the initial dispersive solution, the final film morphology strongly depends on the pH of the initial solution. We distinguish three different regimes, which are illustrated by representative deprotonation levels α = 0.0, 0.2 and 1.0. For the lowest value of α = 0.0 (corresponding to pH → 0), PEDOT chains come together to make a typical granular (micellar) structure with a PEDOT-rich core surrounded by a PSS shell, see Fig. 4(e, h and g). In the side view of a dried film (Fig. 4(f)), a sharp interface between PEDOT- and PSS-rich regions is clearly visible. One can recognize a high concentration of Cl⁻ ions in the central PEDOT-rich region. Fig. 4(h) presents a top view zoom of the interface between the central PEDOT-rich core and the outer PSS-rich shell to show the perfect phase separation. The formation of granular structure is also illustrated in Fig. 5, showing separately PEDOT and PSS chains in the simulation box.

Fig. 5 The snapshot of water, PEDOT- and PSS chains, and ions for (a) α = 0.0, (b) α = 0.2 and (c) α = 1.0 at the hydration level Hy = 10% for the dispersive solution. To show the distribution of water molecules in the polymer matrix we use red and blue colours for water molecules within a distance of 6 angstrom from PEDOT and PSS, respectively. The water molecules which are in the range of 6 angstrom from both PEDOT and PSS are in a cyan colour. The radial distribution between (d) PEDOT and (e) PSS and water molecules for six different α values.

By increasing the deprotonation level to α = 0.1–0.2 the initial PEDOT core is dissolved into the PSS solution and the final film morphology becomes rather homogeneous with a uniform distribution of PEDOT and PSS chains in the entire computational box, see Fig. 4(n and o) and 5. The resulting morphology is similar to the one obtained for the case of the initial homogeneous solution (Section 3.1: Initial homogeneous solution).

At higher pH for α ≈ 0.5–1.0, when more sulfonate groups in PSS chains are deprotonated and thus acquire negative charges, the micellar-type core–shell structure is restored. Fig. 4(q–w) show the starting solution and the final dried film for α = 1.0. (See also Fig. 5, which shows separately PEDOT and PSS chains in the simulation box.) Due to the strong electrostatic attraction between PEDOT and PSS⁻, the PSS⁻ chains penetrate into the dense PEDOT core. The side view (Fig. 4(v)) shows the presence of PSS⁻ and few Na⁺ ions among PEDOT chains. As for the case of the low deprotonation level α discussed above (Fig. 4(f)), the sharp interface between the PEDOT-rich core region and the PSS-rich shell with a high concentration of Na⁺ ions is visible in the side view. This interface is also seen in the top view presented in Fig. 4.

The observed pH dependency of the PEDOT:PSS morphology can be related to the ionic screening effect. We first note that for low and high α, the system at hand is essentially a three-component one composed of PEDOT, PSS/PSSH, and ions, whereas for intermediate α the ion concentration is low, and the system can be considered as a two-component one, composed of PEDOT and PSS/PSSH, see Fig. 5(a–c). The ions are much lighter than the PEDOT or PSS chains and thus have a much higher diffusion coefficient.⁶⁴ For low α the Cl⁻ ions during the early solution stage move into the initial PEDOT core to screen positive PEDOT chains and thus the granular structure is formed (Fig. 5(a)). For high α, the Na⁺ ions are repulsed by positive PEDOT chains and they move outside the initial PEDOT core to screen negative PSS chains (Fig. 5(b)). Because of the strong Coulombic interaction between oxidized PEDOT chains and Cl⁻ ions for low α, and negative PSS chains and Na⁺ ions for high α, the formed granular structures are not dissolved and stay intact. In contrast, for the intermediate α, the ion concentration is low and the system is composed of a blend of two components, PEDOT and PSS/PSSH, which are clearly homogeneously distributed within the computational box (Fig. 5(c)).

The morphology models of PEDOT:PSS suggested in experimental studies vary from a formation of ellipsoidal PEDOT micelles with PSS shells^43,50 to PEDOT islands in PSS shells and a free PSS region,⁵⁸ random coils of PEDOT and PSS,^{27,37,54,56,60} a PEDOT rich core and a PSS rich shell,^{27,48,52,53,61} a pancake-like morphology,^14,47,48 PEDOT- and PSS-rich regions,⁴⁶ and a uniform distribution of PEDOT along PSS chains in solution.⁴⁰ Experimentally, pH is typically controlled by acid treatment. It can be performed in different ways, by dropping acid on the films,^34,35 soaking the film into acid,³⁷ by acid vapor³⁶ or by adding acid to aqueous solution.^22,23 While the details of the methods and corresponding experimental control of pH can be different, all these methods increase the concentration of H⁺ in the blend, which leads to a higher concentration of PSSH as modelled by our simulations. Also there are different experimental models to explain the results of the acidic treatment of PEDOT:PSS, e.g., a coil to a linear/expanded-coil conformation,^36,37,56 continuous network to non-continuous clusters,²⁵ phase separation between PEDOT and PSS,⁴⁰ conformational change of the PEDOT chains and loss of PSS-H,³⁴ and formation of highly ordered and densely packed PEDOT:PSS.³⁵ Our present theoretical results provide a detailed atomistic picture for the morphology of PEDOT:PSS solution and dried films at different pH and demonstrate how the variation of pH can lead to different observed morphologies of PEDOT:PSS films.

3.2.2 Water distribution in the thin film. The changes in the morphology with variation of the deprotonation level α described above are also clearly visible in the water distribution in the PEDOT:PSS film. It should be stressed that the structure of the water clusters and distribution of water in polymer films are of the utmost importance for ion diffusion. In particular, we demonstrated previously that for PEDOT:tosylate the exponential decrease of the diffusion coefficient with the hydration level can be related to the evolution and distribution of water clusters surrounding the polymer matrix.⁶⁴ The snapshots in Fig. 5(a–c) represent the water molecule distribution in different regions of the films for different deprotonation levels α. Clearly, the water molecule distributions are different for different α and the features of the distributions can be traced to the hydrophilic character of PSS chains and hydrophobic character of PEDOT chains. In the micelle-type structure at α = 0.0 the outer PSS-rich region attracts most of the water molecules and the dense PEDOT core has less water, see Fig. 5(a). For α = 0.2, due to the uniform distribution of PEDOT and PSS chains, water molecules are also uniformly distributed in the thin film, see Fig. 5(b). The distribution of the water molecules in the computational domain at α = 1.0 is similar to the one for α = 0.0, which reflects a similar micelle-type character of the morphology of the PEDOT:PSS films for these two cases, where the water density is low in the PEDOT-rich region, see Fig. 5(c).

To quantify the water distribution in PEDOT:PSS films we plot the radial distribution functions PEDOT–water and PSS–water in Fig. 5(d and e). We note that the probability of finding water molecules in the vicinity of a chain is higher for PSS than for PEDOT, which reflects the hydrophilicity of the former as opposed to the hydrophobicity of the latter. For the case of PSS there is a simple trend – by increasing the protonation of the sulfonate group the number of water molecules surrounding PSS increases. For the case of PEDOT, the water distribution around PEDOT chains depends on the relative position of PEDOT and PSS chains and the film morphology. The maximal number of water molecules close to PEDOT chains is observed for α = 0.2. As mentioned above, water tends to stay close to PSS chains. This implies that for α = 0.2 water is situated close to PEDOT chains as well, because of the uniform distribution of PEDOT and PSS chains in this case. In contrast, for both α = 0.0 and α = 1, there is a PEDOT-rich region, and, as a result, the number of water molecules close to PEDOT chains is smaller in comparison to the case α = 0.2. We also calculated the first coordination number for PEDOT and PSS chains, which is defined as the average number of water molecules as the first neighbors of a reference carbon atom. For water molecules for the PSS chain we found that it is independent of α and is around 0.9. For PEDOT the water first coordination number strongly depends on the deprotonation level and varies between 0.63 for α = 1.0 and 0.96 for α = 0.2.

3.3 Quantifying the morphology of PEDOT:PSS films: the radial distribution functions, coordination numbers and SASA

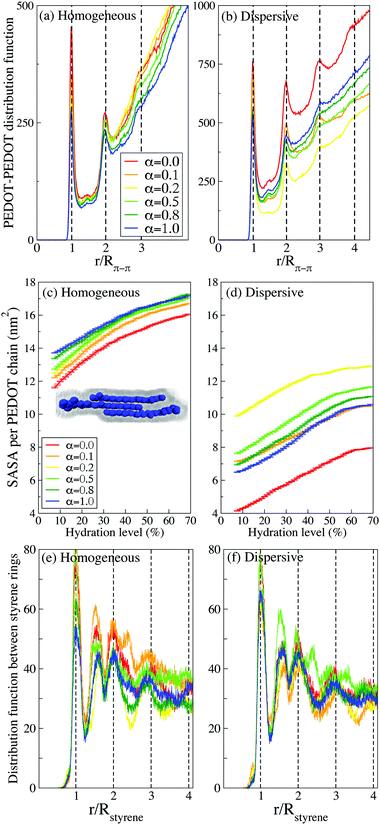
In this section we quantify the morphology of PEDOT:PSS films by examining the number of contacts, the radial distribution functions (RDF), the coordination numbers, and the SASA.

3.3.1 Radial distribution functions, number of contacts and the coordination number. Fig. 6(a and b) show the RDF between PEDOT and PSS chains for homogeneous and dispersive solutions respectively for different values of α. The RDF is calculated in a standard way, see e.g.ref. 63 and 64, where the distance is calculated between the virtual sites in PEDOT and the beads in the PSS backbone. The RDF is normalized by the total number of virtual sites in PEDOT chains. All the distributions exhibit a main peak at ≈5 Å corresponding to the minimal distance between PEDOT and PSS chains. As expected, the main peak is higher for the homogeneous configuration in comparison to the dispersive one, which is related to the formation of PEDOT cores for the latter case. The intensity of the main peak in the RDFs is an indication of the phase separation between the two parts of the polymer. Indeed, for the homogeneous case, the peak intensity is high and rather similar for all α. In contrast, for the case of the initial dispersive solution the peak is highest for α = 0.2 (i.e. for the case when the final film morphology is most homogeneous). The intensity of the peak is smaller for both α > 0.2 and α < 0.2, reflecting formation of the micelle-type structure. The peak is smallest for α = 0, corresponding to the highest phase separation between PEDOT and PSS chains.

Fig. 6 The RDFs between the virtual sites of PEDOT and the PSS backbone for (a) initial random and (b) dispersive configurations. (c) The first coordination number between PEDOT and PSS chains at hydration level Hy = 10%. The variation of the number of contacts between PEDOT and PSS chains with the hydration level for (d) homogeneous and (e) dispersive configurations. (f) Three representative arrangements of PEDOT and PSS chains.

The number of contacts between PEDOT and PSS chains is another useful characteristic to quantify the phase separation between PEDOT and PSS. We define a contact when the distance between two beads is lower than 6 Å, which according to Fig. 6(a and b) includes the sites with the minimal distance between PEDOT and PSS.⁸¹Fig. 6(d and e) show the number of contacts between PEDOT and PSS chains during water evaporation. The number of contacts decreases during water evaporation continuously because the volume of the film decreases and the chains get closer to each other. As expected, the number of contacts is the lowest for the case α = 0, i.e. for the highest phase separation between PEDOT and PSS chains; for higher values of α the number of contacts is almost independent of α. Several representative snapshots illustrating the mutual arrangements and contacts between PEDOT and PSS chains are presented in Fig. 6(f), where side by side stacking of PEDOT chains (blue color) along a PSS chain (green color) is easily recognizable.

Fig. 6(c) shows the first coordination number (CN) between PEDOT and PSS calculated using the RDF, , where g(r) is the RDF, and a ≈ 10 Å is the first minimum of g(r), see Fig. 6(a and b). The coordination numbers are similar for the cases of PEDOT-PSS(backbone), and PEDOT-PSS(sulphonate group), except for the case of the homogeneous initial distribution where the CN between PEDOT and the PSS backbone is higher than the one between PEDOT and the sulfonate group on PSS. At higher pH, α > 0.2, the coordination number is almost independent of α, whereas for a more acidic situation, α < 0.2, the coordination number sharply decreases. This behavior of the CN is directly related to the behavior of the first peak of the RDF discussed above.

3.3.2 Formation of crystallites. PEDOT chains randomly placed in the initial solution assemble themselves in π–π stacks forming nano-crystallites. (Some representative crystallites are highlighted in Fig. 3(d, h and l) and 4(q–w)). The formation of crystallites takes place in the very early stage during times t ∼ 100–120 ns, and the number of stacked PEDOT chains in crystallites does not change during water evaporation. The crystallization is nearly two times slower as compared to PEDOT:tosylate.⁶⁴ To quantify the number of stacks in crystallites we calculate the distance distribution between PEDOT chains. It shows pronounced peaks at integer values of the π–π stacking distance, R_π–π, see Fig. 7(a and b). For the case of the initial homogeneous solution there are two peaks, which corresponds to ∼3 PEDOT chains in each crystallite. For the dispersive initial solution there are three peaks corresponding to ∼4 PEDOT chains in a crystallite. Note that for the latter case the peaks are most pronounced for low and high values of α, i.e. for the cases when PEDOT:PSS exhibits the most pronounced phase separation between PEDOT and PSS. We therefore conclude that the presence of PSS somehow suppresses the crystallite formation.

Fig. 7 The RDFs between PEDOT chains for different deprotonation levels α for (a) initial random and (b) dispersive configurations at hydration level Hy = 10%. The SASA for (c) initial random and (d) dispersive configurations. The inset in (c) illustrates a definition of SASA for a representative crystallite of 3 PEDOT chains. The distribution function between styrene rings for (e) homogeneous and (f) dispersive configurations.

It is instrumental to compare the PEDOT crystallites in PEDOT:PSS with those in PEDOT:TOS. The formation of crystallites in the latter material was studied using atomistic and CG MD simulations respectively in ref. 63 and 64. The RDF in PEDOT:tosylate exhibits typically up to 6 peaks, which is more than twice as large compared to PEDOT:PSS. This is also consistent with the conclusion above that the presence of PSS chains suppresses the crystallite formation.

Our findings reported above concerning the number of chains in crystallites and the relation between the crystallite sizes in PEDOT:PSS and PEDOT:tosylate are in full agreement with the experimental data. Experimentally, the number of chains in crystallites is extracted from the broadening of the diffractions peaks in GIWAXS data using Scherrer's equation.^18,73 The comparison of the calculations to the experimental data can be done in different ways. One can do it indirectly, by also calculating the X-ray spectrum and then using Scherrer's equation to extract the number of chains in crystallites from the calculated peak broadening. Alternatively, one can do it directly, by calculating the distribution functions and simply counting the number of peaks, as presented in Fig. 7(a and b). Note that both methods provide results that are fully consistent with each other.^18,73 However, the latter method underlines the power of computational microscopy, which provides direct access to the molecular organization, in contrast to the experimental GIWAXS technique, which provides this information rather indirectly (i.e. via the peak broadening). The GIWAXS measurements show that PEDOT crystallites in PEDOT:PSS typically consist of 3–4 chains,¹⁷ which is in good agreement with the calculated number of chains as discussed above in this section. It is also noteworthy that GIWAXS measurements consistently show that PEDOT:PSS has smaller crystallites in comparison to PEDOT:tosylate, which was also reproduced in our previous calculations for PEDOT:tosylate.^63,64

Finally, it should be mentioned that the π–π stacking distance in the CG simulations is R_π–π ≈ 4.6 Å, which is somewhat larger than the one obtained from both the atomistic MD simulations and the experimental measurements (R_π–π ≈ 3.5 Å). This discrepancy, which is well-known and inherent to the Martini model, was discussed in detail in ref. 64 and 81 where it was demonstrated that it does not affect any conclusions concerning the morphology of the systems at hand. The evaluation of RDFs between PEDOT planes with water evaporation from solution to dried film for all α is presented in Fig. S5 (ESI†).

A complimentary view on the crystallite formation in PEDOT:PSS is provided by the solvent-accessible surface area (SASA), which is the area given by a rolling spherical probe with the radius of the CG water molecule as illustrated in the inset of Fig. 7(c) for a crystallite composed of three PEDOT chains. Fig. 7(c and d) show the evolution of the average SASA for PEDOT chains during the drying process for different α parameters and different initial configurations (homogeneous and dispersive). For all samples, the SASA decreases as the hydration level decreases because the volume of the thin film decreases and PEDOT chains get closer to each other, hence reducing the available surface for water molecules. Also, the π–π stacking between PEDOT chains reduces the available surface area of PEDOT chains for water molecules and it is therefore expected that the SASA is larger in a material with the smallest crystallites. Indeed, in accordance with our results concerning the crystallite sizes presented above in this subsection, the SASA is larger for the case of the initial homogeneous solution in comparison to the dispersive one, cf.Fig. 7(c and d). For the initial homogeneous solution, the SASA, as expected, is weakly dependent on α, whereas for the initial dispersive solution the SASA strongly depends on the pH and is the largest for α = 0.2 and the smallest for α = 1, which correspond to the most and the least uniform distribution of PEDOT respectively as discussed above.

Finally, we investigate the stacking between styrene rings in PSS chains. There are several experimental studies identifying a broad peak in the GIWAXS spectrum at q = 1.25 Å⁻¹ (d = 5 Å) as stacking between PSS chains.^17,35,44,46 Our calculations however do not show any presence of stacking between PSS chains. Instead, we can attribute the experimentally observed peak to the ordering of styrene rings on the same PSS chain. Fig. 7(e and f) show the distribution function g(r) between styrene rings, which exhibits peaks at integer multiples of r/R_styrene (R_styrene ≈ 4.5 Å is the distance between the styrene rings on a PSS chain, see an illustration in Fig. 6(f)). There is relatively long-range order up to stacking between 3–4 styrene rings for both homogeneous and dispersive samples at all pH. Beside the integer multiples, there is also a pronounced peak at r/R_styrene ≈ 1.5. This peak can be related to bending of the PSS backbone and rotation of styrene rings with respect to nearest neighbours (see an illustration in Fig. 6(f)). Note that the experimental reported GIWAXS peak at q = 1.25 Å⁻¹ (d = 5 Å) is very broad and therefore its origin can be attributed to styrene ring arrangements corresponding to both integer multiples of r/R_styrene and r/R_styrene ≈ 1.5.

4 Conclusion

The conducting polymer PEDOT:PSS is one of the most important and the most experimentally studied conducting polymers with thousands of experimental papers addressing various aspects of its complex morphology. At the same time, a theoretical understanding of its morphology is practically missing. Our study represents a step toward achieving this understanding, where we report a computational microscopy study of this material addressing the most fundamental questions concerning its morphology. In particular, we focus on the effect of the pH on the PEDOT:PSS structure, formation of granular (micellar) regions, phase separation, crystallite formation, and PEDOT and PSS chain orientations.

Our study is based on the Martini coarse grained MD approach that utilizes earlier developed models for water,^74,75 PSS,⁷⁶ and PEDOT,⁶⁴ complemented with a modified PSS-H model that is verified in the present study using all atomistic MD simulations. The effect of pH is modelled by varying the deprotonation level α of the PSS chains (from fully protonated to fully deprotonated, eqn (1)), thus spanning the pH range from pH → 0 to pH ≳ 5. Depending on the pH, Na⁺ or Cl⁻ counterions are introduced to maintain overall neutrality. For the initial configuration we consider two different starting assemblies: a homogeneous solution and a dispersive mixture with a dense core of PEDOT chains in the middle of the simulation box.

Our main results and conclusions can be formulated as follows.

(1) We find that the initial homogeneous solution always leads to a uniform distribution of PEDOT chains in the PSS matrix, whereas the dispersive initial distribution can lead to the dispersive granular-type final morphology with PEDOT-rich and PSS-rich phases. Because the uniform distribution is not consistent with the majority of experiments exhibiting the granular-type morphology, we conclude that in the initial stage of crystallization the PEDOT/PSS solution must have a dispersive character.

(2) For the initial dispersive solution the final morphology strongly depends on the deprotonation level α, and thus on the pH. We can distinguish three different regimes represented by three different deprotonation levels α = 0.0, 0.2 and 1.0 (corresponding to respectively pH → 0, pH ≈ 2.5, and pH ≳ 5). For the first and last regimes the PEDOT:PSS structure exhibits dispersive granular-type morphologies with PEDOT- and PSS-rich regions, whereas for the second regime the final morphology is rather homogeneous. Our results thus show that variation of the pH would lead to changes of the PEDOT:PSS morphology, which finds support in several recent experimental studies. The changes in the morphology with the variation of α described above are also clearly visible in the water distribution in PEDOT:PSS, with water clustering in the PSS-rich region because of the hydrophilic character of PSS.

(3) We demonstrate a formation of crystallites typically composed of several π–π stacked PEDOT chains. We show that the crystallites in PEDOT:PSS are smaller than those in PEDOT:tosylate, which is consistent with the available experimental GIWAXS data.

(4) In order to quantify the morphology of PEDOT:PSS we calculate the distribution functions including PEDOT–PEDOT, PEDOT–PSS, PEDOT–water, and PSS–water distributions. We also calculate the solvent available surface area, the coordination number for PEDOT and the number of contacts between PEDOT and PSS. A broad peak in the experimental GIWAXS spectrum of PEDOT:PSS at q = 1.25 Å⁻¹ (d = 5 Å) is often attributed to stacking between PSS chains. Our calculations however do not show any presence of stacking between PSS chains. Instead, we attribute the experimentally observed peak to the ordering of styrene rings on the same PSS chain.

Finally, we believe that the theoretical insight presented in our study will help to understand the essential features of the PEDOT:PSS morphology not accessible experimentally, and hence would serve as a guide for material design for enhanced performance. Clearly, PEDOT:PSS represents an extremely complex system and our theoretical study is not in a position to address all aspects of its complex morphology. We thus hope that our paper will motivate further theoretical studies of this fascinating material. We also hope that our theoretical predictions would also motivate more detailed experimental studies of the effect of pH on the material morphology.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge fruitful discussion with numerous colleagues including Dagmawi Belaineh Yilma, Magnus Berggren, Xavier Crispin, Aleksandar Mehandzhiyski, Eleni Stavrinidou, and Mats Fahlman. This work was supported by the Troëdssons foundation (896/16), Peter Wallenberg foundation (PWS-2016-0010), the Swedish Research Council via “Research Environment grant” on “Disposable paper fuel cells” (2016 05990), and research project 2017-04474, and the Swedish Energy Agency (Grants No. 43561-1). IZ thanks the Advanced Functional Material center at Linköping University for financial support. The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at NSC and HPC2N.

Notes and references

1. A. Elschner, PEDOT: principles and applications of an intrinsically conductive polymer, CRC Press, Boca Raton, Fla., Taylor Francis [distributor], London, 2011.
2. N. Kim, I. Petsagkourakis, S. Chen, M. Berggren, X. Crispin, M. P. Jonsson and I. Zozoulenko, Electric Transport Properties in PEDOT Thin Films, in Conjugated Polymers: Properties, Processing, and Applications, ed. T. A. Skotheim, J. Reynolds and B. C. Thompson, CRC Press, 2019.
3. C.-K. Cho, W.-J. Hwang, K. Eun, S.-H. Choa, S.-I. Na and H.-K. Kim, Sol. Energy Mater. Sol. Cells, 2011, 95, 3269–3275.
4. S. Stanislav, M. Aneta, V. Jan, S. Eva, H. Michal, K. Lubomir, K. Lukas, W. Martin and V. Martin, J. Biomed. Mater. Res., Part A, 2018, 106, 1121–1128.
5. A. Singh, M. Katiyar and A. Garg, RSC Adv., 2015, 5, 78677–78685.
6. T. Vuorinen, J. Niittynen, T. Kankkunen, T. M. Kraft and M. Mäntysalo, Sci. Rep., 2016, 6, 35289.
7. A. Malti, J. Edberg, H. Granberg, Z. U. Khan, J. W. Andreasen, X. Liu, D. Zhao, H. Zhang, Y. Yao, J. W. Brill, I. Engquist, M. Fahlman, L. Wagberg, X. Crispin and M. Berggren, Adv. Sci., 2016, 3, 1500305.
8. A. Jonsson, Z. Song, D. Nilsson, B. A. Meyerson, D. T. Simon, B. Linderoth and M. Berggren, Sci. Adv., 2015, 1, 1500039.
9. M. Berggren, X. Crispin, S. Fabiano, M. P. Jonsson, D. T. Simon, E. Stavrinidou, K. Tybrandt and I. Zozoulenko, Adv. Mater., 2019, 1805813.
10. D. C. Martin, J. Wu, C. M. Shaw, Z. King, S. A. Spanninga, S. Richardson-Burns, J. Hendricks and J. Yang, Polym. Rev., 2010, 50, 340–384.
11. Y. Wen and J. Xu, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 1121–1150.
12. H. Shi, C. Liu, Q. Jiang and J. Xu, Adv. Electron. Mater., 2015, 1, 1500017.
13. X. Crispin, F. L. E. Jakobsson, A. Crispin, P. C. M. Grim, P. Andersson, A. Volodin, C. van Haesendonck, M. Van der Auweraer, W. R. Salaneck and M. Berggren, Chem. Mater., 2006, 18, 4354–4360.
14. U. Lang, E. Müller, N. Naujoks and J. Dual, Adv. Funct. Mater., 2009, 19, 1215–1220.
15. A. Ugur, F. Katmis, M. Li, L. Wu, Y. Zhu, K. K. Varanasi and K. K. Gleason, Adv. Mater., 2015, 27, 4604–4610.
16. Q. Wei, M. Mukaida, Y. Naitoh and T. Ishida, Adv. Mater., 2013, 25, 2831–2836.
17. O. Bubnova, Z. U. Khan, H. Wang, S. Braun, D. R. Evans, M. Fabretto, P. Hojati-Talemi, D. Dagnelund, J.-B. Arlin, Y. H. Geerts, S. Desbief, D. W. Breiby, J. W. Andreasen, R. Lazzaroni, W. M. Chen, I. Zozoulenko, M. Fahlman, P. J. Murphy, M. Berggren and X. Crispin, Nat. Mater., 2014, 13, 190.
18. S. Rudd, J. F. Franco-Gonzalez, S. Kumar Singh, Z. Ullah Khan, X. Crispin, J. W. Andreasen, I. Zozoulenko and D. Evans, J. Polym. Sci., Part B: Polym. Phys., 2017, 56, 97–104.
19. G. Greczynski, T. Kugler, M. Keil, W. Osikowicz, M. Fahlman and W. Salaneck, J. Electron Spectrosc. Relat. Phenom., 2001, 121, 1–17.
20. J. Hwang, F. Amy and A. Kahn, Org. Electron., 2006, 7, 387–396.
21. S. Kim, S. Y. Kim, M. H. Chung, J. Kim and J. H. Kim, J. Mater. Chem. C, 2015, 3, 5859–5868.
22. F. Kong, C. Liu, H. Song, J. Xu, Y. Huang, H. Zhu and J. Wang, Synth. Met., 2013, 185–186, 31–37.
23. Y. Mochizuki, T. Horii and H. Okuzaki, Trans. Mater. Res. Soc. Jpn., 2012, 37, 307–310.
24. T.-C. Tsai, H.-C. Chang, C.-H. Chen, Y.-C. Huang and W.-T. Whang, Org. Electron., 2014, 15, 641–645.
25. F.-F. Pang, S. Li, W.-Q. Sun and G.-Z. Han, Mater. Chem. Phys., 2017, 186, 246–250.
26. T. Horii, H. Hikawa, Y. Mochizuki and H. Okuzaki, Trans. Mater. Res. Soc. Jpn., 2012, 37, 515–518.
27. D. Alemu, H.-Y. Wei, K.-C. Ho and C.-W. Chu, Energy Environ. Sci., 2012, 5, 9662–9671.
28. J.-S. Yeo, J.-M. Yun, D.-Y. Kim, S. Park, S.-S. Kim, M.-H. Yoon, T.-W. Kim and S.-I. Na, ACS Appl. Mater. Interfaces, 2012, 4, 2551–2560.
29. N. Kim, B. H. Lee, D. Choi, G. Kim, H. Kim, J.-R. Kim, J. Lee, Y. H. Kahng and K. Lee, Phys. Rev. Lett., 2012, 109, 106405.
30. L. Ouyang, C. Musumeci, M. J. Jafari, T. Ederth and O. Inganas, ACS Appl. Mater. Interfaces, 2015, 7, 19764–19773.
31. D. Alemu Mengistie, P.-C. Wang and C.-W. Chu, J. Mater. Chem. A, 2013, 1, 9907–9915.
32. S. Zhang, P. Kumar, A. S. Nouas, L. Fontaine, H. Tang and F. Cicoira, APL Mater., 2015, 3, 014911.
33. J. Ouyang, Displays, 2013, 34, 423–436.
34. Y. Xia and J. Ouyang, ACS Appl. Mater. Interfaces, 2010, 2, 474–483.
35. C. Yeon, S. J. Yun, J. Kim and J. W. Lim, Adv. Electron. Mater., 2015, 1, 1500121.
36. J. Kim, J. G. Jang, J.-I. Hong, S. H. Kim and J. Kwak, J. Mater. Sci.: Mater. Electron., 2016, 27, 6122–6127.
37. C.-C. Lin, C.-K. Huang, Y.-C. Hung and M.-Y. Chang, Jpn. J. Appl. Phys., 2016, 55, 081602.
38. X. Wu, J. Liu and G. He, Org. Electron., 2015, 22, 160–165.
39. A. K. Sarker, J. Kim, B.-H. Wee, H.-J. Song, Y. Lee, J.-D. Hong and C. Lee, RSC Adv., 2015, 5, 52019–52025.
40. P.-W. Sze, K.-W. Lee, P.-C. Huang, D.-W. Chou, B.-S. Kao and C.-J. Huang, Energies, 2017, 10, 716.
41. D. A. Mengistie, M. A. Ibrahem, P.-C. Wang and C.-W. Chu, ACS Appl. Mater. Interfaces, 2014, 6, 2292–2299.
42. K. Aasmundtveit, E. Samuelsen, L. Pettersson, O. Inganäs, T. Johansson and R. Feidenhans'l, Synth. Met., 1999, 101, 561–564.
43. T. Takano, H. Masunaga, A. Fujiwara, H. Okuzaki and T. Sasaki, Macromolecules, 2012, 45, 3859–3865.
44. C. M. Palumbiny, F. Liu, T. P. Russell, A. Hexemer, C. Wang and P. Müller-Buschbaum, Adv. Mater., 2015, 27, 3391–3397.
45. M. N. Gueye, A. Carella, N. Massonnet, E. Yvenou, S. Brenet, J. Faure-Vincent, S. Pouget, F. Rieutord, H. Okuno, A. Benayad, R. Demadrille and J.-P. Simonato, Chem. Mater., 2016, 28, 3462–3468.
46. A. V. Volkov, K. Wijeratne, E. Mitraka, U. Ail, D. Zhao, K. Tybrandt, J. W. Andreasen, M. Berggren, X. Crispin and I. V. Zozoulenko, Adv. Funct. Mater., 2017, 27, 1700329.
47. A. M. Nardes, M. Kemerink, R. A. Janssen, J. A. Bastiaansen, N. M. Kiggen, B. M. Langeveld, A. J. Van Breemen and M. M. De Kok, Adv. Mater., 2007, 19, 1196–1200.
48. J. Rivnay, S. Inal, B. A. Collins, M. Sessolo, E. Stavrinidou, X. Strakosas, C. Tassone, D. M. Delongchamp and G. G. Malliaras, Nat. Commun., 2016, 7, 11287.
49. J. Rivnay, P. Leleux, M. Ferro, M. Sessolo, A. Williamson, D. A. Koutsouras, D. Khodagholy, M. Ramuz, X. Strakosas, R. M. Owens, C. Benar, J.-M. Badier, C. Bernard and G. G. Malliaras, Sci. Adv., 2015, 1, 1400251.
50. J. P. Thomas, L. Zhao, D. McGillivray and K. T. Leung, J. Mater. Chem. A, 2014, 2, 2383–2389.
51. J. Saghaei, A. Fallahzadeh and M. H. Yousefi, Org. Electron., 2015, 19, 70–75.
52. J. Zhou, D. H. Anjum, L. Chen, X. Xu, I. A. Ventura, L. Jiang and G. Lubineau, J. Mater. Chem. C, 2014, 2, 9903–9910.
53. Z. Xiong and C. Liu, Org. Electron., 2012, 13, 1532–1540.
54. J. Gasiorowski, R. Menon, K. Hingerl, M. Dachev and N. S. Sariciftci, Thin Solid Films, 2013, 536, 211–215.
55. T. Horii, Y. Li, Y. Mori and H. Okuzaki, Polym. J., 2015, 47, 695.
56. L. Zhang, H. Deng, S. Liu, Q. Zhang, F. Chen and Q. Fu, RSC Adv., 2015, 5, 105592–105599.
57. J. Y. Oh, M. Shin, J. B. Lee, J.-H. Ahn, H. K. Baik and U. Jeong, ACS Appl. Mater. Interfaces, 2014, 6, 6954–6961.
58. J. Zhou, D. H. Anjum, G. Lubineau, E. Q. Li and S. T. Thoroddsen, Macromolecules, 2015, 48, 5688–5696.
59. M. S. Mahajan, D. M. Marathe, S. S. Ghosh, V. Ganesan and J. V. Sali, RSC Adv., 2015, 5, 86393–86401.
60. B. Xu, S.-A. Gopalan, A.-I. Gopalan, N. Muthuchamy, K.-P. Lee, J.-S. Lee, Y. Jiang, S.-W. Lee, S.-W. Kim, J.-S. Kim, H.-M. Jeong, J.-B. Kwon, J.-H. Bae and S.-W. Kang, Sci. Rep., 2017, 7, 45079.
61. M. Pietsch, M. Y. Bashouti and S. Christiansen, J. Phys. Chem. C, 2013, 117, 9049–9055.
62. N. Rolland, J. F. Franco-Gonzalez, R. Volpi, M. Linares and I. V. Zozoulenko, Phys. Rev. Mater., 2018, 2, 045605.
63. J. F. Franco-Gonzalez and I. V. Zozoulenko, J. Phys. Chem. B, 2017, 121, 4299–4307.
64. M. Modarresi, J. F. Franco-Gonzalez and I. Zozoulenko, Phys. Chem. Chem. Phys., 2018, 20, 17188–17198.
65. J. F. Franco-Gonzalez, N. Rolland and I. V. Zozoulenko, ACS Appl. Mater. Interfaces, 2018, 10, 29115–29126.
66. R. Bhowmik, R. J. Berry, V. Varshney, M. F. Durstock and B. J. Leever, J. Phys. Chem. C, 2015, 119, 27909–27918.
67. R. Bhowmik, R. J. Berry, M. F. Durstock and B. J. Leever, ACS Appl. Mater. Interfaces, 2017, 9, 19269–19277.
68. E. Yildirim, G. Wu, X. Yong, T. L. Tan, Q. Zhu, J. Xu, J. Ouyang, J.-S. Wang and S.-W. Yang, J. Mater. Chem. C, 2018, 6, 5122–5131.
69. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824.
70. L. Monticelli, S. K. Kandasamy, X. Periole, R. G. Larson, D. P. Tieleman and S.-J. Marrink, J. Chem. Theory Comput., 2008, 4, 819–834.
71. S. J. Marrink, A. H. de Vries and A. E. Mark, J. Phys. Chem. B, 2004, 108, 750–760.
72. H. Dong, H. Du, S. R. Wickramasinghe and X. Qian, J. Phys. Chem. B, 2009, 113, 14094–14101.
73. J. F. Franco-Gonzalez, E. Pavlopoulou, E. Stavrinidou, R. Gabrielsson, D. T. Simon, M. Berggren and I. V. Zozoulenko, Nanoscale, 2017, 9, 13717–13724.
74. S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, PLoS Comput. Biol., 2010, 6, e1000810.
75. M. Vögele, C. Holm and J. Smiatek, J. Mol. Liq., 2015, 212, 103–110.
76. M. Vögele, C. Holm and J. Smiatek, J. Chem. Phys., 2015, 143, 243151.
77. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
78. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
79. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
80. M. Parrinello and A. Rahman, Phys. Rev. Lett., 1980, 45, 1196–1199.
81. R. Alessandri, J. Uusitalo, A. De Vries, R. Havenith and S. Marrink, J. Am. Chem. Soc., 2017, 139, 3697–3705.
82. D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701.
83. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19.
84. H. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43.
85. S. Timpanaro, M. Kemerink, F. Touwslager, M. D. Kok and S. Schrader, Chem. Phys. Lett., 2004, 394, 339–343.
86. M. Kemerink, S. Timpanaro, M. M. de Kok, E. A. Meulenkamp and F. J. Touwslager, J. Phys. Chem. B, 2004, 108, 18820–18825.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp07141a

---