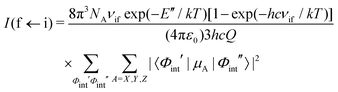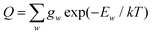A variationally computed room temperature line list for AsH3†
Received
17th November 2018
, Accepted 9th January 2019
First published on 14th January 2019
Abstract
Calculations are reported on the rotation–vibration energy levels of the arsine molecule with associated transition intensities. A potential energy surface (PES) obtained from ab initio electronic structure calculations is refined to experimental data, and the resulting energy levels display sub-wavenumber accuracy for all reliably known J = 0 term values under 6500 cm−1. After a small empirical adjustment of the band centres, our calculated (J = 1–6) rovibrational states reproduce 578 experimentally derived energies with a root-mean-square error of 0.122 cm−1. Absolute line intensities are computed using the refined PES and a new dipole moment surface (DMS) for transitions between states with energies up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 and rotational quantum number J = 30. The computed DMS reproduces experimental line intensities to within 10% uncertainty for the ν1 and ν3 bands. Furthermore, our calculated absorption cross-sections display good agreement with the main absorption features recorded in the Pacific Northwest National Laboratory (PNNL) for the complete range of 600–6500 cm−1.
500 cm−1 and rotational quantum number J = 30. The computed DMS reproduces experimental line intensities to within 10% uncertainty for the ν1 and ν3 bands. Furthermore, our calculated absorption cross-sections display good agreement with the main absorption features recorded in the Pacific Northwest National Laboratory (PNNL) for the complete range of 600–6500 cm−1.
1 Introduction
Arsine (AsH3) is a highly poisonous gas1 which is the direct analogue molecular structure of ammmonia (NH3) and phospine (PH3). Like these two gases it has been detected in the atmospheres of the gas giant planets Jupiter2,3 and Saturn.4 It may therefore be expected to be also present in the atmospheres of gas giant exoplanets.
Arsine is also important for industrial applications as high purity arsine is widely used in the semiconductor manufacturing industry, for example, in processing GaAs surfaces.5–7 Given its highly poisonous nature, with an exposure limit value of 50 ppb mole-concentration,8 the detection of AsH3 escape at such levels is an important safety requirement in this industry.9 It is also monitored in the polymer industry as trace level arsine impurity in ethylene and propylene monomer feedstock gases may contaminate the catalysts, resulting in reduced quality and yield of the polymer products.10
Arsine is also a trace atmospheric pollutant due to emissions from various industrial processes, such as power generation and smelting.11,12 Routine methods for arsine measurement in industry include gas chromatography, electrochemical sensors, colorimetric sensors and Fourier-transform infrared spectroscopy. However, the development of high resolution laser spectroscopy based measurements is a growing area13,14 of research for which detailed line lists are required to model the high resolution absorption spectra.
While there have been a number of studies on the infrared and microwave spectra of arsine, there is no comprehensive line list for the system and there is a lack of information on the intensity of many bands. The situation for absolute line intensities is particularly dire, with existing data confined solely to the measurements reported by Dana et al.15 Previous attempts to model the global vibrational structure16,17 and rovibrational sub-structures,18–24 have focussed predominantly on effective-Hamiltonians, which have limited predictive capability outside the fitted data. In addition, an ab initio potential energy surface (PES) for AsH3 was reported in 1995 by Breidung and Thiel in the form of the cubic anharmonic force fields25 using relativistic effective core potentials (ECPs).
Considering the unsuitability of the current state of AsH3 data for either exoplanet modelling, which necessitates completeness, or industrial monitoring, which necessitates accuracy, we decided to construct a comprehensive line list for arsine which could be used for the applications mentioned above. Our approach to constructing line lists, as exploited in the ExoMol project,26,27 uses potential energy surfaces which have been refined using spectroscopic data but ab initio dipole moment surfaces, which have been shown to give highly accurate predicted transition intensives.28–30 The approach has already been used to compute line lists for the NH3,31–33 PH3,34,35 SbH3,36 and SO337 systems and a line list for PF3 is on the way.38 These studies were based on either a D3h symmetry,31–33,39 in which the tunneling of the so-called umbrella motion was explicitly considered, or a C3v symmetry34,35 in which the tunneling is neglected. Given the high barrier expected for AsH3, the reduced symmetry C3v approach is employed here.
2 Potential energy surface
2.1 Electronic structure calculations
Accurate modelling of heavy elements in quantum chemistry is made particularly challenging by increased relativistic effects, core–core electron correlation and core–valence electron correlation compared to lighter elements. Recovery of the correlation energy has benefited from the recent development of explicitly correlated methods (F12/R12),40,41 which rapidly converge electronic energies towards the complete basis set (CBS) limit with increasing cardinal number n, but must be used in conjunction with suitably optimised basis sets for full effectiveness. To account for scalar relativistic effects, effective core potentials (ECPs) are a computationally inexpensive option. More rigorous treatment is possible with the Douglas–Kroll–Hess (DKH) Hamiltonian, however, so far no satisfactory way has been found of incorporating the DKH Hamiltonian into the F12/R12 framework.42 Although ECPs face the same theoretical hurdles, namely non-commutability with the F12 correlation function, alternative treatments have been found to work well.43,44 For heavy elements where both F12-pseudopotential and standard all-electron DKH based approaches are possible, such as arsenic, the benefits of F12 must therefore be weighed against the penalty of introducing an additional scalar-relativistic approximation. Peterson45 showed that complete basis set (CBS) extrapolated CCSD(T)/aug-cc-pwCVnZ-PP pseudopotential calculations performed almost identically to their DKH Hamiltonian all-electron counterparts in a series of molecular benchmark calculations for post-3d main group elements, including the As2, AsF, AsCl and AsN molecules. They go on to develop a new family of F12-specific cc-pVnZ-PP-F12 basis sets to be used at the CCSD(T)-F12 level, which yield accuracy comparable to the 2–3 times larger aug-cc-pwCV(n+2)Z-PP basis sets used at the standard CCSD(T) level.45,46 Their pseudopotential-F12 optimised approach is the one followed in this work.
All electronic structure calculations were performed using MOLPRO47 and employed the explicitly correlated coupled cluster method CCSD(T)-F12b40,41 with implicit treatment of scalar-relativistic effects via replacement of 10 core electrons with a pseudopotential (PP). Calculations were carried out in the frozen core approximation and utilized the correlation consistent quadruple-zeta, PP-F12 optimised basis set of Hill et al.46 (cc-pVQZ-PP-F12) to represent the As electronic wavefunction and cc-pVQZ-F12 basis sets for the H atoms. Density fitting (DF) for the 2-electron (MP2FIT) and exchange term (JKFIT) integrals employed the cc-pVTZ-PP-F12/MP2Fit and def2-QZVPP/JKFIT basis sets respectively, and for the resolution of the identity of the many-electron F12 integrals (OPTRI) we used the VTZ-PP-F12/OPTRI basis set. For the geminal exponent γ, a value of 1.4a0−1 was used as recommended by Hill et al. All calculations were performed in the ground electronic state, which is sufficiently uncoupled from higher electronic excitations so that non-adiabatic effects are expected to be very small.48
To initially qualify the importance of including scalar relativistic effects in our calculations, relativistic corrections ΔEX along 1-dimensional cuts of the potential energy surface PES were calculated (shown in Fig. 1, along with cuts through the AVQZ surface for reference). This was done by first shifting the potential energy curves by their respective energies at equilibrium, listed in Table 1, where we note the relatively small absolute energies of the ECP based calculations owing to their implicit treatment of 10 core electrons. We then have ΔEX = EX1 − EX2 where EX1 = AVnZ-PP/AVnZ-DK and EX2 = AVnZ for the pseudopotential/all-electron calculations. Here, and in all subsequent DKH calculations, the DKH Hamiltonian has been expanded to the 8th-order (DKH8) using an optimal unitary parametrisation. In Fig. 1 only quadruple-zeta (n = 4) results are presented as they were seen to differ by no more than 3 cm−1 from the respective 5-zeta (n = 5) curves. Clearly the inclusion of scalar relativistic effects are important, and both approximations have a similar effect on the total energy. However, the pseudopotential approximation tends to raise the energy at stretched geometries and lower the energy at contracted geometries, relative to the all-electron calculations. It is difficult to asses the effect of this difference within the Hill et al.46 regime for a full-dimensional PES. We therefore opted to generate a second 6D surface at the AVQZ-DKH8 level of theory (henceforth denoted AVQZ-DK), to provide a benchmark for our VQZ-PP-F12 based ab initio nuclear motion calculations. The results of these calculations are presented in Section 3.
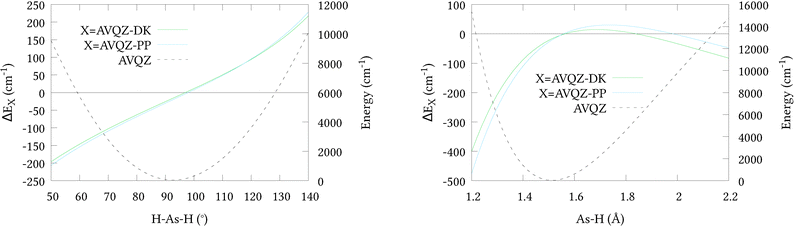 |
| | Fig. 1 One dimensional cuts of the relativistic corrections for the (r1 = r2 = r3 = 1.51 Å; α1 = α2 = 92.1°; 50 ≤ α3 ≤ 140°) bond angle and (r1 = r2 = 1.51 Å; 1.2 ≤ r3 ≤ 2.2 Å; α1 = α2 = α2 = 92.1°) bond length displacements. | |
Table 1 Equilibrium energies calculated at the CCSD(T) level of theory using different basis sets and Hamiltonians
| Basis |
Energy/Eh |
| AVQZ |
−2236.17795527 |
| AVQZ-DK |
−2261.02359376 |
| AVQZ-PP |
−333.14700414 |
| AV5Z |
−2236.18098311 |
| AV5Z-DK |
−2261.02786843 |
| AV5Z-PP |
−333.14983002 |
It is known that beyond the 4th-order expansion the DKH Hamiltonian depends slightly on the chosen paramterization of the unitary transformations applied.49 Thus, additional DKH4 calculations were performed on a subset of the DKH8 PES geometries. Between the 4th and 8th-order the resulting electronic energies were seen to differ by less than 0.1 cm−1 above their equilibrium values. For the purpose of benchmarking the ECP based nuclear motion calculations, therefore, this dependency is not expected to be significant.
2.2 Nuclear geometry grid
Our grid of nuclear geometries was built by combining 1D–6D sub-grids. Our 1D grid consisted of a cut along the r1 = r2 = r3 stretch with, α1 = α2 = α3 = αeq, and a cut along the α1 = α2 = α3 bend with r1 = r2 = r3 = req. Each additional degree of freedom was then added by allowing either an additional As–H bond length or the H–As–H bond angle to vary. Because this method causes the number of points to grow so rapidly, the range and intervals of r and α were reduced with each increasing degree of freedom using the 1D cuts as a guide. This also helped to limit the range of electronic energies generated, as large distortions in the geometry can lead to unnecessarily high values of energy that are not needed in the fit.
In order to ensure each grid point was fully unique we applied the C3v molecular symmetry group transformations prior to computing the electronic energy. If two grid points were transformed into one another, then one was discarded. Finally, any energetically sparse regions were filled by generating additional geometries that were estimated to fall within our desired range. The 1D cuts provided an initial guide to the electronic energy, then intermediate versions of our PES were used to more accurately choose geometries. Our final grid consisted of 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873 nuclear geometries within the range 1.10 ≤ ri ≤ 3.74 Å and 37° ≤ αi ≤ 130°, with electronic energies extending to 27
873 nuclear geometries within the range 1.10 ≤ ri ≤ 3.74 Å and 37° ≤ αi ≤ 130°, with electronic energies extending to 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, although ∼38
000 cm−1, although ∼38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 of these were below 10
000 of these were below 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (1.25 ≤ ri ≤ 1.9 Å and 60° ≤ αi ≤ 126°). The additional points in the 10
000 cm−1 (1.25 ≤ ri ≤ 1.9 Å and 60° ≤ αi ≤ 126°). The additional points in the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–27
000–27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range predominantly belonged to the As–H dissociative stretch, which is where holes commonly appear if the function is not suitably constrained at high energy. Grid points for our AVQZ-DK reference PES were chosen by randomly sampling 16
000 cm−1 range predominantly belonged to the As–H dissociative stretch, which is where holes commonly appear if the function is not suitably constrained at high energy. Grid points for our AVQZ-DK reference PES were chosen by randomly sampling 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 396 equally energetically distributed points from our VQZ-PP-F12 grid, which spanned the bond lengths 1.3 ≤ ri ≤ 1.8 Å, bond angles 65° ≤ αi ≤ 130° and energies below 15
396 equally energetically distributed points from our VQZ-PP-F12 grid, which spanned the bond lengths 1.3 ≤ ri ≤ 1.8 Å, bond angles 65° ≤ αi ≤ 130° and energies below 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1.
000 cm−1.
Each grid point computed at the CCSD(T)-F12b/cc-pVQZ-PP-F12 level took approximately 10–15 minutes to compute on the UCL's Legion computing cluster. This was increased to 20–30 min for the DKH Hamiltonian-based calculations, owing to the increased computational demand of explicitly treating the 10 core electrons.
2.3 Analytic representation
To represent the PES analytically we used the same functional form as for NH3 and PH3.50 The potential is represented as a polynomial expansion| | 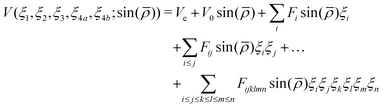 | (1) |
in terms of the internal coordinates,| | | ξk = 1 − exp(−a(rk − req)), (k = 1, 2, 3), | (2) |
| | 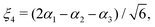 | (3) |
| | 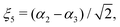 | (4) |
| | 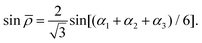 | (5) |
In eqn (1)| | 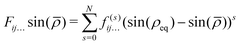 | (6) |
and rk is the As–Hk bond length, αj is the jth H–As–H bond angle (opposite to the jth bond), req is the equilibrium value of rk, a is a molecular parameter, and ρeq is the equilibrium value of the umbrella mode ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) . V0 represents the pure inversion potential and f(s)ij… are the fitting parameters. Points are given as energy (Ei) dependant weights (wi)
. V0 represents the pure inversion potential and f(s)ij… are the fitting parameters. Points are given as energy (Ei) dependant weights (wi)| | 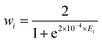 | (7) |
as used by Polyansky et al.51 We could usefully fit terms in the potential up to the 5th order resulting in a root-mean-square (RMS) deviation of 0.7 cm−1 for the 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 678 nuclear geometries. For our all-electron reference PES, the weighted RMS error increased to 1.2 cm−1, most likely due to the proportionally fewer points close to equilibrium. However it should be noted that adding more points to the fit had little effect on the computed vibrational term values reported in Section 3.
678 nuclear geometries. For our all-electron reference PES, the weighted RMS error increased to 1.2 cm−1, most likely due to the proportionally fewer points close to equilibrium. However it should be noted that adding more points to the fit had little effect on the computed vibrational term values reported in Section 3.
The final set of expansion parameters for our ab initio PES is included in the ESI,† along with our grid of nuclear geometries and an Fortran 90 routine to evaluate the analytic expression.
3 Nuclear motion calculations
To calculate rovibrational energy levels we used the variational nuclear motion program TROVE. The general methodology of TROVE is well documented,52,53 with its specific application to XY3-type molecules detailed in ref. 31, and so only a brief description is provided here.
Rovibrational basis functions are constructed as symmetrised linear combinations of 1D primitive-basis-function products,
| | | |ν, J, K, m, τrot〉 = [|J, K, m, τrot〉|n1〉|n2〉|n3〉|n4〉|n5〉|n6〉]Γir | (8) |
where the 1D stretching functions (|
n1〉, |
n2〉, |
n3〉) and bending functions (|
n4〉, |
n5〉, |
n6〉) are obtained by solving the corresponding one-dimensional Schrödinger equations using the Numerov–Cooley approach
54,55 for the stretches, and 1D harmonic oscillator eigenfunctions for the bends. The rotational basis set is built from rigid-rotor functions. In the above equation,
Γir represents one of the irreducible representations of
C3v spanned by |
ν,
J,
K,
m,
τrot〉. For details of the symmetrisation procedure in TROVE the reader is directed to
ref. 53. A multi-step contraction scheme was employed to limit the vibrational, then rovibrational basis set size. This is outlined in the following paragraphs and in Section 6.2.
Owing to the structural similarities between AsH3 and other XY3-type molecules which have been investigated in the past, variational calculations could be performed with relative ease once a PES and DMS had been constructed, and required only a few molecule specific parameters to be defined: atomic mass, molecular symmetry group, Z-matrix, equilibrium parameters and the definition of our 1-D grids upon which the wavefunctions are evaluated. In fact, this is true for any 3–5 atom molecule, provided the molecular symmetry (MS) group has been programmed into TROVE, this includes a recent extension to treat linear molecules.56 Currently TROVE allows for the following MS groups: C2v, C3v, D3h, D2d, C2h, Td, D2h and Dnh with n > 157 (see also ref. 53, where TROVE treatment of the symmetry groups is described). Here we use the C3v symmetry which means that the inversion mode is not fully represented and any tunneling splitting is neglected. We note that the study of deuterated arsine, AsH2D could also be conducted using the same Born–Oppenheimer PES but would require a different symmetrisation procedure in TROVE. Such a study is possible but the lower symmetry and denser vibrational spectrum associated with the D atom would make such a calculation computationally more expensive.
As arsenic has only one stable isotope, 75As, all reported nuclear motion calculations were performed for 75AsH3.
Within the limitations of our PES, the accuracy of our variational calculation is determined predominantly by (i) the size of our nuclear-motion basis set; and (ii) our Taylor-type expansion of the kinetic energy operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and our re-expansion of the potential function V in terms of linearised coordinates. We choose to restrict the former via a polyad number P. The polyad number is an integer that represents the total quanta of vibrational excitations in terms of the lowest energy fundamental. For AsH3
and our re-expansion of the potential function V in terms of linearised coordinates. We choose to restrict the former via a polyad number P. The polyad number is an integer that represents the total quanta of vibrational excitations in terms of the lowest energy fundamental. For AsH3
| | | P = 2(n1 + n2 + n3) + n4 + n5 + n6 | (9) |
where
n1 +
n2 +
n3 is the total number of stretching quanta and
n4 +
n5 +
n6 is the total number of bending quanta, corresponding to the primitive functions |
ni〉 (
i = 1,…,6) in
eqn (8). For our comparison of the VQZ-PP-F12 and AVQZ-DK based
ab initio PESs we chose to include in our variational calculations all vibrational states with
P ≤
Pmax = 14 as used previously for NH
3 and PH
3.
31,34 This resulted in our vibrational eigenvalues to converge within 0.1 cm
−1 below 6000 cm
−1 for the stretches, and as much as 3 cm for the bending overtones. Our
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
and
V expansions we take to the 6th and 8th order, respectively. Increasing them to the 8th and 10th order changed the vibrational term values reported throughout this work by <0.1 cm
−1 for the stretches, and <0.7 cm
−1 for the bends. For highly excited bending overtones, such as the 5 and 6-quanta bends, the convergence error due to our
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
and
V expansions may be several wavenumbers.
Table 2 shows the 26 lowest-lying experimentally derived vibrational states compared to our calculations. Term values known to sub-wavenumber accuracy are taken from Sanzharov et al.;16 the remaining eight bands are from the work by Halonen et al.58 and have an estimated 2 cm−1 uncertainty, although this may be larger for the 5050–5200 cm−1 bands.59 Using the VQZ-PP-F12 and AVQZ-DK PESs the experimentally derived values of the four fundamentals are reproduced to within 10 cm−1 and 14 cm−1 respectively. Whilst far from the accuracy achieved in previous studies on NH3 and PH3, our results are comparable to the achievements of Nikitin et al. in their recent ab initio study of GeH4,60 and we deem it reasonable considering the greater contribution of relativistic effects, core–core electron correlation and core–valence electron correlation associated with heavier atoms. For the overtones and combination bands the quality of our ab initio predictions steadily decreases in proportion to the error on the fundamentals, except for the 2νl=04 band which is independently examined in Section 6.2. Most importantly, the VQZ-PP-F12 surface consistently and significantly outperforms the VQZ-DK surface. Given the factor of 2 reduction in computational time, this highlights the value of the work by Hill, Peterson and co-authors.45,46
Table 2 Differences between experimentally derived band centres and our calculated values computed using all-electron DKH and pseudopotential-F12 based PESs. All numerical values are energies given in units of cm−1
| Band |
Symmetry |
Obs. |
VQZ-PP-F12 |
AVQZ-DK |
Obs–calc.PP-F12 |
Obs–calc.DK |
|
Experimental uncertainties of Halonen et al.58 are estimated to be 2 cm−1 or more.
|
|
ν
2
|
A
1
|
906.752 |
904.812 |
905.058 |
1.940 |
1.694 |
|
ν
4
|
E
|
999.225 |
994.460 |
994.132 |
4.765 |
5.093 |
| 2ν2 |
A
1
|
1806.149 |
1802.443 |
1802.451 |
3.706 |
3.698 |
|
ν
2 + ν4 |
E
|
1904.115 |
1897.551 |
1897.465 |
6.564 |
6.650 |
| 2νl=04 |
A
1
|
1990.998 |
1982.116 |
1981.574 |
8.882 |
9.424 |
| 2νl=24 |
E
|
2003.483 |
1988.246 |
1987.651 |
15.237 |
15.832 |
|
ν
1
|
A
1
|
2115.164 |
2108.659 |
2105.000 |
6.505 |
10.164 |
|
ν
3
|
E
|
2126.432 |
2116.469 |
2112.542 |
9.963 |
13.890 |
|
ν
1 + ν2 |
A
1
|
3013a |
3006.718 |
3002.875 |
6.3 |
10.1 |
|
ν
1 + ν4 |
E
|
3102a |
3089.255 |
3084.866 |
12.7 |
17.1 |
| 2ν1 |
A
1
|
4166.772 |
4151.833 |
4143.187 |
14.939 |
23.585 |
|
ν
1 + ν3 |
E
|
4167.935 |
4152.229 |
4143.527 |
15.706 |
24.408 |
| 2νl=03 |
A
1
|
4237.700 |
4222.006 |
4214.312 |
15.694 |
23.388 |
| 2νl=23 |
E
|
4247.720 |
4229.805 |
4221.816 |
17.915 |
25.904 |
| 2ν1 + ν2 |
A
1
|
5057a |
5041.541 |
5030.916 |
15.5 |
26.1 |
|
ν
1 + ν2 + ν3 |
E
|
5057a |
5041.191 |
5030.920 |
15.8 |
26.1 |
| 2ν1 + ν4 |
E
|
5128a |
5111.286 |
5100.477 |
16.7 |
27.5 |
| 2ν03 + ν2 |
A
1
|
5128a |
5113.615 |
5104.249 |
14.4 |
23.8 |
|
ν
1 + ν3 + ν4 |
E
|
5158a |
5137.282 |
5127.176 |
20.7 |
30.8 |
|
ν
1 + ν3 + ν4 |
A
1
|
5158a |
5137.555 |
5127.471 |
20.4 |
30.6 |
| 3ν1 |
A
1
|
6136.340 |
6116.822 |
6101.231 |
19.518 |
35.109 |
| 2ν1 + ν3 |
E
|
6136.330 |
6116.793 |
6101.192 |
19.537 |
35.138 |
|
ν
1 + 2νl=03 |
A
1
|
6275.830 |
6257.116 |
6243.540 |
18.714 |
32.290 |
|
ν
1 + 2νl=23 |
E
|
6282.350 |
6261.282 |
6247.600 |
21.068 |
34.750 |
| 3νl=13 |
E
|
6294.710 |
6270.037 |
6256.059 |
24.673 |
38.651 |
| 3νl=33 |
A
1
|
6365.950 |
6340.980 |
6327.902 |
24.970 |
38.048 |
4 Refinement
In order to achieve so-called ‘spectroscopic’ accuracy in our variational nuclear motion calculations it is a common practice to empirically refine the chosen ab initio PES to experimental data. In this case our chosen starting point PES is the VQZ-PP-F12 surface. A theoretical description of the refinement procedure has been previously reported for the case of NH3,50 and our method for AsH3 is similar. Namely, small corrections to the parameters fjk… in eqn (1) are made, so as to minimise the sum of squared residuals61| | 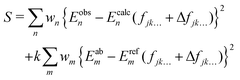 | (10) |
The energies Ecalcn are obtained by diagonalising the matrix representation of the Hamiltonian,where ΔV has the same form as eqn (1), except that fjk… is replaced by the adjustable set of parameters Δfjk…. In the above equation wi is the weight applied, Eobsn is the experimentally derived energy and Eabm and Erefm are the energies of the ab initio and refined PESs when evaluated on our grid of nuclear geometries. The second term in eqn (10) ensures that our refined potential retains the general shape of the ab initio surface, how strongly we force it to do so is controlled by the constant k. In order to find the set of parameters Δfjk… for which the above function is minimised, we employ an iterative least-squares fitting algorithm, which requires only the energies and their derivatives with respect to the adjustable parameters.
Because As is heavier than N or P, the rotational energies of AsH3 are more closely spaced than those of NH3 and PH3, and so more highly populated at room temperature. Particular attention was therefore paid to optimising the equilibrium bond lengths and bond angles. This optimisation was performed prior to refinement by using the hyperfine resolved rotational energies of Tarrago et al.,62 which we averaged using the spin-statistical weights ({A1, A2, E} = {16, 16, 16}), and a Newton–Gauss style procedure with a step size of ±0.002 Å and ±0.002 rad. Although TROVE is capable of computing quadrupole-hyperfine effects,63 requiring only a quadrupole moment surface and electric field gradient tensor in addition to the PES and DMS, the resulting splittings are small (roughly a few MHz) and so not considered here.
For the full nonlinear least squares refinement we allowed for corrections to harmonic and certain cubic terms in our PES, and used 322 experimentally derived energies with J = 6 compiled from ref. 18–22 and 62. These sampled the following vibrational bands: the fundamentals ν1, ν2, ν3, ν4; overtones 2ν1, 2ν2, 2ν3, 2ν4, 3ν1, 3ν3; and combination bands ν1 + ν3, ν2 + ν4, 2ν1 + ν3, ν1 + 2ν3. Because we could find no rotationally excited states belonging to the ν2 and ν4 bands in the literature, only their band centres were included in the refinement. The vibrational band centres measured by Halonen et al.58 were not included due to the large estimated uncertainty. The complete list of experimental energies included in the refinement, along with their assignments, are included in the ESI.†
Weights of wn = 0.1 were distributed to all experimentally derived rovibrational states except for purely rotational states, which were given weights of 1000.0, and the 2νl=04 band of Yang et al.,20 for which we struggled to match experimental energies to our calculated energies owing to conflicting quantum labels, and so gave a weight of 0.0. Weights were adjusted on the fly using Watson's robust fitting scheme.64 A scaling factor of k = 1 × 10−4 was initially applied to the 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 678 ab initio points Eabm included in the fit. As the refinement progressed this was incrementally decreased to 1 × 10−6 so as to reduce the relative contribution of the ab initio data. Care was taken throughout to ensure the refined PES did not deviate substantially from the ab initio surface, and we note that for all ab initio grid points, the energy difference between the refined and geometry optimised ab initio PES's is less than 10% that of the ab initio PES above its zero-point energy (ZPE).
678 ab initio points Eabm included in the fit. As the refinement progressed this was incrementally decreased to 1 × 10−6 so as to reduce the relative contribution of the ab initio data. Care was taken throughout to ensure the refined PES did not deviate substantially from the ab initio surface, and we note that for all ab initio grid points, the energy difference between the refined and geometry optimised ab initio PES's is less than 10% that of the ab initio PES above its zero-point energy (ZPE).
Our final fitted PES is called AsH3-CYT18 below; it is presented as subroutine in the ESI.†
5 Dipole moment surface
5.1 Electronic structure calculations
The electric dipole moment is equal to the first derivative of the electronic energy with respect to an external electric field. This can be approximated using a numerical finite-difference procedure whereby the dipole moment, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) , is related to the electronic energy in the presence of a weak uniform electric field ΔF acting along the space fixed XYZ axis,
, is related to the electronic energy in the presence of a weak uniform electric field ΔF acting along the space fixed XYZ axis,| | 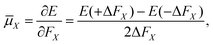 | (12) |
| | 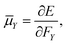 | (13) |
| | 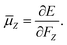 | (14) |
Thus evaluation of the dipole moment at a given nuclear geometry requires seven electronic structure calculations, the seventh being an initial zero-field calculation. A field strength of 0.002 a.u. was deemed sufficiently small to accurately approximate the first derivative without approaching the numerical noise.30 As with our PES, electronic structure calculations were carried out at the CCSD(T)-F12b level of theory with a cc-pVQZ-PP-F12 basis set for the arsenic atom, and cc-pVQZ-F12 for the hydrogens. Due to the sevenfold increase in computational demand of the DMS over the PES, dipole moments were calculated on a reduced grid of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points, generated by randomly sampling our PES grid.
000 points, generated by randomly sampling our PES grid.
5.2 Analytic representation
In a similar spirit to our PES, the ab initio DMS was expressed analytically using the symmetrized molecular bond (SMB) representation.31 In this representation the electronically averaged dipole moment ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) is constructed as symmetrized projections onto the molecular bonds with the dipole moment components (
is constructed as symmetrized projections onto the molecular bonds with the dipole moment components (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) A1,
A1, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Ea,
Ea, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Eb) in the molecule fixed axis system given by 4th order polynomial expansions,
Eb) in the molecule fixed axis system given by 4th order polynomial expansions,| | 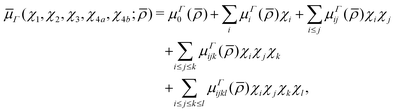 | (15) |
where Γ = A1, Ea and Eb are the irreducible components of C3v,| | | χk = Δrk(1 − exp(−Δrk))2, (k = 1, 2, 3) | (16) |
| | 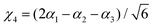 | (17) |
| | 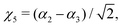 | (18) |
| | 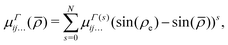 | (19) |
μΓ(s)ij… are the expansion parameters, Δrk = rk − req and ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) is the same as in eqn (1). The dipole moment components (
is the same as in eqn (1). The dipole moment components (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Ea,
Ea, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Eb) are transformed as linear combinations of each other by the C3v group operations and so transform together as an E-symmetry. For this reason the parameters
Eb) are transformed as linear combinations of each other by the C3v group operations and so transform together as an E-symmetry. For this reason the parameters 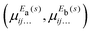 must fit together and
must fit together and 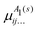 are fitted separately. For an extensive discussion on the SMB representation of the dipole moment function the reader is directed to ref. 31.
are fitted separately. For an extensive discussion on the SMB representation of the dipole moment function the reader is directed to ref. 31.
The final fit required 261 parameters and reproduced the ab initio data with an RMS difference of 0.0008 Debye for energies up to 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, which is comparable to the level of numerical noise in the finite differences procedure. The DMS expansion parameter set and a Fortran 90 routine to construct the DMS is included in the ESI.†
000 cm−1, which is comparable to the level of numerical noise in the finite differences procedure. The DMS expansion parameter set and a Fortran 90 routine to construct the DMS is included in the ESI.†
6 Results
6.1 Structural parameters
Table 3 shows the various structural parameters of AsH3 computed at different levels of theory, compared to those of our refined PES and those derived from experiment. Ab initio calculations of the equilibrium values of r and α were performed using the geometry optimisation procedure in MOLPRO. Both VQZ-PP-F12 and AVQZ-DK level calculations are seen to somewhat overestimate req and αeq when compared to experimental values, a feature that is exacerbated by the exclusion of relativistic effects altogether (rAVQZeq = 1.52375 Å, αAVQZeq = 92.5553° and rAV5Zeq = 1.523653 Å, αAV5Zeq = 92.54910°). As expected, the effect of our equilibrium geometry adjustment results in equilibrium bond lengths and angles much closer to that of experimental results.65 This is reflected in the good agreement between our purely rotational energies and spin-statistics averaged hyperfine resolved rotational energies of Tarrago et al.62 (see Table 4). There are small systematic residuals as large as 0.01 cm−1, suggesting our treatment of the rotational motion could be improved by further tweaking the equilibrium parameters. However, doing so would undoubtedly spoil the vibrational accuracy so we decided against it.
Table 3 Experimental and predicted structural constants of 75AsH3
|
|
AsH3-CYT18 |
VQZ-PP-F12 |
AVQZ-DK |
AV5Z-DK |
Exp65 |
|
r
eq/Å |
1.511394 |
1.520269 |
1.521481 |
1.520432 |
1.511060 |
|
α
eq/° |
92.04025 |
92.21595 |
92.17049 |
92.18705 |
92.0690 |
|
r
SP/Å |
1.4688 |
1.4663 |
1.4670 |
|
|
| ΔE(barrier)/cm−1 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 495 495 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187 187 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 171 171 |
|
|
Table 4 Differences between calculated rotational energies, in cm−1, and the hyperfine resolved values of62 which we averaged using the spin statistical weights
|
J
|
K
|
Sym. |
Obs. |
Obs.–calc.ref |
| 1 |
0 |
A
2
|
7.503018 |
−0.000368 |
| 1 |
1 |
E
|
7.249824 |
−0.000381 |
| 2 |
1 |
E
|
22.253842 |
−0.001287 |
| 2 |
2 |
E
|
21.494930 |
−0.000807 |
| 3 |
0 |
A
2
|
45.005427 |
−0.003161 |
| 3 |
1 |
E
|
44.753718 |
−0.002935 |
| 3 |
2 |
E
|
43.997254 |
−0.002248 |
| 3 |
3 |
A
1
|
42.732027 |
−0.001078 |
| 3 |
3 |
A
2
|
42.732025 |
−0.001077 |
| 4 |
1 |
E
|
74.742676 |
−0.005085 |
| 4 |
2 |
E
|
73.989211 |
−0.004375 |
| 4 |
3 |
A
|
72.729005 |
−0.003149 |
| 4 |
3 |
A
2
|
72.728988 |
−0.003184 |
| 4 |
4 |
E
|
70.955354 |
−0.001422 |
| 5 |
0 |
A
2
|
112.460919 |
−0.007935 |
| 5 |
1 |
E
|
112.211432 |
−0.007705 |
| 5 |
2 |
E
|
111.461647 |
−0.007010 |
| 5 |
3 |
A
1
|
110.207627 |
−0.005823 |
| 5 |
3 |
A
2
|
110.207557 |
−0.005824 |
| 5 |
4 |
E
|
108.442621 |
−0.004109 |
| 5 |
5 |
E
|
106.157387 |
−0.001816 |
| 6 |
1 |
E
|
157.148421 |
−0.010773 |
| 6 |
2 |
E
|
156.403009 |
−0.010103 |
| 6 |
3 |
A
1
|
155.156374 |
−0.008751 |
| 6 |
3 |
A
2
|
155.156164 |
−0.009170 |
| 6 |
4 |
E
|
153.401598 |
−0.007307 |
| 6 |
5 |
E
|
151.129706 |
−0.005092 |
As yet, the inversion barrier height ΔE (barrier) of AsH3 remains unmeasured. The previous highest-level predictions are those by Schwerdtfeger et al.66 in 1992, who calculated a value of 13079.3 cm−1 at the Moeller–Plesset (MP2) level of theory. This is somewhat lower than our CCSD(T) values of just over 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, shown in Table 3. The minimum energy path over the barrier reduces the As–H bond lengths to their so-called saddle-point value rSP at a planar geometry. Of this, the predicted value of 1.457 Å by Schwerdtfeger et al. is in reasonable agreement with our own (see Table 3). For comparison, the NH3 barrier height is measured to be 1786.8 cm−1 occurring for rSP = 0.99460 Å,67 and for PH3 the calculated values of Sousa–Silva et al.39 are currently the most reliable, predicting a value of 11
000 cm−1, shown in Table 3. The minimum energy path over the barrier reduces the As–H bond lengths to their so-called saddle-point value rSP at a planar geometry. Of this, the predicted value of 1.457 Å by Schwerdtfeger et al. is in reasonable agreement with our own (see Table 3). For comparison, the NH3 barrier height is measured to be 1786.8 cm−1 occurring for rSP = 0.99460 Å,67 and for PH3 the calculated values of Sousa–Silva et al.39 are currently the most reliable, predicting a value of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 cm−1 at 1.3611 Å. Whereas the NH3 inversion splitting is well known to be ≈0.79 cm−1 for the ground vibrational state, it has been predicted but not observed in PH339,68 and so it is unlikely to be observed in AsH3 for some time.
130 cm−1 at 1.3611 Å. Whereas the NH3 inversion splitting is well known to be ≈0.79 cm−1 for the ground vibrational state, it has been predicted but not observed in PH339,68 and so it is unlikely to be observed in AsH3 for some time.
6.2 Rovibrational energies
Rovibrational energy level calculations were performed up to J = 30 using the AsH3-CYT18 PES in conjunction with the nuclear motion program TROVE. Model input parameters were kept the same as reported in Section 3, including our Pmax = 14 vibrational basis. With a basis set of this size the vibrational Hamiltonian E-symmetry block has 2571 roots. Therefore, given the 2J + 1 multiplication factor for rotationally exited states, it was necessary to perform additional basis set truncations to reduce the computational cost. Firstly, our purely vibrational energies Eivib were truncated at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. These, upon multiplication with rigid symmetric rotor wavefunctions, form the basis of our full rovibrational calculation, which we term the (J = 0)-contracted basis. Our second truncation, performed only once where J exceeded 21, is therefore to remove all (J = 0)-contracted eigenfunctions with energy greater than Eivib + Eirotor = 16
000 cm−1. These, upon multiplication with rigid symmetric rotor wavefunctions, form the basis of our full rovibrational calculation, which we term the (J = 0)-contracted basis. Our second truncation, performed only once where J exceeded 21, is therefore to remove all (J = 0)-contracted eigenfunctions with energy greater than Eivib + Eirotor = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, where Eirotor is the eigenvalue of a symmetric rigid rotor.
000 cm−1, where Eirotor is the eigenvalue of a symmetric rigid rotor.
Our complete list of calculated energies is available from the ExoMol website (http://www.exomol.com), along with associated local mode quantum labels (n1, n2, n3, n4, n5, n6, Γvib, J, K, Γrot and Γtot). Here (n1, n2 and n3) are stretching quantum numbers, (n4, n5 and n6) are bending quantum numbers, K is the projection of the total rotational angular momentum J onto the molecular axis of symmetry, and (Γvib, Γrot and Γtot) are the vibrational, rotational and total symmetry in C3v. The local mode vibrational quantum numbers can be converted to the normal mode representation using symmetry rules (see Down et al.69), under the assumption that the total number of stretching and bending quanta are conserved between representations. Included in the ESI,† is a list of calculated vibrational states that have been converted to the normal mode representation for n1 + n2 + n3 ≤ 4 and n4 + n5 + n6 ≤ 4. This covers all strong bands under 7000 cm−1, and should aid any future labelling of AsH3 spectra.
Table 5 compares the calculated J = 0 term values under 7000 cm−1, computed using our refined PES, AsH3-CYT18, with the experimentally observed values.16,58 Vibrational labels above 5000 cm−1 are tentative. The refined PES reproduces empirical energies with a marked improvement over the ab initio surface (see Table 2). All bands included in the refinement, except for the 2νl=24 band, display sub-wavenumber accuracy. Based on our energy residuals for J = 1–6 states belonging to the 2νl=24 band, which fall within ±1.0 cm−1 of the experimental value, we strongly suspect the empirical band origin20 of 2003.483 cm−1 is incorrect. From a comparison of our J = 1, 2 energy residuals, we expect the true value to be closer to 1997.5 cm−1. Interestingly, for the bands at 3000 and 5000 cm−1 measured by Halonen et al.,58 all calculated J = 0 term values, except for the 2ν1 + ν2 and ν1 + ν2 + ν3 bands, fall within a few wavenumbers of the experimental value despite being omitted from the refinement. This illustrates the interpolative power of the refinement, and suggests that even bands not yet observed experimentally should be predicted with reasonable accuracy by our refined PES. Alternative matches for the 5057 cm−1 bands within our energies list would be the ν1 + 3ν14 (predicted at 5052.561 cm−1) and ν3 + 3ν41(A2) (5052.758 cm−1) bands. However, considering that these bands are not predicted to be observable at room temperature, the discrepancies are more likely due to resonance interactions that are not well modelled in our PES.
Table 5 Agreement between our calculated energy levels and those derived from experiment. All calculations used our refined PES, AsH3-CYT18. J = 0 comparisons are before employing the EBSC, and J = 1–6 comparisons are afterwards. Energy units are cm−1
| Band |
Symmetry |
J = 0 |
J = 1–6 |
| Obs. |
Calc. |
Obs.–calc. |
σ
ebscrms
|
|
Experimental uncertainties of Halonen et al.58 are estimated to be 2 cm−1 or more.
|
|
ν
2
|
A
1
|
906.752 |
906.109 |
0.643 |
— |
|
ν
4
|
E
|
999.225 |
998.833 |
0.393 |
— |
| 2ν2 |
A
1
|
1806.149 |
1806.161 |
−0.012 |
0.048 |
|
ν
2 + ν4 |
E
|
1904.115 |
1904.046 |
0.069 |
0.131 |
| 2νl=04 |
A
1
|
1990.998 |
1990.293 |
0.705 |
0.262 |
| 2νl=24 |
E
|
2003.483 |
1997.315 |
6.168 |
0.207 |
|
ν
1
|
A
1
|
2115.164 |
2114.938 |
0.227 |
0.027 |
|
ν
3
|
E
|
2126.432 |
2126.102 |
0.330 |
0.068 |
|
ν
1 + ν2 |
A
1
|
3013a |
3016.531 |
−3.5 |
— |
|
ν
1 + ν4 |
E
|
3102a |
3100.438 |
2.4 |
— |
| 2ν1 |
A
1
|
4166.772 |
4166.694 |
0.078 |
0.067 |
|
ν
1 + ν3 |
E
|
4167.935 |
4167.877 |
0.058 |
0.059 |
| 2νl=03 |
A
1
|
4237.700 |
4237.407 |
0.293 |
0.046 |
| 2νl=23 |
E
|
4247.720 |
4247.842 |
−0.122 |
0.241 |
| 2ν1 + ν2 |
A
1
|
5057a |
5040.690 |
16.3 |
— |
|
ν
1 + ν2 + ν3 |
E
|
5057a |
5040.799 |
16.2 |
— |
| 2ν1 + ν4 |
E
|
5128a |
5129.956 |
−2.0 |
— |
| 2ν03 + ν2 |
A
1
|
5128a |
5131.122 |
−3.0 |
— |
|
ν
1 + ν3 + ν4 |
E
|
5158a |
5155.741 |
2.3 |
— |
|
ν
1 + ν3 + ν4 |
A
1
|
5158a |
5156.434 |
1.6 |
— |
| 3ν1 |
A
1
|
6136.340 |
6136.846 |
−0.506 |
— |
| 2ν1 + ν3 |
E
|
6136.330 |
6136.859 |
−0.529 |
— |
|
ν
1 + 2νl=03 |
A
1
|
6275.830 |
6275.814 |
0.017 |
0.051 |
|
ν
1 + 2νl=23 |
E
|
6282.350 |
6282.414 |
−0.064 |
0.049 |
| 3νl=13 |
E
|
6294.710 |
6294.695 |
0.015 |
0.050 |
| 3νl=33 |
A
1
|
6365.950 |
6365.759 |
0.191 |
0.030 |
The residual differences between our calculated J = 0 term values and those of the experimental values can be removed from the final line list by utilising an empirical basis set correction (EBSC),31 whereby our calculated band centres are simply replaced by the corresponding experimental values. We employed the EBSC for all experimentally known bands taken from ref. 16, except the suspicious 2νl=24 band. Fig. 2 displays the difference between our calculated energies and those derived from experiment for states with J ≤ 6 taken from ref. 18–22 and 62 after employing the EBSC. The corresponding root-mean-square errors (σebscrms), split by vibrational band, are shown in Table 5. Although there is some deterioration in quality with J, this is slow and systematic in most cases, reassuring us that our calculations can safely be extended to higher rotational excitations. Agreement for the 2ν2 and stretching bands is particularly pleasing, and all calculated J = 1–6 energies, barring those belonging to the 2ν23 band, are calculated to within ±0.2 cm−1 of the experimental values. Judging by the systematic offset of the 2ν23 band in Fig. 2, the experimental band center used in the EBSC is most likely ≈0.2 cm−1 lower than the true value. Slightly larger σebscrms values are observed for the 2ν04, 2ν24 and ν2 + ν4 bands. Whereas the 2ν24 and ν2 + ν4 bands display clear J–K dependencies, it is difficult to discern any such trend for the 2ν04 band, which was omitted from the refinement altogether. Two possible reasons for this are either corrupt experimental data, or perturbation interactions due to nearby states that are not correctly represented by our PES. Even so, the 0.207 cm−1 root-mean-square error is very reasonable.
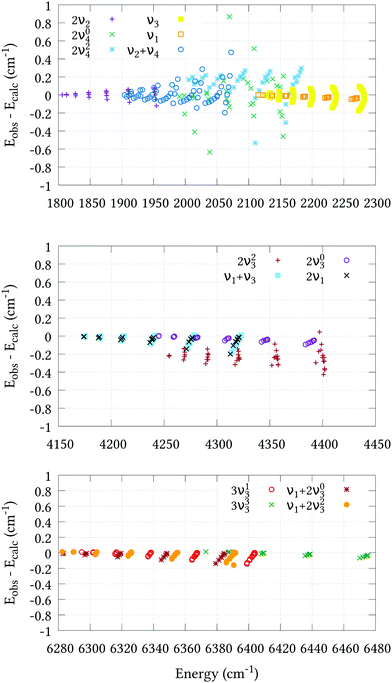 |
| | Fig. 2 Agreement between the observed J = 1–6 energy levels and the calculated values of this work using our refined PES and the EBSC. The 2ν2, ν2 + ν4, 2ν1 and ν3 bands (upper plot) were taken from ref. 18; the 2ν04 and 2ν24 bands (upper plot) were taken from ref. 19; the 2ν1 and ν1 + ν3 bands (middle plot) were taken from ref. 20; the 2ν03 and 2ν23 bands (middle plot) were taken from ref. 21; and the 3ν13, 3ν33, ν1 + 2ν23 and ν1 + 2ν03 bands (bottom plot) were taken from ref. 22. | |
6.3 Line intensity predictions
To simulate absolute absorption intensities we use the expression,| | 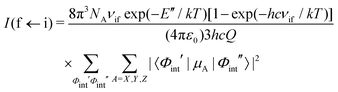 | (20) |
where Φint′ and Φint′′ are the upper and lower state wavefunctions that respectively correspond to energies E′ and E′′. νif is the transition frequency, μA is the electric dipole moment along the A = X, Y and Z axis, T is the absolute temperature and Q(T) the partition function given by,| | 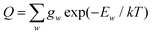 | (21) |
In the above equation, Ew is the energy and gw is the total degeneracy of state w. Note that we are using the same symbol E for the energies (Joule) and term values or wavenumbers (cm−1), whereas conventionally the latter should be Ẽ.
The nuclear spin statistical weights for AsH3 are {16, 16, 16} for states of {A1, A2, E} symmetry, and so gw = 16(2Jw + 1). No calculated or experimentally derived values of the partition function could be found in the literature, so we provide partition function values in the ESI,† for temperatures ranging from 10 to 500 K in intervals of 10 K. Fig. 3 illustrates the convergence of Q as the rotational basis is increased from including only J = 0 states (Jmax = 0), to all computed states with J ≤ 30 (Jmax = 30). In reality there will be additional contributions from our vibrational basis (Pmax = 14) and PES; however, these are difficult to quantify. The room temperature partition function was calculated to be Q(T = 296) = 8250.2801 using Jmax = 30, which we estimate to be better than 99% converged.
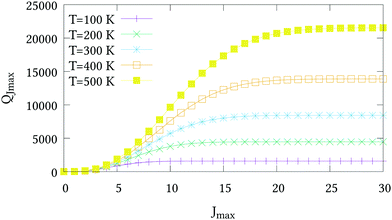 |
| | Fig. 3 The partition functions QJmax of AsH3 at different temperatures versus the maximum J value used in eqn (21). | |
Line list calculations were performed using the AsH3-CYT18 PES and the cc-pVQZ-PP-F12 DMS detailed in Section 5. Transitions involve states with energies up to 10 500 cm−1, rotational excitation up to J = 30 and a maximum lower state energy of 3500 cm−1. The final line list consists of 3.6 million absorption lines in the range of 0–7000 cm−1 with an intensity greater than 1 × 10−28 cm−1 per (molecule cm−2) at 296 K. An overview is presented in Fig. 4. It is available to download from the ExoMol website (http://www.exomol.com), where it is provided in the ExoMol format.70 Summarily, this consists of a .states file which contains the complete list of rovibrational states with associated energies and quantum numbers, and a .trans file which contains the complete list of transitions, each identified by an upper and lower state index (in the .states file), Einstein A-coefficient, and transition wavenumber.
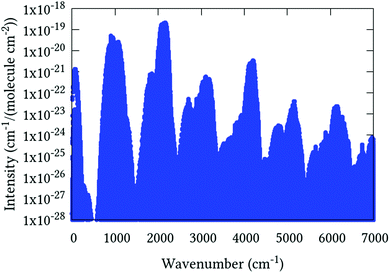 |
| | Fig. 4 Overview of complete J = 0–30 line list computed at 296 K. | |
Several sources of experimental absorption data exist for AsH3. In the following paragraphs our intensity calculations are validated by comparison with only the most recent and reliable sources. For the first test of our absolute intensities we compare our calculated band intensities with those obtained by Zheng et al.,71 shown in Table 6. Zheng et al. produced a 3-dimensional DMS based on density functional theory calculations, and compared the resulting absolute vibrational band intensities to the values obtained by direct integration of absorbance spectra, which they provide with 20–40% estimated uncertainty. Due to multiple bands overlapping only the combined intensity of bands with the same local mode quanta are presented in some cases. For the ν1 and ν3 fundamentals we compare well with the experimental values, reproducing the observed values within 2% and 14%, respectively. Zheng et al. only provide the measured intensity of the sum of the 2ν1 and ν1 + ν3 bands, which are stronger by 17%. No measurements of the weaker 2νl=03 and 2νl=23 bands are given, most likely due to difficulties resolving them without accurate theoretical line positions. Finally, for the three-quanta stretches, our calculated intensities are typically 2–3 times weaker than the measured values. However, it is difficult to estimate the reliability of these measurements, given the recorded spectrum is only medium-resolution (Δν = 0.2 cm−1) and the bands are weak.
Table 6 Comparison of observed and calculated band intensities. Column 1 refers to the local mode quantum numbers assigned by TROVE, where sym is the total symmetry. The units of intensity are 10−18 cm−1 per (molec cm−2). The value under/is the total intensity of the bands with the same quantum numbers n1n2n3
| (n1,n2,n3;sym) |
Band |
Bend centre |
I
obs
71
|
I
calc
71
|
I
calc (this work) |
| (100;A1) |
ν
1
|
2115.164 |
11.4/44.1 |
10.7/40.4 |
11.2/44.9 |
| (100;E) |
ν
3
|
2126.432 |
29.7 |
32.7 |
33.7 |
| (200;A1) |
2ν1 |
4166.772 |
/0.618 |
0.157/0.427 |
0.225/0.722 |
| (200;E) |
ν
1 + ν3 |
4167.935 |
— |
0.270 |
0.497 |
| (110;A1) |
2νl=03 |
4237.700 |
— |
0.0117/0.0123 |
0.0143/0.0163 |
| (110;E) |
2νl=23 |
4247.720 |
— |
0.000671 |
0.00201 |
| (300;A1) |
3ν1 |
6136.340 |
/0.00989 |
0.00456/0.00656 |
0.00337/0.00548 |
| (300;E) |
2ν1 + ν3 |
6136.330 |
— |
0.00200 |
0.00211 |
| (210;A1) |
ν
1 + 2νl=03 |
6275.830 |
/0.00275 |
0.00112/0.00182 |
0.000734/0.00116 |
| (210;E) |
ν
1 + 2νl=23 |
6282.350 |
— |
0.000104 |
0.0000741 |
| (210;E) |
3νl=13 |
6294.710 |
— |
0.000596 |
0.000356 |
| (111;A1) |
3νl=33 |
6365.950 |
— |
0.0000650 |
0.0000934 |
Dana et al.15 measured absolute intensities of 387 lines belonging to the ν1 and ν3 bands. Their line measurements range from 2010 to 2235 cm−1 although they make no attempt to measure the Q-branch from 2110 to 2140 cm−1, presumably owing to the density of lines. Table 7 compares our calculated line positions and intensities to the experimentally measured values for 14 randomly selected strong lines measured by Dana et al. In all cases our calculated intensity values are within ±10% of the experimental value, although there is a slight tendency to be higher. Nevertheless, this is reassuring given our 14% discrepancy with the ν3 band as measured by Zheng et al.71
Table 7 Comparison of calculated and observed15 line positions and intensities belonging to the ν1 and ν3 bands
|
J' |
K′ |
Sym′ |
J′′ |
K′′ |
Sym′′ |
Band |
ν
obs
15
|
I
obs
15
|
ν
calc
|
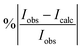
I
calc
|
|
| 9 |
6 |
E
|
10 |
7 |
E
|
ν
3
|
2051.894 |
4.799 × 10−20 |
2052.082 |
4.992 × 10−20 |
4.03 |
| 9 |
7 |
E
|
10 |
8 |
E
|
ν
3
|
2052.548 |
5.755 × 10−20 |
2052.767 |
6.079 × 10−20 |
5.63 |
| 7 |
1 |
A
2
|
8 |
0 |
A
1
|
ν
3
|
2064.460 |
4.396 × 10−20 |
2064.468 |
4.773 × 10−20 |
8.57 |
| 7 |
6 |
E
|
8 |
7 |
E
|
ν
3
|
2067.961 |
1.038 × 10−19 |
2068.139 |
1.110 × 10−19 |
6.95 |
| 4 |
4 |
E
|
5 |
5 |
E
|
ν
3
|
2090.433 |
1.572 × 10−19 |
2090.542 |
1.699 × 10−19 |
8.04 |
| 4 |
1 |
A
1
|
5 |
0 |
A
2
|
ν
3
|
2088.098 |
5.876 × 10−20 |
2088.087 |
6.423 × 10−20 |
9.31 |
| 5 |
4 |
E
|
6 |
5 |
E
|
ν
3
|
2082.601 |
1.250 × 10−19 |
2082.714 |
1.320 × 10−19 |
5.64 |
| 3 |
3 |
E
|
4 |
4 |
E
|
ν
3
|
2097.659 |
1.462 × 10−19 |
2097.738 |
1.571 × 10−19 |
7.49 |
| 2 |
2 |
E
|
1 |
1 |
E
|
ν
3
|
2140.716 |
8.659 × 10−20 |
2140.678 |
9.453 × 10−20 |
9.17 |
| 2 |
1 |
A
1
|
1 |
0 |
A
2
|
ν
3
|
2141.069 |
8.949 × 10−20 |
2141.053 |
9.612 × 10−20 |
7.41 |
| 6 |
6 |
E
|
5 |
5 |
E
|
ν
3
|
2168.331 |
1.965 × 10−19 |
2168.331 |
2.093 × 10−19 |
6.48 |
| 8 |
5 |
E
|
7 |
5 |
E
|
ν
1
|
2172.196 |
3.114 × 10−20 |
2172.262 |
3.301 × 10−20 |
5.99 |
| 8 |
7 |
E
|
9 |
7 |
E
|
ν
1
|
2045.190 |
2.459 × 10−20 |
2045.261 |
2.326 × 10−20 |
5.40 |
| 8 |
8 |
E
|
9 |
8 |
E
|
ν
1
|
2045.319 |
1.310 × 10−20 |
2045.397 |
1.328 × 10−20 |
1.36 |
| 10 |
7 |
E
|
9 |
7 |
E
|
ν
1
|
2185.605 |
2.026 × 10−20 |
2185.716 |
2.114 × 10−20 |
4.35 |
The PNNL database provides a composite spectrum of pure AsH3 up to 6500 cm−1 measured at 5, 25 and 50 °C. For comparison, we generated synthetic T = 298.15 K spectra using a J = 0–30 line list convoluted with a Voigt profile with half-width at half-maxima (HWHM) of 0.09 cm−1. Although linewidths are well known to depend on the upper and lower state quantum numbers, the strongest dependency being J and K, as far as we know no such data exists for AsH3, and we found the value of 0.09 cm−1 reasonably approximated to the PNNL linewidths on average. To convert the PNNL absorbance spectra into cm2 per molecule a multiplication factor of 9.28697 × 10−16 is necessary.
Fig. 5 shows an overview of our synthetic spectrum compared to PNNL, with the key absorption features expanded in Fig. 6–15. Qualitative agreement is very good, particularly for the ν1/ν3 (see Fig. 8 and 9) and ν2/ν4 (see Fig. 6 and 7) fundamentals, and the 2ν1/ν1 + ν3/2ν03/2ν23 band system (shown Fig. 12 and 13). Note that despite only including the ν2 and ν4 band centres in the refinement, their rotational structures are reproduced well. In the 2920–3260 cm−1 region (shown Fig. 10 and 11) the dominant sources of opacity are predicted to be the strong ν1 + ν4 and ν3 + ν4 (A1) (calculated band centre 3119.400 cm−1) bands, and the slightly weaker ν2 + ν3 (3023.706 cm−1) and ν1 + ν2 bands. Considering that no associated experimental energies were included in the refinement, the level of agreement is satisfying. Above 5000 cm−1 most absorption features are lost in the PNNL background noise; only the 2ν1 + ν4, ν2 + 2ν03 and ν1 + ν3 + ν4 bands (our labelling) are clearly visible between 5000 and 5250 cm−1 (see Fig. 14). There is a tenuous absorption bump in the PNNL at 5050 cm−1 for which we appear to be offset by roughly 15 cm−1, confirming our discrepancies with the 2ν1 + ν2 and ν1 + ν2 + ν3 band centres measured by Halonen et al.58 (see Table 5). In the 6000–6400 cm−1 region (see Fig. 15) the salient feature is the 3ν1 and 2ν1 + ν3 Q-branch at 6135 cm−1, for which we clearly underestimate the intensity. Although in line with our comparisons with Zheng et al.71 (see Table 6) it is difficult to quantify this, or indeed draw any conclusions regarding the weaker ν1 + 2ν3/3ν3 bands, without additional high-resolution experimental data.
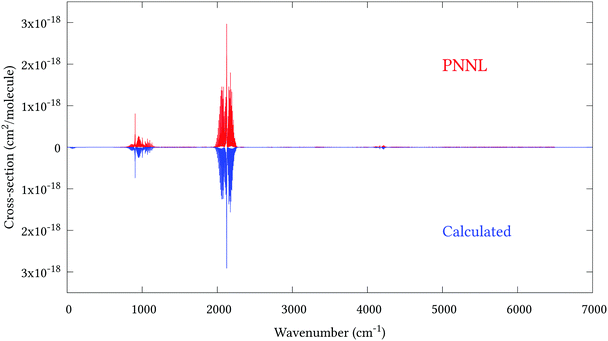 |
| | Fig. 5 Overview of synthetic J = 0–30 spectrum recorded at 298.15 K compared to PNNL. 0–7000 cm−1 region. | |
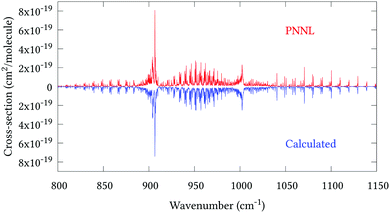 |
| | Fig. 6 Expansion of synthetic J = 0–30 spectrum computed at 298.15 K compared to PNNL. 800–1150 cm−1 region. | |
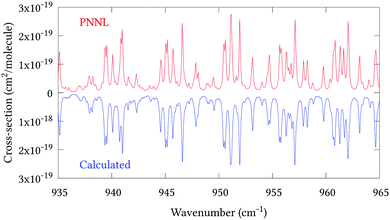 |
| | Fig. 7 Expansion of synthetic J = 0–30 spectrum computed at 298.15 K compared to PNNL. 935–965 cm−1 region. | |
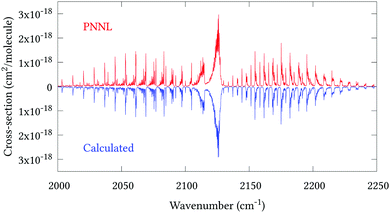 |
| | Fig. 8 Expansion of synthetic J = 0–30 spectrum computed at 298.15 K compared to PNNL. 2000–2250 cm−1 region. | |
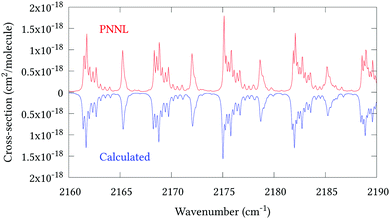 |
| | Fig. 9 Expansion of synthetic J = 0–30 spectrum computed at 298.15 K compared to PNNL. 2160–2190 cm−1 region. | |
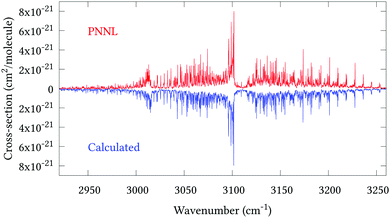 |
| | Fig. 10 Expansion of synthetic J = 0–30 spectrum computed at 298.15 K compared to PNNL. 2920–3260 cm−1 region. | |
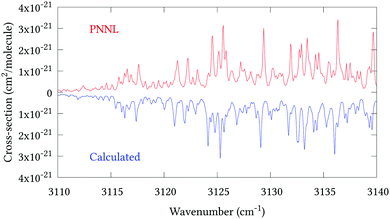 |
| | Fig. 11 Expansion of synthetic J = 0–30 spectrum computed at 298.15 K compared to PNNL. 3110–3140 cm−1 region. | |
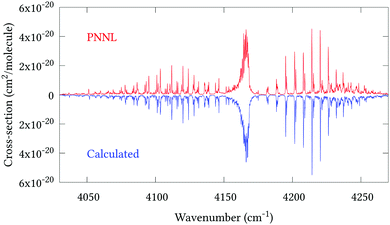 |
| | Fig. 12 Expansion of synthetic J = 0–30 spectrum computed at 298.15 K compared to PNNL. 4035–4285 cm−1 region. | |
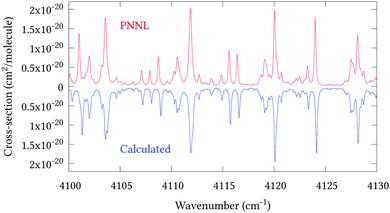 |
| | Fig. 13 Expansion of synthetic J = 0–30 spectrum computed at 298.15 K compared to PNNL. 4100–4130 cm−1 region. | |
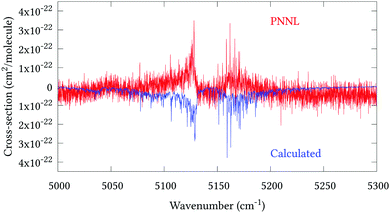 |
| | Fig. 14 Expansion of synthetic J = 0–30 spectrum computed at 298.15 K compared to PNNL. 5000–5300 cm−1 region. | |
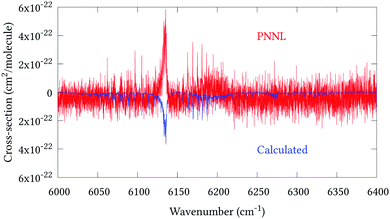 |
| | Fig. 15 Expansion of synthetic J = 0–30 spectrum computed at 298.15 K compared to PNNL. 6000–6400 cm−1 region. | |
The largest source of error in our intensity calculations will undoubtedly be the DMS. To improve on the CCSD(T)-F12b/cc-pVQZ-PP-F12 method by Hill et al.,46 large CCSD(T)/aug-cc-pwCVnZ-DK (n = 4, 5) calculations would likely be necessary (for example, including additional post-CCSD(T) corrections see ref. 72), which are currently computationally unmanageable for a fully 6D surface. Secondarily, the PES quality must be considered. Line intensities are inexorably connected to the PES through the wavefunctions in eqn (20), and accurate modelling of intensity transfer between lines (the so-called ‘intensity stealing’) relies on the correct representation of rotation–vibration resonances in the PES. Therefore, from a nuclear motion point-of-view, high-resolution measurements complete with line intensities and quantum assignments, particularly for the 800–1200, 2900–3300 and 5000–5300 cm−1 regions, would be most beneficial for future modelling.
7 Conclusion
We have produced the first full-dimensional PES and DMS for the arsine molecule. Both PES and DMS were computed at the CCSD(T)-F12b/cc-pVQZ-PP-F12 level of theory, with implicit treatment of scalar relativistic effects via replacement of 10 core electrons with a relativistic pseudopotential. A comparison with standard CCSD(T)/aug-cc-pVQZ-DK based calculations employing the DKH8 Hamiltonian, showed that CCSD(T)-F12b/cc-pVQZ-PP-F12 level theory resulted in significantly more accurate nuclear motion calculations.
Geometry optimisation and empirical adjustment of harmonic and certain cubic terms in the pVQZ-PP-F12 PES resulted in J = 1–6 rotational energies with a root-mean-square error of 0.0055 cm−1, and vibrational term values accurate to within 1 cm−1 for all reliably known experimental band centres under 6400 cm−1. Utilising the empirical basis set correction scheme, 578 experimentally derived (J = 1–6) rovibrational energies are reproduced with an RMS of 0.122 cm−1. Vibrational term value comparisons with eight approximately known band centres showed that six agreed within 3.5 cm−1 despite being omitted from the refinement. The remaining two displayed ∼16 cm−1 discrepancies, most likely due to overlooked resonances.
Rotational–vibrational line intensity calculations were performed using the refined PES and ab initio DMS, in conjunction with variational nuclear motion calculations. The resulting line list, with full quantum assignments, extends to 7000 cm−1 and is complete up to 300 K. Comparisons with multiple experimental sources show our intensity predictions to be reliable, in particular, good overall agreement with the main absorption features present in PNNL is noted. Our complete line list with quantum assignments is available from the ExoMol website (http://www.exomol.com) in ExoMol format.70
As far as we know, arsenic is the heaviest element for which there exists an associated variationally-computed infrared molecular line list. Considering that the quantum chemistry methods employed here are available for most p-block main group elements,46 the outlook for studying similar systems in future is positive.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
PAC thanks EPSRC for a CASE studentship under grant EP/L504889/1 and Servomex for industrial sponsorship. The authors are grateful to Grant J. Hill for his help with electronic structure calculations. SY and JT thank STFC for support under grant ST/M001334/1. The authors acknowledge the use of the UCL Legion High Performance Computing Facility (Legion@UCL), and associated support services, for the completion of this work, along with the STFC DiRAC HPC Facility supported by BIS National E-infrastructure capital grant ST/J005673/1 and STFC grants ST/H008586/1 and ST/K00333X/1.
References
- D. Pakulska and S. Czerczak, Int. J. Occup. Med. Environ. Health, 2006, 19, 36–44 Search PubMed.
- K. S. Noll, T. R. Geballe and R. F. Knacke, Astrophys. J., 1989, 338, L71–L74 CrossRef CAS.
- K. S. Noll, H. P. Larson and T. R. Geballe, Icarus, 1990, 83, 494–499 CrossRef.
- B. Bezard, P. Drossart, E. Lellouch, G. Tarrag and J. P. Maillard, Astrophys. J., 1989, 346, 509–513 CrossRef CAS.
- A. A. Khandekar, B. E. Hawkins, T. F. Kuech, J. Y. Yeh, L. J. Mawst, J. R. Meyer, I. Vurgaftman and N. Tansu, J. Appl. Phys., 2005, 98, 123525 CrossRef.
- C.-W. Cheng, J. Hennessy, D. Antoniadis and E. A. Fitzgerald, Appl. Phys. Lett., 2009, 95, 082106 CrossRef.
- D. Kohen, S. Bao, K. H. Lee, K. E. K. Lee, C. S. Tan, S. F. Yoon and E. A. Fitzgerald, J. Cryst. Growth, 2015, 421, 58–65 CrossRef CAS.
- Health and Safety Executive, EH40/2005 Workplace exposure limits, 2018.
- H. M. Chein, Y. D. Hsu, S. G. Aggarwal, T. M. Chen and C. C. Huang, Atmos. Environ., 2006, 40, 1901–1907 CrossRef CAS.
-
F. Feyerherm and J. Wasson, The Analysis of Trace Contaminants in High Purity Ethylene and Propylene Using GC/MS, 2005.
-
R. Maggs and S. Moorcroft, A Review of Arsenic in Ambient Air in the UK, 2000.
- J. Matschullat, Sci. Total Environ., 2000, 249, 297–312 CrossRef CAS PubMed.
- V. S. Starovoitov and S. A. Trushin, Pure Appl. Opt., 1993, 2, 505 CrossRef CAS.
- K. C. Cossel, F. Adler, K. A. Bertness, M. J. Thorpe, J. Feng, M. W. Raynor and J. Ye, Appl. Phys. B: Lasers Opt., 2010, 100, 917–924 CrossRef CAS.
- V. Dana, J. Y. Mandin, G. Tarrago, W. B. Olson and B. Bezard, J. Mol. Spectrosc., 1993, 159, 468–480 CrossRef CAS.
- N. Sanzharov, C. Leroy, O. Ulenikov and E. Bekhtereva, J. Mol. Spectrosc., 2008, 247, 1–24 CrossRef CAS.
- L. Pluchart, C. Leroy and A. Mourbat, J. Mol. Spectrosc., 2003, 218, 1–11 CrossRef CAS.
- O. N. Ulenikov, A. E. Cheglokov, G. A. Shevchenko, M. Winnewisser and B. P. Winnewisser, J. Mol. Spectrosc., 1993, 157, 141–160 CrossRef CAS.
- O. N. Ulenikov, A. B. Malikova, B. P. Winnewisser and M. Winnewisser, J. Mol. Spectrosc., 1995, 172, 330–343 CrossRef CAS.
- S.-F. Yang, X. G. Wang and Q.-S. Zhu, Spectrochim. Acta, Part A, 1997, 53, 157–163 Search PubMed.
- S.-F. Yang, H. Lin, D. Wang and Q.-S. Zhu, J. Chem. Soc., Faraday Trans., 1998, 94, 1397–1401 RSC.
- D. Wang, H. Lin, X.-G. Wang and Q.-S. Zhu, Spectrochim. Acta, Part A, 1998, 55, 109–119 CrossRef.
- H. Lin, O. N. Ulenikov, S. Yurchinko, X.-G. Wang and Q.-S. Zhu, J. Mol. Spectrosc., 1998, 187, 89–96 CrossRef.
- L. Hai, O. N. Ulenikov, I. M. Olekhnovitch, W. Dong, C. Xi-yi, H. Lu-yuan and Z. Qing-shi, Chin. Phys., 2000, 9, 113 CrossRef CAS.
- J. Breidung and W. Thiel, J. Mol. Spectrosc., 1995, 169, 166–180 CrossRef CAS.
- J. Tennyson and S. N. Yurchenko, Mon. Not. R. Astron. Soc., 2012, 425, 21–33 CrossRef CAS.
- J. Tennyson, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 698–715 CAS.
- O. L. Polyansky, K. Bielska, M. Ghysels, L. Lodi, N. F. Zobov, J. T. Hodges and J. Tennyson, Phys. Rev. Lett., 2015, 114, 243001 CrossRef PubMed.
- O. L. Polyansky, N. F. Zobov, I. I. Mizus, A. A. Kyuberis, L. Lodi and J. Tennyson, J. Quant. Spectrosc. Radiat. Transfer, 2018, 210, 127–135 CrossRef CAS.
- E. K. Conway, A. A. Kyuberis, O. L. Polyansky, J. Tennyson and N. Zobov, J. Chem. Phys., 2018, 149, 084307 CrossRef PubMed.
- S. N. Yurchenko, R. J. Barber, A. Yachmenev, W. Thiel, P. Jensen and J. Tennyson, J. Phys. Chem. A, 2009, 113, 11845–11855 CrossRef CAS PubMed.
- S. N. Yurchenko, R. J. Barber and J. Tennyson, Mon. Not. R. Astron. Soc., 2011, 413, 1828–1834 CrossRef CAS.
- P. A. Coles, R. I. Ovsyannikov, O. L. Polyansky, S. N. Yurchenko and J. Tennyson, J. Quant. Spectrosc. Radiat. Transfer, 2018, 219, 199–212 CrossRef CAS.
- C. Sousa-Silva, S. N. Yurchenko and J. Tennyson, J. Mol. Spectrosc., 2013, 288, 28–37 CrossRef CAS.
- C. Sousa-Silva, A. F. Al-Refaie, J. Tennyson and S. N. Yurchenko, Mon. Not. R. Astron. Soc., 2015, 446, 2337–2347 CrossRef CAS.
- S. N. Yurchenko, M. Carvajal, A. Yachmenev, W. Thiel and P. Jensen, J. Quant. Spectrosc. Radiat. Transfer, 2010, 111, 2279–2290 CrossRef CAS.
- D. S. Underwood, S. N. Yurchenko, J. Tennyson and P. Jensen, J. Chem. Phys., 2014, 140, 244316 CrossRef PubMed.
- B. P. Mant, K. L. Chubb, A. Yachmenev, J. Tennyson and S. N. Yurchenko, Mol. Phys., 2019 Search PubMed , in press.
- C. Sousa-Silva, S. N. Yurchenko and J. Tennyson, J. Chem. Phys., 2016, 145, 091102 CrossRef PubMed.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- F. A. Bischoff, E. F. Valeev, W. Klopper and C. L. Janssen, J. Chem. Phys., 2010, 132, 214104 CrossRef PubMed.
- F. A. Bischoff, S. Höfener, A. Glöβ and W. Klopper, Theor. Chem. Acc., 2008, 121, 11–19 Search PubMed.
- H.-J. Werner, G. Knizia and F. R. Manby, Mol. Phys., 2011, 109, 407–417 CrossRef CAS.
- K. A. Peterson, C. Krause, H. Stoll, J. G. Hill and H.-J. Werner, Mol. Phys., 2011, 109, 2607–2623 CrossRef CAS.
- J. G. Hill and K. A. Peterson, J. Chem. Phys., 2014, 141, 094106 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- A. B. Alekseyev, R. J. Buenker and H.-P. Liebermann, J. Chem. Phys., 2012, 136, 224307 CrossRef PubMed.
- T. Nakajima and K. Hirao, Chem. Rev., 2011, 112, 385–402 CrossRef PubMed.
- S. N. Yurchenko, R. J. Barber, J. Tennyson, W. Thiel and P. Jensen, J. Mol. Spectrosc., 2011, 268, 123–129 CrossRef CAS.
- O. L. Polyansky, R. I. Ovsyannikov, A. A. Kyuberis, L. Lodi, J. Tennyson, A. Yachmenev, S. N. Yurchenko and N. F. Zobov, J. Mol. Spectrosc., 2016, 327, 21–30 CrossRef CAS.
- S. N. Yurchenko, W. Thiel and P. Jensen, J. Mol. Spectrosc., 2007, 245, 126–140 CrossRef CAS.
- S. N. Yurchenko, A. Yachmenev and R. I. Ovsyannikov, J. Chem. Theory Comput., 2017, 13, 4368–4381 CrossRef CAS PubMed.
- B. V. Numerov, Mon. Not. R. Astron. Soc., 1924, 84, 592–602 CrossRef.
- J. W. Cooley, Math. Comput., 1961, 15, 363–374 Search PubMed.
- K. L. Chubb, A. Yachmenev, J. Tennyson and S. N. Yurchenko, J. Chem. Phys., 2018, 149, 014101 CrossRef PubMed.
- K. L. Chubb, P. Jensen and S. N. Yurchenko, Symmetry, 2018, 10, 137 CrossRef.
- M. Halonen, L. Halonen, H. Buerger and P. Moritz, J. Phys. Chem., 1992, 96, 4225–4231 CrossRef CAS.
- T. Lukka, E. Kauppi and L. Halonen, J. Chem. Phys., 1995, 102, 5200–5206 CrossRef CAS.
- A. V. Nikitin, M. Rey, A. Rodina, B. M. Krishna and V. G. Tyuterev, J. Phys. Chem. A, 2016, 120, 8983–8997 CrossRef CAS PubMed.
- S. N. Yurchenko, M. Carvajal, P. Jensen, F. Herregodts and T. R. Huet, Chem. Phys., 2003, 290, 59–67 CrossRef CAS.
- G. Tarrago, V. Dana, J.-Y. Mandin, S. Klee and B. P. Winnewisser, J. Mol. Spectrosc., 1996, 178, 10–21 CrossRef CAS.
- A. Yachmenev and J. Küpper, J. Chem. Phys., 2017, 147, 141101 CrossRef PubMed.
- J. K. G. Watson, J. Mol. Spectrosc., 2003, 219, 326–328 CrossRef CAS.
- M. Carlotti, G. Di Lonardo and L. Fusina, J. Mol. Spectrosc., 1983, 102, 310–319 CrossRef CAS.
- P. Schwerdtfeger, L. J. Laakkonen and P. Pyykkö, J. Chem. Phys., 1992, 96, 6807–6819 CrossRef CAS.
- T. Rajamäki, M. Kallay, J. Noga, P. Valiron and L. Halonen, Mol. Phys., 2004, 102, 2297–2310 CrossRef.
- S. Okuda and H. Sasada, J. Mol. Spectrosc., 2018, 346, 27–31 CrossRef CAS.
- M. J. Down, J. Tennyson, J. Orphal, P. Chelin and A. A. Ruth, J. Mol. Spectrosc., 2012, 282, 1–8 CrossRef CAS.
- J. Tennyson, S. N. Yurchenko, A. F. Al-Refaie, E. J. Barton, K. L. Chubb, P. A. Coles, S. Diamantopoulou, M. N. Gorman, C. Hill, A. Z. Lam, L. Lodi, L. K. McKemmish, Y. Na, A. Owens, O. L. Polyansky, T. Rivlin, C. Sousa-Silva, D. S. Underwood, A. Yachmenev and E. Zak, J. Mol. Spectrosc., 2016, 327, 73–94 CrossRef CAS.
- J.-J. Zheng, S.-G. He, Y. Ding, L.-Y. Hao, X.-H. Wang, S.-M. Hu and Q.-S. Zhu, Chem. Phys. Lett., 2002, 352, 435–440 CrossRef CAS.
- N. J. DeYonker and K. A. Peterson, J. Chem. Phys., 2013, 138, 164312 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Including the final line list, partition function and other spectroscopic data are available from the ExoMol website, http://www.exomol.com. See DOI: 10.1039/c8cp07110a |
|
| This journal is © the Owner Societies 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 and rotational quantum number J = 30. The computed DMS reproduces experimental line intensities to within 10% uncertainty for the ν1 and ν3 bands. Furthermore, our calculated absorption cross-sections display good agreement with the main absorption features recorded in the Pacific Northwest National Laboratory (PNNL) for the complete range of 600–6500 cm−1.
500 cm−1 and rotational quantum number J = 30. The computed DMS reproduces experimental line intensities to within 10% uncertainty for the ν1 and ν3 bands. Furthermore, our calculated absorption cross-sections display good agreement with the main absorption features recorded in the Pacific Northwest National Laboratory (PNNL) for the complete range of 600–6500 cm−1.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873 nuclear geometries within the range 1.10 ≤ ri ≤ 3.74 Å and 37° ≤ αi ≤ 130°, with electronic energies extending to 27
873 nuclear geometries within the range 1.10 ≤ ri ≤ 3.74 Å and 37° ≤ αi ≤ 130°, with electronic energies extending to 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, although ∼38
000 cm−1, although ∼38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 of these were below 10
000 of these were below 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (1.25 ≤ ri ≤ 1.9 Å and 60° ≤ αi ≤ 126°). The additional points in the 10
000 cm−1 (1.25 ≤ ri ≤ 1.9 Å and 60° ≤ αi ≤ 126°). The additional points in the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–27
000–27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range predominantly belonged to the As–H dissociative stretch, which is where holes commonly appear if the function is not suitably constrained at high energy. Grid points for our AVQZ-DK reference PES were chosen by randomly sampling 16
000 cm−1 range predominantly belonged to the As–H dissociative stretch, which is where holes commonly appear if the function is not suitably constrained at high energy. Grid points for our AVQZ-DK reference PES were chosen by randomly sampling 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 396 equally energetically distributed points from our VQZ-PP-F12 grid, which spanned the bond lengths 1.3 ≤ ri ≤ 1.8 Å, bond angles 65° ≤ αi ≤ 130° and energies below 15
396 equally energetically distributed points from our VQZ-PP-F12 grid, which spanned the bond lengths 1.3 ≤ ri ≤ 1.8 Å, bond angles 65° ≤ αi ≤ 130° and energies below 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1.
000 cm−1.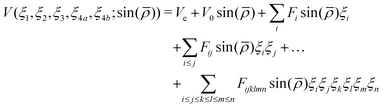
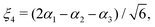
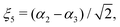
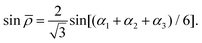
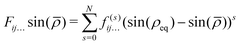
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) . V0 represents the pure inversion potential and f(s)ij… are the fitting parameters. Points are given as energy (Ei) dependant weights (wi)
. V0 represents the pure inversion potential and f(s)ij… are the fitting parameters. Points are given as energy (Ei) dependant weights (wi)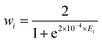
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 678 nuclear geometries. For our all-electron reference PES, the weighted RMS error increased to 1.2 cm−1, most likely due to the proportionally fewer points close to equilibrium. However it should be noted that adding more points to the fit had little effect on the computed vibrational term values reported in Section 3.
678 nuclear geometries. For our all-electron reference PES, the weighted RMS error increased to 1.2 cm−1, most likely due to the proportionally fewer points close to equilibrium. However it should be noted that adding more points to the fit had little effect on the computed vibrational term values reported in Section 3.
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and our re-expansion of the potential function V in terms of linearised coordinates. We choose to restrict the former via a polyad number P. The polyad number is an integer that represents the total quanta of vibrational excitations in terms of the lowest energy fundamental. For AsH3
and our re-expansion of the potential function V in terms of linearised coordinates. We choose to restrict the former via a polyad number P. The polyad number is an integer that represents the total quanta of vibrational excitations in terms of the lowest energy fundamental. For AsH3![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and V expansions we take to the 6th and 8th order, respectively. Increasing them to the 8th and 10th order changed the vibrational term values reported throughout this work by <0.1 cm−1 for the stretches, and <0.7 cm−1 for the bends. For highly excited bending overtones, such as the 5 and 6-quanta bends, the convergence error due to our
and V expansions we take to the 6th and 8th order, respectively. Increasing them to the 8th and 10th order changed the vibrational term values reported throughout this work by <0.1 cm−1 for the stretches, and <0.7 cm−1 for the bends. For highly excited bending overtones, such as the 5 and 6-quanta bends, the convergence error due to our ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and V expansions may be several wavenumbers.
and V expansions may be several wavenumbers.
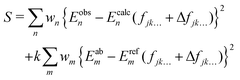
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 678 ab initio points Eabm included in the fit. As the refinement progressed this was incrementally decreased to 1 × 10−6 so as to reduce the relative contribution of the ab initio data. Care was taken throughout to ensure the refined PES did not deviate substantially from the ab initio surface, and we note that for all ab initio grid points, the energy difference between the refined and geometry optimised ab initio PES's is less than 10% that of the ab initio PES above its zero-point energy (ZPE).
678 ab initio points Eabm included in the fit. As the refinement progressed this was incrementally decreased to 1 × 10−6 so as to reduce the relative contribution of the ab initio data. Care was taken throughout to ensure the refined PES did not deviate substantially from the ab initio surface, and we note that for all ab initio grid points, the energy difference between the refined and geometry optimised ab initio PES's is less than 10% that of the ab initio PES above its zero-point energy (ZPE).![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) , is related to the electronic energy in the presence of a weak uniform electric field ΔF acting along the space fixed XYZ axis,
, is related to the electronic energy in the presence of a weak uniform electric field ΔF acting along the space fixed XYZ axis,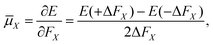
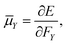
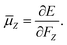
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points, generated by randomly sampling our PES grid.
000 points, generated by randomly sampling our PES grid.
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) is constructed as symmetrized projections onto the molecular bonds with the dipole moment components (
is constructed as symmetrized projections onto the molecular bonds with the dipole moment components (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) A1,
A1, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Ea,
Ea, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Eb) in the molecule fixed axis system given by 4th order polynomial expansions,
Eb) in the molecule fixed axis system given by 4th order polynomial expansions,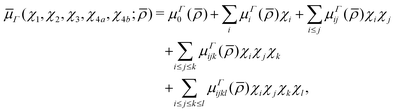
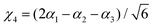
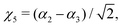
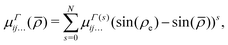
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) is the same as in eqn (1). The dipole moment components (
is the same as in eqn (1). The dipole moment components (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Ea,
Ea, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Eb) are transformed as linear combinations of each other by the C3v group operations and so transform together as an E-symmetry. For this reason the parameters
Eb) are transformed as linear combinations of each other by the C3v group operations and so transform together as an E-symmetry. For this reason the parameters 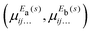 must fit together and
must fit together and 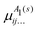 are fitted separately. For an extensive discussion on the SMB representation of the dipole moment function the reader is directed to ref. 31.
are fitted separately. For an extensive discussion on the SMB representation of the dipole moment function the reader is directed to ref. 31.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, which is comparable to the level of numerical noise in the finite differences procedure. The DMS expansion parameter set and a Fortran 90 routine to construct the DMS is included in the ESI.†
000 cm−1, which is comparable to the level of numerical noise in the finite differences procedure. The DMS expansion parameter set and a Fortran 90 routine to construct the DMS is included in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 495
495![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187
187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 171
171![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, shown in Table 3. The minimum energy path over the barrier reduces the As–H bond lengths to their so-called saddle-point value rSP at a planar geometry. Of this, the predicted value of 1.457 Å by Schwerdtfeger et al. is in reasonable agreement with our own (see Table 3). For comparison, the NH3 barrier height is measured to be 1786.8 cm−1 occurring for rSP = 0.99460 Å,67 and for PH3 the calculated values of Sousa–Silva et al.39 are currently the most reliable, predicting a value of 11
000 cm−1, shown in Table 3. The minimum energy path over the barrier reduces the As–H bond lengths to their so-called saddle-point value rSP at a planar geometry. Of this, the predicted value of 1.457 Å by Schwerdtfeger et al. is in reasonable agreement with our own (see Table 3). For comparison, the NH3 barrier height is measured to be 1786.8 cm−1 occurring for rSP = 0.99460 Å,67 and for PH3 the calculated values of Sousa–Silva et al.39 are currently the most reliable, predicting a value of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 cm−1 at 1.3611 Å. Whereas the NH3 inversion splitting is well known to be ≈0.79 cm−1 for the ground vibrational state, it has been predicted but not observed in PH339,68 and so it is unlikely to be observed in AsH3 for some time.
130 cm−1 at 1.3611 Å. Whereas the NH3 inversion splitting is well known to be ≈0.79 cm−1 for the ground vibrational state, it has been predicted but not observed in PH339,68 and so it is unlikely to be observed in AsH3 for some time.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. These, upon multiplication with rigid symmetric rotor wavefunctions, form the basis of our full rovibrational calculation, which we term the (J = 0)-contracted basis. Our second truncation, performed only once where J exceeded 21, is therefore to remove all (J = 0)-contracted eigenfunctions with energy greater than Eivib + Eirotor = 16
000 cm−1. These, upon multiplication with rigid symmetric rotor wavefunctions, form the basis of our full rovibrational calculation, which we term the (J = 0)-contracted basis. Our second truncation, performed only once where J exceeded 21, is therefore to remove all (J = 0)-contracted eigenfunctions with energy greater than Eivib + Eirotor = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, where Eirotor is the eigenvalue of a symmetric rigid rotor.
000 cm−1, where Eirotor is the eigenvalue of a symmetric rigid rotor.