Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spatially resolved ultrasound diagnostics of Li-ion battery electrodes
James B.
Robinson
 *,
Maximilian
Maier
,
George
Alster
,
Tomos
Compton
,
Dan J. L.
Brett
*,
Maximilian
Maier
,
George
Alster
,
Tomos
Compton
,
Dan J. L.
Brett
 * and
Paul R.
Shearing
* and
Paul R.
Shearing
 *
*
Electrochemical Innovation Lab, Department of Chemical Engineering, UCL, London, WC1E 7JE, UK. E-mail: j.b.robinson@ucl.ac.uk; p.shearing@ucl.ac.uk; d.brett@ucl.ac.uk; Web: http://www.ucl.ac.uk/electrochemical-innovation-lab
First published on 18th December 2018
Abstract
The importance of reliable battery diagnostic systems has grown substantially in recent years as a result of the use of high power Li-ion battery packs in an increasingly diverse range of applications. Here, spatially resolved ultrasound acoustic measurements are used to analyse the condition of Li-ion electrodes. Ultrasonic measurements are performed on a commercial mobile phone battery over the full operating voltage window with the lithiation and delithiation of electrodes observed at 36 locations on the surface of the cell. X-ray computed tomography was performed on the cell to ascertain the internal architecture and features that enabled the architecture of the battery to be correlated with the acoustic signature. Analyses of the acoustic signals obtained suggest that the anode and cathode layers can be identified by examining the change in attenuation associated with the charging process. It is also seen that expansions of the electrode layers are inhibited by the presence of the anode current collecting tab in the battery which leads to spatial inhomogeneities in the expansion of the electrode layer examined within the cell.
1. Introduction
The proliferation of Li-ion batteries since their introduction in the late 20th century has been well reported, with the technology increasingly finding applications in high power devices such as automotive powertrains.1–3 In addition to the decreased cost of Li ion cells, their improved safety has also aided the widespread adoption of the technology. In spite of this, concerns remain regarding the potential risk of such cells, with recent high profile incidents being widely reported.4–7 These events have further increased the drive for novel, low-cost diagnostic techniques aimed at monitoring the performance and durability of batteries in operando, which is particularly relevant for the automotive sector.A wide range of diagnostic techniques for Li-ion batteries have been described in the literature;8 these techniques are commonly used in battery management systems, to facilitate the safe operation of battery packs, with typical systems monitoring parameters including, but not limited to, voltage, current and temperature. Such methods have largely focussed on obtaining correlative measurements to understand the state-of-charge (SoC) and state-of-health (SoH) of the battery or pack: Wu et al. have detailed the vast array of diagnostic techniques used in automotive applications including model-based solutions.9 While these techniques can be highly effective, they rely upon correlative effects and inferences associated with indirect measurements that may not hold during extreme conditions such as cell failure, and generally do not provide spatially resolved insight into the batteries condition. In contrast, direct measurements of a cell can identify the degradation and failure of a cell irrespective of the electrochemical or thermal effects which may occur during operation or failure.
Direct measurements of internal changes in the structure of a battery can be performed using X-ray techniques;10–12 however, this is an expensive and often time-consuming process and is not practical in many real-world applications. In contrast, the use of ultrasound techniques to understand changes in the battery architecture is relatively low in cost and can be performed in operando. Acoustic emission spectroscopy, which uses a passive acoustic transducer to detect noises associated with structural changes in systems, has been employed to understand electrochemical devices: Rhodes et al.13 used acoustic emission spectroscopy (AES) to investigate the degradation of Si anodes, that show significant expansion upon lithiation, resulting in the fracture of the electrode. This change in the anode structure results in material and capacity loss and was successfully correlated to the acoustic signals measured. It was observed that the initial charge cycle resulted in the largest degree of particle fracturing, with further cycles also causing some fracturing of the electrode. Fuel cells have also been analysed in a similar manner, with a number of authors14,15 investigating the seals in high-temperature solid oxide fuel cells using acoustic emission spectroscopy. The performance of membranes used in polymer electrolyte fuel cells has also been examined using acoustic techniques16–18 these works investigated a range of phenomena surrounding the complex physical and chemical operation of PEMFCs.
More recently, studies have used ultrasonic time-of-flight (ToF) analysis to interrogate the behaviour of batteries. This technique utilises a narrow ultrasonic pulse, which passes through a sample and is recorded as the signal is reflected back from the interface between different materials or structures. By understanding this acoustic signature, direct measurement of changes in the structure, for instance, cracking or expansion and contraction, can be obtained. Hsieh et al. used acoustic ToF analyses to describe the typical acoustic properties of several battery types and demonstrated the potential to correlate time-of-flight techniques to the state-of-health and charge of batteries in operando.19 Further work examined degradation associated with the cycling of cells with a model which requires no a priori knowledge of the cell to predict degradation.20 Primary Zn-MnO2 cells have also been examined with the change in the state-of-charge of the cell visible as a result of the change in density of the anode, associated with the discharging process.21 Ladpli et al. have also described the use of acoustic measurements to monitor the bulk state of health and charge of Li-ion cells;22 however, to the authors’ knowledge, no spatially resolved, ultrasonic analysis has been published on battery systems.
In this work, spatially resolved acoustic measurements were performed on a commercial mobile phone battery in order to understand the changes in the internal structures of the cell associated with the charging process. X-ray micro computed tomography (CT) was used to understand variations in signal due to the architecture of the cell and highlights the importance of the placement location and appropriate analysis of the data recorded using an ultrasonic transducer on the surface of the battery.
2. Experimental
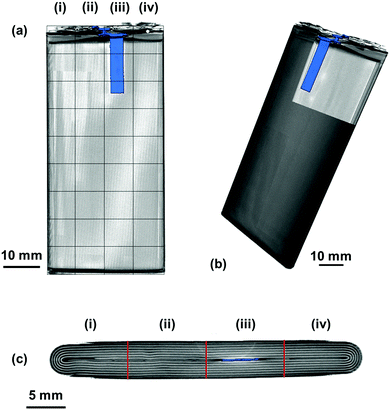
Ultrasound measurements were performed on a commercial 2800 mA h battery designed for a mobile telephone (Samsung J5) of dimensions 9.5 × 4.5 × 0.5 cm. The battery, which was composed of a LiCoO2 cathode with a graphite anode, was analysed from an uncycled state in order to mitigate against any structural effects that may occur as a result of cell degradation over multiple cycles. The measurements were performed on the cell at open circuit potentials (OCPs) ranging from 3.0–4.2 V in 0.1 V increments. To achieve the required voltages, the battery was charged from the initial SOC at 100 mA (0.035 C) until the desired voltage, at which point the voltage was held constant until the current dropped below 10 mA. At each voltage increment, the battery was left to rest at OCP for at least an hour to allow for any relaxation effects. In order to obtain reproducible ultrasound analysis over the full range of voltages, the battery was divided into a matrix containing 36 separate regions, each of 1 cm2 in area, as illustrated in Fig. 1.All ultrasound measurements were performed using an Olympus Epoch 650 ultrasonic flaw detector (Olympus Corp., Japan) using a 6 mm diameter piezoelectric transducer that operated at a frequency of 5 MHz (M110-RM, Olympus Corp., Japan). Measurements were performed by placing the transducer in the centre of the area of interest (1–36) with a thin layer of ultrasonic gel (VWR International, USA) between the transducer and the battery. Consistent pressure between the transducer and the battery was obtained by placing a 100 g weight on top of the transducer for each measurement. Measurements were obtained using a 70 dB acoustic gain with no delay imposed on the measurements; the use of this gain was determined as a result of experiments to determine the largest magnitude of the signal response possible for the initial interface layers without oversaturating the receiver. The resolution of the output of the acoustic reading was limited to 495 discrete measurements to describe the reflection signals. As a result, the duration of the measurements was limited to a 6 μs range which provided a resolution of 12.8 ns in the acquired signals. This provided information on the first eleven reflection peaks associated with material interfaces with sufficient signal responses to enable confident analysis. Further depth information could be achieved at the expense of signal-to-noise ratio by increasing the initial signal gain and extending the range analysed using the Epoch 650. The Epoch was controlled using an open source python based software designed by Steingart described in a previous work.19,23 This allowed each measurement to be obtained as a .json file upon which further analysis could be performed.
To gain an insight into the internal architecture of the cell, X-ray CT of the Samsung J5 cell was performed using a Nikon XT-225 instrument (Nikon Metrology, Tring, UK). These scans were performed at an accelerating voltage of 200 kV and a beam power of 80 W using a tungsten target. In total, 3176 projections were obtained for the scan with the geometric magnification of the system resulting in a pixel size of approximately 52 μm, which enabled the full visualisation of the electrode layers and safety and operational devices within the cell. Reconstruction of the radiographic images was performed using Nikon CT Agent with visualisation achieved using Avizo Fire (FEI, France).
3. Results and discussion
To fully understand the significance and ascribe the correct response of the ultrasound signals obtained, it is helpful to have an a priori knowledge of the internal structures of the cell – particularly the number of interfaces between different layers within the battery itself. In this work, X-ray CT was used to provide this information in a non-destructive manner, as seen in Fig. 2.The variations in the internal architecture of the cell can be seen in both the cross-section and plan orthogonal slices in Fig. 2. The anode current collecting tab shown in Fig. 2(d) is seen to protrude into the rolled electrodes by approximately 20 mm; this is seen to cause distortions through the centre of the electrode architecture, as seen in Fig. 2(c). Further anisotropy can be seen towards either edge of the electrode roll, with gaps visible as a result of the packaging process. These variations in the layering of the cell result in a non-uniformity in the depths between the outer casing of the cell and the interfaces between different layers.
The accuracy of acoustic measurements are heavily dependent on a range of factors, with the contact pressure between the transducer and the object being investigated being one of the most significant. In all instances, a constant force was applied to the top of the transducer to maintain uniform contact between the sensor and the cell. The reproducibility of the signal responses was confirmed by obtaining five measurements for each location, with the average used for each measurement to reduce error in the readings, and was found to be in good agreement in all instances. It was observed that the standard deviation of the averaged signal increased slightly at higher times of flight in some instances due to the higher attenuation of the acoustic waves which occurs at longer ToF, this is a result of the increased mass through which the acoustic waves must propagate. An example of the averaged signals is shown in Fig. 3.
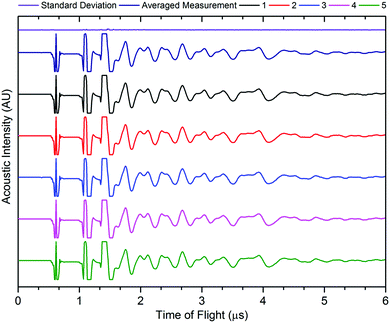 | ||
| Fig. 3 Example signal response for five readings from the same point on the cell, with averaged signal and standard deviation. | ||
The signal responses shown in Fig. 3 contain a number of key features which are consistent throughout all of the experiments: the first, a sharp peak seen at approximately 0.6 μs, is associated with the contact between the transducer and the battery. This contact peak is located in the same position for all measurements and, as such, can be considered an artefact of the signal response. Following on from this, the subsequent response begins to elucidate information about the internal cell structure. In each case, a peak is indicative of an interface between different materials as discussed previously. The precise location of the second and third peaks visible in Fig. 3 cannot be ascertained due to the magnitude of the acoustic signal, which exceeded the maximum gain measured by the device. By accepting the loss of information at these ToFs (which will correspond largely to interfaces between the transducer and the battery shell), it is possible to provide more relevant information that will occur at longer ToF. It can be seen from Fig. 3 that the acoustic peaks are typically measured as doublets, i.e. two peaks located close to each other. It is also evident that the amplitude of the signal decreases through the depth of the battery. This decay in the signal is as a result of several phenomena including wave spreading, attenuation of the signal and interference between the acoustic waves as they pass through the medium of the battery.
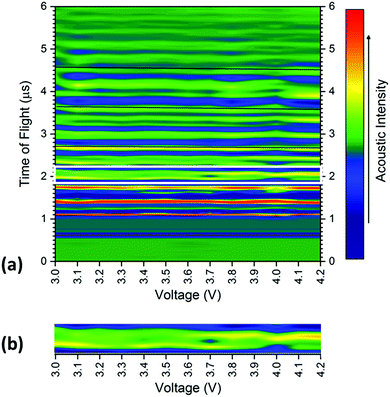
The averaged signal as shown in Fig. 3 was obtained for all positions on the battery between 3.0–4.2 V at 0.1 V increments, with the results shown for a single transducer location in Fig. 4. The consistency in the general location of peaks is evident in Fig. 4; with regions of high acoustic intensity (analogous to the peak locations in Fig. 3) alternating with regions of low intensity. It can however; be seen, that the precise location of the peaks shift throughout the charging of the cell, with concurrent peaks also showing changes in the maximum intensity indicative of a physical change in the corresponding electrodes.
In general, there is a trend towards a lower ToF associated with an increased state-of-charge; this is most evident in the peaks located at 2.6, 3.65 and 4.6 μs. The contraction of all peaks as a result of the charging process is consistent with results demonstrated by Koyama et al.,24 who determined that volume expansion occurs in both LiCoO2 and graphite electrodes during the charging process. In this work, as the transducer is placed normal to the electrodes, expansion in the electrodes corresponds to a negative shift in the time-of-flight, as seen in Fig. 1 and 3. There is also a noticeable deviation in the acoustic intensity of the peaks as a result of the charging process: it can be seen that the amplitude of the peak located at 2 μs decreases with increased state-of-charge, in contrast, the second peak in the doublet, located at 2.1 μs undergoes the opposite change. It is suggested that this change in amplitude occurs due to the change in composition, and in turn the density, of the electrodes to which these peaks refer. During the charging process, the half reactions which occur in the cell are represented by:
| Cathode: LiCoO2 → Li1−xCoO2 + xLi+ + xe− | (1) |
| Anode: xLi+ + 6C + xe− → LixC6 | (2) |
The degree-of-lithiation will affect the density of each electrode; with increased lithiation resulting in a higher density anode and corresponding lower density of the active material in the cathode. Additionally the degree-of-lithiation will affect the dimensions of both electrodes, in this instance through the charging process both electrodes expand.24,25
The acoustic impedance of a system is given by:26
| Z = ρcx,y,z | (3) |
As a product of the velocity of the sound wave (c) through the material, and the density (ρ) of the material the acoustic impedance is a challenging parameter to obtain experimentally in a battery. This is due to the local gradients in SoC which are known to occur27,28 and the highly heterogeneous structure within a full cell which make obtaining accurate local densities difficult and resulting in expansions in the electrodes. These local effects, will will, in turn, affect the peak location obtained from the interfaces which cause reflections. It can be seen from eqn (3) that a higher density electrode will attenuate more signal. In addition to signal change in the attenuation of the signal, the electrode density changes caused by a change in SOC will also result in a change in the speed of sound (c) through the material. The speed of sound is related to the elastic modulus (E) according to the Newton–Laplace equation as shown below:
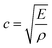 | (4) |
These effects have previously been discussed by Hseih et al.19 who discussed the importance of material density on acoustic wave propagation in battery materials. However, it is important to note the extent of change in the acoustic impedance will be greater than the change in velocity of the acoustic wave propagation as a result of a change in density in material (the acoustic impedance scales linearly with denisty changes, whereas the velocity scales with the inverse square root). As a result of this difference, it is possible to infer changes in the density of the electrode, and furthermore the degree of lithiation, from variations in both the acoustic intensity and change in the reflection peak location of the signal. While obtaining exact values are challenging, general trends in the changes in attenuation and velocity can be acquired by calculating a theoretical change in density at both electrodes. In this case the change in density can be described by eqn (5), with the change in mass obtained through a mass balance calculated using the half-reactions shown in eqn (1) and (2) and the change in volume obtained experimentally.
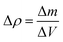 | (5) |
Performing this analysis for the materials used in this work, shown in Table 1, assuming a unit volume which undergoes delithiation of the active material in the cathode from LiCoO2 to Li0.5CoO2 and a corresponding lithiation of the graphite in the anode to LiC6 with the changes in volume obtained from Koyama et al.24 By performing these calculations it is seen that the density of LiCoO2 decreases with the density of the graphite in the anode increasing due to the charging process. It has been reported that the elastic modulus of both spinel and olivine structured materials (such as those commonly employed in battery electrodes) remains relatively constant over the full lithiation range.29 For the purposes of this calculation it is considered constant enabling (as has been done in previous acoustic works19) an estimation of the change in velocity of the acoustic waves in a graphite/LiCoO2 battery.
| Mass 0% SOC (kg mol−1) | Mass 100% SOC (kg mol−1) | % Mass change (%) | Volume expansion24 (%) | Δρ (%) | ΔZ (%) | Δc (%) | |
|---|---|---|---|---|---|---|---|
| Li1−xCoO2 | 97.872 | 94.402 | −3.476 | 1.9 | −1.866 | −1.367 | −0.938 |
| LixC6 | 72.064 | 79.005 | 6.941 | 13.1 | 0.735 | 0.857 | 0.367 |
By performing this calculation based on the figures shown in Table 1 is can be shown that the changes in the velocities in the active cathode material and graphitic anode are −0.93% and 0.37% respectively. These velocity changes are; however, based on a 100% change in SOC and will only provide an estimate of the changes at any localised point. These changes also do not take account of the composite structure of the electrodes which contain a range of other materials including binders and conductivity enhancers, in addition to the current collecting layers and electrolyte within this system. The changes in density can also provide an approximation to the change in acoustic impedance by assuming equivalence between the speed of sound through the material and the velocity of the acoustic wave propagating through the material. Once more a constant modulus is assumed in line with previous work with the calculation obtained according to eqn (6).
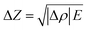 | (6) |
Using the values calculated in Table 1 it can be shown that the charging process for the cell used in this work results in a change in acoustic impedance in both electrodes. It can be seen that the impedance of the anode increases by approximately 0.85% with a corresponding decrease in attenuation of 1.36% observed in the cathode.
The changes in the magnitude of the acoustic signal for the doublet located at approximately 2 μs, as highlighted in Fig. 4, show an apparent decrease in density in the earliest peak with an increase in the second peak of the pair. These contrasting changes in the magnitude are indicative of a change in lithiation state of each of the electrodes and enable the peaks to be assigned to a particular electrode. The decrease in magnitude, and, by inference density, in the first peak suggests the peak can be ascribed to the cathode, with the second doublet located at approximately 2.1 μs demonstrating behaviour anticipated by the anode. These behaviours are consistent with the trends observed using XCT which show the initial cathode double layer being located closest to the housing of the battery with the positive electrode following before the pattern is repeated.
To quantify the changes in the signals across the voltage range, the discrete points that comprise Fig. 4 were isolated with the changes in the time-of-flight and signal intensity analysed over two separate times-of-flight and voltages respectively, these are shown in Fig. 5.
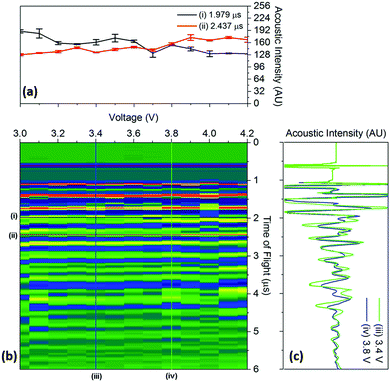 | ||
| Fig. 5 Raw data colourmap (corresponding to the smoothed data shown in Fig. 4) of the acoustic intensity for a single position (b) with (a) a quantification of the changes in manitude of the acoustic signal for two times-of-flight located at (i) 1.979 μs and (ii) 2.437 μs and (c) time-of-flight investigated at two voltages (iii) 3.4 V and (iv) 3.8 V associated with the charging process for a position 6 in the battery. | ||
It can be seen that the changes in acoustic intensity shown in Fig. 5(a) show a similar trend to those discussed previously, with the amplitude of the signal of the two peaks changing in opposite directions as a result of the charging of the cell. It must be noted that the error bars shown in Fig. 5(a) only account for the uncertainty in the amplitude measurement and do not account for any uncertainty associated with the time measurement which may result in further uncertainty in the amplitude signal due to the shape of the peaks. The magnitude of the acoustic intensity peak (ascribed to a cathode layer) located at 1.979 μs, can be seen to decrease from 189–130 AU, with the magnitude of the second peak (an anode layer, identified by comparing the theoretical and measured changes in attenuation of the peaks) located at 2.437 μs increasing from 128–167 AU. These changes in the acoustic intensity across the range of the charging profile correspond to an approximate 30% change for both peaks, suggesting that changes in the signal amplitude correlate to the degree-of-lithiation of the respective electrodes. As seen in Table 1, small changes in the acoustic impedance are observed in both electrodes, with the anode displaying increased impedance and the cathode a reduced one. The magnitude of the changes observed in Fig. 5(a) are larger than the change in the magnitude of impedance; however, the relationship between the acoustic impedance and attenuation has been established to be highly non-linear.30 Similar changes in the attenuation can also be observed throughout the acoustic spectra as seen in Fig. 4, indicating that each doublet is comprised of a single anode and cathode peak, which enables identification of the layer. This has the potential to be a powerful tool for battery monitoring systems; although, while the extent of external noise has not been assessed in this case it has been shown that the standard deviation in the analysis performed in this work never exceeds 5% highlighting the low error in the measurements. Furthermore it should be noted that this technique would prove highly effective in identifying regions of gassing within Li-ion cells. As previously mentioned the signal is attenuated through a range of phenomena; however, the presence of even a small layer of gas would be sufficient to significantly impede the signal, identifying such a region.
The changes in the ToF associated with the charging process are also shown in Fig. 5(c). As discussed previously, the charging of LiCoO2/graphite batteries causes the expansion of both electrodes, with the time-of-flight reducing as a result of the movement of the electrode interfaces towards the transducer. To quantify this, the centre of all of the peaks obtained from 1.5–5 μs were analysed between 3.4–3.8 V. The magnitude of the peak shift was seen to be limited to less than 4% in all cases, with the average peak shifting by 1.74 ± 0.89%. Work conducted by Koyama et al. shows that the linear strain in electrodes similar to the ones used in this work, result in linear expansions in both electrodes; with linear expansions of 4.2% in graphite and 0.6% in LiCoO2 reported.24 However, the expansion in graphite will depend on the degree-of-lithiation with a large number of lithiation states available in graphite that can accept the insertion of Li ions in various ratios, i.e. LixC6, LixC12, LixC32.30 Additionally, the ratio of the capacities of the anode to cathode will also affect the degree-of-lithiation, with the anode expanding less in a cathode-limited cell which has an excess of anode material, resulting in a lower degree-of-lithiation in this electrode.
Quantification of the linear expansion of a LiCoO2/graphite battery performed previously24 shows that charging the cell to an OCP of 3.9 V results in a net 2.2% linear expansion in the electrodes. This result is of a similar magnitude to that measured using acosutic time of flight analysis in this work (which showed an expansion of 1.7–3.6%). However, it is important to also consider the change in local density of the electrodes which both the acoustic impedance and the speed of sound through the material, and as such, will result in errors should direct correlation between the TOF shift and physical position of the layers be inferred in such a complex system.
Despite these limitations in ascertaining exact positions in the battery using ToF analysis, it is possible to access the relative changes in the internal structure by observing the changes in ToF. This was performed in order to investigate the importance of transducer placement in performing ultrasonic investigations on a battery. The variations in ToF between 3.0 and 4.2 V are shown for all 36 positions across the battery in Fig. 6. In all cases, the same single peak located at approximately 2.7 μs was used to calculate the shift. This peak was chosen as it did not contain a doublet, indicating the electrode layer examined in this analysis was a single electrode, as doublet peaks may convolute the analysis and result in an error as a result of the changes in intensity and peak location. It was seen that this peak shifted linearly across the range of voltages with a negative shift seen in the majority of positions. As these measurements were performed at steady state open circuit potentials it is assumed that localised potential distributions are small, which in turn, enables the cell to be described using a single velocity and impedance at any one voltage.
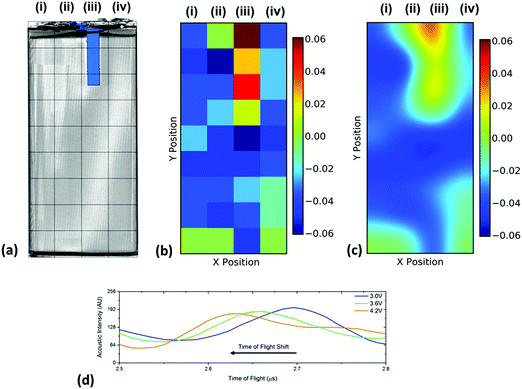 | ||
| Fig. 6 Spatial variations in the time-of-flight across the battery showing (a) the position index of the battery overlaid on a volume rendering of the cell and the location of the current collecting tab which is located in the centre of the jelly roll as shown in Fig. 2(c), (b) the raw change in ToF data between 3.0 and 4.2 V and (c) an smoothed data set identifying regions of change in TOF. Also shown in (d) is a sample of the shift for the single peak analysed that was initially located at approximately 2.7 μs showing the linear nature of the shift in TOF. | ||
It is clear in Fig. 6 that there are a large number of positions in which the peak shift is similar; this is particularly the case in the two left-hand columns (1–29, 2–30). It is also noticeable that the row at the bottom of the battery (33–36) shows a reduced peak shift compared to the bulk of the cell. In analysing the X-ray CT results, it was seen that a proportion of this region contained no electrode material and was solely comprised of empty space and casing, which, in addition to the bends in the electrode stacks seen in Fig. 2(c) result in this non-uniform behaviour.
The most significant deviation from the behaviour of the bulk of the cell occurs in locations 3, 7 & 11. These regions are the areas that contain the anode current collecting tab: as the current collecting tab is fixed into location, due to its connection to the casing and the anode, the electrode layers must expand around the tab. In doing so the expansion seen in the layers unaffected [for instance those in column (i)] is seen to be substantially different in magnitude. Indeed, in this region the peak shift is also seen to be positive, indicating a contraction in the electrode interface away from the transducer. It is suggested that the presence of this current collecting tab inhibits the expansion of the electrode layers surrounding the connection of the tab, resulting in increased stress the causes the contraction of the layers in this region. The tab effectively acts as an ‘anchor point’ limiting the local movement in the electrode architecture, this phenomena has been previously observed in coin cells by Eastwood et al.31 The effect of the tab can also be seen expanding into neighbouring regions resulting in the comparative reduced expansion of the layers beside the tab when compared to those in column (i). These regions; whilst showing an expansion, as with the bulk regions, can be seen to have a slightly reduced peak shift when compared to the locations located further away from the tab.
4. Conclusions
Spatially resolved ultrasonic acoustic measurements were performed over the full operating window of a commercial Li-ion battery to investigate the changes associated with charging on the internal structure. The change in density of electrodes as a result of lithiation and delithiation was visualised through analysis of the change in ultrasonic signal intensity. This showed the potential to evaluate the state-of-charge of the cell with both the anode and cathode showing linear changes in acoustic intensity as a result of the charging process which can be used as a direct measurement to identify changes in the condition of the battery. Indeed through using this technique, the state-of-health of the battery could also be interrogated by monitoring the deviations in the characteristic behaviour of the cell or pack. The increase in signal attenuation of the anode was seen to be approximately equal to the decrease in attenuation of the cathode, suggesting the changes in attenuation were solely due to the change in lithiation state of the electrode.Analysis of the time-of-flight shifts associated with the charging process showed agreement with the reported behaviour of the materials which formed the battery, with both the anode and cathode expanding during the charging. It was observed that the change in location of the peaks was of a similar magnitude to reported linear expansions which occur in LiCoO2/graphite batteries as a result of charging. X-ray micro-tomography was performed that revealed the anode current collecting tab passed approximately one-third of the way into the battery, which coincided with variations in the time-of-flight shift in the spatially resolved acoustic measurements. Rather than the expansion observed in the electrode layers of the bulk battery, a contraction in the time-of-flight shift was observed, suggesting the current collecting tab inhibited the movement of the electrode layers in this region.
The technique described here has the potential to offer relatively economical, real-time data as a diagnostic tool, with the high-resolution information providing information for individual electrode layers. The approach could also be used for rapid assessment of battery structure as an end-of-life assessment tool.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the EPSRC funding for supporting the work of Robinson through the UCL Doctoral Prize Fellowship scheme (EP/M507970/1) and the EPSRC for supporting the energy storage work in the Electrochemical Innovation Lab (EP/R020973/1; EP/R023581/1; EP/N032888/1; EP/N001583/1. EP/P009050/1; EP/M009394/1; EP/M014371/1). The authours would also like to acknowledge the Royal Academy of Engineering for funding Robinson through the UKIC Postgraduate Fellowship Scheme (ICRF1718\1\34). The authors also acknowledge the STFC for supporting Shearing and Brett (ST/K00171X/1) and Royal Academy of Engineering for supporting Shearing. The authors would like to acknowledge Daniel A. Steingart for his assistance and for supplying the code used to obtain the data.References
- M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- L. Lu, X. Han, J. Li, J. Hua and M. Ouyang, J. Power Sources, 2013, 226, 272–288 CrossRef CAS.
- B. Scrosati, J. Hassoun and Y.-K. Sun, Energy Environ. Sci., 2011, 4, 3287–3295 RSC.
- G. P. Beauregard, Report of Investigation: Hybrids Plus Plug in Hybrid Electric Vehicle, U.S. Department of Energy, Idaho National Laboratory, 2008 Search PubMed.
- JTSB, Aircraft Serious Incident Investigation Report, All Nippon Airways Co., LTD JA804A, 2014.
- AAIB, Report on the serious incident to Boeing B787-8, ET-AOP London Heathrow Airport on 12 July 2013, 2015.
- NTSB, Aircraft Incident Report, Auxiliary Power Unit Battery Fire, Japan Airlines Boeing 787-8, JA829J, 2014.
- L. Lu, X. Han, J. Li, J. Hua and M. Ouyang, J. Power Sources, 2013, 226, 272–288 CrossRef CAS.
- C. Wu, C. Zhu, Y. Ge and Y. Zhao, J. Nanomater., 2015, 9 Search PubMed.
- D. P. Finegan, M. Scheel, J. B. Robinson, B. Tjaden, I. Hunt, T. J. Mason, J. Millichamp, M. Di Michiel, G. J. Offer, G. Hinds, D. J. L. Brett and P. R. Shearing, Nat. Commun., 2015, 6, 6924 CrossRef CAS PubMed.
- J. Robinson, D. Finegan, T. Heenan, K. Smith, E. Kendrick, D. Brett and P. R. Shearing, J. Electrochem. Energy Convers. Storage, 2017, 011010 CrossRef.
- J. B. Robinson, J. A. Darr, D. S. Eastwood, G. Hinds, P. D. Lee, P. R. Shearing, O. O. Taiwo and D. J. L. Brett, J. Power Sources, 2014, 252, 51–57 CrossRef CAS.
- K. Rhodes, N. Dudney, E. Lara-Curzio and C. Daniel, J. Electrochem. Soc., 2010, 157, A1354–A1360 CrossRef CAS.
- B. Dev and M. E. Walter, Fuel Cells, 2015, 15, 115–130 CrossRef CAS.
- B. Dev, M. E. Walter, G. B. Arkenberg and S. L. Swartz, J. Power Sources, 2014, 245, 958–966 CrossRef CAS.
- B. Legros, P. X. Thivel, Y. Bultel, M. Boinet and R. P. Nogueira, J. Power Sources, 2010, 195, 8124–8133 CrossRef CAS.
- B. Legros, P.-X. Thivel, Y. Bultel, M. Boinet and R. P. Nogueira, Electrochem. Solid-State Lett., 2009, 12, B116–B118 CrossRef CAS.
- B. Legros, P. X. Thivel, F. Druart, Y. Bultel and R. Nogueira, 8th International Symposium on Advanced Electromechanical Motion Systems & Electric Drives Joint Symposium, IEEE, 2009, pp. 1–6 Search PubMed.
- A. G. Hsieh, S. Bhadra, B. J. Hertzberg, P. J. Gjeltema, A. Goy, J. W. Fleischer and D. A. Steingart, Energy Environ. Sci., 2015, 8, 1569–1577 RSC.
- G. Davies, K. W. Knehr, B. Van Tassell, T. Hodson, S. Biswas, A. G. Hsieh and D. A. Steingart, J. Electrochem. Soc., 2017, 164, A2746–A2755 CrossRef CAS.
- S. Bhadra, A. G. Hsieh, M. J. Wang, B. J. Hertzberg and D. A. Steingart, J. Electrochem. Soc., 2016, 163, A1050–A1056 CrossRef CAS.
- P. Ladpli, F. Kopsaftopoulos and F.-K. Chang, J. Power Sources, 2018, 384, 342–354 CrossRef CAS.
- D. A. Steingart, Accessed August, 2018, https://github.com/dansteingart/nodeforwarder.
- Y. Koyama, T. E. Chin, U. Rhyner, R. K. Holman, S. R. Hall and Y. M. Chiang, Adv. Funct. Mater., 2006, 16, 492–498 CrossRef CAS.
- X. Wang, Y. Sone, G. Segami, H. Naito, C. Yamada and K. Kibe, J. Electrochem. Soc., 2007, 154, A14–A21 CrossRef CAS.
- L. C. Lynnworth, IEEE Trans. Sonics Ultrason., 1965, 12, 37–48 Search PubMed.
- J. Liu, M. Kunz, K. Chen, N. Tamura and T. J. Richardson, J. Phys. Lett., 2010, 1, 2120–2123 CAS.
- D. P. Finegan, E. Tudisco, M. Scheel, J. B. Robinson, O. O. Taiwo, D. S. Eastwood, P. D. Lee, M. D. Michiel, B. Bay, S. A. Hall, G. Hinds, D. J. L. Brett and P. R. Shearing, Adv. Sci., 2016, 3, 1500332 CrossRef PubMed.
- Y. Qi, L. G. Hector, C. James and K. J. Kim, J. Electrochem. Soc., 2014, 161, F3010–F3018 CrossRef CAS.
- K. G. Gallagher, D. W. Dees, A. N. Jansen, D. P. Abraham and S.-H. Kang, J. Electrochem. Soc., 2012, 159, A2029–A2037 CrossRef CAS.
- D. S. Eastwood, V. Yufit, J. Gelb, A. Gu, R. S. Bradley, S. J. Harris, D. J. L. Brett, N. P. Brandon, P. D. Lee, P. J. Withers and P. R. Shearing, Adv. Energy Mater., 2014, 4, 1300506 CrossRef.
| This journal is © the Owner Societies 2019 |