Unexpected trends in the hydrophobicity of fluorinated amino acids reflect competing changes in polarity and conformation

Abstract

Fluorination can dramatically improve the thermal and proteolytic stability of proteins and their enzymatic activity. Key to the impact of fluorination on protein properties is the hydrophobicity of fluorinated amino acids. We use molecular dynamics simulations, together with a new fixed-charge, atomistic force field, to quantify the changes in hydration free energy, ΔG_Hyd, for amino acids with alkyl side chains and with 1 to 6 –CH → –CF side chain substitutions. Fluorination changes ΔG_Hyd by −1.5 to +2 kcal mol⁻¹, but the number of fluorines is a poor predictor of hydrophobicity. Changes in ΔG_Hyd reflect two main contributions: (i) fluorination alters side chain–water interactions; we identify a crossover point from hydrophilic to hydrophobic fluoromethyl groups which may be used to estimate the hydrophobicity of fluorinated alkyl side-chains; (ii) fluorination alters the number of backbone–water hydrogen bonds via changes in the relative side chain-backbone conformation. Our results offer a road map to mechanistically understand how fluorination alters hydrophobicity of (bio)polymers.

---

1 Introduction

The preferential interaction between apolar solutes in water – the hydrophobic effect – is a key factor driving protein folding,^1,2 structural stability with respect to changes in temperature^3,4 (thermal stability) and interactions with other proteins and ligands.^5,6 The hydrophobic effect reflects the balance between solute–water interactions and direct, predominantly dispersive, solute–solute interactions.^7,8 Understanding how to use amino acid mutations to control the hydrophobic effect is critical to develop new protein-based drugs, biodevices and materials.^9–13 Simultaneously, minimizing changes in solute–solute packing upon mutations is desirable to ensure that protein structure – and thus function – is preserved.^14,15 This is, however, difficult with the limited pool of canonical hydrophobic amino acids because their side chains differ in structure and volume. Fluorinated versions of those amino acids, i.e. those where hydrogen atoms in side chain groups are substituted by fluorine (see Fig. 1), can solve this problem while simultaneously enhancing other properties of interest.^3,16–19 Even fluorinating only a few residues may enhance the hydrophobicity and passive diffusion of peptides through membranes,²⁰ the proteolytic resistance²¹ and anti-microbial activity of proteins,²² in addition to tuning their thermal stability,²³ making this synthetic approach of wide interest.^24–28

Fig. 1 Molecular structures, commonly used names and abbreviations for the amino acids under study. Each amino acid residue is capped at the N-terminus with an acetate group (ACE, –COCH₃) and at the C-terminus with an N-methyl group (NME, –NHCH₃). Abbreviations for fluorinated amino acids follow a three-character nomenclature: initial character of parent (non-fluorinated) amino acid name (E, P, V, I, L); number of fluorine atoms (1, 2, 3, 4, 6); fluorination site (δ carbon as D, γ carbon as G or, in the case of chiral center formation following fluorination, R or S).

Still, a caveat of using fluorination to control protein properties remains: do we understand the factors influencing the hydrophobic effect involving fluorinated amino acids? The answer is, simply, that we do not. Here we focus on one factor contributing to the hydrophobic effect: solute–water interactions, for simplicity referred to as solute hydrophobicity. The hydrophobicity of solutes is usually characterized by their hydration free energies.⁸ The hydrophobicity of fluorinated amino acids has been qualitatively estimated by considering the surface area of its side chain (the larger the surface area, the larger the hydrophobicity)^29,30 and its side chain polarity (the larger the polarity, the smaller the hydrophobicity),²³ but detailed mechanistic understanding is still lacking.^16,19 Understanding the origins of fluorination-induced changes in hydrophobicity depends critically on our ability to accurately quantify interactions between amino acids and their environment. We demonstrate that this quantification is now possible using molecular dynamics simulations and fixed-charge, all-atom models. The approach presented here is general, and may be used to investigate the hydrophobicity of any fluorinated (bio)polymer or small molecule.

2 Computational methods

We used the TIP4P-Ew (ref. 31) water model, the AMBER14 (ff14sb; ref. 32) force field for the canonical amino acids and the GAFF force field for methane, ethane and propane. Note that AMBER14 and GAFF use the same Lennard-Jones parameters. For the remaining amino acids and for the fluorinated small molecules, we used a force field developed by us (previous own work³³ and ESI† Sections 1 and 2) based on AMBER14 (amino acids) or GAFF (small molecules). The main difference between our force field for fluorinated molecules and GAFF/AMBER14 lies in the ε and σ Lennard-Jones (LJ) parameters of fluorine, and of hydrogen (H_F) bonded to a fluorinated carbon. The LJ parameters of fluorine were optimized to reproduce the hydration free energies of CF₄ and the molar volume of a 50% mix of CF₄ and CH₄; subsequently, those of H_F were optimized to reproduce the hydration free energy and the molar volume of CHF₃. We chose these target properties because the hydrophobic effect and packing in the hydrophobic core are key for protein stability. In total, we tested 46 (σ_FF,ε_FF) and 24 (σ_HFHF,ε_HFHF) pairs. LJ interactions between different atoms are calculated using the standard combination rules used in the AMBER force field. Atomic partial charges were obtained following the GAFF (small molecules) or AMBER (amino acids) protocols. We note that the requirement of compatibility with the protein force field implies that we retain the point charge representation. This representation has known shortcomings when modeling carbon-bound chlorine, bromine or iodine because these halogens exhibit σ-holes (a positive area in the electrodensity distribution of the halogen atom, surrounded by a negative belt) which this charge model cannot represent.³⁴ Carbon-bound fluorine, however, retains a negative potential in its entire surface and the level of anisotropy in its electronic charge distribution is small.^35–37 For that reason, single point charge models have been used to model the interactions of fluorinated sites with water and with other organic molecules: e.g., Schyman & Jorgensen,³⁴ Ibrahim³⁸ and Ho³⁹ apply their models of σ-holes to carbon-bound chlorine, bromine and iodine, but retain a point charge representation for fluorinated sites. Point charge models perform less well in the case of fluorinated aryl groups because the σ-hole perturbation extends into the β-carbons; when modeling fluorinated aryl molecules, other promising models such as those based on permanent atomic multipole charges^37,40,41 might be advantageous. This extended perturbation occurs via the π electrons,³⁷ and consequently is not expected to be nearly as significant for fluorinated alkyl groups, which are the sole focus of the present work.

Free energy calculations were performed with Gromacs 5.0^42–48 and molecular dynamics simulations to calculate other observables were performed with AMBER 14.⁴⁹ All systems were assembled using the built-in tools of the software package used to perform the simulations. A summary of the most relevant parameters used during the production runs is given in ESI† Table 2. Simulations used a time-step of 2 fs and constraints (LINCS⁵⁰ in Gromacs, SHAKE⁵¹ in Amber) were applied to all bonds involving hydrogen atoms. Integration of the equations of motion was done using a leap-frog Langevin algorithm. van der Waals interactions were shifted to zero between 1.0 and 1.2 nm, and long-range dispersion corrections were applied to both pressure and energy. Long-range electrostatics were treated with the PME scheme with a 1.2 nm cutoff, a grid spacing of 0.1 nm (AMBER) or 0.12 nm (Gromacs) and a 4th (AMBER) or 6th (Gromacs) order interpolation. Production runs were done in the NpT ensemble. The Monte Carlo^49,52 (AMBER) or Berendsen⁵³ (Gromacs) barostats were used with a relaxation time of 1 ps for an isotropic coupling of system pressure to 1 bar; temperature coupling was handled by the leap-frog Langevin integrator with a collision frequency of 1 ps⁻¹ and a target temperature of 298 K.

Hydration free energies were calculated using Free Energy Perturbation (FEP) and Bennett Acceptance Ratio^54,55 (BAR), following the protocol we have previously adopted³³ and described in ESI† Section 2.1. Briefly, in each case, simulations consisting of a single solute molecule in water were conducted, first decoupling coulombic interactions and then LJ interactions. The coupling parameter λ_C for the coulombic interactions was scaled linearly and assumed 21 equally-spaced values between 0 and 1; decoupling the LJ interactions was done over 59 states, with unevenly-spaced λ_LJ values between 0 and 1. At each state, we performed a steepest-descent minimization, BFGS minimization, 100 ps of NVT equilibration and 100 ps of NpT equilibration before collecting statistics for 2 ns. Five independent production runs were performed for each amino acid; three production runs were performed for each (fluoro)alkane.

Molecular dynamics simulations consisted of a steepest descent minimization, a conjugated gradient minimization, a 200 ps NVT heating from 0 K to 298 K, a 1 ns NpT equilibration and a 25 ns NpT production run; in the minimization, heating and equilibration steps the coordinates of the backbone atoms were restrained with a 20 kcal mol⁻¹ potential. These trajectories were used to extract the data used as input for eqn (1), and were also used as input for the APBS⁵⁶ software to estimate the electrostatic hydration free energy of the amino acids using the linearized Poisson–Boltzmann equation, as described in more detail in ESI† Section 3.1.

3 Results & discussion

Change in ΔG_Hyd with fluorination depends on the chirality and location of the fluorinated site and on amino acid identity

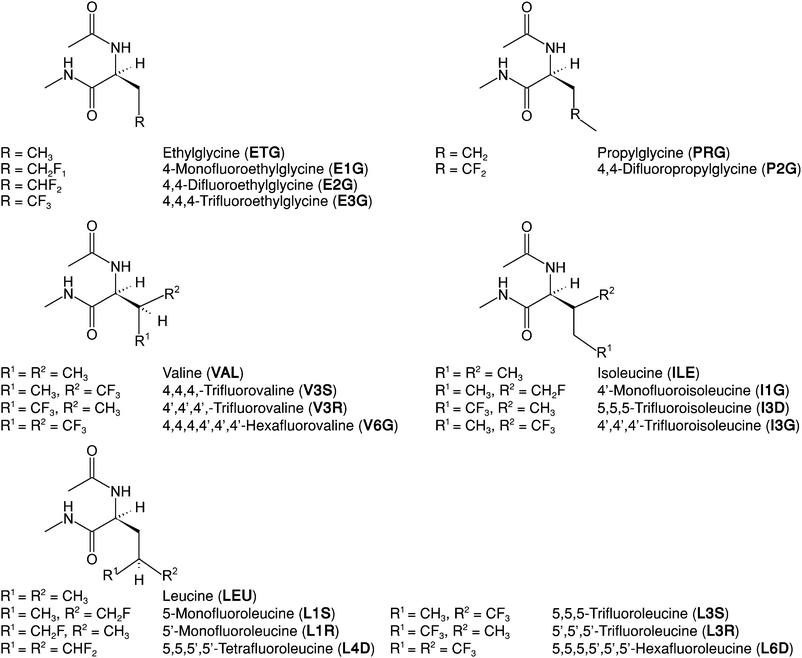
We calculated hydration free energies as a measure of the hydrophobicity of 16 fluorinated amino acids and their 5 non-fluorinated counterparts, totaling 21 aliphatic amino acids (see Fig. 1). These free energies are shown in ESI† Table 4 and Fig. 2; we reported some of these values in a prior publication.³³ The ΔΔG_Hyd values have an associated standard deviation of 0.1 to 0.3 kcal mol⁻¹ (see ESI† Table 4), enabling the precise detection of differences between amino acids.

Fig. 2 Coulombic contribution (Coul), Lennard-Jones contribution (LJ) and sum of the contributions (total) to the differences in hydration free energy (ΔΔG_Hyd) between fluorinated and non-fluorinated amino acids. Each bar is the average of five independent simulations.

The amino acids with one or more –CH₃ → –CF₃ substitutions (here termed fully fluorinated) are, as expected, always more hydrophobic (positive ΔΔG_Hyd) than their non-fluorinated counterparts,^3,19,57 but the change in free energy is not constant per fluorinated group. Even more surprisingly, amino acids with –CH₃ → –CH₂F/–CHF₂ and –CH₂– → –CF₂– substitutions (here termed partially fluorinated) display a range of ΔΔG_Hyd values from −1.5 kcal mol⁻¹ to +1 kcal mol⁻¹, regardless of the number of fluorine atoms. ΔΔG_Hyd depends strongly and non-intuitively on the chirality (R/S) and location (γ vs. δ) of the fluorinated sites, and on the identity of the amino acid.

Calculated ΔG_Hyd for fluorinated C1–C3 alkanes compares well with experiment

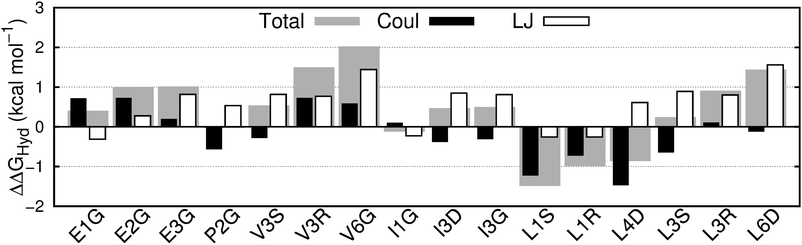
Experimental hydration free energies for amino acids are not available, so we cannot directly assess the accuracy of our predictions. To test the accuracy of our force field, we applied it to all fluorinated variants of methane, ethane and propane for which experimental hydration free energies could be found.⁵⁸ These small molecules are the closest analogues to the side chains of the amino acids investigated here. The free energies of hydration for the fluorinated small molecules are shown in Fig. 3 and ESI† Table 4. We show also the free energies of hydration of methane, ethane and propane, to illustrate the accuracy of the AMBER force field for the alkyl side chains of amino acids. The force field for fluorinated molecules reproduces the experimental hydration free energy very well in most cases. The Average Unsigned Error (AUE) is 0.25 kcal mol⁻¹, lower than reported previously for fluorinated molecules: AUE = 0.36 kcal mol⁻¹ for 4 fluorinated (aromatic) molecules using a permanent multipole charge model for the molecules and the TIP3P water model;⁴¹ AUE = 0.5 to 0.9 kcal mol⁻¹ for 6 fluorinated (primarily aliphatic) molecules using various version of the GAFF, CHARMM and OPLS force fields and SPC or TIP3P water.^59–61 The largest deviation using our model is seen for CH₃F, whose ΔG_Hyd is 0.7 kcal mol⁻¹ too negative. Differences between di- and trifluorinated amino acids should be well captured, but monofluorinated alkyl groups are likely excessively hydrophilic in our model.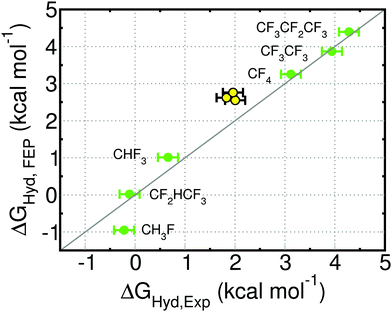

Fig. 3 Free energy of hydration (ΔG_Hyd) of the indicated fluorinated molecules (green), and of methane, ethane and propane (yellow) obtained with simulation (FEP) or experimentally (Exp.; from ref. 58). CF₄ and CHF₃ were used during parameterization. The statistical uncertainty in the FEP values is the size of the symbol. See ESI† Table 4 for free energy values.

The predicted hydration free energies for methane, ethane and propane are too positive by 0.5 to 0.8 kcal mol⁻¹. These results suggest that the predicted ΔΔG_Hyd for amino acids (Fig. 2) may be systematically too negative by 0.5 to 0.8 kcal mol⁻¹. The AMBER force field for proteins, upon which we build the force field for fluorinated amino acids, has been extensively improved for decades and is able to reproduce experimentally-measured structure and dynamics of folded small proteins.^62–68 Efforts to continue developing this force field are on-going in multiple groups⁶⁸ and are now preferentially driven by experimental data on peptides and both folded and intrinsically disordered proteins, rather than on small molecules. Given the state-of-the-art, we opted to keep the Lennard-Jones parameters for the alkane side chains.

Despite these quantitative deviations between our calculated ΔG_Hyd and experiment, our model yields the correct trend in hydrophobicity for all small molecules, fluorinated or not. Our main result – the large dependence of ΔΔG_Hyd,FEP on the identity of the amino acid and characteristics of the fluorinated site – is not affected by these force field shortcomings. Below we show that this dependence is in fact largely due to fluorination-induced conformational changes that alter the number of backbone–water hydrogen bonds. Fluorination-induced changes in conformation in our simulations result from steric hindrance and favorable electrostatic carbonyl–CF interactions, both of which can be captured, at least qualitatively, by all-atom, fixed charge force fields.

The surprising variation in ΔΔG_Hyd is largely coulombic in origin

Decomposing the hydration free energy into Lennard-Jones and coulombic contributions can be naturally done in simulations, and gives valuable insight into the origin of the observed trends. The Lennard-Jones contribution to ΔΔG_Hyd (Fig. 2) is constant and positive per fully fluorinated group, positive but not constant for difluorinated amino acids and negative and constant for monofluorinated amino acids. Despite this variation in the LJ contribution to the free energy of hydration, the wide variation in ΔΔG_Hyd, particularly in the case of the partially fluorinated amino acids, is actually dominated by the coulombic contribution to the free energy. This contribution varies seemingly unpredictably (Fig. 2), with each type of fluorination leading to either positive or negative ΔΔG^Coul_Hyd: e.g., compare E2G with P2G, E1G with L1S, L1R and I1G, V3S with V3R. Previous reports on the dependence of lipophilicity on fluorine-induced polarity changes support the idea that the contribution of electrostatics to hydrophobicity is far from intuitive.^69,70 Neither contribution shows visible correlation with local hydration around the fluorinated site, as measured by the radial distribution function of water around the fluorinated sites (ESI† Section 5.2.4, Fig. 8A and B).

Developing an analytical solvation model to understand how fluorination affects ΔG_Hyd

Can we understand the origin of these hydration free energies? To answer this question we model the fluorination-induced change in hydration free energy in terms of linear, multivariate models of the form , where k_i are fitting parameters and Y_i are observables that should affect the hydration free energy and can be easily calculated in short molecular dynamics simulations. The LJ contribution to ΔΔG_Hyd is dominated by the energy (work) required to form a solute-sized cavity in water to accommodate the larger fluorine atoms. This contribution (Table 1) is proportional to the change in solvent accessible surface area (ΔSASA) of the amino acid,^71,72 and can be easily quantified by measuring ΔSASA in molecular dynamics simulations, and multiplying it by the LJ component of ΔG_Hyd per surface area unit of methane, which is essentially identical to that of CF₄ (ESI† Table 9).

Table 1 Values of the fitting parameters from eqn (1), and associated standard errors and P-values

Fitting parameter	Value	Error	P-value
NA: not applicable.a Calculated via error propagation.
k 1 (ΔA; kcal mol^−1 Å^−2)	0.053	0.001^a	NA
k 2 (ΔhCO; kcal mol^−1 H-bond^−1)	−3.590	0.350	0.000
k 3 (ΔhNH; kcal mol^−1 H-bond^−1)	−3.020	0.780	0.012
k 4 (ΔΦ^+; kcal mol^−1 H2O^−1)	0.115	0.044	0.022
k 5 (hCH2F; kcal mol^−1 H-bond^−1)	−2.619	0.396	0.000
k 6 (hCF2; kcal mol^−1 H-bond^−1)	−1.808	0.270	0.000
k 7 (hCF3; kcal mol^−1 H-bond^−1)	−0.780	0.222	0.004

---

The polar contribution is dominated by the interaction of a distribution of atom-centered point charges with water. This contribution can be estimated in multiple manners.^33,69,70,73 We first attempted to model the polar contribution as the sum of three terms, one proportional to a global quantity, the dipole moment μ, representing the molecular charge distribution, and the other two proportional to local quantities, the number of hydrogen bonds between water and amines (h_NH) or carbonyls (h_CO) in the backbone.‡ Fitting the ΔΔG_Hyd values calculated with FEP using a linear multivariate model (ESI† eqn (5)) consisting of the sum of the contributions arising from changes in SASA, μ, h_NH, and h_CO due to fluorination was unsuccessful: the resulting fitting parameters had unphysical values, e.g., a positive energetic contribution of the dipole moment, and overly large errors (ESI† Table 6). We also attempted to model our data using an analogous version of this model, but where the area term reflects the difference in hydration free energy between CH₄ and CF₄. This second model (ESI† eqn (6)) has proven successful to understand hydrophobicity of tri- and hexa-fluorinated amino acids,³³ but it fails (ESI† Fig. 4) when applied to the partially fluorinated amino acids. Given that the contributions of solute–water hydrogen bonds and the Lennard-Jones interactions to the hydration free energies are well-known,^33,71,73 we interpret these results as an inability of the molecular dipole moment to describe electrostatic solute–water interactions in a quantitative manner, at least for solutes as diverse as the current set of amino acids. We next attempted to characterize how fluorination alters the solute–water electrostatic interactions with another commonly used global descriptor: solving the linearized Poisson–Boltzmann (PB) equation, where the solvent is modeled as a continuum, as described in ESI† Section 3.1. Given the apparently simple problem we were trying to model, we were surprised to find that the electrostatic component of the hydration free energy calculated using PB hardly correlates with the reference FEP values (ESI† Fig. 2A). The absence of correlation suggests that it is imperative to model the solvent as discrete water molecules. Thus, when aiming for a correct characterization of how aqueous solvation of biopolymers changes with mutations, not only the solute but also the solvent must be modeled without the use of global or mean-field descriptors.

Backbone–water hydrogen bonds dominate the polar interactions between the backbone and water;⁷³ the unresolved issue is how to describe polar interactions between the side chain and water. We find that these can be characterized by the electrostatic potential, Φ, at the position of the water oxygen atoms in the first hydration shell of the side chains, as described in ESI† Section 4. The corresponding probability distributions of Φ for the fluorinated amino acids, shown in ESI† Fig. 2B–F, show large negative potential regions together with, in some cases, regions of more positive potentials than observed for the parent amino acid. The more positive potential, almost exclusive to mono- and difluorinated species, arises from a larger exposure of the positively charged carbon skeleton of the side chain, left partially unshielded by hydrogen in mono- and difluorinated groups (see ESI† Section 4 and Fig. 3). The negative potential region, observed for all amino acids, can be attributed to the fluorine atoms. Water molecules near fluorine atoms often assume configurations that meet the geometric criteria for HOH⋯FC hydrogen bonds, as discussed in ESI† Section 5.2, so we consider that these weak hydrogen bonds exist. This interpretation is consistent with ab initio calculations, and spectroscopic measurements;^74–77 the strong correlation between ¹⁹F NMR isotropic chemical shifts and the type of fluorine–protein interactions observed in the Protein Data Bank also suggest that hydrogen bonds to fluorinated alkyl groups exist, and are strongest for groups with low degrees of fluorination,⁷⁸ as we also observe (ESI† Table 7).

Our final model (eqn (1)) reflects the above results. We capture the impact of the fluorination-induced differences on side chain–water electrostatic interactions in two ways, via the average number of water–fluorine hydrogen bonds established by each amino acid (the h_CHnFm terms, where n = 0, 1, 2 and m = 1, 2, 3, in eqn (1)) and via the fluorination-induced change in the number of water molecules experiencing the positive potential region of the side chain (the ΔΦ⁺ term in eqn (1)). Fitting eqn (1) to the ΔΔG_Hyd data shown in Fig. 2 yields the parameters in Table 1; see ESI† Section 5.2 for details of the fit.

ΔΔG_Hyd = k₁ΔA + k₂Δh_CO + k₃Δh_NH + k₄ΔΦ⁺ + k₅h_CH2F + k₆h_CF2 + k₇h_CF3 (1)

Fig. 4 shows the correlation between the FEP-calculated hydration free energies and the ones calculated using eqn (1). The model describes the changes in ΔG_Hyd following fluorination well for most cases, with an adjusted R-squared of 0.86 and an AUE = 0.26 kcal mol⁻¹. Poorer agreement occurs for E1G, for which it yields a value of ΔΔG_Hyd which deviates 0.5 kcal mol⁻¹ from the value given by the FEP simulations and actually has the wrong sign, and for E2G, L4D and L3S, for which deviations are 0.7, 0.5 and 0.5 kcal mol⁻¹ each. Our prior work suggests that the source of these large deviations might be entropic,³³ and we speculate it might be related to changes in solute conformational entropy, which are not included in eqn (1). Clarifying this point is outside the scope of the present work. The systematic error expected in ΔΔG_Hyd,FEP because of the inaccuracy associated with the AMBER force field for alkane side chains (see Fig. 3 and associated discussion above) does not jeopardize the good correlation seen in Fig. 4. That systematic error is also present in ΔΔG_Hyd,model, in the k₁ term associated with the change in area. Future applications of eqn (1) to force field versions that better reproduce the hydration free energies of alkanes can easily be done by re-optimizing the k₁ term.

Fig. 4 Correlation between the hydration free energy differences between fluorinated and non-fluorinated amino acids calculated with FEP (ΔΔG_Hyd,FEP) or eqn (1) (ΔΔG_Hyd,model). Data points are presented as mean ± standard deviation of five independent simulations. The color code indicates the number of fluorine atoms: red = one; yellow = two; green = three; cyan = four; blue = six. The gray line indicates perfect correlation.

Decomposing the contributions to ΔΔG_Hyd

The performance of the multivariate model is sufficiently good to enable insight into the mechanisms of fluorination-induced changes in solvation, by decomposing the individual contributions to ΔΔG_Hyd as seen in Fig. 5.

Fig. 5 Contribution of the changes in surface area (ΔA), hydrogen bonds between water and carbonyls (Δh_CO) or amines (Δh_NH), water molecules exposed to a large positive electrostatic potential (ΔΦ⁺) and hydrogen bonds between water and fluorine in mono- (h_CH2F), di- (h_CF2) or trifluorinated (h_CF3) amino acids to the total change in hydration free energy (ΔΔG_Hyd), between fluorinated and non-fluorinated amino acids, calculated using eqn (1).

Surface area. Within derivatives of the same amino acid, the surface area increases ΔΔG_Hyd proportionally to the number of fluorine atoms (ESI† Fig. 5). The magnitude of the increase per fluorine atom depends on the amino acid identity, which implies that the hydration shells around each side chain are disturbed to a different degree, when accommodating the hydrogen → fluorine substitution – compare, e.g. E2G with P2G.

Backbone–water hydrogen bonds. The contribution of hydrogen bonds between water and carbonyl groups is always positive because fluorination reduces the number of these hydrogen bonds by steric blockage. The magnitude of this contribution, for fluorinated variants of a given amino acid, is again proportional to the number of fluorine atoms in the side chain. In contrast, the contribution of amine–water hydrogen bonds varies between positive and negative because fluorination may increase or decrease the number of these hydrogen bonds. Steric blockage occurs because of fluorine's large size and, for some amino acids, because fluorination changes the preferential conformation of the side chain as discussed in ESI† Section 6. These results are consistent with previous reports indicating that CF and carbonyl groups interact favorably,^79,80 and that changes in the conformational preference of fluorinated alkyl groups affect a molecule's lipophilicity, membrane permeability and inhibitory activity.^25,81,82

Side-chain polarity. The most interesting contributions arise from the polarity of the fluorinated side chain. The large, positive electrostatic potential affecting hydration waters adds an average +0.4 kcal mol⁻¹ to the ΔΔG_Hyd of all partially fluorinated amino acids, and a near-zero, positive, contribution to the trifluorinated amino acids; the largest deviations come from I1G and I3D, for which this contribution is +0.8 kcal mol⁻¹. As indicated above, this contribution stems from the partial shielding of the positively charged carbons occurring in partially fluorinated groups. Regarding the water–fluorine hydrogen bonds, they are much weaker than those with the carbonyl or amine groups, and decrease in stability in the order –CH₂F > –CHF₂/–CF₂– > –CF₃, as indicated by the relative magnitudes of the relevant parameters in Table 1. These trends are expected: our simulations show that the distance between the water oxygen and the fluorine is smaller in groups with fewer fluorines (ESI† Table 7) indicating an increase in hydrogen bond strength, and other experiments and ab initio calculations have shown the same trends.^78,83 Despite the weakness of the hydrogen bonds between water and the di- and tri-fluorinated groups, they nevertheless play an important role: e.g., they are present ≈15% of the time per fluorine in CF₃ groups (ESI† Table 8); for comparison, the number of water–methyl configurations per side chain CH group meeting the hydrogen bond criteria in the non-fluorinated amino acids is almost negligible (≈3%). The magnitude of the hydrogen bond contributions to ΔΔG_Hyd per fluorine atom also follows the order –CH₂F > –CHF₂/–CF₂– > –CF₃, with the average values being −1.79, −0.60 and −0.13 kcal mol⁻¹ per fluorine, respectively;§ the weak water–fluorine hydrogen bonds to –CF₃ contribute on average a non-negligible −0.39 kcal mol⁻¹ –CF₃⁻¹.

Contributions of the side chain to ΔΔG_Hyd are largely constant per CF_x substituent

The values of the free energy contribution per water–fluorine hydrogen bond yielded by the multivariate model anticorrelate surprisingly well with the LJ contribution of the area per fluorine atom (ESI† Fig. 6), suggesting that the energy cost associated with (overall repulsive) water–fluoromethyl LJ interactions is partially offset by the energy gain from the formation of water–fluorine hydrogen bonds. This point is illustrated in Fig. 6, where the ratio of the area and water–fluorine hydrogen bond contributions is plotted against the number of fluorine atoms. It is clear that the contribution of each fluorinated group to the hydration free energy is fairly constant. P2G, bearing the only non-terminal fluorination site in this set of amino acids, has a much lower cavity-forming penalty, thereby escaping this trend. The notable dependency of ΔΔG_Hyd on the chirality and location of the fluorinated site and the identity of the amino acids cannot be explained solely in terms of local changes in solvation around the fluorinated site.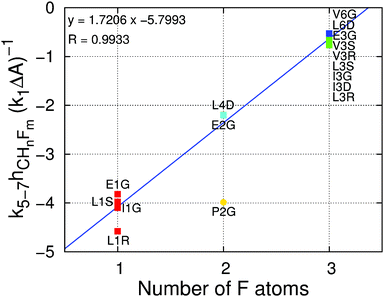

Fig. 6 Ratio of the contribution of the water–fluorine hydrogen bonds to the contribution of the surface area to the ΔΔG_Hyd (k_5–7h_CHnFm(k₁ΔA)⁻¹) versus the number of fluorine atoms per fluoromethyl group. Contributions are calculated using eqn (1). The color code indicates the number of fluorine atoms: red = one; yellow = two; green = three; cyan = four; blue = six. The blue line is a linear fit to the data points (excluding P2G, shown as a circle) with the corresponding equation and regression coefficient at the top left.

For one hydrogen → fluorine substitution, the hydrogen bonding over-compensates the cavity-formation cost. As the number of substitutions increases, the penalty for cavity formation per fluorine is reduced, showing that the perturbation due to the insertion of the first fluorine atom is large but further insertions perturb the water network to a smaller extent. Simultaneously, the energy gain per fluorine from water–fluorine hydrogen bonds is decreased for multiple fluorine insertions, likely due to the less negative partial charges on fluorine and the fewer H_F atoms, which interact favorably with water (see ESI† Section 2.3). Interestingly, there is a crossover point, associated with the number of fluorine substitutions, after which the energy cost surpasses the energy gain; in other words, there is a transition between a locally hydrophilic moiety to a locally hydrophobic moiety. Inspecting Fig. 6 we find that the number of fluorine atoms required to perform the transition is 2.8. This crossover point has associated uncertainty arising from the systematic deviations in the hydration free energies observed for small alkanes with the GAFF/Amber force field (see Fig. 3 and discussion above). Even considering this uncertainty, it appears that trifluoromethyl groups, by themselves, impart only a small increase in amino acid hydrophobicity, because the positive Lennard-Jones component of the hydration free energy is partially offset by the weak but still favorable water–fluorine hydrogen bonds.

RDFs of water around the fluorinated site do not give insight into local contributions to the ΔG_Hyd

Given that the impact of fluorination on local solvation is fairly constant for groups with the same number of fluorine atoms (Fig. 6), we investigated whether these local changes in solvation correlate well with the radial distribution function (RDF) of water around methyl or fluoromethyl groups. Specifically, we calculated the excess free energy, ΔΔG_Shell,PMF, necessary to populate the first hydration layer of methyl or fluoromethyl groups from the potential of mean force associated with each radial distribution function. Our results (ESI† Section 5.2.4 and Fig. 8C) show that such a correlation is at best very weak. We could also not find correlations between ΔΔG_Shell,PMF and the Coulomb and Lennard-Jones components of the hydration free energy (ESI† Fig. 8A and B). Radial distribution functions describe solvation along a single reaction coordinate, which may be insufficient to give quantitative or semi-quantitative insight into local hydrophobicity. In contrast, proximal radial distribution functions – those calculated perpendicular to the surface of the molecule – appear near universal for proteins⁸⁴ and have proven useful to estimate hydration free energies of small molecules and peptides.^85,86 Exploring their usefulness for fluorinated molecules is outside the scope of the present work.

4 Concluding remarks

We present an all-atom, fixed-charge force field for amino acids with fluorinated alkyl side chains that is compatible with the AMBER force field for proteins. With it we investigate how mono-, di- and trifluorination alter amino acid solvation. Our predictions indicate that side chain fluorination alters the hydration free energy of amino acids in surprising ways: ΔΔG_Hyd strongly depends on the chirality and location of the fluorinated site and on the identity of the amino acid. Using a simple, analytical solvation model (eqn (1)), we trace back these dependencies to the multiple mechanisms by which fluorination modifies solvation of amino acids: there is a cost of introducing larger fluorine atoms, gains and costs associated with the higher polarity of fluorinated alkyl groups, and gains or costs from altering the number of backbone–water hydrogen bonds as a result of changed conformational preferences. For small molecules, it is often possible to predict the sign and even estimate the magnitude of the change in hydrophobicity upon fluorination. In contrast, for complex molecules ‘the devil is in the details’: the contribution of each mechanism to the overall hydrophobicity depends on conformational preferences and interactions between different parts of the molecule, making rules-of-thumb insufficient. For example, monofluorination does not always make amino acids more hydrophilic; similar increases in the solvent-exposed surface area of different molecules do not imply that the molecules will experience similar increases in hydrophobicity. Solvent accessible surface area descriptors of hydration free energies remain useful for complex molecules, but only when other contributions are properly accounted for.

The parameter values associated with the solvation model we present will be quantitatively affected by inaccuracies in the force field, but the necessity of this type of approach, the functional form of the solvation model, and the importance of conformational changes and of backbone–water interactions in the non-intuitive variation of ΔG_Hyd with fluorination will remain.

Molecular dynamics studies with custom-tailored force fields and phenomenological solvation models based on discrete rather than mean-field descriptors are key to gain mechanistic insight on solvation, as exemplified in this work. The force field and solvation model we present lay the foundation to interpret how fluorination alters the hydrophobicity of other (bio)polymers. In its current form, the force field can be used to gain semi-quantitative insight on how fluorination affects packing in the hydrophobic core, or the contribution of water-protein interactions to protein stability. Further developing the force field for fluorinated proteins will require the experimental determination of the structure of both folded and intrinsically disordered proteins, the solubility of small peptides, and the free energies of hydration of amino acids or molecules of similar complexity. If the vapor pressure of the pure compound in liquid form is known together with its aqueous solubility, the free energy of hydration can be immediately calculated assuming ideality.⁵⁸ We deliberately restricted the present study to amino acids for which synthesis protocols exist,¹⁹ and we hope that a direct comparison between experiment and simulation will be possible in the future.

The solvation model given by eqn (1) and applied here to amino acids can also be used to interpret molecular dynamics results of other small molecules containing the same functional groups, and extended for other functional groups. The solvation model is also directly relevant for proteins: together with short molecular dynamics simulations of proteins in the folded and unfolded ensembles, it can be used to gain quick insight into how fluorination-induced changes in protein–water interactions contribute to changes in the free energy of folding. Good sampling of the folded protein ensemble can easily be achieved in many cases with molecular dynamics simulations; to sample the unfolded protein ensemble, one can take advantage of a number of algorithms.^87–91 Future work by our group will attempt to extend the solvation model to include mechanisms by which fluorination alters intra-protein non-bonded interactions. This extension is necessary to obtain a complete picture of the mechanisms by which fluorination alters the thermal stability of proteins.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

JRR was funded by the International Max Planck Research School on Multiscale Bio-Systems. We thank Marco Ehlert and René Genz from the IT team of the MPIKG for their help. We thank Dr Valerio Molinari and Dr Alexandra Latnikova for their critical reading of the manuscript. Open Access funding provided by the Max Planck Society.

References

1. R. Zhou, X. Huang, C. J. Margulis and B. J. Berne, Science, 2004, 305, 1605–1609.
2. R. C. Harris and B. M. Pettitt, J. Phys.: Condens. Matter, 2016, 28, 083003.
3. E. N. G. Marsh, Acc. Chem. Res., 2014, 47, 2878–2886.
4. C. N. Pace, H. Fu, K. L. Fryar, J. Landua, S. R. Trevino, B. A. Shirley, M. M. Hendricks, S. Iimura, K. Gajiwala, J. M. Scholtz and G. R. Grimsley, J. Mol. Biol., 2011, 408, 514–528.
5. S. Ye, B. Loll, A. A. Berger, U. Mülow, C. Alings, M. C. Wahl and B. Koksch, Chem. Sci., 2015, 6, 5246–5254.
6. A. M. Davis and S. J. Teague, Angew. Chem., Int. Ed., 1999, 38, 736–749.
7. D. Ben-Amotz, J. Phys. Chem. Lett., 2015, 6, 1696–1701.
8. D. Ben-Amotz, Annu. Rev. Phys. Chem., 2016, 67, 617–638.
9. K. A. Brogden, Nat. Rev. Microbiol., 2005, 3, 238–250.
10. M. Zasloff, Nature, 2002, 415, 389–395.
11. S. T. Henriques, M. N. Melo and M. A. R. B. Castanho, Biochem. J., 2006, 399, 1–7.
12. Y.-W. Cui, H.-Y. Zhang, J.-R. Ding and Y.-Z. Peng, Sci. Rep., 2016, 6, 24825.
13. B. J. Harris, X. Cheng and P. Frymier, J. Phys. Chem. B, 2016, 120, 599–609.
14. B. C. Buer, J. L. Meagher, J. A. Stuckey and E. N. G. Marsh, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4810–4815.
15. B. C. Buer, J. L. Meagher, J. A. Stuckey and E. N. G. Marsh, Protein Sci., 2012, 21, 1705–1715.
16. A. A. Berger, J.-S. Völler, N. Budisa and B. Koksch, Acc. Chem. Res., 2017, 50, 2093–2103.
17. F. Agostini, J.-S. Völler, B. Koksch, C. G. Acevedo-Rocha, V. Kubyshkin and N. Budisa, Angew. Chem., Int. Ed., 2017, 56, 9680–9703.
18. N. C. Yoder and K. Kumar, Chem. Soc. Rev., 2002, 31, 335–341.
19. M. Salwiczek, E. K. Nyakatura, U. I. Gerling, S. Ye and B. Koksch, Chem. Soc. Rev., 2012, 41, 2135–2171.
20. M. Oliver, C. Gadais, J. García-Pindado, M. Teixidó, N. Lensen, G. Chaume and T. Brigaud, RSC Adv., 2018, 8, 14597–14602.
21. V. Asante, J. Mortier, H. Schlüter and B. Koksch, Bioorg. Med. Chem., 2013, 21, 3542–3546.
22. H. Meng and K. Kumar, J. Am. Chem. Soc., 2007, 129, 15615–15622.
23. C. Jäckel, M. Salwiczek and B. Koksch, Angew. Chem., Int. Ed., 2006, 45, 4198–4203.
24. T. Liang, C. N. Neumann and T. Ritter, Angew. Chem., Int. Ed., 2013, 52, 8214–8264.
25. E. P. Gillis, K. J. Eastman, M. D. Hill, D. J. Donnelly and N. A. Meanwell, J. Med. Chem., 2015, 58, 8315–8359.
26. G. Pupo, F. Ibba, D. M. H. Ascough, A. C. Vicini, P. Ricci, K. E. Christensen, L. Pfeifer, J. R. Morphy, J. M. Brown, R. S. Paton and V. Gouverneur, Science, 2018, 360, 638–642.
27. J.-S. Völler, M. Dulic, U. I. Gerling-Driessen, H. Biava, T. Baumann, N. Budisa, I. Gruic-Sovulj and B. Koksch, ACS Cent. Sci., 2016, 3, 73–80.
28. M. Imiołek, G. Karunanithy, W.-L. Ng, A. J. Baldwin, V. E. Gouverneur and B. G. Davis, J. Am. Chem. Soc., 2018, 140, 1568–1571.
29. R. L. Baldwin, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 13052–13056.
30. D. Chandler, Nature, 2005, 437, 640–647.
31. H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, J. Chem. Phys., 2004, 120, 9665–9678.
32. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713.
33. J. R. Robalo, S. Huhmann, B. Koksch and A. Vila Verde, Chem, 2017, 3, 881–897.
34. W. L. Jorgensen and P. Schyman, J. Chem. Theory Comput., 2012, 8, 3895–3901.
35. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757.
36. P. Metrangolo, J. S. Murray, T. Pilati, P. Politzer, G. Resnati and G. Terraneo, Cryst. Growth Des., 2011, 11, 4238–4246.
37. K. El Hage, T. Bereau, S. Jakobsen and M. Meuwly, J. Chem. Theory Comput., 2016, 12, 3008–3019.
38. M. A. A. Ibrahim, J. Phys. Chem. B, 2012, 116, 3659–3669.
39. M. Carter, A. K. Rappé and P. S. Ho, J. Chem. Theory Comput., 2012, 8, 2461–2473.
40. T. Bereau, C. Kramer and M. Meuwly, J. Chem. Theory Comput., 2013, 9, 5450–5459.
41. F. Hédin, K. El Hage and M. Meuwly, J. Chem. Inf. Model., 2016, 56, 1479–1489.
42. H. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56.
43. E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model., 2001, 7, 306–317.
44. D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
45. B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
46. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
47. S. Páll, M. J. Abraham, C. Kutzner, B. Hess and E. Lindahl, International Conference on Exascale Applications and Software, 2014, pp. 3–27.
48. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25.
49. D. A. Case, V. Babin, J. T. Berryman, R. M. Betz, Q. Cai, D. S. Cerutti, T. E. Cheatham III, T. A. Darden, R. E. Duke, H. Gohlke, A. W. Goetz, S. Gusarov, N. Homeyer, P. Janowski, J. Kaus, I. Kolossváry, A. Kovalenko, T. S. Lee, S. LeGrand, T. Luchko, R. Luo, B. Madej, K. M. Merz, F. Paesani, D. R. Roe, A. Roitberg, C. Sagui, R. Salomon-Ferrer, G. Seabra, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu and P. A. Kollman, AMBER 14, 2014.
50. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
51. J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
52. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 1989.
53. H. J. Berendsen, J. v. Postma, W. F. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
54. C. H. Bennett, J. Comput. Phys., 1976, 22, 245–268.
55. M. R. Shirts, E. Bair, G. Hooker and V. S. Pande, Phys. Rev. Lett., 2003, 91, 140601.
56. N. A. Baker, D. Sept, S. Joseph, M. J. Holst and J. A. McCammon, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10037–10041.
57. C. Gadais, E. Devillers, V. Gasparik, E. Chelain, J. Pytkowicz and T. Brigaud, ChemBioChem, 2018, 19, 1026–1030.
58. A. V. Marenich, C. P. Kelly, J. D. Thompson, G. D. Hawkins, C. C. Chambers, D. J. Giesen, P. Winget, C. J. Cramer and D. G. Truhlar, Minnesota Solvation Database – version 2012, 2012.
59. D. Shivakumar, Y. Deng and B. Roux, J. Chem. Theory Comput., 2009, 5, 919–930.
60. D. Shivakumar, J. Williams, Y. Wu, W. Damm, J. Shelley and W. Sherman, J. Chem. Theory Comput., 2010, 6, 1509–1519.
61. D. Shivakumar, E. Harder, W. Damm, R. A. Friesner and W. Sherman, J. Chem. Theory Comput., 2012, 8, 2553–2558.
62. D. E. Shaw, P. Maragakis, K. Lindorff-Larsen, S. Piana, R. O. Dror, M. P. Eastwood, J. A. Bank, J. M. Jumper, J. K. Salmon, Y. Shan and W. Wriggers, Science, 2010, 330, 341–346.
63. K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins, 2010, 78, 1950–1958.
64. K. Lindorff-Larsen, N. Trbovic, P. Maragakis, S. Piana and D. E. Shaw, J. Am. Chem. Soc., 2012, 134, 3787–3791.
65. K. A. Beauchamp, Y.-S. Lin, R. Das and V. S. Pande, J. Chem. Theory Comput., 2012, 8, 1409–1414.
66. S. Piana, J. L. Klepeis and D. E. Shaw, Curr. Opin. Struct. Biol., 2014, 24, 98–105.
67. P. Robustelli, S. Piana and D. E. Shaw, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E4758–E4766.
68. P. S. Nerenberg and T. Head-Gordon, Curr. Opin. Struct. Biol., 2018, 49, 129–138.
69. Q. A. Huchet, B. Kuhn, B. Wagner, H. Fischer, M. Kansy, D. Zimmerli, E. M. Carreira and K. Müller, J. Fluorine Chem., 2013, 152, 119–128.
70. Q. A. Huchet, B. Kuhn, B. Wagner, N. A. Kratochwil, H. Fischer, M. Kansy, D. Zimmerli, E. M. Carreira and K. Müller, J. Med. Chem., 2015, 58, 9041–9060.
71. C. Tan, Y.-H. Tan and R. Luo, J. Phys. Chem. B, 2007, 111, 12263–12274.
72. V. H. Dalvi and P. J. Rossky, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13603–13607.
73. C. A. Hunter, Chem. Sci., 2013, 4, 1687–1700.
74. S. Mondal, B. Biswas, T. Nandy and P. C. Singh, Phys. Chem. Chem. Phys., 2017, 19, 24667–24677.
75. W. Caminati, S. Melandri, I. Rossi and P. G. Favero, J. Am. Chem. Soc., 1999, 121, 10098–10101.
76. H.-J. Schneider, Chem. Sci., 2012, 3, 1381–1394.
77. J. Thomas, N. A. Seifert, W. Jäger and Y. Xu, Angew. Chem., Int. Ed., 2017, 56, 6289–6293.
78. C. Dalvit and A. Vulpetti, ChemMedChem, 2011, 6, 104–114.
79. J. A. Olsen, D. W. Banner, P. Seiler, B. Wagner, T. Tschopp, U. Obst-Sander, M. Kansy, K. Müller and F. Diederich, ChemBioChem, 2004, 5, 666–675.
80. D. O'Hagan, Chem. Soc. Rev., 2008, 37, 308–319.
81. Q. A. Huchet, W. B. Schweizer, B. Kuhn, E. M. Carreira and K. Müller, Chem. – Eur. J., 2016, 22, 16920–16928.
82. Q. A. Huchet, N. Trapp, B. Kuhn, B. Wagner, H. Fischer, N. A. Kratochwil, E. M. Carreira and K. Müller, J. Fluorine Chem., 2017, 198, 34–46.
83. R. E. Rosenberg, J. Phys. Chem. A, 2012, 116, 10842–10849.
84. B. Lin and B. M. Pettitt, J. Chem. Phys., 2011, 134, 106101.
85. B. Lin, K.-Y. Wong, C. Hu, H. Kokubo and B. M. Pettitt, J. Phys. Chem. Lett., 2011, 2, 1626–1632.
86. S.-C. Ou and B. M. Pettitt, J. Phys. Chem. B, 2016, 120, 8230–8237.
87. T. P. Creamer, R. Srinivasan and G. D. Rose, Biochemistry, 1995, 34, 16245–16250.
88. N. C. Fitzkee and G. D. Rose, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 12497–12502.
89. J. Estrada, P. Bernado, M. Blackledge and J. Sancho, BMC Bioinf., 2009, 10, 104.
90. Y. Seki, Y. Shimbo, T. Nonaka and K. Soda, J. Chem. Theory Comput., 2011, 7, 2126–2136.
91. S. A. Ali, M. I. Hassan, A. Islam and F. Ahmad, Curr. Protein Pept. Sci., 2014, 15, 456–476.

---

Footnotes

† Electronic supplementary information (ESI) available: Description of force fields and simulation details, hydration free energies, electrostatic potential in the vicinity of amino acid side chains, linear models to reproduce the calculated hydration free energies, radial distribution functions, conformational changes in fluorinated side chains. AMBER-format force fields for mono- and di-fluorinated amino acids. See DOI: 10.1039/c8cp07025c

‡ Hydrogen bonds exist if the donor–acceptor distance <3.5 Å and the donor-hydrogen-acceptor angle is between 135° and 180°.

§ Values calculated from the relevant h_CHmFn values in ESI† Table 8 and the corresponding k parameter in Table 1.

---