Extremely large differences in DFT energies for nitrogenase models

Abstract

Nitrogenase is the only enzyme that can cleave the triple bond in N₂, making nitrogen avaiable for other organisms. It contains a complicated MoFe₇S₉C(homocitrate) cluster in its active site. Many computational studies with density-functional theory (DFT) of the nitrogenase enzyme have been presented, but they do not show any consensus – they do not even agree where the first four protons should be added, forming the central intermediate E₄. We show that the prime reason for this is that different DFT methods give relative energies that differ by almost 600 kJ mol⁻¹ for different protonation states. This is 4–30 times more than what is observed for other systems. The reason for this is that in some structures, the hydrogens bind to sulfide or carbide ions as protons, whereas in other structures they bind to the metals as hydride ions, changing the oxidation state of the metals, as well as the Fe–C, Fe–S and Fe–Fe distances. The energies correlate with the amount of Hartree–Fock exchange in the method, indicating a variation in the amount of static correlation in the structures. It is currently unclear which DFT method gives the best results for nitrogenase. We show that non-hybrid DFT functionals and TPSSh give the most accurate structures of the resting active site, whereas B3LYP and PBE0 give the best H₂ dissociation energies. However, no DFT method indicates that a structure of E₄ with two bridging hydride ions is lowest in energy, as spectroscopic experiments indicate.

---

Introduction

Nitrogenase (EC 1.18/19.6.1) is the only enzyme in nature that can cleave the triple bond in N₂ to form ammonia and make nitrogen available for cell metabolism.^1–3 It is present in a few groups of bacteria and archaea.^1–3 The nitrogenase reaction is essential to the life on earth – although 78% of the atmosphere is N₂, nitrogen is often the limiting factor for plant growth and a main component of synthetic fertilisers.³ In fact, the industrial Haber–Bosch process to form ammonia consumes ∼1% of the world's energy supplies, produces half of the total biologically available nitrogen on earth⁴ and is a major factor in the recent human population explosion.³

Crystallographic studies have shown that the nitrogenase is a large α₂β₂ heterotetramer.^5–9 The catalytic centre is the MoFe₇S₉C(homocitrate) FeMo cluster bound to the protein by a cysteine and a histidine residue. In some enzymes, the Mo ion is replaced by vanadium or iron.¹⁰ The protein also contains a Fe₈S₇Cys₆ cluster, called the P cluster, which transfers electrons. The electrons are provided by another protein, called the Fe protein, which binds two ATP molecules. Hydrolysis of the ATP molecules triggers the dissociation of the Fe protein, opening up for additional electron transfers.

Nitrogenase catalyses the N₂ + 8e⁻ + 8H⁺ + 16ATP → 2NH₃ + H₂ + 16ADP + 16P_i reaction. It is typically described by the Lowe–Thorneley scheme, involving nine intermediates, E₀–E₈, differing in the number of electrons and protons delivered to the enzyme.¹¹ Nitrogenase has been extensively studied by a great wealth of biochemical, spectroscopic and kinetic methods and several of the intermediates have been trapped and characterised.^1–3,12,13 Of particular interest is E₄, which is believed to be the species that binds N₂ concomitant with the release of H₂ by reductive elimination.³

The experimental studies have been supplemented by many density functional theory (DFT) studies, which can give an detailed atomistic and energetic picture of the reaction mechanism.^3,13–26 Unfortunately, they have led to strongly diverging mechanistic suggestions. For example, some studies have proposed that N₂ is sequentially protonated first on one N atom, which dissociates into NH₃ before the second atom is protonated,^23,25 whereas other studies have suggested that it is alternatively protonated on the two N atoms, forming N₂H₂ and N₂H₄ intermediates.^22,26 Likewise, there is no agreement on how N₂ binds to the cluster, e.g. side-on to one Fe ion,²² with one N atom bridging two Fe ions, after the dissociation of one of the sulfide ions,²³ in the centre of the cluster, displacing a triply protonated carbide ion,²⁴ or forming a covalent bond to the carbide ion.^25,26

In fact, there is not even any consensus regarding the structure of the central intermediate E₄. For example, Hoffman and coworkers have proposed models with two protonated sulfide ions and two bridging hydride ions,²⁷ in agreement with spectroscopic results, whereas Siegbahn has argued that it is energetically much more favourable to triply protonate the central carbide ion.²⁸ Recently, we have performed a systematic combined quantum mechanical and molecular mechanical (QM/MM) study of the possible protonation states of the FeMo cluster, providing a great wealth of possible structures for the various intermediates in the reaction mechanism.²⁹ Here, we examine ten of these and show extreme energy differences between different DFT methods, partly explaining the discrepancy found in previous studies. We also discuss which DFT method gives the more accurate results, by studying the geometry of the resting E₀ state and H₂ dissociation from E₄ and E₂.

Methods

The protein

All calculations are based on the 1.0 Å crystal structure of nitrogenase from Azotobacter vinelandii (PDB code 3U7Q).⁷ The setup of the protein is identical to that of our previous studies.^29–31 The entire heterotetramer was included in the calculations and the DFT calculations were concentrated on the FeMo cluster in the C subunit. The P clusters and the FeMo cluster in subunit A were modelled by MM in the fully reduced and resting states, respectively.³⁰

The protonation states of all residues were the same as before:³⁰ all Arg, Lys, Asp, and Glu residues were charged, except Glu-153, 440, and 231D (a letter “D” after the residue number indicates that it belongs to that subunit; if no letter is given, it belongs to subunit C; subunits A and B are identical to the C and D subunits). Cys residues coordinating to Fe ions were deprotonated. His-274, 451, 297D, 359D and 519D were assumed to be protonated on the ND1 atom, His-31, 196, 285, 383, 90D, 185D, 363D and 457D were protonated on both the ND1 and NE2 atoms (and therefore positively charged), whereas the remaining 14 His residues were modelled with a proton on the NE2 atom. The homocitrate was modelled in the singly protonated state with a proton shared between the hydroxyl group (which coordinates to Mo) and the O1 carboxylate atom. This protonation state was found to be the most stable in a recent extensive QM/MM, molecular dynamics and quantum-refinement study³⁰ and it is also supported by another study.³²

The protein was solvated in a sphere with a radius of 65 Å around the geometrical centre of the protein. 160 Cl⁻ and 182 Na⁺ ions were added to neutralise the protein and give an ionic strength of 0.2 M.³³ The final system contained 133 915 atoms. The added protons, counter ions and water molecules were optimised by a simulated annealing calculation (up to 370 K), followed by a minimisation, keeping the other atoms fixed at the crystal-structure positions.³⁰

All MM calculations were performed with the Amber software.³⁴ For the protein, we used the Amber ff14SB force field³⁵ and water molecules were described by the TIP3P model.³⁶ For the metal sites, the MM parameters were the same as in our previous investigation.³⁰ The metal sites were treated by a non-bonded model³⁷ and charges were obtained with the restrained electrostatic potential method, obtained at the TPSS/def2-SV(P) level of theory^38,39 and sampled with the Merz–Kollman scheme.⁴⁰

QM/MM calculations

The QM/MM calculations were performed with the ComQum software.^41,42 In this approach, the protein and solvent are split into two subsystems: system 1 (the QM region) was relaxed by QM methods, whereas system 2 contained the remaining part of the protein and the solvent. It was kept fixed at the original coordinates (equilibrated crystal structure).³⁰

In the QM calculations, system 1 was represented by a wavefunction, whereas all the other atoms were represented by an array of partial point charges, one for each atom, taken from the MM setup. When there is a bond between systems 1 and 2, the hydrogen link-atom approach was employed: the QM system was capped with hydrogen atoms (hydrogen link atoms, HL), the positions of which are linearly related to the corresponding carbon atoms (carbon link atoms, CL) in the full system.^41,43 All MM atoms were included in the point-charge model, except the CL atoms.⁴⁴

The total QM/MM energy in ComQum was calculated as^41,42

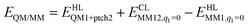where E^HL_QM1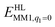+ptch2 is the QM energy of the QM system truncated by HL atoms and embedded in the set of point charges modelling system 2 (but excluding the self-energy of the point charges). is the MM energy of the QM system, still truncated by HL atoms, but without any electrostatic interactions. Finally, 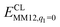is the classical energy of all atoms in the system with CL atoms and with the charges of the QM region set to zero (to avoid double-counting of the electrostatic interactions). Thus, ComQum employs a subtractive scheme with electrostatic embedding and van der Waals link-atom corrections.⁴⁵ The geometry optimisations were continued until the energy change between two iterations was less than 2.6 J mol⁻¹ (10⁻⁶ a.u.) and the maximum norm of the Cartesian gradients was below 10⁻³ a.u.

QM calculations

All QM calculations were performed with the Turbomole software (versions 7.1 and 7.2).⁴⁶ We employed 13 different DFT methods, TPSS,³⁸ PBE,⁴⁷ BP86,^48,49 BLYP,^48,50 B97D,⁵¹ PBE0,⁵² TPSS,⁵³ B3LYP,^48,50,54 BHLYP,⁵⁵ M06,⁵⁶ M06-L,⁵⁷ M06-2X,⁵⁶ and M06-HF.⁵⁸ TPSS, PBE, BP86, BLYP, B97D and M06-L are (meta-) generalized gradient approximation (GGA) functionals, with no admixture of Hartree–Fock (HF) exchange. The other DFT methods are hybrid functionals with 10% (TPSSh), 20% (B3LYP), 25% (PBE0), 27% (M06), 50% (BHLYP), 54% (M06-2X), and 100% (M06-HF) HF exchange (% HF). All calculations employed the def2-SV(P) basis set,³⁹ because previous studies have shown that increasing the basis set to def2-TZVPD changes the relative energies by less than 16 kJ mol⁻¹.^29,31 The calculations were sped up by expanding the Coulomb interactions in an auxiliary basis set, the resolution-of-identity approximation.^59,60 Empirical dispersion corrections were included with the DFT-D3 approach⁶¹ and Becke–Johnson damping,⁶² using parameters optimised for each DFT method, as implemented in Turbomole for all functionals except M06, M06-L, M06-2X and M06-HF (for which no parameters are available because the methods should include dispersion effects by parameterisation).

It should be noted that the M06-2X and M06-HF functionals were constructed for main-group thermochemistry and charge-transfer excitations, respectively, and are not recommended for systems with significant static correlation, like transition metals.⁵⁶ The same applies also to BHLYP with its large amount of HF exchange.⁶³ These three methods reproduce the structure of the resting state quite poorly (Fig. S3, ESI†) and they often give rise to a qualitative change in the geometry of the optimised structures of models 5–7 and 9 (Table S1, ESI†). Therefore, these three functionals were excluded from the figures in the main article, but the results are included in the ESI† (Fig. S1–S3), because they emphasize the trends with respect to % HF.

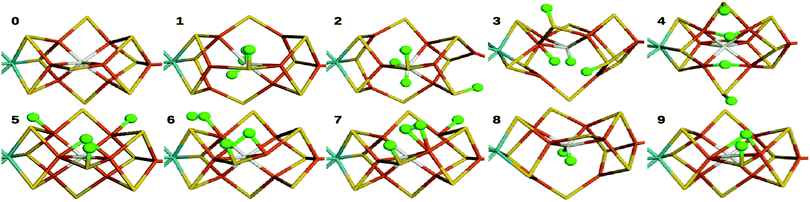
The FeMo cluster was modelled by MoFe₇S₉C(homocitrate) (CH₃S)(imidazole), where the last two groups are models of Cys-275 and His-442. In addition, all groups that form hydrogen bonds to the FeMo cluster within 3.5 Å in the crystal structure⁷ were also included, viz. Arg-96, His-195 and Arg-359 (sidechains), Gly-356, Gly-357 (backbone), as well as two water molecules. In total, the QM system contained 113–117 atoms (depending on the E_n state, i.e. the number of added protons) and it is shown in Fig. 1. Following recent Mössbauer, anomalous dispersion and QM investigations,^13,24,64,65 we used the oxidation state-assignment Mo^IIIFe^II₃Fe^III₄ of the metal ions in the resting (E₀) state, giving a net charge of −5 for the QM system. We studied three oxidation states of the FeMo cluster, obtained by adding 0, 2 or 4 electrons to the resting states, denoted E₀, E₂ and E₄. One proton was added together with each electron, so the net charge of the cluster was −3 for all three states.

Fig. 1 The FeMo cluster illustrating the QM system used in all QM/MM calculations and the naming of the atoms in the cluster.

Experiments have shown that the ground spin state of E₀ and E₂ are quartets with a surplus of three α electrons, whereas E₄ is a doublet.^3,13 These spin states were used in all calculations. The electronic structure of all QM calculations was obtained with the broken-symmetry (BS) approach:¹⁸ for each model, we used the best of the 35 possible BS states³¹ found in our previous study.²⁹ These states are specified in Table 1, which also give further description of the various models (which atoms are protonated and the number of bonds within the cluster). The 13 calculations with different DFT methods for each complex were started with the same wavefunction, to ensure that they belong to the same BS state. Bond lengths involving the added protons are described in Table S2 (ESI†) for all models optimised with the 13 DFT methods, spin densities on the metals are collected in Table S6 (ESI†), whereas Table S7 (ESI†) list the coordinates for the complexes.

Table 1 Description of the ten models, listing the E_n state, the positions of the added protons (atom names are shown in Fig. 1; the number in brackets indicates the direction of the proton^a 27), the BS state,^b the number of bonds of various types (a Fe–Fe interaction is assumed to be broken if it is 0.5 Å longer than in the resting state; the Fe–S and Fe–C bonds are considered broken if they are 0.3 Å longer than in the resting state), and the number of Fe(II) ions in the FeMo cluster (n, formal assignment, assuming that all metal-bound hydrogen atoms are hydride ions)

	E	Position of the H atoms^a				BS State^b	# Fe–X bonds				# other bonds			n
		H1	H2	H3	H4		Fe	S	C	H	S–H	C–H	H–H
a S2B(3) means that the proton on S2B points towards S3A; C(2367) means that the proton is on the Fe2–Fe3–Fe6–Fe7 face and similar for C(3457) and C(2456); S2A(Fe1) and S2A(Mo) mean that the proton on S2A points towards Fe1 or Mo, respectively; Fe2/6(5) or (3) means that the hydride ion bridging Fe2 and Fe6 points towards S5A or S3A; S5A(2) means that the proton on S5A points towards S2B; Fe3/7(2) means that the hydride ion bridging Fe3 and Fe7 points towards S2B; hydride ions terminally bound to one Fe ion are trans to the central carbide ion. b The BS states are defined by which three Fe ions have a negative spin,^31viz. Fe2, 3, and 5 for BS7-1, Fe2, 3 and 4 for BS2, Fe1, 2 and 5 for BS10-1, Fe1, 3 and 7 for BS9-2, Fe1, 5 and 7 for BS6-2, Fe3, 4 and 6 for BS7-3 and Fe3, 4 and 5 for BS8-6. c H2 bound end-on to Fe5. d H2 bound side-on to Fe2.
0	E0					BS7-1	12	22	6	0	0	0	0	3
1	E4	S2B(3)	C(2367)	C(3457)	C(2456)	BS2	4	21	2	0	1	3	0	7
2	E4	S2B(3)	C(2367)	C(3457)	S2A(Fe1)	BS2	8	21	3	0	2	2	0	7
3	E4	S2B(3)	C(2367)	Fe6/7	S2A(Mo)	BS10-1	9	21	5	1	2	1	0	5
4	E4	S2B(3)	Fe2/6(5)	S5A(2)	Fe3/7(2)	BS9-2	12	22	6	2	2	0	0	3
5	E4	S2B(3)	Fe2/6(3)	Fe4	Fe5	BS6-2	12	22	6	3	1	0	0	1
6	E4	S2B(3)	Fe2/6(3)	Fe5^c	H2	BS7-3	12	22	6	2	1	0	1	3
7	E4	S2B(3)	Fe2^d	Fe4	Fe2^d	BS7-3	12	22	6	3	1	0	1	3
8	E2	C(3457)	C(2367)			BS8-6	7	22	4	0	0	2	0	5
9	E2	S2B(3)	Fe2/6(3)			BS7-3	12	22	6	1	1	0	0	3

---

Undoubtedly, the present calculations involve several approximations, e.g. the use of single QM/MM structures and small basis sets without any inclusion of entropy or thermal effects. However, the extremely large difference between the DFT results will undoubtedly remain also in improved calculations.

Results

In this study, we compare energies and geometries of 10 models of the FeMo cluster in the E₄, E₂ or E₀ state, shown in Fig. 2, calculated with 13 different DFT methods. All structures were optimised with QM/MM individually for each DFT method. The aim is to describe and understand the large variation of the results obtained with the various methods and to gain some understanding of which method gives the more reliable results.

Fig. 2 Structures of the 10 studied nitrogenase models, 0–9. Mo, Fe, S and C are shown in cyan, orange, yellow and grey, respectively. Added hydrogen atoms are shown in green balls. For clarity, only the central atoms in the cluster are shown.

E₄ states

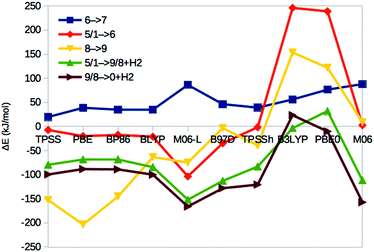
We first compare the relative stability of the best protonation states of E₄ obtained with either the B3LYP (1) or TPSS (5) functionals in our extensive study, ΔE₁₅.²⁹ As can be seen from Fig. 2, both structures are protonated on one of the μ₂ sulfide ions (S2B), whereas the other three protons are on the central carbide ion in 1 but on Fe ions in 5. Protonation of the carbide leads to significant distortions of the FeMo cluster (cf.Table 1), but the carbide ion remains inside the cluster in our QM/MM calculations,²⁹ in variance to the QM-cluster calculations by Siegbahn, in which the protonated carbide ion moves to the periphery of the cluster.⁶⁶

From the relative energies in Fig. 3 (blue curve), it can be seen that the (meta) GGA functionals (TPSS, PBE, BP86, BLYP, M06-L and B97D) predict that structure 5 is 8–242 kJ mol⁻¹ more stable than structure 1. On the other hand, the hybrid functionals (TPSSh, B3LYP, PBE0 and M06) predict that structure 1 is 39–353 kJ mol⁻¹ more stable than structure 5. The latter agrees with Siegbahn's suggestion (based on B3LYP calculations) that it is much more favourable to protonate the central carbide than the metal ions.²⁸ However, a similar study based on a GGA functional would have reached the opposite conclusion.

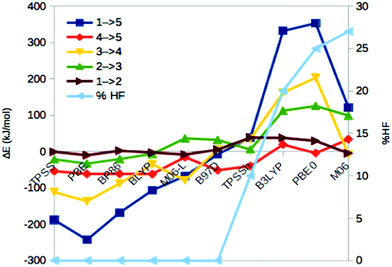Fig. 3 Energies for the 1 → 5, 4 → 5, 3 → 4, 2 → 3 and 1 → 2 isomerisations, obtained with ten different DFT methods. The cyan line shows % HF for the various methods (right axis).

Thus, the various DFT methods give ΔE₁₅ results that differ by up to 595 kJ mol⁻¹. This is 4–30 times larger variation than what is found in other systems.^67–69 For example, Fig. 4 shows the reaction energies of the N₂ + 3H₂ → 2NH₃ reaction, divided into three steps (involving the formation of N₂H₂, N₂H₄ and finally two NH₃ molecules). It can be seen that the 13 DFT functionals give results that agree within 35–38 kJ mol⁻¹. In particular, all methods agree that the first step (formation of N₂H₂) is strongly uphill (by 167 kJ mol⁻¹ on average), whereas the other two steps are downhill by 102 and 154 kJ mol⁻¹ on average, respectively.

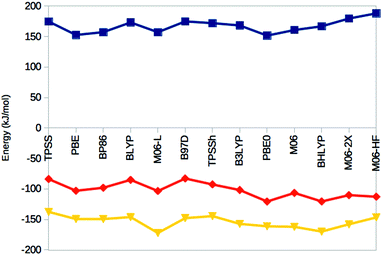Fig. 4 Reaction energies for the N₂ + H₂ → N₂H₂ (top, blue), N₂H₂ + H₂ → N₂H₄ (middle, red) and N₂H₄ + H₂ → 2 NH₃ (bottom, yellow) reactions, obtained in the gas phase with the 13 DFT methods.

The hybrid functionals involve a varying amount of Hartree–Fock exchange (% HF, 10–27%), as is also shown in Fig. 3 (cyan line and right axis). There is a fair correlation between ΔE₁₅ and % HF, R² = 0.75, although M06 breaks the trend. In fact, we also used three functionals with a larger % HF, which increased the correlation to 0.88 and the energy range to 1097 kJ mol⁻¹ (Fig. S1, ESI†), but since such methods are normally not recommended for transition-metal systems^56,63 and they gave qualitative changes in the structure of 5, we present these results in the ESI.† For the N₂ + 3H reactions, the correlation to the % HF is appreciably weaker, 0.03–0.42.

If the structures are not optimized with each DFT functional, the variation is even larger, 862 kJ mol⁻¹ (using the B3LYP structure for 1 and the TPSS structure for 5; Table S3, ESI†), showing the importance of optimizing the individual structures when the energy differences are so large. However, the correlation of ΔE₁₅ obtained with or without geometry optimization is very high, 0.98.

In 1, there are three protons on the central carbide, whereas in 5, they are instead (as hydride ions) on Fe ions. To further understand the large variation in the DFT results, we did similar calculations on three structures (2, 3 and 4) with intermediate protonation, viz. with 2, 1 and no protons on the carbide and with 0, 1 and 2 metal-bound hydride ions, respectively (cf.Fig. 2). In fact, structure 4 is one of the E₄ structures suggested by the Hoffman group (based on BP86 calculations) with two hydride ions bridging two Fe ions each and two protons on sulfide ions.²⁷ From Fig. 3 (red line), it can be seen that ΔE₄₅ is similar for most functionals, with 5 being more stable than 4 by 5–62 kJ mol⁻¹. Only B3LYP and M06 give the opposite ordering (by 19–34 kJ mol⁻¹). However, there is a quite strong correlation between ΔE₄₅ and % HF, R² = 0.8.

In model 3, there is only one hydride ion and the carbide ion is singly protonated. Interestingly, ΔE₃₄ shows an appreciably larger variation among the functionals (Fig. 3, yellow). In general, 3 is less stable than 4 according to the GGA functionals (by 35–137 kJ mol⁻¹), whereas the opposite is true with the hybrid functionals (by 35–203 kJ mol⁻¹). However, with B97D and M06, they are of a similar energy. There is a fair correlation between ΔE₃₄ and % HF (R² = 0.58; 0.76 with all 13 functionals).

Finally, model 2 has no hydride ions and a doubly protonated carbide ion. From Fig. 3 (green line), it can be seen that the GGA functionals, except M06-L and B97D indicate that 3 is 7–33 kJ mol⁻¹ more stable than 2, whereas the other methods give the opposite result by 5–125 kJ mol⁻¹. There is a strong correlation between ΔE₂₃ and % HF (R² = 0.78 or 0.92). If we instead compare the stability of structures 2 and 1, i.e. the effect of moving a proton from a sulfide to the carbide (brown line in Fig. 3), we find that the GGA functionals and M06 indicate that structures 2 and 1 are close in energy (−10 to 2 kJ mol⁻¹), whereas the other hybrid functionals indicate that structure 1 is 29–39 kJ mol⁻¹ more stable than structure 2. There is only a low correlation between ΔE₁₂ and % HF (0.3, but it increases to 0.75 with all 13 DFT functionals).

Thus, the large variation in ΔE₁₅ among the DFT functionals is caused mainly by ΔE₃₄ and ΔE₂₃. This indicates that the variation is related to at least two factors. The isomerizations 4 → 5, 3 → 4 and 2 → 3 all involve a change in the number of hydride ions and therefore also the formal oxidation state of the Fe ions (a hydride ion has two more electrons than a proton; therefore, the number of Fe(II) ions in the structures 1–5 are 7, 7, 5, 3 and 1, respectively), so that structures 1 and 5 actually differ by six levels in the formal oxidation state of the metal ions. On the other hand, 3 → 4, 2 → 3 and 1 → 2 involve the formation of C–H bonds, associated with a distortion of the FeMo cluster, leading to partial cleavage of Fe–C, Fe–S and Fe–Fe bonds. This is detailed in Table 1, in which it can be seen that eight of the Fe–Fe distances have elongated by more than 0.5 Å and four of the Fe–C bonds and one of the Fe–S bonds are elongated by more than 0.3 Å in 1, compared to 5 or the resting E₀ state. Models 2 and 3 have a lower number of broken bonds (cf.Table 1). Apparently, the variation among the DFT methods is the largest when both effects apply.

H₂ binding and dissociation

To gain some additional information about how the energies vary with the DFT functionals, we studied also the binding and dissociation of H₂ from the E₄ and E₂ states of the MoFe cluster. First, we included two complexes with H₂ bound to the FeMo cluster in the E₄ state, both with a proton on S2B. Structure 6 has H₂ bound end-on to Fe5 and the fourth H is bridging Fe2 and Fe6, whereas in structure 7, H₂ is bound side-on to Fe2 and with the fourth H on Fe4 (cf.Fig. 2; atom names are shown in Fig. 1). For all methods, end-on binding (6) was more favourable than side-on binding (7), by 20–88 kJ mol⁻¹ (Fig. 5, blue line). Moreover, with the GGA functionals, 6 was more stable than 5 (the most stable E₄ structure with those functionals) by 7–104 kJ mol⁻¹ (Fig. 5, red line). On the other hand, 1 was appreciably more stable than 6 for the B3LYP and PBE0 functionals (by 239–246 kJ mol⁻¹), whereas the two structures were isoenergetic within 2 kJ mol⁻¹ with TPSSh and M06.

Fig. 5 Energies for the 6 → 7, 5/1 → 6, 8 → 9, 5/1 → 9/8 + H₂ and 9/8 → 0 + H₂ reactions, obtained with ten different DFT methods (using the structure with the lowest energy for 5/1 and 9/8 for each method).

Next, we studied two structures of the E₂ state (i.e. with two protons and electrons less), one with the two protons on the central carbide (8) and the other with one proton on the S2B μ₂ sulfide and one hydride ion bridging Fe2 and Fe6 (9; cf.Fig. 2). They are the best E₂ structures obtained in our previous study with B3LYP and TPSS, respectively.²⁹ As expected, the GGA functionals, but also TPSSh, suggest that 9 is 3–203 kJ mol⁻¹ more stable than 8, whereas the other hybrid functionals favour 8 by 9 (M06) or 122–153 kJ mol⁻¹ (Fig. 5, yellow line). The correlation of ΔE₈₉ to % HF is 0.6.

With these structures, we can estimate the dissociation energy of H₂ from either 5 or 1. It is favourable for all GGA functionals (5 → 9 + H₂) by 68–152 kJ mol⁻¹. For the hybrid functionals (1 → 8 + H₂), H₂ dissociation is also favourable by 3–112 kJ mol⁻¹, except for PBE0 (Fig. 5, green line).

Finally, we studied also the resting state of the enzyme (E₀; 0) to obtain an estimate of the dissociation energy of H₂ from E₂ (9/8 → 0 + H₂). Fig. 5 (brown line) shows that it is favourable for all GGA functionals, as well as TPSSh and M06 by 88–166 kJ mol⁻¹, whereas it is unfavourable for B3LYP and nearly thermoneutral for PBE0.

Geometry of the resting state

For E₀, we can also compare the QM/MM structures with the crystal structure of nitrogenase (3U7Q).⁷ It is at such a high resolution (1.0 Å) that it can be used to calibrate the DFT geometries. In fact, it has been used to determine the broken-symmetry state of the FeMo cluster and the protonation of the homocitrate ligand.³²Fig. 6 shows the root-mean-squared deviation (RMSD), as well as the mean absolute deviation (MAD) and maximum deviation of the metal–ligand and metal–metal distances for the various DFT methods. It can be seen that TPSSh gives the lowest RMSD (0.06 Å), whereas the best metal–ligand distances are obtained with PBE and BP86 (giving the lowest MAD = 0.02 Å) or BLYP (lowest maximum deviation, 0.06 Å). On the other hand, the best metal–metal distances are obtained with B97D and TPSSh (MAD = 0.02 Å) or BLYP methods (maximum deviation of 0.07 Å). Thus, TPSSh and the GGA functionals (except M06-L) give the best structures, appreciably better than those of the other hybrid functionals.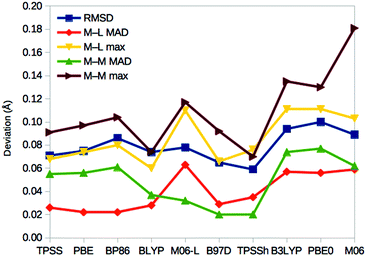

Fig. 6 Performance of the various DFT methods for the structure of the resting E₀ state compared to the crystal structure.⁶ For each method, the RMSD for the Mo, Fe, S and C atoms of the cluster, as well as the directly connected ligand S, O and N atoms are given, together with the MAD and maximum deviation for the 34 metal–ligand (M–L) distances and the 15 short (<3 Å) metal–metal (M–M) distances.

Spin densities

The geometry optimisations with different DFT functionals were started from the same wavefunction, to keep them as similar as possible. We used the experimentally observed spin state and the best BS state obtained for each structure in our previous investigation (listed in Table 1).²⁹ These were obtained by B3LYP for structures 1–3 and 8, and by TPSS for the other structures. Thus, we did not attempt to find better BS states for the other DFT functionals, which would be extremely time-consuming and would have mixed in differences caused by the use of different BS states.

The spin densities obtained for the eight metal ions in the various calculations are listed in Table S6 (ESI†). It can be seen that for most structures, the calculations with different DFT functionals remained in the same BS states, defined by the Fe ions with negative spin densities. However, for two structures, some DFT calculations gave qualitatively differences. For 6, most calculations were in the BS7-3 state, characterised with large negative spin populations on Fe3, Fe4 and Fe6 (≤−2.4). However, the three GGA functionals PBE, BP86 and BLYP gave negative spin populations on the same three Fe ions, but that on Fe6 was small, −0.5 and Fe2 also had a negative spin of intermediate size, around −1.5 (therefore corresponding to the BS6-2 state). We could find the other state also with these functionals, but during geometry optimisation, they changed back to the original state, except for BLYP, for which it is 12 kJ mol⁻¹ less stable than the original state. Still, this difference in the spin states is not reflected in the energies in Fig. 5.

For 4, all DFT calculations give large negative spin populations on Fe1 and Fe3. However, for five of the functionals (the GGA functionals, except M06-L), Fe7 had a small population on Fe7 (−1.2 for B97D or −0.1 for the others), whereas for the other functionals, the population is large and negative. Again, the other state could be found but it typically changed back during geometry optimisation. For BLYP, TPSSh and B3LYP, both states could be found, with energy differences of 12–97 kJ mol⁻¹. In this case, the difference in the wavefunction is reflected in the energies in Fig. 3, which shows an increased stability for 4 for the functionals giving a high spin population on Fe7.

In addition, there are also systematic differences between the spin densities obtained with the various methods. First, the magnitude of the spin populations increases with % HF. It is in general the lowest for BLYP, PBE and BP86 (2.5 on average) and the largest for PBE0 (3.6). The spin on the seven Fe ions also becomes more similar when % HF increases. For example, the difference between the maximum and minimum absolute spin populations of structure 1 is 1.0 for PBE and BP86, but only 0.2 for PBE0.

The difference is even larger for the spin on the Mo ion. It is negative in all structures, except 5. With the TPSS, PBE, BP86 and BLYP functionals, it is in general small in magnitude, 0.2–0.5, but increased to 0.8–1.0 for structures 1 and 2. However, for M06-L and the hybrid functionals, it is appreciably higher, by 0.6–0.8 on average. For structures 1 and 2, these functionals indicate a high-spin state of Mo (spin populations of 1.6–2.5), which are not consistent with ⁹⁵Mo ENDOR experiments.^70–72

Discussion

We have studied how the relative energies of various protonation and H₂-bound states vary when they are calculated with ten different DFT methods. The results in Fig. 3 and 5 show an extremely large variation of the relative energies, up to 600 kJ mol⁻¹, which often correlate to % HF of the methods. A strong dependence on DFT for relative energies and a correlation to % HF have been observed previously for several types of systems. For example, Reiher et al. studied the energy difference between the high- and low-spin states for a number of Fe(II)S₄NL complexes with L = NH₃, N₂H₄, CO, NO⁺, PH₃ and PMe₃.⁶⁷ They showed that predictions obtained by B3LYP and BP86 differed by 94–122 kJ mol⁻¹ and that variants of B3LYP with % HF varying between 0 and 25% gave energies that varied by up to 160 kJ mol⁻¹. They observed that for % HF between 10 and 15%, the results agreed with experiments and recommended the B3LYP* method with 15% HF. This is the method used by Siegbahn for energies (but not structures) for nitrogenase.²⁸

Likewise, for the homolytic Co(III)–C bond dissociation energy in methyl corrin (coenzyme B₁₂ without sidechains), Jensen and Ryde reported a difference of 57 kJ mol⁻¹ between B3LYP and BP86 (51–66 kJ mol⁻¹ for related models with different axial ligands and metals, Co, Fe or Ni).⁶⁸ Later, more functionals were studied, increasing the variation to 139 kJ mol⁻¹ (66 kJ mol⁻¹ excluding BHLYP) and showing a correlation to % HF of R² = 0.89.⁷³

For the oxy-transfer reaction in Mo-dependent dimethylsulfoxide reductase, Li et al. reported a variation of 116 kJ mol⁻¹ for the activation energy and 103 kJ mol⁻¹ for the reaction energy over eight DFT functionals (63 and 61 kJ mol⁻¹ excluding BHLYP). The correlation to % HF was 0.95 and 0.98.⁷⁴ The results were calibrated by using LCCSD(T0) calculations, which showed that for the activation energy, B3LYP gave the best result (9 kJ mol⁻¹ error), whereas for the reaction energy, GGA functionals gave better results (errors of 1–6 kJ mol⁻¹). Similar results were obtained if geometries were optimised with the various methods or if also W was considered.⁶⁹

Thus, previous studies of metalloenzymes have sometimes showed a large variation in the results of different DFT methods, especially for spin-state energies or when the oxidation state of the metal changes. However, the variation observed for nitrogenase is 4–10 times larger than what has been observed before.

Of course, the prime question is which of the DFT methods (if any) can be trusted. In general, hybrid DFT functionals give appreciably better results than GGA functionals for main-group thermochemistry, e.g. with a weighted MAD of 21, 27 and 38 kJ mol⁻¹ for M06-2X, B3LYP and TPSS, respectively, for the recent GMTKN55 test set (and even better results for double hybrid functionals).⁷⁵ Hybrid functionals remain better for some transition-metal complexes, in particular with hard ligands.^67,76 However, there are ample examples of transition-metal complexes (especially with softer ligands), for which GGA methods give better results than hybrid functionals, e.g. for reactions related to the nitrogenase reaction,⁷⁷ for [NiFe]-hydrogenase models^78,79 and for complexes with nitride and carbonyl ligands.⁸⁰ In a recent test of 41 closed-shell organometallic reactions, PBE0 gave the best results among the DFT functionals employed in the present study, but the MAD was not much higher for TPSSh and TPSS (11, compared to 12 and 14 kJ mol⁻¹), whereas B3LYP was appreciably worse, 21 kJ mol⁻¹.⁸¹ Clearly, the performance of DFT methods depend on the system studied, probably depending on the importance of static correlation.⁸⁰

An alternative is to select the functional based on comparisons with experimental observations. In this study, we have compared several properties. Spectroscopic evidence indicate that the E₄ state has two bridging hydride ions.³ Unfortunately, the results in Fig. 3 show that none of the DFT functionals suggest that the best E₄ structure is 4, which has two bridging hydride ions.

Moreover, experiments indicate that four electrons and protons should be added to the resting state before it may bind N₂. Of course, it is then essential that H₂ does not form and dissociate before N₂ binds; otherwise two electrons and protons have been consumed with no gain. However, the energies in Fig. 5 indicate that all methods except B3LYP and PBE0 give strongly favourable H₂ dissociation energies from both E₄ and E₂.

On the other hand, the results in Fig. 6 show that the TPSSh and GGA methods (except M06-L) best reproduce the crystal structure of the resting state. Thus, our calculations indicate that it may be hard to find a DFT method that gives good results for all properties of the FeMo cluster in nitrogenase.

Conclusions

We have shown that nitrogenase models with different protonation states give an unprecedentedly large variation in relative energies obtained with different DFT methods, up to 600 kJ mol⁻¹. This variation is connected to differences in the formal oxidation state of the Fe ions in the cluster (number of hydride ions), as well as to the number of Fe–C and Fe–H bonds. This explains the large discrepancy between mechanisms suggested by different groups.^27,28 Unfortunately, there is currently no quantum mechanical method that can be used to calibrate the DFT methods for a cluster of the size and electronic complexity as the one in nitrogenase. Instead, we suggest that energies are calculated with several DFT methods to check the sensitivity of the results. We have attempted to calibrate the methods by using experimental data. Unfortunately, GGA functionals and TPSSh give the best geometries, whereas B3LYP and PBE0 give better H₂-dissociation energies but a high-spin Mo state for the best E₄ structures. None of the tested methods indicate that the best E₄ state has two bridging hydride groups. This calls for some humility in the interpretation of DFT results on nitrogenase. Undoubtedly, there is an urgent need of more accurate methods that can treat systems of the complexity of the FeMo cluster.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by grants from the Swedish Research Council (project 2014-5540), from COST through Action CM1305 (ECOSTBio), by the Royal Physiographic Society in Lund and by a scholarship to LC from the China Scholarship Council. The computations were performed on computer resources provided by the Swedish National Infrastructure for Computing (SNIC) at Lunarc at Lund University and HPC2N at Umeå University.

References

1. B. K. Burgess and D. J. Lowe, Chem. Rev., 1996, 96, 2983–3012.
2. B. Schmid, H.-J. Chiu, V. Ramakrishnan, J. B. Howard and D. C. Rees, in Handbook of Metalloproteins, John Wiley & Sons, Ltd, 2006, pp. 1025–1036.
3. B. M. Hoffman, D. Lukoyanov, Z.-Y. Yang, D. R. Dean and L. C. Seefeldt, Chem. Rev., 2014, 114, 4041–4062.
4. B. E. Smith, Science, 2002, 297, 1654–1655.
5. J. Kim and D. C. Rees, Science, 1992, 257, 1677–1682.
6. O. Einsle, F. A. Tezcan, S. L. A. Andrade, B. Schmid, M. Yoshida, J. B. Howard and D. C. Rees, Science, 2002, 297, 1696.
7. T. Spatzal, M. Aksoyoglu, L. Zhang, S. L. A. Andrade, E. Schleicher, S. Weber, D. C. Rees and O. Einsle, Science, 2011, 334, 940.
8. T. Spatzal, K. A. Perez, O. Einsle, J. B. Howard and D. C. Rees, Science, 2014, 345, 1620–1623.
9. O. Einsle, J. Biol. Inorg. Chem., 2014, 19, 737–745.
10. R. R. Eady, Chem. Rev., 1996, 96, 3013–3030.
11. R. N. F. Thorneley and D. J. Lowe, in Molybdenum Enzymes, ed. T. G. Spiro, Wiley, New York, 1985, pp. 221–284.
12. K. M. Lancaster, M. Roemelt, P. Ettenhuber, Y. Hu, M. W. Ribbe, F. Neese, U. Bergmann and S. DeBeer, Science, 2011, 334, 974–977.
13. R. Bjornsson, F. A. Lima, T. Spatzal, T. Weyhermüller, P. Glatzel, E. Bill, O. Einsle, F. Neese and S. DeBeer, Chem. Sci., 2014, 5, 3096–3103.
14. F. Tuczek, in RSC Metallobiology Series 7, ed. R. Hille, C. Schulzke and M. L. Kirk, Royal Society of Chemistry, Cambridge, 2017, pp. 223–274.
15. I. Dance, J. Biol. Inorg. Chem., 1996, 1, 581–586.
16. K. K. Stavrev and M. C. Zerner, Int. J. Quantum Chem., 1998, 70, 1159–1168.
17. P. E. M. Siegbahn, J. Westerberg, M. Svensson and R. H. Crabtree, J. Phys. Chem. B, 1998, 102, 1615–1623.
18. T. Lovell, J. Li, T. Liu, D. A. Case and L. Noodleman, J. Am. Chem. Soc., 2001, 123, 12392–12410.
19. H. Xie, R. Wu, Z. Zhou and Z. Cao, J. Phys. Chem. B, 2008, 112, 11435–11439.
20. J. Kästner and P. E. Blöchl, J. Am. Chem. Soc., 2007, 129, 2998–3006.
21. P. P. Hallmen and J. Kästner, Z. Anorg. Allg. Chem., 2015, 641, 118–122.
22. I. Dance, Z. Anorg. Allg. Chem., 2015, 641, 91–99.
23. J. B. Varley, Y. Wang, K. Chan, F. Studt and J. K. Nørskov, Phys. Chem. Chem. Phys., 2015, 17, 29541–29547.
24. P. E. M. Siegbahn, J. Am. Chem. Soc., 2016, 138, 10485–10495.
25. M. L. McKee, J. Phys. Chem. A, 2016, 120, 754–764.
26. L. Rao, X. Xu and C. Adamo, ACS Catal., 2016, 6, 1567–1577.
27. D. Lukoyanov, N. Khadka, D. R. Dean, S. Raugei, L. C. Seefeldt and B. M. Hoffman, Inorg. Chem., 2017, 56, 2233–2240.
28. P. E. M. Siegbahn, J. Comput. Chem., 2018, 39, 743–747.
29. L. Cao and U. Ryde, J. Chem. Theory Comput., 2018, 14, 6653–6678.
30. L. Cao, O. Caldararu and U. Ryde, J. Phys. Chem. B, 2017, 121, 8242–8262.
31. L. Cao and U. Ryde, Int. J. Quantum Chem., 2018, 118, e25627.
32. B. Benediktsson and R. Bjornsson, Inorg. Chem., 2017, 56, 13417–13429.
33. B. M. Barney, J. Mcclead, D. Lukoyanov, M. Laryukhin, T. Yang, D. R. Dean, B. M. Hoffman and L. C. Seefeldt, Biochemistry, 2007, 46, 6784–6794.
34. D. A. Case, J. T. Berryman, R. M. Betz, D. S. Cerutti, T. E. Cheatham, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, T. Luchko, R. Luo, B. Madej, K. M. Merz, G. Monard, P. Needham, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. E. Roitberg, R. Salomon-Ferrer, C. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, D. M. York and P. A. Kollman, AMBER 2014, University of California, San Francisco, 2014.
35. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713.
36. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
37. L. Hu and U. Ryde, J. Chem. Theory Comput., 2011, 7, 2452–2463.
38. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
39. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
40. B. H. Besler, K. M. Merz and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439.
41. U. Ryde, J. Comput.-Aided Mol. Des., 1996, 10, 153–164.
42. U. Ryde and M. H. M. Olsson, Int. J. Quantum Chem., 2001, 81, 335–347.
43. N. Reuter, A. Dejaegere, B. Maigret and M. Karplus, J. Phys. Chem. A, 2000, 104, 1720–1735.
44. L. Hu, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2011, 7, 761–777.
45. L. Cao and U. Ryde, Front. Chem., 2018, 6, 89.
46. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100.
47. J. P. Perdew, K. Burke, M. Ernzerhof, B. Kieron and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
48. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
49. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822–8824.
50. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
51. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
52. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982.
53. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
54. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
55. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
56. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
57. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
58. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126–13130.
59. K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–289.
60. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124.
61. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
62. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
63. H. S. Yu, S. L. Li and D. G. Truhlar, J. Chem. Phys., 2016, 145, 130901.
64. T. Spatzal, J. Schlesier, E.-M. Burger, D. Sippel, L. Zhang, S. L. A. Andrade, D. C. Rees and O. Einsle, Nat. Commun., 2016, 7, 10902.
65. R. Bjornsson, F. Neese and S. DeBeer, Inorg. Chem., 2017, 56, 1470–1477.
66. P. E. M. Siegbahn, Inorg. Chem., 2018, 57, 1090–1095.
67. M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55.
68. K. P. Jensen and U. Ryde, J. Phys. Chem. A, 2003, 107, 7539–7545.
69. J. Li, M. Andrejic, R. A. Mata and U. Ryde, Eur. J. Inorg. Chem., 2015, 3580–3589.
70. S. Raugei, L. C. Seefeldt and B. M. Hoffman, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10521–10530.
71. R. A. Venters, M. J. Nelson, P. A. McLean, A. E. True, M. A. Levy, B. M. Hoffman and W. H. Orme-Johnson, J. Am. Chem. Soc., 1986, 108, 3487–3498.
72. D. Lukoyanov, Z.-Y. Yang, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, J. Am. Chem. Soc., 2010, 132, 2526–2527.
73. U. Ryde, R. A. Mata and S. Grimme, Dalton Trans., 2011, 40, 11176–11183.
74. J. Li, R. A. Mata and U. Ryde, J. Chem. Theory Comput., 2013, 9, 1799–1807.
75. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215.
76. M. Lundberg and P. E. M. Siegbahn, J. Comput. Chem., 2005, 26, 661–667.
77. I. Dance, Mol. Simul., 2018, 44, 568–581.
78. M. G. Delcey, K. Pierloot, Q. M. Phung, S. Vancoillie, R. Lindh and U. Ryde, Phys. Chem. Chem. Phys., 2014, 16, 7927–7938.
79. G. Dong, Q. M. Phung, S. D. Hallaert, K. Pierloot and U. Ryde, Phys. Chem. Chem. Phys., 2017, 19, 10590–10601.
80. J. N. Harvey, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2006, 102, 203–226.
81. S. Dohm, A. Hansen, M. Steinmetz, S. Grimme and M. P. Checinski, J. Chem. Theory Comput., 2018, 14, 2596–2608.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp06930a

---