Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical X-ray absorption spectroscopy database analysis for oxidised 2D carbon nanomaterials†
Fabian
Weber
 ab,
Jian
Ren
ab,
Jian
Ren
 ac,
Tristan
Petit
ac,
Tristan
Petit
 a and
Annika
Bande
a and
Annika
Bande
 *a
*a
aInstitute of Methods for Material Development, Helmholtz-Zentrum Berlin für Materialien und Energie GmbH, Albert-Einstein-Str. 15, 12489 Berlin, Germany. E-mail: annika.bande@helmholtz-berlin.de; Tel: +49 30 8062-42026
bInstitute of Chemistry and Biochemistry, Freie Universität Berlin, Takustr. 3, 14195 Berlin, Germany
cDepartment of Physics, Freie Universität Berlin, Arnimallee 14, 14195 Berlin, Germany
First published on 6th March 2019
Abstract
In this work we provide a proof of principle for a theoretical methodology to identify functionalisation patterns in oxidised carbon 2D nanomaterials. The methodology is based on calculating a large number of X-ray absorption spectra of individually excited carbon atoms in different chemical environments using density functional theory. Since each resulting spectrum gives a fingerprint of the local electronic structure surrounding the excited atom, we may relate each spectrum to the functionalisation pattern of that excited atom up to a desired neighbourhood radius. These functionalisation pattern-specific spectra are collected in a database, that allows fast composition of X-ray absorption spectra for arbitrary structures in density functional theory quality. Finally, we present an exemplary application of the database approach to estimate the relative amount of functional groups in two different experimental samples of carbon nanomaterials.
1 Introduction
Oxidised 2D carbon nanomaterials such as graphene oxide (GO) and its derivatives have gained a lot of interest over the past years. Some representatives of these resource-sustainable and environmentally-friendly materials can either be directly used as photocatalysts for water-splitting with tunable band-gaps,1 or can serve as precursor materials for the production of reduced graphene oxide2,3 as well as biocompatible diagnostics or drug-carrying nanoparticles.4,5 For all of these applications, the extent and type of surface functionalisation is of major importance since it determines not only the electronic structure of the 2D material6 but also other important properties like colloidal stability and surface charge.7 Although its first discovery dates back over 150 years,8 the atomic structure of GO however remains highly debated. The reason for this is the inhomogeneous functionalisation during the preparation procedure. GO is most commonly produced by modifications of Hummers' method,9 in which layers of graphite are first intercalated by sulfuric acid in the presence of sodium nitrate and then oxidised by potassium permanganate.10 Here, the choice of specific reaction and work-up conditions has a direct impact on properties like the stoichiometry11 and the density of holes in the resulting honeycomb scaffold.3 Additionally, initial structural defects in the precursor material in combination with a ‘pseudo-random’ functionalisation with oxygen on the surface,12 ultimately lead to a situation where each nanoparticle in principle needs to be considered unique in terms of its atomic structure. Nonetheless, several properties like the surface charge, acidity13 and photocatalytic properties14 have shown general trends with respect to the overall degree of oxidation (i.e. the average percentage of oxygen-functionalised carbon atoms in a reaction batch). Hence, it can be assumed that such properties are dependent on local features present among all particles rather than on the exact total structures. To understand and optimize the physico-chemical properties for future applications of GO it is therefore desirable that one can extract the most recurrent local functionalisation patterns from an experimental sample.The mission of finding possible local functionalisation patterns is ongoing research in various fields of physical, analytical and theoretical chemistry in which many different structural models have been proposed over the course of time.15–19 Some of the milestones that show the complementary nature of this structural analysis can be summed up as follows: with its first reported syntheses, elemental analyses were conducted that confirmed the non-stoichiometric character of graphite oxide.8 Following the advent of X-ray powder diffraction, the comparison with powder diffraction images of graphite lead to the conclusion that the carbon network of six-membered rings was mostly preserved after oxidation.20–22 Due to the scarce diffraction characteristics, however, no systematic ordering of the oxygen atoms could be detected. These initial measurements already gave rise to an overall structural understanding as ‘stacked two-dimensional macromolecular sheets’ that were assumed to be physically separable into monolayers.22 First infrared spectroscopy measurements supported the existence of carboxyl, aliphatic hydroxyl and epoxy groups.23 With the development of electron microprobe diffraction techniques the monolayer stacking was proven.24 Using this technique, it was also validated that no long-range order for the oxygen functionalisation exists and that the oxygen atoms were most likely bound as hydroxyl or epoxy groups on the sheet surface.24 The basis of the most widely accepted structural model so far was established by Lerf and Klinowski after 13C solid state nuclear magnetic resonance (SSNMR) measurements that are capable of locally probing the atomistic surrounding of nuclei of a specific element.11,19,25 Their findings validated the existence of carbon–carbon double bonds and lead to the conclusion that GO contained graphitic besides oxidized regions proportional to the degree of oxidation. Further improvements to their structural model have been made since, by SSNMR of 13C enriched samples12 and high-resolution transmission electron microscopy images.26
Another field of spectroscopy that provides contributions in terms of element-specific and local structural analysis is X-ray absorption (XA) spectroscopy, where highly energetic X-ray photons are used to excite core electrons into unoccupied orbitals or the ionisation continuum. Since the core electrons are affected by the practically unscreened Coulomb attraction of the spatially close nucleus, each chemical element has specific excitation energies (i.e. absorption edges) at which to probe core-valence transitions. Depending on the excitation energy, different effects may be observed that give rise to three distinguishable energetic regions, namely the pre-edge, X-ray absorption near-edge structure (XANES) and extended X-ray absorption fine structure (EXAFS).
From a theoretical perspective, two main effects contribute to X-ray absorption. The first contribution is connected to the ionisation of the excited core electron and only appears beyond the absorption edge energy. Here, the photoexcited electron is described by continuum wavefunctions that are scattered at several neighbouring atoms. For low ejection energies, (i.e. in the XANES region) several scattering events may occur due to the low mean free path of the ejected electron. Hence, signals in the XANES region contain information on multiple scatterers at once and can be used to identify the nature of functional groups near the excited atom, as well as their relative positioning.27,28 In the EXAFS region, the mean free path of the electron is long and mostly single-scattering events are obtained. Therefore, depending on the periodicity (so called mid-range and long-range order), convoluted oscillatory structures are obtained where the frequency of convolution components can be related to the distance of periodically arranged scattering sites.29 Both effects are covered in the field of multi-scattering theory and have been implemented in programs such as FEFF,30 FDMNES,31 or WIEN2k32 to simulate XANES and EXAFS spectra.
The second contribution is caused by excitation of the core electron into bound and resonance states. While resonance states are difficult to describe, bound final states of excitonic (i.e. extended long-range)33 or molecular (i.e. local short-range) nature can be readily simulated using ab initio quantum chemistry methods such as time-dependent density functional theory (TDDFT) with core-excitation specialized exchange–correlation functionals.34,35
To extract structural information from experimental spectra, there already exist computational procedures based on multi-scattering theory that fit the properties and sites of scatterers to match experimental data in the EXAFS and XANES region. Here, implementations such as IFEFFIT36 use efficient truncations in the scattering expansion length (reciprocal space) or introduce a cutoff radius (real space) in which to optimize the properties of the scattering sites.
However, to the best of our knowledge no similar fitting procedure has been introduced to bound-to-bound state molecular calculations yet, since the non-periodic molecular description of larger systems yields high numbers of bound states, that become prohibitively expensive. To fill this gap, we introduce in this work a methodology that may open up the possibility for such an algorithm. Firstly, we calculate a large number of core-excitations of carbon atoms in different model molecules and then group the resulting spectra with respect to the bonding environment of the excited atom up to a specific radius. These resulting functionalisation specific groups are then used to construct a database, from which we may try to fit the bonding environment of explicit calculations and experimental samples of oxidised 2D carbon nanomaterials.
This paper is structured as follows. First we explain how the database of functionalisation specific spectra is generated in terms of calculation techniques, model structures and how we distinguished the different functional groups. Then, we give a general proof of principle by critically reviewing the choice of a cutoff radius and comparing the resulting spectra of fully-atomistic calculations with compositions from the database. Finally, we show the results of a complementary analysis of two experimental samples of oxidised 2D carbon nanomaterials.
2 Structural aspects and methodology
2.1 Model structure generation
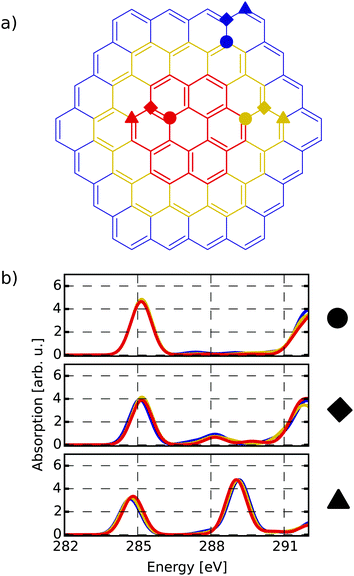
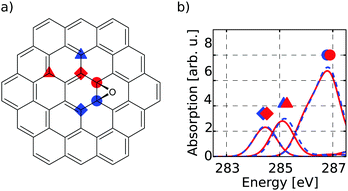
The first target is to generate a meaningful database of local XA spectra. Therefore, we have to select model molecules from which we obtain the database in a sensible way. The goal is that the model structures can mimic the XA response of carbon atoms in basically any environment as close as possible, while keeping the model size as small as possible. In this respect, we used different model molecule sizes that are based on a coronene scaffold (denoted C) and then added further aromatic rings around this structure in two consecutive steps. The next bigger scaffold is then given by circumcoronene (CC) while the largest structural basis is simply referred to as CCC, respectively (see Fig. 1(a)).Besides their pristine forms, the three scaffolds were then functionalised with oxygen-containing groups and hydrogen in several ways to obtain different environments for the individual carbon atoms. Whenever not functionalised, the dangling bonds of the edge-positioned carbon atoms were saturated with one hydrogen atom. By saturation of the graphitic scaffold, several sp3 hybridized carbon atoms are obtained that then represent the properties of carbon dots. This way, a total of sixteen model molecules was prepared on the C scaffold, while twelve belong to the CC group. All in all, this gives rise to 1049 carbon atoms from which we construct the database of individual-atom XA spectra. Additionally, one pristine structure was prepared on the CCC scaffold using a smaller basis set for the XA calculations for at least comparing the effects of different model sizes.
Each model molecule was structurally optimised using the density functional theory (DFT) implementation of the ORCA program suite.37 For this step we use the non-empirical meta-GGA TPSS functional,38 as well as Ahlrichs' def2-SVP basis set.39 Dispersion correction is achieved through Grimme's third order atom-pairwise dispersion correction with Becke-Jones (D3BJ) damping.40,41 To speed up the calculation of the exchange term, the RIJCOSX approximation is used42 with the appropriate def2-SVP/J auxiliary basis sets.43 For each structure a numerical frequency analysis was conducted to confirm optimisation of the structure to its minimum energy. All structures and their total energies may be found as attached .xyz files in the ESI.†
2.2 Calculation of individual-atom spectra
The individual-atom XA spectra were calculated for all model structures as described by DeBeer et al.34 In their work, the authors have shown that for low excitation energies ω0n, reliable results for total XA spectra can be obtained when the excited states n are produced from excitations of single, Pipek–Mezey localised44 core electrons applying the linear-response time-dependent DFT (LR-TDDFT) formalism as implemented in ORCA.37 The total spectrum of a compound can then be obtained from the summation of all contributions of the single excitations. The oscillator strengths in atomic units are obtained as,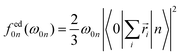 | (1) |
 | (2) |
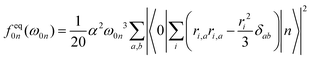 | (3) |
In our work, the orbitals for the LR-TDDFT calculation are obtained by performing a single-point calculation with the BH0.57LYP functional35 on the pre-optimised model structures. This hybrid functional with a high portion of Hartree exchange has been shown to give a very good onset energy for carbon K-edge XA spectra.35 Afterwards, the 1s core-space of the resulting ground-state orbitals is localised using the Pipek–Mezey44 criterion. Note that the procedure was applied regardless of whether the core orbitals were actually degenerate or not, to ensure that the resulting XA spectra can be clearly assigned to different individual atoms.
The individual-atom XA spectra are then obtained from standard LR-TDDFT calculations exciting one specific core-electron at a time into the whole virtual space. For each LR-TDDFT calculation, a total of N = 150 roots is calculated. To account for possible relativistic effects, the zeroth-order regular approximation (ZORA) is used.47 Having obtained both the excited states |n〉 and discrete transition energies ω0n from the LR-TDDFT calculation, we construct XA spectra by applying a Gauss-broadening to the sum of the orientationally averaged discrete oscillator strengths (eqn (1)–(3)) with a full width at half maximum of 1.0 eV.
The underestimation of core excitation energies within TDDFT calculations due to approximating the exchange–correlation functional was treated by adding a global shift of 0.25 eV to all calculated XA spectra. The shift was obtained from performing a number of benchmark calculations on smaller molecules like ethene, ethanol and formic acid, and is in the same order of magnitude as shifts from other DFT functionals that were optimized for X-ray calculations and tested on the same molecules.35
2.3 Database composition of structures
To establish a meaningful way of comparing the individual-atom XA spectra, we apply an automatic indexing scheme that assigns a group descriptor to every individual carbon atom based on the respective local environment, i.e. the neighbouring atoms up to a specified radius. The more neighbours one allows for constructing a descriptor, the more complex it may become and the higher the number of distinguishable environments obtained.To find a balance between accuracy and manageability, the indexing method presented in this work generates group descriptors that consist of the following two components. The first component is based on one of the positions basal, edge and bridge. This determines whether the indexed carbon atom is in the inner region (circles in Fig. 1(a)), at a bridge position (diamonds in Fig. 1(a)) or at the edge (triangles in Fig. 1(a)). To distinguish these positions, the indexing scheme has to take two layers of neighbours into consideration – i.e. the directly bound atoms and their respective bound atoms. We shall refer to this as the next-nearest neighbour (NNN) radius in the following.
The second component of the group descriptor concerns the functionalisation of the indexed carbon atom. To determine this, we chose to use a reduced NNN radius. This means, we nominally look at the nearest and next-nearest neighbours of the indexed atom to be able to distinguish hydroxyl from epoxy groups and such, but then store only the functionalisation of the actual indexed carbon atom, rather than the full surrounding. In other words, we end up with a more simplified group descriptor like “basal C–OH” instead of “basal C–OH bound to three aromatic basal carbon atoms”. The combination of both descriptors then gives rise to a finite number of possible functionalisation patterns, i.e. NNN distinguishable groups.
Using this scheme, we thus may distinguish aromatic atoms (C), hydrogenated atoms (C–H) and hydroxyl atoms (phenolic C–OH and non-phenolic CH–OH). Furthermore, atoms within an epoxy-group (C-Epo and CH-Epo) as well as carbonylic atoms (CHO), ketones (C-Keto) and carboxylic atoms (COOH). Additionally, we make a distinction between the atoms connecting to the carbonylic or carboxylic carbon atoms (C–CHO or C–COOH, respectively) from other aromatic carbon atoms.
A list of how often the different groups are found within the C and CC model structures can be taken from Table 1. Since all functionalised sites were embedded in structurally optimised model structures, atom types that are needed to form the carbon scaffold around functional groups are naturally more often needed to complete a meaningful molecular model structure. After assigning one of the NNN distinguishable groups to each individual-atom XA spectrum, we then construct the catalogue of so-called mean group XA spectra. These are obtained by summing up all individual spectra belonging to one group and divide the result by the number of occurrences. This way, effects caused by electronic transitions beyond the NNN radius are averaged out to some degree (see Section A of the ESI† on conjugation effects), since the individual spectra are in a different embedding environment each time. Nonetheless, it shall be noted that the quality naturally is higher, when more entries are included in the mean spectrum. The mean group XA spectra then reflect the average XA spectrum when exciting a carbon atom in the respective NNN distinguishable environment.
| Group | C | CC | Total |
|---|---|---|---|
| Note, that numbers carrying an asterisk indicate that an additional hydrogen atom is bound to the carbon as well. Also, carboxyl and carbonyl groups were only attached at edge positions, since addition onto the basal plane was not considered sensible for oxidation of a pristine graphene sheet. | |||
| CH | 2/181*/3 | 14/192*/— | 16/373*/3 |
| C | 76/—/84 | 191/—/125 | 267/—/209 |
| C–OH | 4/1/2 | 23/9*/3 | 27/10*/5 |
| C-Epo | 14/3*/7 | 60/2*/16 | 74/5*/23 |
| C–CHO | —/2/— | —/5/— | —/7/— |
| CHO | —/2/— | —/5/— | —/7/— |
| C–COOH | —/2/— | —/8/— | —/10/— |
| COOH | —/2/— | —/8/— | —/10/— |
| C-Keto | —/3/— | —/—/— | —/3/— |
| Sum | 388 | 661 | 1049 |
The composition of total XA spectra is then performed by addition of mean group spectra weighted by the number of carbon atoms that belong to the respective groups in a structure. This way, we may predict the theoretical total XA spectrum for molecular structures within the underlying TDDFT quality in very short times. The other way around, this methodology may open up the possibility to identify spectral features on oxidised carbon materials without prior knowledge of their exact structure.
Take note that the central parameter of this methodology is the choice of indexing radius, because by increasing the indexing radius towards including all atoms of an example molecule, the composition of that molecule from the database will eventually converge to the exact theoretical XA spectrum. The reason for this can be understood when considering an example linear molecule ABCD, where each letter shall represent an atom of a distinguishable environment. The exact theoretical spectrum F[ABCD] is obtained when the core-excitation of every atom is calculated individually and all contributions f are summed up.
| F[ABCD] = f[ABCD] + f[ABCD] + f[ABCD] + f[ABCD] | (4) |
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) [ABCD] following the sum
[ABCD] following the sum![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) [ABCD] = [ABCD] = ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) [ABC] + f[ABCD] + f[ABCD] + [ABC] + f[ABCD] + f[ABCD] + ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) [BCD] [BCD] | (5) |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) are cut off after the next nearest neighbour. Increasing the indexing radius by one would, however, already converge the composition to the exact result. It is important to note though, that the maximum resolution for the indexing radius is still ultimately dictated by the size of the smallest model molecular system from which the database is constructed.
are cut off after the next nearest neighbour. Increasing the indexing radius by one would, however, already converge the composition to the exact result. It is important to note though, that the maximum resolution for the indexing radius is still ultimately dictated by the size of the smallest model molecular system from which the database is constructed.
2.4 Experimental procedure
The aqueous dispersion of micrometer-sized GO was purchased from Graphenea and the carbon dots were purchased from ACS Materials.48 Their X-ray absorption spectra were measured in total electron yield mode from a drop-casted sample on a conductive Si substrate. The C K-edge spectra were measured by scanning the samples in the energy range of 276–310 eV in 0.1 eV steps. Highly oriented pyrolytic graphite (HOPG) was measured using the same parameter as an energy calibration standard for XA spectra. The data was collected at the U49/2 PGM1 beamline of the BESSY II synchrotron radiation source using the LiXEdrom endstation.483 Results and discussion
3.1 Justification of methodology
To facilitate the nomenclature of transitions, we shall denote transitions as σ*(X–Y) or π*(X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Y), where the atom labels in parentheses refer to the atoms involved and the greek letter refers to the type of transition under assumption of local symmetry. Note though, that we do not claim a pure π- or σ-character at any time, but rather give interpretations based on what the virtual Kohn–Sham orbitals (KSO) of a given transition look like. Also the bond order in the labelling is only reflecting the local Lewis structure. Hence, transitions of π*(X–Y) type may occur. Additionally, if there were more than one transition of the same type possible, we use numbers in front of the transition, i.e. 2π*(X
Y), where the atom labels in parentheses refer to the atoms involved and the greek letter refers to the type of transition under assumption of local symmetry. Note though, that we do not claim a pure π- or σ-character at any time, but rather give interpretations based on what the virtual Kohn–Sham orbitals (KSO) of a given transition look like. Also the bond order in the labelling is only reflecting the local Lewis structure. Hence, transitions of π*(X–Y) type may occur. Additionally, if there were more than one transition of the same type possible, we use numbers in front of the transition, i.e. 2π*(X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Y) for a second π* transition.
Y) for a second π* transition.
Firstly, it can be seen that all three positions show a π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) transition feature around 285.1 eV which is in accordance with experimental results.49–53 While this is the only noteworthy peak for the pre-edge region of the basal position (uppermost panel of Fig. 1(b)), the other two positions start to develop a signal around 288.4 eV. This peak, which is caused by transitions into σ*(C–H) orbitals becomes more pronounced for the edge position and shifts to 289.3 eV, which is in line with the experimentally observed value of 289.4 eV in small hydrocarbons.49
C) transition feature around 285.1 eV which is in accordance with experimental results.49–53 While this is the only noteworthy peak for the pre-edge region of the basal position (uppermost panel of Fig. 1(b)), the other two positions start to develop a signal around 288.4 eV. This peak, which is caused by transitions into σ*(C–H) orbitals becomes more pronounced for the edge position and shifts to 289.3 eV, which is in line with the experimentally observed value of 289.4 eV in small hydrocarbons.49
Since the three positions indeed show a different behaviour, the reduced NNN radius correctly distinguishes these different types of atoms. Also, as there are no major differences among each group for the different scaffold sizes, the C and CC scaffolds are assumed to be large enough to describe the three different positions.
 | ||
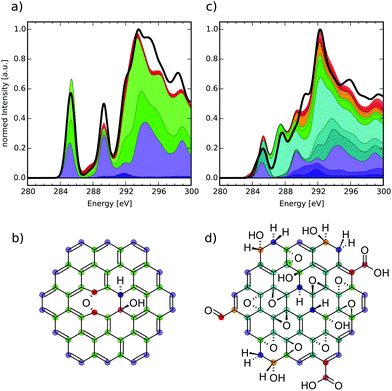
| Fig. 2 (a) Structure of a singly epoxy-functionalised CC model molecule and (b) theoretical near-edge carbon K-edge XA spectra of the highlighted atoms. | ||
The model molecule chosen for this comparison is shown in Fig. 2(a), with the respective carbon K-edge XA spectra in Fig. 2(b). The individual-atom spectra can be connected to different atoms in the structure, corresponding to their color and symbol. Firstly, we shall discuss the circle-marked atoms that would be assigned to the basal C-Epo group by the reduced NNN indexing. Their XA spectra show a pronounced signal just below 287.0 eV (similar to epoxy groups in bulk thin-film graphene oxide at 286.5 eV),50 which can be attributed to π*(C–O) transitions. Both the blue and red spectra are identical, because the atoms are identical with respect to their chemical surrounding as well as molecular symmetry.
The next pair of atoms (highlighted with diamonds) would be assigned as basal C atoms and these atoms are direct neighbours of the basal C-Epo atoms. Their spectra show a signal at 284.7 eV which can be attributed to π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) transitions, which is in qualitative agreement with the experimental value of 285.4 eV in graphite.54 The shift in excitation energy with respect to the experimental reference is likely caused by the proximity to the oxygen atom that is only two bond-lengths away.
C) transitions, which is in qualitative agreement with the experimental value of 285.4 eV in graphite.54 The shift in excitation energy with respect to the experimental reference is likely caused by the proximity to the oxygen atom that is only two bond-lengths away.
Evidence that these direct neighbours are shifted due to the oxygen atom becomes even more apparent, when comparing to a pair of carbon atoms that are three and four bonds away from the oxygen atom, respectively (marked with triangles). In the individual-atom XA spectra, both atoms show a π*-like transition around 285.4 eV, which is in perfect agreement with the experimental value for graphite. However, the two signals are shifted by approximately 0.1 eV with respect to each other, which is due to the fact that one of the atoms (red triangle in Fig. 2(a)) is farther away from the oxygen atom than the other (blue triangle in Fig. 2(a)). Since both of the atoms are otherwise in an identical surrounding with respect to their own next-nearest neighbors, the two carbon atoms seem to have reached a distance from the epoxy-oxygen that is large enough to not affect the individual-atom XA spectrum substantially. Conclusively, in this model molecule the locally excited carbon K-edge XA spectra are sensitive to their surrounding for up to 2–3 Å, i.e. about two bond-lengths.
It has to be noted though, that the triangle-marked atoms would also be assigned as basal C atoms, although their respective π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) transitions lie about 0.7 eV apart from the one of the diamond-marked basal C atoms. While the reduced NNN indexing radius would not be able to distinguish between their environments, already the full NNN indexing radius would indeed be large enough to distinguish these two pairs from each other. With the currently available database size we, however, needed to work with the reduced NNN radius, since otherwise not all possible functionalisation environments would have been covered. Nonetheless, we can use the reduced NNN radius as a first approximation for probing the general usefulness of the overall methodology, since increasing the radius will only improve the quality.
C) transitions lie about 0.7 eV apart from the one of the diamond-marked basal C atoms. While the reduced NNN indexing radius would not be able to distinguish between their environments, already the full NNN indexing radius would indeed be large enough to distinguish these two pairs from each other. With the currently available database size we, however, needed to work with the reduced NNN radius, since otherwise not all possible functionalisation environments would have been covered. Nonetheless, we can use the reduced NNN radius as a first approximation for probing the general usefulness of the overall methodology, since increasing the radius will only improve the quality.
3.2 Analysis of group XA spectra
To obtain the mean group XA spectra from which we compose and decompose the molecular structures, the 1049 individual-atom spectra from the C and CC model molecules were averaged with respect to the assigned group descriptors. Each of these mean group XA spectra then represents the average XA response of one type of functionalisation and can each be analysed to understand the nature of the local transitions. A detailed analysis of all these groups with comparison to various experimental results49–53,55–57 can be found in Section B of the ESI.† Note that beyond approximately 290 eV, the evaluation of signals was only performed qualitatively, since the ionisation edge-jump58 is expected around that energy in experimental spectra. An evaluation of the LR-TDDFT bound-to-bound state transitions is not possible in this region any more, since resonance states and multiple-scattering events are not covered by LR-TDDFT.3.3 Comparison with explicit theoretical spectra
To see how well the methodology is able to reproduce the XA spectrum of a given structure, we shall compare the explicitly calculated spectra for two example model molecules with their respective database compositions. This comparison serves as a quality control for the chosen indexing radius, since the composed spectra ultimately have to converge to the summation of all explicit individual atom contributions for increasing indexing radii (see Discussion at the end of Section 2.3). Similar comparisons for all other structures that were used in this work may be found in Section C of the ESI.†In the first example a comparison to a lowly-functionalised model molecule (see Fig. 3(b)) is made. The solid black line of Fig. 3(a) gives the respective total XA spectrum, when adding up every individual-atom XA response in its exact environment (cf.eqn (4)). The total XA spectrum is dominated by mainly three signals. The first can be identified as a strong π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) transition at 285.0 eV due to a largely conjugated π-electron system that is only slightly disrupted by the central functionalisations. After that, a signal corresponding to σ*(C–H) transitions can be found at 289.1 eV. Finally, for even higher energies a σ*(C–C) signal is obtained at 293.3 eV.
C) transition at 285.0 eV due to a largely conjugated π-electron system that is only slightly disrupted by the central functionalisations. After that, a signal corresponding to σ*(C–H) transitions can be found at 289.1 eV. Finally, for even higher energies a σ*(C–C) signal is obtained at 293.3 eV.
The database composition ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) (ω) for the model molecule in panel (b) at transition energies ω is calculated by addition of the mean group XA spectra
(ω) for the model molecule in panel (b) at transition energies ω is calculated by addition of the mean group XA spectra ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) i(ω) times the number of occurrences of a specific type of atom. The composition is represented by the cumulative addition of colored planes, where each color represents one of the groups from the different mean group XA spectra. The formula below shows how the resulting composition of Fig. 3(a) has been obtained (from bottom to top), while the colored dots in molecule Fig. 3(b) mark the respective species.
i(ω) times the number of occurrences of a specific type of atom. The composition is represented by the cumulative addition of colored planes, where each color represents one of the groups from the different mean group XA spectra. The formula below shows how the resulting composition of Fig. 3(a) has been obtained (from bottom to top), while the colored dots in molecule Fig. 3(b) mark the respective species.
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) (ω) = (ω) = ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) basal basal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH(ω) + 18 CH(ω) + 18![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) edge edge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH(ω) + 12 CH(ω) + 12![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) bridge bridge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C(ω) + 20 C(ω) + 20![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) basal basal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C(ω) + 2 C(ω) + 2![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) basal basal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C-Epo(ω) + C-Epo(ω) + ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) basal basal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C–OH(ω) C–OH(ω) | (6) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) transition at 285.0 eV originates to almost even parts from the edge CH atoms, bridge C atoms and basal C atoms as highlighted also by the colour code. The σ*(C–H) at 289.1 eV on the other hand is almost completely dominated by the edge CH group, since it is also one of the only carbon atom types directly bound to hydrogen. Finally, the σ*(C–C) signal is described by all of the groups present.
C) transition at 285.0 eV originates to almost even parts from the edge CH atoms, bridge C atoms and basal C atoms as highlighted also by the colour code. The σ*(C–H) at 289.1 eV on the other hand is almost completely dominated by the edge CH group, since it is also one of the only carbon atom types directly bound to hydrogen. Finally, the σ*(C–C) signal is described by all of the groups present.
When comparing the black line to the composition, it becomes apparent that the intensities do not match in several regions, while the position of features is well reproduced. The reason for this behaviour is that roughly above 294.0 eV, the intensities begin to smear out for specific signals in some of the mean group XA spectra due to more and more energetic shifts among the multitude of individual-atom spectra. This is probably the case for both signals at 294.8 eV and 298.5 eV, which are not well reproduced by the database composition. While the former one is contained with low intensity in the edge CH group, the latter signal seems to be shifted strongly to higher energies within the database. This is evidence that there are transitions which need a higher indexing radius than the reduced NNN radius for an exact description. However, since these transitions lie beyond the ionisation edge-jump, our approximation using the reduced NNN radius works well enough for the pre-edge region.
Next, we perform the same analysis for a highly-oxidised model molecule (see Fig. 3(d)). The theoretical total XA spectrum (see Fig. 3(c)) is dominated by four transitions. The first transition at 285.2 eV can be identified as a π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) signal that shows a weak shoulder to lower energies caused by π*(C
C) signal that shows a weak shoulder to lower energies caused by π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) transitions of carboxyl and carbonyl groups. The second signal at 287.6 eV is one of σ*(C–O) character and indicates epoxy groups. At 290.5 eV one finds the third peak, which is caused by σ*(C–H) transitions. The last of the dominant signals in the explicit theoretical spectrum can be found at 292.3 eV and is given by σ*(C–C) transitions.
O) transitions of carboxyl and carbonyl groups. The second signal at 287.6 eV is one of σ*(C–O) character and indicates epoxy groups. At 290.5 eV one finds the third peak, which is caused by σ*(C–H) transitions. The last of the dominant signals in the explicit theoretical spectrum can be found at 292.3 eV and is given by σ*(C–C) transitions.
When the spectrum is composed from the database, one can confirm three of these four signals very well in both energetic positioning as well as intensity, with exception of the σ*(C–H) transition. One can furthermore assign more subtle shoulders to specific groups, such as the one at 288.8 eV that is caused mainly from the basal epoxy groups' σ*(C–O) transition as well as the σ*(C–H) transition of the edge CH group. Above around 293.0 eV the intensities again begin to smear out like in the case of the model molecule displayed in Fig. 3(b). Two more signals at 295.9 eV and 299.4 eV can be reproduced qualitatively in the cumulative sum of all group XA spectra. The assignment to one specific type of transition is, however, complicated by the fact that none of the groups is responsible for the signal on its own, but rather all of the groups contribute to the signals to different degrees.
As can be seen, however, both composition XA spectra also yield information beyond qualitative peak assignments, since they can provide the information on how much each functional group relatively contributes to a signal. This is particularly relevant when assigning the near-edge XA spectra of structurally unknown compounds.
3.4 Comparison with experimental spectra
Finally, we present how the database can be used to identify possible functionalisation patterns in two experimental samples of oxidised carbon materials. The first XA spectrum was taken from GO flakes in the micrometer range (see Section 2.4 “Experimental procedure” for measurement details). The second spectrum was taken from an oxidised CD sample with a lateral size below 10 nm.48 For both samples the normed experimental XA spectra (black solid lines in Fig. 4 and 5) as well as estimated compositions of the near-edge features using the database are shown.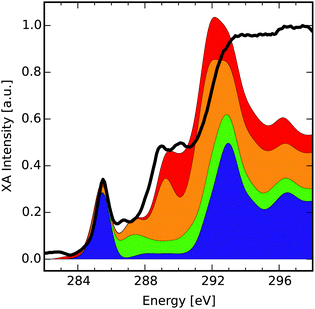 | ||
| Fig. 4 Comparison of the near-edge features of an XA spectrum of graphene oxide (black) with the cumulative sum of four different group XA components. Each component consists of several group XA spectra (see ESI† for detailed composition). | ||
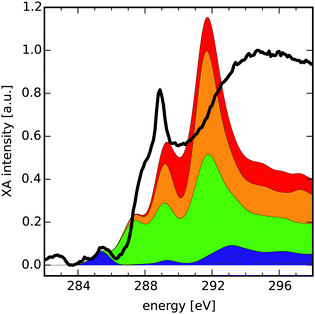 | ||
| Fig. 5 Comparison of a XA spectrum of an oxidised CD sample with the cumulative sum of four different group XA components. Each component consists of several group XA spectra (see ESI† for detailed composition). The spectrum was taken from Ren et al.48 | ||
The compositions provided here are obtained as hand-selected sums of different group XA spectra, which qualitatively reproduce the signals in the pre-edge and low-energy XANES region of the experimental spectra. The selection process was guided along the lines of additional spectroscopic findings,48 like the presence or absence of characteristic vibrations in the infrared spectrum of the respective sample. Hence, the composition presents the result of complementary methods that may allow for estimation of the relative occurrence of functionalisation patterns in the sample. Note that intensities in the region after the ionisation edge-jump around ≈290 eV in the experimental XA spectra have only qualitative meaning. Also, for easier reading we have further grouped the different mean group XA spectra into four main portions, the detailed decomposition of which can be found in Section D of the ESI.† Take note though, that the provided numbers should be seen as instructive examples for these hand-selected compositions. In future work, such compositions shall be obtained by carefully designed data-scientific fitting tools.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) transitions and is reproduced by the lowermost component (blue) of the composition spectrum. This component, which makes up about 38% of carbon atoms in the composition, itself consists of 88% basal C group. This means that large portions of the sample show a graphitic behaviour, which is in line with previous results on GO as discussed in the introduction. This rather intense feature is followed by a less intense signal at 286.7 eV which we partly recovered within the second lowest and highest components (green and orange, respectively). The green component that makes up for 12% of carbon atoms consists of one part basal and two parts bridge epoxy carbon atoms. It shows a σ*(C–O) transition in this region, however shifted by approximately 0.5 eV to higher energies. The orange component (32% of carbon atoms) adds further π*(C–C) from the basal C–OH, basal CH and edge CH-Epo groups in this region, but is shifted by around 0.8 eV compared to the experimental spectrum. Since the orange component is farther off, we assume that this peak is rather of σ*(C–O) nature.
C) transitions and is reproduced by the lowermost component (blue) of the composition spectrum. This component, which makes up about 38% of carbon atoms in the composition, itself consists of 88% basal C group. This means that large portions of the sample show a graphitic behaviour, which is in line with previous results on GO as discussed in the introduction. This rather intense feature is followed by a less intense signal at 286.7 eV which we partly recovered within the second lowest and highest components (green and orange, respectively). The green component that makes up for 12% of carbon atoms consists of one part basal and two parts bridge epoxy carbon atoms. It shows a σ*(C–O) transition in this region, however shifted by approximately 0.5 eV to higher energies. The orange component (32% of carbon atoms) adds further π*(C–C) from the basal C–OH, basal CH and edge CH-Epo groups in this region, but is shifted by around 0.8 eV compared to the experimental spectrum. Since the orange component is farther off, we assume that this peak is rather of σ*(C–O) nature.
The next two signals can be found at 288.9 eV and 290.2 eV. The first is approximately reproduced by the orange component's peak at 289.2 eV in a mixture of π*(C–C), σ*(O–H), σ*(C–H) contributions of mainly the basal CH, basal C–OH and edge CH-Epo groups. The second signal is captured by the uppermost red component's peak at 290.1 eV (18% of carbon atoms) that mainly consists of σ*(C–O) and σ*(O–H) transitions of the edge CH–OH group. It shall be mentioned, though, that especially these two signals allow for a lot of different interpretations and are heavily discussed in literature. In other reports, the signal around 288.9 eV was assigned to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O transitions related to COOH groups,59,60 interlayer states,61 as well as contaminant effects on the GO surface.6 Although our theoretical study cannot rule out the possibility of interlayer effects or contaminants, we can confirm that the signal at 288.9 eV is, in principle, describable as π*(C
O transitions related to COOH groups,59,60 interlayer states,61 as well as contaminant effects on the GO surface.6 Although our theoretical study cannot rule out the possibility of interlayer effects or contaminants, we can confirm that the signal at 288.9 eV is, in principle, describable as π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) related transition from both carbonylic as well as carboxylic group XA spectra. Nonetheless we believe that in this specific sample, those groups may have limited contribution to the peaks, because adding any of them to the composition XA spectrum would at the same time require a higher absorption intensity around 284 eV to account for π*(C
O) related transition from both carbonylic as well as carboxylic group XA spectra. Nonetheless we believe that in this specific sample, those groups may have limited contribution to the peaks, because adding any of them to the composition XA spectrum would at the same time require a higher absorption intensity around 284 eV to account for π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) transitions. It shall be mentioned that the σ*(C–C) transitions at 293.2 eV and 296.8 eV can be qualitatively reproduced, although with incorrect intensities since they are lying in the region beyond the edge-jump. Overall, based on the coefficients in the sum of individual functional groups in this estimated composition, we also find that the prominent π*-transition signal in the GO sample can be related to a relatively high percentage of 54 at% sp2 hybridized carbon atoms, of which around 75% account for unfunctionalised basal C atoms.
C) transitions. It shall be mentioned that the σ*(C–C) transitions at 293.2 eV and 296.8 eV can be qualitatively reproduced, although with incorrect intensities since they are lying in the region beyond the edge-jump. Overall, based on the coefficients in the sum of individual functional groups in this estimated composition, we also find that the prominent π*-transition signal in the GO sample can be related to a relatively high percentage of 54 at% sp2 hybridized carbon atoms, of which around 75% account for unfunctionalised basal C atoms.
The reason for the energetic shifts when trying to describe the feature at 286.7 eV and 288.9 eV could be the underlying shift for the BH0.57LYP functional, which has been shown to slightly deviate for oxygen rich environments.35 In future work, it shall be investigated whether introducing group-specific shifts during construction of the mean group XA spectra improves the fitting results.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) transitions as appearing in the lowermost component's peak at 285.4 eV (blue, 10% of carbon atoms), which is in turn described by 50% basal C group.
C) transitions as appearing in the lowermost component's peak at 285.4 eV (blue, 10% of carbon atoms), which is in turn described by 50% basal C group.
Next in the experimental spectrum, there is a steep rise in intensity around 287.3 eV that is best reproduced by the peak at 287.4 eV in the second lowest component (green, 40% of carbon atoms). This slightly smeared out signal results from mainly σ*(C–O) transitions of basal C-Epo groups. After that, one observes a very intense peak at 288.9 eV. In our composition the signal is described by the second highest and lowest components (orange and green) which peak at 289.2 eV and 289.1 eV, respectively. The orange components' (31% of carbon atoms) peak is dominated by σ*(C–H) transitions of the bridge CH and basal CH groups, while the green components' signal stems from a mixture of π*(C–C) and σ*(O–H) of the basal C–OH group.
Finally, the region between the intense signal at 287.3 eV and the ionisation edge jump is covered by the red component XA spectrum that peaks around 290.3 eV and makes up the remaining 19% of carbon atoms. In this region it contains σ*(C–O), σ*(O–H) and σ*(C–H) transitions from the edge CH2 and edge CH–OH groups.
Although the intensity of the signal at 288.9 eV is not reproduced by the group XA spectra very well, there may be different reasons for that. One reason could be that due to the averaging process in the formulation of group XA spectra, the intensity of specific groups is smeared out at this exact energy. Similar effects were observed when comparing the theoretical total XA spectra with the database compositions (see Section C of the ESI†), which hints at an insufficient indexing radius. Another reason for the very high intensity of this signal could be an excitation into an excitonic state caused by the quantum confinement of the oxidised CD.62
From the XA groups used in the composition XA spectrum of the oxidised CD, we can estimate that about 9% of the carbon atoms are sp2 hybridized, where more than half of these belong to unfunctionalized basal C atoms. This matches with the comparably low absorption intensity in the π* region of the experimental sample.
4 Conclusion and outlook
With this work we present a proof of principle for a functionalisation dependent C K-edge XA spectra database methodology based on quantum chemistry calculations with the aim to understand and predict XA spectra of graphitic materials. To achieve this we first calculate theoretical XA spectra for 1s excitations of individual carbon atoms in a wide variety of different model molecules by means of linear-response TDDFT. As the resulting spectra are approximately defined by the local environment of the excited carbon atoms, group descriptors are assigned to each carbon atom based on a cutoff radius (i.e. their nearest and next-nearest neighbors). These groups then yield a database of functionalisation-pattern dependent, averaged XA spectra, that eventually converge to the exact behaviour with increasing cutoff radius. We discuss the capabilities and limitations of the approach especially in the context of conjugation effects (see Section A of the ESI†) and choice of cutoff radius.From this database, one can compose theoretical XA spectra of, in principle, any substance that is describable by the underlying model molecules in density functional theory quality. We confirmed this by successful reproduction of theoretical XA spectra from explicit calculations by simple addition of the respective database entries. Finally, we give an instructive example of how the methodology may be used as a complementary tool to analyse the functionalisation patterns from experimental XANES spectra of micrometer-sized graphene oxide (GO) flakes and oxidised carbon dots (CD).
We anticipate that the quality of the methodology is mainly limited by the complexity of the descriptors available. Hence, a future measure of improvement shall be the incorporation of more neighbour atoms' environments to the descriptors and expanding the number of model molecules. Furthermore, the underlying calculations will be generally improved by increasing the basis set size or the general level of theory. Finally, a data-scientific fitting algorithm shall be set up such that one is able to fit the composition of a measured experimental sample with respect to the carbon, oxygen and nitrogen pre-edge spectra simultaneously. Applying these multiple requirements will substantially improve the results of the composition methodology.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Volkswagen Foundation for financial support (Freigeist Fellowships No. 89525 and No. 89592).References
- T.-F. Yeh, J. Cihlář, C.-Y. Chang, C. Cheng and H. Teng, Mater. Today, 2013, 16, 78 CrossRef CAS.
- X. Fan, W. Peng, Y. Li, X. Li, S. Wang, G. Zhang and F. Zhang, Adv. Mater., 2008, 4490 CrossRef CAS.
- S. Eigler and A. Hirsch, Angew. Chem., Int. Ed., 2014, 53, 7720 CrossRef CAS PubMed.
- X. Sun, Z. Liu, K. Welsher, J. T. Robinson, A. Goodwin, S. Zaric and H. Dai, Nano Res., 2008, 1, 203 CrossRef CAS PubMed.
- D. Sharma, S. Kanchi, M. I. Sabela and K. Bisetty, Arabian J. Chem., 2016, 9, 238 CrossRef CAS.
- A. Hunt, E. Z. Kurmaev and A. Moewes, Adv. Mater., 2014, 26, 4870 CrossRef CAS.
- D. Konios, M. M. Stylianakis, E. Stratakis and E. Kymakis, J. Colloid Interface Sci., 2014, 430, 108 CrossRef CAS.
- B. C. Brodie, Philos. Trans. R. Soc. London, 1859, 149, 249 CrossRef.
- W. S. Hummers and R. E. Offeman, J. Am. Chem. Soc., 1958, 80, 1339 CrossRef CAS.
- A. M. Dimiev, S. M. Bachilo, R. Saito and J. M. Tour, ACS Nano, 2012, 6, 7842 CrossRef CAS.
- A. Lerf, H. He, M. Forster and J. Klinowski, J. Phys. Chem. B, 1998, 102, 4477 CrossRef CAS.
- W. Cai, R. D. Piner, F. J. Stadermann, S. Park, M. A. Shaibat, Y. Ishii, D. Yang, A. Velamakanni, S. J. An, M. Stoller, J. An, D. Chen and R. S. Ruoff, Science, 2008, 321, 1815 CrossRef CAS.
- T. Szabó, E. Tombácz, E. Illés and I. Dékány, Carbon, 2006, 44, 537 CrossRef.
- Y. Matsumoto, M. Koinuma, S. Ida, S. Hayami, T. Taniguchi, K. Hatakeyama, H. Tateishi, Y. Watanabe and S. Amano, J. Phys. Chem. C, 2011, 115, 19280 CrossRef CAS.
- U. Hofmann and R. Holst, Ber. Dtsch. Chem. Ges. B, 1939, 72, 754 CrossRef.
- G. Ruess, Monatsh. Chem., 1946, 76, 381 CrossRef.
- W. Scholz and H. P. Boehm, Z. Anorg. Allg. Chem., 1969, 369, 327 CrossRef CAS.
- T. Nakajima, A. Mabuchi and R. Hagiwara, Carbon, 1988, 26, 357 CrossRef CAS.
- H. He, T. Riedl, A. Lerf and J. Klinowski, J. Phys. Chem., 1996, 100, 19954 CrossRef CAS.
- U. Hofmann, Eur. J. Inorg. Chem., 1928, 435 CAS.
- U. Hofmann and A. Frenzel, Eur. J. Inorg. Chem., 1930, 1248 CAS.
- U. Hofmann, A. Frenzel and E. Csalán, Eur. J. Org. Chem., 1934, 1 CAS.
- D. Hadži and A. Novak, Trans. Faraday Soc., 1955, 1614 RSC.
- F. Aragon de la Cruz and J. M. Cowley, Nature, 1962, 196, 468 CrossRef.
- A. Lerf, H. He, T. Riedl, M. Forster and J. Klinowski, J. Phys. Chem. B, 1998, 102, 4477 CrossRef CAS.
- K. Erickson, R. Erni, Z. Lee, N. Alem, W. Gannett and A. Zettl, Adv. Mater., 2010, 22, 4467 CrossRef CAS.
- J. J. Rehr, J. Mustre de Leon, S. I. Zabinsky and R. C. Albers, J. Am. Chem. Soc., 1991, 113, 5135 CrossRef CAS.
- J. J. Rehr and A. L. Ankudinov, Coord. Chem. Rev., 2005, 249, 131 CrossRef CAS.
- D. E. Sayers, E. A. Stern and F. W. Lytle, Phys. Rev. Lett., 1971, 27, 1204 CrossRef CAS.
- J. J. Rehr, J. J. Kas, F. D. Vila, M. P. Prange and K. Jorissen, Phys. Chem. Chem. Phys., 2010, 12, 5503 RSC.
- Y. Joly, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 125120 CrossRef.
- K. Schwarz and P. Blaha, Comput. Mater. Sci., 2003, 28, 259 CrossRef CAS.
- P. A. Brühwiler, A. J. Maxwell, C. Puglia, A. Nilsson, S. Andersson and N. Mårtensson, Phys. Rev. Lett., 1995, 74, 614 CrossRef.
- S. DeBeer George, T. Petrenko and F. Neese, Inorg. Chim. Acta, 2008, 361, 965 CrossRef CAS.
- N. A. Besley and F. A. Asmuruf, Phys. Chem. Chem. Phys., 2010, 12, 12024 RSC.
- M. Newville, J. Synchrotron Radiat., 2001, 8, 322 CrossRef CAS.
- F. Neese, WIREs Comput. Mol. Sci., 2018, 8, e1327 CrossRef.
- J. Tao, J. P. Perdew, V. N. Staroverov and E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS.
- F. Neese, F. Wenmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- J. Pipek and P. G. Mezey, J. Chem. Phys., 1989, 90, 4916 CrossRef CAS.
- J. J. Rehr, E. A. Stern, R. L. Martin and E. R. Davidson, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 560 CrossRef CAS.
- J. J. Rehr, J. Phys.: Condens. Matter, 2003, 15, 647 CrossRef.
- C. van Wüllen, J. Chem. Phys., 1998, 109, 392 CrossRef.
- J. Ren, F. Weber, F. Weigert, Y. Wang, S. Choudhury, J. Xiao, I. Lauermann, U. Resch-Genger, A. Bande and T. Petit, Nanoscale, 2019, 11, 2056 RSC.
- I. Ishii and A. P. Hitchcock, J. Electron Spectrosc. Relat. Phenom., 1987, 46, 55 CrossRef.
- R. P. Gandhiraman, D. Nordlund, C. Javier, J. E. Koehne, B. Chen and M. Meyyappan, J. Phys. Chem. C, 2014, 118, 18706 CrossRef CAS.
- A. Nikitin, L.-Å. Näslund, Z. Zhang and A. Nilsson, Surf. Sci., 2008, 602, 2575 CrossRef CAS.
- D. B. Knorr, Jr., C. Jaye, D. A. Fischer, A. B. Shoch and J. L. Lenhart, Langmuir, 2012, 28, 15294 CrossRef.
- S. G. Urquhart, A. P. Smith, H. W. Ade, A. P. Hitchcock, E. G. Rightor and W. Lidy, J. Phys. Chem. B, 1999, 103, 4603 CrossRef CAS.
- P. E. Batson, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 2608 CrossRef CAS.
- J. Zhong, H. Zhang, X. Sun and S.-T. Lee, Adv. Mater., 2014, 26, 7786 CrossRef CAS.
- T. K. Sham, B. X. Yang, J. Kirz and J. S. Tse, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 40, 652 CrossRef CAS.
- R. Lessard, J. Cuny, G. Cooper and A. P. Hitchcock, Chem. Phys., 2007, 331, 289 CrossRef CAS.
- D. Solomon, J. Lehmann, J. Kinyangi, B. Liang and T. Schäfer, Soil Sci. Soc. Am. J., 2005, 69, 107 CrossRef CAS.
- H.-K. Jeong, H.-J. Noh, J.-Y. Kim, M. H. Jin, C. Y. Park and Y. H. Lee, EPL, 2008, 82, 67004 CrossRef.
- D. D'Angelo, C. Bongiorno, M. Amato, I. Deretzis, A. La Magna, E. Fazio and S. Scalese, J. Phys. Chem. C, 2017, 121, 5408 CrossRef.
- D. Pacilé, M. Papagno, A. F. Rodríguez, M. Grioni and L. Papagno, Phys. Rev. Lett., 2008, 101, 066806 CrossRef.
- D. Lee, J. Seo, X. Zhu, J. Lee, H.-J. Shin, J. M. Cole, T. Shin, J. Lee, H. Lee and H. Su, Sci. Rep., 2013, 3, 2250 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp06620e |
| This journal is © the Owner Societies 2019 |